2. 海军装备研究院 北京 100032
2. Naval Academy of Armament, Beijing 100032, China
随着观测手段的提高以及大数据技术的兴起,多时空尺度的海量观测数据,为地理科学带来了巨大的机遇和挑战:若尺度问题得不到有效解决,必将影响地球科学研究的下一步发展[1].面对复合地理空间的多尺度表达问题,需要构建合理普适的地理空间对象尺度模型.文献[2-5]分别针对态势目标、不确定性空间数据、矢量河网目标、城市空间数据库以及城市道路格网等提出了相应的多尺度模型及变换可视化方法.然而普遍存在3方面的问题:尺度模型通用性较低、扩展性差;尺度模型没有考虑不同类型目标在尺度变换过程中的空间关系维护操作;尺度模型实用化程度不高,尚无法构建能应用于实践的数据库.
为解决地理空间集成环境构建中尺度模型的通用性和实用性的问题,实现多类型空间对象的自适应尺度变换,本文基于本体理论,结合地理空间对象的本质特征,构建了一个与对象尺度变换具体算法弱相关的模型,以驱动和实现多类型地理空间对象的多尺度自适应变换.
1 地理空间对象多尺度本体分析 1.1 多尺度模型的本体内涵与综合过程分析哲学概念“本体”被文献[6]引入信息科学并定义为“本体是对公认的概念模型进行的明确并形式化的规范说明”.文献[7-9]在此基础上提出了基于本体的地理空间理论、模型及框架,并应用到军事地理信息[10]等领域.多尺度模型是对地理现实多尺度描述的抽象,是地理本体模型的扩展延伸,因此可以借助本体论思想,挖掘地理空间对象多尺度综合的本质内涵,建立多尺度抽象表达和综合的本体框架,以统一的视图表述对象的多尺度关系,进而实现自动综合.
多尺度综合主要包含两类过程:模型综合与图形综合[11].前者是依据新的用户视点操作数据库,舍掉次要的地物目标,以更加简化、概括的方式描述空间表达的新模型.后者是在图形语言产生视觉冲突时,对点线面等几何目标实施化简综合处理的可视化表达过程[12].然而二者并不独立,模型综合是数据先导,图形综合是表达结果,二者交替贯穿于尺度综合的整个过程.因此将二者看作一个整体来对待,即多尺度综合的领域概念知识,这样有利于构造更具一般性意义的尺度模型.
1.2 多尺度综合算子根据综合对象的不同以及综合操作对目标数据的影响差异,将多尺度综合算法划分为3类操作.
定义1 多尺度变换操作M算子:根据同一对象的不同尺度特征,动态改变部分数据,实现数据模型和几何表现的尺度上卷和下推.该过程中对象要素内涵没有发生变化.此操作算子用符号∑M表示.典型操作如数据化简、夸大等.
定义2 多尺度聚合与分解操作A算子:将多个对象聚合成一个对象,或将一个对象分解成多个对象.该过程中目标要素、数据内容、几何表现和空间关系都发生了变化.此操作算子用∑A表示.典型操作包括选取、合并、关联等.
定义3 多尺度空间关系维护操作S算子:在多尺度变换和聚合分解过程中,维护不同目标之间的位置、拓扑和方向等空间关系,仅改变对象的几何表现,其要素内涵和数据模型没有发生改变.此操作算子用算子符号∑S表示.典型操作包括关系处理、拼接、移位等.
2 地理空间对象多尺度本体模型根据Studer的本体定义[6],本体模型应该包含概念、逻辑和物理3个层次的模型.
2.1 地理空间对象多尺度概念模型根据Perez[13]对本体概念建模的基本原理要求,从5个方面进行阐述.
1) 概念
尺度层级:指当前地理空间对象所处的尺度级别,即分辨率和空间范围.
对象目标:指研究的地理空间对象.
空间特征:表征地理空间对象的位置、图元构造、空间关系等空间属性.
几何特征:表征地理空间对象的几何图元构造和类型.
空间关系:表征地理空间对象之间的拓扑关系、方向关系及距离关系等.
语义特征:表征地理空间对象语义关系和属性.
尺度变换方法:表征地理空间对象在尺度变化过程中其特征发生改变的策略和方法.
2) 关系
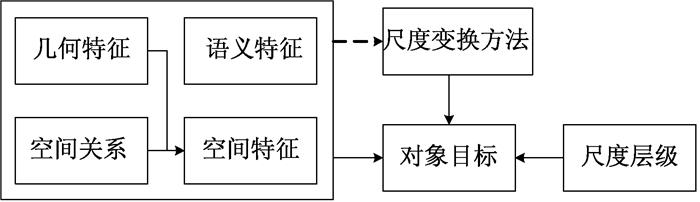
概念之间的关系如图 1所示.其余6个概念是对象目标概念的主要属性,它们之间是属性关系;几何特征和空间关系是空间特征的组成部分,它们之间是部分和整体关系;而语义特征和空间特征又是尺度变换方法的处理对象.
|
图 1 多尺度本体模型概念间的关系 Figure 1 Relations between the concepts of the multi-scale ontology model |
3) 函数
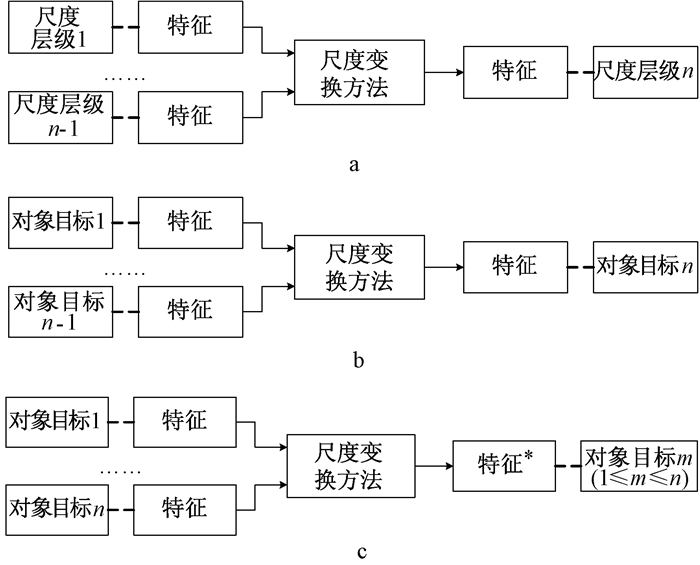
多尺度概念模型有3类函数,如图 2所示.虚线表示概念间的一一对应关系;实线箭头表示概念间的函数映射方向.图 2a表示同一对象在不同尺度下特征之间的函数关系.图 2b表示同一尺度下不同对象合成一个对象的函数关系.图 2c表示了同一尺度下不同对象之间的空间维护函数关系,其中,*指变换后目标的特征发生了改变.
|
图 2 多尺度本体模型函数关系 Figure 2 Functions of the multi-scale ontology model |
4) 公理
描述尺度本体模型中各概念、关系的约束条件和推理关系.约束公理明确地表述概念的值域和概念间的语义关系.推理公理是关于关系之间的推理条件,包括关系间的可逆性、传递性等的描述.
5) 实例
实例是对概念、关系、函数以及公理应用的具体和明确的描述.
2.2 地理空间对象多尺度逻辑模型对于某一目标对象O,其多尺度逻辑模型可表达为三元组公式
| $ O=〈D, K, R〉, $ | (1) |
其中:D表示对象的特征数据集合(对应于几何、空间和属性特征);K为综合算子集合(对应于尺度变换方法);R为数据-算子的关系集合(对应于函数关系,也可称为多尺度综合关系集合).
设λ为尺度标量,用于标定数据的尺度层级.数据集合见公式(2),其中:dλi|O表示对象O在关键尺度λi上的特征数据.不同尺度下dλi|O之间的层次结构没有特定的格式,可针对不同的应用和目标对象类型,按照不同的方式来存储和组织数据,具备极大的灵活性.多尺度综合算子集合为公式(3) 所示,包含了对象O进行多尺度综合时涉及的所有综合算子.公式(4) 为数据与算子的关系集合,描述了对象O在多尺度综合时算子∑i|O和被操作数据dλi|O以及与其他对象O′之间的关系.
| $ D = \left\{ {{d_{{\lambda _i}|O}}|i = 0, 1, \cdots, n} \right\}, $ | (2) |
| $ K = \left\{ {\sum {_{i|O}|i = 0, 1, \cdots, n} } \right\} = \left\{ {\sum {^M} } \right\} \cup \left\{ {\sum {^A} } \right\} \cup \left\{ {\sum {^S} } \right\}, $ | (3) |
| $ R = \left\{ {{r_{i|O}}|i = 0, 1, \cdots, n} \right\} = \left\{ {{R^M}} \right\} \cup \left\{ {{R^A}} \right\} \cup \left\{ {{R^S}} \right\}. $ | (4) |
在尺度λi下,地理空间对象目标集合可以表达如公式(5).公式(6) 表示了M算子操作数据集合D中的其他尺度数据dλ(q)|O生成dλi|O的变换过程.公式(7) 表示λi尺度下对象Ok通过A算子由若干对象O(n)数据dλi|O(n)聚合生成dλi|Ok的过程,公式(8) 表示了对象Ok利用S算子维护同一尺度λi下与其他对象O(p)的三维空间关系而修正dλi|Ok获得新数据
| $ {W_{{\lambda _i}}}\left( {{O_1}, {O_2}, \cdots, {O_p}} \right) = \left\{ {{d_{{\lambda _i}|{O_1}}}, \cdots, {d_{{\lambda _i}|{O_q}}}, {{\hat d}_{{\lambda _i}|{O_{q + 1}}}}, \cdots, {{\hat d}_{{\lambda _i}|{O_p}}}} \right\}, $ | (5) |
| $ {d_{{\lambda _i}|{O_k}}} = r_{{\lambda _i}|{O_k}}^M\left( {\sum {_{\left( 1 \right)|{O_k}}^M}, \cdots, \sum {_{\left( j \right)|{O_k}}^M, {d_{{\lambda _{\left( 1 \right)}}|{O_k}}}, \cdots, {d_{{\lambda _{\left( m \right)}}|{O_k}}}} } \right), k = 1, 2, \cdots, q, m \ne i, $ | (6) |
| $ {d_{{\lambda _i}|{O_k}}} = r_{{\lambda _i}|{O_k}}^A\left( {\sum {_{\left( 1 \right)|{O_k}}^A}, \cdots, \sum {_{\left( j \right)|{O_k}}^A, {d_{{\lambda _i}|{O_{\left( 1 \right)}}}}, \cdots, {d_{{\lambda _i}|{O_{\left( n \right)}}}}} } \right), k = 1, 2, \cdots, q, n \ne k, $ | (7) |
| $ {{\hat d}_{{\lambda _i}|{O_k}}} = r_{{\lambda _i}|{O_k}}^S\left( {\sum {_{\left( 1 \right)|{O_k}}^S}, \cdots, \sum {_{\left( j \right)|{O_k}}^S, {d_{{\lambda _i}|{O_k}}}, \cdots, {d_{{\lambda _i}|{O_{\left( n \right)}}}}} } \right), k = q + 1, \cdots, p, n \ne k. $ | (8) |
艾廷华归纳了4种面向多尺度表达的数据库存储方式[14],然而其主要面向同一类型目标数据且只考虑了Morphing一种尺度变换方法,没有涉及目标聚合以及多种尺度综合方法并存的情况.
结合多尺度逻辑模型,本文认为多尺度数据的存储应该以“关键尺度与综合关系”型为主.数据库中应该存储目标在关键尺度下的对象特征数据D以及关键尺度上的数据-算子关系集合R.而多尺度综合算子集合K则作为通用的处理方法,以知识库的形式存在.关键尺度的含义是指在对象目标的特征数据发生根本变化时的尺度层级.例如,道路目标在尺度变小的过程中,在某一比例尺λ由原来的条带形状变为线状,几何特征发生了根本变化,则该比例尺λ为关键尺度.该尺度下几何特征发生变化前后的数据应该保存在数据库中.
由以上分析和定义可知,针对在特定尺度λ下的目标O,可根据其所在的关键尺度区间[λi-1, λi)(λ∈[λi-1, λi)),查找相应的数据与算子关系ri|O,从知识库中确定所采用的多尺度综合算子∑i|O,并获取可能涉及的其他空间目标的数据dλ|Ok,推导出目标O的数据dλi|O.
3 实验分析本文采用本体构建软件Protégé4.3和推理插件FaCT++验证多尺度本体模型的有效性.为聚焦推理过程,实验模型的基本类缩减为对象目标(objects)、目标数据(data)、尺度变换方法(operator)、尺度层级(scalar)和多尺度综合关系(relation).
3.1 实验1 同一目标不同尺度间的函数关系本实验主要验证公式(6),设定的类属性主要包括尺度层级关系、变换综合关系、等价关系等.设置实例:目标存在从尺度s1到s2的变换综合关系r12,其变换方法为k12.该目标待验证数据dx存在尺度sx∈(s1, s2),其综合关系为rx,对应的综合算子为kx.在relation类下建立子类R12,其充要条件为“使用综合算子k12且变换起始尺度层级≥s1且变换目标尺度层级≤s2”.建立同级子类RX,充要条件为“目标尺度层级在(s1, s2) 范围内”.利用推理机可以得到r12∈R12和rx∈RX,进一步设定RX⊆R12,可以得到kx≡k12.由此可验证公式(6),同一目标可以根据其尺度范围,结合相应的变换综合关系和综合算子,实现由关键尺度向任意尺度的数据转换.
3.2 实验2 多目标形成唯一目标的函数关系本实验主要验证公式(7),设置实例:目标o1~o4在关键尺度s存在变换综合关系r,聚合生成目标oo,其变换方法为k.目标ox待验证数据dx在尺度s的综合关系为rx,对应的综合算子为kx.在relation类下建立子类R,其充要条件为“使用综合算子k且综合变换输入目标∈{o1, o2, o3, o4}且综合变换输出目标为oo”.建立同级子类RInfer,其充要条件为“综合变换输入目标∈{o1, o2, o3, o4}且关键尺度为s”.利用推理机可以得到r∈R和rx∈RInfer,进一步设定RInfer⊆R,可以得到kx≡k.由此可验证公式(7),若存在关键尺度多个目标的聚合综合关系,则对于其中任意聚合目标数据都能够得到相应的综合算子,从而进一步可实现聚合转换.
3.3 实验3 多目标空间关系维护的函数关系本实验主要验证公式(8),设置相关实例:目标o1~o4在关键尺度s存在变换综合关系r1~r4,利用变换方法k1~k4,实现数据d1i~d4i到d1o~d4o的转换.目标ox待验证数据dxi在尺度s的综合关系为rx,对应的综合算子为kx.在relation类下建立子类R,其充要条件为“变换综合关系∈{r1, r2, r3, r4}”.建立同级子类RInfer,其充要条件为“综合变换输入目标∈{o1, o2, o3, o4}且关键尺度为s”.在operator类下建立子类O,其充要条件为“综合算子∈{k1, k2, k3, k4}且关联的变换综合关系∈R”.利用推理机可以得到r1~r4∈R和rx∈RInfer,进一步设定RInfer⊆R,可以得到kx∈O,由此可验证公式(8).若存在关键尺度多个目标的空间维护关系,则对于其中任意目标数据都能够得到相应的综合算子,从而进一步可实现空间关系的维护.
4 总结本文在分析现有尺度模型利弊的基础上,结合本体理论对地理空间对象多尺度特性进行分析,从概念、逻辑和物理3个层次设计地理空间对象多尺度模型,并通过实验验证了多尺度模型的推理过程.本文提出的地理空间对象多尺度模型充分考虑了多尺度的本体特性,与具体的对象类型、表达方式和综合方法无关,并可以通过本体工具实现形式化表达,具有较高的通用性和实用价值.下一步将在多尺度自适应变换算法以及三维空间对象多尺度可视化方面开展研究.
| [1] |
遥感学报编辑部. "遥感尺度效应和尺度转换"论坛简报[J]. 遥感学报, 2014, 18(4): 735-740. (  0) 0) |
| [2] |
施群山, 蓝朝桢, 梁静, 等. 空间目标多尺度表达模型及方法[J]. 系统仿真学报, 2016, 28(9): 2235-2245. (  0) 0) |
| [3] |
丁丽君, 闫浩文, 王中辉, 等. 矢量河网渐进式传输的多尺度表达模型[J]. 测绘科学技术学报, 2015, 32(1): 87-90. (  0) 0) |
| [4] |
王艳军, 李朝奎. 多尺度城市地理数据在线联动更新研究[J]. 测绘科学, 2014, 39(10): 48-52. (  0) 0) |
| [5] |
栾学晨, 杨必胜, 李秋萍. 保持城市道路格网模式的街区合并混合整数规划模型[J]. 测绘学报, 2014, 43(4): 426-434. (  0) 0) |
| [6] |
STUDER R, BENJAMINS V R, FENSEL D. Knowledge engineering: principles and methods[J]. Data & knowledge engineering, 1998, 25(1/2): 161-197. (  0) 0) |
| [7] |
孙敏, 陈秀万, 张飞舟. 地理信息本体论[J]. 地理与地理信息科学, 2004, 20(3): 6-11. (  0) 0) |
| [8] |
郭黎, 崔铁军, 刘刚, 等. 基于本体的地理空间信息集成框架与实现[J]. 测绘科学技术学报, 2008, 25(6): 462-465. (  0) 0) |
| [9] |
侯卫生, 刘修国, 吴信才, 等. 面向三维地质建模的领域本体逻辑结构与构建方法[J]. 地理与地理信息科学, 2009, 25(1): 27-31. (  0) 0) |
| [10] |
修佳鹏, 熊燕, 张雷, 等. 基于OWL的战场本体构建方法[J]. 郑州大学学报(理学版), 2007, 39(2): 136-141. (  0) 0) |
| [11] |
艾廷华, 成建国. 对空间数据多尺度表达有关问题的思考[J]. 武汉大学学报(信息科学版), 2005, 30(5): 377-382. (  0) 0) |
| [12] |
曲邦定. 地图自动综合的现状及发展方向[J]. 山西建筑, 2008, 34(22): 345-346. DOI:10.3969/j.issn.1009-6825.2008.22.217 (  0) 0) |
| [13] |
PEREZ A G, BENJAMINS V R. Overview of knowledge sharing and reuse components: ontologies and problem-solving methods[C]//Proceedings of the IJCAI-99 Workshop on Ontologies and Problem-Solving Methods (KRR5). Stockholm, 1999: 242-257. http://hdl.handle.net/11245/1.162618
(  0) 0) |
| [14] |
艾廷华. 多尺度空间数据库建立中的关键技术与对策[J]. 科技导报, 2004(12): 4-8. DOI:10.3321/j.issn:1000-7857.2004.12.002 (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


