2. 徐州工业职业技术学院 信息与电气工程学院 江苏 徐州 221004
2. School of Information and Electrical Engineering, Xuzhou College of Industrial Technology, Xuzhou 221004, China
熵, 最早用来表征物质热力学状态, 通过描述熵和状态变量之间的关系来度量体系的混乱程度[1].熵具有灵敏度高、抗干扰能力强等优势, 已被广泛应用于故障诊断、误差测试、图像分割及质量评估、信用评价等不同领域[2-18].文献[12]提出了基于熵权法的灰色点估计权重计算方法, 并结合小样本数据进行了参数估计的仿真实例实验, 验证了方法的有效性.文献[13]提出了一种新型的电机轴承故障检测与分类的混合模型.用计算振动信号的置换熵来检测轴承的故障, 该方法对电机轴承故障的检测和分类具有一定的有效性和鲁棒性.文献[14]研究了图像模糊信息的多属性决策问题, 建立了一种基于模糊交叉熵的多属性决策方法, 并验证了该方法的可行性和有效性.文献[15]提出了基于最大熵值的灵武长枣彩色图像分割方法, 实现了图像分割的准确性, 提高了机器识别的精度, 为灵武长枣智能采集提供理论依据.文献[16]在图像分割中提出了一种新的基于熵的图像阈值方法, 该方法在分割NDT图像、红外图像和其他图像方面具有一定的优越性.文献[17]提出了机械设计方案模糊熵权综合评价, 将模糊熵应用于减小振动装置的优化设计方案评定.文献[18]提出了一种新的建筑施工企业信用评价模型, 将层次分析法与熵权法相结合来计算指标权重, 并验证了模型的有效性、合理性.
熵的种类繁多, 度量序列混乱程度的能力也不尽相同, 如何判断不同种类熵描述混沌能力的大小, 且如何选择一种合适的手段对时间序列进行处理以更好地凸显熵的特征则变得具有重要的现实意义.
本文通过计算仿真信号信息熵、近似熵及模糊熵这3种常用熵值, 证明了模糊熵在不同的噪声比例下都能很好地度量序列的复杂程度, 并在一特定值时不会在较大程度上影响计算效率.且提出了基于经验模态分解和相关系数原理的虚假本征模态函数(intrinsci mode function, IMF)筛选方法, 求出了各阶真实本征模态函数的模糊熵, 计算出各阶真实本征模态函数的能量比例, 加权平均求出模糊熵值.实验结果表明, 经验模态分解模糊熵值比直接计算模糊熵值稳定, 能更好地度量序列的混乱程度.
1 三种熵的定义与性能比较 1.1 信息熵设有随机变量X={x1, x2, …, xn}, p(x)为输出概率函数, 则变量X的信息熵为
| $ H\left( x \right) = - \mathop \sum \limits_{i = 1}^n p({x_i})\log (p({x_i})). $ |
1) 设m维矢量X(i)由序列u(i)组成, 即X(i)=[u(i), u(i+1), …, u(i+m-1)], 其中i=1, 2, …, N-m+1.
2) 定义X(i)与其余矢量X(j)之间的距离
3) 按照给定阈值r(r>0), 统计出每个i值对应的d[X(i), X(j)] < r的数目与总矢量个数N-m+1的比值, 记:Cim(r), 即Cim(r)={d[X(i), X(j)] < r}/(N-m+1).
4) 将Cim(r)取对数, 再对所有的i求均值, 记ϕm(r), 表示为
5) 再对m+1重复上述步骤, 得到ϕm+1(r), 得到近似熵
1) 假定给定的时间序列X=[x(1), x(2), …, x(N)]的模式维数为m, 则可通过原始时间序列构建m维向量Xm(i)=[x(i), x(i+1), …, x(i+m-1)]-u(i), 其中i=1, 2, …, N-m+1.令
2) 设向量Xm(i), Xm(j)之间的距离为
3) 引入模糊隶属度函数
| $ A_{ij}^m = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{ }}(d_{ij}^m = 0),}\\ {{\rm{ }}\exp [ - \ln \left( 2 \right){{(\frac{{d_{ij}^m}}{r})}^2}],}&{(d_{ij}^m > 0).} \end{array}} \right. $ |
4) 定义函数
5) 对m+1维模式维数重复上述步骤,
6) 得到原时间序列的模糊熵为FuzzyEn(m, r, N)=ln ϕm(r)-ln ϕm+1(r).当模式维数m=1, 2, 相似容限r=(0.1~0.25)·SD时, 模糊熵的分类效果较佳, 具有良好的统计性[19-20].
1.4 3种熵的性能比较为了比较3种不同的熵的性能, 本文用仿真信号加以验证.信号表达式为
| $ x = a \cdot \sqrt {\sin \frac{1}{4}{\rm{ \mathsf{ π} }}n} + \left( {1 - a} \right) \cdot rand\left( {1, 300} \right), $ | (1) |
其中:a在0.1~0.9间, 以0.1为间隔等间距取点;n为[0, 20]间等分的300个数, 在Matlab中可用n=linspace(0, 20, 300)完成;rand(1, 300)在Matlab中用以实现1行300列区间为(0, 1)的随机数.所以, 仿真信号表示的含义为
对仿真信号分别求取信息熵、近似熵和模糊熵, 并统计了在Matlab中的运行时间, 如表 1和表 2所示.
|
|
表 1 a取不同值时仿真信号信息熵、近似熵、模糊熵值 Table 1 The value of the simulation signal information entropy, approximate entropy and fuzzy entropy with different a |
|
|
表 2 a取不同值时仿真信号信息熵、近似熵、模糊熵运行时间 Table 2 he run time of the simulation signal information entropy, approximate entropy and fuzzy entropy with different a |
据文献[21]知:熵在描述随机事件的不确定性时, 熵值与不确定性成正比, 由表 1可知, 从衡量序列复杂度的角度看, 相比于信息熵, 近似熵和模糊熵具有更好的性能.近似熵和模糊熵值随噪声含量的不同, 变化较信息熵更为明显.当a>0.3, 即噪声比例超过70%时, 近似熵的值会有所降低.此时, 近似熵已不能较好度量一时间序列的混乱程度.相比于近似熵, 模糊熵在不同的噪声比例下都能很好地度量序列的复杂度.
由表 2可知, 信息熵由于算法简单, 运算量小, 计算速度很快, 耗时最短.近似熵和模糊熵由于算法复杂, 计算运行时间较长.但相比于近似熵的运行时间, 模糊熵运行时间不足近似熵运行时间的十分之一.综上, 虽然模糊熵的运行时间长于信息熵, 但其值在0.6 s附近波动, 不会在较大程度上影响计算效率, 且考虑到模糊熵的优良性能, 可以认为在3种常用的熵值中, 模糊熵的优势最为明显.
2 改进的经验模态分解 2.1 经验模态分解信号经EMD自适应分解后会得到有限个从高频到低频, 而且可以是不等带宽的、包含了信号真实物理信息、能够反映信号内部波动性的分量, 把所得的各阶分量称为IMF分量.这些IMF分量满足:在一完整的数据段内, 极值点和过零点的数目必须相同或至多相差1;信号关于时间轴对称, 即无论信号处于哪一时刻, 由其局部极大值构成的上包络和局部极小值构成的下包络的平均值为零[22-23].具体分解步骤如下.
1) 确定信号x(t)所有局部极大值点, 利用3次样条曲线连接所有局部极大值点, 形成上包络.
2) 确定信号x(t)所有局部极小值点, 利用3次样条曲线连接所有局部极小值点, 形成下包络.
3) 计算出上、下包络线的均值, 记为m1:x(t)-m1=h1.理想的, 如果h1满足IMF的两个条件, 则h1就为x(t)的一个IMF.
4) 若h1不是x(t)的一个IMF, 则把h1作为原始信号, 重复步骤(1)~(2)得到上下包络线的新的均值m11:h1-m11=h11.
判断h11是否满足IMF条件, 如不满足, 则再重新循环k次, 有h1k-1-m1k=h1k.使得h1k满足IMF条件, 令c1=h1k, c1即为信号x(t)的第一个IMF.
5) 将得到的c1从x(t)中分离出来, 有r1(t)=x(t)-c1(t).
把r1(t)作为原始信号, 重复步骤(1)~(4)可得到信号的第2个IMF:c2.往复循环n次, 就可得到属于x(t)的n个IMF, 同时:
| $ \left\{ \begin{array}{l} {r_2}\left( t \right) = {r_1}\left( t \right) - {c_2}\left( t \right), \\ {r_3}\left( t \right) = {r_2}\left( t \right) - {c_3}\left( t \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\; \vdots \\ {r_n}\left( t \right) = {r_{n - 1}}\left( t \right) - {c_n}\left( t \right). \end{array} \right. $ |
当rn(t)成为一个单调函数不能再分解时, 循环结束, 由此得到
虚假IMF是原信号在EMD自适应分解时产生的, 不能体现信号的真实成分, 会对原信号的分析造成一定的影响.相关系数可以反映分解得到的各阶IMF与原信号的相关程度, 通过设定阈值来剔除虚假IMF分量.相关系数的定义为
| $ \rho = \frac{{\mathit{\boldsymbol{c}}\left( {1, 2} \right)}}{{\sqrt {\mathit{\boldsymbol{c}}\left( {1, 1} \right) \cdot \mathit{\boldsymbol{c}}\left( {2, 2} \right)} }} = \left( {\mathop \sum \limits_{k = 0}^n x\left( k \right)IMF\left( k \right)} \right)/\sqrt {\mathop \sum \limits_{k = 0}^n {x^2}\left( k \right)\mathop \sum \limits_{k = 0}^n IM{F^2}\left( k \right)} . $ |
其中:c为矩阵[x, IMF]的协方差矩阵;x(t)为原始信号.
下面以一仿真信号为例说明, 仿真信号x(t)为
| $ \begin{array}{l} x\left( t \right) = \left( {1 + 0.8\sin \left( {2{\rm{ \mathsf{ π} }} \cdot 6.5t} \right)} \right)\cos \\ \left( {2{\rm{ \mathsf{ π} }} \cdot 30t + 0.6\sin \left( {2{\rm{ \mathsf{ π} }} \cdot 10t} \right)} \right) + \sin \left( {2{\rm{ \mathsf{ π} }} \cdot 100t} \right). \end{array} $ |
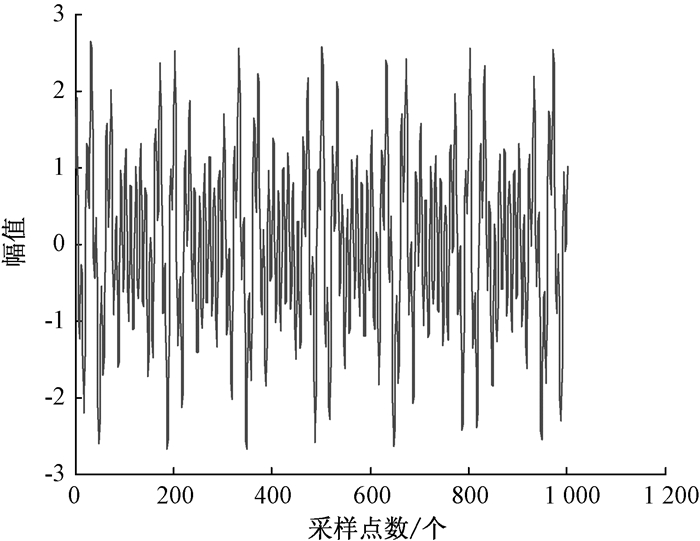
设置采样频率fs=1 000 Hz, 时间t在[0, 1]间以0.001等间隔取点.仿真信号x(t)波形如图 1所示.该信号由一个100 Hz的正弦信号和基频为30 Hz、调制频率为10 Hz的调幅信号叠加而成.其调幅部分的幅值为a(t)=1+0.8sin (2π·6.5t).所以有0.2≤a(t)≤1.8.
|
图 1 仿真信号x(t)波形 Figure 1 The waveform of emulation signal x(t) |
接着对调频部分分析, 对t求导得到角频率
| $ \begin{array}{l} w = \frac{{{\rm{d}}\left( {2{\rm{ \mathsf{ π} }} \cdot 30t + 0.6\sin \left( {2{\rm{ \mathsf{ π} }} \cdot 10t} \right)} \right)}}{{{\rm{d}}t}} = \\ 60{\rm{ \mathsf{ π} }} + 12{\rm{ \mathsf{ π} }}\cos \left( {20{\rm{ \mathsf{ π} }} \cdot t} \right). \end{array} $ | (2) |
由式(2)即可得到频率
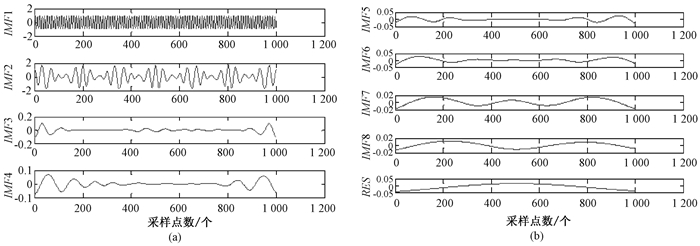
对x(t)进行EMD处理, 可得到8个IMF分量和1个余项.如图 2和图 3所示.
|
图 2 x(t)经EMD处理后的结果 Figure 2 The results of x(t) obtained after EMD processing |
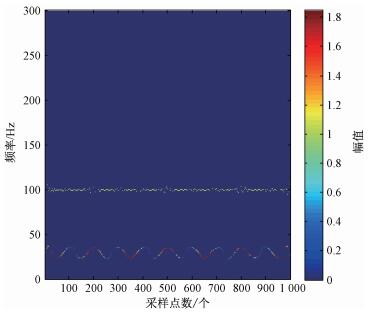
|
图 3 真实IMF合成的Hilbert谱 Figure 3 Real IMF synthetic Hilbert spectrum |
IMF1和IMF2分别对应着信号100 Hz的正弦成分和调频调幅成分, 对应x(t)的解析式可发现IMF3至RES均为多余分量.这是由于EMD在分解时采用3次样条差值方法造成的.求取除余项外各阶IMF与原信号的相关系数, 见表 3.可以发现, IMF1和IMF2与原始信号的相关系数明显大于其余IMF与原信号的相关系数.在这里, 设定阈值为0.2.即当IMF与原信号的相关系数大于0.2时, 该阶IMF为真实分量, 否则该阶IMF为虚假分量.对该较为复杂的仿真信号的分析表明, 原信号与其经EMD处理后得到的IMF的相关系数可以在一定程度上判别真实IMF与虚假IMF.
|
|
表 3 各阶IMF与原信号的相关系数 Table 3 The correlation coefficient between IMF and original signal |
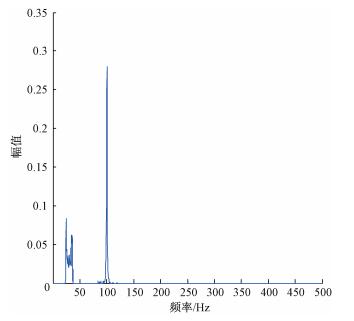
将虚假IMF分量剔除后, 对前两阶IMF合成Hilbert谱和边际谱, 如图 3和图 4所示.从谱图中可以清晰地反映出信号的真实成分:信号由100 Hz正弦信号和调频调幅信号叠加而成, 调频调幅部分的幅值波动范围在0.2~1.8, 频率范围在24~36 Hz.
|
图 4 真实IMF合成的边际谱 Figure 4 Real IMF synthetic marginal spectrum |
上述对3种熵的分析证明了模糊熵具有更好的性能和实用价值.改进的EMD方法可以将信号自适应分解到不同的频段上, 使信号成分在真实IMF分量中得到更好的体现.本节将改进的EMD方法与模糊熵算法进行有机的结合, 即对原信号进行EMD分解, 运用相关系数法筛选出真实IMF分量, 求出每一阶真实IMF分量的能量百分数.计算每阶IMF的模糊熵与能量百分数的乘积, 最后通过加权平均得到最终的模糊熵值.
下面在式(1)所表示的仿真信号中选取3个有代表性状态, 即时间序列极度混乱(a=0.1)、较为混乱(a=0.5)和几乎不混乱(a=0.9)状态, 在这3种情况下改进EMD方法的模糊熵值见表 4.
|
|
表 4 a取不同值时加权模糊熵值 Table 4 The value of weighted fuzzy entropy with different a |
从总体上看, 相比于表 1中a取0.1、0.5和0.9时模糊熵的值, 3种不同状态下的加权模糊熵值间的差距要大于模糊熵值.这说明用改进EMD方法求出的加权模糊熵值能更好地区分出不同状态下仿真信号混乱程度的差异.
对以上3种不同状态下的仿真信号分别求取30次加权模糊熵和模糊熵, 计算出两种熵值的标准偏差, 如表 5所示.
|
|
表 5 两种算法下的模糊熵标准偏差 Table 5 The fuzzy entropy standard deviation of the two algorithms |
由表 5可知, 在3种不同的状态下, 加权模糊熵的标准偏差均小于模糊熵的标准偏差, 这说明应用改进EMD算法求解得出的加权模糊熵稳定性更好.
4 结束语1) 本文通过仿真信号对用以度量序列混乱程度的常用的3种熵进行了分析和比较, 证明了模糊熵的优势.
2) 本文提出了一种改进的EMD方法, 即通过相关系数原理剔除经EMD分解得到的虚假IMF分量, 使分解得到的真实IMF更好地体现信号的成分.
3) 本文将改进的EMD方法和模糊熵结合, 即用各阶真实IMF分量的模糊熵与各阶真实IMF分量在全部真实IMF分量的能量百分数相乘, 得到新的模糊熵.实验结果表明相比于原始信号的模糊熵, 新模糊熵对时间序列混乱程度的区分度更加明显, 其值也更加稳定.
基于以上结论, 我们下一步的研究是, 将改进的经验模态分解方法与信息熵、近似熵进行结合, 并通过实验进行对比分析, 扩展所提方法的应用范围.
| [1] |
PAPOULIS A. Probability, random variables and stochastic processes[M]. New York: Mc Graw-Hill, 2004.
(  0) 0) |
| [2] |
鲁小云. 犹豫模糊粒计算中信息熵研究[J]. 计算机工程与应用, 2017, 53(7): 171-176. (  0) 0) |
| [3] |
杨宁.基于熵理论的矿业城市系统分析与评价研究[D].北京: 中国地质大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-11415-1016068395.htm
(  0) 0) |
| [4] |
郑近德.局部特征尺度分解方法及其在机械故障诊断中的应用研究[D].湖南: 湖南大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10532-1015579812.htm
(  0) 0) |
| [5] |
恩德, 张凤磊, 张昭, 等. 模糊熵在车载环境下语音端点检测中的应用[J]. 计算机工程与应用, 2016, 52(10): 147-150. DOI:10.3778/j.issn.1002-8331.1505-0135 (  0) 0) |
| [6] |
刘乐.基于局部均值分解的滚动轴承故障诊断系统研究与应[D].山西: 中北大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10110-1017167220.htm
(  0) 0) |
| [7] |
周访滨.测量数据误差分布的熵及其应用研究[D].湖南: 中南大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014395937.htm
(  0) 0) |
| [8] |
蔡晔, 曹一家, 谭玉东, 等. 基于标准化结构熵的电网结构对连锁故障的影响[J]. 电工技术学报, 2015, 30(3): 36-43. DOI:10.3969/j.issn.1000-6753.2015.03.005 (  0) 0) |
| [9] |
刘乐, 孙虎儿, 谢志谦. 基于SVD-LMD模糊熵与PNN的滚动轴承故障诊断[J]. 机械传动, 2017, 41(3): 172-176, 181. (  0) 0) |
| [10] |
张良, 张前图. 基于LCD模糊熵和流行学习的故障特征提取方法[J]. 机械强度, 2016, 38(184): 225-230. (  0) 0) |
| [11] |
陈恺, 陈芳, 戴敏, 等. 基于萤火虫算法的二维熵多阈值快速图像分割[J]. 光学精密工程, 2014, 22(2): 517-523. (  0) 0) |
| [12] |
杨文光, 吴云洁, 王建敏. 基于熵权法的小样本灰色置信区间估计[J]. 郑州大学学报(理学版), 2016, 48(1): 51-56. (  0) 0) |
| [13] |
ZHANG X Y, LIANG Y T, ZHOU J Z, et al. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM[J]. Measurement, 2015, 69: 164-179. DOI:10.1016/j.measurement.2015.03.017 (  0) 0) |
| [14] |
WEI G W. Picture fuzzy cross-entropy for multiple attribute decision making problems[J]. Journal of business economics and management, 2016, 17(4): 491-502. DOI:10.3846/16111699.2016.1197147 (  0) 0) |
| [15] |
WANG Y T, DAI Y P, XUE J R, et al. Research of segmentation method on color image of lingwu long jujubes based on the maximumentropy[J]. Eurasip journal on image and video processing, 2017, 2017: 34. DOI:10.1186/s13640-017-0182-5 (  0) 0) |
| [16] |
NIE F Y, ZHANG P F, LI J Q, et al. A novel generalized entropy and its application in image thresholding[J]. Signal processing, 2017, 134: 23-34. DOI:10.1016/j.sigpro.2016.11.004 (  0) 0) |
| [17] |
李福海, 朱凌宏. 机械设计方案模糊熵权综合评价[J]. 装备制造技术, 2010(1): 64-65, 76. DOI:10.3969/j.issn.1672-545X.2010.01.024 (  0) 0) |
| [18] |
王刚, 罗勇. 基于专家可信度的熵权-AHP建筑施工企业信用评价[J]. 郑州大学学报(理学版), 2015, 47(3): 121-126. DOI:10.3969/j.issn.1671-6841.2015.03.023 (  0) 0) |
| [19] |
李永波, 徐敏强, 赵海洋, 等. 基于层次模糊熵和改进支持向量机的轴承诊断方法研究[J]. 振动工程学报, 2016, 29(1): 184-192. (  0) 0) |
| [20] |
杨望灿, 张培林, 王怀光, 等. 基于EEMD的多尺度模糊熵的齿轮故障诊断[J]. 振动与冲击, 2015, 34(14): 163-167. (  0) 0) |
| [21] |
YUAN L, KESAVAN H K. Minimum entropy and information measure[J]. IEEE transactions on systems, man and cybernetics-part c: application and reviews, 1998, 28: 488-491. DOI:10.1109/5326.704595 (  0) 0) |
| [22] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the royal society of London A, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 (  0) 0) |
| [23] |
黎恒.经验模态分解中关键问题的优化理论与方法研究[D].西安: 西安电子科技大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10701-1016245827.htm
(  0) 0) |
 2018, Vol. 50
2018, Vol. 50


