巨灾损失的分布拟合在巨灾保险损失建模和风险评估中占有基础性的地位。巨灾保险损失分布广且不均,既有大量的小额损失,也有少量的大额损失,其分布常呈现厚尾形态。在较早的文献中多运用伽马分布、对数正态分布、威布尔分布等单一分布拟合巨灾损失,无法准确拟合出巨灾损失的厚尾特点[1-2]。近年的文献中提出了组合分布模型的思路[3-6]。部分学者基于极值理论对巨灾受灾人数进行分布拟合[7-8],并且部分文献更多地注重了巨灾损失的厚尾特点[9-10]。
在构建组合分布模型的建模思路下,任何两个分布都可以按需构成组合分布模型,从而得到比单一分布模型更精准的拟合效果。本文运用对数广义误差分布代替对数正态分布,并结合广义帕累托分布构建组合分布模型,同时采用Bakar提出的混合权重方法来计算权重,构建出了LogGED-GPD的组合分布模型。对全球洪水巨灾损失数据进行了实证分布拟合,得到了LogGED-GPD的组合分布模型的拟合效果优于单一的LogGED和对数正态分布(Lognormal)模型,在一定程度上为今后全球洪水巨灾损失的分布拟合方法提供了参考依据。
1 LogGED-GPD组合分布模型的构建 1.1 对数广义误差分布正态分布和对数正态分布在概率和统计的理论和应用中都发挥了重要作用,尾部比正态分布更厚的对数正态分布已被广泛用于风险管理、信用风险评估等领域。对数广义误差分布是对数正态分布的自然扩展,在对数正态分布应用的领域,对数广义误差分布可以有更好的拟合效果。对数广义误差分布的定义如下。
设ξ为遵循标准广义误差分布的随机变量,其中υ>0。令η=exp(ξ),则ξ遵循以υ为参数的对数广义误差分布,记为η~LogGED(υ)。当υ=1时,LogGED退化为对数拉普拉斯分布;当υ=2时,LogGED退化为对数正态分布。
1.2 广义帕累托分布McNeil首次提出了使用广义帕累托分布对超过高阈值的数据进行建模的理论,他的分析中指出了对数正态分布的尾部较薄,无法准确拟合出超过高阈值的大损失数据[11]。在讨论起赔点和保费计算时,普通帕累托分布导致拟合结果过于不切实际,因此尾部区域位于对数正态分布和帕累托分布之间的广义帕累托分布,更适用于拟合超过高阈值的大损失数据。设G(x)为广义帕累托分布的分布函数,则
| $ G(x)= \begin{cases}1-\left(1+\frac{\xi x}{\tau}\right)^{-\frac{1}{\xi}}, & \xi \neq 0, \\ 1-\exp \left(-\frac{x}{\tau}\right), & \xi=0。\end{cases} $ |
G(x)为双参数的分布函数,其中τ>0。当ξ≥0时,x≥0;当ξ < 0时,0≤x≤-τ/ξ。当ξ=0时,广义帕累托分布退化为指数分布。本文基于巨灾损失数据的背景下进行研究,为x>0且ξ≠0的特殊情况。设g(x)为广义帕累托分布的密度函数,则
Bakar等提出了一种新的构建双参数组合模型的方法[5],即混合权重ϕ和阈值θ两个参数由组合模型中的其他参数表示。设f(x)为组合模型的密度函数,
| $ f(x)= \begin{cases}\frac{1}{1+\phi} \cdot h^{*}(x), & 0<x \leqslant \theta, \\ \frac{\phi}{1+\phi} \cdot g^{*}(x), & \theta<x<\infty,\end{cases} $ |
参数ϕ的表达式为
结合本文提出的LogGED-GPD组合分布模型,根据对数广义误差分布和广义帕累托分布的密度函数和分布函数,将参数ϕ写成公式,
| $ \begin{array}{l} \phi=-\frac{\frac{1}{H(\theta)} \cdot \frac{\mathrm{d} H(\theta)}{\mathrm{d} \theta}}{\frac{1}{1-G(\theta)} \cdot \frac{\mathrm{d}(1-G(\theta))}{\mathrm{d} \theta}}=-\frac{\left(1+\frac{\xi \theta}{\tau}\right)^{-\frac{1}{\xi}}}{\frac{v \cdot \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t}{2^{1+\frac{1}{v}} \sigma \Gamma\left(\frac{1}{v}\right)}} \cdot \frac{\frac{d}{\mathrm{~d} \theta} \cdot \frac{v \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t}{2^{1+\frac{1}{v}} \sigma \Gamma\left(\frac{1}{v}\right)}}{\frac{d}{\mathrm{~d} \theta} \cdot\left(1+\frac{\xi \theta}{\tau}\right)^{-\frac{1}{\xi}}}=\\ \frac{\tau\left(1+\frac{\xi \theta}{\tau}\right)}{\theta \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t} \cdot \frac{d}{\mathrm{~d} \theta} \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t=\frac{(\tau+\xi \theta) \exp \left(-\frac{1}{2}\left|\frac{\ln \theta}{\sigma}\right|^{v}\right)}{\theta \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t}。\end{array} $ |
可以将LogGED-GPD组合分布模型的密度函数重新参数化。
当0 < x≤θ时,
| $ \begin{array}{l} f(x-)=\frac{1}{1+\phi} \cdot \frac{h(x)}{H(x)}=\frac{1}{1+\frac{(\tau+\xi \theta) \exp \left(-\frac{1}{2}\left|\frac{\ln \theta}{\sigma}\right|^{v}\right)}{\theta \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t}} \cdot \frac{{\frac{{v{x^{ - 1}}\exp \left( { - \frac{1}{2}{{\left| {\frac{t}{\sigma }} \right|}^v}} \right)}}{{{2^{1 + \frac{1}{v}}}\sigma \Gamma \left( {\frac{1}{v}} \right)}}}}{{\frac{{v\int_0^{\ln \theta } {\exp } \left( { - \frac{1}{2}{{\left| {\frac{t}{\sigma }} \right|}^v}} \right){\rm{d}}t}}{{{2^{1 + \frac{1}{v}}}\sigma \Gamma \left( {\frac{1}{v}} \right)}}}} = \\ \frac{\theta \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t}{\theta \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t+(\tau+\xi \theta) \exp \left(-\frac{1}{2}\left|\frac{\ln \theta}{\sigma}\right|^{v}\right)} \cdot \frac{\exp \left(-\frac{1}{2}\left|\frac{\ln x}{\sigma}\right|^{v}\right)}{x \int_{0}^{\ln x} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t} ; \end{array} $ |
当θ < x < ∞时,
| $ \begin{aligned} &f(x+)=\frac{\phi}{1+\phi} \cdot \frac{g(x)}{1-G(x)}= \\ &\frac{\theta \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t \quad}{\theta \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t+(\tau+\xi \theta) \exp \left(-\frac{1}{2}\left|\frac{\ln \theta}{\sigma}\right|^{v}\right)} \cdot \frac{(\tau+\xi \theta) \exp \left(-\frac{1}{2}\left|\frac{\ln \theta}{\sigma}\right|^{v}\right)}{\theta \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t}= \\ &\frac{(\tau+\xi \theta) \exp \left(-\frac{1}{2}\left|\frac{\ln \theta}{\sigma}\right|^{v}\right)}{\ln \int_{0}^{\ln \theta} \exp \left(-\frac{1}{2}\left|\frac{t}{\sigma}\right|^{v}\right) \mathrm{d} t+(\tau+\xi \theta) \exp \left(-\frac{1}{2}\left|\frac{\ln \theta}{\sigma}\right|^{v}\right)} \cdot \frac{1}{\tau+\xi x}。\end{aligned} $ |
最后,整理后可得LogGED-GPD组合分布模型的密度函数为
| $ f\left( x \right)\left\{ {\begin{array}{*{20}{l}} {\frac{{\theta \int_0^{\ln \theta } {\exp } \left( { - \frac{1}{2}{{\left| {\frac{t}{\sigma }} \right|}^v}} \right){\rm{d}}t}}{{\theta \int_0^{\ln \theta } {\exp } \left( { - \frac{1}{2}{{\left| {\frac{t}{\sigma }} \right|}^v}} \right){\rm{d}}t + (\tau + \xi \theta )\exp \left( { - \frac{1}{2}{{\left| {\frac{{\ln \theta }}{\sigma }} \right|}^v}} \right)}} \cdot \frac{{\exp \left( { - \frac{1}{2}{{\left| {\frac{{\ln x}}{\sigma }} \right|}^v}} \right)}}{{x\int_0^{\ln x} {\exp } \left( { - \frac{1}{2}{{\left| {\frac{t}{\sigma }} \right|}^v}} \right){\rm{d}}t}},}&{0 < x \le \theta ,}\\ {\frac{{(\tau + \xi \theta )\exp \left( { - \frac{1}{2}{{\left| {\frac{{\ln \theta }}{\sigma }} \right|}^v}} \right)}}{{\theta \int_0^{\ln \theta } {\exp } \left( { - \frac{1}{2}{{\left| {\frac{t}{\sigma }} \right|}^v}} \right){\rm{d}}t + (\tau + \xi \theta )\exp \left( { - \frac{1}{2}{{\left| {\frac{{\ln \theta }}{\sigma }} \right|}^v}} \right)}} \cdot \frac{1}{{\tau + \xi x}},}&{0 < x < \infty 。} \end{array}} \right. $ |
本文数据来源于达特茅斯洪水观测台提供的全球大型洪水灾害事件档案(http://www.dartmouth.edu/~floods/Archives/index.html),档案中提供的信息来自新闻、政府、仪器和遥感监测,依据全球洪水事件的发生实时更新,详细记录了每次洪水事件的时间、地点、损失等数据,目前记载了从1985—2010年全球发生的3 703件洪水事件。依据美国保险服务所将巨灾定义为损失金额超过2 500万美元以上的巨大经济损失和人员伤亡的事件,本文提取了全球大型洪水事件档案中损失金额超过2 500万美元的全球洪水巨灾样本共计494条。
2.2 描述性统计特征表 1反映了全球洪水损失的描述性统计特征。由全球洪水损失的描述性统计量可以分析出,样本数据的75%分位数远小于平均值,方差很大,说明存在少量异常大的极端损失;偏度值为15.04,分布右侧尾部有更明显的拉长趋势;峰度值为262.73,远大于标准正态分布的峰度值,样本的分布曲线坡度更大,曲线两侧的尾部较厚,直观反映出了尖峰厚尾的特点。偏度值和峰度值的标准误差都较小,反映出采样数据的平均值和总体的平均值差别较小,抽样误差较小,可靠性高。
|
|
表 1 全球洪水损失描述性统计量 Tab. 1 Descriptive statistics of global flood loss |
本文提出的LogGED-GPD模型,数据的分布须具有厚尾性。厚尾分布是指该分布尾部比指数分布的尾部更厚,即
厚尾分布通常可以通过Q-Q图验证。Q-Q图是根据变量的分位数对应于理论分布的分位数绘制的散点图,若经验分布与理论分布一致,则Q-Q图中的点将落在45°对角线上。若Q-Q图的中部为直线,上端向右偏离该直线,呈向下倾斜趋势,则该分布的上尾具有厚尾性;若Q-Q图的中部为直线,下端向左偏离该直线,呈向上倾斜趋势,则该分布的下尾具有厚尾性。运用SPSS做出全球洪水巨灾样本的对数Q-Q图,见图 1。从图 1中的Q-Q图中可以看出,全球洪水损失数据具有厚尾分布的特点,满足LogGED-GPD模型对数据的基本要求。
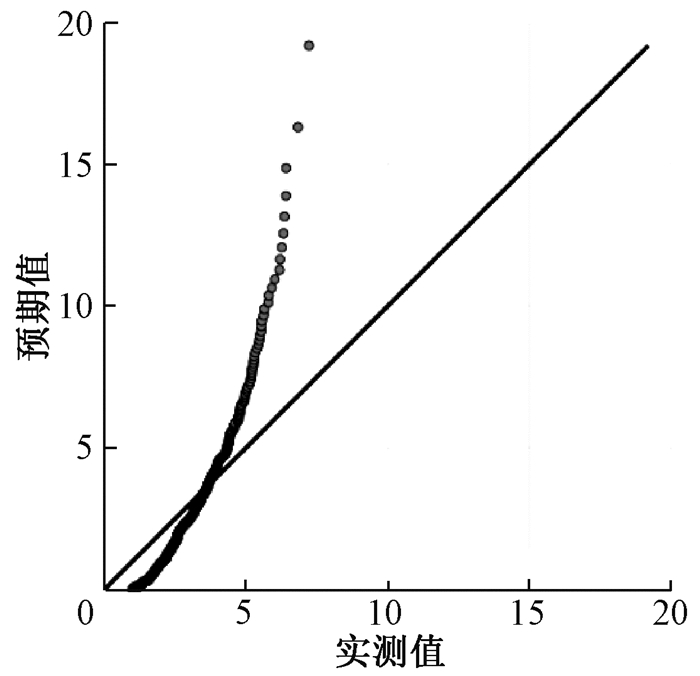
|
图 1 样本的对数Q-Q图 Fig. 1 Logarithmic Q-Q plot of sample |
由于不同等级的洪水巨灾造成的损失数量级差异较大,直接使用原始数据会影响拟合精度,因此在数据预处理阶段采用取对数的方法,消除原始数据在数量级上的差异,提高拟合精度。
将所得参数分别带回LogGED-GPD分布的分布函数中,并与单一的LogGED和Lognormal分布做拟合比较。通过K-S检验和卡方检验,验证样本数据的总体分布是否与拟合的分布存在显著差异。
单样本K-S检验是用来检验一个数据的观测经验分布是否符合已知的理论分布。K-S检验统计量的定义为
卡方检验是验证样本的经验分布函数与拟合分布函数之间的偏离程度,卡方值越小,经验分布函数与拟合分布函数之间的偏离程度越小,拟合效果越好。提出原假设H0:总体X的分布函数为F(x),其分布律为P{X=xi}=pi, i=1, 2, …, 那么当H0为真时,n次试验中样本落入第i个小区间的频率fi/n与概率pi很接近。则在原假设H0成立的条件下,样本服从自由度为k-1的卡方分布,其检验统计量为
在进行卡方检验时,对全球洪水巨灾损失取对数。全球洪水巨灾损失原始数据分布在区间[25 000 000, 210 000 000 000]内,涵盖了例如1998年中国特大洪灾等世界迄今为止损失金额最大的洪涝巨灾,取对数后分布在[17.034 386, 26.070 343]内,因此以全球洪水巨灾损失取对数后的1为区间宽度进行等距分组,共分为10组,则自由度为9。分别对全球洪水巨灾损失拟合的三种分布模型进行K-S检验和卡方检验,检验结果见表 2。
|
|
表 2 全球洪水巨灾损失拟合分布的参数估计值和检验值 Tab. 2 Parameter estimates and test values of fitting distribution of global flood catastrophe losses |
由表 2可知,在卡方检验中,当p=0.05时,χ2(9)=16.919 0,LogGED-GPD、LogGED、Lognormal三种分布模型均能够通过卡方检验。在K-S检验中,当p=0.05时,D(n, p)=D(494, 0.05)=0.061 189 29, Lognormal分布未能通过K-S检验,LogGED-GPD和LogGED两种分布模型均通过K-S检验,且LogGED-GPD的组合分布模型的拟合效果优于LogGED的单一分布模型。
3 结论本文基于文献中常用的对数正态分布、对数广义误差分布、广义帕累托分布等单一分布模型的基础上,结合组合分布模型可变权重的方法,设计了可变权重的对数广义误差-广义帕累托组合分布模型。运用组合分布模型对全球洪水巨灾损失做了实证分布拟合,验证了LogGED-GPD组合分布模型对全球洪水巨灾损失的拟合效果更优,一定程度上为今后巨灾损失分布的拟合方法提供了参考依据。
| [1] |
COORAY K, ANANDA M M A. Modeling actuarial data with a composite lognormal-pareto model[J]. Scandinavian actuarial journal, 2005, 2005(5): 321-334. DOI:10.1080/03461230510009763 (  0) 0) |
| [2] |
SCOLLNIK D P M. On composite lognormal-pareto models[J]. Scandinavian actuarial journal, 2007, 2007(1): 20-33. DOI:10.1080/03461230601110447 (  0) 0) |
| [3] |
SCOLLNIK D P M, SUN C C. Modeling with weibull-Pareto models[J]. North American actuarial journal, 2012, 16(2): 260-272. DOI:10.1080/10920277.2012.10590640 (  0) 0) |
| [4] |
LIAO X, PENG Z X, NADARAJAH S. Tail behavior and limit distribution of maximum of logarithmic general error distribution[J]. Communications in statistics-theory and methods, 2014, 43(24): 5276-5289. DOI:10.1080/03610926.2012.730168 (  0) 0) |
| [5] |
BAKAR S A, HAMZAH N A, MAGHSOUDI M, et al. Modeling loss data using composite models[J]. Insurance: mathematics and economics, 2015, 61: 146-154. DOI:10.1016/j.insmatheco.2014.08.008 (  0) 0) |
| [6] |
VUKOVIC O. Operational risk modelling in insurance and banking[J]. Journal of financial risk management, 2015, 4(3): 111-112. DOI:10.4236/jfrm.2015.43010 (  0) 0) |
| [7] |
YAO F G, WEN H M, LUAN J Q. CVaR measurement and operational risk management in commercial banks according to the peak valuemethod of extreme value theory[J]. Mathematical and computer modelling, 2013, 58(1/2): 15-27. (  0) 0) |
| [8] |
LEPPISAARI M. Modeling catastrophic deaths using EVT with a microsimulation approach to reinsurance pricing[J]. Scandinavian actuarial journal, 2016, 2016(2): 113-145. DOI:10.1080/03461238.2014.910833 (  0) 0) |
| [9] |
SOLARI S, EGÜEN M, POLO M J, et al. Peaks over threshold (POT): a methodology for automatic threshold estimation using goodness of fit p-value[J]. Water resources research, 2017, 53(4): 2833-2849. DOI:10.1002/2016WR019426 (  0) 0) |
| [10] |
MILJKOVIC T, GRÜN B. Modeling loss data using mixtures of distributions[J]. Insurance: mathematics and economics, 2016, 70: 387-396. DOI:10.1016/j.insmatheco.2016.06.019 (  0) 0) |
| [11] |
MCNEIL A J. Estimating the tails of loss severity distributions using extreme value theory[J]. Astin bulletin, 1997, 27(1): 117-137. DOI:10.2143/AST.27.1.563210 (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


