2. 中讯邮电咨询设计院有限公司 郑州分公司 河南 郑州 450007;
3. 嘉兴职业技术学院 互联网学院 浙江 嘉兴 314036
2. China Information Technology Design & Consulting Institute Co., Ltd. Zhengzhou Branch, Zhengzhou 450007, China;
3. Internet School, Jiaxing Vocational & Technical College, Jiaxing 314036, China
在成像和传输过程中,由于外界因素的干扰,获取的原始图像会引入一些噪声,从而造成图像质量的降低[1]。为了得到具有较高质量的图像,需要通过不同的去噪方法对含有噪声的图像进行处理,以减少噪声对图像的影响[2]。在对图像进行去噪的过程中,为去噪方法提供一些关于图像噪声的先验知识(包括噪声对应的分布及其参数),可以有效地提升这些方法的去噪性能。通常,在实际的图像处理过程中,图像中含有的噪声被假设为服从高斯分布,并且其均值为零,但是该高斯分布对应的方差值并不已知,需要通过设计方法估计该数值的大小[3]。根据在评估图像噪声方差过程中,提取噪声信号的方法不同,现有噪声方差估计方法可以分为三种:基于图像块划分;基于主成分分析(principal component analysis, PCA);基于变换域的方法。
基于图像块划分的噪声方差估计方法首先按照一定的规则将原始含噪图像分为多个矩形图像块,然后从获取的图像块中选取最平滑的一部分,并使用它们的像素灰度方差对图像噪声方差进行评估[3-5]。在这类方法中,平滑图像块选取的准确与否,对其精度具有很大的影响,尤其当未选取到或者选取较少的平滑块时,这类方法的评估噪声方差将会产生较大的误差。此外,基于PCA的噪声方差估计方法主要是利用PCA方法实现噪声方差的评估[6-7]。这类方法在图像内容具有较大的变化时,其准确性会随着参数设定不当而降低。不同于上述两种噪声方差估计方法,基于图像滤波的噪声方差估计方法则是首先利用不同的滤波器对含噪图像进行相应的滤波处理。然后,使用噪声图像与滤波后图像进行差分计算,并将差值结果看作是只包含噪声的图像。最后,根据差分计算的结果估计图像的噪声方差。Zoran等[8]首先利用高频滤波和低频滤波分别对图像进行处理,然后对两次滤波后的图像峰值进行差分计算,并以该结果作为对噪声方差估计的结果。Shin等[9]结合滤波方法和分块方法实现了对噪声方法的估计。尽管这类方法能够取得不错的噪声估计结果,但是当含噪图像中包含的纹理信息变得丰富,在对图像进行滤波处理的结果中会存在较多的高阶成分残留,这些残留将会对噪声方差估计结果的准确性产生较大的影响。
随着BM3D(block-matching and 3D filtering)方法在不同的场景中均可以获得非常好的除噪效果,越来越多的学者在该方法的基础上进行改进,并利用改进后的方法对图像中的噪声大小完成估计[10]。经典的BM3D方法在使用过程中,需要通过人为观察图像才能对该方法的噪声方差参数进行设置,这很大程度上限制了该方法的使用范围。为了扩大BM3D方法的使用范围,徐少平等[11]提出了一种改进的方法。该方法首先利用图像在小波变换域上所蕴含的自然场景统计(natural scene statistics,NSS)规律,并提取相应的特征矢量以描述图像中的噪声水平值。然后,利用支持向量回归技术,对含噪的图像进行训练,并获取相应估计图像噪声水平的模型。最后,利用该模型获取的噪声方差参数实现BM3D方法的自适应。文献[12-13]进一步提出了一种结合图像质量感知特征和局部均值估计技术的图像噪声估计方法,并将该方法应用于BM3D方法。由于不同图像的特征以及局部均值噪声评估方法的高效预测性,该方法的噪声估计性能得到了显著的提高。此外,乔双等[14]提出了一种结合PCA和BM3D的噪声估计方法。该方法使用PCA初步估计噪声的大小,作为参数应用于BM3D方法中。尽管该方法取得了较好的噪声评估性能,但是其适用范围过于单一。
为了能够有效地对图像噪声方差进行估计,本文提出了一种基于BM3D的图像噪声方差估计方法。该方法首先利用具有复杂度低、便于实现等特点的快速噪声评估[15](fast noise level evaluation,F-NLE)方法对含噪图像进行噪声估计,得到对噪声的一个初步估计值,考虑到F-NLE方法对噪声方差估计的结果偏大的特点,本文将初步估计的噪声方差值作为最大值,并依照预先设定的列表长度和步长,获取对应的噪声方差列表。然后,将列表中的每个噪声方差数值作为BM3D方法中需要预设的噪声参数,按噪声方差列表中的顺序对含噪图像进行滤波处理,并获取滤波后相对应的图像列表。在通过实验论证了滤波前后图像的NSS特征存在的差异能够反映图像降噪效果的基础上,对滤波前后图像的NSS特征进行提取。最后,选用获取的NSS特征对应的矢量距离,作为每幅含噪图像所对应的噪声方差参数的权重,并根据局部均值法对图像噪声方差实现最终精确的估计。本文所提出方法的流程图如图 1所示。
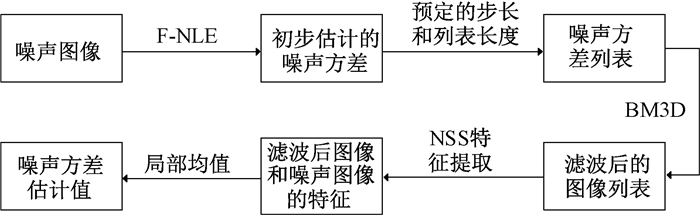
|
图 1 方法流程图 Fig. 1 The flow chart of the method |
本文所提方法的优势主要包括以下三个方面:1) 使用了图像的NSS特征,该特征对图像细节内容不敏感,这有利于提高方法的稳定性;2) 相比于传统的去噪方法,BM3D方法具有更好的去噪效果,这有利于提高方法的准确性;3) 设计的噪声方差估计方法,不仅可以为BM3D方法提供更优的参数,也可以为具有不同噪声大小的图像提供更为精确的估计参数,这有利于提高方法的鲁棒性。
1 BM3D的介绍自2007年BM3D方法被Dabov等提出后,由于该方法同时具备非常好的降噪性能和非常高的执行效率等特点,经常被使用在不同的降噪场景中。该方法主要包括两个操作过程相似的步骤,即初步去噪和最终去噪[10-11]。在这两个去噪的步骤中,每个步骤又被分成三个部分,即相似块匹配和组合、三维滤波、以及滤波后相似块的聚合。具体来讲,BM3D方法首先将含噪图像分割成拥有固定大小、形状规则等特点的图像块,对具有高度相似度的图像块进行匹配,并将这些匹配后的图像块组合成三维数组。然后,使用三维变换对三维数组进行处理,在变换域中利用阈值滤波或者维纳滤波的方法实现对图像块的降噪,并对降噪后的图像块进行三维反变换处理。最后,对反变换得到的图像块进行加权平均处理,并将图像块返回原位置,以获取最终的除噪图像。BM3D方法在对图像除噪的过程中,充分考虑了图像块之间的相似性以及其相对应的稀疏表示,从而实现了对图像中包含的细节信息有效地利用以及保留。
在BM3D方法使用的过程中,需要人为参与预设噪声水平参数。当预设参数的数值大小和真实噪声的大小越接近时,BM3D方法能够取得更好的降噪效果[11-12]。然而,在人为预设参数过程中,该参数的数值大小很容易受到主观的影响,最终导致BM3D方法不能取得理想的降噪效果。因此,实现自适应预设噪声水平参数对于BM3D方法来说是非常有必要的。
2 图像噪声方差估计方法及描述 2.1 噪声方差的初步估计F-NLE去噪方法在对图像的噪声进行估计的过程中,利用了图像的二阶导数信息[15]。考虑到在求取图像二阶信息时,图像中存在的边缘以及纹理部分会产生比较大的二阶导数,并且这些导数会对噪声的估计造成较大的影响。因此,该方法的噪声评估算子N选用两个Laplacian掩蔽算子的差值,其定义为
| $ \boldsymbol{N}=2\left(\left[\begin{array}{rrr} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{array}\right]-\frac{1}{2}\left[\begin{array}{rrr} 1 & 0 & 1 \\ 0 & -4 & 0 \\ 1 & 0 & 1 \end{array}\right]\right)=\left[\begin{array}{rrr} 1 & -2 & 1 \\ -2 & 4 & -2 \\ 1 & -2 & 1 \end{array}\right]。$ | (1) |
假设图像中每个像素点对应的噪声标准差为σ′,那么在N内的图像噪声均值为0,方差变为
| $ \left(4^{2}+4 \cdot(-2)^{2}+4 \cdot 1^{2}\right) \sigma^{\prime 2}=36 \sigma^{\prime 2}, $ |
如果利用I(i, j)*N对图像中的噪声标准差进行计算,σ′2则能够被表示为
| $ \sigma^{\prime 2}=\sum\limits_{I_{\text {image }}}(I(i, j) * \boldsymbol{N})^{2} /(36(W-2)(H-2)), $ | (2) |
式中:W、H分别代表含噪图像的长度和宽度;I(i, j)* N表示含噪图像I在坐标(i, j)处使用N算子进行计算取得的数值。
由于在含噪图像具有丰富纹理信息的情况下,F-NLE方法会将部分复杂纹理和强边缘对应的二阶导数信息错误地计算到噪声的估计数值中,最终导致估计结果的偏大。因此本文在得到噪声方差列表的过程中,将σ′看成是噪声标准差列表对应的最大值,即L1={σ′-nλ, σ′-(n-1)λ, …, σ′},其中:λ表示列表步长;n表示列表长度。在下文中该列表被记为L1={σ1, σ2, …, σn}。利用L1中的数值作为BM3D方法的滤波参数并分别对含噪图像进行去噪处理,得到BM3D方法处理后的图像列表为L2={I1, I2, …, In}。
2.2 NSS特征的提取近年来,相关学者在空域中对图像的NSS模型进行了分析[16],发现当图像出现失真情况时,NSS模型也会产生不同程度的变化。NSS变化的规律仅与图像发生失真的种类和程度有关,与图像中的内容没有太大的关系。考虑到图像受到噪声污染是造成图像发生失真的一种情况,因此,图像的NSS模型会随着噪声的变化产生规律性变化。
在分析图像I的NSS模型之前,需要使用去均值和归一化的方式对图像I进行处理,得到其对应的MSCN(mean subtracted contrast normalized),即
| $ \hat{I}(i, j)=\\\left[I(i, j)-\sum\limits_{k=-K}^{K} \sum\limits_{l=-L}^{L} w_{k, l} I_{k, l}(i, j)\right] /\left[\sqrt{\sum\limits_{k=-K}^{K} \sum\limits_{l=-L}^{L} w_{k, l}\left(I_{k, l}(i, j)-\sum\limits_{k=-K}^{K} \sum\limits_{l=-L}^{L} w_{k, l} I_{k, l}(i, j)\right)^{2}}+C\right], $ |
式中:i∈{1, 2, …, W};j∈{1, 2, …, H};W、H分别代表图像I对应的长度和宽度;C表示常数,通常取值为1,主要为了防止分母变为0;wk, l表示二维的高斯权重系数;K和L分别代表二维高斯窗对应的长度和宽度,通常这两个数值取3。
为了能够量化图像失真和图像NSS统计性质之间的变化规律,常选用非对称广义高斯分布(asymmetric generalized gaussian distribution, AGGD)模型模拟实现该规律[17],AGGD可以表示为
| $ f\left(x ; v, \theta_{r}^{2}, \theta_{l}^{2}\right)= \begin{cases}\frac{v}{\left(\beta_{r}+\beta_{l}\right) \Gamma\left(\frac{1}{v}\right)} \exp \left(-\left(\frac{|x|}{\beta_{1}}\right)^{v}\right), & x<0, \\ \frac{v}{\left(\beta_{r}+\beta_{l}\right) \Gamma\left(\frac{1}{v}\right)} \exp \left(-\left(\frac{|x|}{\beta_{r}}\right)^{v}\right), & x>0,\end{cases} $ |
其中:βr=
为了更好地对AGGD模型进行拟合,一般利用参数集{η, v, βl, βr}来表示,其中η对应AGGD分布的均值,其表达式为
| $ \eta=\left(\beta_{r}-\beta_{l}\right) \Gamma\left(\frac{2}{v}\right) / \Gamma\left(\frac{1}{v}\right)。$ | (3) |
通常,利用距匹配的方法实现对{η, v, βl, βr}的估计[17]。此外,为了能够对图像NSS中邻域对的相关量化处理,选用邻接MSCN系数(公式(4)~(7))的成对组合对四个方向的关系进行模拟,以形成图像的特征元素。四个方向分别是:水平方向H;垂直方向V;主对角方向D1;次对角方向D2。
| $ H(i, j)=\hat{I}(i, j) \hat{I}(i, j+1), $ | (4) |
| $ V(i, j)=\hat{I}(i, j) \hat{I}(i+1, j), $ | (5) |
| $ D 1(i, j)=\hat{I}(i, j) \hat{I}(i+1, j+1), $ | (6) |
| $ D 2(i, j)=\hat{I}(i, j) \hat{I}(i-1, j-1)。$ | (7) |
同样,根据AGGD模型对上述四个方向对应的乘积分布进行模拟。最终,可以在一幅图像中提取到18个NSS特征,这些特征是
为了能够证明图像使用BM3D方法前后的NSS特征差异可以反映出该方法的降噪效果,本文使用两个常用的指标对其进行验证。这两个指标分别是皮尔森线性相关系数(Pearson linear correlation coefficient, PLCC)、斯皮尔曼秩相关系数[18](Spearman rank-order correlation coefficient, SROCC)。使用BM3D方法后,使用图像中真实噪声标准差与BM3D图像进行滤波时所用标准差两者之间差异向量V1,对图像列表具有的降噪效果进行表示,差异向量V1的定义为
| $ \boldsymbol{V}_{1}=\left|L_{1}-\bar{\sigma}\right|=\left[\left|\sigma_{1}-\bar{\sigma}\right|,\left|\sigma_{2}-\bar{\sigma}\right|, \cdots,\left|\sigma_{n}-\bar{\sigma}\right|\right]。$ | (8) |
此外,在使用BM3D方法之后,得到的图像列表对应的NSS特征向量和含噪图像对应的NSS特征向量两者之间存在的差值,能够使用特征矩阵F对其进行表示,特征矩阵F的定义为
| $ \boldsymbol{F}=\left[\begin{array}{c} \left|\boldsymbol{f}^{1}-\boldsymbol{f}^{o}\right| \\ \left|\boldsymbol{f}^{2}-\boldsymbol{f}^{o}\right| \\ \vdots \\ \left|\boldsymbol{f}^{n-1}-\boldsymbol{f}^{o}\right| \\ \left|\boldsymbol{f}^{n}-\boldsymbol{f}^{o}\right| \end{array}\right]=\left[\begin{array}{ccccc} \left|f_{1}^{1}-f_{1}^{o}\right| & \left|f_{2}^{1}-f_{1}^{o}\right| & \cdots & \left|f_{17}^{1}-f_{1}^{o}\right| & \left|f_{18}^{1}-f_{1}^{o}\right| \\ \left|f_{1}^{2}-f_{1}^{o}\right| & \left|f_{2}^{2}-f_{1}^{o}\right| & \cdots & \left|f_{17}^{2}-f_{1}^{o}\right| & \left|f_{18}^{2}-f_{1}^{o}\right| \\ \vdots & \vdots & & \vdots & \vdots \\ \left|f_{1}^{n-1}-f_{1}^{o}\right| & \left|f_{2}^{n-1}-f_{1}^{o}\right| & \cdots & \left|f_{17}^{n-1}-f_{1}^{o}\right| & \left|f_{18}^{n-1}-f_{1}^{o}\right| \\ \left|f_{1}^{n}-f_{1}^{o}\right| & \left|f_{2}^{n}-f_{1}^{o}\right| & \cdots & \left|f_{17}^{n}-f_{1}^{o}\right| & \left|f_{18}^{n}-f_{1}^{o}\right| \end{array}\right], $ |
式中:fi(i=1~n)是L2中第i幅图像对应的NSS特征向量;fo是含噪图像对应的NSS特征向量;σ为含噪图像中真实噪声对应的标准差;σi(i=1~n)是L1中第i个噪声对应的标准差。
本文选用公开数据库LIVE[19]和TID2013[20]中的50幅原始图像,对选用的图像添加不同大小的高斯噪声(标准差的范围是10~100,步长是10),最终共生成500幅含噪图像,对每一幅含噪图像向量V1和F中的每一列向量之间的PLCC、SROCC进行计算。为了能够获取整体性的评价,本文对每一幅图像所有的NSS特征对应的PLCC、SROCC均值进行了计算,其结果均分布在0.94到0.97之间,此时n=8、λ=1。这些分布在0.94到0.97之间的指标数值说明含噪图像按照L1给出的参数完成BM3D滤波后,L2中图像的NSS特征存在的差异可以很好地对σi(BM3D方法的参数)与σ两者之间的相近程度进行反映。根据BM3D方法的特点,当提供的σi数值与σ的数值越接近,即人为参与预先设定的BM3D方法参数越准确,BM3D方法对应的除噪效果就越好,滤波前后的含噪图像就具有越明显的NSS特征差异,进而为本文利用σi实现对σ的估计提供了强有力的依据。
在本文设计的图像噪声方差估计方法中,噪声标准差列表是该方法的基础。只有当噪声标准差列表囊括到图像真实噪声标准差对应的数值时,才能实现在所提出方差估计方法的最后一个步骤中,利用局部均值完成对噪声标准差的精确估计。因此,所选用的标准差具有越大的列表长度和越小的步长,最终得到的方差估计值就会越准确。但是,当噪声标准差列表的长度越长,对应需要使用BM3D方法进行滤波处理的次数就越多,同样对图像NSS特征提取的次数也会变多,这样最终会造成方法运行时间大幅度地增加。所以,在使用设计的方法之前,需要优化列表参数n和λ。根据实验结果,n的范围定为{6, 7, 8, 9, 10},λ的范围定为{0.7, 0.8, 0.9, 1},这样两者共构成了20种组合。利用前文设计的图像集,对参数的所有组合进行实验,使用在每一种参数组合时,18个NSS特征对应的PLCC和SROCC均值,作为选取列表参数的性能指标,所有的实验结果如表 1所示。从表 1可以得出,在考虑方法复杂度的基础上,本文使用的列表参数选用n=7,λ=1的组合。
|
|
表 1 不同n和λ时图像NSS特征与向量V1的相关系数 Tab. 1 Correlation coefficients between image NSS features and V1 with different n and λ |
运用上文所提出的特征可以获得L2中图像对应的NSS特征向量集合{f1, f2, …, fn},这些特征向量均分别对应于L1中的{σ1, σ2, …, σn},使用fo表示待评估图像对应的特征矢量,则最终获取的噪声标准差估计值[12]可以表示为
| $ \sigma_{\text {est }}=\sum\limits_{1 \leqslant i \leqslant n} \omega\left(\boldsymbol{f}^{i}, \boldsymbol{f}^{o}\right) \sigma_{i}, $ | (9) |
式中:ω(fi, fo)表示权重函数,其对应数值的大小主要取决于矢量特征fo和fi的欧氏距离,其定义为
| $ \omega\left(\boldsymbol{f}^{i}, \boldsymbol{f}^{o}\right)=\exp \left(\beta \frac{d\left(\boldsymbol{f}^{i}, \boldsymbol{f}^{o}\right)}{d_{\max }-d_{\min }}\right) / \sum\limits_{1 \leqslant i \leqslant n} \exp \left(\beta \frac{d\left(\boldsymbol{f}^{i}, \boldsymbol{f}^{o}\right)}{d_{\max }-d_{\min }}\right), $ |
其中:β表示控制ω(fi, fo)衰减速度的参数;d(fi, fo)= ‖fo- fi‖ 2表示矢量特征fo和fi的欧式距离;dmin和dmax分别表示{d(f1, fo), …, d(fn, fo)}的最小值和最大值。
考虑到参数β对噪声估计非常重要,以及当图像中存在大小不同的噪声时,图像对应的NSS特征矢量具有差异性,因此本文利用2.1中初步估计的噪声标准差值σ′,实现对参数β的分段整定。选用公开图像数据库LIVE[19]和TID2013[20]中代表性的图像(因为这些图像具有丰富的纹理和情景特征),即图像“stream”、“womanhat”、“bikes”、“statue”、“ocean”、“dancers”。之后,给这些图像分别添加标准差大小不同的高斯噪声(标准差范围为1~100,步长为1),这样共获得600幅含噪声的训练图像(6幅×100个噪声级别)。当β使用不同的数值时,利用公式(9)所预测的评估值与噪声标准差的真实值之间的均方根误差值来筛选最优的β参数值,实验结果如表 2所示。
|
|
表 2 在参数β不同时测试图像的评估均方误差 Tab. 2 Evaluation mean square error of test images in different parameters β |
根据表 2可以得到(加粗的数据表示最优的指标);当噪声为低比例时(即其对应的标准差σ′数值大小在[0, 30]之间时),参数β的数值为6时,得到的误差最小;当噪声为中比例时(即其对应的标准差σ′数值大小在[31, 70]之间时),参数β的数值为7时,得到的误差最小;当噪声为高比例时(即其对应的标准差σ′数值大小在[71, 100]之间时),参数β取值的数值为5时,得到的误差最小。因此,为了能够得到最佳的噪声水平评价值,在每次使用局部均值公式之前,参数β的数值将由预估计噪声标准差参数σ′的数值来决定。
3 实验与分析 3.1 测试数据集及对比方法的选取考虑到本文在对参数β进行训练的过程中利用了LIVE和TID2013图像集中的图像,因此,在对测试图像集进行选取的过程中,采用另外3个公开图像数据库中的225幅图像,包括IVC[19]数据库中的25幅图像,Waterloo[22]数据库中的192幅图像,以及CSIQ[23]数据库中的8幅图像。这些图像具有不同的尺寸,它们的大小从481像素*321像素像素到678像素*678像素。这些图像在使用前首先被处理为灰度图,图像数据集的代表图像如图 2所示。然后,对选取的图像添加高斯噪声,噪声的标准差为10~100,步长为5,共生成4 275幅含噪图像。此外,为了减小噪声随机性对实验结果的影响,对每幅图像的每种噪声标准差均测试50次。

|
图 2 测试图像数据集中的代表图片 Fig. 2 Representative images in the test image data set |
本文选用的对比方法包括基于图像块划分的方法:文献[3]和[5]的方法;基于变换域的方法:文献[6]和[7]的方法;基于图像滤波的方法:文献[8]和F-NLE方法[15]。在对比实验中,对比方法使用的参数均和其原文中使用的最优参数相同。
3.2 性能指标的选取常被应用于对不同噪声估计方法进行评估的准则,主要包括三个指标:方法平均估计误差μE;方法估计误差标准差σE;方法总性能MSE。这三个指标均是数值越小,表示所用的噪声估计方法具有更好的估计性能。此外,μE表示噪声估计方法的估计精度,σE相当于噪声估计方法的可靠性。μE、σE和MSE的定义分别为:
| $ \mu_{E}=\sum\limits_{p=1}^{Q}\left(\sum\limits_{l=1}^{P}\left|\sigma_{\mathrm{est}}^{l}-\bar{\sigma}\right| / P\right) / Q, $ | (10) |
| $ \sigma_{E}=\sqrt{\sum\limits_{p=1}^{Q}\left[\left(\sum\limits_{l=1}^{P}\left|\sigma_{\mathrm{est}}^{l}-\bar{\sigma}\right| / P\right)-\mu_{E}\right]^{2} / Q}, $ | (11) |
| $ M S E=\sqrt{\mu_{E}^{2}+\sigma_{E}^{2}}, $ | (12) |
式中:σestl表示第l次的估计值;Q、P分别表示实验对比图像的数量(4 275幅)和对比的次数(50次)。
3.3 实验结果分析
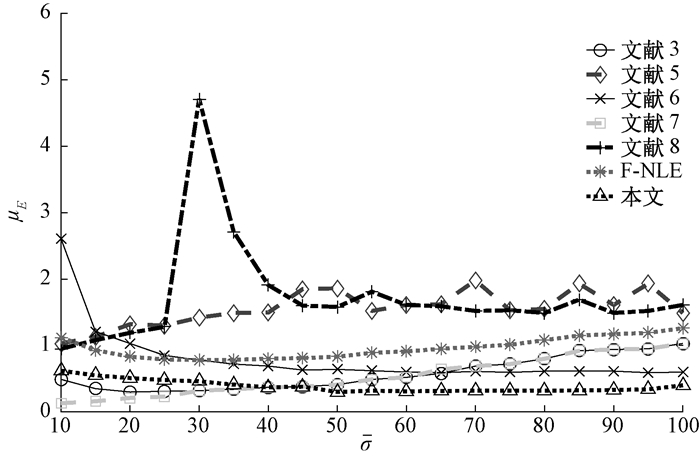
|
图 3 不同方法的μE比较 Fig. 3 The comparsion μE of different methods |

|
图 4 不同方法的σE比较 Fig. 4 The comparsion σE of different methods |
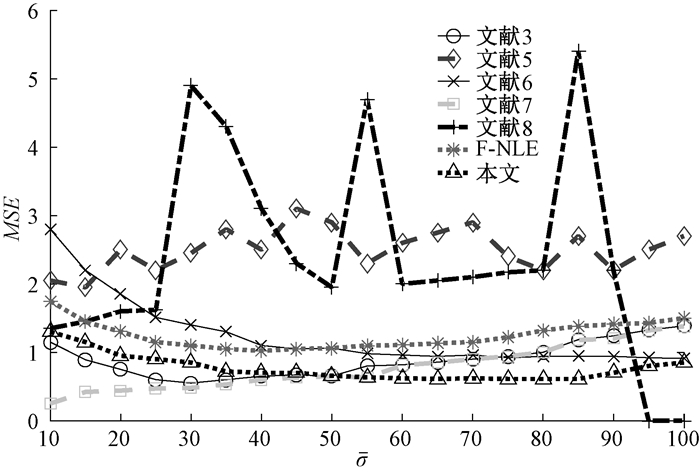
|
图 5 不同方法的MSE比较 Fig. 5 The comparsion MSE of different methods |
1) 随着图像噪声地增大,本文所提方法的μE在整体上始终保持稳定状态,而本文所提方法的σE和MSE则逐步地降低,并且当噪声标准差数值大于50之后,本文所提方法的σE和MSE基本上保持稳定不变,这说明在图像噪声的数值达到一定后,本文所提方法的可靠性非常高,并且非常稳定。
2) 文献[4]和文献[7]在对具有较小噪声的图像进行处理时,μE的数值要低于本文所提出的方法,σE的数值则与本文所提方法相差无几。但是,随着图像噪声水平逐步增大,这两种方法的μE也随之增加,这表明这两种方法的噪声估计性能也随之下降,最终劣于本文所提方法的噪声估计性能。
3) 本文使用了两段结构式的方法对噪声大小进行估计。F-NLE方法获取的μE和σE均比本文所提方法要高,并且本文所提方法的MSE降低非常明显,该数值仅仅是F-NLE方法的1/2。
4) 在任意不同的噪声干扰下,文献[5]和文献[8]的方法无论是在方法的准确性亦或是方法的稳定性上都要低于其他方法,并且这两种方法的μE、σE和MSE均是本文所提方法的2~3倍,这说明本文所提方法相对这两种方法在性能上取得了明显的提升。
4 结论为了能够有效地提高估计图像噪声方差的性能,本文提出了一种基于BM3D的图像噪声方差估计方法。在该方法中,首先使用F-NLE方法获取初级阶段所估计的噪声标准差值,然后根据该标准差,实现了在第二阶段中根据噪声大小的不同,选择最优噪声方差对应的相关参数,有效地提高了本文所提方法的准确性。相比现有的噪声方差估计方法,本文所提方法使用了不受图像内容影响、同时能够高效反映图像噪声方差的NSS特征,该特征的使用显著提高了方法的稳定性以及可靠性。此外,本文所提方法的分段估计思想以及图像的NSS特征不仅可以用在估计图像高斯噪声的方差上,在未来的工作中,也可以将用于估计的F-NLE方法和BM3D方法替换为其他图像噪声模型的估计方法和噪声滤波方法,从而实现对相应图像噪声模型参数的估计。
| [1] |
BHUJLE H V, VADAVADAGI B H. NLM based magnetic resonance image denoising-a review[J]. Biomedical signal processing and control, 2019, 47: 252-261. DOI:10.1016/j.bspc.2018.08.031 (  0) 0) |
| [2] |
LANZA A, MORIGI S, SGALLARI F. Convex image denoising via non-convex regularization with parameter selection[J]. Journal of mathematical imaging and vision, 2016, 56(2): 195-220. DOI:10.1007/s10851-016-0655-7 (  0) 0) |
| [3] |
ZHU X, MILANFAR P. Automatic parameter selection for denoising algorithms using a no-reference measure of image content[J]. IEEE transactions on image processing, 2010, 19(12): 3116-3132. DOI:10.1109/TIP.2010.2052820 (  0) 0) |
| [4] |
SUTOUR C, DELEDALLE C A, AUJOL J F. Estimation of the noise level function based on a nonparametric detection of homogeneous image regions[J]. SIAM journal on imaging sciences, 2015, 8(4): 2622-2661. DOI:10.1137/15M1012682 (  0) 0) |
| [5] |
张承志, 冯华君, 徐之海, 等. 图像噪声方差分段估计法[J]. 浙江大学学报(工学版), 2018, 52(9): 1804-1810. ZHANG C Z, FENG H J, XU Z H, et al. Piecewise noise variance estimation of images based on wavelet transform[J]. Journal of Zhejiang university (engineering science), 2018, 52(9): 1804-1810. (  0) 0) |
| [6] |
PYATYKH S, HESSER J, ZHENG L. Image noise level estimation by principal component analysis[J]. IEEE transactions on image processing, 2013, 22(2): 687-699. DOI:10.1109/TIP.2012.2221728 (  0) 0) |
| [7] |
CHEN G Y, ZHU F Y, HENG P A. An efficient statistical method for image noise level estimation[C]//2015 IEEE International Conference on Computer Vision (ICCV). Santiago: IEEE Computer Society, 2015: 477-485.
(  0) 0) |
| [8] |
ZORAN D, WEISS Y. Scale invariance and noise in natural images[C]//2009 IEEE 12th International Conference on Computer Vision. Kyoto: IEEE Press, 2009: 2209-2216.
(  0) 0) |
| [9] |
SHIN D H, PARK R H, YANG S, et al. Block-based noise estimation using adaptive Gaussian filtering[J]. IEEE transactions on consumer electronics, 2005, 51(1): 218-226. DOI:10.1109/TCE.2005.1405723 (  0) 0) |
| [10] |
DABOV K, FOI A, KATKOVNIK V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE transactions on image processing, 2007, 16(8): 2080-2095. DOI:10.1109/TIP.2007.901238 (  0) 0) |
| [11] |
徐少平, 张兴强, 杨晓辉, 等. 基于噪声估计的自适应块匹配和三维滤波降噪算法[J]. 光电子·激光, 2017, 28(6): 663-673. XU S P, ZHANG X Q, YANG X H, et al. An adaptive BM3D denoising algorithm based on noise level estimation[J]. Journal of optoelectronics ·laser, 2017, 28(6): 663-673. (  0) 0) |
| [12] |
徐少平, 张兴强, 姜尹楠, 等. 局部均值噪声估计的盲3维滤波降噪算法[J]. 中国图象图形学报, 2017, 22(4): 422-434. XU S P, ZHANG X Q, JIANG Y N, et al. Noise level estimation based on local means and its application to the blind BM3D denoising algorithm[J]. Journal of image and graphics, 2017, 22(4): 422-434. (  0) 0) |
| [13] |
郭华平, 刁小宇, 刘宏兵. 一种基于降噪自编码的组合分类算法[J]. 信阳师范学院学报(自然科学版), 2020, 33(4): 657-662. GUO H P, DIAO X Y, LIY H B. Ensemble learning based on denosing autoencoder[J]. Journal of Xinyang normal university (natural science edition), 2020, 33(4): 657-662. DOI:10.3969/j.issn.1003-0972.2020.04.025 (  0) 0) |
| [14] |
乔双, 吴晓阳, 赵辰一, 等. 基于PCA和BM3D的噪声估计方法及其在中子图像去噪中的应用[J]. 原子能科学技术, 2018, 52(4): 729-736. QIAO S, WU X Y, ZHAO C Y, et al. Noise level estimation method based on PCA and BM3D for neutron image denoising[J]. Atomic energy science and technology, 2018, 52(4): 729-736. (  0) 0) |
| [15] |
IMMERKAER J. Fast noise variance estimation[J]. Computer vision and image understanding, 1996, 64(2): 300-302. DOI:10.1006/cviu.1996.0060 (  0) 0) |
| [16] |
RUDERMAN D L. The statistics of natural images[J]. Network: computation in neural systems, 1994, 5(4): 517-548. DOI:10.1088/0954-898X_5_4_006 (  0) 0) |
| [17] |
SHARIFI K, LEON-GARCIA A. Estimation of shape parameter for generalized Gaussian distributions in subband decompositions of vi8eo[J]. IEEE transactions on circuits and systems for video technology, 1995, 5(1): 52-56. DOI:10.1109/76.350779 (  0) 0) |
| [18] |
GU K, XU X, QIAO J F, et al. Learning a unified blind image quality metric via on-line and off-line big training instances[J]. IEEE transactions on big data, 2020, 6(4): 780-791. DOI:10.1109/TBDATA.2019.2895605 (  0) 0) |
| [19] |
SHEIKH H R, WANG Z, CORMACK L, et al. LIVE image quality assessment database release 2[EB/OL]. [2015-04-26]. [2020-05-15]. http://live.ece.utexas.edu/research/quality.
(  0) 0) |
| [20] |
PONOMARENKO N, JIN L N, IEREMEIEV O, et al. Image database TID2013: Peculiarities, results and perspectives[J]. Signal processing: image communication, 2015, 30: 57-77. DOI:10.1016/j.image.2014.10.009 (  0) 0) |
| [21] |
LE CALLET P, AUTRUSSEAU F, Subjective quality assessment Irccyn/IVC database[EB/OL]. (2015-04-04)[2019-01-15]. http://www.irccyn.ec-nantes.fr/ivcdb/.
(  0) 0) |
| [22] |
MA K D, DUANMU Z F, WU Q B, et al. Waterloo exploration database: new challenges for image quality assessment models[J]. IEEE transactions on image processing, 2017, 26(2): 1004-1016. DOI:10.1109/TIP.2016.2631888 (  0) 0) |
| [23] |
LARSON C, CHANDLER DM. Categorical Image Quality (CSIQ) datebase[EB/OL]. (2009-09-12)[2020-05-15]. http://vision.okstate.edu/csiq.
(  0) 0) |
 2021, Vol. 53
2021, Vol. 53


