机器视觉测量作为非接触式测量方法之一[1],在测量过程中具有客观性强、鲁棒性好、重复性高、无损伤等优点,能够满足现代工业生产批量大、检测任务重、检测精度要求高的需求,因此在测量领域得到了广泛的应用[2].
目前,基于机器视觉的圆柱体尺寸检测应用研究非常广泛.文献[3]设计了一套基于机器视觉的西林瓶尺寸自动检测系统;文献[4]设计了一套轴承内外圈尺寸检测和分类系统,以替代人工检测分类;文献[5]应用机器视觉理论研究基于机器视觉的管孔类零件尺寸自动测量系统.在这些研究中都涉及圆柱端面的尺寸测量,但大多数测量方法只简单地应用Canny算子或Sobel算子寻找端面边界,并直接进行圆拟合来进行参数估算.这种方法对于端面图像简单、正常的圆柱样品非常有效,但对于端面存在缺损或端面图像复杂从而使圆边界提取不完整的圆柱,无法进行精确尺寸测量.因此,本文针对端面存在缺损或端面图像复杂的圆柱提出了一种新的测量方法,即通过查找边界点,众数筛选边界点,Kasa算法圆拟合,最终完成对圆直径的精确测量.实验结果表明,该方法适用性强,不仅能够精确测量具有正常端面的圆柱尺寸,同时对端面存在缺损的圆柱也能够进行精确检测,且测量结果达到微米量级.
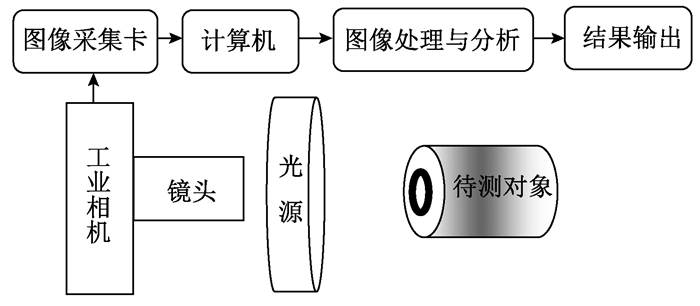
1 测量系统的组成机器视觉测量系统[6]主要由图像采集、图像处理与分析、结果输出三部分构成.图像采集设备通常包含光源、相机、镜头、图像采集卡及计算机等,目的是获取被测物体的光学图像及特征信息,然后通过图像处理算法对采集到的图像进行分析,获取所需要的信息,并将处理结果显示出来.机器视觉测量系统的原理如图 1所示.
|
图 1 测量系统原理 Figure 1 Measurement system principle |
测量方案采用低角度环形光进行照明,图 2给出了本项目中圆柱端面所需要的测量参数,包括外圆直径d1,第2层圆直径d2和中心孔直径d3.外圆和第2层圆之间存在一个倒角区域.

|
图 2 测量参数 Figure 2 Measurement parameters |
图像采集过程中,由于受环境和硬件条件的限制,不可避免地会掺杂部分噪声.因此,在进行尺寸测量之前首先要对图像进行滤波.中值滤波作为一种平滑滤波手段,它能够在降低噪声的同时减小边缘的模糊程度[7],本文选用中值滤波对图像进行平滑处理.
中值滤波可以表示为
| $ {y_i} = \mathop {Med}\limits_D \left\{ {{f_{ij}}} \right\}, $ | (1) |
式中:D为滤波窗口;{fij}代表图像二维数据序列.图像预处理过程如图 3所示,其中图 3(a)为原图像,图 3(b)为中值滤波后图像的效果图.

|
图 3 图像预处理过程 Figure 3 Image pre-processing |
为了对圆柱的尺寸进行精确的测量,需要根据目标对象在图像中的大致位置建立感兴趣区域来查找边界点.首先对目标对象在图像中的位置进行了粗略估算,过程如下:对预处理后的图像进行阈值分割,得到图 3(c)所示的目标对象.由于中心孔区域对中心点坐标的估计存在较大干扰,因此,对阈值分割后的图像进行孔填充,得到如图 3(d)所示的目标区域,最后通过求图 3(d)中区域的重心得到目标对象的中心坐标.
由于受图像复杂背景的影响,使得计算出的重心坐标只是一个粗略的估计值,不能够作为圆参数测量的基准值,但可以在此基础上进一步完成圆柱端面尺寸的精确测量.
2.3 边界点的查找尺寸测量的关键是查找边界点,边界点查找示意图如图 4所示.查找边界点的具体过程如下:

|
图 4 边界点查找示意图 Figure 4 Sketch of boundary points search |
1) 根据2.2中粗略估计得到的圆柱端面图像的中心点坐标,建立测量目标区域,即ROI,如图 4(a)所示.
2) 剖面图如图 4(b)所示,获取ROI内垂直于剖面线方向每列像素点的灰度均值[8],图 4(d)中f1即为ROI内沿剖面线方向的灰度值变化函数图.
3) 求灰度值的一阶导数,并选取一阶导数的局部极值点作为边缘点的候选点,图 4(d)中f2即为灰度值一阶导数函数曲线图.
4) 以目标对象中心点的位置为固定点,如图 4(c)所示,令ROI每隔2°进行一次旋转,并重复2)、3)直到旋转180°,得到如图 4(e)所示的圆边缘候选边界点.
2.4 众数筛检法选取边界点当圆柱端面受损或端面图像较复杂时,直接采用边界点进行圆拟合,会对圆参数的估计产生错误的影响.因此,在进行圆拟合之前要对候选边界点进行一定的筛选,本文提出一种新的众数筛检法对边界点进行选取.众数筛检法选取一组数据中的众数为基点,用Mode表示,之后把该组数据中数值大小在[Mode ± 4]范围内的数据保留下来,将其他数据剔除,即完成筛选.该方法适用于筛除具有固定差值数据中出现的散乱点,如平行线之间数据的散乱点、同心圆之间数据的散乱点.本文所测量的端面存在3个同心圆,因此该方法非常适用.
由2.3节得到的边界点是成组出现的,每一个d1圆上的边界点都有d2和d3圆上的边界点与之对应.在进行众数筛选时以组内边界点之间的距离为参考依据,边界点筛选及圆拟合图像如图 5所示.其中d1与d2圆上的一组边界点如图 5(a)所示,筛选后边界点如图 5(b)所示.

|
图 5 边界点筛选及圆拟合图像 Figure 5 Boundary points selection and circle fitting image |
Kasa代数圆拟合法[9]是速度最快、应用最为广泛的一种圆拟合算法.作为代数距离法的一种,Kasa算法不仅有精确的解析解,且能够克服几何距离法中由于迭代不收敛或收敛到局部最小值所带来的问题.因此,本文选择Kasa算法进行圆参数估计.
Kasa算法以采样点到目标圆的代数距离平方和作为目标函数,推导出拟合圆心坐标和拟合半径的表达式[10].令(xi, yi)表示坐标系中第i个被测量的数据点,共有N个待测量的点,3≤ i≤N,(A, B)为圆心,R为圆的半径,得到的残差公式即目标函数为
| $ \sum\limits_{i = 1}^N {{{\left( {\sqrt {{{\left( {{x_i} - A} \right)}^2} + {{\left( {{y_i} - B} \right)}^2}} - R} \right)}^2} = \mathit{min}\mathit{.}} $ | (2) |
由于(2)式无法求解,因此可以将其转化为
| $ u = {\sum\limits_{i = 1}^N {\left[ {{{\left( {{x_i} - A} \right)}^2} + {{\left( {{y_i} - B} \right)}^2} - {R^2}} \right]} ^2} = \mathit{min}. $ | (3) |
从(3)式中可以看出,u为关于A、B和R的二阶函数,其最小值可以通过如下式子求得:
| $ \frac{{\partial u}}{{\partial A}} = \frac{{\partial u}}{{\partial B}} = \frac{{\partial u}}{{\partial R}} = 0. $ | (4) |
根据(4)式进行求导,并引入新的参数:
| $ C = {R^2} - {A^2} - {B^2}, $ | (5) |
最终可以转化为求A、B、C的线性方程组:
| $ \left\{ \begin{array}{l} 2A\sum {{x_i} + 2B\sum {{y_i}} + CN = \sum {\left( {x_i^2 + y_i^2} \right), } } \\ 2A\sum {x_i^2 + 2B\sum {{x_i}{y_i}} + C\sum {{x_i}} = \sum {\left( {x_i^3 + {x_i}y_i^2} \right), } } \\ 2A\sum {{x_i}{y_i} + 2B\sum {y_i^2} + C\sum {{y_i}} = \sum {\left( {x_i^2{y_i} + y_i^3} \right).} } \end{array} \right. $ | (6) |
通过矩阵运算对线性方程组(6)求解,可以得到A、B、C和R的值.进行圆拟合后得到的边界图像如图 5(c)所示.
3 系统标定和测量结果分析 3.1 系统标定标定的目的是确定被测样品的实际尺寸与采集图像中像素数的量化对应关系,以便将图像中以像素为单位的尺寸转换到物理尺寸上.选用机器视觉中常用的高精度实心圆阵列标定板来对相机进行标定[11].已知标定板中每个圆的标准直径为0.375 mm,选用200万像素的高分辨率工业相机,安装固定好后进行尺寸标定,标定后一个像素的尺寸为8.432 μm.
3.2 测量结果分析为了验证该测量方法的可靠性,用人工和机器视觉两种方法对同一样品外直径进行重复测量[12],测量结果如表 1所示.可以看出,机器视觉的测量精度高于人工测量的精度;此外测量结果的标准差表明,该测量方法比人工测量更加稳定可靠.
|
|
表 1 两种测量方法对同一样品外直径的测量结果 Table 1 The measurement results of outer diameter for the same sample by two methods |
为了验证该测量方法的重复性精度,在机器视觉系统所有条件均保持不变的情况下对同一个端面受损圆柱进行了20次测量,测量数据见表 2.可以看出,d1的重复性误差为0.008 81 mm;d2的重复性误差为0.012 91 mm;d3的重复性误差为0.007 77 mm.圆柱测量误差点线图如图 6所示, 可以看出,3个直径测量值的波动范围都较小,均在±8 μm以内,表明该尺寸测量方法重复性高.

|
图 6 圆柱测量误差点线图 Figure 6 Error points and curves of cylinder measurement |
|
|
表 2 同一样品3个特征尺寸的重复测量结果 Table 2 Repeated measurement results of three feature sizes for the same sample |
为了验证该测量方法的适用性,将该测量方法用于检测表面光滑且无缺陷的其他材料的圆柱端面,最终圆拟合的结果如图 5(d)所示.可以看出, 采用本文提出的测量方法对表面光滑且无损伤的其他材料圆柱同样得到了理想的圆边界,表明该方法不仅能够测量受损圆柱的端面尺寸,同时能够测量表面光滑且无缺陷的管孔圆柱的尺寸,适用性强.但值得注意的是,当受损面积大于50%时,由于准确的边界点过少,可能导致该测量方法失去可信度.
此外,对测量所用时间进行了对比,人工方法测量一个样品外直径的时间约为5 s,而基于Halcon的该尺寸测量方法的时间效率在毫秒量级,能够实现在线实时检测.
由此可见,本文提出的尺寸测量方法具有很高的测量精度和稳定性,测量时间短,且对同类型的圆柱测量具备通用性.
4 结束语通过对受损圆柱进行中值滤波、边界点查找、众数筛选及代数距离法圆拟合,完成了对带孔圆柱多个圆直径尺寸的精确测量,填补了机器视觉测量中关于受损圆柱尺寸精确测量的空白.实验结果表明,本文提出的尺寸测量方法不仅能够精确地测量受损的圆柱,对于标准圆柱同样适用,且重复精度达到±8 μm以内.该测量方法可以满足快速、稳定以及准确性的要求,为表面受损或背景复杂的圆柱内外径测量提供了一种便捷高效的方法.
| [1] |
SHIM J H, NAM T H. Machine vision based automatic measurement algorithm of concentricity for large size mechanical parts[J]. Journal of physics, 2017, 806(1): 012002. (  0) 0) |
| [2] |
IGATHINATHANE C, PORDESIMO L O, BATCHELOR W D. Major orthogonal dimensions measurement of food grains by machine vision using ImageJ[J]. Food research international, 2009, 42(1): 76-84. DOI:10.1016/j.foodres.2008.08.013 (  0) 0) |
| [3] |
杨宗芳, 白剑宇. 基于机器视觉的西林瓶尺寸检测[J]. 计算机测量与控制, 2016, 24(8): 63-66. (  0) 0) |
| [4] |
范帅, 汤绮婷, 卢满怀. 基于机器视觉的轴承内外圈尺寸检测及分类[J]. 自动化仪表, 2016, 37(11): 77-80. (  0) 0) |
| [5] |
张平生, 张桂梅. 基于机器视觉的管孔类零件尺寸测量方法[J]. 机械设计与制造, 2012(12): 139-141. DOI:10.3969/j.issn.1001-3997.2012.12.050 (  0) 0) |
| [6] |
STEGER C, ULRICH M, WIEDEMANN C.机器视觉算法与应用[M].杨少荣, 吴迪静, 段德山, 译.北京: 清华大学出版社, 2008.
(  0) 0) |
| [7] |
SONKA M, HLAVAC V, BOYEL R.图像处理分析与机器视觉[M].艾海舟, 苏延超, 译.北京: 清华大学出版社, 2011.
(  0) 0) |
| [8] |
朱先锋, 潘洪军. 基于Halcon的硒鼓缺陷检测与一维尺寸测量[J]. 吉林大学学报(信息科学版), 2014, 32(3): 308-315. DOI:10.3969/j.issn.1671-5896.2014.03.016 (  0) 0) |
| [9] |
KASA I. A circle fitting procedure and its error analysis[J]. IEEE transactions on instrumentation and measurement, 1976, 25(1): 8-14. (  0) 0) |
| [10] |
祝强, 徐臻. 改进的Kasa算法及其在圆拟合中的精度分析[J]. 测控技术, 2016, 35(1): 30-33. DOI:10.3969/j.issn.1000-8829.2016.01.008 (  0) 0) |
| [11] |
ZHANG Z Y. A flexible new technique for camera calibration[J]. IEEE transactions on pattern analysis and machine intelligence, 2000, 22(11): 1330-1334. DOI:10.1109/34.888718 (  0) 0) |
| [12] |
郑丽丽.基于图像识别的零件几何尺寸检测问题的研究[D].长春: 吉林大学, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10183-2004099808.htm
(  0) 0) |
 2018, Vol. 50
2018, Vol. 50


