2. 西北工业大学 翼型叶栅空气动力国防科技重点实验室 陕西 西安 710072
2. National Key Laboratory of Aerodynamic Design and Research, Northwestern Polytechnical University, Xi'an 710072, China
由于现代民机的摩阻占总阻力的40%~55%, 增大机翼表面的层流区域以期降低摩阻成为设计空气动力学近些年的研究热点[1-3].目前, 自然层流机翼已经在高空长航时无人机[4]、中小型公务机上得到了广泛的应用[5-6], 但针对跨音速的大中型民机尚处于理论与试验阶段, 尤其是后掠效应与实现层流对机翼表面压力分布的要求相互矛盾, 更限制了自然层流技术在中大型民机上的实际应用[7].尽管如此, 自然层流技术依然是提高未来民机性能的发展方向, 而对于大多数在跨声速状态巡航的民机来说, 对跨音速自然层流翼型的深入研究, 必然为真正制造出高性能的层流机翼提供一定的理论依据及技术支持.
维持层流的顺压区长度与激波位置是跨音速自然层流翼型设计的关键, 顺压有利于维持层流, 但过长的顺压区为翼型后缘的压力恢复带来较强的激波, 因此在气动设计中, 需要兼顾这两个关键因素.本文旨在通过压力分布的反设计来协调激波的位置、强度以及顺压区, 并通过考察翼型在不同雷诺数下及不同马赫数下的气动性能, 为跨音速层流翼型的设计提供新方法和新思路.
反设计方法的优点是:在设计人员丰富气动设计经验的基础上, 针对设计要求提出合理压力分布或速度分布, 然后通过求解空气动力学反问题来确定对应的几何外形.近些年发展的特征正交分解(proper orthogonal descomposition, POD)方法是一种高效的数据处理方法, 已经广泛地应用到了诸多领域[8-9], 它通过模态分析的思想提取到数据的主要特征, 用在翼型反设计的优势是在给定目标压力分布和对已知基准翼型形状修改而形成的翼型设计空间的条件下, 通过基于POD的数据重构方法(Gappy POD)就可以反设计得到与给定的目标压力分布相对应的最优翼型形状.
本文采用了一种基于差量采样解的GappyPOD翼型反设计方法, 将该方法成功应用在跨音速层流翼型的反设计中, 针对两种经典的压力分布形态, 进行了精确高效的反设计, 评估了压力分布形态对转捩发生抑制能力的影响.
1 基于差量采样解的Gappy POD方法文献[10]详细介绍了POD方法, Gappy POD方法是POD方法用于已知系统中的填补某一缺失数据的元素时的变形, 通过在系统中获取合适的足够数量采样解(快照样本), 在采样解的基础上提取此系统的基模态, 采用Gappy POD方法[11]可以对该系统中任一缺失数据的元素进行精确填补.
首先定义向量矩阵G及其对应的“标签”向量矩阵n.“标签”向量矩阵n用来识别向量矩阵G中的元素是否缺失.若不缺失nik=1, 若缺失nik=0, 其中nik对应于向量矩阵G中第k个不完全数据向量中的第i个元素的“标签”.假设{φi}i=1m是通过POD方法求得的已知采样集{ui}i=1p的基向量[12].g表示该系统中待填补的向量, 由已经得到的m个POD基来填补近似向量
| $ \mathit{\boldsymbol{\tilde g}} = \mathop \sum \limits_{i = 1}^m {\alpha _i}{\mathit{\boldsymbol{\varphi }}^i}, $ | (1) |
并通过求解Ma=f线性方程组来确定αi, 其中:Mij=(φi, φi)n; fi=(g, φi)n.近似向量
本文研究了一种基于差量采样解的Gappy POD方法, 对原始采样解的结构重新定义, 重新定义采样解集合为Δu=[(u1-u), (u2-u), …, (up-u)], 其中:u表示采样解的平均值; ui|i=1p表示第i个采样解.通过上述方法求解Δu的基向量及系数, 那么最终修正向量可表示为
基于差量采样解Gappy POD方法构建翼型反设计方法分4步:1)根据反设计需要定义合理的设计空间, 利用计算流体力学(computational fluid dynamics, CFD)方法获得设计空间中样本的解, 以此构造快照矩阵; 2)对生成的快照矩阵按文献[10]中的方法求解基向量Φ, 并计算每个基向量的能量; 3)根据所求解问题的需要对低能量模态进行适当截断, 形成对应设计空间的降阶子空间; 4)利用降阶子空间对目标缺失数据进行数据重构.
2.1 CFD数值模拟技术采用有限体积法求解雷诺平均Navier-Stokes方程, 其积分形式为
| $ \begin{array}{l} \frac{{\partial \rho \gamma }}{{\partial t}} + \frac{{\partial \rho \gamma {u_i}}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}[(\mu + \frac{{{\mu _t}}}{{{\sigma _\gamma }}})\frac{{\partial \gamma }}{{\partial {x_i}}}] + {c_{a1}}\rho S{F_{{\rm{length}}}}\\ {F_{{\rm{onset}}}}^{{\rm{0}}{\rm{.5}}}{\gamma ^{0.5}}(1 - {c_{e1}}\gamma ) - {c_{a2}}\rho \mathit{\Omega }{F_{{\rm{turb}}}}\gamma ({c_{e2}}\gamma - 1). \end{array} $ |
引进变量
| $ \begin{array}{l} \frac{{\partial \rho \overline {{{{\mathop{\rm Re}\nolimits} }_{\theta t}}} }}{{\partial t}} + \frac{{\partial \rho \overline {{{{\mathop{\rm Re}\nolimits} }_{\theta t}}} {u_i}}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}[{\sigma _{\theta t}}(\mu + {\mu _t})\frac{{\partial \overline {{{{\mathop{\rm Re}\nolimits} }_{\theta t}}} }}{{\partial {x_i}}}]\\ + {c_{\theta t}}\frac{\rho }{{{t_{{\rm{scale}}}}}}(\overline {{{{\mathop{\rm Re}\nolimits} }_{\theta t}}} - \overline {{{{\mathop{\rm Re}\nolimits} }_{\theta t}}} )(1 - {F_{\theta t}}). \end{array} $ |
本文的快照矩阵是由翼型数据和压力分布构成的, 每一个翼型数据和对应压力分布组成快照矩阵的列向量, 通过在基准翼型的基础上加入扰动量形成多个快照, 依次构成翼型反设计的设计空间.
对于基准翼型的扰动是通过ΔCST翼型参数化方法实现的, 对于在采用类函数变化(class function/shape function transformation, CST)参数化[14]翼型时, 定义
| $ \zeta \left( \psi \right)' = \zeta \left( \psi \right) + {\psi ^{0.5}}\left( {1 - \psi } \right)\mathop \sum \limits_{i = 0}^n \Delta {A_i}{K_i}{\psi ^i}{\left( {1 - \psi } \right)^{n - i}}, $ | (2) |
引入定义
| $ \Delta \zeta \left( \psi \right) = {\psi ^{0.5}}\left( {1 - \psi } \right)\mathop \sum \limits_{i = 0}^n \Delta {A_i}{K_i}{\psi ^i}{\left( {1 - \psi } \right)^{n - i}}, $ | (3) |
因此, 由式(2)和(3)得到ζ(ψ)'=ζ(ψ)+Δζ(ψ).
2.3 反设计方法本文的反设计过程为:1)对快照向量进行POD分解, 得到基向量, 用基向量逼近目标压力分布得到反设计翼型; 2)以反设计得到的翼型为初始翼型, 再进行扰动得到扰动翼型, 加上反设计得到翼型, 进行CFD分析获得快照向量, 将这些快照向量加入原始快照向量库, 如不满足条件, 重复第1、2步; 3)满足收敛条件, 结束.
3 跨音速自然层流翼型反设计本节主要通过两种不同的压力分布形态反设计得到气动外形, 进而在不同雷诺数及马赫数下分析压力分布形态对转捩发生的抑制能力, 同时研究其与阻力发散特性的协调性.
ΔCST参数化上下表面各15个设计变量, 共30个设计变量, 这30个设计变量依次取指定的变量上下限, 共产生60个新翼型, 加上基准翼型共61个.采用文中构建的
对生成的61个翼型形状在如下状态进行CFD计算, 获得采样解:Ma∞=0.74;CL=0.53;Re=6.0×106; 飞行环境湍流度Tu=0.2%;湍流黏性比为10.
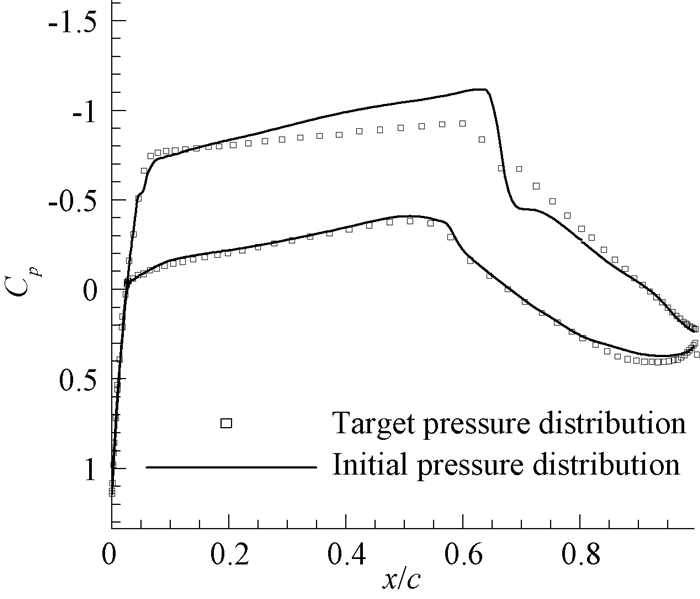
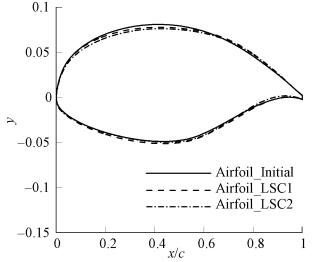
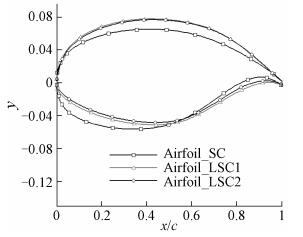
图 1为目标压力分布反设计结果, 可以看出来, 本文的反设计方法对于不同的压力分布都可以得到令人满意的结果, 记此次反设计得到的翼型为AirFoil_LSC2.图 2为初始基准翼型与两个反设计翼型的比较.选取一个设计状态为Ma∞=0.74, CL=0.575, Re=2.0×107, 阻力发散特性较好的传统超临界翼型与上述跨音速自然层流翼型进行对比, 标号分别为:超临界翼型(Airfoil-SC)、Airfoil-LSC1、Airfoil-LSC2, 如图 3所示.
|
图 1 Airfoil-LSC2反设计压力分布与目标压力分布对比 Fig. 1 The pressure distribution comparison between the inverse-design result and the Airfoil-LSC2 one |
|
图 2 初始翼型与两个反设计翼型比较 Fig. 2 The comparison between the initial airfoil and the two inverse-design ones |
|
图 3 超临界翼型与反设计翼型比较 Fig. 3 The comparison between the supercritical airfoil and the inverse-design ones |
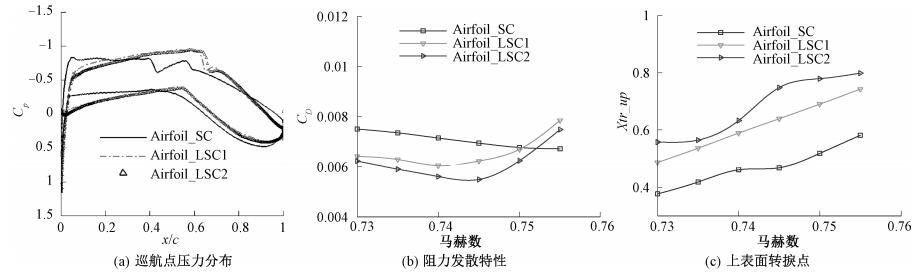
数值模拟3个翼型在雷诺数分别为600万、800万、900万的气动性能.图 4~8给出了各个翼型之间压力分布和阻力发散特性以及层流区随马赫数、雷诺数大小的变化对比.可以看出在雷诺数低于800万时, 随着马赫数的增大, 激波位置后移, 同时上表面转捩位置后移.Airfoil-SC翼型从压力分布上看, 翼型上表面没有明显的顺压梯度, 但依然可以依靠上表面的弱激波维持40%左右的层流区域, 并且层流区域是随着激波位置不断向翼型后缘移动.对于层流理念设计的Airfoil-LSC1和Airfoil-LSC2来说, 翼型上表面层流区域的变化基本与激波位置变化相一致; 从下表面的转捩位置与压力分布的比较来看, 翼型下表面的层流区域的维持是需要压力分布顺压区域的, 顺压区域越长, 层流区越长.从不同雷诺数下的阻力发散特性比较可以看出, 雷诺数在800万以下, 层流理念设计的跨音速层流翼型在层流区大小、阻力系数大小方面有着无可替代的优势, 但阻力发散特性要低于传统超临界翼型, 这是因为自然层流翼型由于顺压梯度的存在, 随着马赫数的增大, 激波不断增强后移, 为激波后翼型压力恢复带来过大的逆压梯度, 因此带来较大的激波阻力(波阻), 过大的波阻削弱了层流摩阻降低的效益, 总阻力的优化在高马赫数时不是特别明显.
|
图 4 600万雷诺数气动特性及层流区比较 Fig. 4 The comparison of aerodynamic performance and laminar region at 6 million Reynolds number |
|
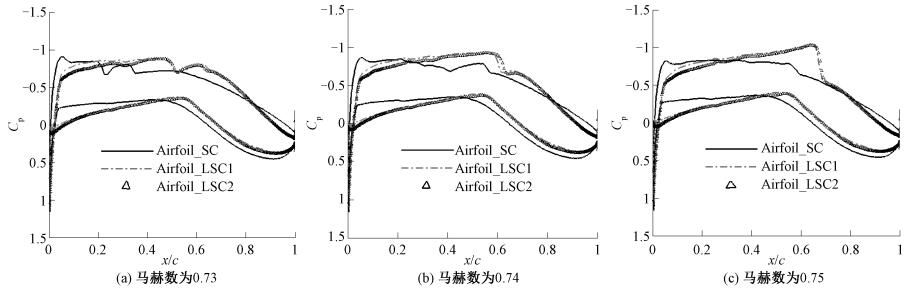
图 5 800万雷诺数压力分布比较 Fig. 5 The comparison of pressure distribution at 8 million Reynolds number |
|
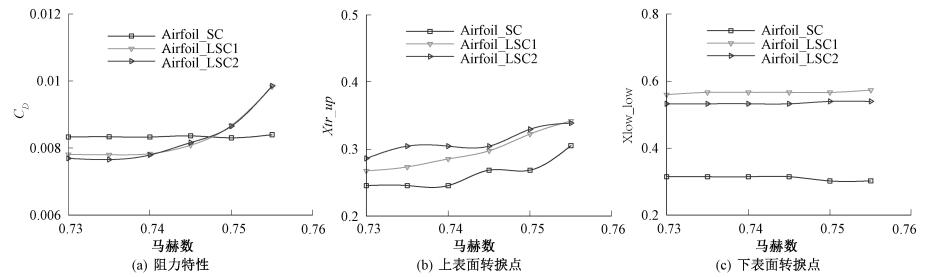
图 6 800万雷诺数气动特性及层流区比较 Fig. 6 The comparison of aerodynamic performance and laminar region at 8 million Reynolds number |
|
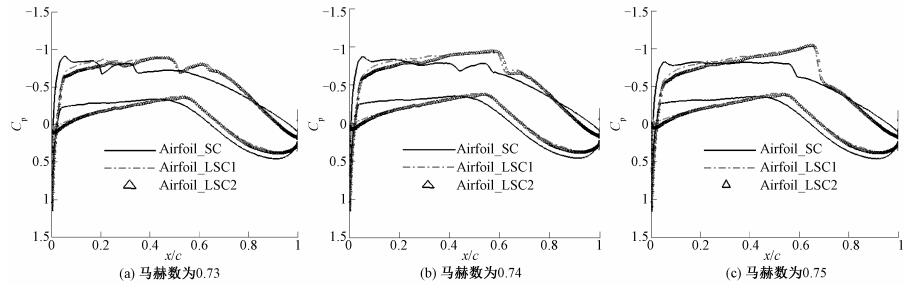
图 7 900万雷诺数压力分布比较 Fig. 7 The comparison of pressure distribution at 9 million Reynolds number |
|
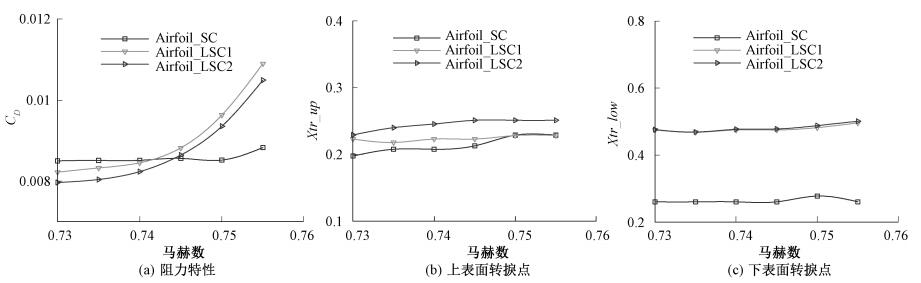
图 8 900万雷诺数气动特性及层流区比较 Fig. 8 The comparison of aerodynamic performance and laminar region at 9 million Reynolds number |
从800万雷诺数及900万雷诺数翼型气动特性的比较可以看出, Airfoil_LSC1、Airfoil_LSC2翼型上表面压力分布在20%~40%弦长区域出现了微小的波动(逆压梯度), 这个微小的波动导致了转捩的发生; 下表面的层流区域的变化基本与顺压区吻合, 层流理念设计的翼型, 可以维持层流区域到60%弦长的位置, 微小的压力分布波动并未影响层流区域的维持.从800万雷诺数之下的翼型压力分布也可以观察到这个小波动, 但在800万雷诺数之下, 这个微小的逆压梯度并未造成转捩的发生, 转捩的发生与激波有很大的关系, 但超过800万雷诺数后, 翼型上表面的转捩对顺压梯度要求变得更加苛刻, 需要对压力分布进行更细致的设计.从800万及900万雷诺数的阻力发散特性可以看出, 在低马赫数时, 层流设计的翼型依然能带来气动效率的提高, 但在马赫数大于0.75时, 由于翼型前部顺压梯度带来过大压力恢复梯度, 陡增了波阻, 降低了翼型的阻力发散特性.
综上, 跨音速自然层流设计的翼型典型的问题是在中高雷诺数下阻力发散特性明显下降, 对顺压区域要求更加严苛; 与传统的超临界翼型对比表明, 在中低等雷诺数下顺压设计的层流翼型阻力特性明显, 阻力发散特性不是很差, 转捩区域与激波位置有很大关系, 微小的逆压梯度并未造成转捩的发生; 在中高等雷诺数下, 抑制转捩的发生需要更严苛的顺压梯度, 阻力发散特性变得更差, 在这种情况下, 可以考虑采用严苛的弱顺压梯度、短顺压长度和及早的弱激波恢复等设计理念进行设计.
4 结论本文基于差量采样解GappyPOD的翼型反设计方法, 对跨声速自然层流翼型进行了反设计, 通过分析设计结果可得到以下结论:
1) 层流理念设计的跨音速翼型在800万雷诺数之下, 层流区域的维持与激波位置有很大的关系, 对顺压区域的要求不太明显, 小的逆压梯度并未造成翼型上下表面转捩的发生; 马赫数小于0.75时, 气动效率明显优于传统的超临界翼型; 马赫数大于等于0.75时, 由于波阻的陡增, 降低了层流带来的气动效率的增益, 因此若考虑阻力发散特性, 需要控制翼型上表面的层流区域, 牺牲设计点的气动效率, 以带来相对较好的阻力发散特性.
2) 层流理念设计的跨音速翼型在雷诺数大于800万时, 层流区域的维持对顺压梯度要求变得严苛, 微小的逆压梯度会造成翼型上表面转捩的发生, 需要对逆压梯度进行更细致的设计, 阻力特性随着马赫数的增大变得更差, 在这种情况下, 需要考虑采用严苛的弱顺压梯度、短顺压长度和及早的弱激波恢复等设计理念进行设计.
| [1] |
STURDZA P. An aerodynamic design method for supersonic natural laminar flow aircraft[D]. Stanford: Stanford University, 2004. https://www.researchgate.net/publication/252824886_An_aerodynamic_design_method_for_supersonic_natural_laminar_flow_aircraft
(  0) 0) |
| [2] |
乔志德. 自然层流超临界翼型的设计研究[J]. 流体力学实验与测量, 1998, 12(4): 23-30. (  0) 0) |
| [3] |
ZHANG Y, FANG X, CHEN H, et al. Supercritical natural laminar flow airfoil optimization for regional aircraft wing design[J]. Areospace science and technology, 2015, 43: 152-164. DOI:10.1016/j.ast.2015.02.024 (  0) 0) |
| [4] |
黄江涛.飞行器气动外形优化设计方法及应用研究[D].西安: 西北工业大学, 2011.
(  0) 0) |
| [5] |
MISSELWITZ F, BERKOWITZ S D, PERZBORN E. Design and development of the Honda Jet[J]. Journal of aircraft, 2005, 42(3): 755-764. DOI:10.2514/1.12268 (  0) 0) |
| [6] |
李权, 段卓毅, 张彦军. 民用飞机自然层流机翼研究进展[J]. 航空工程进展, 2013, 4(4): 399-406. DOI:10.3969/j.issn.1674-8190.2013.04.002 (  0) 0) |
| [7] |
朱自强, 陈迎春, 王晓璐, 等. 现代飞机的空气动力设计[M]. 北京: 国防工业出版社, 2011.
(  0) 0) |
| [8] |
LEGESLEY P, ALONSO J. Investigation of non-linear projection for POD based reduced order models for aerodynamics[C]//39th Aerospace Sciences Meeting and Exhibit. Reno, NV, 2001: 926.
(  0) 0) |
| [9] |
BUITHANH T, DAMODARAN M, WILLCOX K. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition[J]. AIAA Journal, 2004, 42(8): 1505-1516. DOI:10.2514/1.2159 (  0) 0) |
| [10] |
刘浩, 徐敏, 叶茂. 基于特征正交分解的跨声速流场重构和翼型反设计方法研究[J]. 空气动力学学报, 2012, 30(4): 539-545. DOI:10.3969/j.issn.0258-1825.2012.04.019 (  0) 0) |
| [11] |
段焰辉, 蔡晋生, 刘秋洪. 基于代理模型方法的翼型优化设计[J]. 航空学报, 2011, 32(4): 617-627. (  0) 0) |
| [12] |
LANGTRY R B. A correlation based transition model using local variables—part Ⅱ: test cases and industrial applications[J]. Journal of turbomachinery, 2006, 128(3): 423-434. DOI:10.1115/1.2184353 (  0) 0) |
| [13] |
MENTER F R, LANGTRY R B, LIKKI S R. Transition modelling for general purpose CFD codes[J]. Flow turbulence and combustion, 2006, 77(1/4): 277-303. (  0) 0) |
| [14] |
KULFAN B M. Universal parametric geometry representation method[J]. Journal of aircraft, 2008, 45(1): 142-158. DOI:10.2514/1.29958 (  0) 0) |
 2019, Vol. 51
2019, Vol. 51

