在当前信息化时代,随着物联网和云计算的日益发展,生物医学、网络社交、网络信息追踪等许多领域内的数据信息量呈指数增长,并且越来越多的信息被连接起来,以图形形式存储在各个领域[1-2]。由于这些数据信息规模和计算的日益复杂化,给现代图处理系统提出了巨大的挑战。图计算是处理各种数据信息的常用手段之一[3-5],不同压缩格式的数据信息会对图计算问题产生不同的影响,如何选择合适的图数据压缩格式以达到最佳性能需求是一个不可避免的问题。
图可以表示不同实体间复杂的依赖关系[6-7]。图数据可以由不同的压缩格式来表示,不同的图数据压缩格式有不同的表示和复杂度。当前很多研究采用不同的图算法解决方案来提高图数据处理时的性能和效率,但是由于图算法的性能效率由不同图数据压缩格式中边和顶点的处理来确定,在执行过程中,程序的行为不仅会随时间变化而变化,更重要的是不同的图数据压缩格式复杂度会对图算法处理产生不同的影响,因此有效地应用图算法是一项艰巨的任务[8-9]。所以在图算法中如何快速选择合适的数据压缩格式以达到预期的最佳性能是本文的一个重要研究问题[10]。本文针对BFS算法处理不同压缩格式图数据时的性能指标进行特性化分析,为不同条件下应该选择不同压缩格式的数据集提供了依据。
图计算中有5种数据格式:双压缩稀疏列(doubly compressed sparse column,DCSC)[11-13];压缩稀疏列(compressed sparse column,CSC)[14];压缩稀疏行(compressed sparse row,CSR)[15-16];坐标表示(coordinate,COO)[17];独立稀疏列压缩(compressed sparse column independently,CSCI)[18-19]。将这5种数据压缩格式作为遍历类应用广度优先搜索(breadth first search,BFS)算法的输入数据格式进行运行性能事件统计,分析基于BFS算法处理不同压缩格式时的性能指标,性能指标参数包括每周期指令数、数据移动量、功耗、各级cache缺失率以及执行时间等,不同数据压缩格式在BFS算法处理中提供了不同的性能指标。
1 算法及压缩格式分析 1.1 BFS算法广度优先算法是一种常见的图搜索算法,以一种系统的方式搜索图数据中的所有顶点,计算从源点到所有其余顶点所需要遍历的最小边数值,特别是在求解最短路径或者最短步数等问题上有很多的应用[20]。BFS算法的基本思想是给每个活动顶点分配一个深度depth,此深度代表从根节点s到其他所有顶点所需要遍历的最小边数。初始化时,根节点的深度设置为0,并标记为活动状态,将其他活动顶点的深度设置为无穷远,在移动到下一级相邻顶点之前首先对相邻顶点进行探索,在t次迭代后每个顶点与活动顶点的深度公式为[21]depth(v)=min(depth(v), t+1)。若更新导致深度发生变化,则顶点到下一次迭代中变为活动状态。BFS算法伪代码如下。
输入:Graph G(V, E),源顶点s。
输出:dis[n],从源顶点s到其他各个顶点的最短路径长度。
For all n∈V do
d[n]=∞; //顶点n的距离
d[s]=0; //源顶点s的距离
le=1;
state[n]=0; //顶点n的活动状态
state[s]=1; //源顶点s的活动状态
queue < —s; //源顶点s入队
while (queue!=φ) do
for (state[v]=0 & & v是s的邻近点) do
queue < —v;
state[v]=1;
d[v]=min(d[v], le);
le=le+1:
s← v。
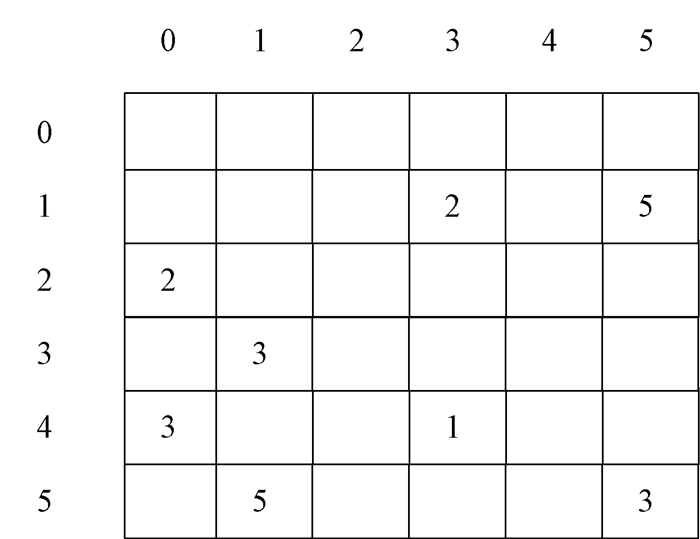
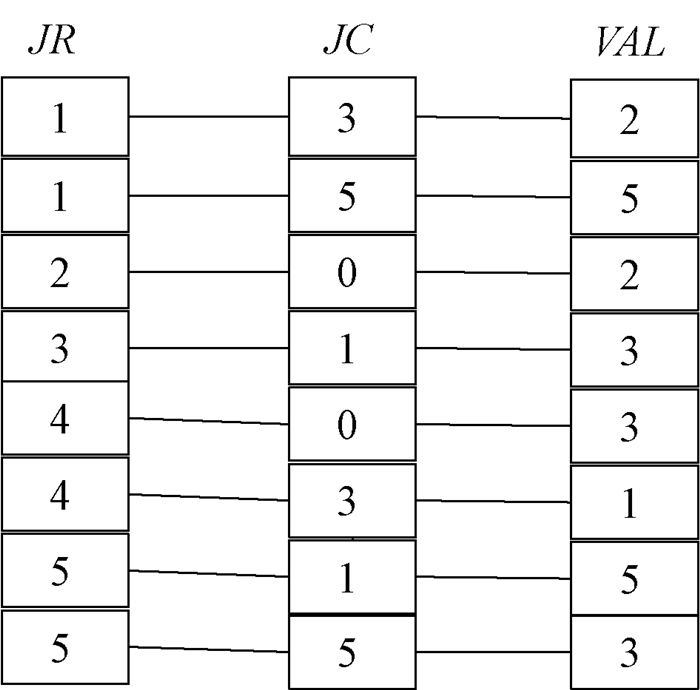
1.2 五种压缩格式分析(1) DCSC压缩格式是CSC压缩稀疏列的拓展。该压缩格式可以有效存储大规模稀疏矩阵[7]。主要是使用JC、CP、JR、VAL 4个数组来存储数据[12-13]。将图 1所示的原始矩阵用DCSC压缩格式表示,表示结果如图 2所示。其中:JC是至少有一个非零元素列的列索引;CP是列指针,可以访问非零元素的列索引;JR是非零元素的列索引中的非零元素相对应的行索引;VAL是列索引和行索引对应的数值。
|
图 1 原始矩阵 Fig. 1 The original matrix |

|
图 2 原始矩阵的DCSC压缩格式 Fig. 2 DCSC compression format of the original matrix |
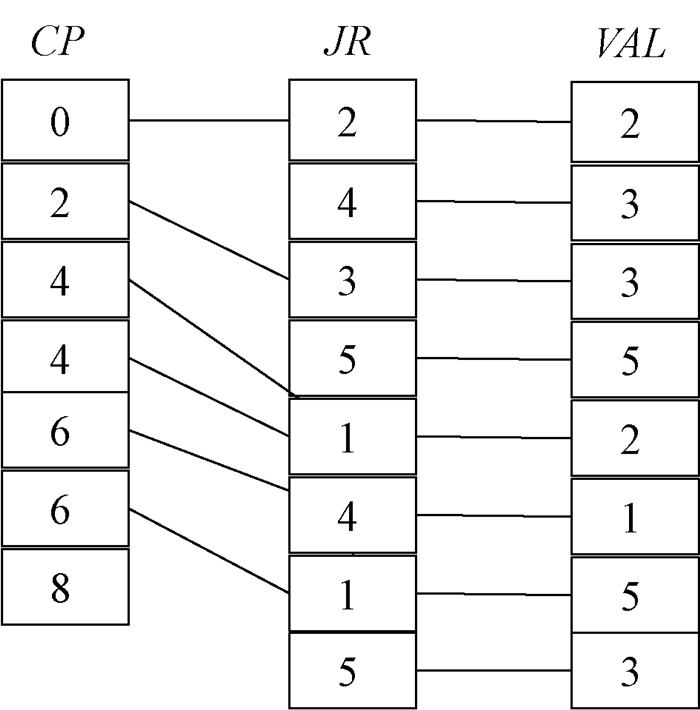
(2) COO压缩格式按坐标表示每一个非零元素,可以直接定位。用3个数组JR、JC、VAL分别表示非零元素所在的行号、列号以及非零元素的数值[17]。原始矩阵使用COO格式表示如图 3所示。
|
图 3 原始矩阵的COO压缩格式 Fig. 3 COO compression format of the original matrix |
(3) CSC压缩格式主要是使用JR、CP、VAL 3个数组来存储数据[14]。原始数据对应的CSC压缩格式表示如图 4所示,其中:JR是非零元素列中的非零元素所对应的行索引;CP是列偏移值,表示某一非零列的第1个非零元素在当前列之前的非零元素的个数;VAL是行索引对应的数值。
|
图 4 原始矩阵的CSC压缩格式 Fig. 4 CSC compression format of the original matrix |
(4) CSR压缩格式按行压缩,与CSC相似,主要是使用CP、JC、VAL 3个数组来存储数据[15-16]。原始数据对应的CSR压缩格式表示如图 5所示,其中:JR是至少有一个非零元素行中的非零元素所对应的列索引;CP是行偏移值,表示某一非零行的第1个非零元素在当前行之前的非零元素的个数;VAL是列索引对应的非零元素值。

|
图 5 原始矩阵的CSR压缩格式 Fig. 5 CSR compression format of the original matrix |
(5) CSCI压缩格式中每列独立压缩后的图数据包括列标识ioc、索引index和数值value,由列标识ioc指示index其余位与数值value的含义。当ioc为“1”,index表示为列索引,value表示邻接稀疏矩阵中该列的非零元素数目; 当ioc为“0”,index表示为当前列的非零元素所在的行号,value表示稀疏邻接矩阵中对应的非零元素值[18-19]。基于图 1原始矩阵,CSCI的压缩结果为(1, 0, 2), (0, 2, 2),(0, 4, 3),(1, 1, 2),(0, 3, 3),以此类推。
2 实验环境与性能指标定义 2.1 硬件平台性能事件统计的运行平台选为4核8线程Intel(R) Core(TM) i5-7200U CPU,该CPU具有6 MB的三级缓存、2.50 GHz时钟频率、4 GB内存,并运行linux内核4.15.0系统,perf性能分析工具,所有代码均使用Dev-cpp.5.11版本进行编译和运行。
2.2 数据集选取本文所使用的实验数据选自斯坦福大学的SNAP (Stanford Network Analysis Project)数据集中Collaboration net-works的ca-AstroPh(http://snap.stanford.edu/data/ca-Astro-Ph.html),以及Social networks的soc-Epinions1(http://snap.stanford.edu/data/soc-Epini-ons1.html),数据的顶点具体信息包括数据集的顶点个数、边数以及内存占用情况如表 1所示。
|
|
表 1 实验所选的数据集 Tab. 1 Data sets selected in the experiment |
本次实验采用的分析工具是基于Linux系统的虚拟机中自带的系统性能分析工具perf[22],通过perf分析工具,应用程序可以利用pmu、tracepoint和内核中的特殊计数器来进行性能分析统计,不仅可以分析指定应用程序的性能问题,也可以分析内核的性能问题。
2.4 性能指标定义分析5种压缩格式的数据对BFS算法的影响。分析的性能和指标参数如下:执行时间(exec.time)、数据移动量(data.mv)、计算量(compute)、每周期指令数(IPC)、各级cache的缺失率(MPKI)、功耗(energy)等指标进行分析比较。
(1) 执行时间。任务的执行时间是从开始执行到完成目标任务所占用的时间,单位为ms。不同压缩格式中每条边的执行时间计算公式为
| $ exec. \;time = tota\_exec\_time/edges _{\circ} $ |
(2) 数据移动量。受延迟和带宽的限制,同一数据集的不同压缩格式下数据移动量是不同的,分析程序性能指标时数据移动量也是一个重要指标,本文中数据移动量表示不同压缩格式下每条边的数据移动量。计算公式是
| $ data. \; m v=( load+store ) / edges _{\circ} $ |
(3) 计算量。在程序执行中,对于同一个算法处理同一个数据集的不同压缩格式时,计算量也是影响性能指标的重要因素之一。不同压缩格式下,数据集处理时计算量的公式为
| $ compute =( instructions-load-store-branch ) / N_{edges } \circ $ |
(4) 每周期指令数。每周期指令数也称IPC(instruction per clock),是一个基本性能指标,是平均每一时钟周期所执行的指令数,计算公式为
| $ I P C= instructions/cycles _{\circ} $ |
(5) 各级cache的缺失率。MPKI(misses per kilo instructions)是一个用来分析cache性能的通用指标,造成cache缺失的因素有数据的大小、cache的映射策略等,因此很难从理论上预估cache的缺失率而导致的时间损耗。利用perf分析工具可以更真实地观察到cache缺失率的情况。用cache_miss表示cache丢失率,instructions表示使用指令数,各级cache的缺失率计算公式为
| $ M P K I=( cache\_misses * 1000) / instructions _{\circ} $ |
(6) 功耗。功耗是图算法处理数据时的重要衡量性能的指标之一,功耗越小越有利于图计算的发展。功耗的计算公式为
| $ Energy =( power/energy - all ) / edges _{\circ} $ |
(7) 皮尔森相关系数(PCC)。皮尔森相关系数(Pearson correlation coefficient,PCC)是一种线性相关系数,是用来反映两个变量线性相关程度的统计量[23]。相关系数用r表示,描述的是两个变量间线性相关强弱的程度,其中n为样本量,r的绝对值越大表明相关性越强。皮尔森相关系数的计算公式为
| $ r=\sum\limits_{i=1}^{n}\left(\left(X_{i}-\bar{X}\right) / \delta X\right)\left(\left(Y_{i}-\bar{Y}\right) / \delta Y\right) /(n-1)_{\circ} $ |
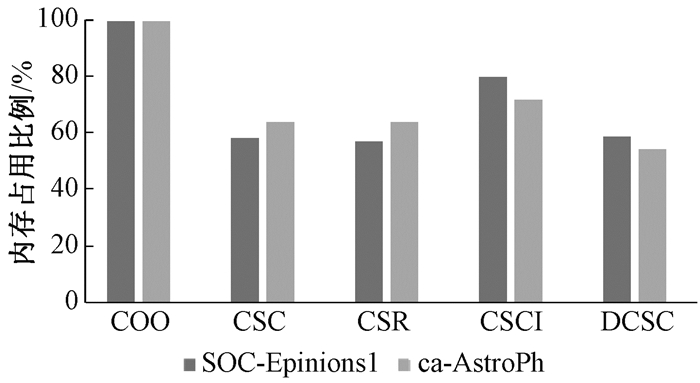
两种不同的数据集在不同压缩格式下的内存占用情况如图 6所示。根据图中统计结果:COO压缩格式占用的内存最大,这是因为COO压缩格式是与原始数据最相近的压缩格式,将原始数据的所有边和顶点的信息以最直接的坐标方式,利用3个数组输出,对数据的压缩程度最小,占用内存较大;DCSC压缩格式占用的内存最小,对数据的压缩程度最大,这是因为DCSC输出4个压缩数组,分别是压缩后的非零列、非零列的偏移值、非零列元素值对应的非零行以及非零元素。若是原始数据足够稀疏,则经过DCSC压缩格式输出后的非零列及非零列偏移两个数组都会进行很大程度的压缩,因此DCSC压缩格式输出数据占用的内存比其他4种压缩格式会更小;CSC和CSR两种压缩格式的输出均是包含偏移值、列/行索引值和权值的3个数组,当稀疏矩阵中的行数和列数相近时,两种压缩格式输出的数据占用的内存大小也趋于相近,所以CSR与CSC两种压缩结果较接近,从图中可以看出CSR与CSC两种压缩格式占用内存相对较小,对数据的压缩程度较大;CSCI压缩格式保证每列独立压缩后的数据,包括列号及该列的非零元素个数、非零元素所在的行号以及非零元素的属性值对应存储全部输出,占用内存空间比DCSC、CSC和CSR大。
|
图 6 两种数据集五种压缩格式下的内存占用情况(归一化到COO格式) Fig. 6 Required memory of two data sets in five compression formats (normalized to COO format) |
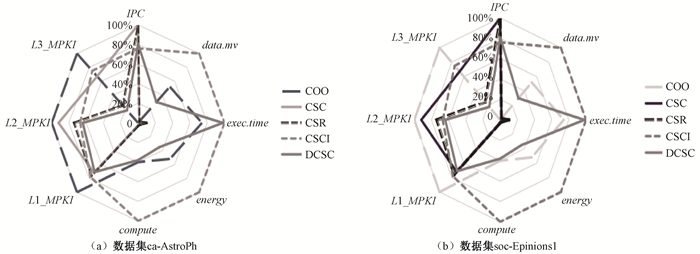
如图 7所示,本文通过雷达图的形式显示了COO、CSC、CSR、DCSC以及CSCI 5种不同压缩格式在BFS算法处理中的性能特性并对其进行分析。雷达图中性能参数包括每个压缩格式实现的ipc、数据移动量、执行时间、功耗以及L1、L2和L3三级数据缓存MPKI。其中,每个指标中度量最大的值为比较标准并视为100%。
|
图 7 两种数据集下五种压缩格式的性能指标 Fig. 7 Performance indicators of five compression formats in two data sets |
(1) 执行时间。两种数据集在不同的压缩格式下每条边的执行时间如表 2所示。可以看出CSCI格式的数据边的执行时间最长,而CSC与CSR压缩格式的数据执行的时间最为接近,两者的边的执行时间最短。在数据量足够大并且数据足够稀疏的时候,DCSC压缩格式的执行时间会越来越短;在数据量较小的时候,DCSC对数据的压缩程度不是很大,因此DCSC的执行时间较长。对于遍历类BFS应用而言,在考虑选择边的执行时间时,优先选择CSC压缩格式或者CSR压缩格式作为数据集的输入格式。
|
|
表 2 两种数据集在不同压缩格式下的执行时间 Tab. 2 The execution time of the two data sets in different compression formats |
(2) 数据移动量。两种数据集在不同压缩格式下每条边的数据移动量如表 3所示。对比5种不同的压缩格式,可以发现CSR压缩格式的数据移动量小于其他4种格式,CSC和CSR的数据移动量接近,数据移动量均偏小。COO、CSCI和DCSC 3种压缩格式的数据移动量相对较大, CSCI压缩格式的数据移动量最大。因此对于遍历类应用而言,在考虑边的数据移动量时,应选择CSR压缩格式作为数据集的输入格式。
|
|
表 3 两种数据集在不同压缩格式下每条边的数据移动量 Tab. 3 The data movement of each side of the two data sets in different compression formats |
(3) 计算量。表 4列出了两种数据集在不同压缩格式下每条边的计算量。可以看出CSR与CSC压缩格式的计算量相对较小,其中CSR压缩格式的计算量最小,而COO与CSCI压缩格式的计算操作相对较多,会成为BFS算法处理时的性能阻碍。因此在优先考虑计算量的情况下,遍历类应用BFS应优先选择CSR压缩格式作为数据集的输入结构,可达到性能最优。
|
|
表 4 两种数据集在不同压缩格式下每条边的计算量 Tab. 4 The calculation amount of each side of the two data sets in different compression formats |
(4) 各级cache的缺失率。两种数据集在5种压缩格式的L1、L2和L3级cache MPKI分别如表 5、表 6和表 7所示。可以看出,在所有压缩格式下,L1级cache MPKI整体大于L2级cache MPKI和L3级cache MPKI;L2级cache MPKI平均小于2,L3级cache MPKI均小于1,综合各级cache MPKI结果对比分析,可以发现COO压缩格式的缺失率最高,DCSC压缩格式具有更小的各级cache MPKI,缺失率低可有效减少时间损耗,因此针对有效提高遍历类应用的缓存命中率可以优先选择DCSC压缩格式。
|
|
表 5 两种数据集在不同压缩格式下L1级cache MPKI Tab. 5 L1 level cache MPKI in different compression formats for the two data sets |
|
|
表 6 两种数据集在五种压缩格式下L2级cache MPKI Tab. 6 L2 level cache MPKI in five compression formats of two data sets |
|
|
表 7 两种数据集在五种压缩格式下L3级cache MPKI Tab. 7 L3 level cache MPKI in five compression formats of two data sets |
(5) 功耗。表 8所示的是5种压缩格式的两种数据集在遍历类算法BFS处理时每条边的功耗。可以看出CSR和CSC压缩格式的数据功耗相对较小,其中CSR功耗最小,CSR压缩格式输出3组数据,输出了行偏移值、每一行非零元素对应的列号以及非零元素的属性值,所以在BFS算法搜索时可以快速找到需要搜索定位的活动顶点与活动顶点连接的点,有效降低了功耗。CSCI压缩格式消耗的能量最大。因此对于遍历类应用BFS而言,减少功耗可优先选择CSR压缩格式。
|
|
表 8 两种数据集在不同压缩格式下每条边的功耗 Tab. 8 The power consumption of each side of the two data sets in different compression formats |
(6) PCC分析。本文将得到的不同性能指标数据继续进行相关系数(PCC)的相关性分析,分别对性能相关与能量相关进行具体分析,如表 9所示。相关系数的取值一般在-1到1之间,若r>0表示正相关,即一个变量随着另一个变量的变化而同方向变化;若r < 0则表示负相关,即一个变量随另一个变量从相反方向变化,r的绝对值越大表示相关性越强。可以看到,各级缓存缺失率总体上与性能和功耗呈现正相关,当性能和能量加强时缺失率也加强,并且IPC、exec.time、data.mv、compute、energy指标与性能和能量密切相关。
|
|
表 9 性能和能量与不同指标的相关性 Tab. 9 The correlation of performance and energy with different indicators |
本文通过对两种数据集的五种压缩格式(COO、CSC、CSR、DCSC、CSCI)在BFS算法上的性能分析发现:处理5种不同压缩格式时,应当优先选择CSR和CSC压缩格式,能有效减少算法的执行时间、计算量、数据移动量以及有效减少功耗;当考虑数据结构算法的应用缓存命中率和内存容量时,可优先选择DCSC压缩格式作为BFS的输入格式,可以有效减少内存使用情况并提高命中缓存率。在进行遍历类应用算法时,可以根据不同的应用环境、性能需求和软硬件条件选择不同的压缩格式,进而可以有效地应对实际需求以提高图计算加速器的性能。
| [1] |
SONG S, LIU X, WU Q Z, et al. Start late or finish early: a distributed graph processing system with redundancy reduction[EB/OL]. [2020-03-10]. https://arxiv.org/abs/1805.12305.
(  0) 0) |
| [2] |
SONG S, LI M, ZHENG X N, et al. Proxy-guided load balancing of graph processing workloads on heterogeneous clusters[C]//45th International Conference on Parallel Processing (ICPP). Philadelphia: IEEE, 2016: 77-86.
(  0) 0) |
| [3] |
MATAM K K, KOO G, ZHA H P, et al. GraphSSD: graph semantics aware SSD[C]//Proceedings of the 46th International Symposium on Computer Architecture. Phoenix: ACM, 2019: 116-128.
(  0) 0) |
| [4] |
SEGURA A, ARNAU J M, GONZÁLEZ A. SCU: a GPU stream compaction unit for graph processing[C]//Proceedings of the 46th International Symposium on Computer Architecture. Phoenix: ACM, 2019: 424-435.
(  0) 0) |
| [5] |
MUKKARA A, BECKMANN N, ABEYDEERA M, et al. Exploiting locality in graph analytics through hardware-accelerated traversal scheduling[C]//51st Annual IEEE/ACM International Symposium on Microarchitecture (MICRO). Fukuoka: IEEE, 2018: 1-14.
(  0) 0) |
| [6] |
MALEWICZ G, AUSTERN M H, BIK A J C, et al. Pregel: a system for large-scale graph processing[C]//Proceedings of the 2010 international conference on Management of data-SIGMOD'10. Indianapolis: ACM, 2010: 135-146.
(  0) 0) |
| [7] |
LOW Y, GONZALEZ J, KYROLA A, et al. Distributed GraphLab: a framework for machine learning in the cloud[EB/OL]. [2012-04-26]. https://arxiv.org/abs/1204.6078.
(  0) 0) |
| [8] |
WU Q Z, FLOLID S, SONG S, et al. Invited paper for the hot workloads special session hot regions in SPEC CPU2017[C]//2018 IEEE International Symposium on Workload Characterization (ⅡSWC). Raleigh: IEEE, 2018: 71-77.
(  0) 0) |
| [9] |
DENG J Y, WU Q Z, WU X Y, et al. Demystifying graph processing frameworks and benchmarks[J]. Science China information sciences, 2020, 63(12): 229101. DOI:10.1007/s11432-019-2807-4 (  0) 0) |
| [10] |
吴城文, 张广艳, 郑纬民. 从系统角度审视大图计算[J]. 大数据, 2015, 1(3): 48-61. WU C W, ZHANG G Y, ZHENG W M. Reviewing large graph computing from a system perspective[J]. Big data research, 2015, 1(3): 48-61. (  0) 0) |
| [11] |
SUNDARAM N, SATISH N R, PATWARY M M A, et al. GraphMat: High performance graph analytics made productive[EB/OL]. [2015-03-25]. https://arxiv.org/abs/1503.07241.
(  0) 0) |
| [12] |
BULUC A, GILBERT J R. On the representation and multiplication of hypersparse matrices[C]//2008 IEEE International Symposium on Parallel and Distributed Processing. Miami: IEEE, 2008: 1-11.
(  0) 0) |
| [13] |
MOFRAD M H, MELHEM R, AHMAD Y, et al. Efficient distributed graph analytics using triply compressed sparse format[C]//2019 IEEE International Conference on Cluster Computing (CLUSTER). Albuquerque: IEEE, 2019: 1-11.
(  0) 0) |
| [14] |
UMUROGLU Y, MORRISON D, JAHRE M. Hybrid breadth-first search on a single-chip FPGA-CPU heterogeneous platform[C]//2015 25th International Conference on Field Programmable Logic and Applications (FPL). London: IEEE, 2015: 1-8.
(  0) 0) |
| [15] |
GONZALEZ J E, LOW Y, GU H, et al. Powergraph: Distributed graph-parallel computation on natural graphs[C]//Proceedings of the 10th USENIX conference on Operating Systems Design and Implementation. Hollywood: USENIX Associatin, 2012: 17-30.
(  0) 0) |
| [16] |
OZDAL M M, YESIL S, KIM T, et al. Energy efficient architecture for graph analytics accelerators[J]. ACM SIGARCH computer architecture news, 2016, 44(3): 166-177. DOI:10.1145/3007787.3001155 (  0) 0) |
| [17] |
ZHOU S J, CHELMIS C, PRASANNA V K. High-throughput and energy-efficient graph processing on FPGA[C]//2016 IEEE 24th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM). Washington: IEEE, 2016: 103-110.
(  0) 0) |
| [18] |
邓军勇, 莉兹·K·约翰, 宋爽, 等. 一种用于图计算加速器的图数据压缩方法及图计算加速器: 中国, CN109919826A[P]. 2019-06-21. DENG J Y, LIZY K J, SONG S, et al. A graph data compression method for graph calculation accelerator and graph calculation accelerator: China, CN109919826A[P]. 2019-06-21. (  0) 0) |
| [19] |
邓军勇, JOHN L K, 宋爽, 等. 一种并行的图计算加速器结构: 中国, 201910107937.1[P]. 2019-02-02. DENG J Y, JOHN L K, SONG S, et al. A parallel graph computing accelerator structure: China, 201910107937.1[P]. 2019-02-02. (  0) 0) |
| [20] |
SHAO Z Y, LI R S, HU D Q, et al. Improving performance of graph processing on FPGA-DRAM platform by two-level vertex caching[C]//Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. New York: ACM, 2019: 320-329.
(  0) 0) |
| [21] |
BULUÇ A, MADDURI K. Parallel breadth-first search on distributed memory systems[C]//Proceedings of 2011 International Conference for High Performance Computing, Networking, Storage and Analysis on-SC'11. Washington: IEEE, 2011: 1-12.
(  0) 0) |
| [22] |
De M A C. The new linux 'perf' tools[EB/OL]. [2010-01-10]. http://vger.kernel.org/~acme/perf/lk2010-perf-paper.pdf.
(  0) 0) |
| [23] |
PANDA R, SONG S, DEAN J, et al. Wait of a decade: did SPEC CPU 2017 broaden the performance horizon?[C]//2018 IEEE International Symposium on High Performance Computer Architecture (HPCA). Vienna: IEEE, 2018: 271-282.
(  0) 0) |
 2021, Vol. 53
2021, Vol. 53


