2. 国网河南省电力公司信息通信公司通信运行部 河南 郑州 450000
2. The Depariment of Communications Operation, State Grid Henan Electric Power Company Information Communication Company, Zhengzhou 450000, China
高压输电线路的弧垂是反映线路安全运行的重要参数,也是输电线路在线监测和动态增容重点关注的指标之一[1-2],当前国内外都非常重视输电线路弧垂的监测研究.现有弧垂的监测方法主要有:图像技术法[3],GPS监测法[4],倾斜角法[5]以及通过导线温度和应力测量弧垂[6-7]等.但是,除了实时监测弧垂变化外,预知和预警弧垂变化也是一个亟待解决的问题,目前还未见有这方面相关的研究.
SVM是一种基于统计学习理论的机器学习算法,已被广泛应用到现代经济和工业领域中[8].文献[9]通过支持向量回归算法建立股票分析模型,对股票价格进行预测分析.文献[10]应用支持向量机算法对混凝土抗压强度进行预测.文献[11]采用支持向量回归算法对山西月度最大电力负荷进行预测.文献[12]进行项目控制预测.因为线路运行的电压、电流、导线的温度,以及周围环境的温度、风速、湿度等都会造成输电线路弧垂的变化[13].本文提出一种基于GA特征自适应赋权的SVM预测高压输电线路弧垂的方法(GA-SVM).该方法主要分为两个阶段:1)根据每个属性对弧垂影响的重要程度不同,使用GA自适应对特征赋权,以突出重要属性,抑制次要或冗余属性. 2)以第一阶段处理过的数据作为SVM的输入,对弧垂进行预测分析.实证研究表明,本文提出的基于GA-SVM预测高压输电线路弧垂的方法是可行和有效的,并且其预测精度优于Bayes算法、KNN算法、决策树算法和BPNN神经网络算法.
1 背景 1.1 输电线路弧垂输电线路任一点的弧垂是指该点与悬线两端连线的铅锤距离,通常所说的弧垂是指一个档距导线段的最大弧垂.输电线路的弧垂是线路设计和安全运行的重要指标,弧垂过小,会导致输电线应力过大,影响输电线路的机械安全;弧垂过大,将导致输电线距离地面太低,会造成对地放电的危险.因此必须保证弧垂在规定的安全范围内.
1.2 支持向量机SVM在构造最优分类超平面时,采用迭代训练算法来减小误差函数. SVM分类模型可以描述为一个数学优化问题,所用公式为
| $ \left\{ \begin{array}{l} \min \alpha \left( w \right) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + c\sum\limits_{i = 1}^n {{\xi _i}} , \\ s, t.{y_i}\left( {\mathit{\boldsymbol{w}} \cdot \phi \left( {{x_i}} \right) + b} \right) \ge 1 - {\xi _i}, \end{array} \right.\;\;\;\;\;\;\;1, 2, \cdots n, $ | (1) |
其中:w为权值向量;c是惩罚系数;ξ是处理不可分数据时的松弛变量;b是偏置量;φ(x)是一个非线性的映射函数,将输入样本映射到高维特征空间.最终,求得SVM分类决策函数为
输电线路弧垂是连续属性,但有时候预测弧垂属于哪一个范围比预测弧垂的确切值更有意义.所以本实验采用等宽离散化方法把弧垂离散化为N个区间.等宽离散化方法是一种典型的无监督离散化方法,是将属性的值域划分为具有相同宽度区间.等宽离散化算法过程如下所示.
输入:属性A,A的个数为M,离散区间个数为N;
输出:离散化后的属性为F.
1) 计算A的最大值MAX和最小值MIN.
2) 计算属性A的离散区间宽度W=(MAX-MIN)/N.
3) F=A
4) For i in M do
5) For j in N do
6) If Ai < =MIN +j*W
7) Fi=j
8) Else
9) Continue
10) End
11) End
12) Return F.
2.2 特征变换特征(属性)变换是指用于属性变量的全体或部分的变换.主要包括两种变换类型:函数变换和标准化(规范化).函数变换是指用一个简单数学函数分别作用于变量的每一个值.假设x是属性变量,常用的函数变换有xk、log (x)、sin (x)、tan (x)、1/x等.标准化的目的是使属性整体值的集合具有特定的性质.特征变换的主要作用包括:1)将不具有正态分布的数据变换为正态分布;2)避免较大值域的变量左右计算结果.根据实验数据分布特征,本文采用标准化变换,所用公式为x′=(x-x)/s,其中:x为均值;s为均方差.创建了1个具有均值为0和标准差为1的新变量x′.为了与标准化变换方法的实验效果对比,本文给出max-min变换法和反正切函数变换法. max-min变换法为x′=(x-Minvalue)/(Maxvalue-Minvalue),变化后的值域为[0, 1];反正切函数变换法为x′=(2arctan (x))/π,变换后的值域为[-1, 1].
2.3 基于GA特征自适应赋权特征权重可以有效提高模型的精确度[14-15].特征权重是对数据的各个特征赋予不同的重要程度,从而达到突出重要特征,抑制次要特征或冗余特征.主要有以下3种方法:1)单一权重方法赋权;2)综合权重方法赋权;3)自适应赋权.自适应赋权是一种客观的赋权方法,不需要人为干预,能更有效地搜索重要特征,抑制次要特征或冗余特征提高模型精度[16-17].本文采用基于GA的特征自适应赋权方法.
GA是一种求解问题高效并行的全局自适应搜索方法[18],以自然选择和遗传理论为基础,在搜索过程中自动获取和积累有关搜索空间知识,并自适应地控制搜索过程以求得最优解.利用遗传算法实现特征自动赋权步骤如下.
1) 基因编码.本文采用表达精确的浮点数编码方法.
2) 种群初始化.随机生成M个染色体组成一个群体,群体内个体的数量即是群体规模,每个初始个体即表示问题的初始解.
3) 计算个体的适应度.适应度函数是唯一评价个体好坏的标准.在GA寻优过程中,一个良好的适应度函数能够指导寻优的方向.为了保证GA能搜索到最优的特征权值,定义的适应度函数为Fitness=N′/N,其中:N′表示进行特征赋权后,能够正确分类训练实例的个数;N表示用于训练实例的总个数.
4) 选择.选择的目的是从当前种群中选出优良的个体为父代.根据个体的适应度,适应度大的个体被选中的概率大.本文采用轮盘赌方法选择优良的个体,设种群的大小为M,每个个体的适应度为Fi,则个体i被选中的概率为
5) 交叉.交叉是遗传算法中最主要的遗传操作,且是产生新个体的主要方式之一.本文采用分散交叉法.
6) 变异.变异是模拟生物进化中的基因突变,它使GA在接近最优解邻域时能够加速向最优解收敛.本文选用高斯函数作为变异函数.
为了对比实验效果,本文在此给出另外两种经常使用的特征赋权方法:互信息权重和熵权重.互信息是信息论中对有用信息的度量,可以看作一个随机变量中包含的另一个随机变量的信息量,包含的信息量越多则权重越大;熵是对信息不确定性的度量,不确定性越大熵值越高,则权重越大.实验数据集的属性集合为{X1,X2,…,Xn},类标属性为Y,令p(xi)为属性Xi的概率分布,p(xi, yi)为属性Xi和Yi之间的联合概率分布,m为属性的个数.则属性的互信息权重为
本文所提出的输电线路弧垂预测模型是一个多阶段的过程:包括数据的特征变换,GA特征自适应赋权,支持向量机预测弧垂,性能评价. GA-SVM预测输电线路弧垂算法过程如下.
输入:训练数据集Train_set,测试集Test_set;
输出:弧垂预测值L.
1) 使用标准化特征变换方法处理训练数据集Train_set,得到Train_set1.
2) 使用遗传算法自适应计算Train_set1的特征权重,得到Train_set2.
3) 使用Train_set2作为SVM的输入,训练SVM.
4) 把测试集Test_set输入到训练好的SVM模型中.
5) 得到弧垂预测值L.
3 实验 3.1 实验数据集实验数据取自郑州市某电力公司,共1 502条记录,每条记录包括6个属性:输电线路温度、环境温度、环境风速、环境湿度、载荷电流、输电线路弧垂.本实验以前5个属性作为GA-SVM算法的输入属性,输电线路弧垂作为预测属性.
3.2 实验性能评估方法实验评估中采用10次十折交叉验证结果的平均正确率,作为GA-SVM预测输电线路弧垂方法的效果评估方法.十折交叉验证方法将数据集随机分成10份,轮流将其中1份作为测试集,另外9份合并作为训练集.平均正确率的计算方法为
在本实验中,使用台湾大学林智仁教授开发的LIBSVM工具箱进行输电线路弧垂预测.其中,支持向量机类型选择c-SVC,核函数选择径向基函数,惩罚系数c和内核参数g使用网格搜索算法进行寻优.网格搜索算法是支持向量机参数寻优常用的一种方法,它将待选取的参数限定在一定的取值范围内,然后将参数按一定的步长分割成一个个网格,同时按次序遍历网格内的所有点,从而获取最优参数组合.网格搜索算法得到的最优参数组合为:惩罚系数c=2 048,内核参数g=0.007 812 5.
3.3.1 不同离散化区间个数的实验结果表 1给出了5种不同等宽离散化区间个数的10次十折实验结果.从表 1可以看出,随着类标属性离散化区间个数的增加,输电线路弧垂的预测准确率逐渐下降.弧垂离散化为3箱的10次十折平均预测准确率为76.68%,比离散化为7箱的平均预测准确率59.95%高16.73%.但是较少的区间划分不能充分反应弧垂的变化,而较多的区间划分准确率又太低.所以综合考虑输电线路弧垂的分布状态,本实验把弧垂等宽离散化分为5个区间.
|
|
表 1 5种不同离散化区间个数的实验结果对比 Table 1 Experimental results comparison of five different discre-tization intervals |
表 2给出了4种特征变换的10次十折实验结果,包括未进行特征变换的SVM方法,MAX-MIN特征变换的SVM方法,反正切特征变换的SVM方法和标准化特征变换的SVM方法.从中可以看出:
|
|
表 2 4种不同特征变换方法的实验结果对比 Table 2 Experimental results comparison of four different feature transformation methods |
1) 未进行特征变换的SVM方法10次十折平均正确率是71.38%,比MAX-MIN特征变换和反正切特征变换的SVM方法平均正确率分别高11.91%和13.16%,比标准化特征变换的SVM方法平均正确率75.10%低3.72%.这说明合理的特征变换能够提高弧垂的预测精度,不当的特征变换则降低预测精度.
2) 标准化特征变换的SVM方法10次十折平均正确率最高,比未进行特征变换的SVM方法提高3.72%,比MAX-MIN特征变换和反正切特征变换的SVM方法分别提高15.63%和16.88%.这说明本文采用的标准化特征变换方法能够更加准确地描述实验数据特征,从而提升弧垂的预测正确率.
3.3.3 特征加权后的实验结果上述实验说明本文提出的标准化特征变换是最佳的特征变换方法,在此基础上,我们采用特征加权方法对实验数据赋权,以突出重要属性,抑制冗余或次要属性. 表 3给出了标准化特征变换并加权后的实验结果.从表 3中可以看出:GA自适应特征赋权方法10次十折实验平均正确率最高,比未加权方法提高2.68%,比熵权重方法提高3.32%,比互信息权重方法提高3.5%.这说明GA自适应特征赋权方法能够进一步突出重要属性,抑制冗余或次要属性,从而提高SVM预测输电线路弧垂的精度.
|
|
表 3 标准化特征变换并加权后的实验结果对比 Table 3 Experimental results comparison of standardized feature transformation and weighting |
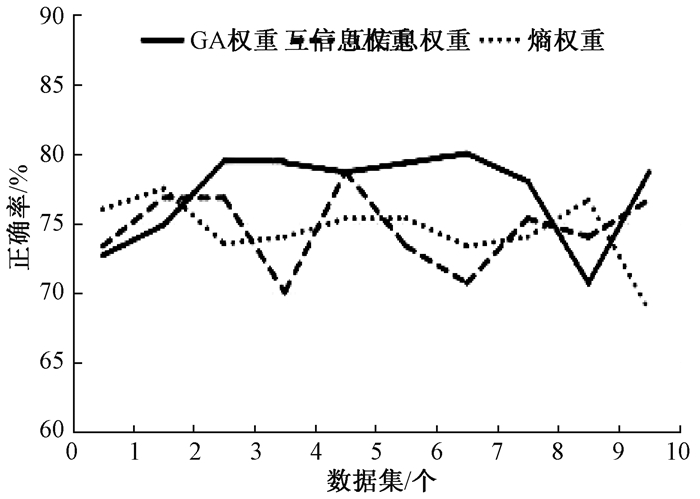
为了更详细地分析特征权重对实验结果的影响,在图 1和图 2中分别给出了10组十折实验的第1组和第2组GA权重、互信息权重和熵权重的正确率曲线.可以看出:
|
图 1 第1组3种特征权重方法正确率曲线对比 Figure 1 Correctness curve comparison of three kinds feature weighting methods in the first group |
|
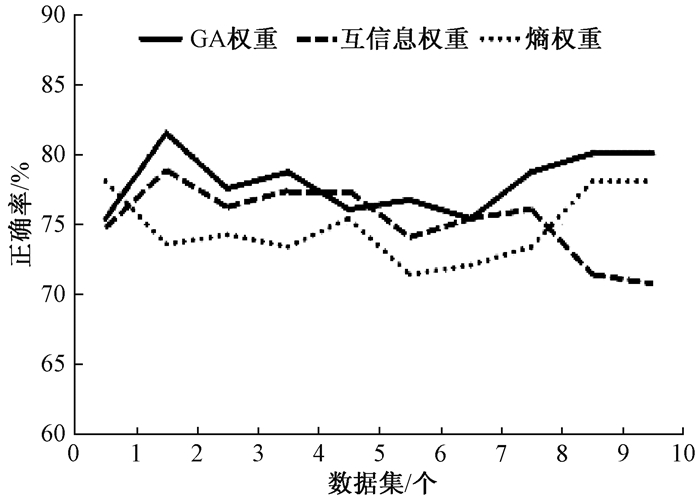
图 2 第2组3种特征权重方法正确率曲线对比 Figure 2 Correctness curve comparison of three kinds feature weighting methods in the second group |
1) 在第1组的10个数据集上,GA权重在其中的6个数据集上优于互信息权重,在1个数据集上等于互信息权重,在2个数据集上低于互信息权重;GA权重在其中的7个数据集上优于熵权重,在3个数据集上低于熵权重.
2) 在第2组的10个数据集上,GA权重在其中的8个数据集上优于互信息权重,在1个数据集上等于互信息权重,在1个数据集上低于互信息权重;GA权重在其中的9个数据集上优于熵权重,在1个数据集上低于熵权重.
3) GA权重的效果在总体上优于互信息权重和熵权重,更适合用于本实验数据集进行特征赋权,以突出重要属性,抑制冗余或次要属性.
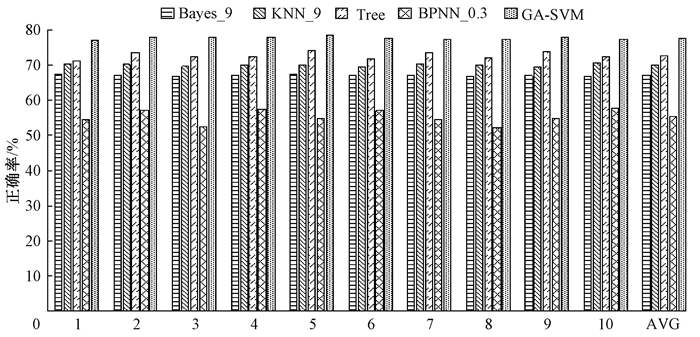
3.3.4 与其他机器学习算法实验对比为了验证本文所提出方法的有效性,图 3给出了贝叶斯算法、KNN算法、决策树算法、BPNN神经网络算法和本文提出的GA-SVM方法的10次十折实验的正确率对比柱状图.贝叶斯算法输入特征离散化采用等宽离散化方法,图中所示Bayes_9表示将每个属性分别离散为9箱后的实验结果. KNN算法的输入属性采用标准化方法变换,图中所示KNN_9表示KNN算法采用9近邻.图中所示Tree表示决策树采用CART算法. BPNN神经网络采用3层网状结构,5个输入节点,10个隐藏层节点,5个输出节点,激活函数选用logsig和purelin,网络训练函数选用traingdm.图中所示BPNN_0.3表示神经网络采用0.3作为学习速率训练BPNN模型.从图 3中可以看出,参与比较的5种算法中,本文所提出的GA-SVM算法预测输电线路弧垂的10次十折正确率均是最优,且明显高于其他4种算法.
|
图 3 5种算法最优结果对比 Figure 3 Five algorithms optimal results comparison |
针对在预测高压输电线路弧垂方面,还未见有相关的研究,本文提出一种基于GA特征自适应赋权的SVM预测高压输电线路弧垂方法(GA-SVM).该方法首先使用GA给实验数据自适应赋权,以突出重要属性,抑制冗余或次要属性,然后再使用SVM预测输电线路弧垂.实证结果表明,本文提出的GA-SVM预测输电线路弧垂的方法是可行有效的,并且优于Bayes算法、KNN算法、决策树算法和BPNN算法. GA-SVM算法模型还有一些不足和待完善的地方,如引入更多和输电线路相关的属性特征,研究不同的SVM参数选择方法对实验精度的影响等.
| [1] |
王红斌, 陈扬, 高雅, 等. 输电线路弧垂对动态增容的影响[J]. 华北电力大学学报(自然科学版), 2014, 41(2): 41-46. DOI:10.3969/j.ISSN.1007-2691.2014.02.07 (  0) 0) |
| [2] |
王孔森, 孙旭日, 盛戈皞, 等. 架空输电线路导线弧垂在线监测误差分析及比较方法[J]. 高压电网, 2014, 50(4): 27-34. (  0) 0) |
| [3] |
王礼田, 邵凤莹, 萧宝瑾. 基于双目视觉稀疏点云重建的输电线路弧垂测量方法[J]. 太原理工大学学报, 2016, 47(6): 747-751. (  0) 0) |
| [4] |
董晓虎, 易东. 基于北斗卫星差分定位技术的输电线路弧垂监测[J]. 电子设计工程, 2015, 23(19): 41-42. DOI:10.3969/j.issn.1674-6236.2015.19.013 (  0) 0) |
| [5] |
陈思明, 闫斌, 周小佳, 等. 基于倾角的输电线路弧垂三维模型算法研究[J]. 计算机应用与软件, 2014, 31(3): 82-84. DOI:10.3969/j.issn.1000-386x.2014.03.022 (  0) 0) |
| [6] |
姚陈果, 张磊, 李成祥, 等. 基于力学分析和弧垂测量的导线覆冰厚度测量方法[J]. 高电压技术, 2013, 39(5): 1204-1209. DOI:10.3969/j.issn.1003-6520.2013.05.027 (  0) 0) |
| [7] |
张江华.高压输电线路弧垂在线监测研究[D].武汉: 华中科技大学, 2012.
(  0) 0) |
| [8] |
SUGANYADEVI M V, BABULAL C K. Support vector regression model for the prediction of loadability margin of a power system[J]. Applied soft computing, 2014, 24: 304-315. DOI:10.1016/j.asoc.2014.07.015 (  0) 0) |
| [9] |
WANG J Z, HOU R, WANG C, et al. Improved v-support vector regression model based on variable selection and brain storm optimization for stock price forecasting[J]. Applied soft computing, 2016, 49: 164-178. DOI:10.1016/j.asoc.2016.07.024 (  0) 0) |
| [10] |
靳江伟, 董春芳, 冯国红. 基于灰色关联支持向量机的混凝土抗压强度预测[J]. 郑州大学学报(理学版), 2015, 47(3): 59-63. DOI:10.3969/j.issn.1671-6841.2015.03.011 (  0) 0) |
| [11] |
尹立.基于支持向量机的某区域电网电力需求的预测研究[D].北京: 北京交通大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10004-1014374681.htm
(  0) 0) |
| [12] |
WAUTERS M, VANHOUCKE M. Support vector machine regression for project control forecasting[J]. Automation in constuction, 2014, 47: 92-106. DOI:10.1016/j.autcon.2014.07.014 (  0) 0) |
| [13] |
MALHARA S, VITTAL V. Mechanical state estimation of overhead transmission lines using tilt sensors[J]. IEEE transactions on power systems, 2010, 25(3): 1282-1290. DOI:10.1109/TPWRS.2009.2038703 (  0) 0) |
| [14] |
DIALAMEH M, JAHROMI M Z. A general feature-weighting function for classification problems[J]. Expert systems with applications, 2017, 72: 177-188. DOI:10.1016/j.eswa.2016.12.016 (  0) 0) |
| [15] |
姬波.信息瓶颈方法的特征权重研究[D].郑州: 郑州大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10459-1013254108.htm
(  0) 0) |
| [16] |
PHAN A V, NGUYEN M L, BUI L T. Feature weighting and SVM parameters optimization based on genetic algorithms for classification problems[J]. Applied intelligence, 2017, 46(2): 455-469. DOI:10.1007/s10489-016-0843-6 (  0) 0) |
| [17] |
PENG L Z, ZHANG H L, ZHANG H B, et al. A fast feature weighting algorithm of data gravitation classification[J]. Information sciences, 2017, 375: 54-78. DOI:10.1016/j.ins.2016.09.044 (  0) 0) |
| [18] |
田晋跃, 王晨阳, 李得志. 基于遗传算法的某工程车辆起步特性研究[J]. 郑州大学学报(理学版), 2016, 48(2): 121-126. (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


