2. 太原理工大学 电气与动力工程学院 山西 太原 030024
2. College of Electrical and Power Engineering, Taiyuan University of Technology, Taiyuan 030024, China
近年来,互联网上的数字信息越来越多,用户也越来越多,导致信息超载。因此,推荐系统应运而生。通常,推荐系统主要被分为三类,即协同过滤推荐系统、基于内容的推荐系统以及混合推荐系统。其中,协同过滤是迄今为止最成功的推荐技术并广泛应用于各种推荐系统中。当前协同过滤推荐系统使用的方法是基于内存的或基于模型的协同过滤算法[1]。基于内存的协同过滤算法可以分为基于用户[2]和基于项目的协同过滤[3]。然而,协同过滤推荐系统随着用户和项目数量的大幅度增加,数据稀疏性和可扩展性以及冷启动问题愈加严重。基于模型的协同过滤算法可以利用降维[4]、聚类[5]、关联规则挖掘[6]等技术缓解上述问题。文献[7]证明基于聚类的协同过滤算法在稀疏数据中推荐效果更佳。文献[8]提出了主成分分析(principal component analysis,PCA)和遗传(genetic algorithm,GA)优化K-means聚类的混合推荐算法,提高了推荐结果准确性。文献[9]提出了一种结合K-means和人工蜂群的混合推荐系统,提高了可扩展性。文献[10]提出一种基于凝聚层次聚类的协同过滤算法。然而,以上方法使用的聚类算法都属于硬聚类,即每个用户或项目只能划分到一个簇中,不符合实际情况。文献[11]首次将模糊C均值(fuzzy C-means,FCM)应用到基于用户的协同过滤推荐算法中,FCM是一种软聚类算法,它可以根据隶属度的不同,将用户划分到多个簇中, 其结果优于其他聚类方法。文献[12]提出了基于项目的模糊聚类推荐系统,该系统将用户定位在合适的簇中,并提供具有最佳用户邻居的推荐,增加了预测的覆盖范围。文献[13]将基于灰狼优化的FCM聚类应用到基于用户的协同过滤推荐系统中,提高了推荐结果的准确率。
然而,上述研究大多都是根据用户对项目的评分数据进行聚类,没有充分利用用户或项目之间的隐含信息。同时,用户或项目在聚类时容易出现局部最优的情况,导致最近邻居选取不准确,降低推荐结果的准确度。因此本文提出了融合用户偏好优化聚类的协同过滤推荐算法(collaborative filtering recommendation algorithm based on user preference optimization clustering, CF-UPOC)。首先根据用户对具有某一类型的项目评分在所有评分中的比例和属于该类型的项目数量在所有项目中的比例来预测用户对该类型的偏好,形成细粒度用户-项目类型偏好矩阵。此外,使用蝙蝠优化的用户模糊聚类算法对该矩阵进行聚类,该算法利用蝙蝠优化算法收敛速度较快、寻优性能较好等优点,对FCM的初始化进行优化,增强了聚类效果并提高了可扩展性。然后从隶属度较高的簇中选取目标用户的最近邻居,提高了最近邻选取的准确性。最后建立用户加权相似度模型进行评分预测并做出推荐,进一步提高了推荐结果准确性。
1 基于用户的协同过滤算法基于用户的协同过滤算法(user-based collaborative filtering,UBCF)[2]利用用户-项目评分矩阵计算目标用户与其他用户之间的相似度,如式(1)所示。然后找出与目标用户相似度较高的前K个用户作为目标用户的最近邻,最后根据最近邻预测目标用户对未评级项目集合中的每个项目的评级分数,选取预测评分较高的前N个项目提供给目标用户。
| $ sim{ _u}(tu,u) = \sum\limits_{i \ \in {\kern 1pt} {\kern 1pt} {I_{tu,u}}} {({R_{tu,i}} - \overline {{R_{{tu}}}} )({R_{u,i}} - \overline {{R_u}} )} /\sqrt {\sum\limits_{i\ \in {\kern 1pt} {\kern 1pt} {I_{tu,u}}} {{{({R_{tu,i}} - \overline {{R_{tu}}} )}^2}} } \sqrt {\sum\limits_{i\ \in {\kern 1pt} {\kern 1pt} {I_{tu,u}}} {{{({R_{u,i}} - \overline {{R_u}} )}^2}} } , $ | (1) |
其中:Itu, u表示目标用户tu和用户u共同评价过的一组项目集合;Ru, i、Rtu, i分别表示用户u、目标用户tu对项目i的评分;
根据公式(1)可以看出, UBCF算法在计算相似度时,需要将目标用户与其他所有用户进行比较。文献[12]对用户-项目评分矩阵中的全部用户进行FCM聚类,降低了利用相似度查找最近邻居的复杂度,缓解了可扩展性问题。但是过度依赖用户-项目评分矩阵,不利用用户或项目之间的隐含信息,相似度的计算可能存在问题,导致最近邻居选取不准确。例如,表 1所列的是用户对不同类型的项目评分表,通过公式(1)可以计算出用户u1和u2的相似度为0,若u1在选取最近邻时,会直接忽略u2。但是根据表 1可以看出,用户u1和u2对类型e1的项目评分较低,对类型e2和e3的项目评分较高。因此,从类型偏好的角度来看,用户u1和u2具有较高的相似性,u2应属于u1的最近邻。另一方面,使用FCM对用户进行聚类容易出现局部最优的情况,影响聚类效果,导致最近邻居选取不准确。
|
|
表 1 用户对不同类型的项目评分表 Tab. 1 User rating table for different types of item |
针对以上问题,本文提出了融合用户偏好优化聚类的协同过滤推荐算法。主要从利用RP-IIP(rating proportion-inverse item proportion)算法形成的细粒度用户-项目类型偏好矩阵、蝙蝠优化的用户模糊聚类以及建立用户加权相似度模型这3个方面对基于用户的协同过滤推荐算法进行改进。
2.1 细粒度用户-项目类型偏好矩阵传统的协同过滤算法在数据建模时过度依赖用户对项目的评分数据,未考虑到用户对项目类型的偏好。本文在数据建模时加入项目类型特征,能够真实地反映出用户兴趣偏好并提高推荐准确性。在推荐系统中,每个项目都有一个或多个类型特征,导致项目的类型数量远小于项目数量,并且用户对不同项目类型的偏好存在较大差异,由此,本文提出一种RP-IIP算法来预测用户对项目类型的偏好,从而生成细粒度用户-项目类型偏好矩阵。该矩阵中的每一行表示用户对不同项目类型的偏好程度。另外,该矩阵维度小于推荐系统中的原始用户-项目评分矩阵,在一定程度上缓解了数据稀疏性。因而本文以此评分矩阵进行建模。
评分比例表示用户对具有类型e的项目评分在所有评分中的比例,
| $ R{P_{u,i}} = \sum\limits_{i\ \in {\kern 1pt} {\kern 1pt} {I_{u,e}}} {{R_{u,i}}} /\sum {{R_u}} , $ | (2) |
其中:RP表示评分比例;分子表示用户u评价过的所有属于类型e的项目的评分总和;分母表示用户u对项目的全部类型的总评分。
反向项目比例表示属于该项目类型的项目数量在所有项目中的比例,它在一定程度上避免了由于属于类型e的热门项目对用户偏好产生的影响,计算方式如式(3)所示,为了避免属于类型e的项目数量为0,本文将分母定义为1+card(Ie),
| $ II{P_{i,e}} = {\rm{ln}} ( card (I)/(1 + card ({I_e}))), $ | (3) |
其中:IIP表示反向项目比例;card(I)表示项目的总数量;card(Ie)表示属于类型e的项目数量。
因此,用户对项目类型的偏好程度根据式(4)计算得出并形成细粒度用户-项目类型偏好矩阵,
| $ {P_{u,e}} = R{P_{u,i}} \cdot II{P_{i,e}} = \sum\limits_{i\ \in {\kern 1pt} {\kern 1pt} {I_{u,e}}} {{R_{u,i}}} \cdot {\rm{ln}} ( card (I)/(1 + card ({I_e})))/\sum {{R_u}} 。$ | (4) |
由RP-IIP算法可以得出,若用户对具有某一类型的项目评分在所有评分中的比例过高,则表示用户更偏爱属于该类型的项目。同时,对于热门项目类型即属于该类型的项目数量较多,根据式(4)计算得出的用户偏好值较低,而对于一些比较冷门的项目类型即属于该类型的项目数量较少,若用户对其评分比例较高,则表示该用户比其他用户更偏爱属于这些冷门类型的项目。
例如,根据表 1所列的用户对不同类型的项目评分表分成用户-项目评分矩阵A和类型-项目矩阵B,如表 2、表 3所示。表 2中数据项表示相应的具体打分,对于未评分的数据项记为0。表 3中当项目具备某一类型时,该项的评分记为1,反之为0。根据表 2和表 3可以构建细粒度用户-项目类型偏好矩阵X,如表 4所示。
|
|
表 2 用户-项目评分矩阵A Tab. 2 User-item rating matrix A |
|
|
表 3 类型-项目矩阵B Tab. 3 Type-item matrix B |
|
|
表 4 细粒度用户-项目类型偏好矩阵X Tab. 4 Fine-grained user-item type preference matrix X |
本文利用蝙蝠优化的用户模糊聚类算法对上一节得到的细粒度用户-项目类型偏好矩阵进行离线聚类,增强了聚类效果并提高了推荐算法的可扩展性。该矩阵可表示为X={x1, x2, …,xi,…,xn}。其中xi表示用户ui对所有项目类型的偏好向量。
2.2.1 FCM聚类算法FCM是一种迭代聚类算法,通过最小化目标函数(5)可以将n个用户划分到c个集群中,
| $ {J_{{\rm{fcm}}}} = (\mathit{\boldsymbol{W}},\mathit{\boldsymbol{C}}) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^c {{{({w_{ij}})}^m}} } d_{ij}^2, $ | (5) |
其中:用户簇隶属度矩阵W=(wij)n×c;wij表示第i个用户属于第j个簇的隶属度;聚类中心矩阵C={c1, c2, …, cc};dij= ‖ xi-cj ‖表示用户ui对所有类型的偏好向量xi和聚类中心cj之间的距离;m表示模糊加权系数,一般取值为2。
目标函数中的每个变量按公式(6)、(7)迭代更新,
| $ {w_{ij}} = 1/\sum\limits_{k = 1}^c {{{({d_{ij}}/{d_{ik}})}^{\frac{2}{{m - 1}}}}} , $ | (6) |
| $ {c_j} = \sum\limits_{i = 1}^n {w_{ij}^m} {\mathit{\boldsymbol{x}}_i}/\sum\limits_{i = 1}^n {w_{ij}^m} 。$ | (7) |
蝙蝠算法是群体智能优化算法[14],它启发于微蝙蝠捕食时的回声定位行为。
蝙蝠的速度vit以及位置xit在第t次迭代期间根据公式(8)~(10)进行修改。
| $ {f_i} = {f_{ {\rm{min}} }} + ({f_{{\rm{ max}} }} - {f_{{\rm{ min }}}})\beta , $ | (8) |
| $ \mathit{\boldsymbol{v}}_i^t = \mathit{\boldsymbol{v}}_i^{t - 1} + (\mathit{\boldsymbol{x}}_i^{t - 1} - {\mathit{\boldsymbol{x}}_{{\rm{best}}}}){f_i}, $ | (9) |
| $ \mathit{\boldsymbol{x}}_i^t = \mathit{\boldsymbol{x}}_i^{t - 1} + \mathit{\boldsymbol{v}}_i^t, $ | (10) |
其中:xbest表示当前全局最优位置;β是[0, 1]之间的随机数;fi是位于[fmin, fmax]之间的随机初始化脉冲频率。在局部搜索期间,对当前全局最优位置进行随机扰动,使用公式(11)生成新位置,
| $ {\mathit{\boldsymbol{x}}_{{\rm{new}}}} = {\mathit{\boldsymbol{x}}_{{\rm{best}}}} + rand \cdot {A^t}, $ | (11) |
其中:rand表示[-1, 1]之间的随机数;At表示在第t次迭代期间所有蝙蝠响度的平均值。
随着种群内的每只蝙蝠逐渐接近最优位置,蝙蝠的响度Ai和脉冲发射率ri根据式(12)、(13)进行修改,
| $ A_i^t = \alpha A_i^{t - 1}, $ | (12) |
| $ r_i^t = r_i^0\left[ {1 - {\rm{exp}} ( - \gamma t)} \right], $ | (13) |
其中:α、γ为常数。
2.2.3 蝙蝠优化的用户模糊聚类算法蝙蝠优化的用户模糊聚类算法思想为:先利用蝙蝠优化算法查找最优的初始聚类中心,再使用最优的初始聚类中心对用户进行FCM聚类。蝙蝠优化算法中的每一只蝙蝠表示一个聚类中心矩阵C={c1, c2, …,cc},并将适应度函数设置为fit(C)=Jfcm(W, C)。
蝙蝠优化的用户模糊聚类算法流程如下。
输入:细粒度用户-项目类型偏好矩阵、用户聚类个数c、蝙蝠种群大小h、最大迭代次数T等参数。
输出:用户簇隶属度矩阵W。
Step1:随机产生初始蝙蝠种群M={C1, C2, …, Ch}并对每一只蝙蝠的速度vi0、脉冲发射率ri0、位置xi0、频率fi以及响度Ai0进行初始化;Step2:使用公式(6)计算隶属度;Step3:使用公式(5)计算每一只蝙蝠的适应度,并选出当前具有最优适应度值的蝙蝠个体;Step4:根据公式(8)~(10)对蝙蝠个体的位置和速度进行修改;Step5:产生一个随机数rand1并对每一只蝙蝠进行遍历,如果rand1>ri,则根据公式(11)生成xnew并计算适应度fit(xnew);
Step6:再产生一个随机数rand2并对每一只蝙蝠进行遍历,如果rand2 < Ai并且fit(xnew) < fit(xi),则接受Step5产生的xnew并根据式(12)、(13)对响度和脉冲发射率进行修改。
Step7:如果迭代次数小于T或者未达到聚类中心收敛条件,则转向Step2继续迭代;否则,输出取得xbest的蝙蝠作为初始聚类中心并进行FCM聚类划分,得到最终的用户簇隶属度矩阵W。
2.3 生成目标用户的最近邻居根据用户的聚类结果,首先从用户簇隶属度矩阵W中找出隶属度大于一定阈值的用户簇组成目标用户的候选邻居簇,这样可以增大最近邻居选取的范围并提高准确性。然后通过相似度计算公式(14)计算目标用户与该簇中的所有候选邻居之间的项目类型偏好相似度,按照降序进行排列,将前K个候选邻居作为目标用户的最近邻居Ntu。
| $ sim{ _e}(tu,u) = \sum\limits_{e\ \in {\kern 1pt} {\kern 1pt} {E_{tu,u}}} {({P_{tu,e}} - \overline {{P_{tu}}} )({P_{u,e}} - \overline {{P_u}} )} /\sqrt {\sum\limits_{e\ \in {\kern 1pt} {\kern 1pt} {E_{tu,u}}} {{{({P_{tu,e}} - \overline {{P_{tu}}} )}^2}} } \sqrt {\sum\limits_{e\ \in {\kern 1pt} {\kern 1pt} {E_{tu,u}}} {{{({P_{u,e}} - \overline {{P_u}} )}^2}} } , $ | (14) |
其中:Etu, u表示目标用户tu和用户u共同评价过的项目的所有类型集合;Ptu, e、Pu, e分别表示的是目标用户tu和用户u对具有类型e的项目的偏好值;
根据公式(15)将用户项目类型偏好相似度sime(tu, u)和传统的用户项目评分相似度simu(tu, u)进行加权求和,建立用户加权相似度模型。
| $ sim (tu,u) = sim{ _e}(tu,u) \cdot \lambda + sim{ _u}(tu,u) \cdot (1 - \lambda ), $ | (15) |
其中:λ为权重因子,取值在[0, 1]之间。当λ=1时,仅考虑用户项目类型偏好相似度;当λ=0时,仅考虑用户项目评分相似度。sime(tu, u)是根据RP-IIP算法预测出的细粒度用户-项目类型偏好矩阵而计算出的相似度,考虑了用户以及项目之间的隐性信息。simu(tu, u)是直接根据用户-项目评分矩阵计算出的相似度。将两者同时考虑并进行加权求和,有利于提高推荐的准确性。权重因子λ的取值对推荐结果的影响在实验部分进行讨论。
最后,通过公式(16)预测目标用户的未评级项目集合中的每个项目的评级。选取预测评级较高的前N个推荐列表提供给目标用户。
| $ {Q_{tu,i}} = \overline {{R_{tu}}} + \sum\limits_{u\ \in {\kern 1pt} {\kern 1pt} {N_{tu}}} { sim } (tu,u) \cdot ({R_{u,i}} - \overline {{R_u}} )/\sum\limits_{u\ \in {\kern 1pt} {\kern 1pt} {N_{tu}}} { sim } (tu,u)。$ | (16) |
本文提出融合用户偏好优化聚类的协同过滤推荐算法的具体流程如下所示。
Step1:利用RP-IIP算法预测用户对项目类型的偏好,构建细粒度用户-项目类型偏好矩阵;
Step2:利用蝙蝠优化的用户模糊聚类算法对细粒度用户-项目类型偏好矩阵中的全部用户进行聚类;
Step3:根据聚类结果找出目标用户的候选邻居簇,并且通过公式(14)计算目标用户与该簇中的所有候选邻居之间的项目类型偏好相似度,并且按照降序进行排列,将前K个候选邻居作为目标用户的最近邻居;
Step4:通过公式(15)将用户项目类型偏好相似度和传统的用户项目评分相似度进行加权求和,建立用户加权相似度模型;
Step5:预测目标用户的未评级项目集合中的每个项目的评级分数并做出推荐。
3 实验与结果 3.1 实验数据集与度量标准本文使用MovieLens100K数据集来验证算法性能,该数据集被公认为是评估推荐算法的主要数据集,包括943个用户为1 682部电影提供的100 000个评分记录,评分范围是1~5分。该数据集十分稀疏,只有6.3%的评分可用。通过对该数据集进行预处理,提取出用户对项目的评分以及项目所属类型保存在用户-项目评分矩阵和类型-项目矩阵中。然后将数据集分成训练集和测试集(80%作为训练集,20%作为测试集)。此外,本文采用了不同的比例分割对数据进行交叉验证,最后取得结果的平均值。
为了检查推荐的质量,本文使用了平均绝对误差(mean absolute error,MAE)这一性能评价指标来度量推荐算法提供的预测评级与目标用户的真实评级之间的平均绝对偏差,计算方式如公式(17)所示。这种度量标准已广泛用于比较和测量推荐系统的性能。
| $ MAE = \frac{1}{M}\sum\limits_{u = 1}^M {{\kern 1pt} {\kern 1pt} \frac{1}{N}} \sum\limits_{i = 1}^N | {R_{u,i}} - {Q_{u,i}}|, $ | (17) |
其中:M表示测试集中目标用户的总数量;N表示测试集提供的项目总数量;Ru, i、Qu, i分别表示用户u对项目i的实际评分和预测评分。
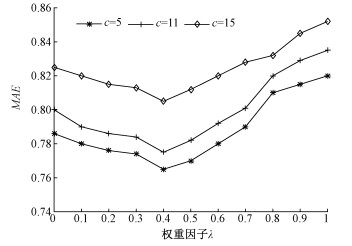
3.2 实验结果分析 3.2.1 最佳权重因子λ的确定为了确定权重因子λ的最佳值,检验该因子对推荐结果的影响,实验中选取最近邻居数量为40,用户聚类个数分别为5、11、15。随着权重因子λ的增长,实验结果如图 1所示。
|
图 1 MAE随权重因子λ的变化情况 Fig. 1 The change of MAE with weighting factor λ |
根据图 1可得,当权重因子λ在[0,0.4]范围内,无论用户的聚类个数取值为多少,MAE随着λ的增加而降低,推荐效果逐渐增加;而当权重因子λ在[0.4,1]范围内,MAE随着λ的增加而增加,推荐效果逐渐减弱。因此,在所提算法中权重因子λ的最佳值为0.4。
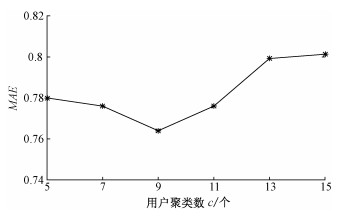
3.2.2 用户最佳聚类个数c的确定为了确定用户的最佳聚类个数c,实验中c值分别选取5、7、9、11、13、15,选取最近邻居数量为40,其MAE结果如图 2所示。根据图 2可得,用户的聚类个数为9时,MAE值最小。因此,用户的最佳聚类个数为9。
|
图 2 MAE随用户聚类个数的变化情况 Fig. 2 The change of MAE with the number of clusters of users |
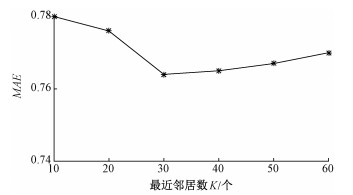
为了确定用户的最佳近邻个数K,实验中K值分别选取10、20、30、40、50、60。实验结果如图 3所示。根据图 3可得,最近邻居个数K在[10, 30]的范围内,MAE随着K的增加而呈现下降趋势,表明推荐效果在该范围内随着最近邻居个数的增加而增加,并且在K=30时,本文算法的MAE最小。而当最近邻居个数K在[30, 60]范围内,MAE随着K的增加而呈现缓慢上升的趋势,但比最近邻居个数K取10、20时的MAE值要低。因此,在所提算法中最近邻居个数K的最佳值为30。
|
图 3 MAE随最近邻居个数的变化情况 Fig. 3 The change of MAE with the number of nearest neighbors |
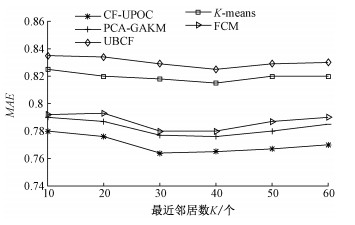
为了验证所提CF-UPOC算法推荐结果的准确性,实验中选取了4种算法与其进行对比,包括K-means、FCM、PCA-GAKM以及UBCF。最近邻个数K分别选取10、20、30、40、50、60。实验结果如图 4所示。根据图 4可以看出,与其他4种算法相比,本文提出的算法取得MAE最小,即推荐结果的准确度最高。K-means、FCM、PCA-GAKM都在UBCF的基础上加入了不同的聚类算法,但仅利用用户-项目评分矩阵,没有充分利用用户或者项目之间的隐含信息,可能造成最近邻居选取不准确的问题,降低了推荐结果的准确性。而本文充分利用用户对项目类型的偏好形成细粒度用户-项目类型偏好矩阵,并在此基础上利用蝙蝠优化的用户模糊聚类算法进行聚类,增强了聚类效果,然后从隶属度较高的簇中选取最近邻居,大大提高了最近邻选取的准确度。最后,建立用户加权相似度模型进行评分预测并做出推荐,进一步提高推荐结果准确性。
|
图 4 CF-UPOC与其他算法的对比 Fig. 4 Comparison of CF-UPOC with other algorithms |
本文从类型偏好角度出发,根据用户对具有某一类型的项目评分在所有评分中的比例和属于该类型的项目数量在所有项目中的比例,形成细粒度用户-项目类型偏好矩阵,并在新的矩阵上利用蝙蝠优化的用户模糊聚类算法进行聚类,从隶属度较高的簇中选取最近邻居,提高了最近邻居选取的准确度。仿真结果表明,本文提出的算法具有较小的MAE,即推荐准确度更高。然而本文算法在相似度计算方式中未考虑时间因素,下一步将结合时间因素来对用户进行推荐,进一步提高推荐准确度。
| [1] |
MANUEL A C J, YANG Y M, MIGUEL T C. A memory-based collaborative filtering algorithm for recommending semantic web services[J]. IEEE Latin America transactions, 2013, 11(2): 795-801. DOI:10.1109/TLA.2013.6533969 (  0) 0) |
| [2] |
ZHANG Z P, KUDO Y, MURAI T. Neighbor selection for user-based collaborative filtering using covering-based rough sets[J]. Annals of operations research, 2017, 256(2): 359-374. DOI:10.1007/s10479-016-2367-1 (  0) 0) |
| [3] |
LI D S, CHEN C, LV Q, et al. An algorithm for efficient privacy-preserving item-based collaborative filtering[J]. Future generation computer systems, 2016, 55: 311-320. DOI:10.1016/j.future.2014.11.003 (  0) 0) |
| [4] |
DE S S, DEHURI S. Machine learning for auspicious social network mining[M]//PANDA M, DEHURI S, WANG G N. Social networking. Switzerland: Springer, 2014: 45-83.
(  0) 0) |
| [5] |
孙焕良, 崔晨, 刘俊岭. 基于动态转移图的时间敏感的旅游路线推荐方法[J]. 郑州大学学报(理学版), 2017, 49(1): 50-57. SUN H L, CUI C, LIU J L. Time-sensitive travel route recommendation method based on dynamic transfer graph[J]. Journal of Zhengzhou university(natural science edition), 2017, 49(1): 50-57. (  0) 0) |
| [6] |
NAJAFABADI M K, MAHRIN M N, CHUPRAT S, et al. Improving the accuracy of collaborative filtering recommendations using clustering and association rules mining on implicit data[J]. Computers in human behavior, 2017, 67: 113-128. DOI:10.1016/j.chb.2016.11.010 (  0) 0) |
| [7] |
WU Y, LIU X D, XIE M, et al. CCCF: improving collaborative filtering via scalable user-item co-clustering[C]//Proceedings of the Ninth ACM International Conference on Web Search and Data Mining. San Francisco, 2016: 73-82.
(  0) 0) |
| [8] |
WANG Z, YU X, FENG N, et al. An improved collaborative movie recommendation system using computational intelligence[J]. Journal of visual languages & computing, 2014, 25(6): 667-675. (  0) 0) |
| [9] |
KATARYA R. Movie recommender system with metaheuristic artificial bee[J]. Neural computing and applications, 2018, 30(6): 1983-1990. DOI:10.1007/s00521-017-3338-4 (  0) 0) |
| [10] |
CHALCO C I, CHASI R B, ORTIZ R H. Hierarchical clustering for collaborative filtering recommender systems[C]//International Conference on Applied Human Factors and Ergonomics. Orlando, 2018: 346-356.
(  0) 0) |
| [11] |
KOOHI H, KIANI K. User based collaborative filtering using fuzzy C-means[J]. Measurement, 2016, 91: 134-139. DOI:10.1016/j.measurement.2016.05.058 (  0) 0) |
| [12] |
BIRTOLO C, RONCA D. Advances in clustering collaborative filtering by means of fuzzy C-means and trust[J]. Expert systems with applications, 2013, 40(17): 6997-7009. DOI:10.1016/j.eswa.2013.06.022 (  0) 0) |
| [13] |
KATARYA R, VERMA O P. Recommender system with grey wolf optimizer and FCM[J]. Neural computing and applications, 2018, 30(5): 1679-1687. DOI:10.1007/s00521-016-2817-3 (  0) 0) |
| [14] |
YANG X S, HOSSEIN G A. Bat algorithm: a novel approach for global engineering optimization[J]. Engineering computations, 2012, 29(5): 464-483. DOI:10.1108/02644401211235834 (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


