2. 上海市信息安全综合管理技术研究重点实验室 上海 200240;
3. 公安部第三研究所 上海 201204;
4. 天津大学 计算机科学与技术学院 天津 300072)
2. Shanghai Key Laboratory of Integrated Administration Technologies for Information Security, Shanghai 200240, China;
3. The Third Research Institute of Ministry of Public Security, Shanghai 201204, China;
4. School of Computer Science and Technology, Tianjin University, Tianjin 300072, China
近年来,随着嵌入式系统、通信网络、泛在计算等技术[1]的不断发展,人类社会已进入以数字化、网络化和智能化为特征的信息化时代,信息感知、泛在计算和管理调控等技术的不断融合,实现了物理空间和信息空间的互联互通和深度融合,最终产生信息物理系统(cyber-physical system,CPS)[2-3]. CPS的概念在2006年由Jones[4]提出,并很快引起了广泛的关注与研究.2014年10月,中德双方举行的第三轮中德政府磋商后发表的《中德合作行动纲要》[5]中宣布,两国将开展“工业4.0”合作,而工业4.0的核心就是构建CPS架构.中国在最近突出强调了推动新型工业化、信息化、城镇化、农业现代化的同步发展,工业和信息化部联合中国电子技术标准研究院,联合印发了《信息物理系统白皮书(2017)》[6].可以看出,CPS系统越来越支撑全球信息化和工业化的深度融合,受到各国的重视和发展.
CPS系统提供了物理空间、信息空间深度融合的智能信息服务平台,目前广泛用于智能电网、通信网络、石油石化、核能、交通运输等关键基础设施领域[7-9].随着通信、计算与控制技术的交叉融合,CPS系统表现出一类新的信息安全问题[10-13],即网络攻击不再局限于信息领域,也能够通过攻击远程终端单元(remote terminal unit,RTU)、可编程逻辑控制器(programmable controller,PLC)等终端设备实现物理破坏.在CPS系统中,由于信息空间和物理空间的相互融合,攻击者可能基于信息空间攻击物理空间,其破坏程度之大、危险系数之高,往往是CPS设计者和管理者始料未及,任何针对CPS的攻击一旦得逞,后果都将不堪设想.为此,如何保障CPS系统安全、稳定、连续、可靠地运行,并对其进行安全风险评估变得十分重要.
近年来,国内外学者围绕上述问题对CPS系统的攻击失效和安全评估问题展开了研究.传统可靠性的分析方法“故障树分析”[14-15],被用于智能交通、电力系统[16-17]等CPS系统的安全评估中,但没有考虑CPS系统中信息网络和物理网络的耦合关系引起的衍生失效问题,而CPS系统失效具有很强的级联失效特性.高洋[18]和Chen[19]等考虑了CPS系统的级联失效特性,并基于相互依赖网络理论,对该失效过程进行了仿真和验证,给出了CPS系统遭受随机攻击下的安全评估模型,但该模型主要依赖于随机攻击的场景进行分析与验证,并没有考虑其他的攻击策略.但在实际的信息物理系统中,系统遭受到的攻击类型,往往是目的性很强的蓄意攻击[20-21], 并给CPS系统带来很大的级联失效风险[22-23].可以看出,上述针对信息物理系统的安全评估方法,主要从单一网络的属性或单一的随机攻击等视角进行分析研究,缺乏对现实中的蓄意攻击下,信息物理系统的级联失效过程和安全评估等进行有效分析.
基于上述分析,本文对现有的信息物理系统进行有效建模;在此基础上,探讨了蓄意攻击策略下系统的级联失效过程;并通过仿真对比实验,给出影响信息物理系统安全性的主要评估要素;最后对本文的研究工作进行总结,并给出下一步的工作展望.
1 相关模型与概念现实中的信息物理系统是由各种各样的网络构成,通常是由信息网络和物理网络组成.通过对现实中的信息物理系统实例进行分析,建立符合信息物理系统特性的模型.这里我们将分析现实中的信息物理系统及其攻击的类型,对现实中的网络攻击方式进行建模,最后我们将简单介绍信息物理系统中的一些基本概念.
1.1 网络模型本文主要是针对信息物理系统的失效问题进行研究与分析.通过研究与分析生活中一些信息物理系统的实例,可以得知组成信息物理系统的两个网络的节点数量一般是不相同的.在信息物理系统中,通信网络的节点数量多于物理网络中的节点数量,因此我们建立了节点数量不同的两个网络,用A表示通信网络,用B表示物理网络.为了对信息物理系统可靠性进行定性分析,在本文中我们假设两个网络间节点的连接为等比连接,即网络B中的每一个节点与网络A中节点连接的数量相同,并规定NA:NB=3:1,即网络B中的一个节点与网络A中的3个节点连接,而且这种连接是完全随机的,网间连接和网内连接是没有任何关系的.在本文中,我们用NA表示通信网络中节点的数量,用NB表示物理网络中节点的数量.不失一般性,我们假定这里两个网络都服从随机网络的网络分布特性.
由前面的分析得知,实际中的信息物理系统,受到攻击的类型往往是蓄意的、有目的性的攻击,该类型的攻击对信息物理系统的影响和危害较大,很容易造成信息物理系统级联失效的衍生效应.因此,这里主要研究蓄意攻击下CPS系统的安全性问题,在本文中,我们用基于概率方程的方式来模拟蓄意攻击过程.
1.2 基本概念在前述建模过程中,信息物理系统中的一个网络受到攻击后,由于两个网络之间相互耦合,A网络中节点的失效会使B网络中的节点失效,B网络中节点的失效又会反过来使A网络中的节点失效,这个过程会迭代进行,这种现象我们称之为级联失效.级联失效会在下面两种情况下停止,一种是组成耦合系统的两个网络完全崩溃,不能保持基本功能;另一种是两个网络中都没有节点被删除,达到一种稳态,这时耦合系统还保持基本的功能.级联失效的过程,是信息物理系统遭受攻击后表现出的一种很重要的特性,与单个网络遭受攻击后节点失效过程完全不同.
当信息物理系统中的一个网络受到攻击以后,网络会分裂成一个较大的簇和一些比较小的簇,我们规定只有满足下面两个条件的节点才能保持功能[22-24].
1) 当前网络中的节点必须与另一个网络中的节点连接.
2) 节点必须在最大连通簇集合内.
满足上述两个条件的节点称之为功能节点.功能节点是网络中很重要的节点,受到攻击后,只有当功能节点还存在时,网络才能保持基本功能,当网络中没有功能节点就说明网络已经完全崩溃.
2 理论分析在本节中我们建立了一个数学框架,来分析信息物理系统在蓄意攻击下的安全性,这个框架是解决蓄意攻击的理论基础.我们通过一定的数学分析将蓄意攻击转化为随机攻击,然后按照分析随机攻击级联失效的理论来研究耦合系统遭受目标攻击后的级联失效.
2.1 蓄意攻击的转化文献[25]中提出了一个概率方程来表示节点去除的概率,我们用Wα(ki)表示在初始蓄意攻击的情况下度数为k的节点i失效的概率,
| $ {W_\alpha }\left( {{k_i}} \right) = \frac{{k_i^\alpha }}{{\sum\limits_{i = 0}^N {k_i^\alpha } }}. $ | (1) |
由式(1)可以看到,当α < 0的时候,公式就无意义,因此节点度数为0的节点就必须被排除,但是在现实的耦合系统中度数为0的节点是存在的,因此为了研究的一般性,我们对上面的方程进行改进,得到
| $ {W_\alpha }\left( {{k_i}} \right) = \frac{{{{\left( {{k_i} + 1} \right)}^\alpha }}}{{\sum\limits_{i = 0}^N {{{\left( {{k_i} + 1} \right)}^\alpha }} }}. $ | (2) |
当α < 0的时候,度数高的节点被保护,度数低的节点有较高的失效概率;当α>0的时候,度数低的节点被保护,度数高的节点有较高的失效概率;当α=0的时候,所有的节点具有相同的失效概率,就是随机失效.当α→+∞的时候,节点按照节点的度的高低顺序依次被删除,相反,当α→-∞时,节点删除的顺序为从低到高依次被删除.
将蓄意攻击转化为随机攻击的主要思想是找到一个等价的网络A′.当蓄意攻击发生后,我们删除了比例为(1-p)的节点,但是我们把剩余节点中导致失效的节点的边保留下来,接下来我们主要是求出剩余节点的度分布Pp(k).用Ap(k)表示剩余节点中度数为k的节点的数量,可以得到
| $ P_{p}(k)=\frac{A_{p}(k)}{p N_{A}}, $ | (3) |
当另一个节点去除的时候,Ap(k)的值为
| $ {A_{(p - 1/N)}}(k) = {A_p}(k) - \frac{{{P_p}(k){{(k + 1)}^\alpha }}}{{\sum\limits_k {{P_p}} (k){{(k + 1)}^\alpha }}}. $ | (4) |
当N→∞时,式(4)对p求导得
| $ \frac{{{\rm{d}}{A_p}(k)}}{{{\rm{d}}p}} = N\frac{{{P_p}(k){{(k + 1)}^\alpha }}}{{\sum\limits_k {{P_p}} (k){{(k + 1)}^\alpha }}}. $ | (5) |
结合式(3)和式(5)可得
| $ - p\frac{{{\rm{d}}{A_p}(k)}}{{{\rm{d}}p}} = {P_p}(k) - N\frac{{{P_p}(k){{(k + 1)}^\alpha }}}{{\sum\limits_k {{P_p}} (k){{(k + 1)}^\alpha }}}. $ | (6) |
为了求解式(6),我们定义一个新的函数
| $ {P_p}(k) = \frac{1}{p}P(k){t^{(k + 1)\alpha }}, $ | (7) |
| $ \sum\limits_{k} P_{p}(k)(k+1)^{\alpha}=\frac{t G_{\alpha}^{\prime}(t)}{G_{\alpha}(t)}. $ | (8) |
因此Pp(k)的生成函数为
| $ G_{A b}(x) \equiv \sum\limits_{k} P_{p}(k) x^{k}=\sum\limits_{k} P_{p}(k) t^{(k+1) \alpha} x^{k}. $ | (9) |
由于网络A中的连接是随机的,在剩余节点中边的删除概率等于剩余节点中边的数量与原始网络中边的数量比值:
| $ \tilde p \equiv \frac{{pN\langle k(p)\rangle }}{{N\langle k\rangle }} = \frac{{\sum\limits_k P (k)k{t^{(k + 1)\alpha }}}}{{\sum\limits_k P (k)k}}, $ | (10) |
其中:〈k〉是原始网络的平均度,〈k(p)〉是蓄意攻击后剩余网络中节点的平均度.我们运用文献[27]中的方法可以求得剩余节点的生成函数,
| $ {G_{Ac}}(x) \equiv {G_{Ab}}(1 - \tilde p + \tilde px). $ | (10) |
式(10)是网络A遭受蓄意攻击后剩余节点的生成函数.蓄意攻击的级联失效和随机攻击的级联失效只是在初始阶段受到攻击时分析的过程不相同,如果我们找到一个网络A′和它的生成函数
| $ \tilde{G}_{A 0}(x)=G_{A b}\left(1+\frac{\tilde{p}}{p}(x-1)\right). $ | (11) |
接下来运用随机攻击的分析过程来继续分析蓄意攻击下的级联失效,主要是用生成函数和渗流理论对级联失效的迭代过程进行详细数理分析,分析每一步失效后网络中功能节点的数量占原网络中节点总数的比值.网络A′的生成函数已经在前面式(11)求得,根据网络A′的生成函数我们可以求得剩余节点的度的分布生成函数,
| $ \tilde{G}_{A 1}(z)=\tilde{G}_{A 0}^{\prime}(z) / \tilde{G}_{A 0}^{\prime}(1). $ | (12) |
当网络A′受到随机攻击删除(1-p)比例的节点后,网络中剩余节点的度分布会发生变化,相应的度分布的生成函数也会变化.网络A′受到随机攻击而被去除节点后,网络中剩余节点的数量是N′A1=p·NA.其中功能节点的数量即最大连通簇中的节点数量与原始网络中节点数量的比值是
| $ g_{A}(p)=1-\tilde{G}_{A 0}\left[1-p\left(1-f_{A}\right)\right], $ | (13) |
其中:fA是关于p的函数,满足
| $ f_{A}=\tilde{G}_{A 1}\left[1-p\left(1-f_{A}\right)\right]. $ | (14) |
在网络B中可以得到与上述相似的理论,运用上述理论我们可以详细分析每一步的级联失效.运用生成函数的方法可以得到级联失效的迭代方程,在下一节中列出具体分析过程.
2.2 网络A′中的随机失效根据前面的分析,我们已经把蓄意攻击转化为随机攻击.在初始攻击时,网络A′发生随机失效,我们假设有(1-p)比例的节点因受到攻击而失效,可以求得剩余节点的数量为
| $ N_{A 1}^{\prime}=p \cdot N_{A}=\mu_{1}^{\prime} \cdot N_{A}, $ | (15) |
其中:μ′1是删除(1-p)比例的节点后剩余节点的数量与原始网络中节点数量的比值,由式(15)可以得到μ′1=p.根据前面的分析可以知道在N′A1中属于最大连通簇的节点数量是
| $ N_{A 1}=g_{A}\left(\mu_{1}^{\prime}\right) \cdot N_{A 1}^{\prime}=\mu_{1}^{\prime} \cdot g_{A}\left(\mu_{1}^{\prime}\right) \cdot N_{A}=\mu_{1} \cdot N_{A}, $ | (16) |
从式(16)中可以得到经过第一次失效后,保持功能的节点数量与原始网络中节点的比值为
| $ \mu_{1}=\mu_{1}^{\prime} \cdot g_{A}\left(\mu_{1}^{\prime}\right). $ | (17) |
由于信息物理系统的耦合性,网络B中节点的功能依赖网络A′中的节点,因此网络B中的节点会因网络A′中节点的失效而失效.由于网络B中的每一个节点与网络A′中3个节点连接,而且网络间的连接是随机的,因此可以得到网络B中有依赖关系的节点数量,
| $ N_{B 2}^{\prime}=\left[1-\left(1-\mu_{1}\right)^{3}\right] \cdot N_{B}=\left(\mu_{1}^{3}-3 \cdot \mu_{1}^{2}+3 \cdot \mu_{1}\right) \cdot N_{B}=\mu_{2}^{\prime} \cdot N_{B}, $ | (18) |
| $ \mu_{2}^{\prime}=\mu_{1}^{3}-3 \cdot \mu_{1}^{2}+3 \cdot \mu_{1}=\mu_{1}^{\prime} \cdot g_{A}\left(\mu_{1}^{\prime}\right) \cdot\left(\mu_{1}^{2}-3 \cdot \mu_{1}+3\right). $ | (19) |
与2.2节分析相似,我们可以求得在N′B2中属于最大连通簇的节点的数量是
| $ N_{B 2}=g_{B}\left(\mu_{2}^{\prime}\right) \cdot N_{B 2}^{\prime}=\mu_{2}^{\prime} \cdot g_{B}\left(\mu_{2}^{\prime}\right) \cdot N_{B}=\mu_{2} \cdot N_{B}, $ | (20) |
从式(20)可得
| $ \mu_{2}=\mu_{2}^{\prime} \cdot g_{B}\left(\mu_{2}^{\prime}\right). $ | (21) |
经过2.2和2.3两小节对级联失效的分析后,可以得到网络A′剩余节点中具有依赖关系的节点的数量. 根据2.2节的随机失效,我们可以得知网络B中的一个节点可能与网络A′中的1个、2个或3个节点连接,也可能不与网络A′中的任何节点连接.在表 1中我们列出了各种连接数量在原始网络中所占的比例.
|
|
表 1 网络B中依赖节点数量所占的比例 Tab. 1 The proportion of the number of dependent nodes in network B |
根据我们对耦合系统的建模,可以知道网内连接和网间连接没有任何关系,完全是随机的,因此网络A′中有依赖关系的节点数量为
| $ \begin{array}{l} N_{A3}^\prime = {\mu _2} \cdot {N_B} \cdot \left[ {C_3^1 \cdot {\mu _1} \cdot {{\left( {1 - {\mu _1}} \right)}^2} \cdot 1 + C_3^1} \right. \cdot \\ \left( {1 - {\mu _1}} \right) \cdot 2 + \mu _1^3 \cdot 3]/\left[ {1 - {{\left( {1 - {\mu _1}} \right)}^3}} \right], \end{array} $ | (22) |
所以N′A3=μ1·gB(μ′2)·NA.从NA1到N′A3,可以得到NA1-N′A3=(1-gB(μ′2))·NA1.
根据文献[27]中的理论,由于在初始阶段删除的节点不属于NB2、NA1和N′A1,因此从NA1中移除的节点等于从N′A1中移除相同比例的节点,所以NA1-N′A3=(1-gB(μ′2))·NA1=(1-gB(μ′2))·N′A1.总的移除的节点占原始网络A′的比例为
| $ 1-\mu_{1}^{\prime}+\left(1-g_{B}\left(\mu_{2}^{\prime}\right)\right) \cdot \mu_{1}^{\prime}=1-\mu_{1}^{\prime} \cdot g_{B}\left(\mu_{2}^{\prime}\right). $ | (23) |
从公式(23)可得μ′3=μ′1·gB(μ′2),因此在N′A3中属于最大连通簇的节点数量为
| $ N_{A 3}=\mu_{3}^{\prime} \cdot g_{A}\left(\mu_{3}^{\prime}\right) \cdot N_{A}=\mu_{3} \cdot N_{A}, \mu_{3}=\mu_{3}^{\prime} \cdot g_{A}\left(\mu_{3}^{\prime}\right). $ |
由于信息物理系统的耦合性,网络B中的节点会因2.4节中网络A′中节点的失效而失效.用与2.2节相似的方法,可以求得网络B中剩余节点中具有依赖关系的节点的数量
| $ N_{B 4}^{\prime}=\left[1-\left(1-\mu_{3}\right)^{3}\right] \cdot N_{B}=\left(\mu_{3}^{3}-3 \cdot \mu_{3}^{2}+3 \cdot \mu_{3}\right) \cdot N_{B}. $ | (24) |
从NB2到N′B4,可得
| $ N_{B 2}-N_{B 4}^{\prime}=\left[1-\left(\mu_{3}^{3}-3 \cdot \mu_{3}^{2}+3 \cdot \mu_{3}\right) / \mu_{2}\right] \cdot N_{B 2}. $ | (25) |
与2.4节分析过程一样,
| $ N_{B 2}-N_{B 4}^{\prime}=\left[1-\left(\mu_{3}^{3}-3 \cdot \mu_{3}^{2}+3 \cdot \mu_{3}\right) / \mu_{2}\right] \cdot N_{B 2}^{\prime}. $ | (26) |
因此,网络B中总的失效的节点数量为
| $ 1-\mu_{2}^{\prime}+\mu_{2}^{\prime} \cdot\left[1-\left(\mu_{3}^{3}-3 \cdot \mu_{3}^{2}+3 \cdot \mu_{3}\right) / \mu_{2}\right]=1-\mu_{1}^{\prime} \cdot\left(\mu_{3}^{2}-3 \cdot \mu_{3}+3\right) \cdot g_{A}\left(\mu_{3}^{\prime}\right), $ | (27) |
所以
| $ \mu_{4}^{\prime}=\mu_{1}^{\prime} \cdot\left(\mu_{3}^{2}-3 \cdot \mu_{3}+3\right) \cdot g_{A}\left(\mu_{3}^{\prime}\right). $ | (28) |
在N′B4中属于最大连通簇的节点数量为:
| $ N_{B 4}=\mu_{4}^{\prime} \cdot g_{B}\left(\mu_{4}^{\prime}\right) \cdot N_{B}, $ | (29) |
| $ {\mu _4} = \mu _4^\prime \cdot {g_B}\left( {\mu _4^\prime } \right). $ | (30) |
根据前面分析级联失效过程的方法,可以知道每一步级联失效后网络中节点的数量,用式(31)表示,
| $ \left\{\begin{array}{l}{\mu_{2 i}^{\prime}=\mu_{1}^{\prime} \cdot\left(\mu_{2 i-1}^{2}-3 \cdot \mu_{2 i-1}+3\right) \cdot g_{A}\left(\mu_{2 i-1}^{\prime}\right)} \\ {\mu_{2 i+1}^{\prime}=\mu_{1}^{\prime} \cdot g_{B}\left(\mu_{2 i}^{\prime}\right)}\end{array}\right., $ | (31) |
其中:μ′1=p,下面我们找到一种方法对式(31)进行详细分析,进而求得临界阈值.
3 实验仿真及分析在本节中,我们主要对前面得到的式(31)进行分析求解,并通过仿真实验对结果进行验证.
3.1 方程求解对于耦合系统的级联失效,虽然我们不知道级联失效具体在哪一步停止,但是当级联失效停止的时候网络不会再失效.因此可得
| $ \left\{\begin{array}{l}{\mu_{2 i}^{\prime}=\mu_{2 i-2}^{\prime}=\mu_{2 i+2}^{\prime}} \\ {\mu_{2 i+1}^{\prime}=\mu_{2 i-1}^{\prime}=\mu_{2 i+3}^{\prime}}\end{array}\right.. $ | (32) |
为了方便分析级联失效的迭代公式,定义变量x、y满足方程组
| $ \left\{\begin{array}{l}{y=\mu_{2 i}^{\prime}=\mu_{2 i-2}^{\prime}=\mu_{2 i+2}^{\prime}} \\ {x=\mu_{2 i+1}^{\prime}=\mu_{2 i-1}^{\prime}=\mu_{2 i+3}^{\prime}, \quad 0 \leqslant x, y \leqslant 1}\end{array}\right.. $ | (33) |
因此式(31)可以用式(34)表示
| $ \left\{\begin{array}{l}{y=p \cdot\left(\left(x \cdot g_{A}(x)\right)^{3}-3 \cdot x \cdot g_{A}(x)+3\right) \cdot g_{A}(x)} \\ {x=p \cdot g_{B}(y)}\end{array}\right.. $ | (34) |
对式(34)消元,可得
| $ x=p \cdot g_{B}\left[p \cdot\left(\left(x \cdot g_{A}(x)\right)^{3}-3 \cdot x \cdot g_{A}(x)+3\right) \cdot g_{A}(x)\right]. $ | (35) |
对于一些常见的网络,比如随机网络和无标度网络,这个方程式的求解是比较困难的,因此我们用画图的方式来求近似解.首先把式(35)写成
| $ \left\{\begin{array}{l}{z=x} \\ {z=p \cdot g_{B}\left[p \cdot\left(\left(x \cdot g_{A}(x)\right)^{3}-3 \cdot x \cdot g_{A}(x)+3\right) \cdot g_{A}(x)\right]}\end{array}\right., $ | (36) |
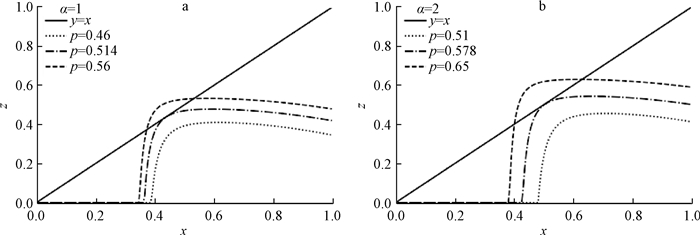
然后根据式(36)在图中把这两条线画出来,两条线相切的时候就是方程(34)的解,我们把求出来的解称为临界阈值pc.具体如图 1所示.从图 1a可以看到,设定3个不同的p值,通过计算曲线与直线之间的距离可以得到比较精确的理论解.从图 1a可以求得α=1时,pc=0.514,其中α是概率方程中的参数.从图 1a可以看到当p值小于临界阈值0.514时,曲线与直线在(0, 1]区间内没有交点,当等于临界阈值pc时,曲线与直线相切,当p值大于临界阈值pc时,曲线与直线有两个交点.用与图 1a中相同的方法我们可以求得α=2时,pc=0.578.图 1中的b图与a图具有相似的规律.至此我们已经求得耦合系统遭受蓄意攻击时的临界阈值,为了确保结果的正确性,我们会通过仿真实验来验证结果的正确性.
|
图 1 对方程(36)的求解 Fig. 1 Solution of equation (36) |
接下来我们对结果进行验证,主要是通过数值模拟来验证结果的正确性.首先创建两个随机网络,网络的节点数量分别为12 000和4 000,然后按照前面所描述的模型,使两个网络连接在一起,即网络A中的3个节点随机与网络B中的1个节点连接,而且这种连接方式是完全随机的.这样我们就使两个网络耦合在一起,用前面提出的概率方程表示蓄意攻击,即根据概率方程来确定每一个节点失效的概率.在模拟级联失效的过程中,每一步级联失效后节点的数量会被保存在文件里,方便对数据进行分析.当组成耦合网络的两个网络中都没有节点被删除,就认为级联失效已经停止.当级联失效停止的时候, 我们会统计每一次级联失效结束时耦合系统中的两个网络剩余节点的数量.
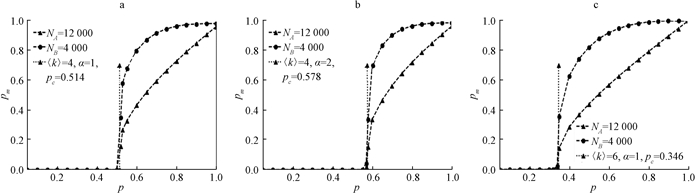
图 2中的横坐标表示网络受到蓄意攻击后没有被攻击的节点数量与原始网络中的节点数量的比值,受到攻击的节点的比例为(1-p),纵坐标表示级联失效停止的时候两个网络中剩余节点的比例.在图 2a中,取α=1,组成耦合系统的两个网络的节点平均度为〈k〉=4;在图 2b中,取α=2,其余与图 2a中的条件一样.对比图 2a和图 2b可以发现, 当α增大,临界阈值pc也在增大,说明网络的可靠性降低了.α的增大说明网络中度比较大的节点受到攻击的概率在增大,因此网络的可靠性降低,实验结果与预期的结果一致,说明我们的结论是正确的.图 2c中取α=1,〈k〉=6,对比图 2a和图 2c可以看到, 随着节点度的增大,临界阈值pc在减小,临界阈值的减小说明耦合系统的可靠性在增强.我们知道当网络的度增大说明网络之间的连接越来越紧密,因此网络的可靠性会增大,实验结果与我们的预期结果一致,进一步验证了结论的正确性.在模拟级联失效的过程中,为了确保实验的正确性,我们对每一个p值重复进行了50次实验,然后取平均值,而且在临界阈值附近多取了两组p值,可以更好地观察在临界阈值附近耦合系统的可靠性.
|
图 2 网络中剩余节点的比例 Fig. 2 The fraction of survivals in both networks |
从图 2中可以看到,当级联失效停止的时候,耦合系统中的一个网络完全崩溃,另一个网络也一定会完全崩溃,同样当一个网络存在一部分功能节点,另一个网络也会存在一部分功能节点,而且功能节点的数量与p值成正比.从图 2中还可以看到,当p值小于临界阈值pc的时候,耦合系统完全崩溃,当p的取值大于临界阈值的时候,耦合系统中的两个网络都会存在一部分功能节点,即耦合系统还保存基本的功能,当p的取值在临界阈值附近的时候,耦合系统可能完全崩溃,也可能保存有基本的功能,又一次验证了我们结论的正确性.
在图 2中的临界阈值附近,即黑色箭头所表示的位置,可以看到当p的取值大于临界阈值的时候,两个网络的变化趋势接近直线上升,这种现象表示当p值大于临界阈值的时候耦合系统不会完全崩溃.从图 2可以看到上面的曲线表示的是B中剩余的节点所占的比例,下面的曲线表示网络A中剩余的节点所占的比例.由于网络攻击发生在网络A中,我们可以看到网络A中的节点所占的比例总是低于网络B中的节点所占的比例.这是网络B中的1个节点与网络A中的3个节点相连接的关系导致,因此网络B中的节点会受到一定程度的保护.对于现实中一些比较重要的耦合系统,我们可以把一些关键的节点连接多条依赖边进行保护,来提高耦合系统的可靠性.
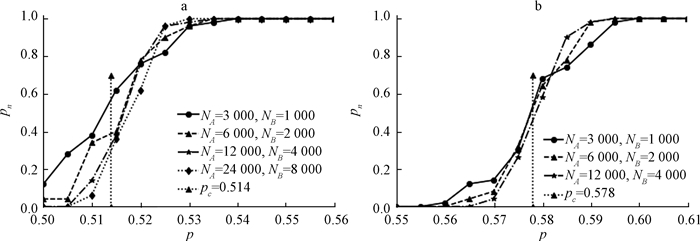
在图 3中我们在临界阈值附近选取多个值进行比较分析,其中纵坐标Pn表示级联失效停止的时候最大连通簇存在的概率.例如,在α=1、〈k〉=4、临界阈值pc=0.514的时候,在[0.50, 0.56]区间内每隔0.005取一个点,每个点进行50次实验,统计耦合系统没有完全崩溃的次数,最后把得到的数据用图 3a表示. 图 3b中取α=2,用与图 3a相同方法验证.从图 3中我们可以看到, 耦合系统的节点数量从小到大依次递增,随着节点数量的增加, 曲线越来越靠近临界阈值,临界阈值用黑色箭头表示,当节点的数量足够大的时候, 曲线会在临界阈值附近产生一阶相变,与在单个网络中的二阶相变是完全不同的.
|
图 3 耦合系统没有完全崩溃的概率 Fig. 3 The probability of having a giant component |
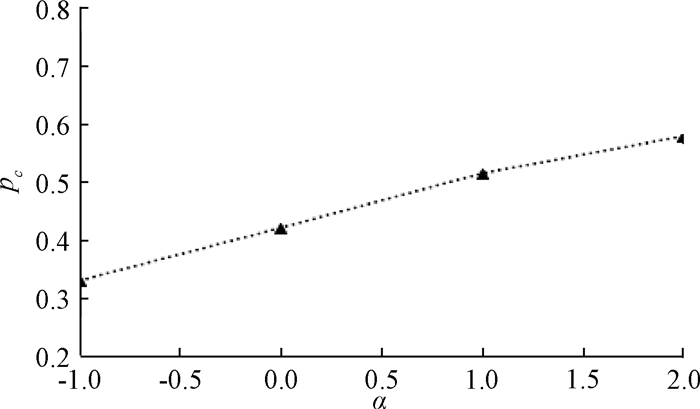
图 4是对比不同α情况下,临界阈值的变化情况,α的取值为-1、0、1、2,对于每一个α的取值, 用上述理论分别求出对应的临界阈值,为了比较pc和α之间的关系,规定在这4种α取值下的耦合系统的平均度相同,平均度的取值都为〈k〉=4,具体变化趋势如图 4表示.图 4中横坐标是概率方程的参数α,纵坐标是临界阈值pc,从图 4中可以看到临界阈值pc和概率方程的参数α成正比关系,随着α的增大pc的值也在不断增大.
|
图 4 pc与α之间的关系 Fig. 4 The relationship between pc and α |
信息物理系统是一个在探索中的、非常有发展前景的研究领域,引起国内外学者对该领域的广泛关注.目前对该领域的研究,主要聚焦在将网络技术、控制技术、通信技术和物理学、网络科学、社会学等相关领域知识相结合,以完善信息物理系统的理论框架,并对信息物理系统的安全性、自治性和高性能进行研究.
本文针对信息物理系统进行安全评估,是保证CPS安全、稳定、连续运行的基础.本文提出了信息物理系统的分析模型和安全评估指标,在蓄意攻击策略下,考虑了信息物理系统对该攻击行为的级联失效过程.在安全估计的度量中,考虑了影响信息物理系统安全性的主要因素,并基于仿真实验给出了对比分析的验证.下一步的研究工作,将进一步优化该模型,提高安全评估模型在大规模信息物理系统中的应用效率;同时在确定影响级联失效的评估要素上,提高分析的成功率,从而实现失效的最小成本修复.
| [1] |
李仁发, 谢勇, 李蕊, 等. 信息-物理融合系统若干关键问题综述[J]. 计算机研究与发展, 2012, 49(6): 1149-1161. (  0) 0) |
| [2] |
何明, 梁文辉, 陈希亮, 等. CPS系统体系结构顶层设计研究[J]. 计算机科学, 2013, 40(11): 18-22. DOI:10.3969/j.issn.1002-137X.2013.11.004 (  0) 0) |
| [3] |
何廷润. "工业4.0"战略中CPS系统的挑战与前瞻[J]. 移动通信, 2014, 38(21): 19-21. DOI:10.3969/j.issn.1006-1010.2014.21.004 (  0) 0) |
| [4] |
JONES D, ROONEY P, BISSELL R E. American competitiveness initiative[J]. World education information, 2006, 16: 1-25. (  0) 0) |
| [5] |
杨解朴. 解读中德创新伙伴关系[J]. 当代世界, 2014(11): 21-23. DOI:10.3969/j.issn.1006-4206.2014.11.006 (  0) 0) |
| [6] |
中国信息物理系统发展论坛.信息物理系统白皮书[R/OL].(2018-03-02)[2018-12-01]. http://www.cesi.cn/201703/2251.html.
(  0) 0) |
| [7] |
张恒.信息物理系统安全理论研究[D].杭州: 浙江大学, 2015.
(  0) 0) |
| [8] |
李钊, 彭勇, 谢丰, 等. 信息物理系统安全威胁与措施[J]. 清华大学学报(自然科学版), 2012, 52(10): 1482-1487. (  0) 0) |
| [9] |
李伯宇, 高飞, 朱建平, 等. 信息物理系统研究与应用综述[J]. 成都信息工程学院学报, 2014, 29(4): 388-393. DOI:10.3969/j.issn.1671-1742.2014.04.011 (  0) 0) |
| [10] |
邢静宇, 张立臣. 信息物理系统安全及相关措施[J]. 计算机系统应用, 2014, 23(6): 1-6. DOI:10.3969/j.issn.1003-3254.2014.06.001 (  0) 0) |
| [11] |
郑明辉, 吕含笑, 段洋洋. 相同敏感值数据集的隐私保护泛化算法[J]. 郑州大学学报(理学版), 2018, 50(2): 35-40. (  0) 0) |
| [12] |
李曦, 孙贝磊, 万波, 等. 安全关键信息物理系统的时序可预测性[J]. 计算机科学, 2017, 44(S2): 490-493. (  0) 0) |
| [13] |
敖伟.信息物理系统中攻击检测与安全状态估计问题研究[D].重庆: 重庆大学, 2017.
(  0) 0) |
| [14] |
蔡亮.基于故障树的信息安全风险评估方法研究[D].武汉: 华中科技大学, 2008.
(  0) 0) |
| [15] |
张晖, 杨小彦, 赵旭剑, 等. 基于社会网络关注度的学科前沿热点挖掘[J]. 郑州大学学报(理学版), 2018, 50(3): 49-55. (  0) 0) |
| [16] |
YOUNES M B, BOUKERCHE A. A performance evaluation of a fault-tolerant path recommendation protocol for smart transportation system[J]. Wireless networks, 2018, 24(2): 345-360. DOI:10.1007/s11276-016-1335-7 (  0) 0) |
| [17] |
邓良辰, 刘艳丽, 柏天缘. 考虑分布式发电的配电网CPS可靠性评估[J]. 电力系统及其自动化学报, 2017, 29(11): 32-38. DOI:10.3969/j.issn.1003-8930.2017.11.006 (  0) 0) |
| [18] |
高洋, 马洋洋, 张亮, 等. 伴随随机攻击的信息物理系统的同步控制[J]. 清华大学学报(自然科学版), 2018, 58(1): 14-19. (  0) 0) |
| [19] |
CHEN X D, ZHOU Y C, ZHOU H, et al. Analysis of production data manipulation attacks in petroleum cyber-physical systems[C]//IEEE/ACM International Conference on Computer-Aided Design(ICCAD). Austin, 2017: 108.
(  0) 0) |
| [20] |
SABALIAUSKAITE G, MATHUR A P. Aligning cyber-physical system safety and security[C]//Asia-Pacific Conference on Complex Systems Design & Management. Singapore, 2015: 41-53.
(  0) 0) |
| [21] |
FANG Y P, ZIO E. Optimizing the resilience of interdependent infrastructure systems against intentional attacks[C]//International Conference on System Reliability and Safety. Milan, 2017: 62-67.
(  0) 0) |
| [22] |
BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025-1028. DOI:10.1038/nature08932 (  0) 0) |
| [23] |
HUANG Z, WANG C, RUJ S, et al. Modeling cascading failures in smart power grid using interdependent complex networks and percolation theory[C]//IEEE International Conference on Industrial Electronics & Applications. Melbourne, 2013: 1023-1028.
(  0) 0) |
| [24] |
BABALOLA A A, BELKACEMI R, ZARRABIAN S. Real-time cascading failures prevention for multiple contingencies in smart grids through a multi-agent system[J]. IEEE transactions on smart grid, 2018, 9(1): 373-385. DOI:10.1109/TSG.2016.2553146 (  0) 0) |
| [25] |
YAGAN O, QIAN D J, ZHANG J S. Optimal allocation of interconnecting links in cyber-physical systems: interdependence, cascading failures, and robustness[J]. IEEE transactions on parallel & distributed systems, 2012, 23(9): 1708-1720. (  0) 0) |
| [26] |
GALLOS L K, COHEN R, ARGYRAKIS P, et al. Stability and topology of scale-free networks under attack and defense strategies[J]. Physical review letters, 2005, 94(18): 188701. DOI:10.1103/PhysRevLett.94.188701 (  0) 0) |
| [27] |
SHAO J, BULDYREV S V, BRAUNSTEIN L A, et al. Structure of shells in complex networks[J]. Physical review E, 2009, 80(3): 036105. DOI:10.1103/PhysRevE.80.036105 (  0) 0) |
 2019, Vol. 51
2019, Vol. 51


