随着VR/AR技术的飞速发展,其技术要求也越来越高。除了通过建模工具构造虚拟的三维场景外,基于视觉技术将真实场景或物体直接转化为三维数据的三维重建技术受到了大量的关注。由于互联网海量图片的存在,以及场景图像的易获取性,许多研究者考虑利用同一个场景或物体在不同视角下的图片,根据视觉原理实现三维重建。
由于所使用的不同视角图片往往来自于不同的拍照环境,没有经过精确标定的相机参数,需要在多幅未标定的图像中通过特征点集匹配来恢复相机位姿,从而得到三维重建结果[1]。相机位姿恢复技术也可用于图像拼接[2],将含有重叠部分的两幅或多幅图像,拼接成一幅包含各图像信息的高分辨率、宽视角图像。恢复多张图像中相机位姿的基础是两张图像中的相机相对位姿的恢复,而相机间的相对位姿信息又包含在图像间的基础矩阵中,因此基础矩阵估算成为研究的重点内容之一。
估算基础矩阵是从一组含有粗差点的数据集中估计最优的矩阵。早期使用的关键点通常为图像中的角点,包括Harris[3]、FAST[4]等,主要根据邻域内的灰度变化来判断一个点是否为角点[5]。为了降低因图像旋转、缩放对角点检测准确性的影响,尺度不变特征变换匹配(scale invariant feature transform, SIFT)算法[6]以其对旋转、缩放等因素的鲁棒性,受到了广泛的关注。特征描述符的维数越高,越会影响算法时效性,将主成分分析(principal components analysis, PCA)算法与SIFT算法结合的PCA-SIFT方法[7]可以有效降低特征维数,提高算法速度。加速稳健特征(speeded up robust features, SURF)算法[8]对关键点的提取效率做了提升,但由于拍摄环境的不同,在特征点集的匹配过程中,完全使用自动的特征点提取与匹配算法往往导致误匹配,进而影响后续的重建精度。
建立了图像之间的特征点匹配关系后,就可以对两幅图像之间的基础矩阵进行估算。传统的8点估计算法[9]计算简单且易于实现,适用于简单图像匹配,但是对复杂情况适应性较差,实际应用比较困难。鲁棒性算法因具有剔除误匹配点、抗噪声干扰的优点,成为研究的主要方向。最小二乘法[10]对异常点敏感,当图像存在大量的异常点时很难准确估计出模型,而随机采样一致(random sample consensus, RANSAC)算法[11]通过迭代,逐步过滤误匹配点并取得最优模型,是目前应用最广泛的鲁棒算法之一。为了进一步提高RANSAC算法的估计精度,文献[12]在基础矩阵估算过程中,引入了特征直线作为几何约束。文献[13]在采用对极几何误差来识别误匹配点,通过去除误匹配点提高基础矩阵的估算精度。但这些方法本身引入了更多需要人为设定的经验性阈值,也带来了计算过程的不稳定性。
本文针对多相机分别采集的多幅图像,引入图像之间的单应变换,实现对基础矩阵的更精确计算。首先提取图像上较强的特征点,在特征点对之间寻找一个单应变换,该单应变换意味着在图像所对应的三维场景中存在着一个平面,而该平面在不同图像上的投影平面之间满足该单应变换。随后再利用位于该平面之外的其余特征点匹配对,对两幅图像之间的可能基础矩阵进行计算,并根据内点数量选择最佳的基础矩阵。该方法利用单应变换作为基础矩阵估计的约束,降低了RANSAC算法对图像间内点比率的依赖,在不提高算法复杂度的前提下,通过提高基础矩阵内点比率来改善其估计精度。实验结果表明,本文算法计算出的基础矩阵在图像点到对极线的距离误差要优于目前主流算法,且鲁棒性较好、运算速度快。
1 对极几何原理 1.1 单应矩阵当图像中的场景存在平面或近似平面,或者存在低时差区域的情况时,可以使用单应变换将该区域位于图像平面上的一个坐标点,映射到另一个图像平面上。这种变换可以表示为
| $ \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}_1} = {\mathit{\boldsymbol{x}}_2}, $ | (1) |
其中:x1和x2分别为两张图像上的坐标点x1和x2的齐次坐标形式;H是一个3×3的非奇异矩阵。当已知某个三维空间点在一幅图像上的投影点位置后,通过单应矩阵,可求出其在另一幅图像上的投影点位置。
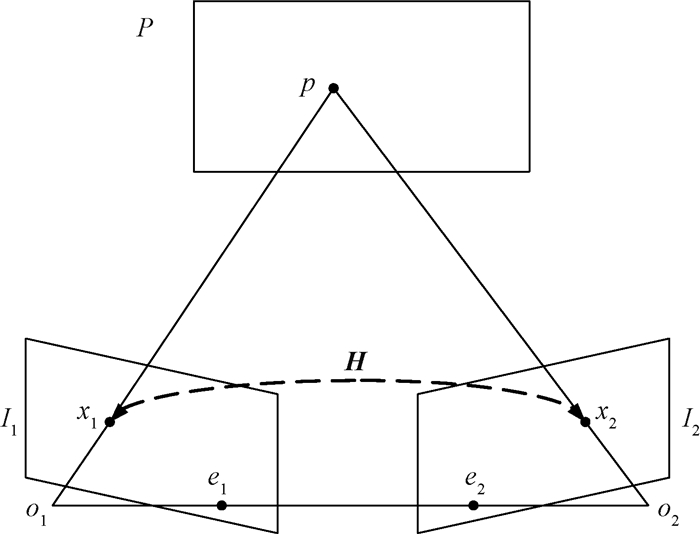
如图 1所示,空间平面P上的一个点p,在图像I1上的投影点为x1,则根据公式1可以得到其在图像I2上的成像点x2。通过公式(1)求出平面P在两幅图像之间的单应矩阵H。
|
图 1 单应变换 Fig. 1 Homography transformation |
由于H包含了‖H‖=1的约束,该矩阵共有8个未知量,需要至少4个特征点匹配对可以计算出来。在实际场景中,得到的匹配对中往往包含噪声,比如由于图像分辨率导致像素位置的偏差,或者特征点的误匹配。通常采用RANSAC算法来提高单应矩阵计算方法的鲁棒性。
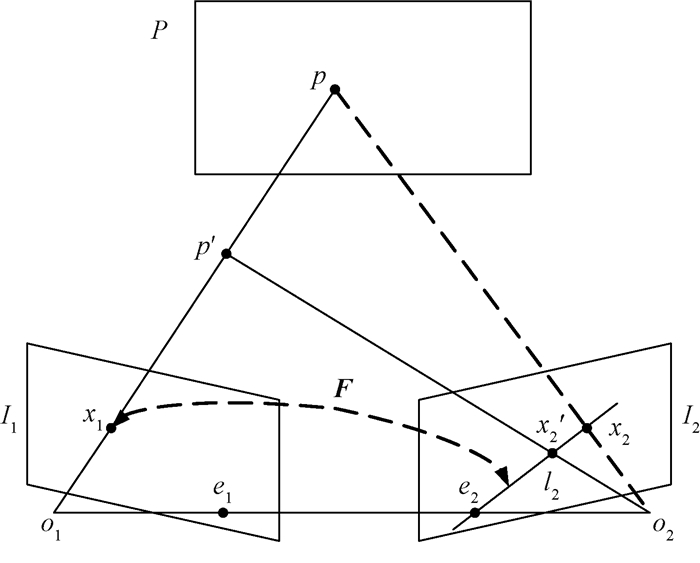
1.2 基础矩阵以上我们分析了在三维空间中位于平面P上的点p在不同图像上的投影成像点所满足的约束。对于不在平面P上的点p′,当对它采用矩阵H进行转换的时候,如图 1所示,会得到错误的投影成像点x2,而实际的投影成像点应当为x′2。也就是说,即使已知p′在图像I1上的投影成像点x1,也无法通过单应矩阵H计算出p′在图像I2上的对应投影成像点。但是,对于两个成像点x2和x′2,它们的连线为直线l2,即x1在图像I2上的对极线。由于拍摄两幅图像的相机参数不同,可通过基础矩阵来描述图像I1上任意一点在图像I2上对应的对极线。
|
图 2 对极几何约束 Fig. 2 Constraint on epipolar geometry |
在任意场景多种结构的两幅图像间对极约束都成立。根据图像上的像点位置,可找到另一幅图像上的对应像点所位于的对极线,
| $ \mathit{\boldsymbol{x}}_2^{\rm{T}}\mathit{\boldsymbol{F}}{x_1} = 0, $ | (2) |
为了求解公式(2)中的基础矩阵F,通常使用8点法,即需要获取8个点对坐标。与单应矩阵的求解方法类似,通过使用RANSAC迭代过滤误匹配点,提高基础矩阵的求解鲁棒性。
2 利用单应变换的基础矩阵求解算法 2.1 算法原理从前述的分析中得知,当图像场景内的点位于相同平面或近似平面时,可以根据某点p在图像I1中的投影点x1的位置,通过单应矩阵H计算出其在图像I2中的对应投影点x2的准确位置。同时,也可以通过基础矩阵F来获得该点在I2中的对极线l2。而x2必然位于l2上。也就是说,该点p在不同图像上的投影坐标应当同时满足公式(1)和公式(2)。
令
| $ \left\{ {\begin{array}{*{20}{c}} {{h_{11}}{u_1} + {h_{12}}{v_1} + {h_{13}} = \left( {{h_{31}}{u_1} + {h_{32}}{v_1} + {h_{33}}} \right){u_2}}\\ {{h_{21}}{u_1} + {h_{22}}{v_1} + {h_{23}} = \left( {{h_{31}}{u_1} + {h_{32}}{v_1} + {h_{33}}} \right){v_2}} \end{array}} \right., $ |
再整理成类似公式(2)的形式,即
| $ \left\{ {\begin{array}{*{20}{c}} {\left( {{u_2}\;\;\;\;\;{v_2}\;\;\;\;\;1} \right) \times \left[ {\begin{array}{*{20}{c}} {{h_{31}}}&{{h_{32}}}&{{h_{33}}}\\ 0&0&0\\ { - {h_{11}}}&{ - {h_{12}}}&{ - {h_{13}}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {{v_1}}\\ 1 \end{array}} \right]{\rm{ = }}0}\\ {\left( {{u_2}\;\;\;\;\;{v_2}\;\;\;\;\;1} \right) \times \left[ {\begin{array}{*{20}{c}} 0&0&0\\ {{h_{31}}}&{{h_{32}}}&{{h_{33}}}\\ { - {h_{21}}}&{ - {h_{22}}}&{ - {h_{23}}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {{v_1}}\\ 1 \end{array}} \right]{\rm{ = }}0} \end{array}} \right., $ | (3) |
进而可以将公式(3)简写为
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}_2^{\rm{T}}{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{x}}_1} = 0}\\ {\mathit{\boldsymbol{x}}_2^{\rm{T}}{\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{x}}_1} = 0} \end{array}} \right., $ | (4) |
其中M1、M2均为由H的参数所构成的矩阵。
如前所述,空间中位于平面P上的点p在不同图像上的投影坐标应当同时满足公式(1)和公式(2),利用这一性质,建立基础矩阵F的各项与单应矩阵H的系数关系。由于基础矩阵F的秩为2,因此将其与公式(4)联立为
| $ \mathit{\boldsymbol{F}} = a{\mathit{\boldsymbol{M}}_1} + b{\mathit{\boldsymbol{M}}_2}, $ | (5) |
将公式(5)代入公式(2),得到
| $ \mathit{\boldsymbol{x}}_2^{\rm{T}}\left( {a{\mathit{\boldsymbol{M}}_1} + b{\mathit{\boldsymbol{M}}_2}} \right){\mathit{\boldsymbol{x}}_1} = 0, $ | (6) |
为了求解公式(6)中的两个未知量a和b,进一步将公式(6)整理为
| $ \left( {\mathit{\boldsymbol{x}}_2^{\rm{T}}{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{x}}_1}} \right)a + \left( {\mathit{\boldsymbol{x}}_2^{\rm{T}}{\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{x}}_1}} \right)b = 0, $ | (7) |
因为H包含了‖H‖=1约束,所以我们可以令h33=1。类似地,对于
| $ a{h_{13}} + b{h_{23}} = - 1。$ | (8) |
式(7)和(8)表示了基础矩阵F的各项与单应矩阵H的系数关系。为了进一步求解其中的两个未知量,需要用到不属于平面P的点p′,其在不同图像上的投影坐标满足公式(2)但不满足公式(1)。将p′在图像I1和I2上的投影成像点坐标代入公式(7)和(8)求解系数a和b,从而根据公式(5)来计算得到基础矩阵F的值。
由于RANSAC方法通过随机选择若干个点作为内点进行基础矩阵估计,其精度较为依赖于内点比率。当图像之间的内点比率较低时,RANSAC方法难以准确找到适合用于估算基础矩阵的若干内点,往往陷于局部最优解。而使用单应变换作为基础矩阵变换估计的前置约束,则有效地利用了满足单应变换的平面信息,在降低计算复杂度的同时,也降低了对内点选择的困难度,并通过最大化基础矩阵的内点数量来确保其更加适应图像上各个像素的变换,也就是提高了基础矩阵的估计精度。
2.2 算法步骤首先在图像I1和I2上采用SURF算法检测特征点,然后通过K-最近邻方法建立两幅图像上特征点的匹配关系,该匹配关系包含一定的噪声。我们对全部匹配对进行过滤,将偏转角度过大或距离过远的匹配对去除。
在对各个特征点的坐标进行归一化[14]之后,通过RANSAC算法可以求得图像I1和I2之间的单应矩阵H。将阈值设为1个像素,即图像I1上的特征点经过单应矩阵变换后,所得到的像素坐标与图像I2上的匹配特征点的距离不应超过1个像素。该约束会倾向于将更多的特征点匹配对标记为外点,并保证所求得的单应矩阵能够很好地满足内点的变换。根据前文的分析,如果1个三维空间中的点p,在图像I1与I2上的投影点x1和x2满足公式1,则点p应当位于平面P上。此时得到的内点即位于该平面上。为了进一步获得平面P在图像之间更准确的单应矩阵H,我们对全部内点根据变换像素与实际特征点之间的误差进行排序,然后利用误差最小的50个内点重新计算单应矩阵H。
我们根据第一次计算H时的外点集合,和第二次计算得到的H,来进行对基础矩阵F的计算。根据式(5)、(7)和(8),对图像之间的各个像素点匹配对计算相应的基础矩阵,并通过统计各个基础矩阵所拥有的内点数量,选择具有最多内点的基础矩阵F。具体算法步骤如下。
for pair(x1, x2)∈Outlier(H)
a, b←solve(x1, x2, M1, M2) //将匹配对的像素齐次坐标代入公式(7)和(8)
Fpair(x1, x2)←aM1+bM2 //根据公式(5)计算基础矩阵
for every pair(xi, xj)
d ←distance(x, l) //计算特征点到相应对极线的距离
if d < δ
Inlier(Fpair(x1, x2)).append(pair(xi, xj)) //将该点对标记为内点
else
Outlier(Fpair(x1, x2)).append(pair(xi, xj)) //将该点对标记为外点
N(Fpair(x1, x2)) ←count(Inlier(Fpair(x1, x2))) //统计内点数量
F←
通过采用上述的算法步骤,我们最大化了F的内点数量,找到符合最多特征点匹配对的基础矩阵变换。在实际中,特征点到对极线的距离阈值δ通常设为1个像素。
3 实验 3.1 数据集我们使用了Middlebury数据集中的2001和2003两部分[14-15]作为实验数据集。该数据集共包含了8个场景,每个场景由9张图像组成。由于该数据集中的场景图像主要为平移运动,缺少旋转和缩放变换,所以我们在其基础上,另外采集了一组场景图像,将其命名为Building,作为Middlebury数据集的补充,如图 3所示。

|
图 3 场景Building图像 Fig. 3 Scene Building image |
我们首先对所有图像进行了裁剪和缩放,将分辨率统一为512×512。然后在各个场景的图像之间建立SURF特征点匹配对,并将其中的部分匹配显示如图 4所示。当对特征点匹配对进行过滤后,部分匹配显示如图 5所示。

|
图 4 场景图像之间的特征点匹配 Fig. 4 Feature point matching between scene images |

|
图 5 场景图像之间过滤后的特征点匹配 Fig. 5 Matching of filtered feature points between scene images |
可以看到,经过过滤后,剩余的匹配对具有相似的角度和距离。这对建立两幅图之间的单应矩阵变换有很大帮助。
3.2 基础矩阵投影为了验证本文提出的基础矩阵计算方法的有效性和鲁棒性,将本文方法与RANSAC算法[10]作对比实验。将图像在不同基础矩阵上的Sampson距离作为对基础矩阵估计精度的评价误差。由于在本文算法中,对于检测出的特征点匹配对进行了过滤,在对比实验中,我们采用了有过滤RANSAC和无过滤RANSAC两种不同的策略。
表 1给出了不同算法在各个图像场景中的平均误差,单位为0.1像素。能够看到3种算法在该项指标上的性能较接近。在大部分场景中,最好与最差结果之间的差距约为0.01像素。
|
|
表 1 各算法的整体平均误差 Tab. 1 The overall average error of each algorithm |
|
|
表 2 各算法的内点率 Tab. 2 The interior point rate of each algorithm |
表 2给出了不同算法在各个图像场景中的内点率,即到对极线的距离小于1个像素的特征点。应当注意的是,该评价是在全部特征点上进行,也就是包含了被过滤的特征点。可以看到,本文算法在内点率上取得了最好的效果,在大部分场景中均提高了2%。
表 3给出了不同算法在各个图像场景中的平均内点误差,单位为0.000 1像素。本文算法在几乎全部场景中的该项指标上均取得了最佳结果,与其他几种算法相比有明显的改进。相应地,有过滤的RANSAC算法平均误差比无过滤时也有所降低。考虑到几种算法在整体平均误差上的差距不大,但在内点率上具有一定差距,说明本文算法所计算出的基础矩阵更好地符合场景中内点的变换,而放大了外点的误差。
|
|
表 3 各算法在内点上的平均误差 Tab. 3 The average error of each algorithm on interior point |
|
|
表 4 各算法在外点上的平均误差 Tab. 4 The average error of each algorithm on outer point |
表 4给出了不同算法在各个图像场景中的平均外点误差,单位为1像素。可以看到,本文算法在大部分场景中获得了最大的外点误差,这也再次验证了前面的分析结论,即本文算法通过更好地拟合内点变换,同时进一步排斥外点,以计算出场景中不同图像之间的基础矩阵。
通过对以上各表中的数据进行分析,本文算法在提高了内点率的同时,显著降低了内点的平均误差,从而体现出了更好的有效性和鲁棒性。这是由于RANSAC方法通过随机选择若干个点作为内点估算基础矩阵,其精度较为依赖于内点比率,容易陷于局部最优解。本文方法将单应变换作为基础矩阵变换估计的前置约束,有效地利用了场景中满足单应变换的平面部分信息,降低了对内点选择的困难度,并通过最大化基础矩阵的内点数量来确保其更适应图像上各个像素的变换,提高了基础矩阵的估计精度。
4 结语本文针对图像场景内的多幅不同视点图像,提出了一种通过单应变换和对极约束的基础矩阵估计算法。该方法利用场景内位于相同平面或近似平面上的空间点,计算图像间的单应变换,再根据对极几何约束,通过平面外的其余空间点,从单应矩阵进一步计算出图像间的基础矩阵。通过在公开图像数据集与自行采集图像数据上进行对比实验,实验结果说明了本文算法的有效性和鲁棒性,能够很好地过滤特征点匹配对中的噪声并去除误匹配,计算出更可靠精度的基础矩阵。在未来的工作中,本文算法可推广至规模更大的图像集上应用,并为不同相机位姿测算、图像拼接、点云恢复、三维重建等工作提供了良好的基础。
| [1] |
SCHÖNBERGER J L, FRAHM J M. Structure-from-motion revisited[C]//2016 IEEE Conference on Computer Vision And Pattern Recognition. Las Vegas, 2016: 4104-4113.
(  0) 0) |
| [2] |
裴红星, 刘金达, 葛佳隆, 等. 图像拼接技术综述[J]. 郑州大学学报(理学版), 2019, 51(4): 1-10, 29. PEI H X, LIU J D, GE J L, et al. A review on image mosaicing techniques[J]. Journal of Zhengzhou University (natural science edition), 2019, 51(4): 1-10, 29. (  0) 0) |
| [3] |
QIAO Y J, TANG Y C, LI J S. Improved harris sub-pixel corner detection algorithm for chessboard image[C]//Proceedings of the 2013 2nd International Conference on Measurement, Information and Control. Harbin, 2013: 1408-1411.
(  0) 0) |
| [4] |
TRAJKOVIĆ M, HEDLEY M. Fast corner detection[J]. Image and vision computing, 1998, 16(2): 75-87. DOI:10.1016/S0262-8856(97)00056-5 (  0) 0) |
| [5] |
WANG Z C, LI R, SHAO Z H, et al. Adaptive harris corner detection algorithm based on iterative threshold[J]. Modern physics letters B, 2017, 31(15): 1750181. DOI:10.1142/S0217984917501810 (  0) 0) |
| [6] |
LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 (  0) 0) |
| [7] |
KE Y, SUKTHANKAR R. PCA-SIFT: a more distinctive representation for local image descriptors[C]//Proceedings of the 2004 IEEE Conference on Computer Vision and Pattern Recognition. Washington, 2004: 506-513.
(  0) 0) |
| [8] |
BAY H, TUYTELAARS T. Surf: speeded up robust features[J]. Computer vision and image understanding, 2008, 110: 346-359. DOI:10.1016/j.cviu.2007.09.014 (  0) 0) |
| [9] |
LI H, HARTLEY R. Feature matching and pose estimation using newton iteration[J]. Lecture notes in computer science (image analysis and processing-ICIAP 2005), 2005, 3617: 196-203. (  0) 0) |
| [10] |
刘经南, 曾文宪, 徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报·信息科学版, 2013, 38(5): 505-512. LIU J N, ZENG W X, XU P L. Overview of total least squares methods[J]. Geomatics and information science of wuhan university, 2013, 38(5): 505-512. (  0) 0) |
| [11] |
MOISAN L, STIVAL B. A probabilistic criterion to detect rigid point matches between two images and estimate the fundamental matrix[J]. International journal of computer vision, 2004, 57: 201-218. DOI:10.1023/B:VISI.0000013094.38752.54 (  0) 0) |
| [12] |
ZHOU F, ZHONG C, ZHENG Q. Method for fundamental matrix estimation combined with feature lines[J]. Neurocomputing, 2015, 160: 300-307. DOI:10.1016/j.neucom.2015.02.033 (  0) 0) |
| [13] |
颜坤, 刘恩海, 赵汝进, 等. 快速鲁棒的基础矩阵估计[J]. 光学精密工程, 2018, 26(2): 461-470. YAN K, LIU E H, ZHAO R J, et al. A fast and robust method for fundamental matrix estimation[J]. Optics and precision engineering, 2018, 26(2): 461-470. (  0) 0) |
| [14] |
SCHARSTEIN D, SZELISKI R. High-accuracy stereo depth maps using structured light[C]//2003 IEEE Conference on Computer Vision and Pattern Recognition. Madison, 2003: 195-202.
(  0) 0) |
| [15] |
SCHARSTEIN D, SZELISKI R, ZABIH R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[C]//Proceedings IEEE Workshop on Stereo and Multi-baseline Vision. Kauai, 2001: 131-140.
(  0) 0) |
 2021, Vol. 53
2021, Vol. 53


