2. 中国科学院 计算技术研究所 计算机体系结构国家重点实验室 北京 100190;
3. 中国科学院大学 人工智能学院 北京 100190;
4. 中国科学院大学 北京 100190
2. State Key Laboratory of Computer Architecture, Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China;
3. School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing 100190, China;
4. University of Chinese Academy of Sciences, Beijing 100190, China
扫描链在数字集成电路的可测试性设计(design for test,DFT)中是不可或缺的,在实际工业设计中具有非常广泛的应用。在一款工业芯片中,扫描单元和它们的时钟电路占整个芯片面积的30%左右[1]。扫描链作为数字电路设计中的一部分,如此高的面积开销也带来了不可避免的扫描链故障。10%~30%的缺陷就可能会导致扫描链失效,而扫描链故障几乎占芯片故障的50%[2-4]。因此,如何有效诊断扫描链故障十分重要。
扫描链故障诊断方法根据是否修改扫描单元设计和扫描链框架分为两类。
第一类扫描链故障诊断方法在不修改扫描单元设计和扫描链框架的前提下提高扫描链诊断质量,该方法不会增加电路开销,对于电路的性能影响较小。文献[4]在扫描链中检测到故障后,将可能的候选故障注入扫描链中,并对各种测试向量进行比特流仿真,进而观测扫描链中的比特流响应。文献[5]提出了一项与扫描测试向量有关的扫描链重连技术,扫描链根据敏感单元进行重新排序,生成新的电路网表和扫描测试向量,然后进行扫描链故障诊断。文献[6]提出了一种与测试向量无关的扫描单元重连可诊断性设计方法,且不需要生成新的电路网表。通过将扫描单元的扇入(fanin)扫描单元交换至其他扫描链的方式增加敏感单元数目,以及使用敏感单元分割非敏感单元的方式减少连续的非敏感单元,从而增加诊断信息。
第二类扫描链故障诊断方法通过修改扫描单元设计或扫描链框架提高扫描链故障诊断质量,该方法可以提高电路的可诊断性,具有较短的诊断时间,但往往会增加电路面积开销。文献[7]提出将一条扫描链中的扫描单元输出端连接到其他扫描链中的扫描单元输入端的诊断方法。在发生故障时,通过观测其他扫描链的移出数据来诊断该扫描链是否发生故障。文献[8]中,在触发器的输出端增加两个分别由使能信号和触发器输出端信号控制的pmos和nmos管,并增加由使能信号驱动的全局诊断线,扫描链中发生固定0故障时,全局诊断线移出数据为1;发生固定1故障时,全局诊断线移出数据为0,从而判断故障类型并通过移出数据发生翻转时的时钟周期区分发生故障的扫描单元。
实际工业设计中为了降低电路的面积和功耗开销,存在较多的多位扫描单元。多位扫描单元中的多个触发器具有相同的时钟域和相同的边沿触发方式,在功能模式中同单位扫描单元一样,执行触发器的功能,存储组合逻辑中的数据,多位扫描单元中的每个触发器分别存储数据,不会相互影响。在扫描模式中,多位扫描单元中的多个扫描单元在扫描链上是相邻的,不能被其他扫描单元分割,依次经过扫描移入阶段、数据捕获阶段、扫描移出阶段,观测扫描移出阶段的数据实现多位扫描单元的故障诊断。通过对已有工作的研究发现,现有的可诊断性设计方法不支持针对多位扫描单元的优化。因此,本文提出了一种面向多位扫描单元的扫描链优化方法。本文的主要贡献包括:
1) 提出了多位敏感单元和固定多位非敏感单元的定义,在后端设计限制下,提出了有助于提高诊断质量的多位扫描单元特性;
2) 提出了满足多位扫描单元约束的扫描链重连可诊断性设计方法;
3) 在ISCAS′89基准电路的实验结果表明,采用所提方法对含有多位扫描单元的电路进行优化后,b17电路SA-0(stuck-at-0,SA-0)和SA-1(stuck-at-1,SA-1)故障的平均诊断分辨率(diagnostic resolution,DR)分别是优化前的12.59倍和13.37倍;s38417电路SA-0和SA-1故障的平均诊断分辨率分别是优化前的19.95倍和3.04倍。
1 研究背景 1.1 敏感单元与诊断质量随着芯片复杂度的提升,集成电路芯片中扫描单元数目越来越多,测试数据量也越来越大。同时,每条扫描链上的扫描单元数目随之增加,导致移入一个测试向量需要更多的时钟周期,测试时间越来越长。实际工业设计中使用扫描压缩技术[9]将多条扫描链压缩至扫描通道中以减少测试数据量和测试时间开销。
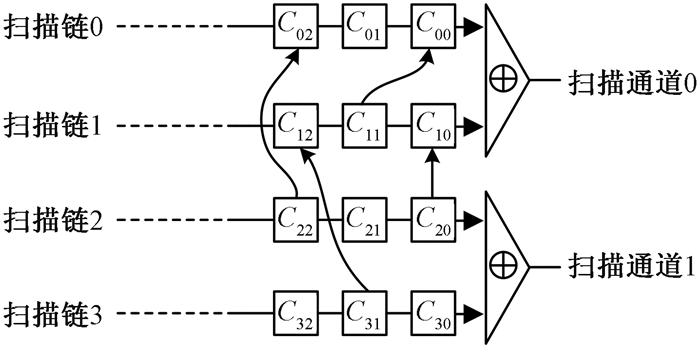
文献[6]指出,在扫描压缩情况下,如果扫描单元CT的所有扇入扫描单元都在其他扫描通道中,那么称CT为敏感单元,否则称为非敏感单元。例如,如图 1所示,电路中有四条扫描链,两条一组分别压缩至两个扫描通道中。C02在扫描通道0中,C02的扇入扫描单元C22在扫描通道1中,因此C02是一个敏感单元,同理,C12和C10也是敏感单元。但是C00和它的扇入扫描单元C11都在扫描通道0中,所以C00是非敏感单元。敏感单元有极大的可能性可以在至少一个测试向量下捕获故障敏感数据,对于故障诊断是十分有利的。因此,敏感单元数目越多,可以提供有效的诊断信息越多。
|
图 1 扫描压缩下的敏感单元 Fig. 1 Sensitive cells under scan |
扫描压缩会损失部分诊断信息。扫描移出阶段,在同一时钟周期内移出数据被压缩的扫描单元称为耦合单元。仍以图 1为例,C11是C01的耦合单元,C20是C30的耦合单元。假如C12发生故障,在数据移入阶段,C10、C11、C12都会出错;在数据捕获阶段,C02和C12是敏感单元,其扇入扫描单元不在扫描链1上,可以捕获正确数据,经过扫描压缩移出后的数据均可以提供有效的诊断信息;而C00的扇入扫描单元是C11,C11在移入阶段已经出错,所以C00可能会捕获错误数据,由于C10的数据与C00的数据同时压缩,导致C00和C10的移出数据都不能提供有效的诊断信息。因此,只有扫描通道中的耦合单元都成为敏感单元才会为故障诊断提供有效的诊断信息。
综上,为了提高扫描链故障的诊断质量,文献[5-6]指出,首先需要增加敏感单元数目,敏感单元数目越多,扫描链故障诊断的效果越好;其次,工业设计流程中,要尽可能使同一扫描通道中的耦合单元都成为敏感单元,从而提高扫描压缩情况下的扫描链故障诊断质量。
1.2 研究动机基于扫描单元重连的可诊断性设计方法有效提高了故障诊断分辨率和诊断质量。然而,实际工业电路中可能存在多位扫描单元,且一些设计流程中前端设计的扫描链会在后端设计过程中被优化,这都限制了现有可诊断性设计方法的应用。
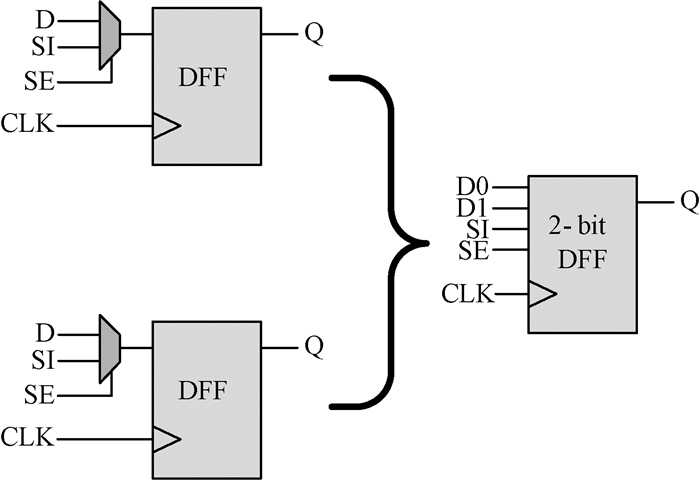
多位扫描单元指同一个扫描单元中包含多个单位扫描单元,也可以理解成把多个完全相同的触发器合并在一个触发器中。这种合并不是简单地把两个或更多的标准触发器直接连在一起,而是晶体管级别的合并,可以大大降低电路的面积开销;由于多个触发器共用同一时钟电路,因此极大地降低电路中的功耗。以两位扫描单元为例,两个单位扫描单元和一个两位扫描单元的关系如图 2所示。
|
图 2 两位扫描单元示例 Fig. 2 2-bit scan cell demonstration |
多位扫描单元的优点使其在实际工业芯片设计中被广泛使用,但现有可诊断性设计方法[5-6]只支持对单位扫描单元进行优化,当面向多位扫描单元时,敏感单元的定义、扫描单元所在扫描链的分配等都不再适用。
另一方面,实际工业设计流程中,前端设计的扫描链在后端设计时可能会被修改,后端设计人员会将扫描单元的顺序进行重新排列,这将导致已有方法[6]针对扫描压缩的耦合单元优化方法失效。在工业电路的后端设计流程中,允许前端将每条扫描链上的扫描单元划分成多个组,组内的扫描单元顺序在后端设计时可能会被改变,但是一个组中的扫描单元不会被重新放置于其他组中。
为了解决上述问题,本文提出了面向多位扫描单元、考虑后端设计限制的多位敏感单元和固定多位非敏感单元的定义,在满足多位扫描单元约束的情况下,提出了多位扫描单元的交换策略,进一步提出了面向多位扫描单元的扫描链重连可诊断性设计方法。
2 所提方法 2.1 优化流程图 3为本文提出的可诊断性设计流程图,该优化算法基于模拟退火启发式算法。首先,随机选择要进行优化的扫描单元M=[C1…Cn],当n≥2时,M表示一个多位扫描单元且位数为n,即M中包含n个单位扫描单元;当n=1时,M表示一个单位扫描单元,位数为1。其次,将与M位于同一扫描通道中的扇入扫描单元交换至其他扫描通道。最后,比较交换前后的电路中的敏感单元比例,如果交换后敏感单元比例变大,则接受此次交换;如果交换后敏感单元比例变小,根据模拟退火启发式算法的原则,以一定的概率接受此次交换。当优化敏感单元数目阶段停止时,根据同一扫描通道中不同扫描链的敏感单元数目,对扫描单元进行分组,即使后端调整了组内扫描单元顺序,依然能够保证耦合单元皆为敏感单元。

|
图 3 本文所提方法流程图 Fig. 3 The flow chart of proposed method |
在扫描压缩的情况下,扫描通道中的耦合单元都是敏感单元才会提供有效的诊断信息。实际工业设计流程中,后端设计人员会对前端设计的扫描链进行新的优化,前端设计的扫描单元顺序可能会被打乱。例如,图 4(a)中是前端设计的扫描链结构,多位扫描单元中的Ne、Nk、Nq都是非敏感单元,数据移出时不能提供有效的诊断信息,前端设计将它们放在同一组耦合单元中,除此之外的其他5组耦合单元都可以提供有效的诊断信息;但是后端设计时可能会将扫描链优化成图 4(b)中所示的扫描单元顺序,此时电路中仅有3组耦合单元可以提供有效的诊断信息。

|
图 4 后端设计对扫描链的优化 Fig. 4 Optimization of scan chain by back-end design |
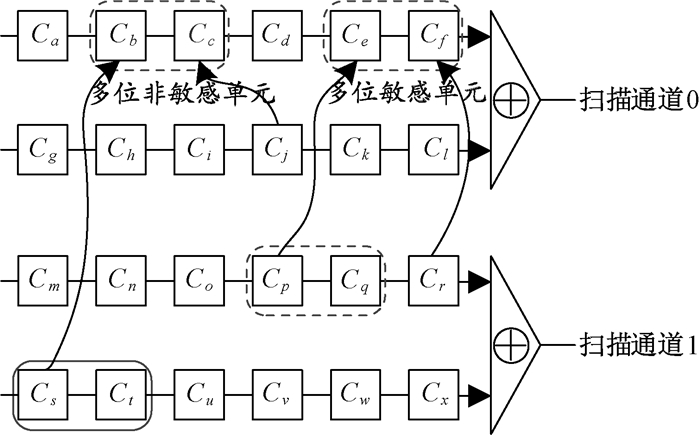
基于上述原因,在单位扫描单元的敏感单元定义仍然有效的前提下,提出面向多位扫描单元的多位敏感单元定义:如果一个多位扫描单元M=[C1…Cn]中所有扫描单元的扇入扫描单元都不在与M相同的扫描通道中,那么多位扫描单元M被称为多位敏感单元,否则称为多位非敏感单元。例如,如图 5所示,[Cb、Cc]是一个两位扫描单元,但是Cc的一个扇入扫描单元Cj与[Cb、Cc]在同一扫描通道中,所以[Cb、Cc]是一个多位非敏感单元;[Ce、Cf]也是一个两位扫描单元,并且该扫描通道中没有[Ce、Cf]的扇入扫描单元,所以[Ce、Cf]是一个多位敏感单元。
|
图 5 多位敏感单元和多位非敏感单元 Fig. 5 Multi-bit sensitive cell and multi-bit non-sensitive cell |
为了提高后端设计约束下的诊断质量,我们进一步提出了扫描单元划分成组的方法。当优化敏感单元数目阶段停止时,根据同一扫描通道中不同扫描链的敏感单元数目,将扫描单元划分成敏感单元组和非敏感单元组,并且允许组内的扫描单元进行交换。在扫描通道中划分敏感单元组时,必须保证所有扫描链的敏感单元组中扫描单元数目相同。由于敏感单元组中只可以放置敏感单元,因此即使后端设计调整了组内扫描单元顺序,依然能够保证耦合单元皆为敏感单元。
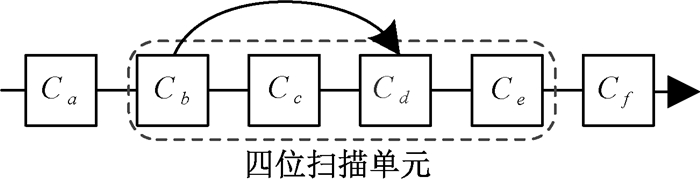
基于多位敏感单元的定义,我们进一步提出了固定多位非敏感单元的定义。如果多位扫描单元中的两个或更多的扫描单元互为扇入、扇出扫描单元,我们称其为固定多位非敏感单元。由于多位扫描单元中的某一位扫描单元和它的扇入扫描单元在同一条扫描链上,所以固定多位非敏感单元一定不能成为多位敏感单元。例如,如图 6所示,[Cb、Cc、Cd、Ce]是一个四位扫描单元,Cb是Cd的一个扇入扫描单元,无论如何交换扇入扫描单元到其他扫描链,Cb与Cd一定会在同一条扫描链上,所以[Cb、Cc、Cd、Ce]是固定多位非敏感单元。
|
图 6 固定多位非敏感单元 Fig. 6 Fixed multi-bit non-sensitive cell |
为了提高多位扫描单元中的敏感单元数目,需要尽可能多地将多位非敏感单元优化为多位敏感单元。为了实现该目标,需要将选中的多位扫描单元M=[C1…Cn]中所有扫描单元的扇入扫描单元交换至其他扫描通道。
首先,需要选择一个多位非敏感单元M作为优化目标。假设{F1…Fm}是多位扫描单元M的扇入扫描单元与其在同一扫描通道中的集合,那么{F1…Fm}中扫描单元的数目越少,使该多位扫描单元成为多位敏感单元所需要交换至其他扫描通道的扫描单元也就越少,换言之,其更容易成为多位敏感单元。因此,我们优先选择具有较小{F1…Fm}集合的多位扫描单元作为优化目标。
然后,判断所选中的多位扫描单元M是否为固定多位非敏感单元。如果是固定多位非敏感单元,意味着其无法成为多位敏感单元,则重新选择要优化的多位非敏感单元。否则,将{F1…Fm}中的所有扫描单元交换至其他扫描通道。
在交换过程中,需要遵循三条原则:扫描链长度不变;多位扫描单元必须连续;多位扫描单元中各扫描单元的顺序不允许改变。图 7为多位扫描单元的优化流程图。进行优化的多位扫描单元为M=[C1…Cn]。需要交换至其他扫描通道的扫描单元集合{F1…Fm}中的每个扫描单元位数不定,以N(F)表示扫描单元F的位数。与{F1…Fm}中的扫描单元进行交换的扫描单元集合用SWAP表示,并且以N(SWAP)表示SWAP中所有扫描单元的位数总和。

|
图 7 多位扫描单元的优化流程图 Fig. 7 Multi-bit scan cell optimization flow chart |
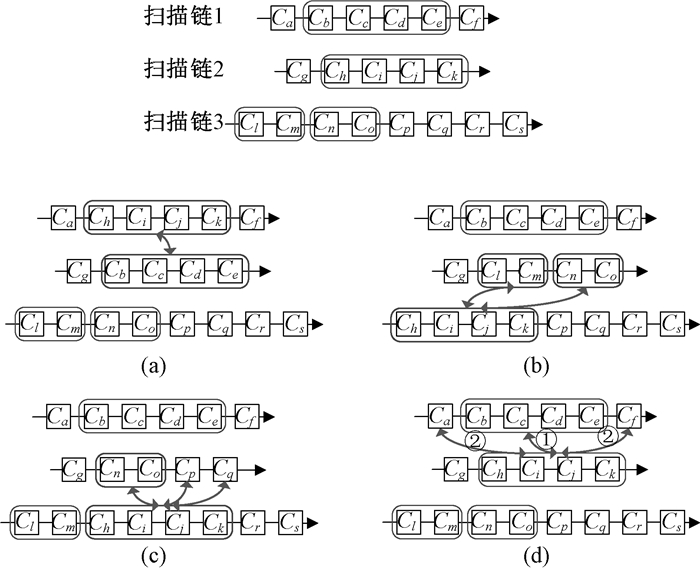
例如,如图 8所示,假设某次迭代从{F1…Fm}中选出要进行交换的扫描单元为扫描链2中的[Ch、Ci、Cj、Ck],因此与其交换的扫描单元集合SWAP须满足N(SWAP)=4。如图 8(a)所示,若选中进行交换的非敏感单元是一个四位扫描单元[Cb、Cc、Cd、Ce],此时N(SWAP)=4,符合交换长度的原则。如图 8(b)所示,若选中进行交换的非敏感单元是扫描链3上的一个两位扫描单元[Cn、Co],将其放入SWAP后,此时N(SWAP)=2,在扫描链3上再次选中一个两位扫描单元[Cl、Cm],此时N(SWAP)=4,符合交换长度原则。如图 8(c)所示,扫描链3上先选中[Cn、Co]的情况下,扫描链3上再次选择其他扫描单元,如果选到一个单位扫描单元Cp,此时N(SWAP)=3,那么需要在扫描链3上再选一个单位扫描单元Cq,此时N(SWAP)=4,符合交换长度原则。如图 8(d)所示,如果第一次选中的非敏感单元为扫描链1中的Cf,此时N(SWAP)=1,扫描链1中只剩一个四位扫描单元[Cb、Cc、Cd、Ce]和一个单位扫描单元Ca,接下来选择该扫描链上的任何扫描单元都无法满足N(SWAP)=4的原则,故无法进行交换。采用图 8中的交换方式,保证交换的扫描单元数目相等的同时,还必须保证交换前后,四位扫描单元[Ch、Ci、Cj、Ck]从扫描移入端到扫描移出端方向的顺序不变且不被其他扫描单元所分割。
|
图 8 四位扫描单元交换长度限制 Fig. 8 Length limitation aim at swaping 4-bit scan cells |
实验采用ISCAS′89中的s38417和b17基准电路,分别包含1 636个和1 415个扫描单元,扫描压缩技术采用嵌入式确定测试(embedded deterministic test,EDT)扫描压缩[9]。基准电路中50%的扫描单元被设置为两位扫描单元,其余50%的扫描单元仍为单位扫描单元,并划分不同数目的扫描链和扫描通道产生多个电路版本进行实验。
对于每个电路版本,分别生成自动测试向量(automatic test pattern generation,ATPG)。然后,对于每个扫描单元,分别注入SA-0和SA-1故障,并分别生成失效日志文件。最终,采用商业工具对失效日志文件进行诊断。诊断精度皆为100%,即所有候选故障都包含了实际注入的故障。故障注入实验中,对扫描链电路的每个扫描单元分别进行SA-0和SA-1故障注入后,对所有扫描单元的诊断分辨率进行分析,形成表格。在本文中,诊断分辨率定义为候选故障单元的数目,理想值为1。
3.2 评估结果与分析表 1给出了基准电路在扫描压缩情况下的SA-0和SA-1故障的诊断分辨率。
|
|
表 1 诊断分辨率 Tab. 1 Diagnostic resolution |
在s38417电路中,通过比较E1电路的未优化版本和优化版本的注错结果发现,SA-0故障下优化版本的最差诊断分辨率是未优化版本的12.29倍,平均诊断分辨率是未优化版本的23.95倍。SA-1故障下优化的版本最差诊断分辨率是未优化版本的5.33倍,平均诊断分辨率是未优化版本的3.76倍。E2电路中,SA-0故障下优化版本的最差诊断分辨率是未优化版本的13.83倍,平均诊断分辨率是未优化版本的17.89倍。SA-1故障下优化版本的最差诊断分辨率是未优化版本的8倍,平均诊断分辨率是未优化版本的2.61倍。E3电路中,SA-0故障下优化版本的最差诊断分辨率是未优化版本的10.38倍;平均诊断分辨率是未优化版本的18.01倍。SA-1故障下优化版本最差诊断分辨率是未优化版本的5.33倍,平均诊断分辨率是未优化版本的2.76倍。平均而言,经过本文所提方法优化后的多位扫描单元电路,对于SA-0故障的优化版本平均诊断分辨率是未优化版本的19.95倍,最差诊断分辨率是未优化版本的12.17倍;对于SA-1故障的优化版本平均诊断分辨率是未优化版本的3.04倍,最差诊断分辨率是未优化版本的6.22倍。
对于b17电路来说,经过本文所提方法优化后的多位扫描单元电路,对于SA-0故障优化版本的平均诊断分辨率是未优化版本的12.59倍,最差诊断分辨率是未优化版本的12.70倍;对于SA-1故障优化版本的平均诊断分辨率是未优化版本的13.37倍,最差诊断分辨率是未优化版本的14.66倍。
对于物理失效分析(physical failure analysis,PFA)来说,可疑故障单元越少越好,可疑故障单元等于1是最理想的情况。但是如果可疑故障单元不超过3,对于物理失效分析都是可以接受的。由表 2可以看出,在s38417电路中,对于SA-0故障来说,未优化版本中DR=1的平均百分比为25.02%,优化版本中DR=1的平均百分比为88.87%;DR≤3的平均百分比由未优化版本的51.93%提高至优化版本的98.35%。对于SA-1故障来说,未优化版本中DR=1的平均百分比为60.55%,优化版本中DR=1的平均百分比为93.58%;DR≤3的平均百分比由未优化版本的85.84%提高至优化版本的99.67%。在b17电路中,对于SA-0故障来说,未优化版本中DR=1的平均百分比为72.63%,优化版本中DR=1的平均百分比为84.17%;DR≤3的平均百分比由未优化版本的77.10%提高至优化版本的96.35%。对于SA-1故障来说,未优化版本中DR=1的平均百分比为69.33%,优化版本中DR=1的平均百分比为90.27%;DR≤3的平均百分比由未优化版本的74.80%提高至优化版本的95.83%。
|
|
表 2 诊断分辨率的百分比 Tab. 2 The percentage of diagnostic resolution |
综上所述,经过本文所提方法的优化后,不仅提高了电路中扫描链故障的平均诊断分辨率和最差诊断分辨率,而且优化后诊断分辨率为1的扫描单元数目大幅提高。对于物理失效分析来说,电路中诊断分辨率小于等于3的扫描单元数目也得到了提高。
4 总结实际工业设计流程中,电路中存在多位扫描单元,且后端设计流程中会对前端设计的扫描单元进行重新排序,但是原有的可诊断性设计方法不支持多位扫描单元的优化,当面向多位扫描单元时,敏感单元的定义、扫描单元所在扫描链的分配等都不再适用。因此本文提出了面向多位扫描单元和后端设计限制的多位敏感单元和固定多位非敏感单元定义,并且提出了面向多位扫描单元的交换策略和可诊断性设计优化方法。ISCAS′89中的s38417基准电路实验结果表明,经过本文所提方法优化后的包含多位扫描单元的扫描链电路,SA-0故障的平均诊断分辨率和最差诊断分辨率分别是未优化的扫描链电路的19.95倍和12.17倍,DR=1的平均百分比由25.02%提高至88.87%,DR≤3的平均百分比由51.93%提高至98.35%;SA-1故障的平均诊断分辨率和最差诊断分辨率则分别是未优化扫描链电路的3.04倍和6.22倍,DR=1的平均百分比由60.55%提高至93.58%,DR≤3的平均百分比由85.84%提高至99.67%。b17基准电路实验结果表明,SA-0故障的平均诊断分辨率和最差诊断分辨率优化扫描电路分别是未优化扫描链电路的12.59倍和12.7倍,DR=1的平均百分比由72.63%提高至84.17%,DR≤3的平均百分比由77.10%提高至96.35%;SA-1故障的平均诊断分辨率和最差诊断分辨率优化扫描链电路分别是未优化扫描链电路的13.37倍和14.66倍,DR=1的平均百分比由69.33%提高至90.27%,DR≤3的平均百分比由74.80%提高至95.83%。
| [1] |
KUNDU S. On diagnosis of faults in a scan-chain[C]//The 11st Annual IEEE VLSI Test Symposium. Atlantic City, 1993: 303-308.
(  0) 0) |
| [2] |
GUO R, VENKATARAMAN S. A technique for fault diagnosis of defects in scan chains[C]//Proceedings of International Test Conference. Baltimore, 2001: 268-277.
(  0) 0) |
| [3] |
YANG J S, HUANG S Y. Quick scan chain diagnosis using signal profiling[C]//International Conference on Computer Design. San Jose, 2005: 157-160.
(  0) 0) |
| [4] |
HUANG Y, GUO R F, CHENG W T, et al. Survey of scan chain diagnosis[J]. IEEE design & test of computers, 2008, 25(3): 240-248. (  0) 0) |
| [5] |
LO W H, HSIEH A C, LAN C M, et al. Utilizing circuit structure for scan chain diagnosis[C]//The 18th IEEE European Test Symposium. Aviqnon, 2013: 1-6.
(  0) 0) |
| [6] |
YE J, HUANG Y, HU Y, et al. Diagnosis and layout aware (DLA) scan chain stitching[C]//The IEEE International Test Conference.Anaheim, 2013: 1-10.
(  0) 0) |
| [7] |
SCHAFER J L, POLICASTRI F A, MCNULTY R J. Partner SRLs for improved shift register diagnostics[C]//IEEE VLSI Test Symposium. Atlantic City, 1992: 198-201.
(  0) 0) |
| [8] |
DOUNAVI H M, TSIATOUHAS Y. Stuck-at fault diagnosis in scan chains[C]//The 9th IEEE International Conference on DTIS. Santorini, 2014: 1-6.
(  0) 0) |
| [9] |
HUANG Y, CHENG W T, RAJSKI J. Compressed pattern diagnosis for scan chain failures[C]//The IEEE International Conference on Test. Austin, 2005: 744-751.
(  0) 0) |
 2021, Vol. 53
2021, Vol. 53


