2. 中南林业科技大学 智慧林业云研究中心 湖南 长沙 410004
2. Research Center of Smart Forest Cloud, Central South University of Forestry and Technology, Changsha 410004, China
特征选择[1]是一种常见的数据降维方法,其基本原理是在不牺牲学习算法性能的前提下,从原始数据集中挑选出使分类器表现最佳的特征子集。这里特征子集的挑选可以看作寻找最优解的问题,在实际应用中常用启发式搜索算法得到所需的特征子集。常见的启发式搜索算法[2]有禁忌搜索(tabu search, TS)算法、差分进化(differential evolution, DE)算法、模拟退火(simulated annealing, SA)算法、粒子群优化(particle swarm optimization, PSO)算法、蚁群优化(ant colony optimization, ACO)算法、遗传算法(genetic algorithm, GA)、人工蜂群(artificial bee colony, ABC)算法等。
具体搜索方式可以分为全局搜索和局部搜索。全局搜索倾向于确定领域内多路径的搜索,局部搜索倾向于在当前节点的相邻状态间搜索。大多数算法无法同时兼顾全局搜索和局部搜索,因此人们往往通过混合多个算法来提升算法性能。例如,张震等[3]利用遗传算子对PSO算法进行优化,得到特征子集初始最优解,再利用TS算法对初始最优解进行搜索,最终得到特征选择的全局最优解。刘玉杰等[4]借助遗传算法来弥补ABC算法全局搜索能力差的问题,提出一种改进的ABC算法用于求解舰载机着舰调度问题。初蓓等[5]提出一种初始化策略和更新机制,在局部播种阶段引入贪婪策略,达到最小化特征个数和最大化分类性能的目的。陈倩茹等[6]针对特征权重对K近邻算法和遗传算法进行优化,利用WKNN算法赋予每个特征权重,再利用自调优自适应遗传算法对部分参数进行调整,实验结果证明了方法的有效性。启发式搜索算法非常适用于特征子集的搜索,因此常被人们应用在特征选择方法中,本文便借助ABC算法和DE算法进行特征子集的选择。
目前,关于ABC算法在特征选择方面的研究有很多。Rao等[7]提出一种基于ABC算法和梯度提升决策树的ABCoGBDT算法,先利用ABC算法对原始特征集进行优化,剔除不相关特征,将优化后的特征集作为GBDT的输入进一步约简特征个数,但传统的ABC算法局部搜索性能较差且易于早熟,一定程度上影响了最终的特征选择结果。Hancer等[8]提出一种基于非支配排序和遗传算子相结合的多目标ABC算法;李光华等[9]将随机森林算法的重要度评分作为蚁群算法的启发信息,实现对整个特征空间的搜索,该特征选择算法可以有效降低特征维度,提升数据分类准确度。
DE算法可以有效规避遗传算法中变异方式的不足。Zorarpaci等[10]提出将DE算法和ABC算法相结合用于特征选择,该混合算法在分类器运行时间、精度等方面均优于常见的经典特征选择技术,并且在差分进化方面也优于纯粹的搜索算法,但只对低维度数据集进行了分析研究。封硕等[11]针对ABC算法收敛性差、后期损害种群多样性等问题,提出一种结合DE算法的自适应ABC算法,该算法在收敛速度和求解精度上有所提升。
本文在ABC算法[12]中引入DE算法[13]思想,利用ABC算法控制参数少、鲁棒性强,适用于高维复杂优化问题的特点,以及DE算法操作简单、搜索精度强的特点,提出一种新型二进制特征选择算法DE_BABC,旨在解决数据挖掘中常见分类任务的特征选择问题。在ABC算法中加入多项式差分变异算子,引入交叉算子和最优保存策略,在4个Benchmark测试函数上验证了所提算法的可行性。对7个常用高维数据集进行降维处理,并与7种经典降维算法进行对比。结果显示,本文算法在寻优效果、收敛速度以及降维程度等方面优于7种经典降维算法。
1 传统人工蜂群算法ABC算法主要由四部分组成:食物源、雇佣蜂、跟随蜂、侦察蜂。食物源即蜜源,雇佣蜂保存优良解,跟随蜂加快搜索速度,侦察蜂打破局部最优。算法寻优过程如下。
1) 蜜源初始化。设蜜源总数为SN,通过式(1)进行初始化,
| $ x_{i j}=x_{\min j}+\mathit{rand}[0, 1]\left(x_{\max j}-x_{\min j}\right), $ | (1) |
其中:xij表示第i个蜜源xi在第j维度的取值,i的取值为{1, 2, …, SN},j的取值为{1, 2, …, D};xminj和xmaxj分别代表第j维的最小值和最大值。蜜源初始化就是对每个蜜源的各个维度通过式(1)赋予一个随机值,生成SN个初始蜜源。
2) 雇佣蜂阶段。雇佣蜂遍历每一个蜜源,在每个蜜源附近利用式(2)搜索新的蜜源,在得到新的蜜源后,计算新旧蜜源的适应度值,依据贪婪法则保留较优蜜源,
| $ v_{i j}=x_{i j}+\varphi\left(x_{i j}-x_{k j}\right), $ | (2) |
其中:vij为雇佣蜂找到的新蜜源;φ为[0, 1]内的随机数。适应度值的计算方式不唯一,应根据实际求解问题而定。
3) 跟随蜂阶段。跟随蜂根据雇佣蜂分享的信息选择蜜源,通过式(3)计算蜜源的概率值pi,以轮盘赌的方式选择所要跟随的蜜源进行开采,从而保证适应度值高的蜜源被开采的概率更大。跟随蜂开采蜜源的逻辑同雇佣蜂一样,根据(4)式搜索新的蜜源,
| $ p_i=\frac{f i t_i}{\sum\limits_\limits{i=1}^{S N} f i t_i}, $ | (3) |
| $ v_{i j}=x_{k j}+\varphi\left(x_{k j}-x_{g j}\right)_{\circ} $ | (4) |
4) 侦察蜂阶段。如果一个蜜源在经过雇佣蜂和跟随蜂的多次开采后仍没有被更新,则该蜜源被认为陷入局部最优。蜜源被更新的情况由参数trail界定。当蜜源被更新保留时,trail值为0;当蜜源未被更新时,trail值加1;当trail值超过初始设定的阈值limit时,则抛弃该蜜源,同时雇佣蜂转化为侦察蜂,利用式(1)寻找新的蜜源代替被抛弃蜜源。
2 DE_BABC算法原理传统的ABC算法和DE算法都用于实数问题的求解,而特征选择问题解的形式为二进制。假设有一个M行N+1列的数据集,每一行代表一组数据,前N列代表N个特征,最后一列代表这一组的标签。特征选择问题是要从这N个特征中找到数量少且分类性能优越的子集。可见,特征选择问题本质上可以理解为选择一个合适的0/1串,串的长度是原始数据集中特征的个数,0是不被选择的特征,1是被选择的特征。因此,对每一个蜜源进行特征编码,将其表示为由二进制符号0和1组成的二进制符号集。
2.1 蜜源初始化利用Bernoulli分布初始化蜜源, 将蜜源的每个维度都赋值为(0, 1)之间的随机数。如果随机数大于0.5,则保留该特征;如果随机数小于0.5,则舍弃该特征。具体公式为
| $ \begin{gathered} p_1=P\left(X_{i j}=1\right)=p, \\ p_0=P\left(X_{i j}=0\right)=1-p, \\ X_{i j}= \begin{cases}0, & \text { if } U(0, 1) \leqslant p, \\ 1, & \text { if } U(0, 1)>p, \end{cases} \end{gathered} $ | (5) |
其中:Xij表示第i个蜜源的第j维特征;U(0, 1)表示(0, 1)之间生成的随机值。因为在二进制蜂群初始化阶段,每个特征保留或舍弃的概率是相等的,所以p值取0.5。
2.2 新型蜜源更新方式传统的雇佣蜂对蜜源的更新方式是在单一维度上进行搜索,全局搜索能力差,易陷入局部最优。本文采用一种新的多项式差分变异算子,多维、快速地遍历更新蜜源。
以某蜜源的第j维特征为例,算法思想为:当初始蜜源Xi特征保留数量小于等于1时,蜜源不进行更新;反之,更新蜜源等于变异蜜源。变异蜜源是由差分蜜源与初始蜜源进行交叉得到的,当差分蜜源第j维特征取值为1时,变异蜜源在该维度上取值也为1,反之,其取值等于初始蜜源。差分蜜源是由邻近蜜源Xr1、Xr2和初始蜜源Xi进行交叉得到的,当初始蜜源第j维特征取值为1,且邻近蜜源Xr1和Xr2在第j维取值相等,差分蜜源在第j维取值为0,反之,其取值为1。依次遍历蜜源所有维度,得到最终更新的蜜源。
设初始蜜源为Xi,在该蜜源附近随机选择两个蜜源Xr1和Xr2,更新后的蜜源Xv为
| $ X_v^j= \begin{cases}X_i^j, & \mathit{sum}\left(X_i^j \leqslant 1\right), \\ X_{\text {mut }}^j, & \mathit{sum}\left(X_i^j \geqslant 2\right) 。\end{cases} $ | (6) |
变异蜜源Xmut为
| $ X_{\mathrm{mut}}^j= \begin{cases}1, & \text { if } X_{\mathrm{diff}}^j=1, \\ X_i^j, & \text { otherwise 。}\end{cases} $ | (7) |
差分蜜源Xdiff为
| $ X_{\text {diff }}^j= \begin{cases}0, & X_i^j=1 \cap\left(X_{r 1}^j=X_{r 2}^j\right), \\ 1, & X_i^j=0 \cap\left(X_{r 1}^j \neq X_{r 2}^j\right) 。\end{cases} $ | (8) |
最终的新蜜源Xvj=(Xi1, Xi2, …, XiD), i={1, 2, …, SN}, j={1, 2, …, D}。
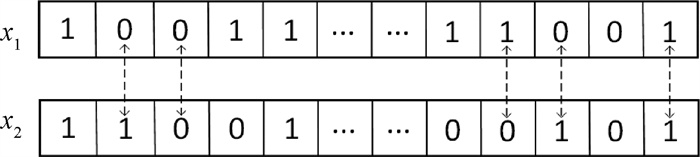
此外,在跟随蜂阶段加入基于交叉算子[14]的自适应局部搜索策略,即在已经更新的蜜源附近随机选择一个蜜源,在两个蜜源个体中任意选择几个维度位置相互交换,进一步提升算法的全局搜索能力。在侦察蜂搜索过程中加入最优保存策略[15],即用当前种群中前N个适应度值较高的蜜源替换种群中适应度值较低的N个蜜源,这样不仅可以提升蜜源的整体质量,还可以加快蜜源收敛速度。蜜源交叉图解如图 1所示。
|
图 1 蜜源交叉图解 Fig. 1 Cross diagram of nectar sources |
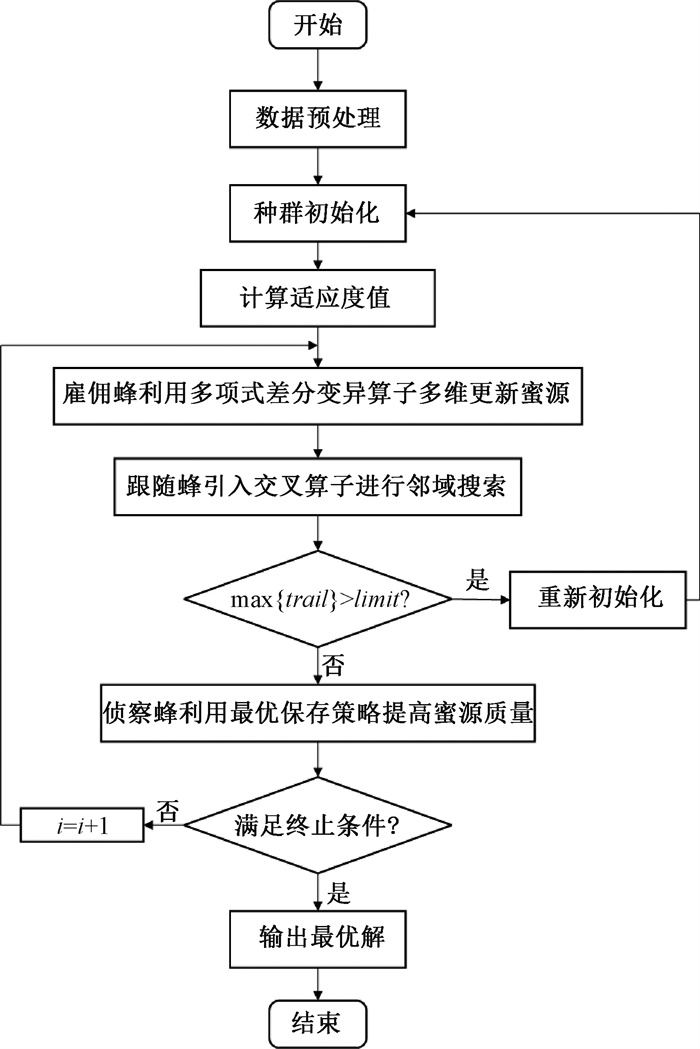
DE_BABC算法结构如图 2所示。
|
图 2 DE_BABC算法结构 Fig. 2 DE_BABC algorithm structure |
DE_BABC算法的具体步骤如下。
第1步:数据集预处理。先对数据集进行缺省值填充,再对标签进行编码预处理。算法输入参数为:蜜源个数SN、雇佣蜂数量、跟随蜂数量、最大迭代次数MSN、蜜源更新次数限制limit;算法最终输出为:最佳蜜源、适应度值、分类准确率。
第2步:蜜源初始化。使用式(1)随机生成初始蜜源Xij={Xi1, Xi2, …, XiD},使用式(9)计算每个蜜源的适应度值fit,
| $ f i t=\frac{a c c}{\operatorname{count}}, $ | (9) |
其中:acc为分类精度;count为最终选择的特征维度数量。
第3步:雇佣蜂阶段。通过式(6)~(8),多项式差分变异算子随机选择蜜源Xij的多个维度进行降维,加快降维速度。判断新蜜源是否属于优秀蜜源,如果是,则不更新。反之,计算新蜜源的适应度值,并与旧蜜源适应度值进行对比,根据贪婪法则保存蜜源。蜜源的好坏通过适应度值的高低来评判,理想的特征子集是特征数量越小越好,分类精度越高越好。
第4步:跟随蜂阶段。跟随蜂通过式(3)计算蜜源Xij被跟随的概率,通过轮盘赌方式选择所要跟随的蜜源,在被跟随的蜜源X1附近随机选择一个蜜源X2与X1做交叉,进一步提高算法搜索能力。
第5步:侦察蜂阶段。当蜜源i未被更新的次数trail达到最大无效次数limit时,该蜜源被当作无效蜜源舍弃。同时负责搜索它的雇佣蜂转变为侦察蜂,在搜索领域通过式(1)随机生成一个新的蜜源替代它,再通过最优保存策略更新当前种群中适应度值较低的蜜源,以提升蜜源整体质量。
第6步:得出最优解。经过上述搜索,保存较优蜜源,去重排序后输出,将排名第一的蜜源作为最优解。将最优特征子集输入XGBoost分类器,采用十倍交叉验证计算其分类精度。
3 仿真实验 3.1 DE_BABC算法性能测试为验证新算法DE_BABC的有效性, 以寻优精度和收敛速度作为评价指标,在Griewank、Rastrigin、Sphere和Rosenbrock 4个Benchmark测试函数上进行验证,所选函数在其各自的定义域内均为多峰函数。Benchmark测试函数具体信息如表 1所示。选择ABC、DE、TS、GA 4种经典搜索算法与新算法进行对比,不同算法在4个Benchmark测试函数上的寻优最小值、平均值和函数极限值结果列于表 2。可以发现,新算法对4个Benchmark测试函数的寻优效果均优于4种经典的启发式搜索算法。
|
|
表 1 Benchmark测试函数具体信息 Tab. 1 Benchmark test functions details |
|
|
表 2 不同算法在4个Benchmark测试函数上的寻优数据对比 Tab. 2 Comparison of optimization data of different algorithms on four Benchmark test functions |
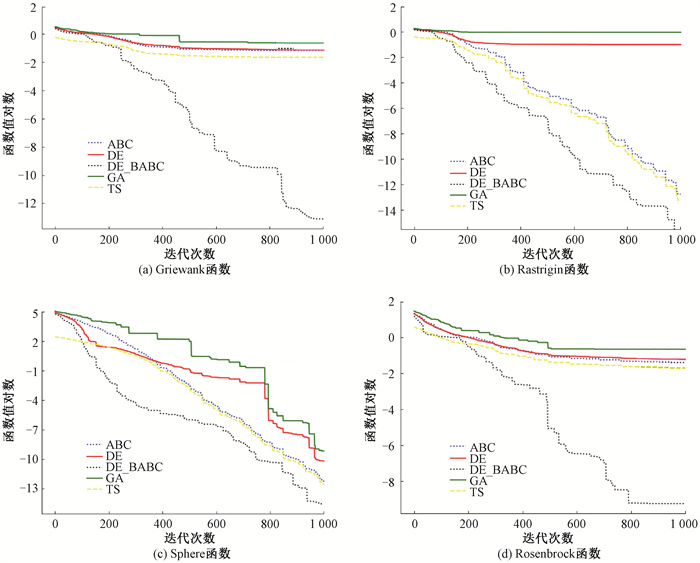
不同算法在4个Benchmark测试函数上的寻优过程如图 3所示。可以发现,新算法的收敛速度与求解精度明显优于其他4种算法,尤其在Griewank函数和Rosenbrock函数上,曲线走势相较其他4种算法收敛更快且寻优结果更佳。对于Rastrigin函数和Sphere函数,ABC和TS算法效果相近,GA和DE算法效果略差,但新算法相较其他4种算法性能更优。
|
图 3 不同算法在4个Benchmark测试函数上的寻优过程 Fig. 3 Optimization process of different algorithms on four Benchmark test functions |
从UCI数据库中选取7个高维数据集,分别为声纳数据集(Sonar)、城市土地覆盖数据集(ULC)、ICF-CY自我问题分类数据集(SCADI)、心律失常数据集(Arr)、语音修复数据集(LSVT)、帕金森氏病数据集(PD)、质谱数据集(Arcene),高维数据集具体信息如表 3所示。采用Sklearn库进行算法实验,种群数为数据集的特征数,蜜源最大更新次数为13,借助XGBoost分类器计算最终分类精度。为处理多分类问题,选择损失函数作为目标函数,学习率为0.2,调节树数量为100个,实验结果取算法迭代50次的平均值。
|
|
表 3 高维数据集具体信息 Tab. 3 High-dimensional data set details |
表 4为DE_BABC算法对7个数据集进行特征选择的结果。将数据集的原特征数与降维后的最小特征数和平均特征数进行对比,其中降维率为原特征数与平均特征数的差值占原特征数的百分比。
|
|
表 4 DE_BABC算法特征选择结果 Tab. 4 Feature selection results of DE_BABC algorithm |
由表 4可知,新算法针对不同数据集的降维效果不尽相同,但其降维率普遍在88%以上。当原特征数小于500时,降维率超过90%;当原特征数大于500时,降维率仍旧可以超过88%。可见,新算法可以有效去除原始数据集中大量的不相关、冗余特征,成功缩减数据集的原始特征维度。
为保证在对数据集进行特征选择的同时,不降低数据集的分类性能,对7个数据集降维前后的分类精度进行了实验分析。将XGBoost与十倍交叉验证相结合作为分类器来评估特征选择后分类的准确性。DE_BABC算法降维前后分类精度对比结果列于表 5。可以看出,新算法对于特征数小于500的数据集,分类精度有明显提升;对于特征数大于500的数据集,分类精度也有一定的提升。可见,新算法在剔除特征的过程中,有效保留了重要特征,在降低维度的同时优化了数据集的分类精度。
|
|
表 5 DE_BABC算法降维前后分类精度对比 Tab. 5 Comparison of classification accuracy of DE_BABC algorithm before and after dimension reduction |
选用随机森林(RF)、正则化(L12)、主成分分析法(PCA)、快速相关滤波算法(FCBF)、递归特征消除法(RFE)、DisABC[16]、MRABC[17] 7种经典的特征选择算法,与DE_BABC算法进行了各项性能指标的对比实验。其中,DisABC和MRABC是在2012年分别由Kashan和Akay等人提出的,并在2015年首次被Hancer等[18]应用于特征选择中。表 6为不同算法对7个数据集的特征选择结果对比情况,选用数据集降维后所保留的平均特征数作为指标。表 7为最佳特征选择情况下不同算法降维后平均分类精度对比情况。其中,RF算法是通过给每个特征值打分取排名靠前的特征,在处理Arcene数据集时发现,RF算法只计算了前94个特征权重值,之后的特征权重全部计算为0,因此RF算法对Arcene数据集只保留了94个特征,而新算法保留了1 165个特征。但最终的分类精度表明,新算法的降维效果要优于RF算法,故RF算法可能存在过度剔除冗余特征的情况。PCA算法要求降维后的特征数必须少于样本数,因此该算法在处理Arcene数据集时,特征保留的个数等于其样本数,与DE_BABC算法保留的特征数量不同。但最终的分类精度表明,新算法的降维效果明显优于PCA算法,故PCA算法也可能存在过度剔除冗余特征的情况。
|
|
表 6 不同算法特征选择结果对比 Tab. 6 Comparison of feature selection results of different algorithms |
|
|
表 7 不同算法降维后平均分类精度对比 Tab. 7 Comparison of average classification accuracy of different algorithms after dimensionality reduction |
分析表 6和表 7的数据可以发现,新算法的维度约简性能在处理高维数据集时效果更显著,而对于特征数小于1 000的数据集,特征选择效果与其他7种算法相近,这是由于数据集中所剩特征的特征权重排名都靠前。而对于更高维的数据集,无论是降维效果还是分类精度相较其他算法都有更好的表现。
综上所述,通过将DE_BABC算法在不同数据集上与7种已有的特征选择算法进行对比,可以发现,新算法不仅可以有效降低数据集的特征维度,且数据集在特征选择之后的分类精度明显优于对比算法。
4 结束语本文提出一种新的模拟人工蜂群的特征选择算法DE_BABC。该算法在传统ABC算法的基础上使用多项式差分变异算子,融入DE算法,提升了算法的全局搜索能力,加快了蜜源更新速度。同时,引入交叉算子和最优保存策略,进一步提升了蜜源质量。通过4个Benchmark测试函数,验证了新算法在寻优精度和收敛速度上相较4种经典的启发式搜索算法都有显著提升。对7个常用高维数据集进行特征选择的实证对比研究,结果表明,相比7种经典降维算法,新算法能够更加有效地降低数据维度,并进一步提升数据分类精度。下一步将结合特征选择结果的稳定性进行深入研究,进一步提升高维数据特征选择算法的性能。
| [1] |
XUE B, ZHANG M J, BROWNE W N, et al. A survey on evolutionary computation approaches to feature selection[J]. IEEE transactions on evolutionary computation, 2015, 20(4): 606-626. (  0) 0) |
| [2] |
LAN S W, FAN W J, YANG S L, et al. A survey on the applications of variable neighborhood search algorithm in healthcare management[J]. Annals of mathematics and artificial intelligence, 2021, 89(8/9): 741-775. (  0) 0) |
| [3] |
张震, 魏鹏, 李玉峰, 等. 改进粒子群联合禁忌搜索的特征选择算法[J]. 通信学报, 2018, 39(12): 60-68. ZHANG Z, WEI P, LI Y F, et al. Feature selection algorithm based on improved particle swarm joint taboo search[J]. Journal on communications, 2018, 39(12): 60-68. (  0) 0) |
| [4] |
刘玉杰, 万兵, 苏析超, 等. 基于IABC算法的舰载机着舰调度[J]. 控制与决策, 2022, 37(7): 1810-1818. LIU Y J, WAN B, SU X C, et al. Aircraft carrier landing scheduling based on IABC algorithm[J]. Control and decision, 2022, 37(7): 1810-1818. (  0) 0) |
| [5] |
初蓓, 李占山, 张梦林, 等. 基于森林优化特征选择算法的改进研究[J]. 软件学报, 2018, 29(9): 2547-2558. CHU B, LI Z S, ZHANG M L, et al. Research on improvements of feature selection using forest optimization algorithm[J]. Journal of software, 2018, 29(9): 2547-2558. (  0) 0) |
| [6] |
陈倩茹, 李雅丽, 许科全, 等. 自调优自适应遗传算法的WKNN特征选择方法[J]. 计算机工程与应用, 2021, 57(20): 164-171. CHEN Q R, LI Y L, XU K Q, et al. WKNN feature selection method based on self-tuning adaptive genetic algorithm[J]. Computer engineering and applications, 2021, 57(20): 164-171. (  0) 0) |
| [7] |
RAO H D, SHI X Z, RODRIGUE A K, et al. Feature selection based on artificial bee colony and gradient boosting decision tree[J]. Applied soft computing, 2019, 74: 634-642. DOI:10.1016/j.asoc.2018.10.036 (  0) 0) |
| [8] |
HANCER E, XUE B, ZHANG M J, et al. Pareto front feature selection based on artificial bee colony optimization[J]. Information sciences, 2018, 422: 462-479. DOI:10.1016/j.ins.2017.09.028 (  0) 0) |
| [9] |
李光华, 李俊清, 张亮, 等. 一种融合蚁群算法和随机森林的特征选择方法[J]. 计算机科学, 2019, 46(S2): 212-215. LI G H, LI J Q, ZHANG L, et al. Feature selection method based on ant colony optimization and random forest[J]. Computer science, 2019, 46(S2): 212-215. (  0) 0) |
| [10] |
ZORARPACI E, ÖZEL S A. A hybrid approach of differential evolution and artificial bee colony for feature selection[J]. Expert systems with applications, 2016, 62: 91-103. (  0) 0) |
| [11] |
封硕, 刘琨. 融合差分进化思想的自适应人工蜂群算法[J]. 郑州大学学报(理学版), 2021, 53(3): 72-78. FENG S, LIU K. Adaptive artificial bee colony algorithm based on differential evolution[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(3): 72-78. (  0) 0) |
| [12] |
KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri: Erciyes University, 2005.
(  0) 0) |
| [13] |
STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. (  0) 0) |
| [14] |
曲志坚, 张先伟, 曹雁锋, 等. 基于自适应机制的遗传算法研究[J]. 计算机应用研究, 2015, 32(11): 3222-3225. QU Z J, ZHANG X W, CAO Y F, et al. Research on genetic algorithm based on adaptive mechanism[J]. Application research of computers, 2015, 32(11): 3222-3225. (  0) 0) |
| [15] |
毕惟红, 任红民, 吴庆标. 一种新的遗传算法最优保存策略[J]. 浙江大学学报(理学版), 2006, 33(1): 32-35. BI W H, REN H M, WU Q B. A new elitist strategy in genetic algorithms[J]. Journal of Zhejiang university (science edition), 2006, 33(1): 32-35. (  0) 0) |
| [16] |
KASHAN M H, NAHAVANDI N, KASHAN A H. DisABC: a new artificial bee colony algorithm for binary optimization[J]. Applied soft computing, 2012, 12(1): 342-352. (  0) 0) |
| [17] |
AKAY B, KARABOGA D. A modified artificial bee colony algorithm for real-parameter optimization[J]. Information sciences, 2012, 192: 120-142. (  0) 0) |
| [18] |
HANCER E, XUE B, KARABOGA D, et al. A binary ABC algorithm based on advanced similarity scheme for feature selection[J]. Applied soft computing, 2015, 36: 334-348. (  0) 0) |
 2023, Vol. 55
2023, Vol. 55


