由于液晶玻璃窑炉温度控制系统是一个大惯性、纯滞后系统,再加上窑温、窑压等多种变量耦合和定时加料对窑炉温度的影响,很难建立精确的系统模型[1].目前,国内液晶玻璃窑炉的控制方法多采用以燃料燃烧提供热能的方式以及传统的PID控制策略.实际中控制系统具有多输入、多输出的强耦合性和严重的非线性,使得该系统对控制性能的要求很高,然而传统PID参数一旦整定计算好之后,在整个控制过程中都是固定不变的,很难满足玻璃窑炉的工艺要求,容易使玻璃出现条纹、气泡和析晶等严重的质量问题.此外,熔化的玻璃是导电的,电助熔系统就是在熔化的玻璃两端施加电压产生电阻热来加热生料,使其在高温下熔化, 其具有以下优点:提高窑内玻璃液对流强度,从而大幅度提高玻璃质量;具有较高的热效率,增加单位产量;减少了火焰对窑壁的侵蚀,可有效延长窑炉寿命并减少环境污染.本文设计了一种气电混合智能控制系统,即同时控制燃气流量和电助熔系统功率来达到温度控制的目的,并提出了一种前馈模糊自适应PID控制策略,实现了玻璃窑炉复杂工况下的智能控制.
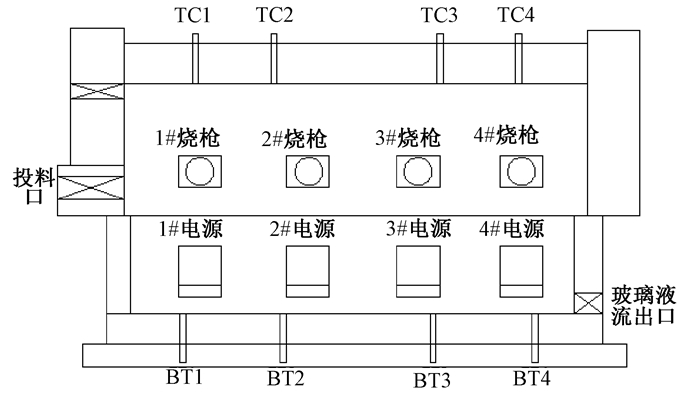
1 玻璃窑炉的结构液晶玻璃窑炉是液晶玻璃基板生产的核心装置,熔解工艺流程有熔化、澄清、均化、冷却四个环节.液晶玻璃窑炉的结构如图 1所示.其中TC1、TC2、TC3、TC4为顶部热电偶,BT1、BT2、BT3、BT4为底部热电偶,1#烧枪、2#烧枪、3#烧枪、4#烧枪为天然气和氧气燃烧口,1#电源、2#电源、3#电源、4#电源为电助熔设备.
|
图 1 液晶玻璃窑炉的结构 Figure 1 Structure of LCD glass furnace |
生产玻璃的生料从投料口投入,烧枪喷出的燃料燃烧主要熔化窑炉上半部的玻璃液,电助熔电极棒(钼电极棒)镶嵌在窑炉底部左右对称位置,一边4个,通过两端施加电压产生电阻热熔化窑炉底部玻璃生料.热电偶检测窑炉各个部分玻璃液的温度,转化成4~20 mA标准电信号传送给工控机.熔化的玻璃液通过流出口流入下一个环节进行进一步的澄清.
液晶玻璃对质量要求极高,原料熔化和澄清在很大程度上决定了液晶玻璃的质量.窑内温度与设定温度只要偏差5~10 ℃,就可能引起熔化和澄清过程的显著变化,导致玻璃发生缺陷,成为废品.液晶玻璃生产工艺要求窑炉玻璃液温度必须达到1 450 ℃,并在此温度下保持一段时间进行澄清,澄清之后的玻璃液从窑炉进入到铂金通道进行再次的澄清,这样严格把关每一步的温度才能最终生产出没有条纹和气泡的平板玻璃.铂铑热电偶的测温范围为0~1 600 ℃,实际生产中用铂铑热电偶作为窑炉玻璃液的温度测量元件.液晶玻璃生产采用电助熔和富氧燃烧方法(在助燃风出风口通入氧气),富氧燃烧使得燃料的燃烧更彻底,电助熔用电能代替了部分化学能,也使窑炉寿命更长.
2 玻璃窑炉温度控制系统 2.1 温度控制系统分析玻璃窑炉温度控制系统分为两部分:一是窑炉主体温度控制系统,通过控制燃气流量完成;二是窑炉底部温度控制系统,通过调节电助熔系统功率完成.
窑炉主体温度控制系统以工艺要求的温度作为设定温度,玻璃窑炉某一处热电偶的测量温度作为实测温度和反馈温度,当实测温度偏离设定温度时,采集的温度数据通过智能控制器输出信号,调节燃料、空气、氧气阀门的开度,达到调节玻璃液温度的目的.窑炉底部温度控制系统也以工艺要求的温度作为设定温度,玻璃窑炉底部某一处热电偶的测量温度作为实测温度和反馈温度,当实测温度偏离设定温度时,采集的温度数据通过PID控制器输出信号,调节电助熔系统的功率,达到调节底层玻璃液温度的目的.
由窑炉结构可以看出,各回路紧密相连、相互影响.为了说明各回路之间温度的耦合作用,以TC1、TC2为例作出分析.假如TC1热电偶检测的玻璃液温度低于设定温度,TC2热电偶检测的温度等于设定温度,那么TC1回路燃气阀门需要增加开度,TC2回路燃气阀门开度不变,一段时间后,TC1检测到的温度到达设定温度,能够推测由于受TC1附近温度升高的影响,TC2附近温度也会升高,这样TC2热电偶检测到的温度就会高于设定温度,继而TC2回路燃气阀门需减小开度,使温度降回至设定温度.
窑炉主体温度控制系统有4个热电偶,4个温度控制回路,底部有4个热电偶,也是4个温度控制回路,一共8个温度控制回路.这8个控制回路之间都有耦合作用,作用的大小有强有弱,取决于回路之间的距离.为了解决各回路温度耦合这一问题,本文加入了前馈控制器.从抑制干扰的角度看,前馈控制可以减轻反馈控制的负担.但是如果对所有实际工业的干扰对象都作出补偿,势必要设计多个前馈通道,增加了投资费用和维护工作量.因此,从经济实用角度出发,只对相邻的主要干扰采取前馈补偿,对其他影响较小的干扰采用反馈控制方式.
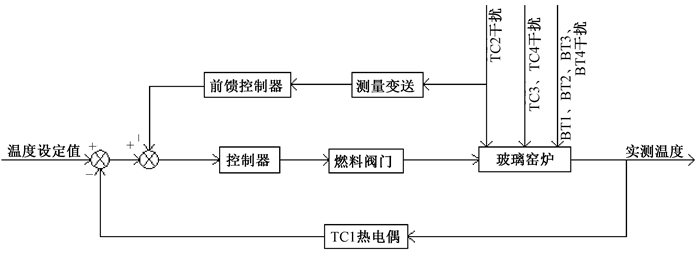
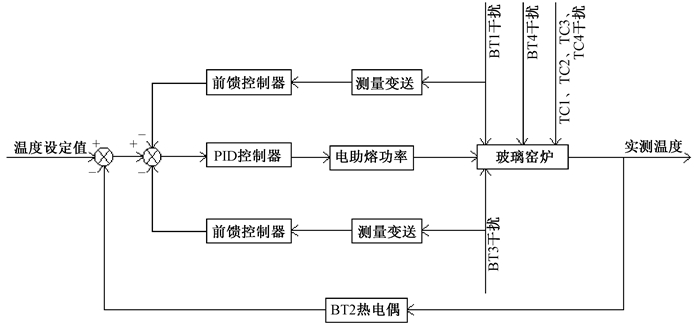
以TC1回路为例的主体控制系统方框图如图 2所示.离TC1回路最近的回路是TC2回路,只对TC2回路的干扰设置前馈控制器.以BT2回路为例的电助熔控制系统方框图如图 3所示.离BT2回路最近的回路是BT1回路和BT3回路,所以对这两个回路的干扰都设置前馈控制器.
|
图 2 主体控制系统方框图 Figure 2 Block diagram of main-body control system |
|
图 3 电助熔控制系统方框图 Figure 3 Block diagram of electric boosting control system |
在热工控制系统中,由于被控对象通常存在一定的滞后,因而从干扰产生到被控量发生变化需要一定的时间.从偏差产生到调节器产生控制作用,再到被控量发生变化又要经过一定的时间,由此可见,反馈控制具有自身局限性.
前馈控制就是直接对扰动进行控制,而不是被动等待扰动产生偏差后再对其进行控制,对克服干扰要比反馈控制及时得多.但是,反馈控制属于开环控制,当前馈控制并没有彻底消除偏差时,系统无法得知这一信息,更无法对其进行校正.
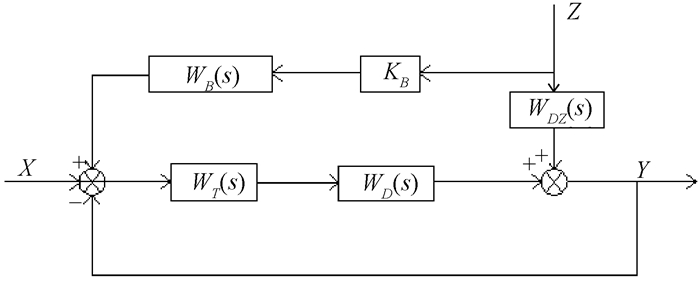
在工程实际中,为克服反馈和前馈的局限性,对一两个主要扰动采用前馈补偿,而对其他非主要干扰采用反馈控制,这种控制系统称为前馈-反馈复合控制系统[2].前馈-反馈原理如图 4所示.其中KB为测量变送器变送系数; WB(s)为前馈控制装置的传递函数; WT(s)为前向通道传递函数; WD(s)为控制通道对象传递函数; WDZ(s)为干扰通道对象传递函数.
|
图 4 前馈-反馈原理 Figure 4 Feedforward and feedback principle |
为了计算干扰与输出之间的关系,假设X(s)=0,则
| $ Y\left( s \right) = \frac{{{W_{DZ}}\left( s \right) + {K_B}{W_B}\left( s \right){W_T}\left( s \right){W_D}\left( s \right)}}{{1 + {W_T}\left( s \right){W_D}\left( s \right)}}\cdot Z\left( s \right). $ | (1) |
要实现完全补偿,须使Y(s)=0,即
| $ {W_B}\left( s \right) =-\frac{{{W_{DZ}}\left( s \right)}}{{{K_B}{W_T}\left( s \right){W_D}\left( s \right)}}. $ | (2) |
玻璃窑炉主体温度控制系统的动态特性可以用1个一阶惯性环节串联1个纯滞后环节表示为
| $ {G_1}\left( s \right) = \frac{{{K_1}{{\rm{e}}^{-\tau s}}}}{{{T_1}s + 1}}, $ | (3) |
式中:K1为放大系数; T1为对象的惯性环节时间参数; τ为对象的纯滞后时间参数.
电助熔控制系统的动态特性可以用一个惯性环节表示为
| $ {G_2}\left( s \right) = \frac{{{K_2}}}{{{T_2}s + 1}}, $ | (4) |
式中:K2为放大系数;T2为对象的惯性环节时间参数.
玻璃窑炉温度控制系统任何一个回路的输出,都是这个回路的输入作用和其他回路耦合作用的共同结果.以TC1回路为例,用数学方法表示为
| $ {Y_1}\left( s \right) = {a_0}{Y_2}\left( s \right) + {a_1}{Y_3}\left( s \right) + {a_2}{Y_4}\left( s \right) + {a_3}{Y_5}\left( s \right) + {a_4}{Y_6}\left( s \right) + {a_5}{Y_7}\left( s \right) + {a_6}{Y_8}\left( s \right), $ | (5) |
式中:a0,a1,…, a6为除TC1回路之外的回路对TC1回路的作用系数.
3 模糊自适应PID智能控制模糊PID控制器以误差e和误差变化率ec作为控制器的输入量,输入量经模糊化与模糊推理之后得出模糊控制器的输出值,PID控制器根据模糊控制的输出值对自身参数进行调节[3].模糊自适应PID控制器的原理如图 5所示[4].控制系统包含一个常规PID控制器和一个具有模糊推理功能的参数校正部分.模糊系统的输入为e和ec,通过已经存储到计算机的模糊推理规则库得到ΔKp、ΔKi、ΔKd,将PID控制器的3个参数Kp、Ki、Kd分别与ΔKp、ΔKi、ΔKd相加,得到调整后的Kp、Ki、Kd,然后由整定后的PID控制器控制被控对象,得到输出信号[5].
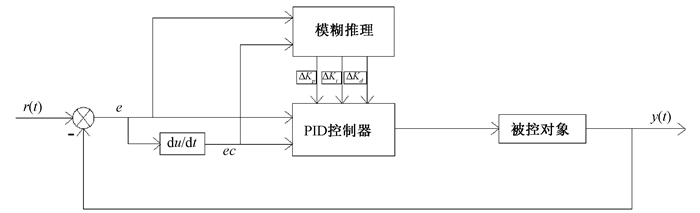
|
图 5 模糊自适应PID控制器的原理 Figure 5 Schematic diagram of fuzzy adaptive PID controller |
模糊控制器的输入变量为e、ec,其论域均取{-60, 60},输出变量为ΔKp、ΔKi、ΔKd,其论域分别取{-6, 6}、{-3, 3}、{-42, 42}.模糊子集均为{NB,NM,NS,ZE,PS,PM,PB},集合中元素分别代表负大、负中、负小、零、正小、正中、正大.各个元素均采用高斯分布[6],输入、输出变量的隶属度函数如图 6所示.
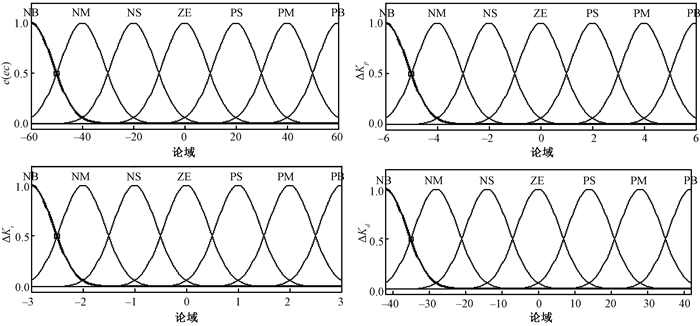
|
图 6 隶属度函数 Figure 6 Diagram of membership function |
模糊控制规则库的建立原则如下:
1) 比例系数Kp的作用是加快系统响应速度,减小系统稳态误差;积分系数Ki的作用是消除系统稳态误差;微分系数Kd的作用是改善系统的动态性能.
2) 当|e|较大时,要提升响应速度,选择较大的Kp,同时为防止积分饱和,取较小的Ki.
3) 当|e|和|ec|为中等大小,为使超调减小,取较小的Kp,Ki、Kd取适中值.
4) 当|e|较小时,为使系统有良好的稳态性能,应增大Kp、Ki.同时为防止系统在设定值附近出现震荡,应适当选取Kd,原则是:当|ec|较小时,Kd取大一点,当|ec|较大时,Kd取小一点.
根据工程经验,建立ΔKp、ΔKi、ΔKd的模糊控制规则表,如表 1~3所示.
|
|
表 1 ΔKp模糊控制规则表 Table 1 The fuzzy-control rule table of ΔKp |
|
|
表 2 ΔKi模糊控制规则表 Table 2 The fuzzy-control rule table of ΔKi |
|
|
表 3 ΔKd模糊控制规则表 Table 3 The fuzzy-control rule table of ΔKd |
根据模糊控制规则表,构造2个输入(e,ec)、3个输出(ΔKp,ΔKi,ΔKd)的模糊控制器,并在模糊规则编辑器中编辑49条控制规则[7].
4 仿真根据实际窑炉系统加入阶跃输入后的响应,设定放大系数K1=1.09,K2=1,惯性时间常数T1=400,T2=600,纯滞后时间常数τ=4 s.使用Matlab软件中的Simulink和Fuzzy模块进行温度控制系统的仿真,仿真模型见图 7,其中模型中的子系统是PID控制器.
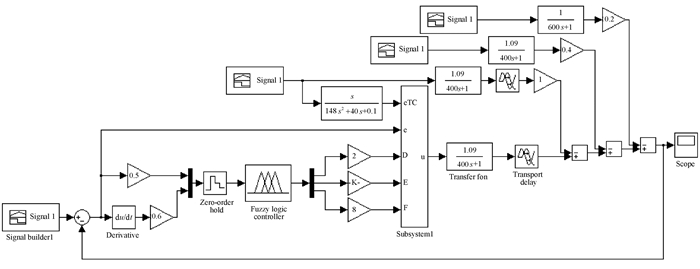
|
图 7 仿真模型 Figure 7 Simulation model |
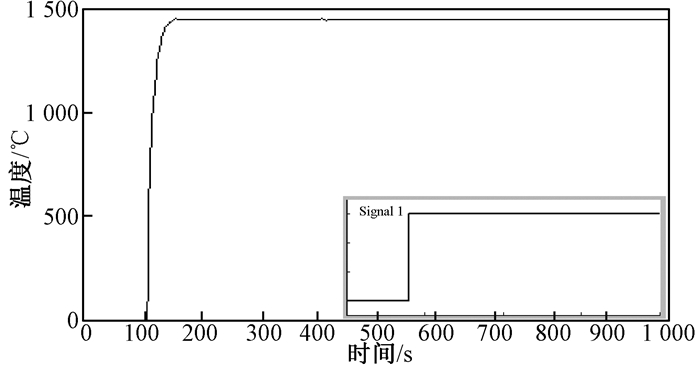
为了证明模糊自适应PID控制的控制效果,将其与传统PID控制进行了比较.为了更好地比较模糊自适应PID控制与传统PID控制之间的优劣,设定各回路之间的耦合干扰为0.温度为1 450 ℃,仿真时间为1 000 s,图 8是模糊自适应PID控制与传统PID控制的对比.结果表明,与传统PID控制相比,模糊自适应PID控制超调量更小,调节时间更短.加入干扰后的温度曲线如图 9所示,曲线在400 s处出现极小的波动,仿真曲线整体平滑稳定.在400 s时,对除TC1之外的回路设置幅值为600 ℃的干扰信号,如图 9右下角小图框所示.
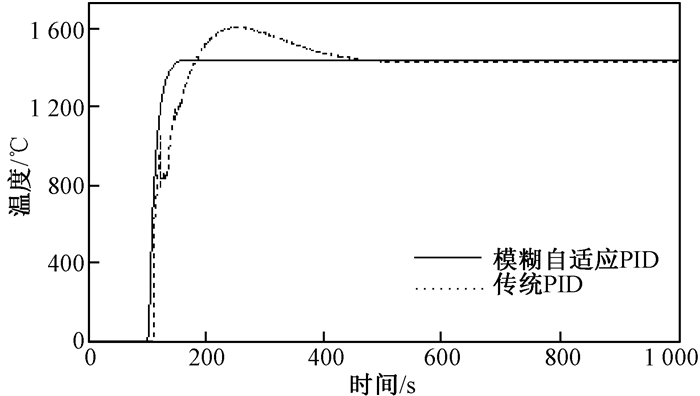
|
图 8 模糊自适应PID控制与传统PID控制的对比 Figure 8 Contrast of fuzzy adaptive PID controller and traditional PID controller |
|
图 9 加入干扰后的温度曲线 Figure 9 Chart of temperature under interference conditions |
气电混合控制能提高熔融效率,增加玻璃产量,模糊自适应PID控制比传统PID控制具有更好的控制效果.前馈-反馈控制能减小反馈系统的压力,保证控制精度.结合了气电混合控制、智能控制和反馈-前馈控制的液晶玻璃窑炉温度控制系统具有良好的控制效果.
| [1] |
MICHAEL C. Classical glass technology[M]. Berlin: Wiley-VCH Verlag, 2006.
(  0) 0) |
| [2] |
WU W, CHOU Y S. Adaptive feedforward and feedback control of non-linear time-varying uncertain systems[J]. International journal of control, 1999, 72(12): 1127-1138. DOI:10.1080/002071799220489 (  0) 0) |
| [3] |
孙建延, 王振成. 模糊PID参数的相平面法整定策略[J]. 河南科技大学学报(自然科学版), 2012, 33(3): 89-92. (  0) 0) |
| [4] |
倪忠远, 李秀志, 吕焕云, 等. 自整定PID-Fuzzy控制器在炉温控制中的应用[J]. 自动化与仪器仪表, 1996(5): 30-34. (  0) 0) |
| [5] |
章卫国, 杨向忠. 模糊控制理论与应用[M]. 西安: 西北工业大学出版社, 2004.
(  0) 0) |
| [6] |
石辛民. 模糊控制及其MATLAB仿真[M]. 北京: 清华大学出版社, 2008.
(  0) 0) |
| [7] |
杨益兴, 崔大连, 周爱军. 模糊自适应PID控制器及Simulink仿真实现[J]. 舰船电子工程, 2010, 30(4): 127-130. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49

