目标跟踪是通过视频图像序列不断估计目标状态的过程,在视频监控、医疗诊断、人机交互等方面都有着非常重要的应用价值。虽然目标跟踪已经被研究几十年[1-2],但由于遮挡、突变运动、尺度变化等外界因素,目标跟踪仍然是计算机视觉领域的重要研究热点。传统跟踪方法大部分都假定了跟踪目标具有运动平滑性条件。然而,实际应用中目标的突变运动时常发生,这将导致跟踪的失败。为了解决这些问题,基于检测的跟踪方法[3]、基于随机采样的跟踪方法[4]等方法被大量提出。
近年来,研究者尝试将群优化算法应用于计算机视觉领域[5-6]。群优化算法可以看作一种在图像序列中搜索目标的全局搜索策略过程。因此,将跟踪问题转化为全局优化问题引起研究者们的高度关注。文献[7]将蝙蝠算法应用到视觉跟踪,该方法可以在各种具有挑战性的条件下稳健地跟踪单个目标。文献[8]提出了基于多样性优化的粒子滤波跟踪算法,该方法将布谷鸟搜索优化算法融入粒子滤波中,增加粒子的多样性,解决粒子退化问题,从而改善跟踪性能。文献[9]提出了混合卡尔曼布谷鸟搜索跟踪器,可以有效地从当前帧到下一帧探索搜索空间,来定位目标的位置。实验结果表明,该方法在计算时间上优于粒子群算法。文献[10]提出了混合正弦余弦算法(sine cosine algorithm, SCA)和差分进化算法(differential evolution, DE)来解决全局优化和目标跟踪问题,该方法通过SCA的全局搜索与DE的局部搜索来改善优化性能,从而使运动目标获得良好的跟踪精度和鲁棒性。文献[11]将时间连续性信息结合到粒子群优化中,在粒子滤波的框架内形成多层重要性采样,获得好的跟踪性能,尤其是对于目标的不确定运动。文献[12]提出了一种基于核相关滤波(kernelized correlation filter, KCF)的布谷鸟搜索扩展的跟踪器,该方法根据置信度映射设计了一个自适应阈值来同时跟踪平滑和突变运动。虽然这些基于优化的跟踪器均取得了较好的跟踪效果,但是对突变运动的跟踪精度方面还需进一步提高。
GOA是一种新颖的仿生群优化算法[13],具有调节参数少的优点,已被成功应用于很多领域[14-15]。但由于GOA存在收敛速度慢,收敛精度低的缺陷。本文提出一种WGOA算法用来解决突变运动跟踪问题。该算法利用变异算子增加种群多样性,提高全局搜索能力,通过惯性权重来改变蚱蜢的位置更新机制,改善算法的局部搜索能力,采用WGOA应用于视觉跟踪,表现出良好的跟踪性能。
1 蚱蜢优化算法GOA是一种基于种群的优化算法,它模拟了自然界中蚱蜢群的行为[13]。这种行为可以归纳为3个主要部分。
1.1 初始化模拟蚱蜢在这一阶段的群集行为的数学模型为
| $ {\mathit{\boldsymbol{P}}_p} = {\mathit{\boldsymbol{S}}_p} + {\mathit{\boldsymbol{G}}_p} + {\mathit{\boldsymbol{A}}_p}, $ | (1) |
其中:Pp是第p个蚱蜢的位置;Sp是蚱蜢群的社会互动因子;Gp是第p个蚱蜢的重力;Ap表示风平流。Sp、Gp和Ap的数学模型为
| $ {\mathit{\boldsymbol{S}}_p} = \sum\limits_{q = 1 \ne p}^N s ({d_{pq}}){\mathit{\boldsymbol{\hat d}}_{pq}};{\mathit{\boldsymbol{G}}_p} = - g{\mathit{\boldsymbol{\hat e}}_g};{\mathit{\boldsymbol{A}}_p} = u{\mathit{\boldsymbol{\hat e}}_w} $ | (2) |
其中:dpq= Pq-Pp是介于第p个蚱蜢和第q个蚱蜢之间的距离;
将公式(2)中的Sp、Gp和Ap代入公式(1),该方程可以表示为
| $ {\mathit{\boldsymbol{P}}_p} = \sum\limits_{q = 1 \ne p}^N s (|{\mathit{\boldsymbol{P}}_q} - {\mathit{\boldsymbol{P}}_p}|)({\mathit{\boldsymbol{P}}_q} - {\mathit{\boldsymbol{P}}_p})/{\mathit{\boldsymbol{d}}_p} - g{\mathit{\boldsymbol{\hat e}}_g} + u{\mathit{\boldsymbol{\hat e}}_w}。$ | (3) |
考虑到公式(3)中的蚱蜢个体将快速的收敛至舒适区,这将导致算法不能收敛至全局最优。因此,公式(3)不能直接用于求解优化问题,为了解决这个问题,文献[13]提出修正后的方程为
| $ \mathit{\boldsymbol{P}}_p^d = c(\sum\limits_{q = 1 \ne p}^N c ((u{b_d} - l{b_d})/2)s(|\mathit{\boldsymbol{P}}_q^d - \mathit{\boldsymbol{P}}_p^d|)(({\mathit{\boldsymbol{P}}_q} - {\mathit{\boldsymbol{P}}_p})/{\mathit{\boldsymbol{d}}_{pq}})) + {\mathit{\boldsymbol{\hat T}}_d}, $ | (4) |
其中:Ppd是第p个蚱蜢在d维搜索空间的分量;ubd和lbd分别是蚱蜢在d维搜索空间的取值上界和取值下界;
为了平衡探索和开发性能以及舒适区、排斥区和吸引区之间的相互转换,参数c可以表示为c=cmax-t(cmax-cmin)/T,其中:cmax、cmin分别是最大值和最小值,本文设置cmax=1,cmin=0.000 1;t是当前迭代次数;T是最大迭代次数。
2 基于WGOA的目标跟踪方法 2.1 WGOA方法 2.1.1 改进原理基本GOA是通过种群之间相互作用不断向目标位置移动,这将导致种群多样性降低,一旦算法陷入局部最优,将很难跳出。因此,在GOA中引入变异算子,使种群位置以一定的概率重新初始化,增加算法全局搜索能力,提高收敛精度。另外,在GOA位置更新过程中引入非线性动态权重可以加快算法后期的搜索速度,提高收敛效率。
2.1.2 变异算子GOA调节参数少,具有较强的搜索能力,但是存在收敛精度较低的问题。本文借鉴DE的变异机制[16],将变异算子引入GOA中,增强种群多样性,避免陷入局部最优,最终实现全局最优。其基本思想是在蚱蜢每次更新过程之后,以一定的概率重新初始化。可以表述为Xi=round(rand*(ubd-lbd))P>Thr,其中:Xi为第i个蚱蜢的位置;P是介于0与1之间的随机数;ubd和lbd分别是蚱蜢在d维搜索空间的取值上界和取值下界。在本文中,Thr=0.98。
2.1.3 动态权重尽管GOA通过变异算子可以增强全局搜索能力,但是在GOA搜索后期,蚱蜢的位置更新仍以公式(4)进行局部搜索,这只能促使蚱蜢向目标位置靠近,但不能更快地收敛至局部最优。针对这个问题,受粒子群优化算法中惯性权重的启发,本文将非线性动态权重引入GOA中,表述为
| $ w = {w_{ {\rm{max}} }} - ({w_{ {\rm{max}} }} - {w_{{\rm{ min}} }}) \times {(t/T)^{1/t}}, $ | (5) |
其中:wmax、wmin分别为动态权重的最大值和最小值,本文设置为wmax=1,wmin=0.000 1。
由式(5)可知:在搜索前期,动态权重较大时,算法的探索能力强,可以保证全局搜索;在算法后期,动态权重变小,增强算法的开发性能,提高收敛速度。改进后的公式为
| $ \mathit{\boldsymbol{P}}_p^d = c(\sum\limits_{q = 1 \ne p}^N c ((u{b_d} - l{b_d})/2)s(|P_q^d - P_p^d|)(({P_q} - {P_p})/{d_{pq}})) + w{\mathit{\boldsymbol{\hat T}}_d}。$ |
综上所述,将变异算子和非线性动态权重引入标准的GOA中,既能增强算法的全局搜索能力,又能提高算法的收敛速度。
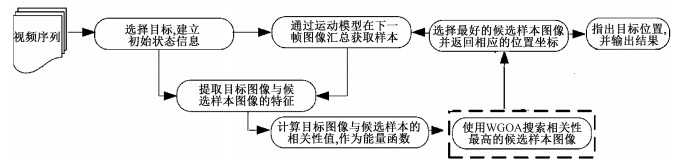
2.2 目标跟踪实现假设图像(状态空间)中存在一个目标(最好的蚱蜢),WGOA的目的是在图像中随机生成一组候选样本(蚱蜢)来寻找目标。基于WGOA的跟踪器可以看作以WGOA作为一种搜索方式,来搜索与目标最为相似的候选样本,其跟踪流程图如图 1所示。
|
图 1 基于WGOA跟踪器流程图 Fig. 1 The flowchart of the WGOA tracker |
由图 1可知,首先,用户在第一帧中选择目标,并建立初始状态向量X=[x, y, s]。其中:[x, y]表示目标在图像上像素坐标的位置;s是尺度参数。其次,依据运动模型(蚱蜢位置更新机制)在下一帧图像中生成候选样本图像,并获取特征信息;然后,使用能量函数计算出目标图像与候选样本图像之间的相关性,其相关性最大的候选样本图像,即为所求的预测目标;最后,将预测目标作为本帧的目标以及下一帧的模板,完成视觉跟踪。其中,虚线框是WGOA作为一种全局搜索策略来寻找与目标最为相似的候选样本图像。在这项工作中,我们的主要贡献是通过改进GOA来生成候选样本图像信息。基于前期的研究工作,采用相似函数作为能量函数[12]。
3 实验结果与分析本实验在Intel(R)Core(TM) i5-7500CPU3.4G计算机上运行,用MatlabR2017b、Windows10操作系统实现。为了验证提出算法的适用性,将实验分为两部分:1) WGOA的性能评估;2)与先进的跟踪器对比。
3.1 WGOA的性能评估为了验证提出的优化算法WGOA的有效性,本实验选取23个基准函数[17]中的5个函数,对提出的优化算法进行性能测试(如表 1所示)。其中:F1和F2为单峰函数;F9、F10和F11为多峰函数。单峰函数只有一个全局解,没有局部解。因此,它们可以用来检测优化算法的收敛速度。多峰函数具有许多局部极小值,这些函数可以反映算法跳出局部优化并实现全局优化的能力。
|
|
表 1 5个基准测试函数 Tab. 1 Five benchmark test functions |
为了验证WGOA具有一定的优势,将WGOA和GOA[13]、SCA[17]、DE[16]进行比较。4种优化算法保持同样的种群大小,n=30和迭代次数T=500,WGOA和GOA中的吸引力强度f=0.5和吸引力长度比例l=1.5;DE算法中的交叉常数设置为0.2,常数因子为0.5。通过WGOA、GOA、SCA和DE对以上5种函数进行30次测试和比较,并使用平均值、标准差和最差值作为统计数据,其实验结果如表 2所示(最好的结果用粗体表示)。从表 2可以看出,对于收敛精度和稳定性方面,WGOA无论在单峰函数还是多峰函数均表现出明显的优势,特别是与GOA相比。因此,WGOA具有很好的全局收敛性能。
|
|
表 2 基准测试函数运行结果 Tab. 2 Results of benchmark test function |
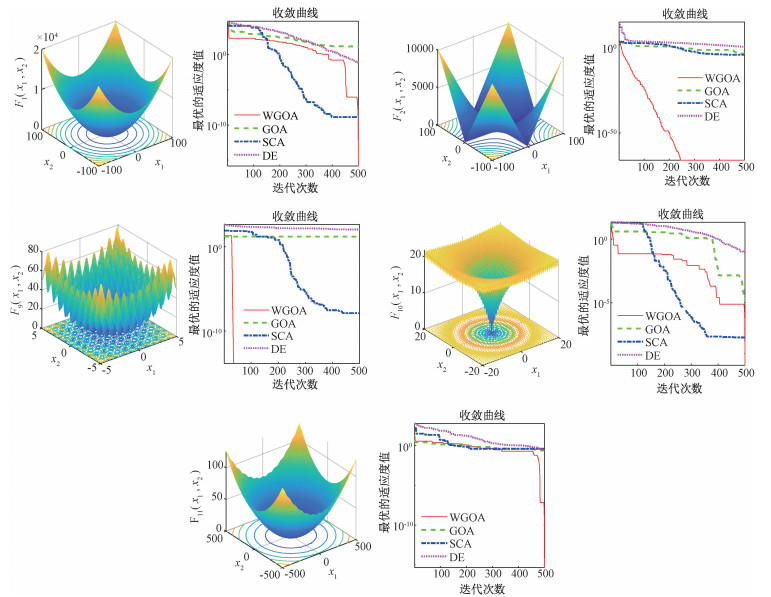
为了能直观地观测4种算法在测试函数中的收敛状况,通过计算每次迭代最优的适应度值来绘制收敛曲线,结果如图 2所示。从图 2可以看出,WGOA相比于其他优化算法而言,具有明显的下降趋势。因此,WGOA具有较快的收敛速度。综上所述,WGOA既能增强全局探索性能,提高收敛精度;又能增强局部开发性能,提高算法的收敛效率。
|
图 2 收敛曲线图 Fig. 2 Convergence curve |
为了验证WGOA在目标跟踪中的可行性,实验选取6个视频序列(FISH、JUMPING、DEER、ZXJ、BLURFACE、FHC)进行测试。4个先进的跟踪器(GOA、KCF[18]、LSST[19], CACF[3])进行比较。在视频序列中,ZXJ和FHC是我们实验室构建的数据集。其他视频序列来自网站http://cvlab.hanyang.ac.kr/tracker_benchmark/datasets.html。我们提取了BLURFACE序列中的306~310帧进行抽帧处理,形成目标的突变运动问题。在这次实验中,参数设置如下:WGOA与GOA的参数保持一致;种群大小n=100;迭代次数T=300;吸引力强度f=0.5;吸引力长度比例l=1.5;而KCF,LSST和CACF跟踪器采用默认值。另外,我们分别从定性和定量两个方面对实验结果进行分析。
3.2.1 定性分析我们对6个视频序列分为两组对跟踪结果进行分析。
1) 一般运动组
选取FISH、JUMPING和DEER视频序列作为一般运动组,跟踪结果如图 3所示。

|
图 3 一般运动组的跟踪结果 Fig. 3 Tracking results of general motion group |
对于FISH视频序列,目标存在光照变化的现象。从图 3(第1行)可以看出,在#0058和#0312帧发生相机抖动,在#0178帧亮度变暗。虽然所有的跟踪器都能成功捕获目标,但是WGOA和KCF的跟踪效果最好。
对于JUMPING视频序列,由于相机抖动导致目标出现严重模糊。从图 3(第2行)可以看出,KCF在#0096帧不幸丢失目标;GOA和CACF在#0262帧也丢失目标;仅有WGOA和LSST成功地跟踪了整个视频序列。
对于DEER视频序列,目标经历了运动模糊和多个相似目标。从图 3(第3行)可以看出,KCF和CACF在#0026帧丢失目标,虽然它们在#0042帧中恢复了跟踪,但仍然无法跟踪整个视频序列。然而,其他的跟踪器完成了整个视频序列。由一般运动组的实验结果可知,WGOA跟踪器在对于平滑运动的视频序列中能保证较好的跟踪效果。
2) 突变运动组
为了验证提出的跟踪器在目标发生突变运动时的跟踪效果,选取ZXJ、BLURFACE和FHC视频序列作为突变运动组,这3个序列的目标均发生大位移现象。跟踪结果如图 4所示。

|
图 4 突变运动组的跟踪结果 Fig. 4 Tracking results of abrupt motion group |
对于ZXJ视频序列,由于相机的连续抖动造成了突变运动,最大位移为70个像素点。从图 4(第1行)可以看出,在#0042帧之前所有的跟踪器均能很好地跟踪目标,但在#0069帧,KCF和LSST丢失目标;GOA在#0110帧也开始偏离目标。因此,WGOA和CACF表现出较好的跟踪效果。
对于BLURFACE视频序列,设计了帧丢失问题。由于在#0153、#0241和#0310帧出现相机的剧烈抖动,导致目标出现模糊现象。从图 4(第2行)可以看出,只有WGOA和GOA跟踪器在#0310帧能成功地跟踪目标并完成了整个视频序列,其他的跟踪器均丢失目标,说明基于优化的跟踪器能较好地解决视频的帧丢失问题。
对于FHC视频序列,最大位移为188个像素点。从图 4(第3行)可以看出,WGOA和CACF均能成功地跟踪整个视频序列,其他跟踪器均丢失目标。总之,对于大位移视频序列,WGOA跟踪器相比于其他跟踪器具有很强的优势。
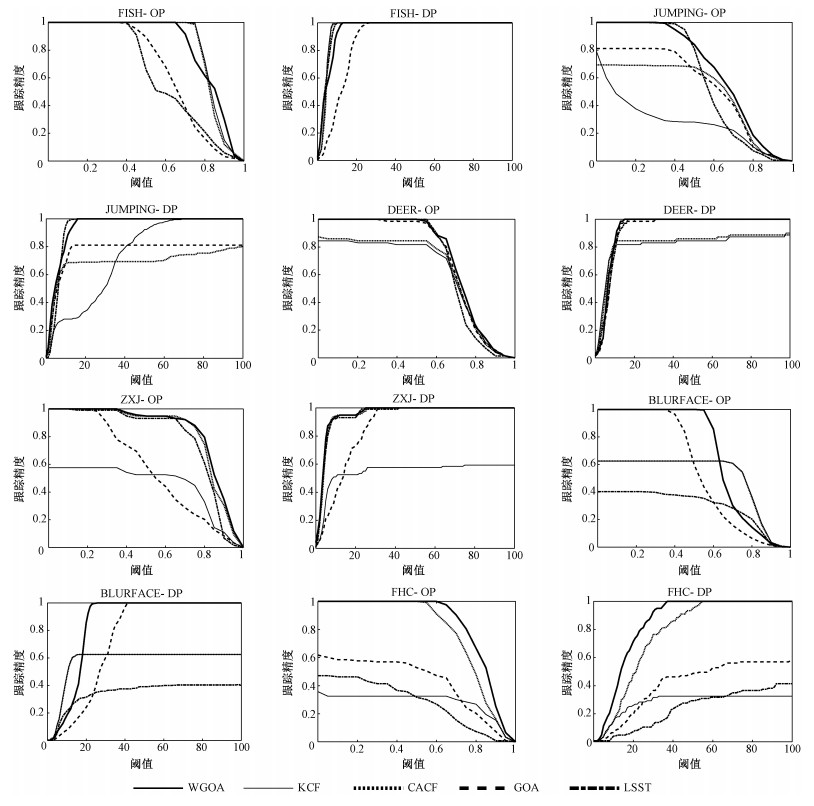
3.2.2 定量分析为了直观地评估这些跟踪器的性能,采用重叠精度(overlap precision, OP)、距离精度(distance precision, DP)和中心位置误差(centre location error, CLE)来计算并观察跟踪结果[20]。表 3给出了平均重叠率,表 4给出了平均中心位置误差,最好的实验结果在表中用粗体表示,并利用平均值来统计所有的视频序列。图 5为OP和DP成功图的平均精度。对于OP成功图,x轴表示阈值范围,y轴表示帧的比率,即重叠量高于阈值的帧数占总帧数的比率。图中的曲线下边面积越大,表示跟踪的效果越好。对于DP成功率图,y轴也代表了帧的比率,表示了预测目标的中心位置与真实位置的距离低于阈值的帧数占总帧数的比率。图中的斜率越高,表示跟踪效果越好。
|
图 5 成功图的平均精度 Fig. 5 The average precision of success plots |
|
|
表 3 平均重叠率 Tab. 3 Average overlap rate |
|
|
表 4 平均中心位置误差 Tab. 4 Average centre location error |
由表 3、表 4和图 5的结果可知,WGOA跟踪器表现出较好的跟踪结果。特别地,对于抽帧处理后的BLURFACE视频序列,CACF丢失了目标,而WGOA跟踪器仍能成功跟踪目标。因此,提出的算法在处理视频帧丢失问题具有一定的优势。
4 结束语本文针对传统跟踪器不能较好地适应突变运动问题,提出了一种基于WGOA的突变跟踪方法。该方法将变异算子融入GOA中,增强算法跳出局部最优的能力,提高收敛精度;利用非线性减小的动态权重可以在算法后期加强局部搜索性能,提高收敛效率;并将提出的WGOA应用到视觉跟踪,用来解决运动的突变问题。实验结果表明,本文方法不仅能有效处理突变运动跟踪问题, 在通常的视频序列上也具有良好的鲁棒性,在未来可与先进跟踪器相结合来实现实时跟踪。
| [1] |
张焕龙, 胡士强, 杨国胜. 基于外观模型学习的视频目标跟踪方法综述[J]. 计算机研究与发展, 2015, 52(1): 177-190. ZHANG H L, HU S Q, YANG G S. Video object tracking based on appearance models learning[J]. Journal of computer research and development, 2015, 52(1): 177-190. (  0) 0) |
| [2] |
何志勇, 蔡乐才, 许继家. 基于Mean Shift算法跟踪视频中运动目标[J]. 郑州大学学报(理学版), 2010, 42(1): 38-40, 48. HE Z Y, CAI L C, XU J J. Tracking moving objects based on Mean Shift algorithm in video[J]. Journal of Zhengzhou university(natural science edition), 2010, 42(1): 38-40, 48. (  0) 0) |
| [3] |
MUELLER M, SMITH N, GHANEM B. Context-aware correlation filter tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York, 2017: 1396-1404.
(  0) 0) |
| [4] |
WANG F S, LI X C, LU M Y. Adaptive Hamiltonian MCMC sampling for robust visual tracking[J]. Multimedia tools and applications, 2017, 76(11): 13087-13106. DOI:10.1007/s11042-016-3699-1 (  0) 0) |
| [5] |
张焕龙, 高增, 张秀娇, 等. 混合模拟退火与蚁狮优化的图像匹配方法[J]. 计算机科学, 2019, 46(6): 328-333. ZHANG H L, GAO Z, ZHANG X J, et al. Image matching method combining hybrid simulated annealing and antlion optimizer[J]. Computer science, 2019, 46(6): 328-333. (  0) 0) |
| [6] |
张焕龙, 张秀娇, 贺振东, 等. 基于布谷鸟搜索的图像匹配方法研究[J]. 郑州大学学报(理学版), 2017, 49(4): 51-56. ZHANG H L, ZHANG X J, HE Z D, et al. The study on image matching method based on cuckoo search[J]. Journal of Zhengzhou university(natural science edition), 2017, 49(4): 51-56. (  0) 0) |
| [7] |
GAO M L, SHEN J, YIN L J, et al. A novel visual tracking method using bat algorithm[J]. Neurocomputing, 2016, 177: 612-619. DOI:10.1016/j.neucom.2015.11.072 (  0) 0) |
| [8] |
刘剑, 郭文博, 李凌燕, 等. 一种基于多样性优化的视频目标跟踪方法[J]. 计算机应用与软件, 2017, 34(1): 137-142. LIU J, GUO W B, LI L Y, et al. A video target tracking method based on diversity optimisation[J]. Computer applications and software, 2017, 34(1): 137-142. DOI:10.3969/j.issn.1000-386x.2017.01.025 (  0) 0) |
| [9] |
LJOUAD T, AMINE A, RZIZA M. A hybrid mobile object tracker based on the modified cuckoo search algorithm and the kalman filter[J]. Pattern recognition, 2014, 47(11): 3597-3613. DOI:10.1016/j.patcog.2014.04.003 (  0) 0) |
| [10] |
NENAVATH H, JATOTH R K. Hybridizing sine cosine algorithm with differential evolution for global optimization and object tracking[J]. Applied soft computing, 2018, 62: 1019-1043. DOI:10.1016/j.asoc.2017.09.039 (  0) 0) |
| [11] |
ZHANG X Q, HU W M, MAYBANK S, et al. Sequential particle swarm optimization for visual tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York, 2008: 1-8.
(  0) 0) |
| [12] |
ZHANG H L, ZHANG X J, WANG Y, et al. Extended cuckoo search-based kernel correlation filter for abrupt motion tracking[J]. IET computer vision, 2018, 12(6): 763-769. DOI:10.1049/iet-cvi.2017.0554 (  0) 0) |
| [13] |
SAREMI S, MIRJALILI S, LEWIS A. Grasshopper optimisation algorithm: theory and application[J]. Advances in engineering software, 2017, 105: 30-47. DOI:10.1016/j.advengsoft.2017.01.004 (  0) 0) |
| [14] |
ARORA S, ANAND P. Chaotic grasshopper optimization algorithm for global optimization[J]. Neural computing and applications, 2019, 31(8): 4385-4405. DOI:10.1007/s00521-018-3343-2 (  0) 0) |
| [15] |
ELMI Z, EFE M O. Multi-objective grasshopper optimization algorithm for robot path planning in static environments[C]//2018 IEEE International Conference on Industrial Technology (ICIT).New York, 2018: 244-249.
(  0) 0) |
| [16] |
STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 (  0) 0) |
| [17] |
MIRJALILI S. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge-based systems, 2016, 96: 120-133. DOI:10.1016/j.knosys.2015.12.022 (  0) 0) |
| [18] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 (  0) 0) |
| [19] |
WANG D, LU H C, YANG M. Robust visual tracking via least soft-threshold squares[J]. IEEE transactions on circuits and systems for video technology, 2016, 26(9): 1709-1721. DOI:10.1109/TCSVT.2015.2462012 (  0) 0) |
| [20] |
WU Y, LIM J, YANG M. Online object tracking: a benchmark[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York, 2013: 2411-2418.
(  0) 0) |
 2020, Vol. 52
2020, Vol. 52


