2. 智能康复装置与检测技术教育部工程研究中心 天津 300130
2. Engineering Research Center of Intelligent Rehabilitation Device and Detect Technology of Ministry of Education, Tianjin 300130, China
家庭服务机器人是机器人发展的重要方向之一,而机械臂控制对服务机器人执行各种类人任务至关重要[1].作为一种复杂的非线性系统,机械臂易受不确定的因素,包括不确定的惯性、未知的重力转矩、未知的摩擦力矩和其他干扰的影响[2].这些难以预测的不确定性影响了机械臂的控制精度及可靠性.因此,必须设计鲁棒控制方法处理上述干扰,以实现预期的性能.
对不确定性及干扰的处理,文献[3-5]提出了多种方法.滑模控制具有较强的鲁棒性和快速响应能力,常被应用于各种非线性不确定系统的控制中,但滑模控制的不连续性会引起控制的抖振.干扰观测器提供了处理干扰和不确定性的另一种方法.和其他干扰估计与抑制方法相比,非线性干扰观测器以其简单直观及严格的稳定性分析得到了广泛的研究和应用.为了估计高度非线性、强耦合的机械臂的未知干扰,文献[6]提出用非线性干扰观测器估计干扰及参数不确定性,然后通过估计值对控制器进行补偿.文献[7]提出了一种新型非线性干扰观测器,解决了干扰观测器的系统设计问题,并将其应用于机械臂控制,但不能实现有限时间控制.文献[8]研究了具有参数不确定性和外部干扰的空间机械臂的鲁棒跟踪控制问题,提出一种基于干扰观测器的输出反馈自适应控制方法,采用模糊逻辑系统来估计和补偿集总干扰.文献[9]针对具有模型不确定性和受外界干扰的机械臂轨迹跟踪控制问题,设计了由非线性控制器、速度观测器和干扰观测器组成的复合控制器,并给出了半全局渐近稳定性条件.
上述控制方法中系统都是渐近稳定的,与渐近稳定系统相比,有限时间稳定系统通常表现出更快的收敛速度和更好的抗干扰性能[10-11].基于干扰观测器的终端滑模控制方法是一个有效的复合控制方法,将干扰观测值作为前馈补偿,能够及时有效地抑制干扰.本文针对五自由度机械臂的运动控制问题,研究一种非奇异终端滑模控制与非线性干扰观测器相结合的复合控制器.将系统模型不确定性和外界干扰作为复合干扰(集总干扰),设计了非奇异终端滑模控制器,以实现对系统的鲁棒控制及跟踪误差的有限时间收敛,同时利用干扰观测器估计集总干扰,对滑模控制器进行前馈补偿以削弱控制抖振.
1 模型描述机械臂的各个关节都为旋转关节,考虑由外界干扰和模型误差组成的复合干扰,串联刚性连接的机械臂模型可以表示为
| $ \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{q}} \right) + \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\dot q}}} \right) = \mathit{\boldsymbol{\tau }} + {\mathit{\boldsymbol{\tau }}_d}, $ | (1) |
式中:q、
通常情况下,机械臂的精确动力学模型难以得到,将模型分为已知部分和不确定部分:M(q)=M0(q)+ΔM(q),C(q,
| $ {\mathit{\boldsymbol{M}}_0}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} + {\mathit{\boldsymbol{C}}_0}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{G}}_0}\left( \mathit{\boldsymbol{q}} \right) = \mathit{\boldsymbol{\tau }} + \mathit{\boldsymbol{d}}, $ | (2) |
式中:d=τd-ΔM(q)
在实际工程中,复合干扰d通常很难获得,需要对其进行估计,但是干扰的估计值与实际值之间存在一定的误差.干扰观测器设计的基本思想是用估计输出与实际输出的差值对估计值进行修正.用
| $ \begin{array}{l} \mathit{\boldsymbol{\dot {\hat d}}} = \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{\hat d}}} \right) = - \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\hat d}} + \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{d}} = \\ - \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\hat d}} + \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\left[ {{\mathit{\boldsymbol{M}}_0}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} + {\mathit{\boldsymbol{C}}_0}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{G}}_0}\left( \mathit{\boldsymbol{q}} \right) - \mathit{\boldsymbol{\tau }}} \right], \end{array} $ | (3) |
式中:L(q,
| $ {{\mathit{\boldsymbol{\dot e}}}_d} + \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right){\mathit{\boldsymbol{e}}_d} = 0. $ | (4) |
选取合适的增益函数L(q,
定义辅助向量z=
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{p}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right) = \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right){\mathit{\boldsymbol{M}}_0}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}}. $ | (5) |
对z求导得:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat d}} = \mathit{\boldsymbol{z}} + \mathit{\boldsymbol{p}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right);}\\ {\mathit{\boldsymbol{\dot z}} = - \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{z}} + \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\left[ {{\mathit{\boldsymbol{C}}_0}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{G}}_0}\left( \mathit{\boldsymbol{q}} \right) - \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{p}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)} \right].} \end{array} $ | (6) |
对观测误差ed求导得
| $ {{\mathit{\boldsymbol{\dot e}}}_d} = - \mathit{\boldsymbol{\dot {\hat d}}} = - \mathit{\boldsymbol{\dot z}} - \mathit{\boldsymbol{\dot p}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right). $ | (7) |
将式(6)代入式(7)得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot e}}}_d} = \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{z}} - \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\left[ {{\mathit{\boldsymbol{C}}_0}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{G}}_0}\left( \mathit{\boldsymbol{q}} \right) - \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{p}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)} \right] - \\ \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right){\mathit{\boldsymbol{M}}_0}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} = \\ - \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\left[ {{\mathit{\boldsymbol{C}}_0}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{G}}_0}\left( \mathit{\boldsymbol{q}} \right) + {\mathit{\boldsymbol{M}}_0}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} - \mathit{\boldsymbol{\tau }}} \right] + \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\left[ {\mathit{\boldsymbol{z}} + \mathit{\boldsymbol{p}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)} \right] = \\ - \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{\hat d}}} \right) = - \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right){\mathit{\boldsymbol{e}}_d}. \end{array} $ | (8) |
选择Lyapunov函数
设计具有较快收敛速度的非奇异快速终端滑模面s为
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{e}} + \mathit{\boldsymbol{A}}{\rm{sig}}{\left( \mathit{\boldsymbol{e}} \right)^\mathit{\boldsymbol{\alpha }}} + \mathit{\boldsymbol{B}}{\rm{sig}}{\left( {\mathit{\boldsymbol{\dot e}}} \right)^\mathit{\boldsymbol{\beta }}}, $ | (9) |
式中:e(t)表示角度跟踪误差,e(t)=q(t)-qd(t);s=[s1, s1, …,sn]T∈Rn,A=diag(a1, a2, …, an),B=diag(b1, b2, …, bn),a1, a2, …, an,b1, b2, …, bn是大于0的常数;α=diag(α1, α2, …, αn),β=diag(β1, β2, …,βn),1 < βi < 2,αi > βi,1≤i≤n;sig(e)α=[|e1|α1sgn(e1), …, |en|αnsgn(en)]T,sgn(·)为符号函数,sig(
针对机械臂动力学模型(2),设计基于非线性干扰观测器的滑模控制律为
| $ \begin{array}{l} \mathit{\boldsymbol{\tau }} = {\mathit{\boldsymbol{M}}_0}\left( \mathit{\boldsymbol{q}} \right){{\mathit{\boldsymbol{\ddot q}}}_d} + {\mathit{\boldsymbol{C}}_0}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{G}}_0}\left( \mathit{\boldsymbol{q}} \right) - {\mathit{\boldsymbol{M}}_0}{\mathit{\boldsymbol{B}}^{ - 1}}{\mathit{\boldsymbol{\beta }}^{ - 1}}\left( {{\mathit{\boldsymbol{I}}_n} + } \right.\\ \left. {\mathit{\boldsymbol{A\alpha }}{\rm{diag}}\left( {{{\left| {{e_i}} \right|}^{{\alpha _i} - 1}}} \right)} \right){\rm{sig}}{\left( {\mathit{\boldsymbol{\dot e}}} \right)^{2{\mathit{\boldsymbol{I}}_n} - \mathit{\boldsymbol{\beta }}}} - \mathit{\boldsymbol{\hat d}} - {\mathit{\boldsymbol{M}}_0}\left[ {{\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{K}}_2}{\rm{sig}}{{\left( \mathit{\boldsymbol{s}} \right)}^\gamma }} \right], \end{array} $ | (10) |
式中:In为n阶单位矩阵;K1=diag(k11, …, k1n),K2=diag(k21, …, k2n),k1i、k2i为大于0的常数;γ=diag(γ1, γ2, …, γn),0 < γ1, …,γn < 1,
|
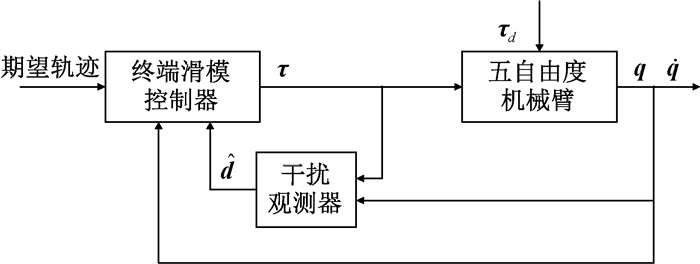
图 1 控制系统框图 Fig. 1 The diagram of control system |
定理1 考虑机械臂动力学模型(2),用干扰观测器方程(6)估计系统集总干扰d,设计非奇异终端滑模函数(9)及控制律(10),则轨迹跟踪误差在有限时间内收敛.
证明 选取Lyapunov函数V2=
| $ {{\dot V}_2} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left[ {\mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{A\alpha }}{\rm{diag}}\left( {{{\left| {{e_i}} \right|}^{{\alpha _i} - 1}}} \right)\mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{{\rm B}\beta }}{\rm{diag}}\left( {{{\left| {{{\dot e}_i}} \right|}^{{\beta _i} - 1}}} \right)\mathit{\boldsymbol{\ddot e}}} \right]. $ | (11) |
对e求二阶导数并代入式(11)得
| $ \begin{array}{l} {{\dot V}_2} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left\{ {\mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{A\alpha }}{\rm{diag}}\left( {{{\left| {{e_i}} \right|}^{{\alpha _i} - 1}}} \right)\mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{{\rm B}\beta }}{\rm{diag}}\left( {{{\left| {{{\dot e}_i}} \right|}^{{\beta _i} - 1}}} \right) \cdot } \right.\\ \left. {\left[ {\mathit{\boldsymbol{M}}_0^{ - 1}\left( { - {\mathit{\boldsymbol{C}}_0}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} - {\mathit{\boldsymbol{G}}_0}\left( \mathit{\boldsymbol{q}} \right) + \mathit{\boldsymbol{\tau }} + \mathit{\boldsymbol{d}}} \right) - {{\mathit{\boldsymbol{\ddot q}}}_d}} \right]} \right\}. \end{array} $ | (12) |
将式(10)代入式(12)得
| $ \begin{array}{l} {{\dot V}_2} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{B\beta }}{\rm{diag}}\left( {{{\left| {{{\dot e}_i}} \right|}^{{\beta _i} - 1}}} \right)\left[ { - \left( {{\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{K}}_2}{\rm{sig}}{{\left( \mathit{\boldsymbol{s}} \right)}^\mathit{\boldsymbol{\gamma }}}} \right) - \mathit{\boldsymbol{M}}_0^{ - 1}\left( {\mathit{\boldsymbol{\hat d}} - \mathit{\boldsymbol{d}}} \right)} \right] = \\ - {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{B\beta }}{\rm{diag}}\left( {{{\left| {{{\dot e}_i}} \right|}^{{\beta _i} - 1}}} \right)\left( {{\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{K}}_2}{\rm{sig}}{{\left( \mathit{\boldsymbol{s}} \right)}^\mathit{\boldsymbol{\gamma }}} - \mathit{\boldsymbol{M}}_0^{ - 1}{\mathit{\boldsymbol{e}}_d}} \right) \le \\ - {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{B\beta }}{\rm{diag}}\left( {{{\left| {{{\dot e}_i}} \right|}^{{\beta _i} - 1}}} \right)\left[ {{\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{s}} + \left( {{\mathit{\boldsymbol{K}}_2} - {\rm{diag}}\left( {\mathit{\boldsymbol{M}}_0^{ - 1}{\mathit{\boldsymbol{e}}_d}} \right){\rm{dia}}{{\rm{g}}^{ - 1}}\left( {{\rm{sig}}{{\left( \mathit{\boldsymbol{s}} \right)}^\mathit{\boldsymbol{\gamma }}}} \right)} \right){\rm{sig}}{{\left( \mathit{\boldsymbol{s}} \right)}^\mathit{\boldsymbol{\gamma }}}} \right]. \end{array} $ | (13) |
若矩阵K2-diag(M0-1ed)diag-1(sig(s)γ)正定,则
| $ {{\dot V}_2} \le - 2{\underline k _1}V_2^2 - {2^{\left( {\gamma + 1} \right)/2}}{\underline k _2}{V_2}^{\left( {\mathit{\boldsymbol{\gamma }} + 1} \right)/2}, $ | (14) |
式中:k1、k2分别为正定对角矩阵Bβdiag(|
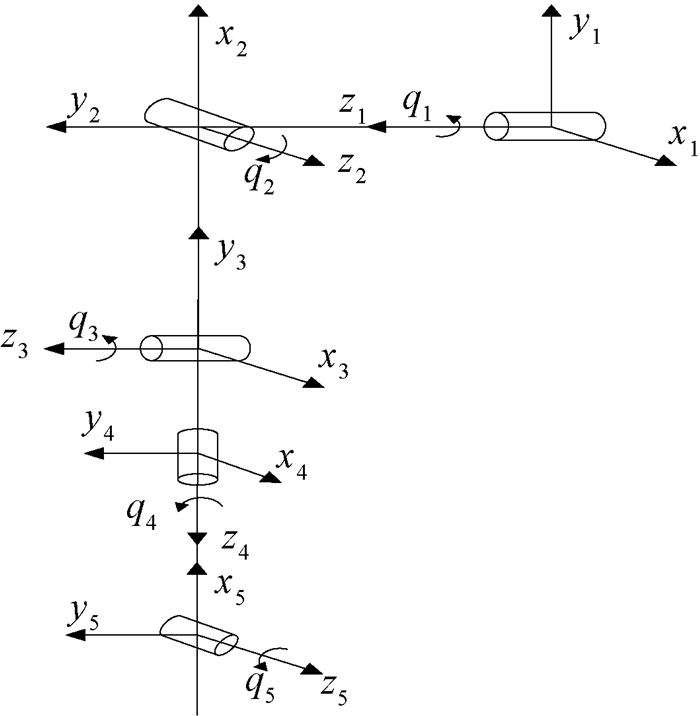
为了验证所提出的控制策略的有效性,对文献[13]中的五自由度机械臂系统进行了仿真分析,其机械臂简图如图 2所示,其中q1为肩关节屈伸角,q2为肩关节外展内收角,q3为肘关节屈伸角,q4为腕关节内旋、外旋角,q5为腕关节屈伸角.以每个关节中心点为原点建立坐标系,各关节绕z轴旋转.
|
图 2 五自由度机械臂简图 Fig. 2 The diagram of five degree-of-freedom robotic manipulator |
式(1)中M(q)、C(q,
|
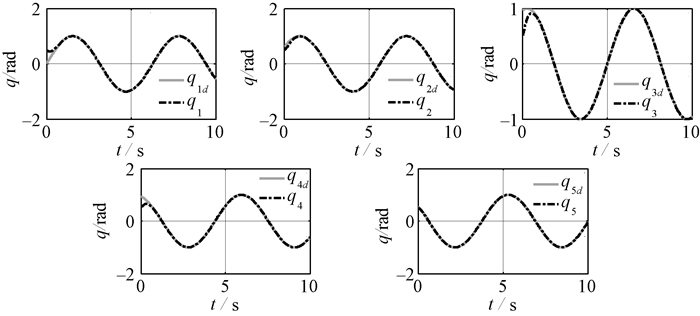
图 3 关节角度跟踪曲线 Fig. 3 Tracking curve of joint angle |
|
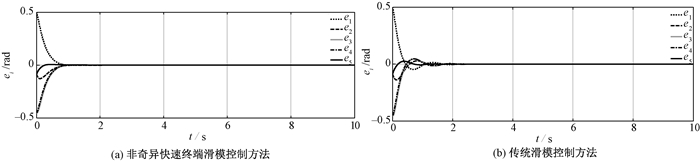
图 4 关节角度跟踪误差 Fig. 4 Tracking error of joint angle |
|
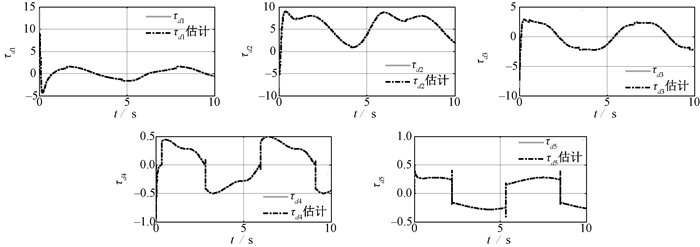
图 5 干扰及干扰估计曲线 Fig. 5 Disturbance and its estimation curve |
|
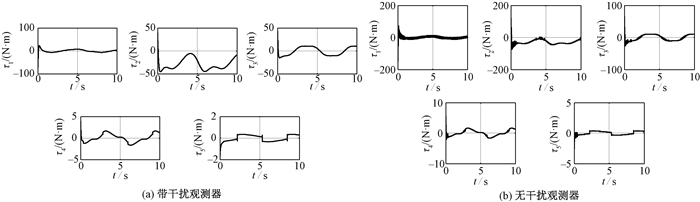
图 6 控制输入 Fig. 6 Control input |
图 3为关节角度跟踪曲线,图 4为关节角度跟踪误差.可以看出,在系统存在模型不确定性和外界干扰情况下,设计的终端滑模控制器能够使机械臂对指令轨迹做出快速响应,跟踪误差在有限时间内收敛.与现有方法相比,本文所提出的控制方法误差收敛速度更快.图 5为干扰及干扰估计曲线,τd1、τd2、τd3、τd4、τd5分别为关节1~5处的复合干扰.可以看出,设计的干扰观测器能够实现对干扰的准确观测,其观测值为控制器提供补偿,采用干扰观测器补偿的方法可以减小控制抖振.为证明干扰观测器的有效性,针对相同的机械臂系统,设计无干扰观测器补偿的滑模控制器,滑模切换项增益不小于干扰上界,即k2i≥‖d‖,其他控制器参数与本文所提出的控制器参数相同,在两种控制器下的控制输入如图 6所示.可以看出,本文所提出的控制器控制力矩曲线连续光滑,基本无抖振(第5个关节控制曲线的不连续是由不连续摩擦引起的),且由于切换增益较小,所需的起始力矩较小,而无干扰观测器补偿的滑模控制器控制力矩存在较强的抖振且起始力矩较大.
5 结论针对五自由度机械臂的控制问题,设计了基于干扰观测器的非奇异终端滑模控制策略.将外界干扰和系统模型不确定性看作集总干扰,利用非线性干扰观测器逼近系统干扰,不需要知道系统干扰的上界且能够削弱控制抖振.设计的非奇异终端滑模面能够使系统在有限时间内收敛,加快了对指令的响应速度.理论分析和仿真结果表明,所提出的干扰观测器能够实现对干扰的准确观测,基于干扰观测器的滑模控制能够有效削弱抖振且使轨迹跟踪误差在有限时间内收敛.
| [1] |
徐昱琳, 杨永焕, 李昕, 等. 基于双目视觉的服务机器人仿人机械臂控制[J]. 上海大学学报(自然科学版), 2012, 18(5): 506-512. DOI:10.3969/j.issn.1007-2861.2012.05.013 (  0) 0) |
| [2] |
CHENG L, HOU Z G, TAN M. Brief paper:adaptive neural network tracking control for manipulators with uncertain kinematics, dynamics and actuator model[J]. Automatica, 2009, 45(10): 2312-2318. DOI:10.1016/j.automatica.2009.06.007 (  0) 0) |
| [3] |
陈志旺, 薛佳伟. 基于不确定逼近的机械手自适应鲁棒预测控制[J]. 控制理论与应用, 2012, 29(5): 635-641. (  0) 0) |
| [4] |
CUONG P V, WANG Y N. Adaptive trajectory tracking neural network control with robust compensator for robot manipulators[J]. Neural computing and applications, 2016, 27(2): 525-536. DOI:10.1007/s00521-015-1873-4 (  0) 0) |
| [5] |
于靖, 陈谋, 姜长生. 基于干扰观测器的非线性不确定系统自适应滑模控制[J]. 控制理论与应用, 2014, 31(8): 993-999. (  0) 0) |
| [6] |
CHEN W H, BALLANCE D J, GAWTHROP P J, et al. A nonlinear disturbance observer for robotic manipulators[J]. IEEE transactions on industrial electronics, 2000, 47(4): 932-938. DOI:10.1109/41.857974 (  0) 0) |
| [7] |
MOHAMMADI A, TAVAKOLI M, MARQUEZ H J, et al. Nonlinear disturbance observer design for robotic manipulators[J]. Control engineering practice, 2013, 21(3): 253-267. DOI:10.1016/j.conengprac.2012.10.008 (  0) 0) |
| [8] |
CHU Z Y, CUI J, SUN F C. Fuzzy adaptive disturbance-observer-based robust tracking control of electrically driven free-floating space manipulator[J]. IEEE systems journal, 2014, 8(2): 343-352. DOI:10.1109/JSYST.2012.2220171 (  0) 0) |
| [9] |
BOUAKRIF F. Trajectory tracking control using velocity observer and disturbances observer for uncertain robot manipulators without tachometers[J]. Meccanica, 2017, 52(4/5): 861-875. (  0) 0) |
| [10] |
LI S H, DU H B, LIN X Z. Finite-time consensus algorithm for multi-agent systems with double-integrator dynamics[J]. Automatica, 2013, 47(8): 1706-1712. (  0) 0) |
| [11] |
WANG X, LI S, SHI P. Distributed finite-time containment control for double-integrator multiagent systems[J]. IEEE transactions on cybernetics, 2014, 44(9): 1518-1528. DOI:10.1109/TCYB.2013.2288980 (  0) 0) |
| [12] |
YU S H, YU X H, SHIRINZADEH B, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11): 1957-1964. DOI:10.1016/j.automatica.2005.07.001 (  0) 0) |
| [13] |
KANG H B, WANG J H. Adaptive control of 5 DOF upper-limb exoskeleton robot with improved safety[J]. ISA transactions, 2013, 52(6): 844-853. DOI:10.1016/j.isatra.2013.05.003 (  0) 0) |
 2019, Vol. 51
2019, Vol. 51


