时间触发以太网(time-triggered ethernet,TTE)发展迅速,被广泛应用于车辆控制[1-2]、航空控制[3]和无线通信等领域[4]。该技术所表现的安全性、实时性和灵活性等特点,符合工业网络的未来发展方向。
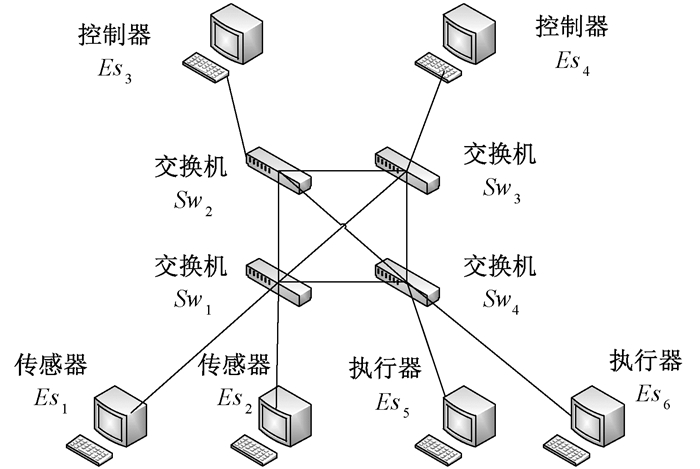
目前,空间网络采用分布式网络架构,如图 1所示。网络中每个节点都是对等个体,网络采用了主从双控制器模式和交换机冗余设计,以保障网络的可靠性和信息传输的实时性。由于基于CSMA/CD传输机制的标准以太网无法保证网络设备的"无冲突通信",空间网络需要引入一种实时通信技术。TTE[5]根据网络中统一的全局时钟进行设备间的通信交互,在遵循IEEE802.3协议的同时兼容SAE AS6802标准,同时支持时间触发通信和事件触发通信。因此,搭载TTE的空间网络有望成为星载系统的主干网络。
|
图 1 航天器控制网络模型 Fig. 1 The network model of satellite control |
网络物理拓扑结构由交换机(switch,Sw)、终端系统(end-system,Es)和物理链路(physical link,Pl)组成。TTE支持三种关键性数据流的传输[7]:时间触发(time-triggered, TT)流、速率受限(rate-constrained, RC)流和尽力传输(best effort, BE)流,其中TT流对抖动和延迟的要求最高。
TTE根据离线生成的调度表进行数据流的转发。调度表时间跨度为矩阵周期(matrix cycle, MC)[8],该周期由多个基本周期(basic cycle, BC)组成。数值上MC等于所有TT流传输周期的最小公倍数,BC等于所有TT流传输周期的最大公约数。合理设计的时间调度表可以实现物理链路上无冲突传输。
目前,调度表的生成方法主要分成两类。第一类是基于可满足模理论[6, 9]的非确定性算法,该算法主要利用随机化思想,通过优化损失函数来生成满足条件的调度表生成解。这类方法包括采用粒子群算法、遗传算法[10]等进化优化算法实现或是通过强化学习方法搜索最优时间触发调度表。另一类算法为确定性算法,采用一系列规则来保证数据流无冲突传输。此类算法具有算法复杂度低、生成结果可验证、增量化调度性强的特点。文献[11]提出基于贪心思想的TT-RMS算法,该算法会计算消息传输截止时间,以判断下一消息最早何时可以传输,以避免消息碰撞。文献[12]提出将TT消息分为二跳消息和非二跳消息进行配置,通过建立一套配置规则,实现消息无冲突传输。航天器控制系统属于硬实时系统,当发生网络拓扑变化时需要进行动态实时调度[13],以迅速恢复系统功能。因此,确定性算法更加适合空间TTE调度。
本文提出一种增强型的确定性的调度算法。首先,本文介绍如何设计消息的传输路径,来提高网络负载均衡度。之后,介绍调度表生成算法,并对于算法正确性,即是否满足调度表基本约束条件进行论述。最后,通过实验证明所提算法设计的合理性。算法本身的确定性生成特点可以满足星上网络需求,同时对多跳消息的支持能力有明显提高。
2 HCS(hop-count schedule)算法模型 2.1 消息路径设计降低消息对关键链路的依赖,可以提高网络负载均衡度。首先,对网络状态进行描述。定义消息集合F={f1, f2, …, fi}, (0≤i≤N),fi表示第i个消息,N为需要传输的TT消息总数。fi.path={v1, v2, …, vn}表示fi的传输路径为v1→v2→…→vn;网络中存在M条物理链路。接着,对网络负载度进行量化分析,如公式(1)~(5)所示,
| $ {\mu _i} = \mathop \sum \limits_{n = 1}^{{N_i}} 1/{T_n}, $ | (1) |
| $ \mu = \mathop \sum \limits_{i = 1}^M {\mu _i}, $ | (2) |
| $ \bar \mu = \mu /M, $ | (3) |
| $ {\sigma _i} = \sqrt {{{({\mu _i} - \bar \mu )}^2}/M} , $ | (4) |
| $ \sigma = \sqrt {\mathop \sum \limits_{i = 1}^M \sigma _i^2/M} 。$ | (5) |
其中:μi为第i条物理链路的负载度;Ni表示经过第i条物理链路的消息数;μ为网络负载度;μ为网络链路平均负载;σi为链路负载均方差;σ为网络负载均方差。负载均衡算法是保证在μ可接受范围内,最小化σ。定义Dijkstra算法下的网络初始负载为U,本文设置阈值k=0.2,表示负载度和均衡度的权衡值。此时网络可容忍的最大网络负载为μ'=(1+k)·U,表示增加k·U的负载量来提高网络均衡度。
保证消息传输速度在可接受范围内,尽可能使网络负载均衡的问题可以转化为:min{σ},s.t.μ*≤μ',μ*表示新生成的消息路径下的网络负载。算法首先对链路负载进行降序排序,选择出链路负载压力最大的链路Plk(必有μk>μ)。假设Plk上有一条数据链路vx→vy,该数据链路存在中继节点[13]vz,如果将传输路径更改为vx→vz→vy时, 可以实现网络均衡度增加(即σ减小)。那么就可以通过增加中继节点的方法进一步实现负载均衡。需要注意的是,满足μ*≤μ'才可以重新配置该消息传输路径。算法具体步骤如下。
1) 根据网络拓扑图G和消息集合F,计算出消息传输的最短路径配置CP;初始化最终配置方案CP*=CP。
2) 根据CP计算μ、μ、σ、σ的值;初始化U=μ;按照链路σ负载降序排列,取出链路负载高于σ的链路放入队列Q。
3) 若Q为空,算法结束;否则,队首元素pl出队,判断pl是否有中继节点,若存在中继节点则进入步骤4);否则,继续执行步骤3)。
4) 找经过pl的所有消息F(pl),按他们消息周期从小到大排序,取其中最小周期对应的一个消息fi;遍历pl的所有中继节点,找到使{μ(源结点到中继节点的边)+μ(中继节点到目标结点的边)}值最小的中继节点,将原有路径修改,得到新消息路径配置CP*;重新计算μ、σ;若μ≤(1+k) ·U,跳转步骤1);否则,回溯路径,执行步骤3)。
2.2 调度表设计 2.2.1 调度表结构本文对调度表的设计采用"时间槽"概念,将一个MC分成若干个大小相同的时间槽,并规定时间槽仅可放置一帧。实际情况中,还要考虑消息的传输延迟和发送延迟来确定时间槽的大小,合理调整时间槽的大小可以提高时间利用率[14]。
调度表将BC作为一行,表分为m=MC/BC行,每行分为n个区,n初始化设置为交换机个数swNum,矩阵表示为m·n的结构。
假设终端Es连接的交换机为Swq,则可以对该Es的调度表的列进行编号,编号规则如式(6)所示,Sw(q+j)表示路径第二跳交换机编号,等式右侧表示该交换机对应列号,具体可参考文献[12]。如果消息路径仅有一跳,则放入0号列。针对二跳消息,如果消息fi第二跳为Sw(q+j), 则对(q+j)号列中再编号,同样满足式(6)。但是,列编号中应当删除已经经过的交换机编号,即q和(q+j),并将二跳消息放入<q+j, 0>号位。这里(q+j)称为一级分区号,0称为二级分区号。对于三跳消息,假设经过的第三跳为Swp,则将消息配置在<q+j, p>位置。对于更多跳的消息,可以按照上述方法继续配置。
| $ Sw(q + j) = \left\{ \begin{array}{l} q + j,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;q + j < swNum + 1,\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;q + j = swNum + 1,\\ q + j - swNum,\;\;q + j > swNum + 1。\end{array} \right. $ | (6) |
归纳调度表结构划分策略, 可以得到式(7),
| $ n = \left\{ \begin{array}{l} 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H = 1, \\ swNum, \;\;\;\;\;\;H{\rm{ }} = 2, \\ A_{swNum}^{H - 1}, \;\;\;\;\;\;\;\;H \ge {\rm{ }}3, \end{array} \right. $ | (7) |
其中:n表示基本周期的分区个数;H表示网络传输的TT消息的最大跳数;A表示排列运算。
假设在如图 1所示的网络中,存在由Es1发送的三个TT帧,其传输路径表示为
| $ {f_1}:E{s_1} \to S{w_1} \to E{s_2};{f_2}:E{s_1} \to S{w_1} \to S{w_2} \to E{s_2};{f_3}:E{s_1} \to S{w_1} \to S{w_4} \to S{w_3} \to E{s_4}。$ |
此时H=3,BC分区数为4×3=12个,Es1一个BC下的调度表分区情况如图 2所示,可以看出f1的分区号为<0, 0>,f1的分区偏移量为9;f2分区号为<2, 0>,f2的分区偏移量为2;f3的分区号为<4, 3>,f3消息的分区偏移量为8。

|
图 2 Es1一个BC下的调度表 Fig. 2 The schedule of Es1 in one BC |
这里给出对于任意消息f,可以通过消息传输路径获得各级分区号f.sectionNo(式(8))、各级分区偏移量f.sectionOffset(式(9))和最终的BC上分区量f.section(式(10))。接下来按照所求f.section按序配置消息。
| $ \forall f \in F, f.{\rm{ }}path = [E{s_q}, {h_1}, {h_2}, \ldots , {h_m}, E{s_p}], S = swNum \to f.{\rm{ }}section\;\\No = [{s_1}, {s_2}, \ldots , {s_{S - 1}}] = [{h_2}, \ldots , {h_m}, 0, \ldots , 0], $ | (8) |
式中:f.path表示消息传输经过h1, h2, …, hm编号的交换机,消息f的区域编号是一个长度为S-1的数组,S代表交换机个数。由f.path可以得到区域编号f.sectionNo。若消息跳数小于S-1,则空余位置用0补充。
| $ \begin{array}{l} \forall f \in F, f.{\rm{ }}path{\rm{ }} = [E{s_q}, {h_1}, {h_2}, \ldots , {h_m}, E{s_p}]{\rm{ }}, S = swNum, n = P(i).{\rm{ }}size\left( {\rm{ }} \right){\rm{ }}, i \in {\rm{ }}[1, m]{\rm{ }}, \\ P(i) = \{ {h_k}|{h_k} \in {\rm{ }}({h_i}, {h_{i - 1}})\;or\;{h_k} \in {\rm{ }}({h_{i - 1}}, S]{\rm{ }} \cup {h_k} \in {\rm{ }}(0, {h_i}){\rm{ }}, k \in {\rm{ }}[1, i - 2]{\rm{ }}\} {\rm{ }}, \\ {t_i} = \left\{ \begin{array}{l} 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m{\rm{ }} = 1, \\ {h_i} - {h_{i - 1}} - n - 1, \;\;\;\;\;\;m \ge 2 \cap {h_i} > {h_{i - 1}}, \\ {h_i} - {h_{i - 1}} + S - n, \;\;\;\;\;m \ge 2 \cap {h_i} < {h_{i - 1}}, \end{array} \right. \end{array} $ | (9) |
式(9)主要计算消息在各级分区的偏移量,n表示前向分区对当前分区的影响值。例如,f3经交换机Sw4,Sw4的分区应当为(0, 1, 2, 3),但是f3之前经过了交换机Sw1,Sw4下分区为(0, 2, 3),所以二级分区号3的偏移量由原来的3变为2。n的计算分为两种情况:1) 当后跳交换机编号大于前跳交换机编号时,n表示交换机hi-1之前经过的编号在(hi, hi-1)范围内的交换机的个数;2) 当后跳交换机编号小于前跳交换机编号时,n的值应当是所经过编号大于在(0, hi)的所有交换机个数。ti表示第i级分区偏移量的计算方法。
| $ \begin{array}{l} \forall f \in F, f.{\rm{ }}path{\rm{ }} = [E{s_q}, {h_1}, {h_2}, \ldots , {h_m}, E{s_p}]{\rm{ }}, S = swNum \to f.{\rm{ }}section\\No{\rm{ }} = [{s_1}, {s_2}, \ldots , {s_{S - 1}}] \to f.{\rm{ }}sectionOffset{\rm{ }} = [{t_1}, {t_2}, \ldots , {t_{S - 1}}] \to \\f.{\rm{ }}section = \mathop \sum \limits_{i = 1}^{m - 2} {t_i}\cdot\mathop \prod \limits_{t = i}^{m - 2} (S - t) + {t_{m - 1}}, \end{array} $ | (10) |
式(10)表示通过分区号和分区偏移量可以计算出消息所在的具体位置f.section,该值等于前m-2个分区偏移量乘以各级分区的分区数。tm-1表示最后一级分区的偏移量。
2.2.2 算法合理性分析算法的合理性主要体现在网络消息传输过程中不会造成消息传输链路"冲突"。由于本算法主要依据为消息传输路径跳数,可以分为两部分论证调度表的生成规则,有效避免冲突。
第一部分是连接不同Sw的Es的调度表结构不同,避免后续链路产生冲突。
第二部分是连接相同Sw的不同Es的调度表结构相同,如何保证消息调度不会产生冲突现象是我们要研究的问题。冲突即同一时间槽,一个物理链路上有两条方向相同的消息。为了避免这种情况,引入"同源消息"[6]概念。在文献[12]中,同源消息定义为:若两条消息由连接在同一个交换机的不同设备发出且所经过的交换机路径相同,则两消息互为"同源消息",记为f1≈f2。意味着f1和f2不能占用同一个时间槽,否则会造成冲突。该定义是针对两条路径定义的,存在另一种情况会产生同源消息。因为当两个多跳消息是由连接到同一个交换机的不同终端发出时,如果传输路径上存在相同的数据链路便会产生冲突,即消息路径上经过大于等于两个相同交换机。例如,Es1→Sw1→Sw4→Sw3→Es4与Es2→Sw1→Sw4→Sw2→Es3两消息都会经过数据链路Sw1→Sw4,如果Sw1同时处理两消息,会发生消息冲突,应做同源消息处理。本文提出的HCS算法,由于对消息路径分辨明确,减少同源消息规模。
针对同源消息,本文采用预先处理的方式记录下所有的同源消息到SS数组中,每当处理f时,对f的所有同源消息进行标注,使其在f所在时间槽为不可占用状态,表示为式(11),
| $ \forall {f_1}, {f_2} \in F, {f_1} \approx {f_2} \to {f_1}.section \ne {f_2}.section。$ | (11) |
1) 计算出TT消息的最大跳数H、每行分区数sectionNum=ASH-1;所有设备的调度表形式为(MC/BC)·sectionNum,(MC/BC)表示行数,sectionNum表示列数。同时,记录同源消息的相关信息到列表SS。消息优先级由传输路径的跳数决定,跳数越小优先级越高。next[MC/BC][sectionNum]矩阵记录BC下的每个分区的槽的使用情况,各分区初始化起点为0。
2) 对排序后的消息fk进行调度。如果k>N,转到4);否则,按照2.2.1方法把fk按照跳数安排到Es对应的分区里,fk会在MC的时间里发送(MC/Pk)次。ti可以由消息路径和网络拓扑计算得到。fk传输时间点可以表示为
3) 沿消息传输路径更新交换机和终端设备的调度表,返回2)。
4) Es的调度表建立完成。
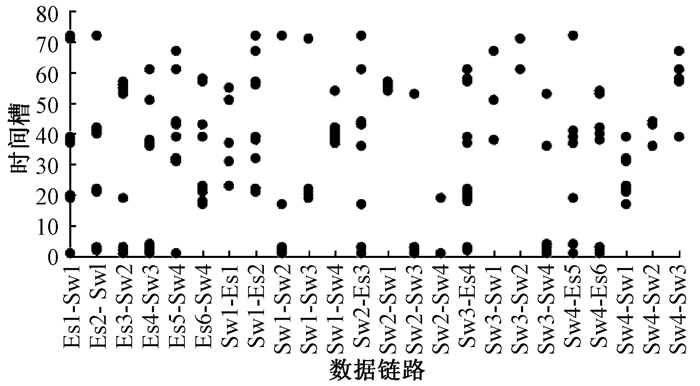
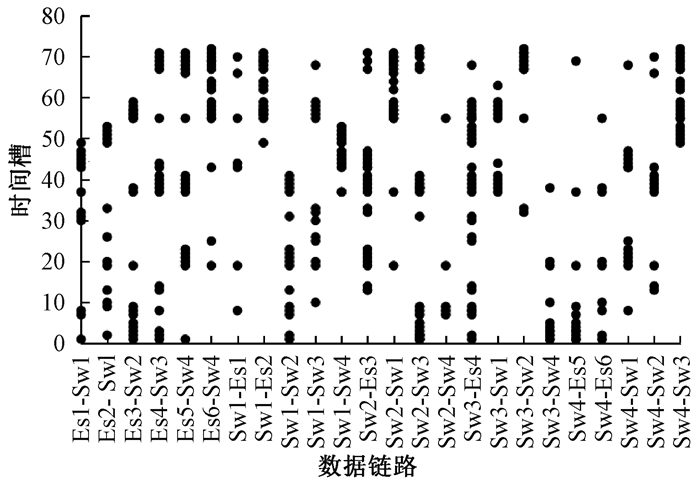
3 实验评估该部分主要证明HCS算法的可行性,仿真网络拓扑结构如图 1所示,包含6个端系统、4个交换机和12条物理链路。调度50条TT消息用于调度表生成,最大路径跳数H=3。TT消息长度不作设置,采用"时间槽"概念设计算法,消息周期为{4 ms,8 ms,16 ms,32 ms }的随机数。因此,MC=32 ms, BC=4 ms,调度表为8行12列的矩阵形式,这里设每行BC包含72个槽,每个槽代表 4/72 ms。图 3(50条消息中有20%的多跳消息)和图 4(100条消息中有80%的多跳消息)显示了在原二跳-非二跳算法下不同的多跳占比消息的配置情况;图 5和图 6显示了在HCS算法下不同的多跳占比消息的配置情况。
|
图 3 (50, 20%)二跳-非二跳算法 Fig. 3 (50, 20%) Two-hop-non-two-hop algorithm |
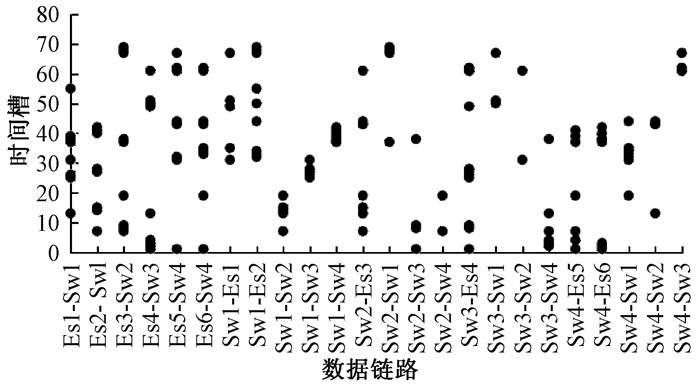
|
图 4 (100, 80%)二跳-非二跳算法 Fig. 4 (100, 80%) Two-hop-non-two-hop algorithm |
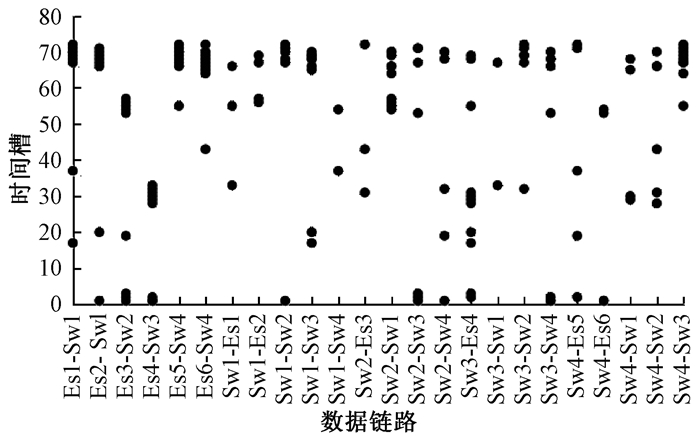
|
图 5 (50, 20%)HCS算法 Fig. 5 (50, 20%) HCS algorithm |
|
图 6 (100, 80%)HCS算法 Fig. 6 (100, 80%) HCS algorithm |
从实验结果可以看出,HCS算法可以完成TT业务的调度;根据各个节点的调度表信息,可以分析出消息的传输路径。当网络出现设备故障时,可以方便定位受影响的TT消息。从图 3和图 5对比可以发现,两种算法都可以合理的调度TT消息,保证网络无冲突运行。但是,随着多跳消息的所占比例的增加,如表 1所示,可以发现二跳-非二跳的算法下TT消息的最大传输片段不断增加,80%多跳消息的传输片段相比20%多跳消息的增加几乎翻倍,而HCS算法下消息没有太大变化。可以看出,HCS对于多跳消息的适应度明显优于原算法。对比图 4和图 6,在100条数据帧,80%的多跳率的情况下,可以明显看出原二跳-非二跳算法出现多个TT传输片段,而HCS下TT分布较为松散。当算法用于星上数据传输时,传输量庞大,原算法产生的大片TT传输片段会长时间占用时间资源和链路资源,造成非TT消息传输失败,HCS相较其能有效减少该情况的发生。
|
|
表 1 多跳消息占比对TT消息配置的影响 Tab. 1 The influence of the proportion of multi-hop messages on TT message configuration |
本文提出了一种根据消息传输跳数来对调度表进行设计的方法。首先从负载均衡和传输时间两个方面,对消息传输路径进行配置。之后,建立一套规则可将TT流合理地安排到调度时间表中。由于调度表的明确划分,能有效避免TT消息"带状化"的现象,RC和BE消息可以减少因长时间等待而造成的失效现象。HCS算法可以有效支持大网络、长距离的数据帧配置,提高系统的实用性。
| [1] |
严翔. 基于工业以太网的列车控制网络性能分析及优化[J]. 机车电传动, 2018(3): 41-44. YAN X. Performance analysis and optimization of train control network based on industrial Ethernet[J]. Electric drive for locomotives, 2018(3): 41-44. (  0) 0) |
| [2] |
WANG N C, YU Q H, WAN H, et al. Adaptive scheduling for multicluster time-triggered train communication networks[C]//IEEE Transactions on Industrial Informatics. New York: IEEE, 2018: 1120-1130.
(  0) 0) |
| [3] |
蒋社稷, 卢海涛, 史志钊, 等. 时间触发以太网在航空电子系统中的应用[J]. 电光与控制, 2015, 22(5): 84-88. JIANG S J, LU H T, SHI Z Z, et al. Application of time-triggered Ethernet in avionics system[J]. Electronics optics & control, 2015, 22(5): 84-88. (  0) 0) |
| [4] |
RODRIGUES E M G, GODINA R, POURESMAEIL E, et al. Hybrid time triggered protocol for home wireless communications[C]//IEEE International Conference on Environment and Electrical Engineering. New York: IEEE, 2017: 1-6.
(  0) 0) |
| [5] |
KOPETZ H, ADEMAJ A, GRILLINGER P, et al. The time-triggered ethernet (TTE) design[C]//IEEE International Symposium on Object-oriented Real-time Distributed Computing. Berlin: Springer, 2005: 22-33.
(  0) 0) |
| [6] |
STEINER W. Synthesis of static communication schedules for mixed-criticality systems[C]//IEEE International Symposium on Object/Component/Service-oriented Real-time Distributed Computing Workshops. New York: IEEE, 2011: 11-18.
(  0) 0) |
| [7] |
STEINER W, BAUER G, HALL B, et al. TT Ethernet dataflow concept[C]//The Eighth IEEE International Symposium on Network Computing and Applications. New York: IEEE, 2009: 146-154.
(  0) 0) |
| [8] |
刘晚春, 李峭, 何锋, 等. 时间触发以太网同步及调度机制的研究[J]. 航空计算技术, 2011, 41(4): 122-127. LIU W C, LI Q, HE F, et al. Research on time-triggerd-ethernet synchronization and scheduling mechanism[J]. Aeronautical computing technique, 2011, 41(4): 122-127. (  0) 0) |
| [9] |
POZO F, RODRIGUEZ-NAVAS G, HANSSON H, et al. SMT-based synthesis of TT ethernet schedules: a performance study[C]//IEEE International Symposium on Industrial Embedded Systems. New York: IEEE, 2015: 1-4.
(  0) 0) |
| [10] |
LI B Q, WANG Y. Hybrid-GA based static schedule generation for time-triggeredEthernet[C]//IEEE International Conference on Communication Software and Networks. New York: IEEE, 2016: 423-427.
(  0) 0) |
| [11] |
方挺, 王勇, 褚文奎, 等. 基于贪心思想的调度表优化算法设计[J]. 计算机工程, 2018, 44(9): 280-285. FANG T, WANG Y, CHU W K, et al. Design of scheduling table optimization algorithm based on greedy thought[J]. Computer engineering, 2018, 44(9): 280-285. (  0) 0) |
| [12] |
ZHENG Z, HE F, XIONG Y. The research of scheduling algorithm for time-triggered ethernet based on path-hop[C]//IEEE/AIAA 35th Digital Avionics Systems Conference. New York: IEEE, 2016: 1-6.
(  0) 0) |
| [13] |
LI Z H, WAN H, PANG Z Y, et al. An enhanced reconfiguration for deterministic transmission in time-triggered networks[C]// IEEE/ACM Transactions on Networking. New York: IEEE, 2019: 1124-1137.
(  0) 0) |
| [14] |
LIU M C, YIN H X, LI H, et al. An efficient scheduling algorithm for adjustable time slots in time-triggered ethernet[C]//IEEE 11th International Conference on Communication Software and Networks. New York: IEEE, 2019: 68-72.
(  0) 0) |
 2021, Vol. 53
2021, Vol. 53

