0 引言

随着移动多媒体社交网络的发展，面向移动设备的社交多媒体的存储、复制与传播变得非常盛行，这不仅演变成大数据问题，而且造成多媒体内容的非法滥用，导致产权纠纷与隐私泄露.如何安全分享移动社交多媒体数据成为移动互联网领域的一个关键性问题.多媒体加密^[1]是一种直接的内容保护技术，但解密内容可被随意支配.因此，除加密外还需要其他技术继续跟踪并监控解密内容的使用，其中水印标志可持续验证版权^[2].虽然联合加密与水印可提供双重保护，但水印不具有可追踪性，而指纹技术则可实现溯源追踪^[3].但是，现有的联合加密与指纹双重保护技术仅限于某些特殊应用场合，不便于在移动多媒体社交网络中推广；此外，如何为移动社交多媒体数据安全分享提供一种轻量级的安全技术，降低服务器端的负载，是移动社交网络领域面临的一项挑战性任务.移动社交多媒体数据安全分享方法的研究能解决内容分享过程中隐私泄露追踪、产权纠纷、个性化服务等难题.该课题的研究涉及多媒体内容分享等研究领域，可为远程医疗、视频监控系统、多媒体传感器网络等诸多相关领域提供安全与隐私保护.

传统的BS码^[3]、正交码^[4]及Tardos码^[5]等经典指纹码为数字指纹技术的发展奠定了基础，但容纳用户数有限.大容量指纹码^[6]和分组码^[7]可容纳更多用户，但不具有社交网络结构自适应性.现有的多媒体个性化策略没有考虑到多客户服务请求的情形^[8]，而对多客户服务请求进行聚类分组，并提供个性化服务策略，是移动社交多媒体数据安全分享的前提.

在多媒体安全保护方面，为提供保密性，可直接进行多媒体加密，实现隐私保护.可利用联合加密与水印嵌入^[9]、加密域信息嵌入技术^[10-11]、联合指纹与解密技术^[12]，通常采用同态加密实现密域信息隐藏^[13]或密域水印嵌入^[14].有别于以上相关技术，本文利用小波变换，提出一种在小波域实现联合指纹嵌入与选择加密的多媒体安全保护，可以直接应用于资源受限环境下的多媒体安全分享.

1 理论基础 1.1 小波变换

对任意函数f(t)的离散小波变换为

$ W{{T}_{f}}\left( m, n \right)=\langle f, {{\psi }_{m, n}}\rangle ={{\int }_{R}}f\left( t \right)\cdot \overline{{{\psi }_{m, n}}\left( t \right)}\text{d}t. $

(1)

若{ψ_{m, n}}_{m, n∈Z}是离散小波的一个框架，A, B分别为上界和下界，若有A=B，则称该框架为紧框架，对应的离散小波逆变换公式为

$ f\left( t \right)=\sum\limits_{m, n}{f\langle f, {{\psi }_{m, n}}\rangle \cdot {{\psi }_{m, n}}\left( t \right)=\frac{1}{A}\sum\limits_{m, n}{W{{T}_{f}}\left( m, n \right)\cdot {{\psi }_{m, n}}\left( t \right).}} $

(2)

当A, B的值均为1时，{ψ_{m, n}}_{m, n∈Z}为离散小波变换的正交基，此时对应的小波逆变换公式为

$ f\left( t \right)=\sum\limits_{m, n}{\langle f, {{\psi }_{m, n}}\rangle \cdot {{\psi }_{m, n}}\left( t \right)=\sum\limits_{m, n}{W{{T}_{f}}\left( m, n \right)\cdot {{\psi }_{m, n}}\left( t \right).}} $

(3)

1.2 混沌映射

Arnold变换的产生公式为

$ \left[\begin{align} &{{x}_{n+1}} \\ &{{y}_{n+1}} \\ \end{align} \right]=\left[\begin{matrix} 1&b \\ a&ab+1 \\ \end{matrix} \right]\left[\begin{matrix} {{x}_{n}} \\ {{y}_{n}} \\ \end{matrix} \right]\text{mod}\left( N \right), $

(4)

式中：a和b是参数，关系到变换的具体细节；n是迭代次数；N是向量的长度.

2 联合指纹与加密

将图像进行小波变换，得到近似分量、低频水平分量、低频垂直分量、高频分量.其中，近似分量包含原图像信息最多，看上去也最接近原始图像；低频分量包含信息其次；高频分量只包含原图细节部分，所含信息最少.

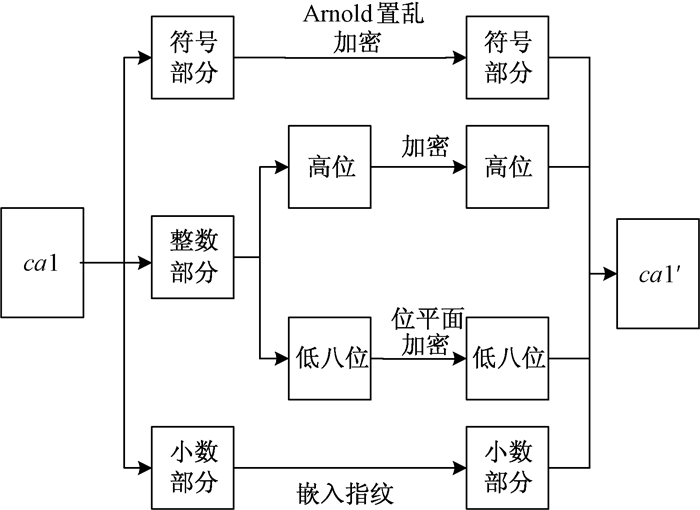
先对近似分量(ca1)进行处理，用一个矩阵来存储符号位，对该矩阵进行Arnold变换，将其进行置乱加密.用一个矩阵来存储小数部分，嵌入指纹序列，对中间整数部分加密之前，把整数部分转换成二进制位平面，转换后位平面的个数会大于8位，将这些位平面分割成高位和低八位，其中低八位采用位平面加密算法，高位先跟指纹序列异或运算，然后进行Arnold变换，改变其位置，整个近似分量部分加密完成，再把它还原成ca1′.根据安全级别的需求，可以对水平分量(ch1)、垂直分量(cv1)进行类似的指纹嵌入与加密.图 1是对近似分量进行指纹嵌入与加密的流程图，具体步骤如下：

Step 1：对各分量的低八位构成的整数矩阵转化为一维向量；对一维向量中的向量元素进行二进制位平面分解以得到8个二进制位面，并将所述多个二进制位面划分为第一位面(表示为向量A₁)和第二位面(表示为向量A₂)，其中它们各含4个位平面.

Step 2：根据初始秘钥key(x₀, u₁)和向量A₁的向量长度对分段线性混沌映射系统进行N₀+L次迭代以得到整数向量X；X₁(i)=mod(floor(X(i)×10¹⁴), 256)+1；将X₁中的各向量元素进行二进制位平面分解以得到多个二进制位面；将多个二进制位面划分以得到秘钥流b₁和秘钥流b₂，它们各含4个位平面.

Step 3：根据公式$ su{{m}_{1}}=\sum\limits_{i=1}^{L}{{{\mathit{\boldsymbol{A}}}_{2}}\left( i \right)} $对向量A₂进行求和，并根据求和结果sum₁对向量A₁中的向量元素向左循环移sum₁位，得到移位向量A₁₁，其中L为向量A₂的长度.

Step 4：根据公式B₁(i)=A₁₁(i)$ \oplus $A₁₁(i-1)$ \oplus $A₂(i)$ \oplus $b₁(i)，对移位向量A₁₁中的第i个向量元素进行加密以得到加密向量B₁；根据公式$ su{{m}_{2}}=\sum\limits_{i=1}^{L}{{{\mathit{\boldsymbol{B}}}_{1}}\left( i \right)} $对加密向量B₁进行求和，并根据求和结果sum₂对向量A₂中的向量元素向左循环移sum₂位，得到移位向量A₂₂，其中L为加密向量B₁的长度.

Step 5：根据公式B₂(i)=A₂₂(i)$ \oplus $A₂₂(i-1)$ \oplus $B₁(i)$ \oplus $b₂(i)，对移位向量A₂₂中的第i个向量元素进行加密以得到加密向量B₂.

Step 6：根据公式$sum=\sum\limits_{i=1}^{L}{{{\mathit{\boldsymbol{B}}}_{1}}\left( i \right)}+{{\mathit{\boldsymbol{B}}}_{2}}\left( i \right) $对加密向量B₁和加密向量B₂进行求和，得到求和结果sum.

Step 7：根据初始秘钥key(y₀, u₂)和公式s₀=mod(y₀+sum/L, 1)得到初值s₀；根据初值s₀对分段线性混沌映射系统进行N₀+2L次迭代处理以得到混沌向量S，并将S划分为相同长度的混沌向量S₁和混沌向量S₂.

Step 8：根据公式Y=mod(floor(S₁×10¹⁴), L)+1将向量S₁转化为整数向量Y，根据公式Z=mod(floor(S₂×10¹⁴), L)+1将向量S₂转化为整数向量Z.

Step 9：根据公式temp=B₂(i)，B₂(i)=B₁(Z(i))，B₁(Z(i))=temp交换加密向量B₁中的向量元素以得到混合向量C₁，以及根据temp=B₁(i)，B₁(i)=B₂(Y(i))，B₂(Y(i))=temp交换加密向量B₂中的向量元素以得到混合向量C₂，其中L为混沌向量S₁或混沌向量S₂中的向量长度，i=1, 2，…，L.

Step 10：对混合向量C₁和混合向量C₂进行重组以得到加密指纹图像.

3 实验结果与分析

实验平台：处理器为Intel(R)双核i5-3230 CPU, 操作系统Windows 8专业版，Matlab 2009.

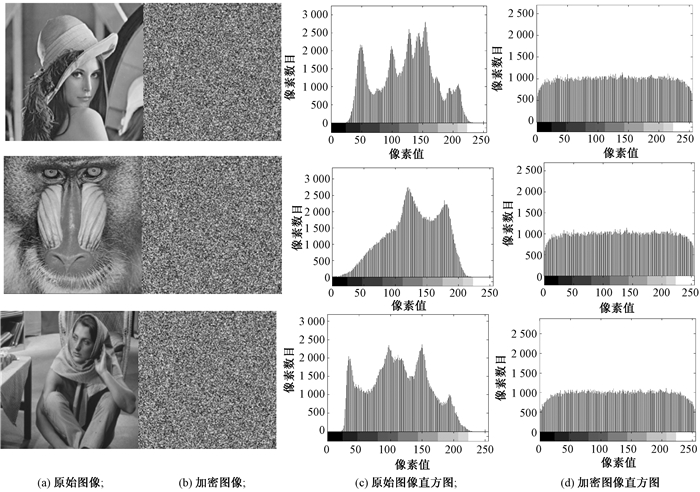
3.1 直方图分析

主要进行了一级小波变换后针对近似分量进行加密的实验，加密结果如图 2所示.相对于原始图像，加密图像变为噪声图像，图像的原始信息从加密图像中完全不可感知.从图 2可以看出，对一级小波变换后的近似分量系数进行加密后，加密图像的直方图趋向一致，说明加密算法可以掩盖原始图像的特征，加密方法是有效的.

3.2 相关性分析

表 1是加密图像和原始图像的像素值的相关系数分析.可以看出，原始图像的各组毗邻像素的相关性很高，接近于1，经过一级变换并对近似分量进行加密后，相关性大大降低，这种情况表明对小波域近似分量进行选择加密，同样会取得好的加密效果，而且选择加密的时间复杂度相对于整幅图像会降低.

3.3 密钥敏感性分析

在解密阶段，用细微变化的密钥去解密同样的加密图像，密钥敏感性如图 3所示.可以看出，用正确的密钥可以将原始图像解密出来，而错误的密钥解密出来的仍然是一张噪声图像.

3.4 相关算法比较分析

本文的叛逆者追踪算法可以在小波域的近似分量检测指纹实施叛逆者追踪，是一种局部指纹检测方式，而文献[9]没有叛逆者追踪技术，只有单纯的水印提取技术，而且直接在空间域提取水印.文献[12]虽然有指纹追踪技术，在量化域对指纹信息进行全局检测，增加了客户端的时间复杂度.相对于其他两种方法，本文算法更适宜于资源受限环境下的多媒体安全分享.

推荐的联合指纹与加密仅仅在DWT中的重要系数进行加密，相对于全加密来说时间复杂度大大降低.尤为重要的是，通过混沌映射可提前产生进行加密操作的参数矩阵.对比一些相关算法，本算法不仅可以实现保密性与可跟踪性，而且可以提高加密效率，降低服务器端与客户端的负载.

表 2为本文算法与其他相关算法的综合性能比较，结果表明，本文推荐的算法不仅可以进行联合指纹与加密技术，而且小波域选择加密的运用，使得加密的数据量大大变少，可以减少服务器端与客户端的资源开销，为该算法应用于资源受限环境提供了技术支撑.

4 结论

与传统多媒体内容保护方法不同，本文推荐的算法是直接在小波域对图像进行联合指纹嵌入与加密处理.指纹技术可对非法泄密者进行溯源追踪，而且可以根据安全级别进行选择加密.对小波域系数进行选择加密，相对于全加密不仅可以缩短加密时间，而且实验结果表明了本文推荐的保护方法的有效性.