随着智能网联汽车和车联网技术的不断发展,复杂场景自动驾驶、沉浸式车载娱乐系统、实时安全检测与预警等新型业务将成为主要的车载应用场景[1],这不仅会造成车联网中移动数据和订阅数据的爆炸式增长,其低时延、高带宽、高可靠性的业务需求也为计算资源有限的车辆终端和云计算服务模式带来了极大的挑战。
边缘计算通过将边缘服务器(edge server,ES)部署在路侧单元(road side unit,RSU)上,可以将原来聚集在云中心的计算资源下沉到靠近车联网用户端的边缘网络设备,有效弥补了云计算中车辆与云端远距离通信导致的延迟干扰和网络负载,扩展了车联网的计算能力,被称为车辆边缘计算(vehicle edge computing,VEC)[2]。根据资源调度和优化对象,车联网中的任务卸载可分为单ES卸载和多ES协作卸载。单ES卸载主要是指一个服务组合或者一次卸载任务执行中只考虑一个ES的情况。例如,文献[3]利用车联网中的用户激励机制,在VEC中引入一个卸载服务提供者,部署一个ES和时间表处理卸载任务的需求。文献[4]针对许多车辆同时争夺通信和计算资源的情况,为了快速有效地为单个车辆作出最佳卸载决策,提出一种基于自学习的车联网分布式计算卸载方案。多ES协作卸载则主要通过多个ES建立协作来实现负载均衡。例如,文献[5]为了降低车载网络的计算服务延迟,提出一种协同边缘计算框架来提高服务和卸载任务的可靠性。文献[6]研究了边缘计算辅助架构中负载计算的新场景,分析了多个车辆之间的任务上传协调、ES/云服务器之间的任务迁移以及ES/云服务器的异构计算能力。然而,相比计算规模宏大的云中心,车联网中体积和规模较小的ES所配备的计算、存储和带宽等资源往往是有限的。
针对车辆端产生的大量任务和数据,ES通常需要合适的资源分配策略以实现任务卸载。文献[7]考虑了多车辆环境中卸载的不确定性,将多个移动车辆的任务卸载到附近的ES,以便车辆能够作出合适的卸载决策,实现最佳的长期回报,解决了VEC中的分布外样本(out of distribution,OOD)检测问题。文献[8]为了解决车联网中复杂的网络状态和海量计算数据导致延迟能耗增加、服务质量下降等问题,提出一种联合计算卸载和资源分配策略。人工智能算法由于具有学习能力强、覆盖范围广、可移植性高等优势,也常用于解决ES资源约束下的任务卸载问题。文献[9]提出一种基于改进的卷积神经网络差分进化算法的推断任务卸载策略,使用云-边协作模型在云和边缘设备之间部署计算任务。文献[10]针对特定的高性能计算任务需求,提出一种基于深度强化学习的边缘计算任务分配与卸载算法。
在上述研究成果中,主要考虑对单一类型任务进行卸载处理。事实上,在VEC场景中,由于车辆的高机动性和用户的不同,造成道路区域内车辆密度和网络拓扑时刻在变化,一些关联因素也随之动态变化,如计算资源、用户喜好、车辆状态、道路环境等,这导致车联网中的计算任务种类繁多,且每种任务具有不同的延迟等性能需求,较之普通场景,任务具有更强的复杂性和差异性。因此,如何在ES的计算、存储和带宽等资源受限的情况下,面向车联网环境中的多类型、差异化任务需求,结合人工智能算法对任务进行有效的卸载,仍然是车联网边缘计算中一个迫切需要解决的问题。基于此,本文综合考虑车辆移动过程中车辆端产生的多样性和差异性的任务卸载需求、车辆密度、车辆网络拓扑以及ES资源限制等问题,以最小化任务时延为目标,提出一种结合深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法的任务卸载模型,解决了多样性和差异性任务在道路区域内动态协作环境下的优化卸载问题。
1 系统模型为了研究VEC中的任务卸载策略,提出了由移动车辆、ES以及云中心构成的三层异构网络模型。假设云中心拥有足够的计算和缓存资源,而ES的资源受到限制,为了降低任务的卸载时延,允许ES之间通过协作来处理车辆的任务卸载请求。
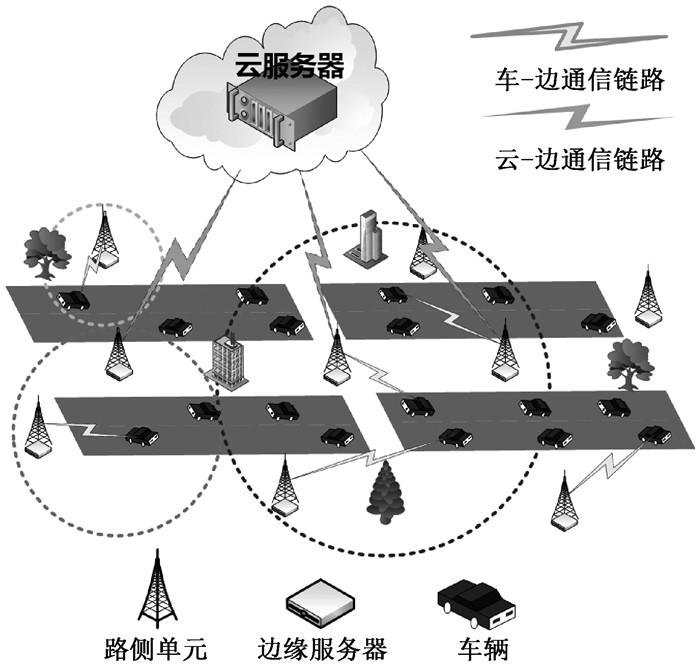
为了进一步分析问题,假设车辆进入道路区域内满足泊松过程,某一时刻系统中车辆表示为V={Vi|i∈N+}。假设共有m个ES部署在RSU上,表示为E={E1, E2, …, Em}。考虑车辆的移动性及车辆密度的动态变化,将时间划分为离散的时间段,允许每个时间段中多个ES形成动态协作簇,解决单个ES资源有限及网络负载均衡问题。三层异构网络模型如图 1所示。
|
图 1 三层异构网络模型 Fig. 1 Three-layer heterogeneous network model |
为了表述任务的多样性和差异化属性,假设某一时刻共产生n个任务,且定义参数元组Z=〈M, L, C〉表示任务属性,其中M={Mi, i∈n, n∈N+},Mi表示任务i的数据量大小。同理,Li表示任务i的类型,Ci表示任务i需要的计算资源。由于ES的计算、存储和带宽等资源受限,车联网用户根据任务类型可以选择在本地、ES协作簇或云中心执行任务卸载请求,以保证任务得到有效处理。因此,对于任务i,其卸载时延可以分为以下3种情况。
1) 本地卸载时延。任务i的本地卸载时延可以表示为
| $ T_i^{\text {local }}=\frac{C_i^{\text {local }}}{F_{\mathrm{V}}}, $ | (1) |
其中:Cilocal表示任务卸载需要的本地计算资源;FV表示车辆的计算能力。
2) ES卸载时延。任务i卸载到ES协作簇的时延主要包括任务上传、任务执行和任务排队。由于任务i上传到ES的时间要小于车辆以最大速度(vmax)驶离当前ES通信半径rc的时间,故任务i上传到ES的时延为
| $ T_i^{\text {up }}=\frac{M_i^{\text {edge }}}{R_i^{\text {edge }}}, T_i^{\text {up }} \leqslant \frac{r_{\mathrm{c}}}{v_{\text {max }}}, $ | (2) |
其中:Miedge表示任务i上传到ES的数据量大小;Riedge表示任务i上传到ES的传输速率,可通过香农公式来计算。
定义Dit表示t时刻任务i卸载到Ej上的动态优先级,Ciedge表示任务i需要ES的计算资源,FE表示ES的计算能力,Srej表示Ej剩余可用资源大小,则任务i在ES上执行的时延为
| $ T_i^{\text {cal }}=D_i^t \cdot \frac{C_i^{\text {edge }}}{F_{\mathrm{E}}}, C_i^{\text {edge }} \leqslant S_{\mathrm{re}}^j \text { 。} $ | (3) |
基于M/M/1排队模型,任务i卸载到ES后被暂放在排队队列中,根据车辆到达时间遵循参数为λi的泊松分布,任务i的排队时延为
| $ T_i^{\text {qu }}=\frac{\lambda_i}{\mu_i\left(\mu_i-\lambda_i\right)}, $ | (4) |
其中:λi表示单位时间内卸载到ES的任务数量;μi表示单位时间内执行的任务数量。
在现有的研究中,任务执行结果的返回时延通常忽略不计,协作簇之间的内部传输时延也可假设为常量。因此,任务i卸载到ES的总时延可以描述为
| $ T_i^{\text {edge }}=T_i^{\text {up }}+T_i^{\text {qu }}+T_i^{\text {cal }} \text { 。} $ | (5) |
3) 云中心卸载时延。当任务i本身数据量超过了本地车载设备和ES的最大执行能力,即Srej < Ciedge,任务i需要的计算资源超过了ES的剩余最大计算能力和剩余带宽资源时,任务将卸载到云中心执行。假设Ricloud表示任务i上传到云端的传输速率,Fcloud表示云端服务器的计算能力,则任务i卸载到云中心的时延为
| $ T_i^{\text {cloud }}=\frac{M_i^{\text {cloud }}}{R_i^{\text {cloud }}}+\frac{C_i^{\text {cloud }}}{F_{\text {cloud }}} 。$ | (6) |
为了研究卸载系统的性能,定义任务i的卸载决策二进制变量αi和βi。αi=1表示任务i在本地计算,αi=0表示任务i不在本地执行。当αi=0且Srej>Ciedge时,即ES剩余可用资源大于任务i需要的计算资源,任务i可以卸载到ES上并被执行,此时βi=1。反之,βi=0,任务i通过ES转发卸载到云中心。
在本系统模型中,要求多样性任务在卸载时延最小的情况下能够达到较高的卸载成功率,则优化问题可以构建为
| $ \begin{aligned} & \min \sum\limits_i^n T_i^{\text {total }}=\min \sum\limits_i^n\left\{\alpha_i T_i^{\text {local }}+\right. \\ & \left.\left(1-\alpha_i\right)\left[\beta_i T_i^{\text {edge }}+\left(1-\beta_i\right) T_i^{\text {eloud }}\right]\right\}, \\ & \text { s.t. } C 1: \alpha_i, \beta_i \in\{0, 1\}, C 2: B_i^{\text {edge }} \leqslant B_{\max }, \\ & C 3: T_i^{\text {up }} \leqslant \frac{r_c}{v_{\text {max }}}, C 4: T_i^{\text {total }} \leqslant T_{i, \max }, \\ & C 5: \forall i \in \mathbf{N}^{+}, n \in \mathbf{N}^{+}, \end{aligned} $ | (7) |
其中:C1表示二进制变量;C2表示车辆可利用的带宽限制;C3表示任务的传输时间限制;C4表示任务卸载总时延小于任务的最大截止时间;C5表示i和n的取值范围。
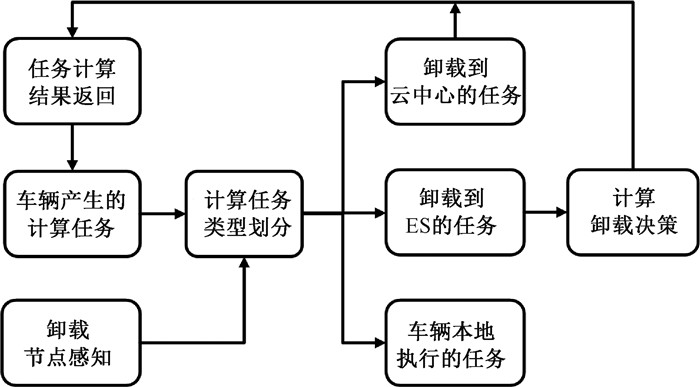
本文的优化问题模型是非线性的变量相乘,因此优化问题是一个具有NP-Hard性质的非线性整数规划问题。为了对问题进行求解,基于DDPG提出一种面向多样性和差异性任务的卸载算法TPDC-DDPG。TPDC-DDPG首先针对车联网环境下产生的大量多样性任务进行动态优先级的建立,然后根据道路区域内车辆的密度和网络拓扑结构建立ES动态协作簇,最后基于DDPG实现卸载决策。具体卸载决策过程如图 2所示。
|
图 2 TPDC-DDPG卸载决策过程 Fig. 2 TPDC-DDPG offloading decision process |
由于不同任务的卸载时延约束有差别,为了提升系统的整体卸载效率,结合任务的类型和任务的紧迫程度,构建了任务动态优先级划分模型。假设Li表示任务i的类型,Uit表示任务i的紧迫程度且由最大延迟容忍度决定,则在t时刻Ej上接收到的第i个任务的动态优先级Dit可以表示为
| $ D_i^t=\partial_1 L_i+\partial_2 U_i^t, $ | (8) |
其中:Uit=1/(Ti, max-Tave),Ti, max表示任务i的最大延迟容忍度,Tave表示任务处理的平均时间;∂1、∂2表示加权因子,且∂1+∂2=1(∂1, ∂2∈[0, 1])。Uit越大,表示任务越紧迫。
为了对车辆端产生的不同任务进行优先级划分,定义n个任务的集合为
| $ H=\left\{\left(x_1, y_1\right), \left(x_2, y_2\right), \cdots, \left(x_n, y_n\right)\right\}, $ | (9) |
其中:xi∈X=Rn;yi∈Y={-1, +1}。
若给出关于任务集合H的超平面w·x+b=0,其中w表示特征向量,b表示常数,则式(8)提出的任务优先级划分问题可以转化为凸二次规划问题,
| $ \begin{aligned} & \min _{\boldsymbol{w}, b} \frac{1}{2}\|\boldsymbol{w}\|^2+G \sum\limits_{i=1}^n \xi_i, \\ & \text { s.t. } y_i\left(\boldsymbol{w} \cdot x_i+b\right) \geqslant 1-\xi_i, \xi_i \geqslant 0, i=1, 2, \cdots, n, \end{aligned} $ | (10) |
其中:ξ=(ξ1, ξ2, …, ξi)T;G表示惩罚参数,目标是使‖w‖最小以达到
对式(10)的凸二次规划问题进行求解,引入拉格朗日乘子φ、ω构造拉格朗日函数,
| $ \begin{aligned} & L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\varphi}, \omega)=\frac{1}{2}\|\boldsymbol{w}\|^2+G \sum\limits_{i=1}^n \xi_i- \\ & \sum\limits_{i=1}^n \varphi_i\left[y_i\left(\boldsymbol{w} \cdot x_i+b\right)-1+\xi_i\right]-\sum\limits_{i=1}^n \omega_i \xi_i, \end{aligned} $ | (11) |
其中:φi≥0;ωi>0。则式(11)可以转换为求解拉格朗日对偶问题,即
| $ \max\limits_{\varphi, \omega} \min\limits_{\boldsymbol{w}, b, c} L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\varphi}, \omega) 。$ | (12) |
通过微分可求得L(w, b, ξ, φ, ω)对w, b, ξ的极小值,将L(w, b, ξ, φ, ω)代入式(12),由此得对偶问题的最优解φ*=(φ1*, φ2*, …, φn*)T。选择φ*的一个分量φj*满足条件0 < φj* < G,计算b*=yi-
| $ \boldsymbol{w}^* \cdot x+b^*=0。$ | (13) |
最终,可以得到关于集合H的优先级分类决策函数f(x)=sign(w*·x+b*)。
3 ES动态协作簇的建立为了降低任务卸载的时延,提出一种基于网络密度和负载均衡的动态协作簇构建方法,根据优化问题中约束C3的ES通信半径和道路区域内车辆密度建立ES动态协作簇。事实上,道路区域内车辆密度是动态变化的,车辆产生的计算任务也是在动态变化的,传统的固定ES协作簇会造成整体的任务卸载效率降低。在同一段道路区域内的不同时刻,根据车辆密度和任务量的不同,可以自适应调整其协作域大小。假设每个ES的通信半径为rc, 结合区域内车辆密度,ES动态协作簇的建簇半径rEj的计算公式为
| $ r_{E_j}= \begin{cases}\frac{d_{E_j}}{\bar{d}_E} \cdot r_{\text {c}}, & d_{E_j} \geqslant \bar{d}_E, \\ r_{\text {c}}, & \text { 其他 }, \end{cases} $ | (14) |
其中:rc≤rEj≤rmax, rmax表示最大建簇半径;dEj表示Ej所在区域内车辆密度;dE表示所有车辆的平均密度,即
| $ \bar{d}_E=\frac{\sum\limits_{j=0}^m d_{E_j}}{m} 。$ | (15) |
为了形成密度和工作负载更均衡的协作簇,在得到每个ES协作簇的建簇半径后,可以在其协作簇内选择权重最高的ES作为簇头服务器。假设WEj是由半径为rEj的簇的工作负载和面积确定的权重,则
| $ W_{E_j}=\frac{\sum\limits_{E_j \in E_{C S}} \vartheta_{E_j}}{{\rm{ \mathsf{ π} }} r_{E_j}^2}, $ | (16) |
其中:ϑEj是Ej的工作负载大小;ECS是以Ej为簇头形成的协作簇集合。
选出权重最高的Ej后,在以rEj为半径的簇内,将距离最近且在行驶轨道路径上权重不高于Ej的ES依次加入簇头为Ej的簇中, 由此可最终形成动态协作簇。需要注意的是,簇头Ej并不一定是簇的物理中心,考虑车辆的移动性,簇的形成与其移动轨迹有较强的关联性。
4 基于DDPG的任务卸载决策在VEC系统中,连续移动的车辆在任务卸载的过程中会产生较大的状态空间。同时,考虑当前卸载资源分配对后续时间点的长期影响,采用基于DDPG的TPDC-DDPG来解决任务卸载问题。常用的卸载算法对于智能体的选择主要考虑ES的剩余可用资源,将任务和ES作为共同智能体,使得系统整体获得最大的奖励,以达到优化问题的目的。
为了描述方便,定义四元组Q=〈S, A, R, P〉来表示马尔科夫决策(Markov decision process,MDP)模型。其中:S表示状态空间;A表示动作空间;R表示奖励函数;P表示状态转移概率。状态空间S是ES剩余可用计算资源的状态和车辆产生的任务状态的集合。集合Sre={Sre1, Sre2, …, Srem}表示ES剩余可用计算资源的状态,即剩余可用资源的大小;集合Stask={Stask1, Stask2, …, Staskn}表示车辆产生的任务状态,即任务优先级和数据量大小等属性。动作空间A是指在每一个时间间隔t内,车辆结合当前任务的状态选择任务卸载到哪里。ES结合自身剩余可用计算资源状态选择如何执行卸载任务,因此动作空间包括了任务卸载决策集合{αi, βi}。
智能体在t时刻的状态St下采取动作At后,任务的状态和ES剩余可用资源的状态都会发生变化,这决定了t+1时刻的状态St+1下采取的动作At+1,用S×A×S表示系统的状态转移概率P。任务卸载的目标是卸载的整体时延最小,因此系统奖励函数R定义为
| $ R\left(S_t \mid S_{t+1}, A_t\right)=-T_i^{\text {total }} \text { 。} $ | (17) |
本文提出的TPDC-DDPG任务卸载算法的主要步骤如下。
输入:Srej,Staski,αi,βi,Ciedge,t,St,At。
输出:最优奖励R*。
1:初始化状态空间S里的状态Srej,Staski;
2:设置初始值αi,βi;
3:根据Srej,Staski,Ciedge计算智能体t时刻在状态St下的动作At;
4:if Ci≪Ciedge
αi=1,任务i在本地执行;
5:else if αi=0 ‖ Srej≥Ciedge
βi=1, 任务i卸载到Ej执行;
6:else βi=0, 任务i卸载到云服务器执行;
7:计算系统状态转移概率S×A×S和下一时刻的状态St+1采取的动作At+1;
8:更新状态空间S, 动作空间A, 计算奖励函数R;
9:循环迭代。
5 仿真结果分析本节对任务卸载策略进行仿真实验和性能分析,实验平台为pytorch1.11.0,工具采用pycharm。具体参数设置如下:系统总带宽为20 MHz,服务器数量为5~10台,服务器计算资源为10 GHz,最大迭代次数为500,折扣因子为0.9,传输功率为100 mW,噪声功率为10-7 MW。
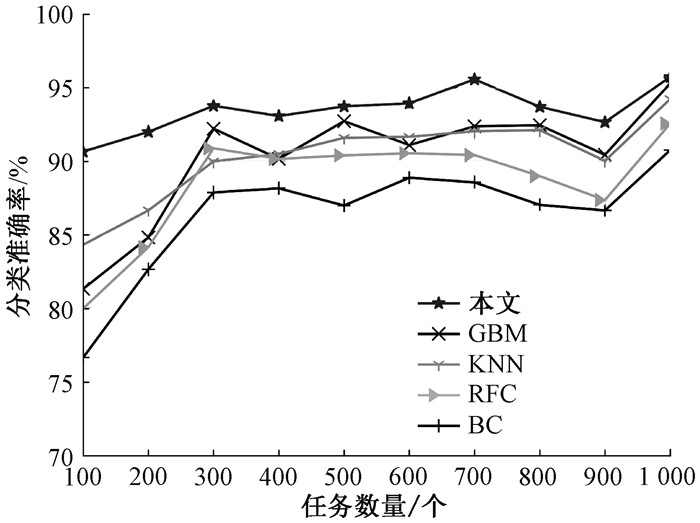
为了验证系统性能,与通用梯度回归(GBM)算法、k近邻(KNN)算法、随机森林(RFC)算法以及分支切割(BC)算法进行了任务分类的对比实验。图 3给出了不同算法的任务分类准确率结果。可以看出,随着任务数量的上升,某一类型任务的样本数量也在增加,任务分类时相同类型任务可参考的特征集中某一特征的样本数量也相应增多,这样能够更加精准地对任务进行分类。因此,任务分类准确率在波动中上升。
|
图 3 不同算法的任务分类准确率 Fig. 3 Task classification accuracy of different algorithms |
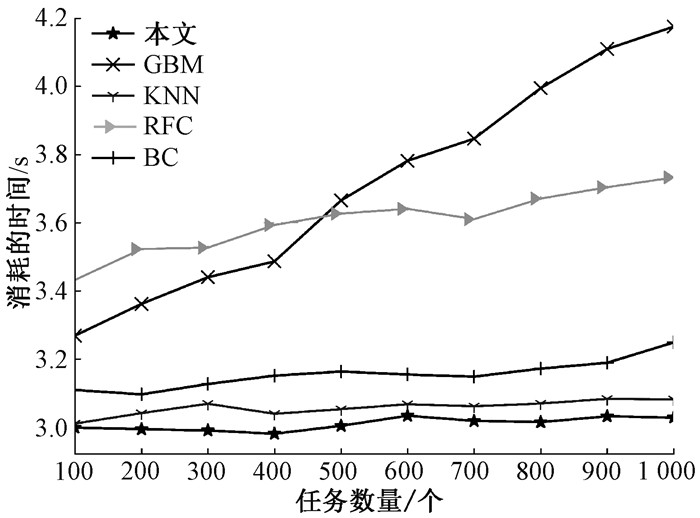
图 4给出了不同算法的任务分类效率结果。可以看出,随着任务数量的增加,在进行任务分类时系统整体的计算量也在增大,任务分类所消耗的时间出现了小幅度增加。
|
图 4 不同算法的任务分类效率 Fig. 4 Task classification efficiency of different algorithms |
由图 3和图 4还可以看出,本文提出的任务优先级分类方法在不同任务数量时任务分类准确率和任务分类效率都相对更高。
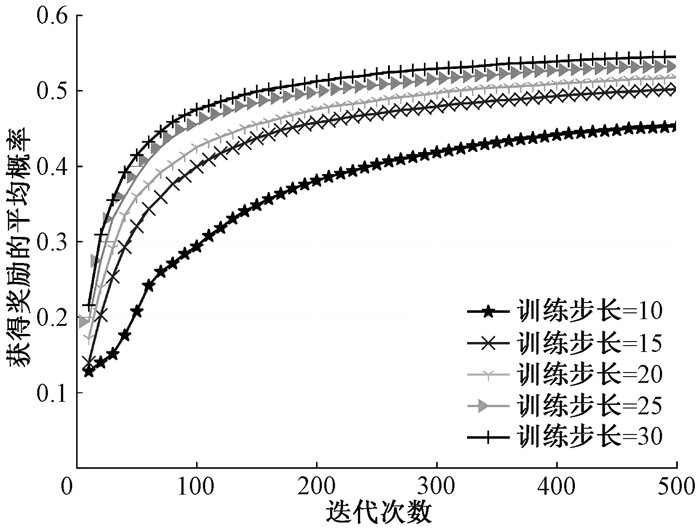
假设每个时刻每个车辆产生100~200个随机任务,且每个任务有不同的优先级。图 5显示了车辆数量为10时不同迭代次数下训练步长与获得奖励的平均概率之间的关系。可以看出,训练步长越大,每次训练时总体获得奖励的平均概率也越大。
|
图 5 训练步长与获得奖励的平均概率之间的关系 Fig. 5 The relationship between the training step length and the average probability of obtaining rewards |
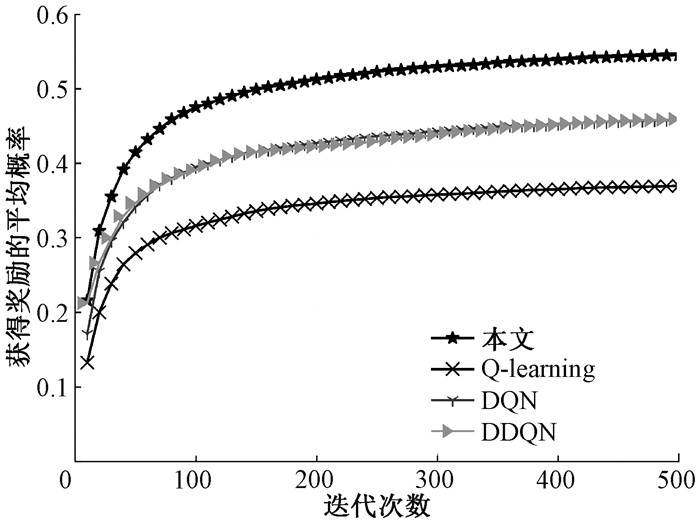
为了评价本文算法的卸载效果,与其他卸载算法如Q-learning、DQN、DDQN进行了对比分析。图 6给出了不同算法的收敛性对比结果。
|
图 6 不同算法的收敛性对比 Fig. 6 Convergence comparison of different algorithms |
由图 6可以看出,随着迭代次数的增加,本文算法在迭代400次左右时达到稳定,总体获得奖励的平均概率为0.540,而DQN、DDQN、Q-learning在迭代420次左右时达到稳定,总体获得奖励的平均概率分别为0.454、0.455、0.366。这得益于TPDC-DDPG算法利用了确定性策略梯度进行迭代更新,收敛更快、更平稳。
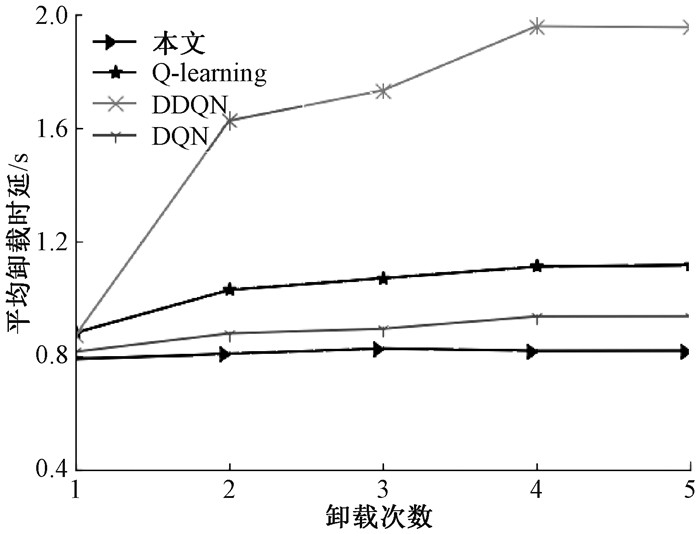
图 7显示了车辆数量为10时卸载次数对平均卸载时延的影响。卸载次数是指车辆在移动过程中连续产生任务的离散时间段数量,当卸载次数为5时,所有车辆连续5个时间段均产生随机数量的任务。
|
图 7 不同算法的平均卸载时延对比 Fig. 7 Comparison of average offloading delay of different algorithms |
由图 7可以看出,随着卸载次数的增加,本文算法的平均卸载时延有小幅度的波动。这是由于随着卸载次数的增加,系统中ES的剩余资源存在变化,同时每个时间段车辆产生的任务数量也会随机变化。整体来说,本文算法的平均卸载时延小于其他三种算法。
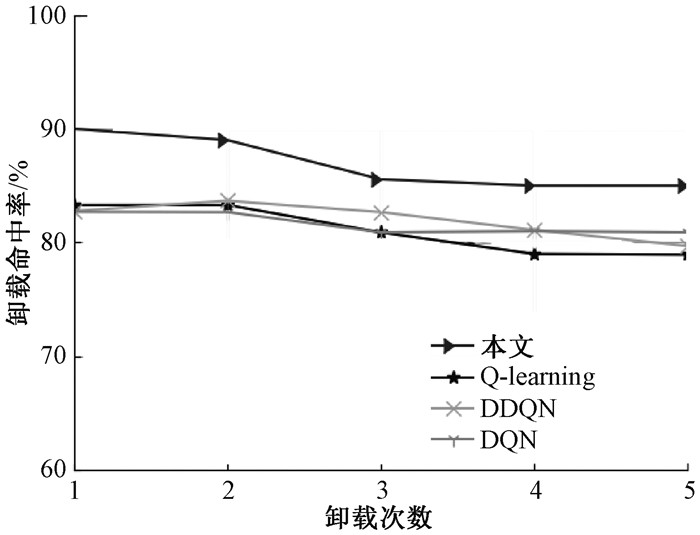
图 8显示了卸载次数对卸载命中率的影响。卸载命中率是指车辆卸载任务时成功卸载的任务数量和系统中产生的总任务数量之间的比值。
|
图 8 不同算法的卸载命中率对比 Fig. 8 Comparison of offloading hit rates of different algorithms |
由图 8可以看出,随着卸载次数的增加,任务数量增加,ES剩余可用资源的减少会造成卸载命中率的小幅度下降。但是,随着卸载次数的增多,卸载命中率会趋于稳定的值,本文算法相比其他三种算法卸载命中率最高。
6 结语针对未来车联网中计算任务呈现出多样性和差异性的情况,本文以最小化时延为目标,通过对任务进行预处理,结合任务种类提出了基于最大延迟容忍度的动态优先级划分方法,并根据区域内车辆密度建立ES动态协作簇,实现了车联网中面向移动场景的任务动态协作卸载策略。实验结果表明,本文提出的卸载算法具有很好的收敛性,在有较高卸载命中率的情况下,能有效降低差异性任务的平均卸载时延。本文提出的卸载算法虽然取得了一定的效果,但在实现过程中动态协作簇的建立与移动轨迹结合尚未形成完善的理论体系。未来工作将考虑在用户安全与隐私保护的前提下,研究面向移动轨迹的协作卸载,进一步提升车辆移动场景中的卸载效率。
| [1] |
KONG X J, WANG K L, HOU M L, et al. A federated learning-based license plate recognition scheme for 5G-enabled Internet of Vehicles[J]. IEEE transactions on industrial informatics, 2021, 17(12): 8523-8530. DOI:10.1109/TII.2021.3067324 (  0) 0) |
| [2] |
CHEN C, LIU L, WAN S H, et al. Data dissemination for industry 4.0 applications in Internet of Vehicles based on short-term traffic prediction[J]. ACM transactions on Internet technology, 2022, 22(1): 1-18. (  0) 0) |
| [3] |
HUANG X M, YU R, YE D D, et al. Efficient workload allocation and user-centric utility maximization for task scheduling in collaborative vehicular edge computing[J]. IEEE transactions on vehicular technology, 2021, 70(4): 3773-3787. DOI:10.1109/TVT.2021.3064426 (  0) 0) |
| [4] |
LUO Q Y, LI C L, LUAN T H, et al. Self-learning based computation offloading for Internet of Vehicles: model and algorithm[J]. IEEE transactions on wireless communications, 2021, 20(9): 5913-5925. DOI:10.1109/TWC.2021.3071248 (  0) 0) |
| [5] |
LI M S, GAO J, ZHAO L, et al. Deep reinforcement learning for collaborative edge computing in vehicular networks[J]. IEEE transactions on cognitive communications and networking, 2020, 6(4): 1122-1135. DOI:10.1109/TCCN.2020.3003036 (  0) 0) |
| [6] |
DAI P L, HU K W, WU X, et al. A probabilistic approach for cooperative computation offloading in MEC-assisted vehicular networks[J]. IEEE transactions on intelligent transportation systems, 2022, 23(2): 899-911. DOI:10.1109/TITS.2020.3017172 (  0) 0) |
| [7] |
ZHU X Y, LUO Y Y, LIU A F, et al. Multiagent deep reinforcement learning for vehicular computation offloading in IoT[J]. IEEE Internet of Things journal, 2021, 8(12): 9763-9773. DOI:10.1109/JIOT.2020.3040768 (  0) 0) |
| [8] |
WANG K, WANG X F, LIU X. A high reliable computing offloading strategy using deep reinforcement learning for IoVs in edge computing[J]. Journal of grid computing, 2021, 19(2): 15. DOI:10.1007/s10723-021-09542-6 (  0) 0) |
| [9] |
王瑄, 毛莺池, 谢在鹏, 等. 基于差分进化的推断任务卸载策略[J]. 计算机科学, 2020, 47(10): 256-262. WANG X, MAO Y C, XIE Z P, et al. Inference task offloading strategy based on differential evolution[J]. Computer science, 2020, 47(10): 256-262. DOI:10.11896/jsjkx.190800159 (  0) 0) |
| [10] |
WANG J X, WANG L T. Mobile edge computing task distribution and offloading algorithm based on deep reinforcement learning in Internet of Vehicles[J]. Journal of ambient intelligence and humanized computing, 2021, 1-11. (  0) 0) |
 2024, Vol. 56
2024, Vol. 56


