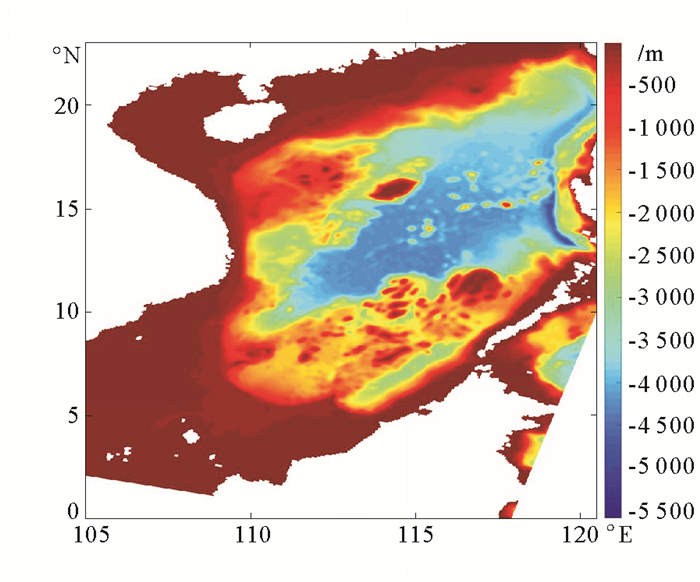
南海是西太平洋最大的边缘海,水深超过5 500 m。它是一个半封闭的海盆,被中国,菲律宾,婆罗岛,和中南半岛包围(见图 1)。海水通过台湾海峡和吕宋海峡与中国东海和西太平洋交换,通过加里曼丹海峡与印度洋交换。由于流入南海的水主要来自穿过吕宋海峡的太平洋水,南海海水的水文性质变化与太平洋水存在密切联系[1]。
|
图 1 南海地形分布 Fig. 1 The topographic distribution of the South China Sea |
ENSO是全球气候变化的主要模态,并通过大气循环和洋流循环将赤道太平洋的异常信号传递到其他热带海域以及热带外海域,从而影响其他海洋的水文变化。Klein等[2]将ENSO事件对各个海域表面温度的影响解释为“大气桥”和热惯性。目前对于ENSO对南海影响的研究主要分为两个方面,分别研究了南海表面高度和表面温度与ENSO的关系。研究使用的数据主要包括卫星数据[3-5]和模型数据[6-11]。Soumya等[12]研究了南海表面高度与太平洋和印度洋表面高度的关系,通过海表面高度与气候指数的线性回归分析发现印度洋偶极子指数(IOD)贡献了南海西南部年际变化的40%,ENSO贡献了南海西南部的30%和东南部的40%。Cheng等[13]使用了循环平稳经验正交函数(Cyclostationary EOF, CSEOF)分解法,分解潮汐表数据,卫星数据和OGCM模型数据三种海表面高度数据,证实南海表面高度的年际波动与ENSO异常有关。Rong等[14]发现南海表面高度和海表面温度的响应完全异相,并且发现南海表面高度与水深100 m处的温度具有很好的相关性。Thompson等[15]使用一个区域洋流模型研究南海的混合层温度的季节平均与年际异常,当混合层较深时,南海混合层深度具有较强的季节信号。Thompson等[15]同时研究发现了海气热量交换是改变混合层温度最主要的原因,垂向混合是一个较弱的负反馈。Zhou等[4]提出了南海的海表面温度引起了几种从南海到其他地区的正压波,同时发现东亚和南印度洋存在反气旋涡旋,在北太平洋和西南太平洋存在气旋涡旋。这说明海表面温度也可以对大气循环产生影响。Wang等[16]研究发现了南海El Niño年的温度异常存在一个双峰现象,其中太阳短波辐射是出现第一个暖锋的主要原因,Ekman流和地转流是之后温度降低的原因,经向地转流是温度再次上升的原因。同样的结论出现在Huang等[9]的研究中。此外,Huang等[9]还比较了El Niño年与La Niña年的双峰结构,总体上,El Niño年南海表面温度异常的双峰结构更加稳定。Qiu等[3]提出了南海表面温度异常在ENSO成熟期的主要特征是西南部和东北部的异相,海气热量交换和吕宋海峡流入的冷水是南海东北部负温度异常的主要原因,大气环流的减弱和南海西边界流的减弱是南海西南部正温度异常的主要原因。
前人关于南海物理过程对ENSO的响应进行过大量的研究[3, 6-7, 12, 16],对南海表面高度与ENSO事件关系的研究已经有了从季节循环和年际尺度的研究[13],但对南海表面温度的研究的关注点主要在El Niño年份特征和南海表面温度异常的空间特征。且此前南海表面温度的研究使用的方法多为传统经验正交分解法(EOF)[3, 17-18]。EOF提供了一个平稳的方法处理空间变量,是一个单个空间映射的基函数,并通过时间确定空间分布的振幅调制,而真实海洋水文性质的空间分布存在明显的季节循环变化特征。本文使用一种新的方法——循环平稳的经验正交函数分解法(CSEOF)分析南海表面温度的季节和年际变化特征。数据的平稳性是普通EOF的基本假设,即协方差函数不依赖于原始时间序列。平稳性假设往往不能充分解释地球物理学与气候学的变量,即使在去除周期信号的前提下。循环平稳经验正交分解法(CSEOF)作为替代普通EOF分析或其他基于平稳性假设的特征分析技术的方法,可以正确识别时间相关的响应特性并准确地从数据中提取具有物理意义的模式及其时空演化[19]。传统EOF不能很好体现数据中存在的多种循环平稳信号(如年周期和ENSO信号),而CSEOF允许空间模态随时间变化,因此在处理这些数据时具有明显的优势。
关于CSEOF研究分析方法,目前已有一些研究应用在大气海洋科学分析中。Wu等[20]基于CSEOF研究热带太平洋海域上层海洋热含量的年际变化特征。Kim等[21]的研究指出,CSEOF方法可以分析北极海冰的损失与北极扩大机制的联系。Sun等[22]用CSEOF和典型相关分析(CCA)发展了韩国降雨量预报的经验统计系统。通过和观测数据对比,证明CSEOF-CCA方法可以对韩国季节降水变化做有效预测。Kim等[23]以CSEOF方法为基础分析朝鲜半岛的验潮数据和重构数据,并借此估计当地海平面变化。
1 数据和方法介绍 1.1 数据介绍本研究主要结合卫星数据与高分辨率数值模拟结果进行分析,相对于卫星数据,模型的分辨率更高,可以较好的反映中尺度动力学特征,因此两者对比也有助于本文了解中尺度过程的影响。本文使用的卫星数据来源于美国国家海洋和大气管理局提供的最优插值海表温度数据[24](Optimal Interpolation Sea Surface Temperature, OISST,https://www.ncdc.noaa.gov/oisst)。这组数据结合了多种观测数据,包括卫星、船测、和浮标数据,通过插值建立成一个全球的网格数据,并使用偏值调节处理卫星和船测的数据,得到一个空间表面温度图。OISST的空间精度是0.25°,本文使用的空间范围是100°E~120.5°E,0°~23°N。卫星数据的时间范围是1982年至今,为了和模型数据能够选取相同的时间区间,因此本文选取的时间范围为1982—2007年。
模型数据来源于长期积分的高分辨率数值模型结果,本文使用区域海洋模型(Regional Ocean Modeling System, ROMS)对南海进行了5 km分辨率的模拟,该分辨率可以较好的模拟中尺度过程,因此对比卫星与模型数据结果也可以对中尺度过程的作用有所了解。模型垂直方向上分为50层,表层强迫来源于Coordinated Ocean-ice Reference Experiments Version 2 (CORE v2,http://data1.gfdl.noaa.gov/nomads/forms/core/COREv2.html)数据集,边界条件与初始条件来源于Simple Ocean Data Assimilation (SODA 2.1.6,http://apdrc.soest.hawaii.edu/datadoc/soda_2.1.6.php)数据集。值得提及的是,模型未采用外部SST数据逼近的方式来矫正模型表面温度场,模型海表面温度变化主要受太阳辐射、气温及海洋过程影响。模型还包含了潮汐强迫,其数据来源于TPXO(http://volkov.oce.orst.edu/tides/global.html)全球潮汐模型[25]。本文加入模式分析意在观察高分辨率的模型数据与粗分辨率的卫星数据的在CSEOF空间分布中的异同,研究中尺度过程对ENSO信号的响应。此外,由于卫星数据没有潜热通量、短波辐射热通量以及海表面净热通量的数据,分析南海表面温度延迟响应的物理机制时只能依赖模型数据。
1.2 循环平稳经验正交函数分解法将数据分解成不太复杂的模式使本文理解物理系统的复杂响应更加容易,最简单且最常用的分解函数是经验正交分解函数(EOF)。EOF定义如下:
| $ T\left( {r, t} \right) = \sum\limits_i { L{V_i}\left( r \right)P{C_i}\left( t \right)}。$ |
EOF方法将数据T分解成由单一空间模态(LV)和相应时间序列(PC)组成的集合,LV是由一个随机时间序列(PC)调制的物理过程。LV称作负载向量,PC被称为主成分时间序列(PCTS)。每一组负载向量和主成分时间序列组成一个简单EOF模态。因此,EOF的每一模态的LV是时间独立的,并且只有振幅随着时间变化。然而,一个物理系统的特殊响应不是固定不变的,年周期信号出现在很多气候变量中,它们以一年为周期振荡,但是在年际尺度上同样存在振幅的变化,引起了一个可调制的年际周期。
CSEOF不是简单的特征值分解,普通EOF的协方差矩阵是不随时间变化的,即假定信号是平稳的,这种假设在真实过程中往往并不成立,CSEOF将协方差矩阵设为一随时间变化的给定先验周期的函数。另外CSEOF特征值分解的本征函数不再是傅里叶函数,而是Bloch函数,是普通EOF的一种拓展[26]。Kim等[26]首次提出使用循环平稳EOF的方法分析地球物理信号中随时间变化的空间模态和年际尺度的波动。CSEOF定义如下:
| $ \begin{array}{l} T\left( {r, t} \right) = \sum\limits_j {L{V_j}\left( {r, t} \right)P{C_j}\left( t \right), } \\ \;\;\;\;\;LV\left( {r, t} \right) = LV\left( {r, t + d} \right)。\end{array} $ |
CSEOF方法将空间时间数据T分解为由空间模态(LV)和相应的时间序列(PCTS)组成的模态。与传统EOF相比,CSEOF最大的差异是空间模态LV是随着时间改变的。模态间混合对于传统EOF是普遍存在的问题,CSEOF可以更好的表现气候信号并减少模态间的混合。近期的研究[27]已经证明了使用CSEOF可以有效的提取季节循环和ENSO信号,并且计算前不需要移除季节循环信号[26-29]。本文使用卫星与模型的月平均数据并以一年为固定周期时,每个CSEOF模态由12个负载向量和1个主成分时间序列组成。
2 结果与分析 2.1 模型数据验证为确保模型数据模拟的准确性,本文首先对比了卫星海表温度数据(OISST)和ROMS模型数据的海表温度,以及卫星AVISO数据和ROMS模型数据的海表面高度异常的季节平均和年际变化。
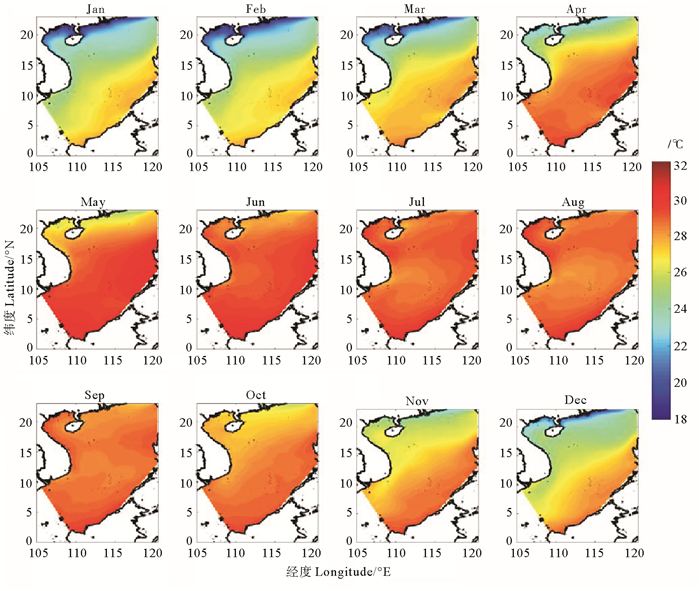
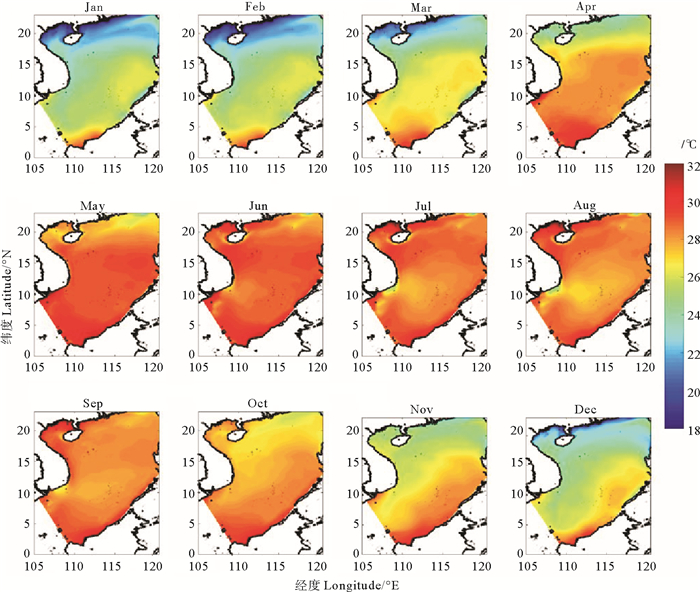
图 2和3分别是卫星数据和模型数据在1982—2007年期间的海表温度季节平均。从图中可以看到,总体上季节平均比较相似,在冬季,模型数据和卫星数据在南海西南部存在一个冷舌区域,这个现象与Liu等[30]文章中描述的南海西南部冷舌区域一致,主要是由于南海西边界流带来南海北部的冷水引起此处温度较低,这个区域在11—2月比较明显。在7—9月,模型数据中南海西南部越南沿岸存在一个较低温度的区域,而卫星数据中并不明显,这主要是由于在较高分辨率的模型中夏季西南季风引起的沿岸上升流带来的冷水。
|
图 2 卫星数据表面温度1982年到2007年季节平均 Fig. 2 The seasonal cycle of satellite data of sea surface temperature from 1982 to 2007 |
|
图 3 ROMS模型数据表面温度1982年到2007年季节平均 Fig. 3 The seasonal cycle of ROMS model dataof sea surface temperature from 1982 to 2007 |
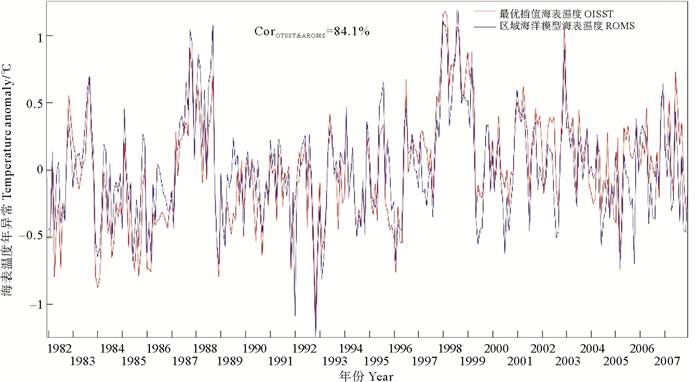
图 4是分别使用1982—2007年的月平均卫星数据和模型数据计算的海表温度年际异常结果。其中红线是卫星的数据计算结果,而蓝线是模型数据结果。从图中可以看到,两种数据的相关系数较高,达到了84.1%。图中本文可以看到在比较明显的El Niño年,如1982—1983、1987—1988和1997—1998年可以观察到温度异常存在一个暖双峰结构,这个现象与Wang等[16]发现的双峰结构相似,第一个暖峰值在El Niño年的冬季出现,第二个暖锋在第二年的夏季出现。在La Niña年,冷双峰的结构并不明显,如1988—1989、1995—1996、1999—2000年中,只有1989年出现了较明显的冷双峰现象。这与Huang等[9]发现的La Niña年与El Niño年的不对称性相符,部分La Niña年的温度异常只出现单峰现象。
|
图 4 卫星数据和ROMS模型数据表面温度年际异常 Fig. 4 Interannual surface temperature anomaly of satellite data and ROMS model data |
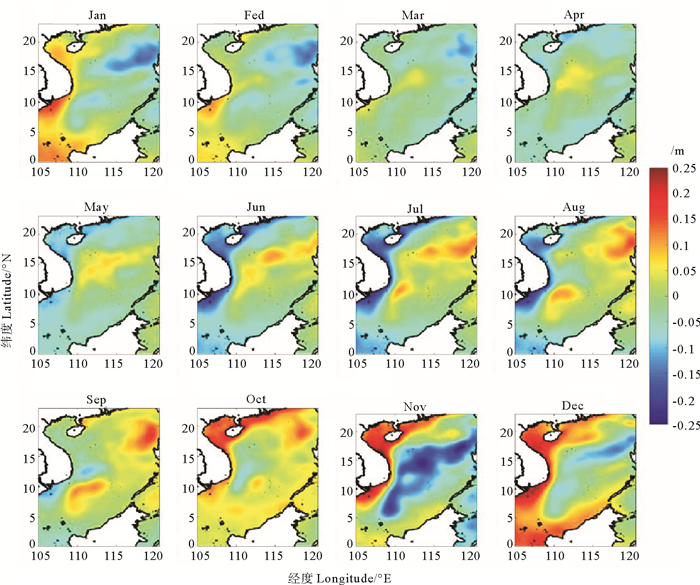
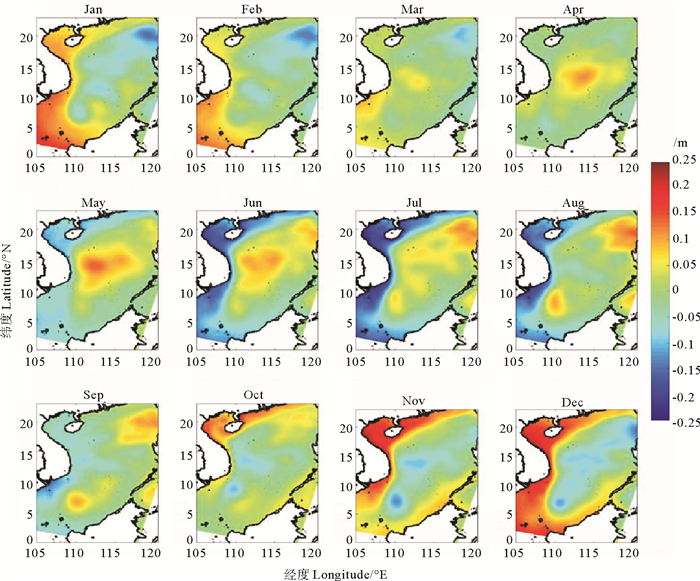
图 5和6分别是卫星数据和模型数据的南海表面高度异常的季节循环。直接比较海表面高度,模型数据和卫星数据存在较大差异,其原因为模型数据和卫星数据选取的参考面不同。因此,使用海表面高度数据计算季节平均后,在每个点减去季节平均。对比图 5和6,模型数据对海表面高度异常的模拟较好。在冬季,海表面高度异常呈现西南部高,东北部低的特点;在夏季相反,海表面高度西南部低,东北部高。南海的动力学受到冬季的东北季风(11—2月)和夏季的西南季风(6—8月)影响[12],这影响了海表面高度的季节循环。尽管两种数据南海的表面高度异常季节平均相关性很好,但是由于模型不包含任何数据同化,表面高度异常的年际变化相关性较为一般。
|
图 5 AVISO卫星数据1993—2007年表面高度异常 Fig. 5 The surface height anomaly of AVISO satellite data from 1993 to 2007 |
|
图 6 ROMS模型数据1993—2007年表面高度异常 Fig. 6 The surface height anomaly of ROMS model data from 1993 to 2007 |
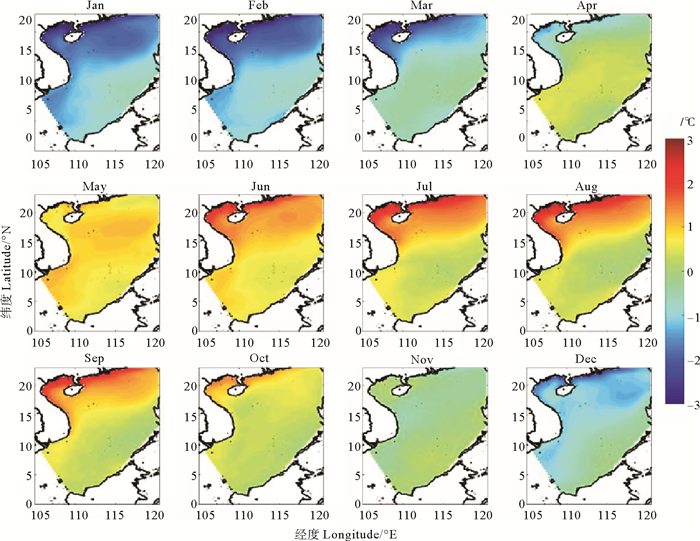
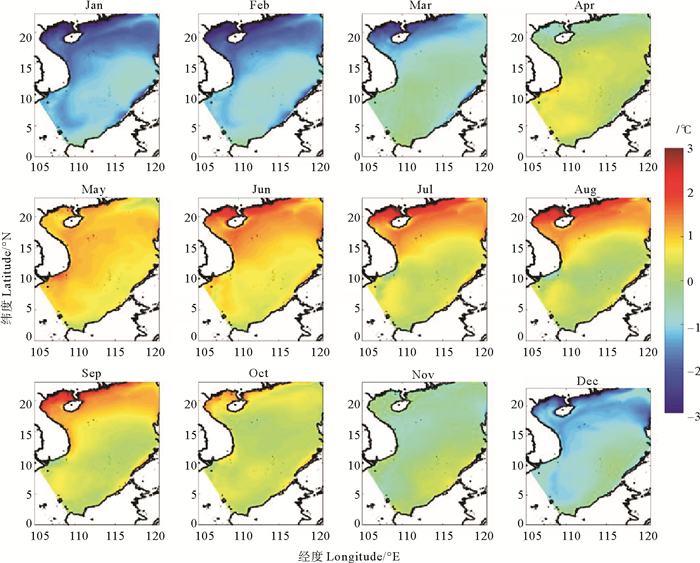
Hamlington等[27]使用包含AVISO、Topex/Poseidon、OSTM等多种数据的卫星测高数据集证明了CSEOF分析可以从数据中提取出季节循环和ENSO信号。本文对卫星数据南海表面温度数据做CSEOF分析,并将计算结果与ROMS模型数据的CSEOF结果对比。CSEOF的第一模态是季节循环信号,也是卫星数据和模型数据中的最主要模态。图 7是卫星数据南海表面温度的CSEOF第一模态空间分布,去趋势的卫星数据中,第一模态解释了大约88.7%。Sun等[28]对北太平洋表面温度使用CSEOF分解,第一模态解释了95.68%,说明海表温度的季节循环占所解释的方差比重较大。第一模态空间分布的最大值和最小值分别在夏季(2月)和夏季(8月)的南海北部靠近广东省附近,南海南部的振幅比较小。图 8是ROMS模型数据计算得到的CSEOF第一模态空间分布,这与图 7十分相似。模型数据第一模态解释了约90%。在CSEOF第一模态的空间分布中,在冬季(12—3月)南海整体均为降温变化,最大降温出现在北部,存在达到-3 ℃的冷中心,南海南部降温较小。在夏季(6—9月)南海整体均为升温变化,最大升温同样在北部,存在达到3 ℃的暖中心。南海季节循环信号中,南海主要受太阳辐射影响,整体呈现同相变化的特征,振幅最大区域主要分布在北部湾和中国南部沿海地区,这主要受南海北部水深较浅的影响,使此区域更容易受到长、短波辐射以及水平平流的影响。在5、10和11月,南海的CSEOF第一模态南北部差异较小。6、7、8和9月在第一模态出现了北部高温,南部低温的特点,在季节循环中南北部差异不明显(见图 2)。总体上,模型与卫星的季节平均空间分布非常相似,引入了中尺度过程未对季节信号产生显著影响。
|
图 7 卫星数据南海表面温度CSEOF第一模态空间分布 Fig. 7 The first mode space distribution of CSEOF based on satellite data of surface temperature in the South China Sea |
|
图 8 ROMS模型数据CSEOF第一模态空间分布 Fig. 8 The first mode space distribution of CSEOF based on ROMS model data of surface temperature in the South China Sea |
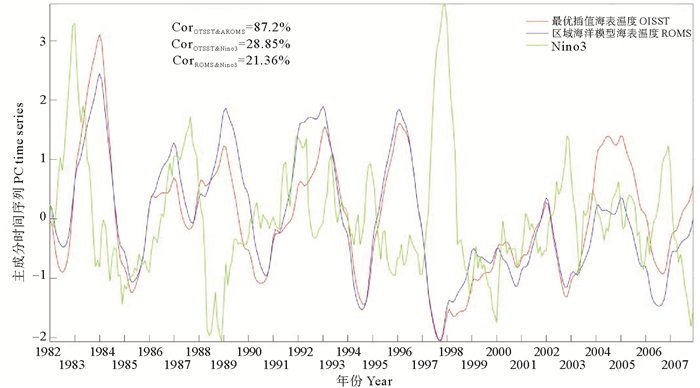
图 9展示了卫星数据和ROMS模型数据的CSEOF第一模态主成分的对比,可以看出,两种数据拟合的很好,相关系数达到约87.2%。同时,通过滞后相关分析CSEOF第一模态主成分与Nino3指数发现,Nino3指数领先第一模态时间序列12个月是相关性最大,两者相关指数一般。与卫星数据时间序列的相关系数为28.85%,相关关系的p值小于0.01%;与模型数据则为21.36%,相关关系的p值为0.02%。这说明南海表面温度年变化和ENSO信号存在适度的相关性。总体上,卫星数据的南海表面温度的年变化比模型数据振动幅度大(见图 9)。在El Niño年,如1982—1983, 1987—1988和1997—1998年,表面温度的时间序列都出现较明显的下降。在La Niña年,如1983—1984,1988—1989, 1995—1996年,季节循环的振幅出现显著增加。这种相反的关系指明了ENSO信号对南海表面温度季节循环的振动存在显著影响。
|
图 9 卫星数据和模型数据CSEOF第一模态时间序列与Nino3指数对比 Fig. 9 The comparison of the Nino3 index and the first mode time series of CSEOF based on the satellite data and the model data |
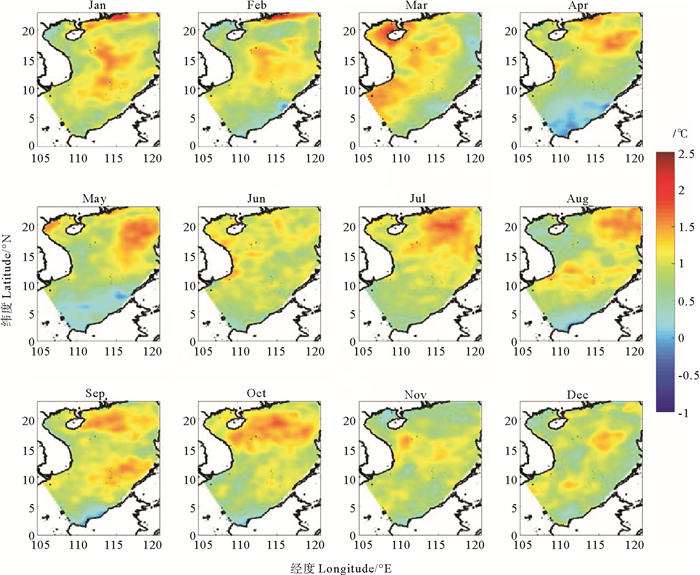
Cheng等[6]使用CSEOF方法分析南海表面高度的卫星数据、模型数据、潮汐表数据,发现CSEOF第二模态代表了ENSO信号的影响。图 10为卫星数据计算得到的CSEOF第二模态,解释了约3.6%的方差。图 11是模型数据第二模态空间分布,解释了约2.14%方差。
|
图 10 卫星数据南海表面温度CSEOF第二模态空间分布 Fig. 10 The second mode space distribution of CSEOF based on satellite data of surface temperature in the South China Sea |
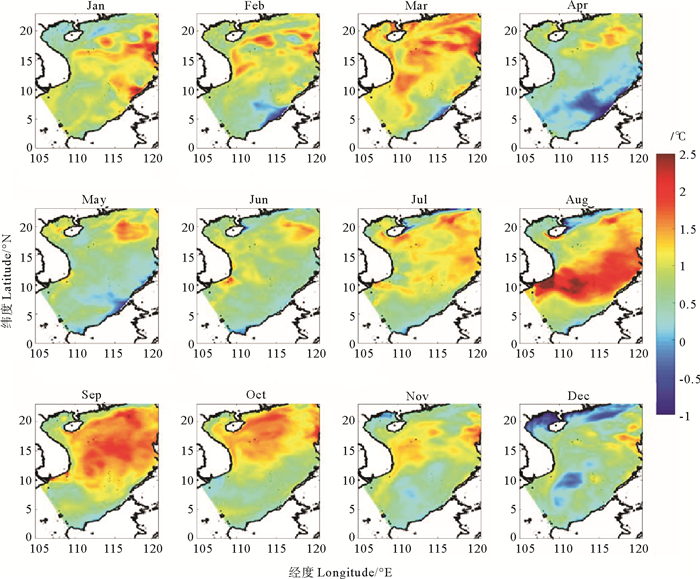
图 10中显示,在El Niño年,大部分模态的东北部温度为正值,只有3月的东北部区域温度为负值,4—5月的南海南部马来西亚群岛附近存在小于0 ℃的低温区域。此外,在11—3月,南海中南部越南沿岸温度约为1 ℃。图 11是ROMS模型数据CSEOF第二模态的空间分布,通过比较两种数据的ENSO信号,本文发现在El Niño年南海温度异常总体为正值,从4—6月,正温度区域主要分布在南海北部,温度最高达到1.5 ℃,7月开始,正温度区域慢慢向南发展,到冬季,正温度区域分布在南海东南部。总体上,CSEOF第二模态的空间分布中,振幅正值基本分布在南海的中部和北部,南海南部和北部呈异相变化的特征,在4和5月较为明显。ROMS模型数据与卫星数据第二模态空间分布相比,存在一些不同之处,如ROMS模型数据3月南海东北部吕宋海峡附近表面温度为正值,而卫星数据则相反;模型数据8月越南南部海岸附近温度异常较高,最高超过了2.5 ℃,而卫星数据温度异常在1 ℃;模型数据12月南海中南部温度存在小于0 ℃的海域,卫星数据此区域都是正值。Liu等[30]研究发现,在越南南部大陆坡上存在一个强烈的西边界流,并带来了南海北部的冷水,在El Niño年,冬季季风减弱,引起南海环流减小,因此冬季南海中南部变暖。Liu等[8]文章中说明,在El Niño年,东北季风减弱,引起海洋失热减少,对应得热增多,因此冬季南海北部的温度变化为正值。7月开始,南海表面温度异常正值区域向南延伸,在8和9月,南海中南部区域表面温度为正,与卫星数据相比,模型数据在8月南海中南部的温度异常高于卫星数据。在Xie等[5]的研究中,夏季的西南季风引起了南海中南部越南沿岸的上升流,在El Niño年,夏季风减小,因此上升流带来的冷水减少,表面温度上升。在4—9月可以观测到南海南部温度为负值,可能是由于El Niño年夏季西南季风减弱,因此带来的热量减少引起的。
|
图 11 ROMS模型数据南海表面温度CSEOF第二模态空间分布 Fig. 11 The second mode space distribution of CSEOF based on ROMS model data of surface temperature in the South China Sea |
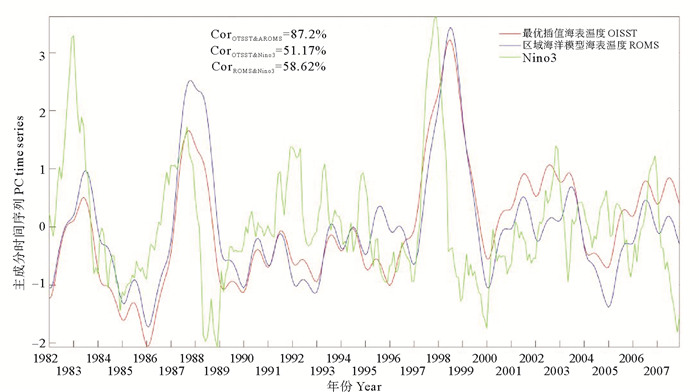
图 12对比了两种数据CSEOF第二模态的主成分时间序列以及与Nino3指数,证明表面温度第二模态的时间序列与ENSO相关。对于南海温度CSEOF年变化的研究显示,El Niño年的主成分时间序列为正(1982—1983, 1986—1987,1991—1992,1997—1998),而La Niña年则相反(1984—1985, 1988—1989)。南海表面温度空间模态中正的区域在El Niño年会上升,例如吕宋海峡西侧。卫星数据与模型数据的时间序列接近,相关系数达到87.74%。Nino指数与两种数据主成分时间序列滞后相关,通过两种数据的滞后相关性分析发现,卫星数据与模型数据达到最大相关系数的时间略有不同。Nino3指数领先卫星数据时间序列6个月时相关系数最大,而模型数据则是8个月,因此,在Nino3指数领先两种数据时间序列7个月时两种数据都较大,与卫星数据的相关系数达到51.17%,模型数据为58.23%,两数据相关关系的p值均小于0.01%。Fang等[17]的研究使用1993—2003年的卫星观测数据证明了Nino3.4指数领先南海表面温度异常EOF第一模态时间序列8个月,Klein等[2]使用南海表面温度1983—1992年的卫星观测数据,对表面温度异常用EOF方法分析发现其自定义ENSO指数领先南海表面温度异常5个月,研究不同的ENSO指数和选取不同的时间范围可能是结论产生差异的原因。ENSO引起的表面温度异常存在滞后相关性的原因将在2.4节详细介绍。
|
图 12 卫星数据和ROMS模型数据的CSEOF第二模态以及与Nino3指数对比 Fig. 12 comparison of the Nino3 index and the second mode time series of CSEOF based on the satellite data and the model data |
Klein等[2]结合船测数据与卫星观测数据,发现El Niño现象引起大气环流的改变,从而引起其他海域上空云覆盖量和表面蒸发的变化。在El Niño年云覆盖的减少增加了海洋吸收太阳辐射的净热通量,同时,蒸发的减少降低了海洋潜热通量的热量耗散,进而增加了海洋表面的净热通量。这些关系与概念构成了“大气桥”的定义,联系了赤道太平洋表面温度异常和其他海域的表面温度异常。
海洋表面蒸发的热量直接对应潜热通量,海洋上空云覆盖的改变直接影响太阳短波辐射的热量。因此为了验证“大气桥”理论,本文对ROMS模型数据中的潜热通量和太阳短波辐射热通量做CSEOF分析。潜热通量CSEOF前二模态占比分别为65.86%和6.62%;太阳短波辐射热通量的CSEOF前二模态占比分别为81.29%和4.43%。通过潜热通量和短波辐射热通量前二模态的主成分时间序列与Nino3指数的滞后相关性分析发现,潜热通量的第一模态和短波辐射热通量的第二模态与Nino3指数相关性高。蒸发引起的潜热通量的季节循环不够明显,可能引起ENSO对潜热通量的季节信号影响较大,因此潜热通量的第一模态主成分时间序列与Nino3指数相关性高。
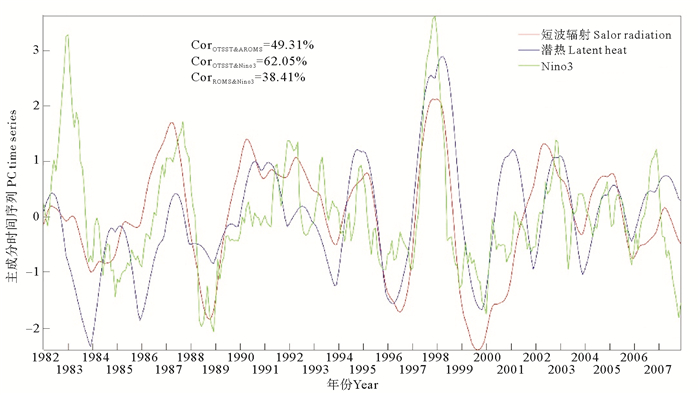
图 13是潜热通量CSEOF第一模态主成分时间序列,太阳短波辐射CSEOF第二模态主成分时间序列以及Nino3指数的对比。通过滞后相关性分析,可以确定Nino3指数与潜热通量和太阳短波辐射热通量的时间序列在无滞后时间时相关系数最大。其中,Nino3指数与潜热通量的相关系数为38.41%,与太阳短波辐射的相关系数为62.05%。KLEIN等[2]提出了一个假设,海表面温度异常对云层覆盖和蒸发的响应符合下面的公式:
| $ \frac{\partial }{{\partial t}}{\rm{SST' = }}\left( {F'/\rho cH} \right) - \left( {{\rm{SST'/}}\lambda } \right)。$ |
|
图 13 南海表面潜热通量的CSEOF第一模态时间序列以及表面太阳短波辐射CSEOF第二模态的时间序列与Nino3指数对比 Fig. 13 The comparison of the Nino3 index and the first mode time series of surface latent heat flux and the second mode time series of surface short wave radiation in Southern South China Sea |
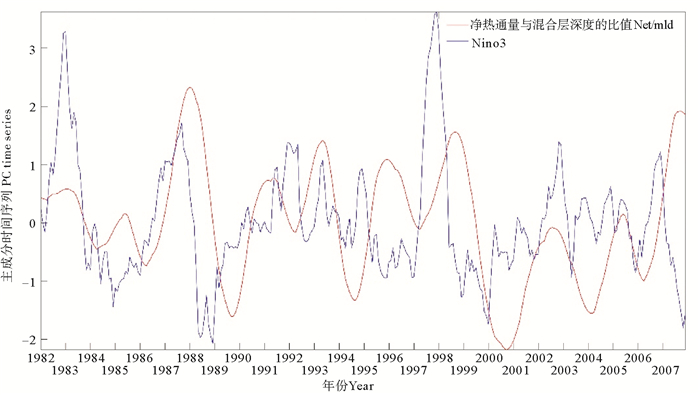
式中:SST′是表面温度异常值;F′是净表面通量的异常值,即由云层覆盖和蒸发异常引起的表面通量变化;ρ是海水密度;c是海水的比热;H是混合层深度;λ是滞后的时间尺度。上述公式表达了混合层中的垂直对流过程,温跃层下的夹带过程过程或者是任何与ENSO无关的过程可能是阻碍海洋表面温度过快反映于净热通量的原因。为了确认混合层对于表面温度变化的延缓作用,对ROMS模型数据表面净热通量与混合层深度的比值做CSEOF分解。Qiu等[31]分析了5种计算混合层深度的方法,并对比南海北部不同方法得到的混合层深度,得到温度方法是计算该区域更好的方法的结论。鉴于其研究区域与本文相似,采用了相同的方法计算混合层深度,即与表层温度差为0.6 ℃的深度。图 14是净热通量与混合层深度比值的CSEOF第二模态时间序列与Nino3指数的对比,通过滞后相关性分析发现,在Nino3指数领先9个月时,相关系数最大,达到49.96%。模型数据表面温度滞后Nino3指数为8个月,尽管结论与表面温度不尽相同,不可否认的是混合层与净热通量共同延缓了表面温度的过快响应。
|
图 14 南海表面净热通量与混合层深度比值的CSEOF第二模态的时间序列与Nino3指数对比 Fig. 14 The comparison of the Nino3 index and the second mode time series of the ratio of net surface heat flux to mixed layer depth in the South China Sea |
本文主要基于卫星数据与高分辨率ROMS模型数据运用循环经验正交函数的方法研究了南海表面温度的季节循环和年际变化。在El Niño年,两种数据的第一模态时间序列都因ENSO出现明显的下降信号,第一模态主成分与Nio指数有适度相关性,但比第二模态相关性低,证明南海表面温度的季节变化也会受ENSO信号影响。目前关于ENSO信号传递到南海的时间没有确切的结论,Fang等[17]使用EOF分析方法研究发现Nino3.4指数领先南海表面温度特征8个月,Klein等[2]研究发现ENSO信号与南海表面温度特征延迟为5个月,原因可能是不同区域的ENSO信号传递到南海需要不同的时间。CSEOF第一模态的空间分布中,南海北部振幅较大,且与季节平均空间分布相似,在冬季温度低,夏季温度高。
CSEOF第二模态代表了ENSO对南海表面温度的影响,其时间序列与Nino指数的滞后相关性高,达到50%以上。ENSO信号领先第二模态时间序列约7个月,说明ENSO信号通过大气作用传递到南海具有一些延迟性。南海西边界流在El Niño年由于季风减弱而减弱,影响CSEOF第二模态空间分布冬季中南部的高温,夏季西南季风减弱引起的越南南部海域上升流减弱是南海夏季西南部高温的原因,冬季东北季风减弱,使南海东北部失热减少引起南海东北部高温。ROMS模型数据和卫星数据第二模态空间分布存在一定程度的不同,相比而言模型数据的空间变化更为复杂,这主要是由于较高分辨率的模型包含了更多中尺度过程,而两者的时间变化仍存在较高的一致性。
本文选取Nino3指数比较南海表面温度与ENSO的关系,此外,表面温度和Nino3.4指数以及Nino4指数的关系同样存在一定的滞后相关性。其中,Nino3.4指数领先表面温度第二模态时间序列8个月时,相关性最高,模型数据相关系数为51%,卫星数据为43.36%。Nino4指数领先表面温度第二模态时间序列9个月时相关性最高,模型数据相关系数为36.8%,卫星数据为33.13%。
通过验证ROMS模型数据的潜热通量与太阳短波辐射热通量与ENSO间的关系,可以确定El Niño现象发生时,太平洋表面温度异常通过大气循环,影响南海上空云覆盖以及表面蒸发的改变,从而影响表面温度的改变。ENSO对南海表面热通量的影响是无延迟的,混合层的平流过程和垂向混合过程延缓表面温度的改变,因此ENSO现象对南海表面温度的影响具有延迟性。
| [1] |
Fang G, Wang Y, Wei Z, et al. Interocean circulation and heat and freshwater budgets of the South China Sea based on a numerical model[J]. Dynamics of Atmospheres and Oceans, 2009, 47(1-3): 55-72. DOI:10.1016/j.dynatmoce.2008.09.003
(  0) 0) |
| [2] |
Klein S A, Soden B J, Lau N C. Remote sea surface temperature variations during ENSO: Evidence for a tropical atmospheric bridge[J]. Journal of Climate, 1999, 12(12): 917-932.
(  0) 0) |
| [3] |
Qiu F, Pan A, Zhang S, et al. Sea surface temperature anomalies in the South China Sea during mature phase of ENSO[J]. Chinese Journal of Oceanology and Limnology, 2016, 34(3): 577-584. DOI:10.1007/s00343-016-4290-3
(  0) 0) |
| [4] |
Zhou M, Wang G. Responses of atmospheric circulation to sea surface temperature anomalies in the South China Sea[J]. Ocean Science Discussions, 2015, 11(6): 1693-1710.
(  0) 0) |
| [5] |
Xie S, Xie Q, Wang D, et al. Summer upwelling in the South China Sea and its role in regional climate variations[J]. Journal of Geophysical Research Oceans, 2003, 108(C8): 3261. DOI:10.1029/2003JC001867
(  0) 0) |
| [6] |
Cheng Y, Hamlington B D, Plag H P, et al. Influence of ENSO on the variation of annual sea level cycle in the South China Sea[J]. Ocean Engineering, 2016, 126: 343-352. DOI:10.1016/j.oceaneng.2016.09.019
(  0) 0) |
| [7] |
Rong Z, Liu Y, Zong H, et al. Interannual sea level variability in the South China Sea and its response to ENSO[J]. Global & Planetary Change, 2007, 55(4): 257-272.
(  0) 0) |
| [8] |
刘雪, 林霄沛. ENSO背景下南海海表温度异常的跷跷板模态[J]. 中国海洋大学学报(自然科学版), 2013, 43(12): 83-87. Liu X, Lin X. The sea surface temperature see saw pattern in South China Sea during ENSO[J]. Journal of Ocean University of China Deriodical, 2013, 43(12): 83-87. (  0) 0) |
| [9] |
Huang Z, Du Y, Wu Y, et al. Asymmetric response of the South China Sea SST to El Niño and La Niña[J]. Journal of Ocean University of China, 2013, 12(2): 272-278. DOI:10.1007/s11802-013-2169-x
(  0) 0) |
| [10] |
Yan H, Soon W, Wang Y. A composite sea surface temperature record of the northern South China Sea for the past 2500 years: A unique look into seasonality and seasonal climate changes during warm and cold periods[J]. Earth-Science Reviews, 2015, 141: 122-135. DOI:10.1016/j.earscirev.2014.12.003
(  0) 0) |
| [11] |
Soumya M, Vethamony P, Tkalich P. Inter-annual sea level variability in the southern South China Sea[J]. Global & Planetary Change, 2015, 133: 17-26.
(  0) 0) |
| [12] |
Thompson B, Tkalich P. Mixed layer thermodynamics of the Southern South China Sea[J]. Climate Dynamics, 2014, 43(7-8): 2061-2075. DOI:10.1007/s00382-013-2030-3
(  0) 0) |
| [13] |
Wang C, Wang W, Wang D, et al. Interannual variability of the South China Sea associated with El Niño[J]. Journal of Geophysical Research Oceans, 2006, 111: C03023. DOI:10.1029/2005JC003333
(  0) 0) |
| [14] |
Fang G, Chen H, Wei Z, et al. Trends and interannual variability of the South China Sea surface winds, surface height, and surface temperature in the recent decade[J]. Journal of Geophysical Research Oceans, 2006, 111: 10.
(  0) 0) |
| [15] |
Wang Z, Zhai F, Li P. A shift in the upper-ocean temperature trends in the South China Sea since the late 1990s[J]. Acta Oceanologica Sinica, 2016, 35(11): 44-51. DOI:10.1007/s13131-016-0947-1
(  0) 0) |
| [16] |
Kim KY, Hamlington B D, Na H. Theoretical foundation of cyclostationary EOF analysis for geophysical and climatic variables: Concepts and examples[J]. Earth-Science Reviews, 2015, 150: 201-218. DOI:10.1016/j.earscirev.2015.06.003
(  0) 0) |
| [17] |
吴晓芬, 许建平, 张启龙, 等. 热带西太平洋海域上层海洋热含量的CSEOF分析[J]. 热带海洋学报, 2011, 30(6): 37-46. Wu X, Xu J, Zhang Q, et al. CSEOF analysis of the upper ocean heat content in the tropical western Pacific[J]. Journal of tropical ocean, 2011, 30(6): 37-46. DOI:10.3969/j.issn.1009-5470.2011.06.006 (  0) 0) |
| [18] |
Kim KY, Hamlington B D, Na H, et al. Mechanism of seasonal Arctic sea ice evolution and Arctic amplification[J]. Cryosphere Discussions, 2016, 10(5): 1-29.
(  0) 0) |
| [19] |
Sun M, Kim G. Quantitative monthly precipitation forecasting using cyclostationary empirical orthogonal function and canonical correlation analysis[J]. Journal of Hydrologic Engineering, 2016, 21(1): 04015045. DOI:10.1061/(ASCE)HE.1943-5584.0001244
(  0) 0) |
| [20] |
Kim K Y, Kim Y. A comparison of sea level projections based on the observed and reconstructed sea level data around the Korean Peninsula[J]. Climatic Change, 2017, 142(1-2): 23-36. DOI:10.1007/s10584-017-1901-8
(  0) 0) |
| [21] |
Banzon V, Smith T M, Chin T M, et al. A long-term record of blended satellite and in situ sea-surface temperature for climate monitoring, modeling and environmental studies[J]. Earth System Science Data, 2016, 8(1): 165-176. DOI:10.5194/essd-8-165-2016
(  0) 0) |
| [22] |
Egbert G D, Erofeeva S Y. Efficient inverse modeling of barotropic ocean tides[J]. Journal of Atmospheric & Oceanic Technology, 2002, 19(2): 183-204.
(  0) 0) |
| [23] |
Kim K Y, North G R, Huang J. EOFS of one-dimensional cyclostationary time series: Computations, examples, and stochastic modeling[J]. Journal of the Atmospheric Sciences, 2010, 53(7): 1007-1017.
(  0) 0) |
| [24] |
Hamlington B D, Leben R R, Nerem R S, et al. Reconstructing sea level using cyclostationary empirical orthogonal functions[J]. Journal of Geophysical Research Oceans, 2011, 116: C12015. DOI:10.1029/2011JC007529
(  0) 0) |
| [25] |
Sun M, Kim G. Quantitative monthly precipitation forecasting using cyclostationary empirical orthogonal function and canonical correlation analysis[J]. Journal of Hydrologic Engineering, 2016, 21(1): 04015045.
(  0) 0) |
| [26] |
Hamlington B D, Leben R R, Strassburg M W, et al. Cyclostationary empirical orthogonal function sea-level reconstruction[J]. Geoscience Data Journal, 2015, 1(1): 13-19.
(  0) 0) |
| [27] |
Liu Q, Jiang X, Xie S P, et al. A gap in the Indo-Pacific warm pool over the South China Sea in boreal winter: Seasonal development and interannual variability[J]. Journal of Geophysical Research Oceans, 2004, 109: 10.
(  0) 0) |
| [28] |
Qiu C, Mao H, Yu J, et al. Sea surface cooling in the Northern South China Sea observed using Chinese sea-wing underwater glider measurements[J]. Deep Sea Research Part Ⅰ Oceanographic Research Papers, 2015, 105: 111-118. DOI:10.1016/j.dsr.2015.08.009
(  0) 0) |
 2019, Vol. 49
2019, Vol. 49

