自然海况中,海洋工程结构物常受到海风、波浪、海流等作用,其中风荷载约占总荷载10%左右。由于海风的随机性和脉动性以及水中的漂浮结构物或者船舶的自身特性,导致海风对海上结构物的作用是一个极其复杂的过程,因此模拟符合实际海洋环境中的随机风对研究浮体结构或者漂浮物受到的作用力来说显得尤为重要[1]。
目前,国内关于随机风的模拟已经取得一些成果。季春群[2-3]在讨论海洋工程试验有关风要求时,假定阵风由无限多个正弦形式的波动风速叠加而成,并应用Longuet-Higgins随机模型,列出了实现风速过程的表达式。张云彩[1]利用谱特性首次对具有API谱的随机风进行了试验室模拟。2006年,唐筱宁[4]根据大量的物理模型试验,提出了采用不同船模模型比尺来确定风速比尺的建议。夏云强[5]研究了模型相似性、比尺效应、风速比尺,给出了重力相似条件下风速比尺的修正系数,比较了风场的开敞式方案和风洞式方案。彭涛[6]借助数学模型和物理模型给出了模拟风场时的一些建议,如实验区与风阵的距离以及池壁的距离。以上研究对于模拟的结果,谱形波动较大,谱能随频率变化较为剧烈,本文尝试减小模拟风谱的波动性,减缓谱能随频率变化,使模拟谱更贴近目标谱线。
1 风谱模拟理论风谱种类众多,应用较多的有Davenport谱、Harris谱、Ochi&Shin谱、API谱[7-11]等。模拟方法大致有三种,如简谐波合成法、线性滤波法、小波分析法。本文采用简谐波叠加法模拟风谱,根据Shinozuka理论[12],随机过程样本G(t)可以用下式表示:
| $ \begin{align} &G\left( t \right)=g\left( n\cdot \Delta t \right)= \\ &\sum\limits_{j=1}^{M}{\sqrt{2{{S}_{v}}\left( {{\omega }_{j}} \right)\Delta \omega }\text{cos}\left( {{w}_{j}}n\Delta t+{{\varphi }_{j}} \right)+{{V}_{0}}}。\\ \end{align} $ |
其中:Sv为随机过程G(t)的风功率谱;ωj为第j个角频率值;Δω为角频率增量;φj为均匀分布在区间(0,2π)内的随机变量;V0为平均脉动风速;
风谱分为陆地风谱和海洋风谱,其代表分别为API谱和Davenport谱。API随机脉动风功率谱表达式为:
| $ \begin{align} &S\left( f \right)={{\left[\sigma {{\left( z \right)}^{2}} \right]}^{2}}/{{f}_{p}}\times 1/{{\left[1+1.5\frac{f}{{{f}_{p}}} \right]}^{5/3}}, \\ &或S\left( \omega \right)={{\left[\sigma {{\left( z \right)}^{2}} \right]}^{2}}/{{\omega }_{p}}\times 1/{{\left[1+1.5\frac{\omega }{{{\omega }_{p}}} \right]}^{5/3}} \\ \end{align} $ |
其中:
| $ {{f}_{p}}=0.025\times \frac{V\left( z \right)}{\left( z \right)};{{\omega }_{p}}=2\pi {{f}_{p}}; $ |
| $ \sigma \left( z \right)=0.15\times {{(\frac{z}{{{z}_{s}}})}^{\text{-}0.125}}\ \ \ \ z\le {{z}_{s}}; $ |
| $ \sigma \left( z \right)=0.15\times {{(\frac{z}{{{z}_{s}}})}^{\text{-}0.275}}\ \ \ \ \ z>{{z}_{s}}。$ |
式中:S(f)为随机风脉动功率谱;V(z)为z高度处的平均风速;zs为标准高度,一般取20 m;fp为由风谱测量获得的平均频率;σ(z)为z高度位置风速脉动的标准差。
Davenport风谱公式如下:
| $ \begin{align} &S\left( \omega \right)={{\frac{145900C\omega }{1+{{\left( \frac{191\omega }{V} \right)}^{2}}}}^{\frac{4}{3}}}, \\ &或\frac{f\cdot S\left( f \right)}{C{{V}^{2}}}=\frac{4{{X}^{2}}}{{{\left[1+{{X}^{2}} \right]}^{\frac{4}{3}}}} \\ \end{align} $ |
其中:X=1 200f/V;f为风速的脉动频率;C为粗糙度系数;ω为风速脉动圆频率;V为风速;S(ω)为随机风脉动功率谱。
2 两类风谱的试验室模拟在海洋工程的模拟试验中,对于风场模拟的正确程度既没有明确的规定也没有既定的标准,一些研究[3, 5]在此方面做了积极的尝试, 在实践中一般要求风速满足以下三个要求:平均风速误差控制在5%左右;风速标准差10%左右;模拟风谱与目标谱要保持一致,谱面积相差控制在10%左右。
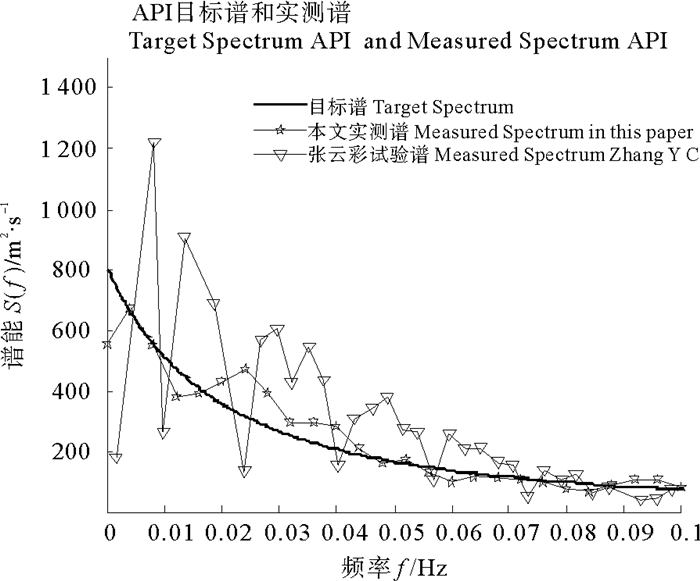
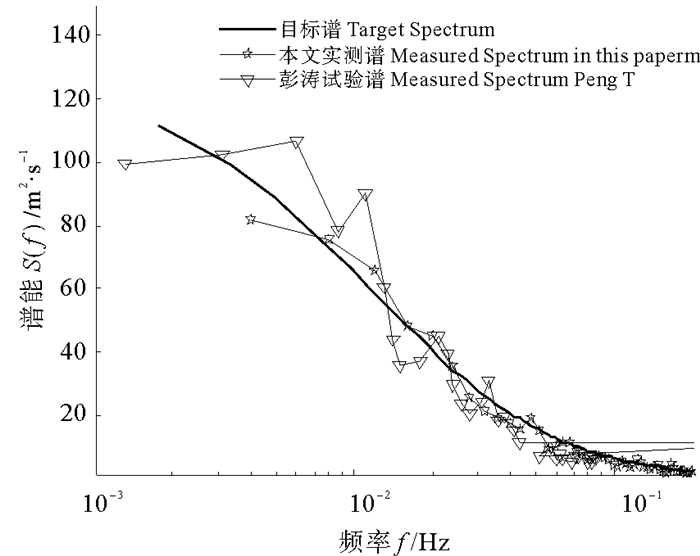
2.1 风谱的模拟验证研究本文首先采用伺服驱动方法对张云彩等[1]和彭涛等所做相关试验[5]分别进行了模拟,以此来验证本文的模拟方法的有效性。图 1本文测点布置图,图 2为本文试验结果与张云彩[1]试验结果的对比情况。试验中API风谱脉动风模拟试验采用给定风速42.69 m/s,风压中心高度z=22.27 m,计算风频率范围为0.005~0.7(rad/s)。张彩云在试验中选用模型比尺为1/70,风速采样时间1 290 s,采样频率为20 Hz;本次试验采用比尺1/140,风速采样时间1 200 s,采样频率为4 Hz。图 3为本文试验结果与彭涛等所做试验的对比情况,试验风压中心高度取10 m,平均风速为12 m/s。本文模型比尺1/40,采样频率为4 Hz。

|
图 1 测点布置平面图 Fig. 1 Arrangement plan of measuring points |
|
图 2 与张云彩等试验结果对比图 Fig. 2 Comparison with the test of Zhang Yun-Cai |
|
图 3 与彭涛等试验结果对比图 Fig. 3 Comparison with the test of Peng Tao |
从试验结果看(图 2~3),与目标曲线相比较,两条试验风谱曲线在高频区(如f>0.07 Hz)与目标谱曲线均非常吻合,但在低频区长周期段(如f < 0.07 Hz)则出现了一定程度的波动性。由于本文对控制数据进行了插值计算,使得控制风速信号变化不过于剧烈,从模拟的结果看,本文实测谱曲线更贴近目标谱,波动性小并具有更好的稳定性。
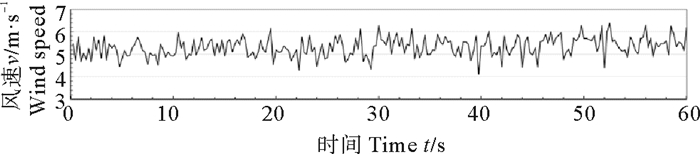
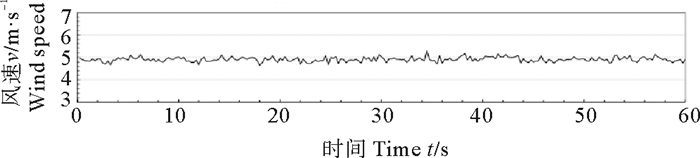
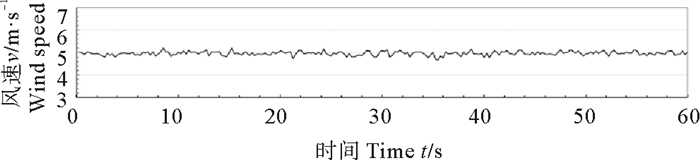
2.2 两类风谱的对比研究为满足试验环境风速偏差的要求,首先要选择合理的风区,并对其风速过程进行试验研究。以风速5 m/s为例,在吹风口不同的位置对风速进行了试验数据的采集,采集点距离风口分别为1.5 m(A测点)、3.0 m(B测点)、4.5 m(C测点)、6.0 m(D测点)、7.5m(E测点)。图 4~6为部分测点测得的同一平均风速下的过程线。表 1中列出了5个测点的风过程各相关参数的统计结果,可见对本次试验所考虑的五个测点,C测点之前的点位风速偏差较大,C测点以后的点位才满足风速控制偏差5%和风速控制标准差10%的要求,原因是风机风口位置风场波动较大,需要传播一段距离后才会变得均匀、稳定,因此风的有效试验段应该与风机口保持一定的距离,在本次试验中试验段处于进风口4.5~7.5 m范围内。
|
图 4 测点A的风过程线 Fig. 4 Wind speed process of the measuring point A |
|
图 5 测点C的风过程线 Fig. 5 Wind speed process of the measuring point C |
|
图 6 测点E的风过程线 Fig. 6 Wind speed process of the measuring point E |
|
|
表 1 风过程参数统计表 Table 1 Parametric statistics table of the wind speed process |
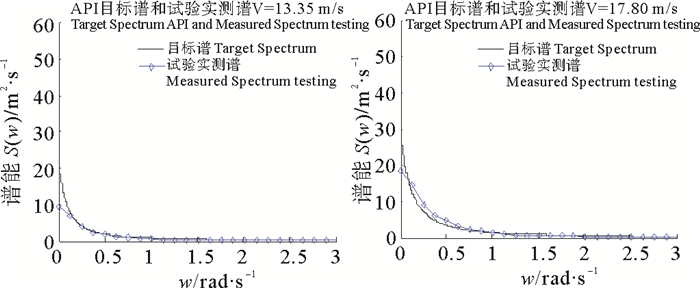
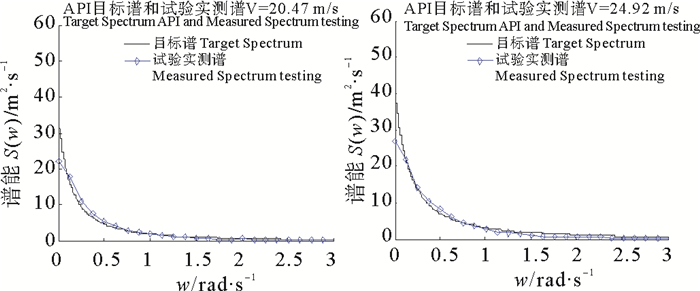
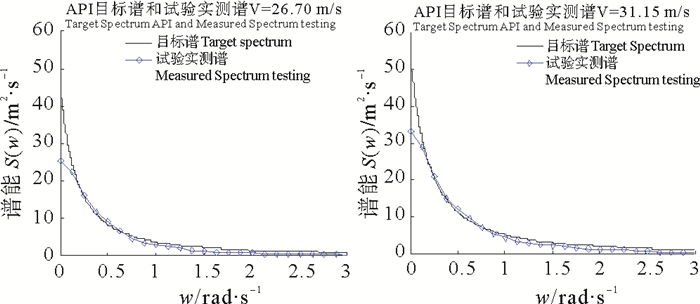
同时,在本次试验中对于目标风谱面积和实测风谱面积偏差也进行了控制。实测谱是由风速仪在试验区测得的风过程数据生成的谱。图 7~12列出了API风谱和Davenport谱的目标谱形和实测谱形。
|
图 7 V=13.35 m/s, 17.8 m/s时,API实测风谱与目标谱形对比 Fig. 7 V=13.35 m/s, 17.8 m/s, Comparison with target spectrum |
|
图 8 V=20.47 m/s, 24.9 m/s时,API实测风谱与目标谱形对比 Fig. 8 V=20.47 m/s, 24.9 m/s, Comparison with target spectrum |
|
图 9 V=26.7 m/s,31.15 m/s时,API实测风谱与目标谱形对比 Fig. 9 V=26.7 m/s, 31.15 m/s, Comparison with target spectrum |
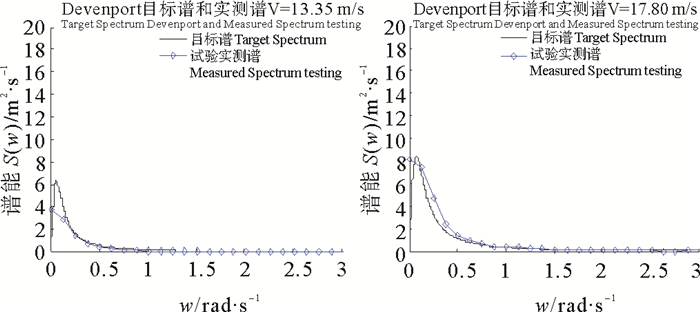
|
图 10 V=13.35 m/s,17.80 m/s时,Davenport实测风谱与目标谱形对比 Fig. 10 V=13.35 m/s, 17.80 m/s, Comparison with target spectrum |
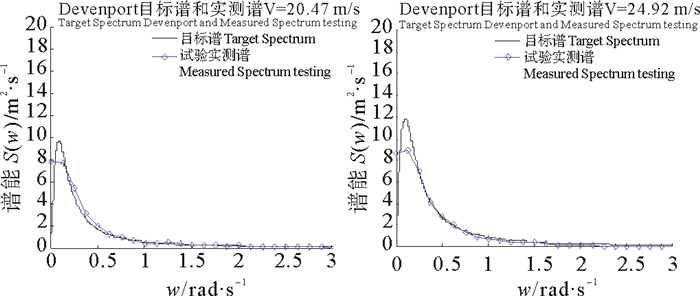
|
图 11 V=20.47 m/s, 24.92 m/s时,Davenport实测风谱与目标谱形对比 Fig. 11 V=20.47 m/s, 24.92 m/s, Comparison with target spectrum |
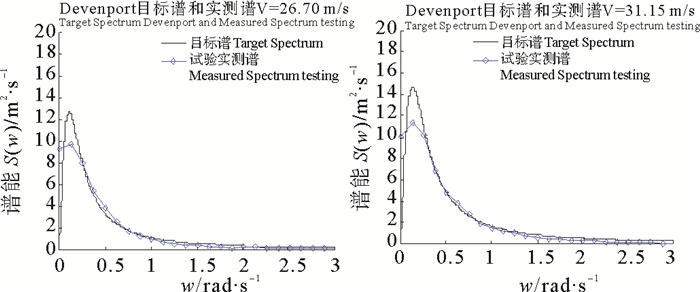
|
图 12 V=26.7 m/s, 24.92 m/s时,Davenport实测风谱与目标谱形对比 Fig. 12 V=26.7 m/s, 24.9 m/s, Comparison with target spectrum |
从API谱和Davenport谱的谱形上来看两者的谱形并不相同,前者为渐近线,后者为一条抛物线,但风能均集中在低频区,即长周期区间。从图中看实测风谱与目标风谱线关系,每一条实测风谱线与目标风谱线均保持相同的走向和相同的变化趋势,只是在较低风速时,实测风谱的谱能有所降低,这是由于在模拟风过程的时候,由于外界环境的影响,风能有所衰减,但这对谱模拟的影响不大。
表 2为API谱和Davenport谱谱特性随机风过程谱面积统计数据,实测风谱的谱面积与目标谱谱面积均有所偏差,两者并不能完全与目标谱吻合。时平均风速较低时,谱面积偏差会大些且偏差并不稳定, 时平均风速较高时,谱面积偏差会小些。例如API谱特性随机风过程中,时平均风速13.4 m/s,谱面积偏差达到15%,风速为八级风、十级风时,谱面积偏差均有所降低,最大不超过12%,最小仅为0.2%;Davenport谱特性随机风过程中,时平均风速13.4、17.8 m/s,谱面积偏差约为13%,风速为20.5、24.9、26.7、31.2 m/s时,谱面积偏差最大不超过10%,最小仅为4.4%。模拟的六级风、八级风、十级风、十一级风模拟谱面积均控制在10%左右,模拟效果较好,六级风实测谱偏差较大,究其原因是模拟风速偏小风能损失相对较大。在这一系列的随机风过程中,实测风谱的值很难达到谱峰的位置,但这影响不了模拟谱面积与目标谱面积比。从总体上来说,API风谱和Davenport风谱面积偏差率基本能满足试验要求。
|
|
表 2 API谱和Davenport谱特性随机风的谱面积统计 Table 2 The wind spectrum area deviation about API and Davenport |
API风谱与Davenport风谱的风过程均表现了一定的随机性和脉动性,为了找出两者之间的差别,又分别研究了具有谱特性的一系列随机风过程,图 13~18,并对此随机风过程进行了特征值统计,数据统计如表 3。
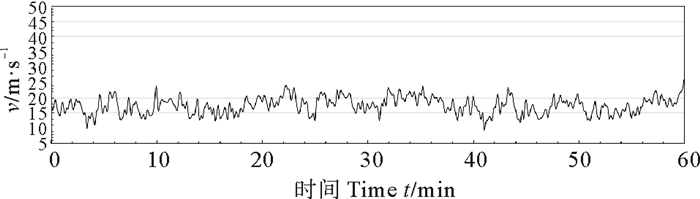
|
图 13 API谱特性风过程线V=17.8 m/s Fig. 13 Wind speed process of API spectrum V=17.80 m/s |
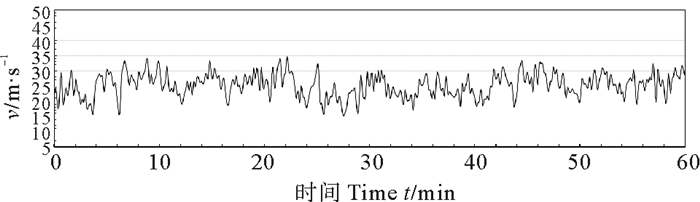
|
图 14 API谱特性风过程线V=24.92 m/s Fig. 14 Wind speed process of API spectrum V=24.92 m/s |
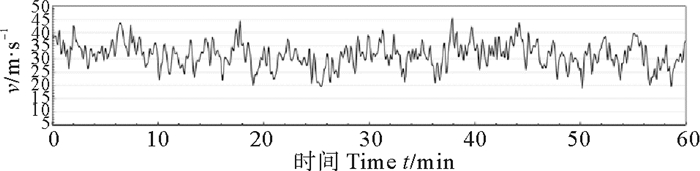
|
图 15 API谱特性风过程线V=31.15 m/s Fig. 15 Wind speed process of API spectrum V=31.15 m/s |
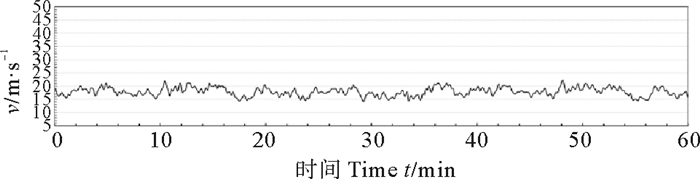
|
图 16 Davenport谱特性风过程线V=17.8 m/s Fig. 16 Wind speed process of Davenport spectrum V=17.8 m/s |
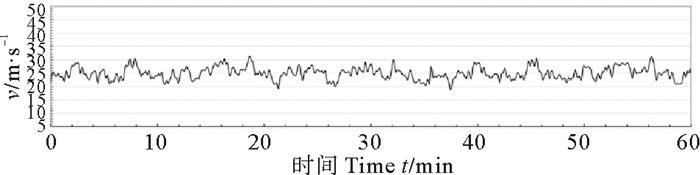
|
图 17 Davenport谱特性风过程线V=24.92 m/s Fig. 17 Wind speed process of Davenport spectrum V=24.92 m/s |
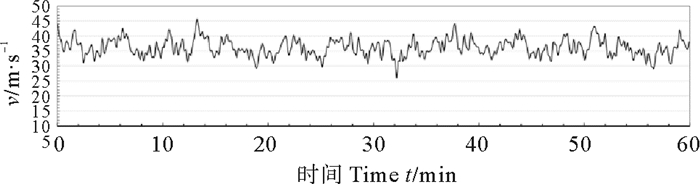
|
图 18 Davenport谱特性风过程线V=31.15 m/s Fig. 18 wind speed process of Davenport spectrum V=31.15 m/s |
|
|
表 3 两随机风过程风速特性值统计表 Table 3 Parametric statistics table of the wind speed process about API and Davenport |
在相同时平均风速、相同风历时情况下,如风速为17.8 m/s历时1 h,API随机风过程的波动性要比Davenport谱风大。这也可从表 3的特征值统计表中看出,最大风速项API谱均比Davenport大,最小风速项前者均比后者小,说明API谱风过程速度变化范围大,波动性强,试验数据显示,API谱随机风过程风速的波动幅度为Davenport谱随机风波动幅度的1.5~2.0倍。
3 结语文章基于Shinozuka理论,依据随机风风谱的有关特性,在试验室成功进行了两种谱特性随机风的模拟,并与其他随机风试验结果进行了对比分析,参照有关谱模拟的要求,对API谱和Davenport谱进行了模拟与分析。模拟结果显示,模拟的时平均风速越低,实测谱面积偏差越大;相反,模拟的风速越高,实测谱面积偏差就越小。对比两类风谱,API谱风速波动较Davenport谱大,两者之间存在较大的差异性。通过对一系列随机风过程的试验模拟,分别从风速偏差、风速标准差和谱面积偏差三方面进行控制,验证了谱特性随机风过程的有效性和合理性,可作为海洋工程试验中的风环境。
| [1] |
张云彩. 阵风及其谱模拟[J]. 海洋工程, 1996, 14(2): 20-27. ZHANG Yun-cai. Gust simulation[J]. Ocean Engineering, 1996, 14(2): 20-27. (  0) 0) |
| [2] |
季春群, 黄祥鹿. 海洋工程模型试验的要求及试验技术[J]. 中国海洋平台, 1996, 11(5): 234-237. JI Chun-qun, HUANG Xiang-lu. Test requirement and technology in model experiment of ocean engineering[J]. China Offshore Platform, 1996, 11(5): 234-237. (  0) 0) |
| [3] |
季春群, 盛振邦. 海洋工程环境条件模拟[J]. 中国海洋平台, 1996, 11(4): 191-193. JI Chun-qun, SHENG Zhen-bang. Environment simulation of ocean engineering[J]. China Ocean Platform, 1996, 11(4): 191-193. (  0) 0) |
| [4] |
唐筱宁, 夏运强, 杨洪旗, 等. 波浪物理模型试验中风速比尺确定方法初探[J]. 海岸工程, 2006, 25(1): 1-5. TANG Xiao-ning, XIA Yun-qiang, YANG Hong-qi, et al. A preliminary study on the determination method of wind speed scale in physical wave model test[J]. Coastal engineering, 2006, 25(1): 1-5. (  0) 0) |
| [5] |
夏运强, 李华军, 唐筱宁. 海洋工程物理模型试验中风场模拟方法研究[J]. 工程力学, 2008, 25(1): 28-33. XIA Yun-qiang, LI Hua-jun, TANG Xiao-ning. Wind simulation in physical model experiment of ocean engineering[J]. Engineering Mechanics, 2008, 25(1): 28-33. (  0) 0) |
| [6] |
彭涛, 杨建民, 李俊. 海洋工程试验池中风场模拟[J]. 海洋工程, 2009, 27(2): 8-13. PENG Tao, YANG Jian-min, LI Jun. Simulation of wind field in a laboratory basin[J]. Coastal engineering, 2009, 27(2): 8-13. (  0) 0) |
| [7] |
Davenport A G. The Spectrum of Horizontal Gustiness Near Ground in High Winds[J]. Royal Meteor Soc, 1961(87): 194-211.
(  0) 0) |
| [8] |
Suresh Kumar K. Random number sensitivity in simulation of wind loads[J]. Wind and Structures, 2000, 3(1): 1-10. DOI:10.12989/was.2000.3.1.001
(  0) 0) |
| [9] |
Harris R I. The Nature of the Wind, Modern Designing of Wind Sensitive Structures[M]. Const Ind Res & Inf Assn London, 1971, 29-55.
(  0) 0) |
| [10] |
SIMIU E. Wind spectra and dynamic along wind response[J]. Journal of the Structural Division, ASCE, 1974, 100(9): 1897-1910.
(  0) 0) |
| [11] |
舒新玲, . 风荷载测试与模拟技术的回顾与展望[J]. 振动与冲击, 2002, 21(3): 6-10. SHU Xin-ling, ZHOU Dai. Review and prospect on measurement and simulation techniques of wind load[J]. Journal of vibration and shock, 2002, 21(3): 6-10. (  0) 0) |
| [12] |
Shinozuka M. Digital simulation of random processes and its applications[J]. Sound and Vibration, 1972, 25(1): 111-128. DOI:10.1016/0022-460X(72)90600-1
(  0) 0) |
| [13] |
阎石, 郑伟. 间谐波叠加法模拟风谱[J]. 沈阳建筑大学学报(自然科学版), 2005, 21(1): 1-4. YAN Shi, ZHENG Wei. Wind load simulation by superposition of harmonic[J]. Journal of Shenyang Jianzhu University(Natural Science), 2005, 21(1): 1-4. (  0) 0) |
 2018, Vol. 48
2018, Vol. 48

