2. 中国海洋大学物理海洋教育部重点实验室 深海前沿研究中心 海洋高等研究院,山东 青岛 266100;
3. 青岛海洋科学与技术试点国家实验室,山东 青岛 266237
计算流体力学是一门借助于计算机求解流体动力学方程的新兴学科,通过代码编写程序进行数值模拟与仿真,实现流体动力学演变特征的流体实验测试、模拟和预报[1-4]。计算模式建立、计算理论方法发展和科学与工程应用是计算流体力学三个主要研究内容[5]。
进入21世纪以来,计算流体力学随着计算能力的提升而迅速发展,当前已经形成具有算法高效化、模式精细化和应用领域多元化等鲜明特点的学科发展局面。在地球科学领域,数值模拟最早出现在大气科学,Richardson[6]将有限差分格式引入大气中的天气图分析和相关数学求解研究中,至今,地球流体计算及数值预报研究已有超过100年的历史。百年来大气和海洋的数值计算与模拟取得了巨大进步,形成了计算地球流体动力学这一新兴交叉学科[7-9]。目前,建立在中国自主设计制造的每秒百亿亿次浮点运算高性能超级计算机基础上,我们已经能够很大程度上实现地球系统在实验室的“数值孪生”,从而使得在实验室里研究任何地球系统中的自然过程成为可能,这又将推动地球科学的理论和技术更加蓬勃、迅猛的发展。我们完全可以期望,在不久的将来,地球系统数值模拟可以用数值定量的形式来精准预报、预测地球环境的未来,实现人类打造宜居地球的梦想。
Benjamin等[10]回顾了自1919年开始的人工预报和数值天气预报的演化进程,并划分了4个时代,从观测、理论和数值预报等方面详细阐述。沈学顺等[11]阐述了中国数值天气预报自主创新的历史,在计算格式、模式动力框架和四维变分同化等方面都取得了颇具影响的研究成果。此外,前人通过撰写科学家的人物传记,记录了计算地球流动力学的发展进程[12-16]。本文结合最新研究动态对该学科内容进行系统性回顾,延用Benjamin等[10]100年展望回顾文章中的时间划分方法,将计算地球流体力学100年来取得的进展划分为四个阶段:第一阶段(1919—1939年)、第二阶段(1939—1956年)、第三阶段(1956—1985年)和第四阶段(1985—2018年)。
1 第一阶段(1919—1939年):起源19世纪后期至第二次世界大战(20世纪40年代初)是计算地球流体力学发展的萌芽阶段。这一时期,社会对于预报的需求不断增加,科技发展使得观测和通信手段都有所改进,但是由于世界范围内的计算技术、观测技术和气象科学等发展的不成熟,人们所能获取到的观测资料十分有限,只能通过经验法则结合简单观测资料外推的方式预报天气,预报结果的准确性也难以保证[7]。
1.1 理论研究进展基于Newton、Maxwell等人在18—19世纪使用欧拉方程得到的基础物理成果,流体动力学概念和流体动力学方程在这一阶段共同发展,奠定了现代气象科学的基础。早在1913年,近代气象学奠基人之一的Vilhelm Bjerknes就提出了将物理学的理论方程组应用到实际大气中,根据已观测到的大气状态计算未来的大气状态;几年以后,Lewis Fry Richardson对这种设想进行了实践,不过由于当时计算工具的落后,这种设想无疑只是一个“梦想”[17]。虽然关于数值天气预报的初次实践以失败告终,但是Richardson所设计的整套数值方案,尽管依赖于“人工”计算,但已经具有当今数值模式的雏形。
1.2 第一阶段代表性人物气象数值模式发展历程中的早期代表性人物是Bjerknes家族和Lewis Fry Richardson(见图 1)。

|
图 1 第一阶段代表性人物及所构想的由人工“电脑”完成的“预报工厂”[6] Fig. 1 Representative scientists in the first period and "forecast factory"conceived by Richardson on a "human being" computer[6] |
Carl Bjerknes(1825—1903年)毕业于斯德哥尔摩大学,是挪威数学家、物理学家与流体动力学家。子承父业,Vilhelm Bjerknes(1862—1951年)在1892年取得博士学位后任教于瑞典斯德哥尔摩大学,并于1904年提出通过求解一个非线性偏微分方程组来预测天气的思想,定义了“预报是气象学的终极问题”[18],奠定了数值天气预报和计算地球流体力学发展的总基调。Jacob Bjerknes(1897—1975年)继承了祖父和父亲的流体动力学研究,在克里斯蒂亚尼亚大学取得博士学位后,历任卑尔根气象局局长(1931)、挪威地球物理研究所气象学教授(1932)和麻省理工学院教师(1933—1934年),并于1940年成为加州大学洛杉矶分校的气象学教授,主攻大气环流研究;其1952年利用高空火箭拍摄的照片进行的天气分析和预报,属于最早利用太空技术进行的气象研究工作。Lewis Fry Richardson(1881—1953年)是英国著名数学家、物理学家,现代气象学的奠基人之一。他首先发展了有限差分法,提出用数学物理方法求解天气预报问题并进行了早期的尝试[17],于1922年出版了《利用数值方法的天气预报》。书中详细叙述了进行预报所需要的动力学模型、数学过程及计算实例。图 1为Richardson构想的“预报工厂”[16, 19]。该设想为此后气象领域的数值研究方法提供了启发性思路,成为后来数值天气预报发展的重要引索。
学科的起源总是基于生存需求的朴实思考。在第一阶段,社会对预报需求的增加及工业革命等历史事件推动了该阶段的理论和观测技术的发展。Bjerknes等人基于18世纪的基础物理成果丰富了流体动力学的理论基础,卑尔根等气象学派的建立推动了国际气象学者间的交流与学习。囿于较为落后的算力条件与观测技术,尽管以Richardson为首的科学家们所做出的数值天气预报尝试都以失败告终,但是为此后计算地球流体力学的发展提供了宝贵的经验与构想。在该阶段,凭借此前的基础物理“养分”,计算地球流体力学开始生根发芽。
2 第二阶段(1939—1956年):雏形第二阶段见证了技术进步和飞跃对气象学,尤其是预报技术产生的重大影响。第二次世界大战,以及之后的“冷战”都和这一阶段取得的科技进步息息相关。在第二阶段初期,天气预报很大程度上受到20年前卑尔根气象学院基础工作的影响。
2.1 发展的时代背景第二次世界大战中,有效利用空军力量是战争取胜的关键,因此第二次世界大战“风暴前期”,人们再次认识到提高天气预报精度的重要性。当时,电子计算机还不存在,自动画图软件也不存在,所以只能用纸笔来记录观测数据,用铅笔和橡皮来分析;再加上描图纸和一张发光的桌子,就是用来完成预报任务的全部工具了。那时典型的工作场景在图 2中展示。由于受到当时预报环境限制,很多复杂的天气分析程序不得不简化[20-22]。

|
( 资料来源:NOAA/NCEP天气预报中心。Data from: NOAA/NCEP weather forecast center. ) 图 2 1950s年代在华盛顿的美国中央分析中心工作的预报员 Fig. 2 Weather rapporters working at the United States Central Analysis Centre in Washington in 1950s |
John von Neumann是著名数学家,也是第一台计算机的关键设计师。他认识到,流体运动中的非线性传输需要强大的计算能力来估算,因此,1947年他在普林斯顿大学高等研究所(Institute for Advanced Study)组建了一个由Charney领导的科学家小组。到1950年初,计算过程的细节已经解决,在马里兰州阿伯丁试验场的电子数字积分器和计算机(ENIAC)在一个月内成功地进行了4次24小时预报,结果出人意料的准确。这项工作指出了涡度非线性平流的重要性,在另一篇具有里程碑意义的论文[23]中有所描述。
普林斯顿小组的工作引起了关注,到了20世纪50年代初,人们普遍认识到计算机生成的预报是以刻画地球流体力学的控制方程为基础的。气象小组利用一个三层准地转模式,测试了1950年11月美国东海岸强风暴[24]和其他气旋。这些尝试并没有全部取得成功,但引发了科学家们的思考,他们认为使用更加准确的原始方程进行预报可能会得到更好的结果。
2.3 第二阶段代表性人物瑞典裔美国著名气象学家Carl Gustaf Rossby(1898—1957年)在20岁那年取得了斯德哥尔摩大学数学、天文学、力学学士学位。硕士毕业后Rossby来到美国,在美国气象局短暂工作后,被美国航空基金会聘用,开创了美国第一条民航航线的气象服务系统,名显美国气象学界。1946年8月Rossby同Neumann在普林斯顿大学召开了第一次讨论数值预报的会议,此次会议的召开推动了以数值天气预报为基础的地球系统数值模拟由理论到现实的飞跃;1950年Rossby回到瑞典,和斯德哥尔摩大学联合成立气象研究所。
Joseph Smagorinsky(1924—2005年)是美国著名气象学家、美国国家海洋和大气管理局(NOAA)和地球物理流体动力学实验室(Geography Fluid Dynamical Laboratory)的创始主任,是结合计算机和数学模型对全球气候演变趋势进行扩展预测的先驱(详见4.1)。Smagorinsky受邀来到普林斯顿高等研究院,使用电子数值积分器和电子计算机ENIAC对方程进行求解,之后检验了对流层中部大尺度运动的可预报性,证明了利用数值过程进行天气预报具有良好的应用前景。Smagorinsky是最早尝试利用数值天气预报新方法,将预报时间延长到1~2 d的研究人员之一。他在1963年发表了一篇开创性的论文[25],介绍了他使用大气动力学原始方程来模拟大气环流的研究,从根本上改变了表征气候和大气物理过程发展的建模方法。Smago-rinsky扩展了早期的天气模式,将诸如风、云量、降水、气压和辐射等变量包括在内。后来,他与同事Lilly、Deardorff共同开发了大涡模拟,这是第一个在数值模式中解释大气湍流的实用技术。
总之,第二阶段在理论认知上有较大提升。由于第二次世界大战的爆发,对天气预报提出了更急迫和更高的需求。第一台计算机诞生,并且认识到流体运动中的非线性传输需要强大的计算能力,并且在此阶段,在ENIAC计算机进行了4次24小时预报,结果出人意料的准确。但此阶段进行的其它数值预报结果差强人意,因此,引发了科学家意识到使用更加准确的原始方程可能会取得更好的结果的思考和探索。
3 第三阶段(1956—1985年):数值天气预报的形成与发展 3.1 形成与发展的历程20世纪50年代初数值天气预报兴起,在天气预报员经过对科学和技术的快速适应过程后,天气预报逐渐走向成熟。在第三阶段出现了第一个天气预报模式,用于模拟斜压波的发展,并改进温带气旋预测。第一次实时数值预报于1954年底在瑞典率先产生。此后1955年初美国新的联合数值天气预报小组也独立进行实时预报,但直到1958年,美国才向天气预报员提供基于数值预报的天气图。早期的预报模式受到计算机能力的限制,开发人员必须综合考虑分辨率(水平方向和垂直方向,及其相应的时间步长)、预测持续时间、区域大小等。随着计算机能力的提高,分辨率、时间步长等都更加精细,提高了预测的准确性和及时性。
1956年,在法兰克福举行的数值天气预报国际研讨会上,来自美国、日本和11个欧洲国家的50多名与会者展示了开发的天气预报模式。美国、英国、瑞典、德国和比利时正在发展数值预报方法。1960年,在东京举行的数值天气预报研讨会与会人数扩展到了131名。同年,日本气象厅(Japan Meteorological Agency)进行了首次实时数值预报运行,这是第三个采用单层正压模式的国家[26]。其他国家开始利用原始方程(Primitive Equation)来进行模式预报。1966年,德国气象局(Deutscher Wetterdienst,DWD)推出了一种用于业务预报的模式,同年美国气象局推出了6层原始方程模式。日本气象厅于1975年引进北半球原始方程、推出4层原始方程模式,水平分辨率为381 km。引入了非绝热过程,尤其是深对流驱动的非绝热过程,但也导致了虚假的“网格点风暴”问题[27]。1972年,英国气象局推出了10层原始方程模式[28]。
多层数值预报模式开始通过对次网格尺度过程的参数化来改进模拟能力,包括水蒸气及其相位变化、对流、辐射、湍流以及地球表面的热、湿和动量交换,并结合各种成分来描述非绝热和黏性效应。Richardson[6]很早就认识到,成功的天气预报必须包括更多的动力过程。20世纪70年代,随着全球模式的引入,业务化数值天气预报取得了飞跃性进展,第一次飞跃是1972年美国将6层原始方程模式扩展为9层2.58°经纬度版本[29]。欧洲中期数值天气预报中心(ECMWF)在1979年推出了一个类似的模式,水平分辨率为1.875 8°,有15个垂向分层,是第一个业务化模式。利用高效的傅立叶变换,Robert(1969年)开发了谱模式。半球谱模式于1976年在加拿大和澳大利亚投入使用。区域模式可以更高分辨率地反映大气过程。Phillips[30]测试了一个模式,即美国嵌套网格模式(NGM)并于1985年正式启用。在第三阶段所有的模式都采用了静力近似假定。
3.2 第三阶段代表性人物John von Neumann是美籍匈牙利数学家、计算机科学家、物理学家,被后人称为“现代计算机之父”。1933年,担任普林斯顿大学教授的Neumann将自己的研究领域逐渐从纯数学向应用数学转换,开始准备研制计算机的计划。1944年,Neumann来到宾夕法尼亚大学摩尔工程学院,正式成为美国第一台通用电子计算机(ENIAC,Electronic Numerical Integrator and Computer,电子数字积分计算机)研制项目的顾问。1945年末,他成功地说服了普林斯顿高等研究院高层全力支持ENIAC项目,并且意识到数值天气预报是计算机在数学应用领域面临的最重要的挑战之一。1946年8月,Neumann在高等研究院组织并主持了第二个对计算流体力学具有历史意义的会议。这次会议集结了一批美国当时最有思想的气象学家,目的是使用ENIAC做出准确的天气预报。Jule Gregory Charney提出了用于描述大气运动的简化方程组和滤波方法,从而与项目组建立了更加紧密的联系。后来Charney加入该项目的气象小组,参考1922年Richardson的工作,确定采用Jacob Bjerknes的倾向方程进行预报试验方案。1950年,项目组利用一层正压滤波模式,通过Neumann在计算机上的编程,成功进行了历史上第一次24小时天气预报[14]。
解决了预报方案难题的Charney是20世纪最伟大的气象学家,他对气象学、大气动力学和物理海洋学的贡献是难以估量的。Charney高中毕业时已经熟读了大部分关于微积分的书籍,之后进入加州大学洛杉矶分校学习数学和物理学[13]。1947年春,Charney来到了奥斯陆气象研究院,研究如何从基础流体动力学方程中发展出一套可解的方程组。Charney返回美国后,担任Neumann团队中气象小组的负责人,并着手解决一系列关键的技术问题。1952年春,Charney和他的团队首次对1950年感恩节期间的温带气旋进行了事后模拟,该气旋在中大西洋地区造成了大量雨雪,但在当时未能得到成功预报。在尝试了两个模式却完全没有模拟出低压系统的爆发性增强后,第三个模式——个简单的2层正压模式成功了。尽管得到的低压中心远在实际中心的400 km以外,但是这个计算机产生的结果依然能够帮助预报员模拟出影响东海岸的雨雪天气[31]。这次预报结果比实际天气迟到了18个月,却是数值预报历史上的巨大成功。之后在Charney的帮助下,美国气象局、空军和海军于1954年在马里兰州苏特兰建立了一个联合数值天气预报小组,用于大规模大气流动模式的日常运行和天气的日常预报。美国气象局很快又成立了一个专门面向研究的小组,由Charney领导,使用计算机进行基本的大气和海洋研究,极大地推进了计算地球流体力学的发展进程。
中国的数值模拟研究和数值天气预报的发展离不开顾震潮、巢纪平和廖洞贤等老一辈气象学家的不懈努力。顾震潮(1920—1976年)是中国现代大气科学的主要开拓者之一,他独创性地提出了数值天气预报可以是一个“演化”问题,而不必是一个初值问题,并指导廖洞贤于1956年发表了一个较为简单的数值预报实验结果。顾震潮又带领巢纪平等在1957年成功地用2层准地转模式,完成了亚洲区域的24小时和48小时的数值天气预报实验。巢纪平是中国科学院院士,长期从事数值天气预报、中小尺度大气动力学、积云动力学和热带大气动力学等领域的研究并取得了重要成果。廖洞贤是中国早期从事数值天气预报的先驱者之一,他在1955年首次用图解法,对2层模式进行500 hPa形势进行数值预报求解,预报出导致大规模寒潮的天气形势的演变特征,这是我国第一张数值天气预报图,从此我国有了数值天气预报业务[32]。之后他发表了有关动力气象、数值预报和天气学的论文60余篇,在模式设计、计算方法等方面都有深入研究。
总结起来,该阶段以几个主要事件的时间节点为主线。1954年,在瑞典诞生了第一个实时数值预报;1955年初,美国新的联合数值天气预报小组产生;1956年,在法兰克福举行的数值天气预报国际研讨会上,来自美国、日本和11个欧洲国家的50多名与会者展示了开发的天气预报模式;其时,美国、英国、瑞典、德国和比利时正在发展原始方程模式的数值预报方法。1960年,在东京举行了数值天气预报研讨会。同年,日本气象厅进行了首次实时数值预报运行。20世纪70年代,随着全球模式的引入,业务化数值天气预报取得了飞跃性进展,第一次飞跃是1972年美国将6层原始方程模式扩展为9层2.58°经纬度版本。欧洲中期数值天气预报中心(ECMWF)在1979年推出第一个业务化模式。同时,中国也形成了自己的初期大气海洋环境数值预报业务化系统。
4 第四阶段(1985—2018年):从大气海洋数值模拟到地球系统模式及气候变化 4.1 大气模式及海气耦合模式的发展近几十年来,数值方法几乎主导了大气与海洋的预报进程,是计算流体力学向自动化、智能化与现代化快速迈进的一个阶段。20世纪90年代后,对气象卫星的投入不断提高,新型探空数据的引进,以及更加有效的区域模式的出现,使得数值模式的发展迈向了新的台阶;传统的人工制作预报图在这个阶段正式走向终结,取而代之的是基于计算机的气象业务和服务自动化系统(如美国的AFOS工作站),预报员的职责也由订正预报结果转为决策和与非气象人员进行交流;观测手段的提高与预报方法的发展有效解决了此前棘手的极端天气预报等问题,预报准确性得到了实质性提高[10]。
在这个阶段,世界范围内数值天气预报和计算地球流体力学获得迅猛发展,以致各国数值预报中心如雨后春笋出现,并取得丰硕成果。如美国国家大气研究中心(NCAR)通过地面、探空等多种观测手段与卫星观测资料的积累,制作并发布了质量优良的再分析数据产品和实时预报数据(https://ncar.ucar.edu/who-we-are/history),对其他再分析系统开发机构提供了参照的范本,在世界范围内具有深远的影响力;欧洲中期数值天气预报中心(ECMWF)通过建立以谱模式为基础的数值模拟和预报,开发了一套完备的数据同化系统,提供了覆盖天气、气候不同尺度的实时业务化预报与再分析数据产品(https://www.ecmwf.int/en/about/what-we-do),为政府公共决策提供科学依据、为科研机构提供基础性的数据支撑。另外的一个典型代表是现位于美国普林斯顿大学校园的地球流体动力学实验室(GFDL)。1953年,Smagorinsky在跟随Neumann和Charney完成学业后,Smagorinsky接受了美国气象局的职位,成为了联合数值天气预报单元的先驱者之一;1955年,在Neumann的鼓动下,美国气象局在其指导下成立了环流研究部,从此开始了利用计算机使用数学模式研究气候演变的生涯。Joseph认为他的任务是继续Neumann和Charney计算机建模程序的最后一步:建立一个三维的、全球的、原始方程的大气环流模式。GFDL的发展历史及部分成果如表 1所示,是20世纪后半叶及本世纪初计算地球流体发展的一个缩影。
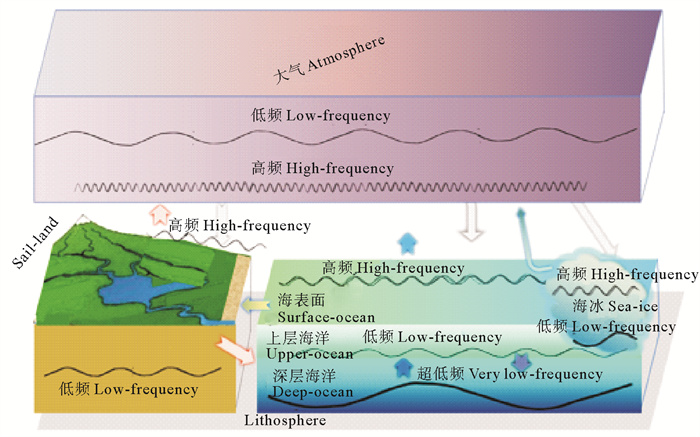
4.2 地球系统科学的建立与全球气候变化地球系统科学中一个具有基础性的研究领域是气候变化,它和人类生存环境息息相关。气候关心的时间尺度从季节年际到数世纪,因此合理模拟地球表面流体在较长时间内的运动需要考虑陆面的植被土壤、海冰生消等相关水热变化过程,形成如图 3所示“地球系统”耦合模式的基本框架。
|
图 3 地球表面各圈层物理过程及其耦合相互作用的时空尺度关系 Fig. 3 The spatio-temporal scale relationship between the physical processes of each layer on the earth surface and their coupling interactions |
陆面是天气/气候/地球系统的重要组成部分, 其物理、化学、生物过程深刻影响着陆地与大气、陆地与海洋之间的能量和物质交换。大气内部存在大尺度的慢变运动,但其局部表现为天气过程的快变特征。海面主要受到太阳辐射、风场和天体引潮力作用,存在潮汐、海浪和风、海流等快变运动,且通过海气界面与大气发生显著的质量及水热交换;海洋水体通常具有稳定层结——由浅至深,表现为上层低频、深层超低频的慢变特征。海冰在高纬和极地作为海气之间的一个交换驿站而存在,调制大气海洋的辐射效果,且有明显的季节变化特征,陆地上的冰盖变化相对缓慢。各圈层通过海气界面、冰气界面、陆气界面、陆海交界带、冰海交界面交换传递自身发展的信号而耦合在一起,相互作用共同调制天气气候状态的演变。准确描述各组成部分之内的物理、化学、生物过程,计算各分量之间的物质和能量交换, 对提高天气气候数值预报预测精度, 充分理解全球变化带来的水安全、粮食安全、生态环境恶化等问题的形成机制, 并制定相应对策, 具有重要的科学和社会意义。
含大气-陆面-海洋-海冰4个基本分量的耦合气候模式是政府间气候变化专门委员会(Intergovernmental Panel on Climate Change,IPCC)作气候评估的基本工具。在IPCC框架下的世界气候研究计划(World Climate Research Programme,WCRP)耦合模拟工作组(Working Group on Coupled Modelling,WGCM)发起的国际耦合模式比较计划(Coupled Model Intercomparison Project,CMIP)成为气候变化关键问题的研究利器。自1995年以来,WGCM已经先后开展6次耦合模式比较计划(CMIP1-6),CMIP1-6提供的模式数据支撑了大量的学术成果,同时为IPCC评估报告提供了重要依据[34-39]。
IPCC大致每6年发布一次评估报告,分别在1990、1995、2001、2007和2013年完成,这些报告已成为国际社会认识和了解气候变化问题的主要科学依据(见表 2)。
|
|
表 2 IPCC历次报告主题(根据IPCC官网资料整理[40-41]) Table 2 Themes of IPCC reports (organized according to IPCC official website data[40-41]) |
随着超级计算机的发展,尤其是新型节能高效超级计算机的快速发展,越来越高分辨率的数值模拟是当今地球环境科学研究的发展趋势[42]。作为在CMIP5基础上新增的科学实验,CMIP6框架下的高分辨率模式比较计划(High Res MIP)利用超级计算机显著提高了大气和海洋模式的时空分辨率,大气模式最高分辨率可以提高到25 km,而海洋模式最高分辨率可以提高到10 km[42]。
台风以及超强台风的预报对于人民生产生活具有重要意义,但是在科学上却是一个挑战性的课题。模式的表现力提升远不仅仅表现在台风问题上,高分辨率模拟可以显著提高全球平均温度变化,海表面温度和混合层深度的季节变化,极端天气,以及极端天气和大气之间的关系等。因此,计算资源的不断发展,模式分辨率提高,物理过程更具现实代表性是未来模式发展的大趋势。随着分辨率增加,可以更加精准地刻画台风的发生、发展、中尺度涡旋的生成和移动、黑潮流轴的结构和强度以及中小尺度涡旋的相互作用等[43-44],因此台风的可预报性显著升高。图 4显示了1950—2018年间高分辨率和低分辨率模拟的全球热带气旋轨迹及其与观测值的比较。除热带南大西洋外,低分辨率中热带气旋的年数量在所有海盆都被严重低估,热带北大西洋尤为严重:低分辨率中的热带气旋数量每年不到1个,而在观测中每年有12个, 该区高分辨率(6个)和低分辨率模式都低估了热带气旋的数量,但高分辨模式会更接近实测结果。从图 4我们也看到,即使是目前的高分辨率模式,对于超强热带气旋c5的模拟,离观测也还差得很远。高分辨率地球系统模式未来的发展面临诸多挑战。

|
( 图像底部不同的颜色表示不同的风暴强度类别,经向虚线分隔不同的海盆[42]。Different colors at the bottom of the figure represent different storm intensity categories. The numbers below the colors represent the maximum wind speed rarges at the center of the storm. Separate different basins through the virtual line[42]. ) 图 4 1950年—2018年间,观测(a)以及高分辨率模式(b)、低高分辨率模式(c)模拟的热带气旋频率轨迹 Fig. 4 Tropical cyclone trajectories from observation (a) and simulated by high-resolution model (b), low-resolution model (c) between 1950 and 2018 |
得益于电子计算机等现代化计算工具的诞生和科学家们的不懈努力,在计算地球流体力学发展的第四阶段,以人工经验为主的研究和预报方式逐渐被客观定量的数值模拟和预报方式取代,地球气候科学作为一门基础应用学科,走上实证科学的现代化轨道,天气气候预报预测的准确性不断提高。计算地球流体力学在该阶段不断扎根于科技发展的土壤,逐渐变得枝繁叶茂。
5 未来发展:机遇和挑战中国自主设计制造的高性能计算机发展迅速,基于超级计算的地球系统数值模拟对现实的刻画也越来越具有代表性,但仍存在以下发展空间:(1)现有大气模式分辨率不够高,模式中不能允许对流云现象发生,不能够解析大气风暴气旋精细结构;不能支持像青藏高原这样的复杂下垫面对大气环流的深层次影响机制研究;解析云对流现象,需要大气分辨率达到3 km,而目前耦合模式难以达到此精度,受分辨率所限,只能采用参数化方案来近似估算云对流过程,这会增加大气的不确定性,并限制了对局地重大灾害、极端天气事件(如台风生成和发展)的数值预报水平。(2)海洋模式分辨率不够高,不能够允许海洋亚中尺度现象发生,也不能够解析中尺度海洋涡及锋面精细结构,不支持准确模拟和预报热带气旋生成所需的局地上层海洋暖核精细结构;解析海洋次中尺度结构需要海洋模式分辨率达到1 km,全球海洋模式目前很难达到此分辨率,因此,不能支持复杂海底地形对海洋环流的影响,严重地限制了海洋环流的模拟水平和海洋环境中重大灾害事件的预警水平。(3)生物地球化学过程涉及生命生消过程,因此不能简单地总结为纯粹的物理和化学过程;除了将生命现象还原为基础的物理、化学过程以外,还必须将竞争、分配、繁衍、演替、自控等行为抽象成数学规律,由于生物地球化学过程本身涉及随时间而变的自然环境,因此在解决此类问题时需要将管理调度与模式调控相结合,进而演变成自然控制论范畴的问题;生物地球化学过程本身的特殊性与复杂性导致现阶段地球系统模式解决生物地球化学过程的技术仍不够成熟,且缺少定量的风险分析与效果评估;生物地球化学过程本身就是碳循环的过程,因此,能科学地代表生物地球化学过程的地球系统模式也是一个实现“双碳”(“碳达峰”“碳中和”)战略的科学研究和效果测试平台。(4)由于地球系统模式涉及众多学科与繁杂的数据资料,目前地球系统模式的研发工作仍然缺乏系统的管理和组织、国家层面的协调与持续的经费支持,有限的研究团队分散在不同的单位独立立项研发,会导致产生不必要的重复研究和资源浪费,降低了模式研发效率,不利于当今地球系统仿真模拟的快速发展。
无缝隙天气气候一体化预报,即同一模式预报过程产生天气和气候不同时间尺度的预报预测结果,短时间尺度结果为天气预报,长时间尺度结果则为气候预报,是未来天气气候预报的一个重要发展方向,可以解决目前天气预报不准确、气候预报众说纷纭的现状,利于打造宜居地球的最终目标。高分辨率耦合地球系统模式,以及相应的高精度再分析数据,在实现无缝隙天气气候一体化预报过程中将起到至关重要的作用。所谓再分析,是利用数学模型中的动力学和物理学规律,抽取观测信息并投影到模式空间,校正模式模拟篇差,重建历史天气气候时空连续演变的过程,它集成观测分析和理论研究成果,形成完整描述地球气候系统中各要素的历史演变数据流;如果说数值模式是人体的骨络,观测资料是人体的肌肉,已有的理论研究成果是人体的心脏和主要血脉的话,同化产生分析数据就类似于骨髓造血赋予肌肉生命力的过程,形成的分析数据就是一个有灵有肉的生命整体了。这样的分析数据是理解地球流体演变中各种动力和物理过程机理的基石,当前时刻的分析数据能反映模式初始化到当前时刻的三维流体连续演变情景,是对未来进行预报预测的初始条件。基于实证科学原理,利用这样的分析数据研究各种大气海洋过程,不断地纠偏校误,在预报实践中不断地改进模式和观测网结构及观测手段,更新的模式和观测体系又可更新分析数据,形成“再”分析数据集,通过这样循环往复的过程,地球科学在过去半个多世纪获得了迅猛的发展;不断地研制再分析数据集、改进模式和初始化,是这个发展过程的核心。
研制超高分辨率耦合地球系统模式,将地球系统各分量中的各种多源观测信息整合,不仅对解决当前地球科学的基础科学前沿问题具有重要意义,而且能够满足国家重大战略需求。清晰认知全球变化对极端天气气候灾害现象的影响机制、提高它们的预报预测精度,是全人类改进生存环境面临的共同挑战,是对打造宜居地球的有力支撑,是构建人类命运共同体在地球科学领域的具体落实。
未来,以越来越具现实世界代表性的高分辨率耦合地球系统模拟为最终目标,尚有以下几点科学技术挑战:(1)越来越高分辨率的模式,模拟更加精确的多尺度相互作用过程,要求数值方案对现实中的能量串级和逆串级有更加精准的表达能力;(2)越来越高分辨率的模式对各流体分量边界层过程的数值方案提出了更高的要求,比如更加精细的海气、陆气交界面过程描述及相关的湍流混合参数化设计,以及更具现实代表性的生物地球化学过程;(3)越来越高分辨率的预报预测需要更加平衡协调的多尺度非线性强耦合同化来制作模式初始条件和历史再分析数据集,以推动天气气候现象的机理认知和可预报性研究;(4)超高分辨率模拟和预报预测要求在更加节能、计算能力更强的的高性能计算机上发展更加高效并行的模式算子和数值计算方案;(5)超高分辨率模拟和预报预测需要时间上高频次、空间上高密集的观测资料来进行检验评估。
6 结语回顾计算流体动力学发展的百年历史,Richardson、Rossby、Charney和von Neumann等科学家的出现极大地推动了这门学科的发展,他们的学术思想、研究成果和科研经历都深刻地影响了当时自然科学理论和计算技术的发展。本文以地球系统数值模拟为例回顾了数值计算与模拟的发展历史;展望未来,该领域的研究热点将继续在模式架构,如地球系统耦合模式及其高分辨率模拟计算[45]、多时空尺度的“无缝隙”预报[46]、集合预报与非线性系统可预报性[47]、多源数据分析和“大数据”应用[48]和超级计算机发展[49-50]等方向取得突破。
| [1] |
Gad-el-Hak M. Nine decades of fluid mechanics[J]. Fluids Eng, 2016, 138(10): 100802. DOI:10.1115/1.4033961 (  0) 0) |
| [2] |
张磊成, 果晓东, 赵恩铎, 等. 计算流体力学(CFD)发展简述[C]. 北京: 北京力学会第二十三届学术年会会议论文集, 2017: 101-103. Zhang L C, Guo X D, Zhao E Y, et al. A Brief Introduction to the Development of Computational Fluid Dynamics (CFD)[C]. Beijing: Proceedings of the 23rd Annual Conference of Beijing Society of Theoretical and Applied Mechanics, 2017: 101-103. (  0) 0) |
| [3] |
杨楠山, 史立地, 张月. 20世纪后半叶以来计算流体力学的发展探究[J]. 科技经济导刊, 2017(14): 66-69. Yang N S, Shi L D, Zhang Y. Exploring the development of computational fluid dynamics[J]. Journal of Science and Technology Economy, 2017(14): 66-69. (  0) 0) |
| [4] |
王兵波, 刘海力. 计算流体力学的发展及应用研究[J]. 南方农机, 2018, 49(9): 145-150. Wang B B, Liu H L. Research on the development and application of computational fluid dynamics[J]. Southern Agricultural Machinery, 2018, 49(9): 145-150. DOI:10.3969/j.issn.1672-3872.2018.09.113 (  0) 0) |
| [5] |
余金伟, 冯晓锋. 计算流体力学发展综述[J]. 现代制造技术与装备, 2013(6): 25-26. Yu J W, Feng X F. Review of the development of computational fluid dynamics[J]. Modern Manufacturing Technology and Equipment, 2013(6): 25-26. DOI:10.16107/j.cnki.mmte.2013.06.023 (  0) 0) |
| [6] |
Richardson L F. Weather Prediction by Numerical Process[M]. Cambridge: Cambridge University Press, 1922: 236-237.
(  0) 0) |
| [7] |
廖洞贤. 国外数值天气预报的历史回顾和未来的展望[J]. 广西气象, 1985(1): 1-4. Liao D X. Historical review of foreign numerical weather prediction and future prospects[J]. Guangxi Meteorology, 1985(1): 1-4. (  0) 0) |
| [8] |
纪立人. 数值天气预报发展进程中若干亮点的回顾及其启迪[J]. 气象科技进展, 2011, 1(1): 40-43. Ji L R. Review of some highlights in the development of numerical weather forecasting and its inspiration[J]. Progress in Meteorological Science and Technology, 2011, 1(1): 40-43. (  0) 0) |
| [9] |
廖洞贤. 近10年我国数值天气预报的进展(1980—1989)[J]. 气象学报, 1990, 48(1): 17-25. Liao D X. Progress of numerical weather prediction in China in the past 10 years(1980—1989)[J]. Journal of Meteorology, 1990, 48(1): 17-25. (  0) 0) |
| [10] |
Benjamin S G, Brown J M, Brunet G, et al. 100 Years of Progress in Forecasting and NWP Applications[J]. Meteor Monographs, 2019, 59: 1-66. (  0) 0) |
| [11] |
沈学顺, 王建捷, 李泽椿, 等. 中国数值天气预报的自主创新发展[J]. 气象学报, 2020, 78(3): 451-476. Shen X S, Wang J J, Li Z C, et al. Development of independent innovation in numerical weather forecasting in China[J]. Journal of Meteorology, 2020, 78(3): 451-476. (  0) 0) |
| [12] |
Bolin B. Carl-Gustaf-Rossby in memoriam[J]. Tellus, 1957, 9: 257-258. (  0) 0) |
| [13] |
Phillips N A. Jule Charney's influence on meteorology[J]. Bull Am Meteorol Soc, 1982, 63: 492-498. DOI:10.1175/1520-0477(1982)063<0492:JCIOM>2.0.CO;2 (  0) 0) |
| [14] |
贾朋群, 张萌. 现代数值天气预报之父——记美籍匈牙利数学和气象学家冯·诺依曼[J]. 气象科技进展, 2014, 4(6): 111-114. Jia P Q, Zhang M. The father of modern numerical weather forecasting: A Memoir of Hungarian-American Mathematician and Meteorologist Von Neumann[J]. Progress in Meteorological Science and Technology, 2014, 4(6): 111-114. (  0) 0) |
| [15] |
周炎. 顾震潮学术道路及其思想研究[D]. 南京: 南京信息工程大学, 2018. Zhou Y. Study on Gu Zhenchao's Academic Path and His Thoughts[D]. Nanjing: Nanjing University of Information Science and Technology, 2018. (  0) 0) |
| [16] |
Ward M D, Back to the Future: Richardson's Multilateral Arms Race Model//Gleditsch N, eds. Lewis Fry Richardson: His Intellectual Legacy and Influence in the Social Sciences. Pioneers in Arts, Humanities, Science, Engineering, Practice[M]. [s. l. ]: Springer Cham, 2020, 27: 57-72.
(  0) 0) |
| [17] |
朱抱真. 第一讲数值天气预报的历史发展和现状[J]. 气象, 1983(6): 40-44. Zhu B Z. First lecture on the historical development and current status of numerical weather forecasting[J]. Meteorology, 1983(6): 40-44. (  0) 0) |
| [18] |
Bjerknes V. Das problem der Wettervorhersage betrachtet vom Stadtpunkt der Mechanik and Physik[J]. Meteor Z, 1904(21): 1-7. (  0) 0) |
| [19] |
NOAA. NOAA Celebrates 200 Years of Science Service and Stewardship[EB/OL]. [2007-12-31]. https://celebrating200years.noaa.gov/.
(  0) 0) |
| [20] |
Petterssen S. Weather Analysis and Forecasting[M]. New York: McGraw- Hill Academic Press, 1940: 505.
(  0) 0) |
| [21] |
Petterssen S. Motion and Motion Systems. Vol. I, Weather Analysis and Forecasting[M]. 2nd. New York: McGraw-Hill, 1956: 428.
(  0) 0) |
| [22] |
Saucier W J. Principles of Meteorological Analysis[M]. Chicago: University of Chicago Press, 1955: 438.
(  0) 0) |
| [23] |
Charney J G, Fjörtoft R, von Neumann J. Numerical integration of the barotropic vorticity equation[J]. Tellus, 1950, 2(4): 237-254. (  0) 0) |
| [24] |
Smith C D. The destructive storm of November 25—27, 1950[J]. Monthly Weather Review, 1950, 78: 204-209. (  0) 0) |
| [25] |
Smagorinsky J. General circulation experiments with the primitive equations[J]. Monthly Weather Review, 1963, 91(3): 99-164. (  0) 0) |
| [26] |
Nitta T, Saito K. Early History of the Operational Numerical Weather Prediction in Japan[R]. Washington: NOAA/NCEP, 2004.
(  0) 0) |
| [27] |
Kasahara A. A numerical experiment on the development of a tropical cyclone[J]. Journal of the Atmospheric Sciences, 1961, 18: 259-282. (  0) 0) |
| [28] |
Bushby F H, Timpson M S. A 10-level atmospheric model and frontal rain[J]. Quart J Roy Meteor Soc, 1967, 93-17. (  0) 0) |
| [29] |
Stackpole J. The NMC 9-layer Global Primitive Equation Model on a Latitude-Longitude Grid[R]. Washington: NMC Office Note in NOAA, 1978. https://repository.library.noaa.gov/view/noaa/12745.
(  0) 0) |
| [30] |
Phillips N. The Nested Grid Model[R]. Washington: NOAA, 1979.
(  0) 0) |
| [31] |
Charney J G, Phillips N A. Numerical integration of the quasi-geostrophic equations for barotropic and simple baroclinic flows[J]. Journal of the Atmospheric Sciences, 1953, 10(2): 71-99. (  0) 0) |
| [32] |
廖洞贤. 简化的两个参变数模型的图解数值预报[J]. 气象学报, 1956, 27(2): 153-166. Liao D X. Simplified graphical numerical prediction of two covariate models[J]. Journal of Meteorology, 1956, 27(2): 153-166. (  0) 0) |
| [33] |
NOAA. CSS Timelines[EB/OL]. [2020-10-31]. https://www.gfdl.noaa.gov/wp-content/uploads/pix/about_us/timeline.html/.
(  0) 0) |
| [34] |
Hibbard K A, Meehl G A, Cox P, et al. A strategy for climate change stabilization experiments[J]. Eos Transactions American Geophyssical Union, 2007, 88(20): 21-221. (  0) 0) |
| [35] |
Eyring V, Bony S, Meehl G A, et al. Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization[J]. Geoscientific Model Development, 2016, 9(5): 1937-1958. (  0) 0) |
| [36] |
Meehl G A, Coauthors. Decadal prediction: Can it be skillful?[J]. Bulletin of the American Meteorological Society, 2009, 90(10): 1467-1486. (  0) 0) |
| [37] |
Taylor K E, Stouffer R J, Meehl G A. An overview of cmip5 and the experiment design[J]. Bulletin of the American Meteorological Society, 2012, 93(4): 485-498. (  0) 0) |
| [38] |
周天军, 邹立维, 陈晓龙. 第六次国际耦合模式比较计划(CMIP6)评述[J]. 气候变化研究进展, 2019, 15(5): 445-456. Zhou T J, Zou L W, Chen X L. Review of the Sixth International Coupled Model Comparison Program (CMIP6)[J]. Advances in Climate Change Research, 2019, 15(5): 445-456. (  0) 0) |
| [39] |
Petrie R E, Denvil S, Ames S, et al. Coordinating an operational data distribution network for CMIP6 data[J]. Geoscientific Model Development, 2021, 14(1): 629-644. (  0) 0) |
| [40] |
IPCC. History of the IPCC[EB/OL]. (2021-05-30)[2022-08-31]. https://www.ipcc.ch/about/history/.
(  0) 0) |
| [41] |
IPCC. Reports. [EB/OL]. (2021-06-09)[2022-08-31]. https://www.ipcc.ch/reports.
(  0) 0) |
| [42] |
Chang P, Zhang S, Danabasoglu G, et al. An unprecedented set of high-resolution earth system simulations for understanding multiscale interactions in climate variability and change[J]. Journal of Advances in Modeling Earth Systems, 2020, 12(12): 1-52. (  0) 0) |
| [43] |
Li M K, Zhang S Q, Wu L X, et al. An examination of the predictability of tropical cyclone genesis in high-resolution coupled models with dynamically downscaled coupled data assimilation initialization[J]. Advances in Atmospheric Sciences, 2020, 37(9): 939-950. (  0) 0) |
| [44] |
Li M K, Zhang S Q, Wu L X, et al. A high-resolution Asia-Pacific regional coupled prediction system with dynamically downscaling coupled data assimilation[J]. Science Bulletin, 2020, 65(21): 1849-1858. (  0) 0) |
| [45] |
董文杰, 袁文平, 滕飞, 等. 地球系统模式与综合评估模型的双向耦合及应用[J]. 地球科学进展, 2016, 31(12): 1215-1219. Dong W J, Yuan W P, Teng F, et al. Bidirectional coupling and application of earth system models and integrated assessment models[J]. Advances in Earth Sciences, 2016, 31(12): 1215-1219. (  0) 0) |
| [46] |
王毅, 周庆亮, 代刊, 等. 全球数据处理和预报系统发展及展望[J]. 气象科技进展, 2019, 9(2): 6-10. Wang Y, Zhou Q L, Dai J, et al. Global data processing and forecast system development and outlook[J]. Progress in Meteorological Science and Technology, 2019, 9(2): 6-10. (  0) 0) |
| [47] |
朱跃建. 基于最新全球集合预报系统的可预报性评估[J]. 大气科学学报, 2020, 43(1): 193-200. Zhu Y J. Forecastability assessment based on the latest global ensemble forecast system[J]. Journal of Atmospheric Sciences, 2020, 43(1): 193-200. (  0) 0) |
| [48] |
刘帅, 陈戈, 刘颖洁, 等. 海洋大数据应用技术分析与趋势研究[J]. 中国海洋大学学报(自然科学版), 2020, 50(1): 154-164. Liu S, Chen G, Liu Y J, et al. Analysis and trend research of marine big data application technology[J]. Periodical of Ocean University of China, 2020, 50(1): 154-164. (  0) 0) |
| [49] |
吴琦, 倪裕芳, 黄小猛. 基于"神威·太湖之光"的区域海洋模式并行优化[J]. 计算机研究与发展, 2019, 56(7): 1556-1566. Wu Q, Ni Y F, Huang S M. Parallel optimization of regional ocean model based on "Shenwei-TaihuLight"[J]. Computer Research and Development, 2019, 56(7): 1556-1566. (  0) 0) |
| [50] |
宋振亚, 刘卫国, 刘鑫, 等. 海量数据驱动下的高分辨率海洋数值模式发展与展望[J]. 海洋科学进展, 2019, 37(2): 161-170. Song Z Y, Liu W G, Liu X, et al. Development and outlook of high-resolution numerical ocean model driven by massive data[J]. Advances in Marine Science, 2019, 37(2): 161-170. (  0) 0) |
2. The Key Laboratory of Physics and Oceanography, Ministry of Education, Ocean University of China, Deep Sea Frontier Research Center, Institute of Oceanography, Qingdao 266100, China;
3. Pilot National Laboratory of Marine Science and Technology (Qingdao), Qingdao 266237, China
 2022, Vol. 52
2022, Vol. 52

