生物炭是酸性土壤修复的重要新型材料，农作物秸秆是生产生物炭的重要原料，因此生物炭技术作为农作物秸秆开发利用的新型技术，既变废为宝，又节能减排；而生物炭技术应用是否可行，与农作物秸秆收集成本、热解加工成本以及炭补偿金和农业效益持续时间等密切相关，而影响农作物秸秆收集成本的关键因素是原材料运输距离^[1-3]。

农作物秸秆无论用于制作生物炭、成型燃料还是发电，在其经济效益分析过程中，农作物秸秆的收集、运输都是具有重要影响的因素^[4-5]。于晓东在秸秆发电燃料收加储运过程模拟分析中，通过分析不同模式下的成本变化趋势，对不同收购量及不同收购半径情况下秸秆收购，提出理想的优化模式，即集中收集和分散收集相结合模式。认为无论是单纯的集中收集加工模式还是分散的收集加工模式，从收集成本考虑，都不是理论上的最佳模式，建议应该在距离电厂几十公里范围内适当设几个收购点，同时，电厂内的料场也应该设置燃料的破碎及打包设备，便于收购电厂周边近距离的秸秆，这样可以有效降低燃料成本^[6]。马放等在秸秆能源化工程原料运输半径经济和环境评价中对原料收购半径经济评价模型、原料收购半径环境评价模型进行了评价，并提出了秸秆能源转化密度的概念，通过研究表明在哈尔滨地区建设沼气、乙醇、热电联产和成型燃料工程时，运输半径分别为37、35、22和4 km左右，此时工程的单位利润最大^[7]。

邢爱华在生物质资源收集过程成本、能耗及环境影响分析中，建立了描述秸秆收集过程成本、能耗和污染物排放的数学模型，讨论了压缩对秸秆收集成本、能耗及环境的影响，并对收集过程的成本和能耗进行了敏感性分析，并通过数据分析获知，压缩后的运输成本占不压缩运输成本的1/3，但同时增加了压缩成本^[8]。朱金陵等在玉米秸秆成型燃料生命周期评价中从能源消耗和环境排放出发，分析了玉米秸秆生长、运输、压缩成型及成型燃料运输、燃烧利用等过程，建立了秸秆成型燃料的生命周期能源消耗、环境排放分析模型。研究表明，秸秆运输、压缩成型、燃料运输等环节都需要消耗能源，压缩成型能耗占总能耗95.2%，但压缩后密度提高，便于运输和储存，可以高效利用^[9]。

同时生物炭经济可行性与各国实际情况密切相关，对于发达国家(地区)和发展中国家(地区)，劳动力成本、机械、运输和能源的经济成本不同，其生物炭的经济性完全不同。因此对发达国家(地区)与其他非发达国家(地区)在农作物秸秆生产生物炭的经济性评估方面应该分别考虑。

通过以上分析发现，相关学者虽然在农作物秸秆生物炭生产影响因素或者农作物秸秆收集运输方面进行了相关研究，但是均没有建立一个广泛适用的农作物秸秆收购半径和收集站设置计算方法。为便于政府和企业决策，本文通过分析影响农作物秸秆生物炭生产基地建设的相关参数，建立了农作物秸秆收购半径与农作物秸秆收集站位置设置的数学模型，实现节约运输成本、优化运输模式、提高运输效率。

1 农作物秸秆收购半径数学模型建立 1.1 方法和参数

为了便于分析，采用盈亏平衡分析方法(I=P×Q-VC×Q-FC)^[10-11]，对影响生物炭生产基地的销售收入、变动成本和固定成本作如下归类：

(1) 单位质量农作物秸秆转化为生物炭的相关销售总收入为a；

(2) 单位质量单位距离农作物秸秆的运输总费用为b；

(3) 单位质量农作物秸秆变动总成本为c；

(4) 生物炭生产固定资产总投资为d。

上述参数提到的秸秆的质量可由农作物秸秆分布的面密度ρ(即单位面积秸秆的质量)与秸秆的分布面积确定。本文假定秸秆均匀分布，即ρ为常数。

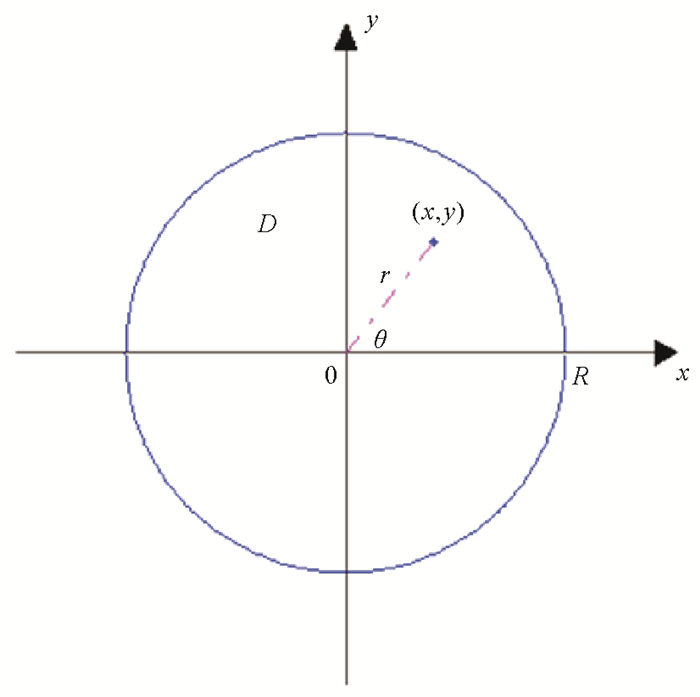
1.2 农作物秸秆收购半径数学模型建立

设秸秆均匀分布在圆盘形区域D内，半径为R。生物炭基地位于圆心，如图 1所示以圆心为原点建立坐标系。区域内任意一点(x, y)处的农作物秸秆到生产基地距离为$r=\sqrt{{{x}^{2}}+{{y}^{2}}}$，取值范围为[0, R]。

根据盈亏平衡分析方程，列出利润函数：

$ \begin{align} &I\left( R \right)=a\rho \text{ }\!\!\pi\!\!\text{ }{{R}^{2}}-c\rho \text{ }\!\!\pi\!\!\text{ }{{R}^{2}}-\iint\limits_{D}{b\sqrt{{{x}^{2}}+{{y}^{2}}}\rho \text{d}S}-d= \\ &\ \ \ \ \ \ \ \ \ \ \ \left( a-c \right)\rho \text{ }\!\!\pi\!\!\text{ }{{R}^{2}}-\int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{\text{d}\theta }\int_{0}^{R}{b\rho r\cdot r\text{d}r}-d= \\ &\ \ \ \ \ \ \ \ \ \ \ \left( a-c \right)\rho \text{ }\!\!\pi\!\!\text{ }{{R}^{2}}-\frac{2}{3}b\rho \text{ }\!\!\pi\!\!\text{ }{{R}^{3}}-d, \\ \end{align} $

为求最大利润，令

$ I'\left( R \right) = 2\left( {a - c} \right)\rho {\rm{ \mathsf{ π} }}R - 2b\rho {\rm{ \mathsf{ π} }}{R^2} = 0, $

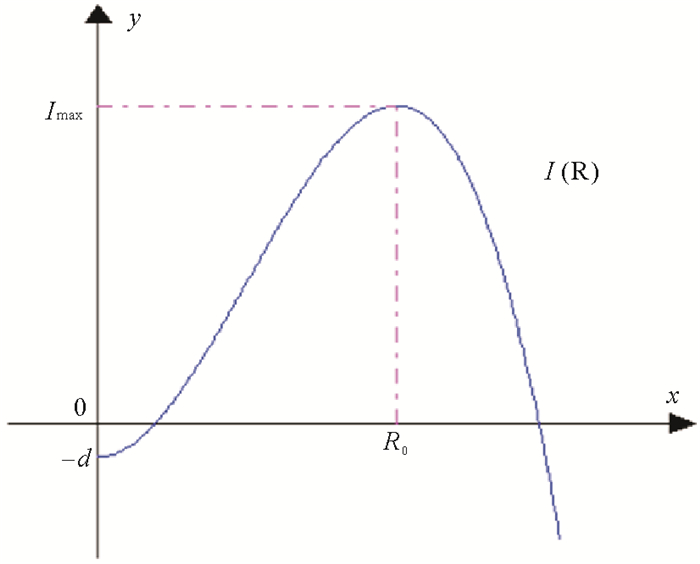
得I(R)的最大值点为(见图 2)

$ {R_0} = \frac{{a - c}}{b}, $

从而，最大利润为

$ {I_{\max }} = \frac{1}{3}\rho {\rm{ \mathsf{ π} }}\frac{{{{\left( {a - c} \right)}^3}}}{{{b^2}}} - d。$

通过以上分析发现，决定生物炭生产基地农作物秸秆收购半径R₀的关键因素是单位质量农作物秸秆带来的收益和单位质量单位距离农作物秸秆运输费用，与农作物秸秆面密度ρ大小无关，而最大收益I_max与农作物秸秆面密度ρ密切相关。

2 农作物秸秆收集站模型的建立

农作物秸秆具有松散、密度低、形状不规则等特点，在进行生物炭加工前需要预处理，形成符合生物炭炉要求的大小尺寸和密度，既有利于工厂化生产又提高了工作效率。而这一过程的实施地点对生产成本具有重大影响，即将这一预处理过程由“在生物炭生产基地进行”移到“农作物秸秆收集站进行”，这样为后续由收集站运输原料到生物炭生产基地节约了大量运输成本，因此收集站设置在离生物炭生产基地多远非常重要。

由于秸秆分布均匀，故ρ为常数，不妨设ρ=1。运输单位面积(等同于单位质量)的秸秆单位距离所需的运输费用为b。收集站将秸秆压缩打包，从而运输单位面积单位距离压缩打包后秸秆所需运输费用降为q。令$\theta =\frac{q}{b}$，显然0＜θ＜1。如果要在D上建一个或多个收集站，应如何选址才会使收集运输D上的全部秸秆至生产基地所需的总费用最低。

2.1 设立一个收集站的最优选址模型

不失一般性，设收集站建在x轴上的点(h, 0)处，其中0≤h≤R。此时，运输秸秆至生产基地有如下两种方式：(a)将平面中的点(x, y)处单位面积的秸秆直接运至生产企业的费用为$b\sqrt{{{x}^{2}}+{{y}^{2}}}$；(b)将平面中的点(x, y)处单位面积的秸秆先经过位于(h, 0)处的收集站再运至生产基地的费用为 $b\sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+qh$。

易知，以上两种运输方式费用相等的点(x, y)满足：

$ b\sqrt {{x^2} + {y^2}} = b\sqrt {{{\left( {x - h} \right)}^2} + {y^2}} + qh, $

即

$ \sqrt {{x^2} + {y^2}} - \sqrt {{{\left( {x - h} \right)}^2} + {y^2}} = \theta h, $

此为以(0, 0)和(h, 0)为焦点的双曲线的一个分支。令$C=\frac{h}{2} $，$A=\frac{\theta h}{2}$，$B=\sqrt{{{C}^{2}}-{{A}^{2}}}$=$\frac{h}{2}\sqrt{1-{{\theta }^{2}}}$即得双曲线的标准方程：

$ \frac{{{{\left( {x - \frac{h}{2}} \right)}^2}}}{{\frac{{{\theta ^2}{h^2}}}{4}}} - \frac{{{y^2}}}{{\frac{{\left( {1 - {\theta ^2}} \right){h^2}}}{4}}} = 1\left( {x > \frac{h}{2}} \right)。$

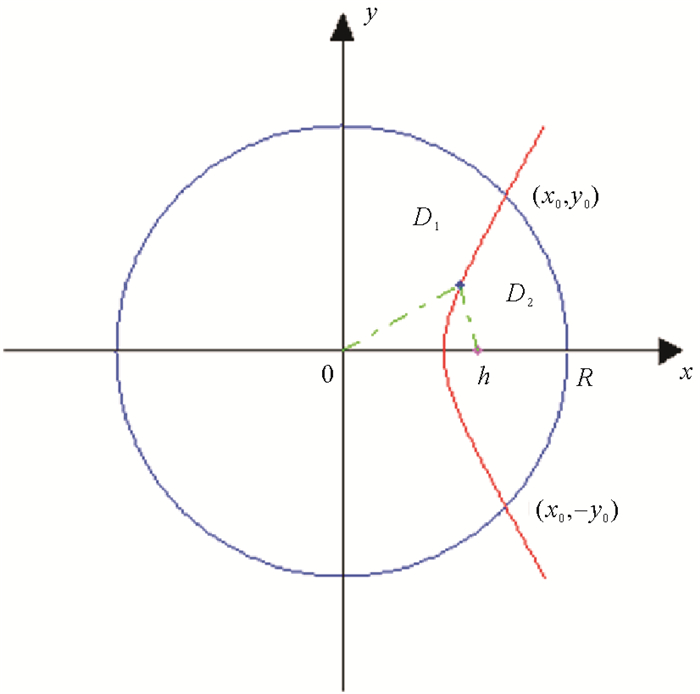
如图 3所示，圆盘D被上述曲线分成D₁和D₂两部分，其中D₁上的点(x, y)按方式(a)运输的费用 $b\sqrt{{{x}^{2}}+{{y}^{2}}}$小于按方式(b)运输的费用 $b\sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+qh$；D₂上的点(x, y)按方式(a)运输的费用$b\sqrt{{{x}^{2}}+{{y}^{2}}}$大于按方式(b)运输的费用$b\sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+qh$。从而在增设一个收集站的情况下，收集运输D上全部秸秆至生产基地所需的总费用为

$ \begin{align} &f\left( h \right)=\iint\limits_{{{D}_{1}}}{b\sqrt{{{x}^{2}}+{{y}^{2}}}\text{d}S}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \iint\limits_{{{D}_{2}}}{\left( b\sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+qh \right)\text{d}S}= \\ &\ \ \ \ \ \ \ \ \ \ \ \iint\limits_{D\backslash {{D}_{2}}}{b\sqrt{{{x}^{2}}+{{y}^{2}}}\text{d}S}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \iint\limits_{{{D}_{2}}}{\left( b\sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+qh \right)\text{d}S}= \\ &\ \ \ \ \ \ \ \ \ \ \ \iint\limits_{{{D}_{2}}}{\left( b\sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+qh-b\sqrt{{{x}^{2}}+{{y}^{2}}} \right)\text{d}S}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \iint\limits_{D}{b\sqrt{{{x}^{2}}+{{y}^{2}}}\text{d}S}= \\ &\ \ \ \ \ \ \ \ \ \ \ b\iint\limits_{{{D}_{2}}}{\left( \sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+\theta h-\sqrt{{{x}^{2}}+{{y}^{2}}} \right)\text{d}S}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \frac{2}{3}\pi b{{R}^{3}}, \\ \end{align} $

记

$ g\left( h \right)=\iint\limits_{{{D}_{2}}}{\left( \sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+\theta h-\sqrt{{{x}^{2}}+{{y}^{2}}} \right)\text{d}S}, $

从而

$ f\left( h \right) = bg\left( h \right) + \frac{2}{3}{\rm{ \mathsf{ π} }}b{R^3}。$

收集站的最优选址问题归结为选取合适的h值，使得总费用f(h)最低。由f(h)和g(h)单调性相同，此问题归结为求g(h)的最小值点。

由方程组

$ \left\{ \begin{array}{l} {x^2} + {y^2} = {R^2}\\ \frac{{{{\left( {x - \frac{h}{2}} \right)}^2}}}{{\frac{{{\theta ^2}{h^2}}}{4}}} - \frac{{{y^2}}}{{\frac{{\left( {1 - {\theta ^2}} \right){h^2}}}{4}}} = 1\;\;\;\;\;\;\left( {x > \frac{h}{2}} \right) \end{array} \right. $

得双曲线与圆盘D边界交点为(x₀, y₀)和(x₀, -y₀)，其中

$ \left\{ \begin{array}{l} {x_0} = \frac{{\left( {1 - {\theta ^2}} \right)h}}{2} + \theta R\\ {y_0} = \frac{{\sqrt {1 - {\theta ^2}} }}{2}\sqrt {4{R^2} - 4\theta hR - \left( {1 - {\theta ^2}} \right){h^2}} \end{array} \right., $

从而

$ \begin{array}{l} g\left( h \right) = \\ \int_{ - {y_0}}^{{y_0}} {{\rm{d}}y} \int_{\alpha \left( y \right)}^{\beta \left( y \right)} {\left( {\sqrt {{{\left( {x - h} \right)}^2} + {y^2}} + \theta h - \sqrt {{x^2} + {y^2}} } \right){\rm{d}}x} , \end{array} $

其中对于-y₀＜y＜y₀，

$ \left\{ \begin{array}{l} \alpha \left( y \right) = \frac{h}{2} + \frac{{\theta h}}{2}\sqrt {\frac{{{y^2}}}{{\frac{{\left( {1 - {\theta ^2}} \right){h^2}}}{4}}} + 1} \\ \beta \left( y \right) = \sqrt {{R^2} - {y^2}} \end{array} \right.。$

考虑到上述积分中被积函数和积分区域的复杂性，结合数值积分的方法讨论g(h)的最小值点。

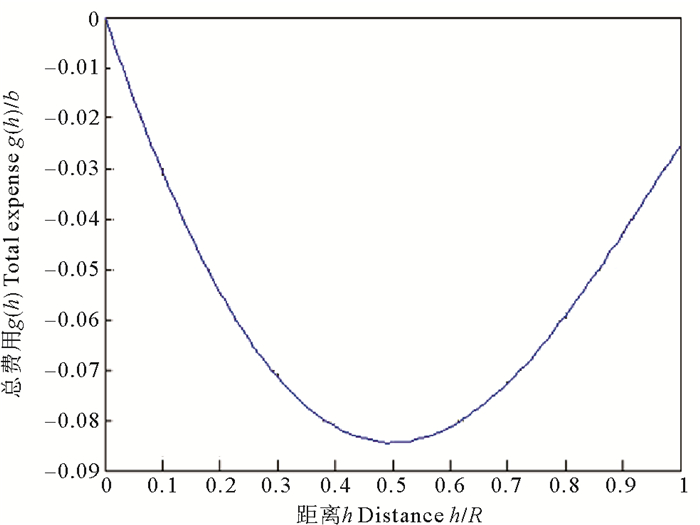
取R=1，θ=0.5，h的步长为0.01R。用数值积分近似计算g(h)并绘制其图像(见图 4)。

此时，g(h)的最小值点h₀=0.49，最小值g(h₀)=-0.084 5，总运费f(h₀)=bg(h₀)+$\frac{2}{3}$πb R³=2.009 9b，相对于不设置收集站时的运费$\frac{2}{3}$πb R³=2.094 4b，费用的节省比例

$ \omega = \frac{{ - bg\left( {{h_0}} \right)}}{{\frac{2}{3}{\rm{ \mathsf{ π} }}b{R^3}}} = 4.03\% 。$

在表 1中，针对不同θ值，给出在最优位置增设收集站时，节省的费用比例。取R=1。

2.2 设立多个收集站的最优选址模型

如果要在D上建n个收集站(n≥2)，应如何选址才会使收集运输D上的全部秸秆至加生产基地所需的总费用最低？

如果n个收购站可在D上自由设置，则此问题的计算复杂度较高。为此我们仅在如下假设条件下，考虑上述问题的最优解。

模型假设：n个收集站均匀分布在生产基地周围，即收集站到生产基地的距离均相等(设距离为h)，且相邻两个收集站与生产基地连线的夹角相等(等于 $\frac{2\pi }{n}$，见图 5)。

不失一般性，设其中一个收集站位于x轴。利用相邻两个收集站的中垂线，可将区域D划分成相等的n个扇形区域(每个扇形的圆心角为$\frac{2\pi }{n}$)。根据就近原则，每个扇形区域上的秸秆，或者直接运到生产基地，或者先经过此扇形区域上的收集站再运输至生产基地。因此，对多个收集站选址问题的研究只需针对其中一个扇形讨论即可。将一个扇形区域记为D₀。类似于2.1中的讨论，D₀被双曲线

$ \frac{{{{\left( {x - \frac{h}{2}} \right)}^2}}}{{\frac{{{\theta ^2}{h^2}}}{4}}} - \frac{{{y^2}}}{{\frac{{\left( {1 - {\theta ^2}} \right){h^2}}}{4}}} = 1\;\;\;\;\;\;\;\left( {x > \frac{h}{2}} \right), $

分成了D₀₁和D₀₂两部分，其中D₀₁上的秸秆直接运至生产基地费用较低，D₀₂上的秸秆先经过收集站再运至生产基地费用较低。根据交点位置分为图 6和7两种情况。

可通过双曲线与区域D边界的交点坐标(x₀, y₀)判定出现的是情形1还是情形2。具体来说：当${{x}_{0}}<R\text{cos}\frac{\pi }{n}$，即$h<\frac{2R(\cos\frac{\pi }{n}-\theta )}{1-{{\theta }^{2}}}$时，出现情形1；当${{x}_{0}}\ge R\text{cos}\frac{\pi }{n}$，即$ h\ge \frac{2R(\cos\frac{\pi }{n}-\theta )}{1-{{\theta }^{2}}}$时，出现情形2。

类似于2.1的讨论，收集运输D₀上的全部秸秆至生产基地所需的费用为：

$ \begin{align} &{{f}_{0}}\left( h \right)=\iint\limits_{{{D}_{01}}}{b\sqrt{{{x}^{2}}+{{y}^{2}}}\text{d}S}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \iint\limits_{{{D}_{02}}}{\left( b\sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+qh \right)\text{d}S}= \\ &\ \ \ \ \ \ \ \ \ \ \ b\iint\limits_{{{D}_{02}}}{\left( \sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+\theta h-\sqrt{{{x}^{2}}+{{y}^{2}}} \right)\text{d}S}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \frac{2}{3n}\pi b{{R}^{3}}, \\ \end{align} $

记

$ \begin{align} &{{g}_{0}}\left( h \right)= \\ &\iint\limits_{{{D}_{02}}}{\left( \sqrt{{{\left( x-h \right)}^{2}}+{{y}^{2}}}+\theta h-\sqrt{{{x}^{2}}+{{y}^{2}}} \right)\text{d}S}, \\ \end{align} $

从而

$ {f_0}\left( h \right) = b{g_0}\left( h \right) + \frac{2}{{3n}}{\rm{ \mathsf{ π} }}b{R^3}, $

因此，在设置n个收购站时，收集运输D上的全部秸秆至生产基地所需的总费用为：

$ f\left( h \right) = n{f_0}\left( h \right) = nb{g_0}\left( h \right) + \frac{2}{3}{\rm{ \mathsf{ π} }}b{R^3}。$

对于情形1：双曲线与扇形区域D₀的半径相交，如图 6所示，设区域D₀₂边界的四个顶点坐标分别为(x₁, y₁)、(x₁, -y₁)、(x₂, y₂)、(x₂, -y₂)，由方程组

$ \left\{ \begin{array}{l} y = \tan \frac{{\rm{ \mathsf{ π} }}}{n} \cdot x\\ \frac{{{{\left( {x - \frac{h}{2}} \right)}^2}}}{{\frac{{{\theta ^2}{h^2}}}{4}}} - \frac{{{y^2}}}{{\frac{{\left( {1 - {\theta ^2}} \right){h^2}}}{4}}} = 1\;\;\;\;\;\;\;\left( {x > \frac{h}{2}} \right), \end{array} \right. $

解得

$ \left\{ \begin{array}{l} {x_1} = \frac{{\left( {1 - {\theta ^2}} \right)\left( {1 + \theta \sec \frac{{\rm{ \mathsf{ π} }}}{n}} \right)h}}{{2 - 2{\theta ^2}{{\sec }^2}\frac{{\rm{ \mathsf{ π} }}}{n}}};\\ {y_1} = \frac{{\left( {1 - {\theta ^2}} \right)\left( {\sin \frac{{\rm{ \mathsf{ π} }}}{n} + \theta \tan \frac{{\rm{ \mathsf{ π} }}}{n}} \right)h}}{{2\cos \frac{{\rm{ \mathsf{ π} }}}{n} - 2{\theta ^2}\sec \frac{{\rm{ \mathsf{ π} }}}{n}}}; \end{array} \right. $

由方程组

$ \left\{ \begin{array}{l} y = \tan \frac{{\rm{ \mathsf{ π} }}}{n} \cdot x\\ {x^2} + {y^2} = {R^2}\;\;\;\;\;\;\;\;\;\left( {x > \frac{h}{2}} \right), \end{array} \right. $

解得

$ \left\{ \begin{array}{l} {x_2} = R\cos \frac{{\rm{ \mathsf{ π} }}}{n}\\ {y_2} = R\sin \frac{{\rm{ \mathsf{ π} }}}{n} \end{array} \right.。$

从而当 $h<\frac{2R(\cos\frac{\pi }{n}-\theta )}{1-{{\theta }^{2}}}$时，

$ \begin{array}{l} {g_0}\left( h \right) = \int_{ - {y_1}}^{{y_1}} {{\rm{d}}y} \int_{\alpha \left( y \right)}^{\beta \left( y \right)} {\left( {\sqrt {{{\left( {x - h} \right)}^2} + {y^2}} + \theta h - } \right.} \\ \left. {\sqrt {{x^2} + {y^2}} } \right){\rm{d}}x + 2\int_{{y_1}}^{{y_2}} {{\rm{d}}y} \int_{\gamma \left( y \right)}^{\beta \left( y \right)} {\left( {\sqrt {{{\left( {x - h} \right)}^2} + {y^2}} + \theta h - } \right.} \\ \left. {\sqrt {{x^2} + {y^2}} } \right){\rm{d}}x, \end{array} $

其中

$ \gamma \left( y \right) = \cot \frac{{\rm{ \mathsf{ π} }}}{n} \cdot y。$

对于情形2：双曲线与扇形区域D₀的弧相交，如图 7所示，交点坐标为(x₀, y₀)和(x₀, -y₀)。

从而当 $h\ge \frac{2R(\cos\frac{\pi }{n}-\theta )}{1-{{\theta }^{2}}}$时，

$ \begin{array}{l} {g_0}\left( h \right) = \int_{ - {y_0}}^{{y_0}} {{\rm{d}}y} \int_{\alpha \left( y \right)}^{\beta \left( y \right)} {\left( {\sqrt {{{\left( {x - h} \right)}^2} + {y^2}} + \theta h - } \right.} \\ \left. {\sqrt {{x^2} + {y^2}} } \right){\rm{d}}x。\end{array} $

同样本文结合数值积分方法讨论此最优选址问题。

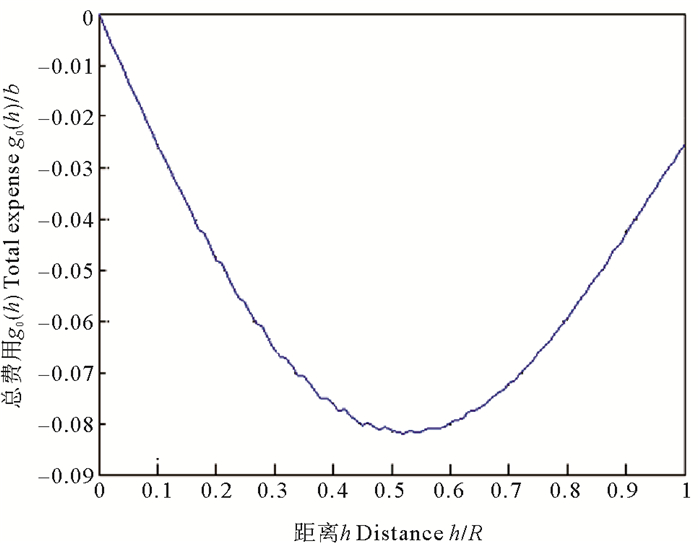
如增设n=5个收集站，取R=1，θ=0.5，h的步长为0.01R。用数值积分近似计算g₀(h)并绘制其图像(见图 8)。

此时，g₀(h)的最小值点h₀=0.52，最小值g₀(h₀)=-0.082 0，总运费f(h₀)=nb g₀(h₀)+$\frac{2}{3}$πb R³=1.684 4b，相对于不设置收集站时总运费的节省比例

$ \omega = \frac{{ - nbg\left( {{h_0}} \right)}}{{\frac{2}{3}{\rm{ \mathsf{ π} }}b{R^3}}} = 19.57\% 。$

在表 2中，本文针对不同n值，给出在最优位置增设收集站时，节省的费用比例。取R=1，θ=0.5。

3 结果与分析

(1) 农作物秸秆分布广、能源密度低、收集成本高，因此农作物秸秆收集运输成本对实施农作物秸秆生物炭技术影响很大，因此以盈亏平衡分析(I=P×Q-VC×Q-FC)为基础，通过数学工具建立了生物炭生产基地农作物秸秆收购半径数学模型，获得最优半径为R₀=$\frac{a-c}{b}$。分析发现，农作物秸秆收购最优半径R₀与农作物秸秆面密度ρ无关，因此无论生物炭生产基地设在哪个农业产区，其获得最大利润时农作物秸秆收购半径大小是由参数a, b, c决定的，目前我国农业主产区参数a, b, c值相近，经过调研赋值后，半径R₀可计算为常数，因此R₀可以作为我国北方实施农作物秸秆生物炭技术的统一参考值。

(2) 通过对生物炭生产基地建设参数分析发现，提高运输效率是在管理过程中节约成本的唯一可控途径。农作物秸秆经过打包压缩后再运输，节约了运输成本。压缩是农作物秸秆进入炭炉之前的必须程序，但是压缩时序即是运输前压缩还是运输到生物炭生产基地后压缩，对整个运输成本产生重要影响。本文将压缩提前到运输前实施，即依托村镇为单位实施压缩程序，将原先在生物炭生产基地进行的程序前移到村镇收集站实施，大幅度提高了运输效率。当农作物秸秆经收集站运输至生产基地费用占直接运输至生产基地费用50%时，即θ=0.5，收集站位置h为0.49R，节约费用比例为4.03%；随着运输效率的提高，节约比例逐步增加，当经收集站运输费用占直接运输费用10%时，收集站位置h为0.59R，节约比例增至11.51%。

(3) 在对称性假设的前提下，我们进一步讨论了增设n个收集站的最优选址问题。从结果看，当n≤4时，总运费的节省比例与收集站的个数n近似正比。而当n≥5时，每增加一个收集站所能增加的总运费节省比例效率开始降低。这些结果的取得对于在实际问题中如何增设收集站以提高秸秆的收购效率提供了理论依据。

4 模型改进与推广

本文就秸秆均匀分布在圆盘形区域的理想情形，讨论了生物炭生产基地和收集站的最优选址问题。文中所建立的模型可在以下几个方面进行改进和推广：

(1) 秸秆的分布区域是任意的平面有界区域，如：矩形区域。

(2) 秸秆的分布密度不均匀。

(3) 农作物秸秆运送到生物炭生产基地或收集站的距离不是直线距离，而是沿一定的道路交通网进行计算。

(4) 考虑农作物的的周期性、秸秆回收设备的折旧、投资的时间成本等因素对利润函数的影响。