海啸是造成人员伤亡和经济损失最严重的自然灾害之一。在1987年第42届联合国大会上,海啸被确定为“国际减轻灾害十年”活动的自然灾害之一。从地理位置和历史海啸记录角度分析,我国沿海地区存在受到海啸危害的可能性。海啸地震容易发生在地壳运动剧烈的海沟地区和年轻的地壳造山带[1]。中国南海与菲律宾板块相邻且与马尼拉海峡邻接,其地质构造容易发生海啸。最近的研究[2]认为,在南海海槽附近将会发生9.0级的地震,不仅会影响南海海域,而且在东海和黄海也将产生影响。根据历史海啸记录,公元前47年在山东莱州湾发生了我国有记录以来最早的一次海啸;1498年9月20日日本四国东南海域发生8.6级地震引起的大海啸,波及到我国东北海域;1992年1月4—5日在海南岛西南海域发生弱群震,位于榆林港的验潮站记录到最大海啸波振幅达78 cm[3]。据统计,截止到公元1966年,我国近海发生25次海啸,其中破坏性海啸8~9次[4]。中国沿海地势较低,即使震级中等的海啸也将会对中国沿海产生影响。沿海城市的城市建设和经济发展都很发达,人口密度高,一旦海啸发生将会对社会发展造成严重损失,影响经济发展和国家建设。
国外学者进行海啸危险性灾害分析开始于1980年代。Rikitake与Aida[5]利用概率方法分析了2000—2010年间日本岛屿遭受某阈值的海啸波袭击的可能性。Annaka与Satake等[6]提出通过构造逻辑树的方法建立了海啸波高和超越概率的关系。Choi等[7]用对数正态分布拟合得到的海啸波高,从而获得韩国沿海各地点的海啸波高统计分布特点。Geist等[8]根据地震灾害分析方法提出了海啸灾害分析方法,当研究地点有足够的海啸爬高数据时,对发生频次与爬高进行经验分析;当历史海啸爬高数据不足时,则采用蒙特卡罗模拟方法结合海啸传播数值模型计算爬高。Parsons等[9]结合500 a的海啸爬高观测数据与数值模型结果对加勒比地区绘制了海啸灾害图。González等[10]结合海啸淹没模型与地震灾害概率评估方法提出了海啸灾害概率评估方法,并在俄勒冈州的海边地区建立了第一张海啸淹没概率图。Liu等[2]采用数值计算模型模拟了中国南海附近的假设海啸,并结合海啸发生概率推导海啸风险概率公式,据此计算中国南海沿海重要城市在未来100 a内海啸波高超过2.0 m和1.0~2.0 m之间的概率。Liu等[11]计算了一次震级8.0发生在马尼拉俯冲带的假设海啸的传播时间和海啸振幅分布,并对中国南海建立海啸预警预报提出了技术建议。
全球矩心矩张量(Global Centroid Moment Tensor,Global CMT)是5.5级以上的全球地震目录,记录了自1976年以来各次历史地震的详细参数,包括发生时间、震源深度、震源位置、矩心矩张量、倾斜角等[12]。本文采用Global CMT中的历史地震记录,筛选可能对中国沿海产生海啸威胁的历史地震,利用Method of Splitting Tsunami (MOST)海啸传播模型模拟这些历史地震可能引发的海啸增水。目前有许多海啸数值模式,本文采用美国国家海洋大气管理局海啸研究中心采用的MOST模型,该模型被40余次的实际海啸验证其计算的准确与快速[13-14]。
采用的历史地震记录从1962年开始,资料年限很短且每年发生在太平洋7级及以上的地震次数并不多,采用复合分布来估计长期地震矩震级及离岸海啸振幅的重现值。
复合分布主要解决资料年限较短的问题。Feller[15]在Neyman[16]等研究的基础上提出的新型传染分布的基础上构造出适用于描述传染行为的复合分布族。马逢时与刘德辅[17]提出复合极值理论解决了资料年限较短时分布拟合较差的问题,其通过构造Poisson-Gumbel复合极值分布推算了台风海况下多年一遇设计波高。董胜等[18]、Wang等[19]分别采用复合极值分布理论研究了风暴潮或台风海况下海浪波高的重现值。
本文简要介绍了MOST海啸传播模型,据此模拟历史地震引发的海啸增水过程,对历史地震的发生频次进行统计分布,确定了适于中国沿海离岸海啸振幅统计分析的模型,对中国沿海的离岸海啸振幅进行分布拟合,计算其长期重现值并给出重现期为1 000和2 500 a时中国沿海海啸振幅超过某阈值的海域。
1 MOST海啸传播模型MOST模型采用非线性浅水方程(Nonlinear Shallow-Water Equation,NSW)研究海啸波的演变过程[20]。描述海啸演变过程的浅水方程如下:
| $ \left\{ \begin{align} & \ \ {{h}_{t}}+{{\left( uh \right)}_{x}}+{{\left( vh \right)}_{y}}=0 \\ & {{u}_{t}}+u{{u}_{x}}+v{{u}_{y}}+g{{h}_{x}}=g{{d}_{x}} \\ & {{v}_{t}}+u{{v}_{x}}+v{{v}_{y}}+g{{h}_{y}}=g{{d}_{y}} \\ \end{align} \right., $ | (1) |
初始条件为
| $ \left\{ \begin{align} & h\left( x, y, 0 \right)={{h}_{0}}\left( x, y \right) \\ & u\left( x, y, 0 \right)={{u}_{0}}\left( x, y \right) \\ & v\left( x, y, 0 \right)={{v}_{0}}\left( x, y \right) \\ \end{align} \right., $ | (2) |
式中:h=η (x, y, t)+d (x, y, t),η (x, y, t)为波浪振幅,d (x, y, t)为静水深;u (x, y, t)和v (x, y, t)分别为向岸方向和沿岸方向的深度平均速度;g为重力加速度。
| $ \left\{ \begin{array}{l} \;\;\;\;{h_t}+{\left( {uh} \right)_x}=0\\ {u_t}+u{u_x}+g{h_x}=g{d_x}\\ \;\;\;\;{v_t}+u{v_x}{\rm{=}}0 \end{array} \right., $ | (3) |
与
| $ \left\{ \begin{array}{l} \;\;\;\;{h_t}+{\left( {vh} \right)_y}=0\\ {v_t}+v{v_y}+g{h_y}=g{d_y}\\ \;\;\;\;{u_t}+v{u_y}{\rm{=}}0 \end{array} \right.。$ | (4) |
采用黎曼不变量表示出以上两式,式(3)可表示为
| $ \left\{ \begin{array}{l} {p_t}+{\lambda _1}{p_x}=g{d_x}\\ {q_t}+{\lambda _2}{q_x}{\rm{=}}g{d_x}\\ \;\;v'+{\lambda _3}v'=0 \end{array} \right., $ | (5) |
式中:p、q以及v′为黎曼不变量,p=u+2(gh)1/2,q=u-2(gh)1/2,v′=v;λ1、λ2以及λ3 为系统特征值,λ1=u+(gh)1/2,λ2=u-(gh)1/2,λ3=u。实际上,3个特征值λ1、λ2以及λ3为特征线族的斜率集合。Titov和Synolakis[22]采用中心有限差分算法解方程(5)得到黎曼不变量p、q、v′,进而表示出h、u、v。
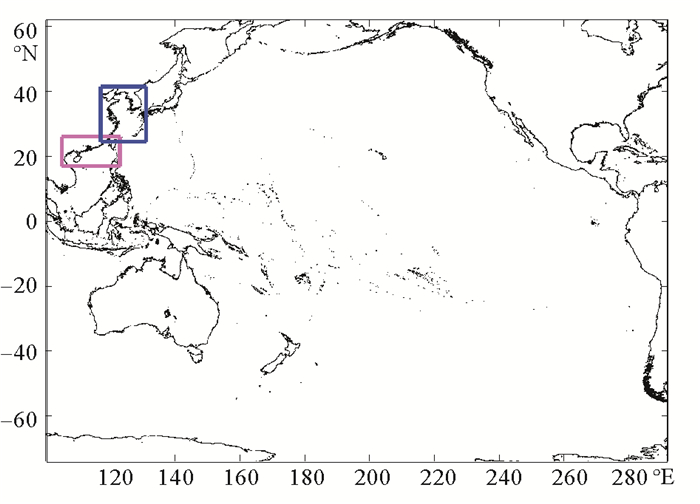
2 历史地震引起的海啸增水收集Global CMT地震目录中的7级及以上的可能对中国沿海产生海啸威胁的292次历史地震数据。采用Okada弹性空间地震位移模型[23]模拟计算各历史地震产生的海底变形,作为MOST海啸传播模型的初始条件,模拟各历史地震可能引发的海啸传播过程。计算网格采用两层嵌套形式。粗网格来自ETOPO1地形模型,网格分辨率为4 arc min,网格范围为100.0167 °E ~ 67.9833°W,73.9598°S ~ 62.0001°N。在中国沿海区域采用细网格,计算网格精度为1 arc min,网格范围如图 1中的蓝色方框和玫红色方框的范围。根据CFL条件,4 arc min的粗网格和1 arc min的细网格对应的时间步长分别设为8和3 s。基于MOST模型计算结果,对中国沿岸50 m水深处各历史地震产生的海啸振幅进行统计分析。
|
图 1 计算区间地形及网格设置 Fig. 1 Bathymetry of calculation region and grid setting |
本文采用Poisson分布描述7级及以上的历史地震每年发生频次的概率分布。Global CMT地震目录中自1976—2013年发生271次震级7级及以上的地震,平均每年发生次数λ=7.131 6,参数估计置信区间为[6.282 5, 7.980 7]。图 2显示7级及以上地震发生频率的直方图及Poisson分布拟合情况。对其进行K-S检验,h=0通过检验,说明采用Poisson分布拟合7级及以上的地震的发生频次概率分布是可行的。

|
图 2 7级及以上地震发生频次直方图与Poisson分布拟合 Fig. 2 Histogram of earthquakes occurrence times with Magnitude over 7 and the Poisson distribution fitting |
研究表明2011年3月11日日本地震的重现期约为500~1 200 a[24],本文分别假设此海啸的重现期为500、1 000 a。采用Poisson-Lognormal (P-L)分布、Poisson-Weibull (P-W)分布及Poisson-Generalized Extreme Value (P-GEV)分布拟合香港附近海域50 m水深处某点海啸振幅,其超越概率如图 3。

|
图 3 海啸振幅分布的超越概率图 Fig. 3 Exceedance probability of tsunami amplitude |
比较图 3(a)与(b)发现,当随机变量数值较小时,三种分布的拟合结果相差并不明显;当随机变量取极大值时,相比于Weibull分布与GEV分布,Lognormal分布的计算结果与实测值最接近。而且当2011年3月11日的日本海啸重现期设为500 a时,Lognormal分布的拟合结果优于此海啸重现期设置为1 000 a的情况。计算此次海啸重现期分别设置为1 000和500 a时,采用P-L分布、P-W分布及P-GEV分布拟合实测值,同时计算了对应于不同重现期的海啸增水重现值,结果如表 1。
|
|
表 1 海啸振幅不同重现期对应的重现值 Table 1 Return values of tsunami amplitude corresponding to different return periods |
表 1显示了当2011年3月11日日本海啸的重现期分别假设为1 000和500 a时采用复合分布拟合历史地震引发的海啸增水时不同重现期对应的重现值。香港地区附近水深50 m处某点模拟得到的海啸增水为12.10 cm。由表 1可见,当假设2011年3月11日日本海啸的重现期为1 000 a时,P-GEV分布高估了不同重现期所对应的重现值;P-W分布低估了其重现值(7.35 cm),而P-L分布的估计值更接近计算结果,但也存在一定程度的高估(17.06 cm)。从上述分析发现,假设2011年日本海啸的重新期是1 000 a得到的重现值计算结果,P-L分布估计偏高,而P-W分布估计偏低。当假设2011年3月11日日本海啸的重现期为500 a时,由P-L分布得到的500 a一遇的海啸振幅为13.03 cm,与计算的结果比较接近。P-W分布的重现值为7.23 cm,小于计算值。由此可见,当假设2011年3月11日日本海啸重现期为500 a时,采用P-L分布拟合历史地震引发的海啸增水并计算长期重现值时计算结果比较准确。
2.3 中国沿岸海啸振幅的重现值通过对香港地区的海啸增水分析知当假设极大值即2011年3月11日日本海啸的重现期为500 a时,采用P-L分布推求多年一遇重现值是比较准确的。故本文假设此日本海啸的重现期为500 a,采用P-L分布推求中国沿海50 m水深处各点的长期重现值(见图 4)。

|
图 4 中国沿海各处50 m水深处海啸振幅对应不同重现期的重现值。 Fig. 4 Return values of offshore tsunami amplitude corresponding to different return periods in different points along China coasts |
该图中各点处不同颜色的线段表示对应不同重现期计算得到的重现值,线段长短表示重现值大小。
经过统计得到重现期为100、500、1 000、1 500、2 000和2 500 a时,中国沿海50 m水深处海啸振幅最大值均发生在广东省汕头市附近(117.8167°E,22.1667°E),分别为20.82、46.35、63.62、76.08和94.71 cm。图 5标出了中国沿海50 m水深处,1 000 a一遇的海啸振幅超过20和25 cm的区域。图 6标出了2 500 a一遇时海啸振幅超过25和50 cm的区域。

|
图 5 中国沿海50 m水深处千年一遇的最可能发生的变量组合中海啸振幅超过(a)20 cm、(b)25 cm的范围 Fig. 5 he area where the tsunami amplitude is higher than 20 cm (a) and 25 cm (b) with the return period 1000 years |

|
图 6 中国沿海50 m水深处2 500 a一遇的最可能发生的变量组合中海啸振幅超过(a)25 cm、(b)50 cm的范围 Fig. 6 The area where the tsunami amplitude is higher than 25 cm (a) and 50 cm (b) with the return period 2 500 a |
由图 5知,重现期为1 000 a时,广东省东北部海域、福建省西南部、浙江省北部海域和上海市附近海域的离岸海啸振幅超过20 cm;广东省东北部海域、福建省西南部海域的离岸海啸振幅超过25 cm。由图 6知,当重现期提高到2 500 a时,海啸离岸振幅超过25 cm的海域有广东省东北部海域、福建省西南部和东北部海域、台湾大部分邻近海域、浙江省和上海市附近海域,而广东省东北部海域、福建省西南部海域及台湾南部和东部海域的离岸海啸振幅达到50 cm。
3 结论本文主要讨论了采用MOST海啸传播模型计算历史地震可能在中国沿海附近引发的海啸增水并采用一维概率模型研究海啸增水的统计特性,从而为中国沿海城市及海洋工程建设提供重要的参考依据。
(1) 收集可能对中国沿海产生海啸危害的历史地震记录,采用MOST海啸传播模型计算了这些历史地震可能引发的海啸增水。Poisson分布可以描述选用的历史地震的发生频次分布特征。
(2) 通过对香港地区的海啸增水统计分析发现,相比于P-W分布与P-GEV分布,P-L分布可以比较准确地拟合离岸海啸增水的概率分布,故采用P-L分布拟合中国沿海各点的离岸海啸增水并计算出各处的长期重现值。
(3) 给出了重现期分别为1 000和2 500 a时,海啸增水分别超过20、25和25、50 cm的海域。当重新期为2 500 a时,广东省东北部海域、福建省西南部海域及台湾南部和东部海域的离岸海啸振幅达到50 cm。
| [1] |
Fukao Y. Tsunami earthquakes and subduction processes near deep-sea trenches[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1979, 84(B5): 2303-2314. DOI:10.1029/JB084iB05p02303
(  0) 0) |
| [2] |
Liu Y, Santos A, Wang S M, et al. Tsunami hazards along Chinese coast from potential earthquakes in South China Sea[J]. Physics of the Earth and Planetary Interiors, 2007, 163(1): 233-244.
(  0) 0) |
| [3] |
叶琳, 王喜年, 包澄澜. 中国的地震海啸及其预警服务[J]. 自然灾害学报, 1994, 3(1): 100-103. Ye L, Wang X, Bao C. Tsunami in the China Seas and its warning service[J]. Journal of Natural Disasters, 1994, 3(1): 100-103. (  0) 0) |
| [4] |
包澄澜. 海啸灾害及其预警系统[J]. 国际地震动态, 2005(1): 14-18. Bao C. Tsunami disaster and its pre-warning system[J]. Recent Developments in World Seismology, 2005(1): 14-18. (  0) 0) |
| [5] |
Rikitake T, Aida I. Tsunami hazard probability in Japan[J]. Bulletin of the Seismological Society of America, 1988, 78(3): 1268-1278.
(  0) 0) |
| [6] |
Annaka T, Satake K, Sakakiyama T, et al. Logic-tree approach for probabilistic tsunami hazard analysis and its applications to the Japanese coasts[M]. Birkhäuser Basel: Tsunami and Its Hazards in the Indian and Pacific Oceans, 2007, 577-592.
(  0) 0) |
| [7] |
Choi B H, Hong S J, Pelinovsky E. Simulation of prognostic tsunamis on the Korean coast[J]. Geophysical Research Letters, 2001, 28(10): 2013-2016. DOI:10.1029/2000GL012534
(  0) 0) |
| [8] |
Geist E L, Parsons T. Probabilistic Analysis of Tsunami Hazards[J]. Natural Hazards, 2006, 37(3): 277-314. DOI:10.1007/s11069-005-4646-z
(  0) 0) |
| [9] |
Parsons T, Geist E L. Tsunami probability in the Caribbean region[M]. Birkhäuser Basel: Tsunami Science Four Years after the 2004 Indian Ocean Tsunami, 2009, 2089-2116.
(  0) 0) |
| [10] |
González F I, Geist E L, Jaffe B, et al. Probabilistic tsunami hazard assessment at Seaside, Oregon, for near- and far-field seismic sources[J]. Journal of Geophysical Research: Oceans (1978-2012), 2009, 114(C11).
(  0) 0) |
| [11] |
Liu P L F, Wang X, Salisbury A J. Tsunami hazard and early warning system in South China Sea[J]. Journal of Asian Earth Sciences, 2009, 36(1): 2-12. DOI:10.1016/j.jseaes.2008.12.010
(  0) 0) |
| [12] |
Helffrich G R. How good are routinely determined focal mechanisms? Empirical statistics based on a comparison of Harvard USGS and ERI momentensors[J]. Geophys Jour Int, 1997, 131: 714-750.
(  0) 0) |
| [13] |
Tang L, Titov V V, Wei Y, et al. Tsunami forecast analysis for the May 2006 Tonga tsunami[J]. Journal of Geophysical Research: Oceans (1978-2012), 2008, 113(C12).
(  0) 0) |
| [14] |
Wei Y, Bernard E N, Tang L, et al. Real-time experimental forecast of the Peruvian tsunami of August 2007 for US coastlines[J]. Geophysical research letters, 2008, 35(4).
(  0) 0) |
| [15] |
Feller W. On a general class of 'contagious' distribution[J]. The Annals of Mathematical Statistics, 1943, 14(4): 389-400. DOI:10.1214/aoms/1177731359
(  0) 0) |
| [16] |
Neyman J. On a new class of 'contagious' distribution, applicable in entomology and bacteriology[J]. Annals of Math Stat, 1939, 10: 35-57. DOI:10.1214/aoms/1177732245
(  0) 0) |
| [17] |
马逢时, 刘德辅. 海洋工程建筑中设计波高推算的新方法[J]. 科学通报, 1979(1): 33-37. Ma F, Liu D. New method to estimate design wave height in ocean engineering[J]. Science Bulletin, 1979(1): 33-37. (  0) 0) |
| [18] |
Dong S, Liu W, Zhang L Z, et al. Long-term statistical analysis of typhoon wave heights with Poisson-maximum entropy distribution[C]. //The Proceedings of 28 the International Conference on Ocean, Offshore and Polar Engineering, Hawaii, USA, OMAE79278, 2009, 2: 189-196. https://www.researchgate.net/publication/267605004_Long-Term_Statistical_Analysis_of_Typhoon_Wave_Heights_With_Poisson-Maximum_Entropy_Distribution
(  0) 0) |
| [19] |
Wang L P, Sun X G, Lu K B, Xu D L. A maximum-entropy compound distribution for extreme wave heights of typhoon-affected sea areas[J]. China Ocean Engineering, 2012, 26(1): 49-58. DOI:10.1007/s13344-012-0004-6
(  0) 0) |
| [20] |
Titov V V, Synolakis C E. Numerical modeling of tidal wave runup[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1998, 124(4): 157-171. DOI:10.1061/(ASCE)0733-950X(1998)124:4(157)
(  0) 0) |
| [21] |
Yanenko N N. The method of fractional steps[M]. New York: Springer, 1971.
(  0) 0) |
| [22] |
Titov V V, Synolakis C E. Modeling of breaking and nonbreaking long-wave evolution and runup using VTCS-2[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1995, 121(6): 308-316. DOI:10.1061/(ASCE)0733-950X(1995)121:6(308)
(  0) 0) |
| [23] |
Okada Y. Internal deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 1992, 82(2): 1018-1040.
(  0) 0) |
| [24] |
Tsimopoulou V, Jonkman S N, Kolen B, et al. A multi-layered safety perspective on the tsunami disaster in Tohoku, Japan[C]. //FLOODrisk 2012: The 2nd European Conference on FLOODrisk Management" Science, Policy and Practice: Closing the Gap", Rotterdam, The Netherlands, 20-22 November 2012; Authors version. 2012. https://www.researchgate.net/publication/263417283_A_multi-layered_safety_perspective_on_the_tsunami_disaster_in_Tohoku_Japan
(  0) 0) |
 2018, Vol. 48
2018, Vol. 48


