2. 中国科学院海洋研究所,山东 青岛 266100
南海是一个半封闭海,吕宋海峡较为宽阔且水深较大,它将南海与太平洋连通,是南海与外界水体交换的主要通道。横跨吕宋海峡的巨大海岭因其剧烈的地形变化,会诱发强内潮并传入南海北部海区,吕宋海峡是世界海洋中内潮的重要生成源地之一。另外,南海北部具有宽广的大陆架和大陆坡,陆架区潮汐现象显著,在此处也有明显的内潮生成。针对南海内潮的研究,方欣华等[1]对南海内波的分布、现场观测、特征及生成源等进行了系统的阐述和总结,为南海内潮的研究奠定了坚实的基础。利用数值模式对内潮进行数值模拟,是研究海洋内潮的生成和传播机制的有效途径之一。Miao等[2]的研究成果表明, 吕宋海峡处生成的内潮会向西传播至东沙群岛;向西南传播至南海海盆。Wang等[3]采用非静力的MITgcm模式估计了南海海域潮汐混合情况,研究指出吕宋海峡是南海内潮能量的主要来源,在吕宋海峡双海脊附近垂向扩散系数为~10-2 m2·s-1,在南海海盆底层垂向扩散系数达到(10-3~10-1) m2·s-1,在底层以上的水体中垂向扩散系数约为(10-4~10-3)m2·s-1。随着海洋观测技术的进步和观测资料的增多,如何充分利用现有的观测数据实现对内潮的高精度模拟,已成为一个急需解决的问题。在数学物理反问题的框架下,伴随同化方法能够最大限度的合理使用有限的观测资料,它能够在动力学框架上实现海洋数值模式与海洋多元观测数据的有机结合,是获取稳定可靠高时空分辨率海洋环境要素场的有效工具。大量研究成果表明,伴随同化方法在物理海洋研究中占有越来越重要的地位[4]。目前,国内外学者已开始利用伴随同化方法进行内潮研究[5-8]。随着海洋观测技术的进步和观测资料的增多[9],如何充分利用现有的观测数据实现海洋内潮的高精度模拟,已成为一个急需解决的问题。而目前所积累的大量的观测数据,如多源遥感资料、ARGO温盐剖面资料和现场观测资料等,则为伴随同化方法在内潮数值模拟中的实现提供了强有力的数据支持。
在海洋观测中,合理规划潜标的布放位置有利于充分发挥每套潜标的作用,使获取的实测数据能够更加准确、全面地包含海洋物理过程的主要信息,从而提高海洋观测的效率和质量。基于南海现有的潜标布放位置,利用伴随同化方法对潜标布放位置进行优化,其优化结果可以为南海潜标布放提供参靠。本文主要探讨了南海观测站点分布的优化问题,结构如下:首先,本文对两层等密度坐标内潮模型进行简要介绍;进而,利用该模型对南海M2内潮进行数值模拟,探讨研究南海观测站点优化问题;最后,在第4节是对全文的总结。
1 模型 1.1 正向模型本文采用两层等密度坐标模型,该模型是一个非线性的原始方程模型,在垂向采用等密度坐标,水平方向采用球坐标,考虑静压近似和自由海面[10]。假设每一层的密度ρk(k=1, 2)是常数,可以得到内模态方程如下[11]:
正向模型第一层:
| $ \frac{{\partial {q_1}}}{{\partial t}} + \frac{1}{{R\cos \phi }}\frac{{\partial \left( {{q_1}{u_1}} \right)}}{{\partial \lambda }} + \frac{1}{{R\cos \phi }}\frac{{\partial \left( {{q_1}{v_1}\cos \phi } \right)}}{{\partial \phi }} = 0, $ | (1a) |
| $ \begin{array}{l} \frac{{\partial {u_1}}}{{\partial t}} + \frac{{{u_1}}}{{R\cos \phi }}\frac{{\partial {u_1}}}{{\partial \lambda }} + \frac{{{v_1}}}{R}\frac{{\partial {u_1}}}{{\partial \phi }}-\frac{{{u_1}{v_1}\tan \phi }}{R}-\\ \;\;\;\;f{v_1}-{A_h}\mathit{\Delta }{u_1} + \frac{{{A_v}\bar \rho }}{{{q_1}\bar h}}\left( {{u_1} - {u_2}} \right) + \\ \;\;\;\;\frac{g}{{R\cos \phi }}\frac{\partial }{{\partial \lambda }}\sum\limits_{m = 1}^l {\left( {\frac{{{q_m}}}{{{\rho _m}}} - {h_m}} \right) = 0, } \end{array} $ | (1b) |
| $ \begin{array}{l} \frac{{\partial {v_1}}}{{\partial t}} + \frac{{{u_1}}}{{R\cos \phi }}\frac{{\partial {v_1}}}{{\partial \lambda }} + \frac{{{v_1}}}{R}\frac{{\partial {v_1}}}{{\partial \phi }} + \frac{{u_1^2\tan \phi }}{R} + \\ \;\;\;\;f{u_1} + \frac{g}{R}\frac{\partial }{{\partial \phi }}\sum\limits_{m = 1}^2 {\left( {\frac{{{q_m}}}{{{\rho _m}}}-{h_m}} \right)}-\\ \;\;\;\;{A_h}\mathit{\Delta }{v_1} + \frac{{{A_v}\bar \rho }}{{{q_1}\bar h}}\left( {{u_1}-{u_2}} \right) = 0。\end{array} $ | (1c) |
底层:
| $ \frac{{\partial {q_2}}}{{\partial t}} + \frac{1}{{R\cos \phi }}\frac{{\partial \left( {{q_2}{u_2}} \right)}}{{\partial \lambda }} + \frac{1}{{R\cos \phi }}\frac{{\partial \left( {{q_2}{v_2}\cos \phi } \right)}}{{\partial \phi }} = 0, $ | (2a) |
| $ \begin{array}{l} \frac{{\partial {u_2}}}{{\partial t}} + \frac{{{u_2}}}{{R\cos \phi }}\frac{{\partial {u_2}}}{{\partial \lambda }} + \frac{{{v_2}}}{R}\frac{{\partial {u_2}}}{{\partial \phi }}-\frac{{{u_2}{v_2}\tan \phi }}{R}-\\ f{v_2} + \frac{g}{{R\cos \phi }}\frac{\partial }{{\partial \lambda }}\sum\limits_{k = 1}^2 {\left( {\frac{{{q_k}}}{{{\rho _2}}}-{h_k}} \right)} - {A_h}\mathit{\Delta }{u_2} - \\ \frac{{{A_v}\bar \rho }}{{{q_2}\bar h}}\left( {{u_1} - {u_2}} \right) + \frac{{\kappa {\rho _2}{u_2}}}{{{q_2}}}\sqrt {{{\left( {{u_2}} \right)}^2} + {{\left( {{v_2}} \right)}^2}} = 0, \end{array} $ | (2b) |
| $ \begin{array}{l} \frac{{\partial {v_2}}}{{\partial t}} + \frac{{{u_2}}}{{R\cos \phi }}\frac{{\partial {v_2}}}{{\partial \lambda }} + \frac{{{v_2}}}{R}\frac{{\partial {v_2}}}{{\partial \phi }} + \frac{{u_2^2\tan \phi }}{R} + \\ \;\;\;\;f{u_2} + \frac{g}{R}\frac{\partial }{{\partial \phi }}\sum\limits_{k = 1}^2 {\left( {\frac{{{q_k}}}{{{\rho _2}}}-{h_k}} \right)}-\\ \;\;\;\;{A_h}\mathit{\Delta }{v_2}-\frac{{{A_v}\bar \rho }}{{{q_2}\bar h}}\left( {{v_1} - {v_2}} \right) + \\ \;\;\;\frac{{\kappa {\rho _2}{v_2}}}{{{q_2}}}\sqrt {{{\left( {{u_2}} \right)}^2} + {{\left( {{v_2}} \right)}^2}} = 0。\end{array} $ | (2c) |
其中:t代表时间;λ和ϕ分别是东经和北纬;u和v分别表示潮流在λ和ϕ方向上的流速分量。各层动态质量q1=ρ1(h1+η1-η2), q2=ρ2(h2+η2)。其中hk为各层初始静止厚度,除底层外也只与k有关,与λ和ϕ无关;ηk为各层上界面的扰动高度;R是地球半径;g是重力加速度;f=2Ωsinϕ是Coriolis参数;Ω为地球自转角速度; Ah是水平涡动粘性系数和垂向涡动粘性系数;Δ是拉普拉斯算子,且
| $ \begin{array}{l} \mathit{\Delta }\left( {u, v} \right) = \frac{1}{{{R^2}{{\cos }^2}\phi }}\frac{{{\partial ^2}\left( {u, v} \right)}}{{\partial {\lambda ^2}}} + \\ \;\frac{1}{{{R^2}\cos \phi }}\frac{\partial }{{\partial \phi }}\left[{\cos \phi \frac{{\partial \left( {u, v} \right)}}{{\partial \phi }}} \right]。\end{array} $ |
式中:Av为表层摩擦系数;κ为底摩擦系数;ρ=(ρ1+ρ2)/2,h=(h1+h2)/2。定义正压流为各层流速的质量加权平均值,即:
| $ Q = {q_1} + {q_2}, U = \frac{{{q_1}{u_1} + {q_2} + {u_2}}}{Q}, V = \frac{{{q_1}{v_1} + {q_2}{v_2}}}{Q}。$ |
将内模态各层动量方程以Qk为权重加权平均,各层连续方程直接相加,即可得到外模态方程:
| $ \frac{{\partial Q}}{{\partial t}} + \;\frac{1}{{R\cos \phi }}\frac{{\partial \left( {QU} \right)}}{{\partial \lambda }} + \frac{1}{{R\cos \phi }}\frac{{\partial \left( {QV\cos \phi } \right)}}{{\partial \phi }} = 0, $ | (3a) |
| $ \frac{{\partial U}}{{\partial t}}-fV + {M_\lambda } + {R_U} + \frac{{\kappa {\rho _2}{u_2}}}{Q}\sqrt {{{\left( {{u_2}} \right)}^2} + {{\left( {{v_2}} \right)}^2}} = 0, $ | (3b) |
| $ \frac{{\partial V}}{{\partial t}} + fU + {M_\phi } + {R_V} + \frac{{\kappa {\rho _2}{u_2}}}{Q}\sqrt {{{\left( {{u_2}} \right)}^2} + {{\left( {{v_2}} \right)}^2}} = 0。$ | (3c) |
其中:
| $ \begin{array}{l} {M_\lambda }\frac{g}{{R\cos \tilde \omega }}\frac{\partial }{{\partial \lambda }}\left( {\frac{Q}{\rho }-h} \right) + \frac{{g{q_2}}}{{QR\cos \tilde \omega }}\left( {\frac{1}{{{\rho _2}}}-\frac{1}{{{\rho _1}}}} \right)\frac{{\partial {q_1}}}{{\partial \lambda }}, \\ {M_\phi } = \frac{g}{R}\frac{\partial }{{\partial \phi }}\left( {\frac{Q}{\rho }-h} \right) + \frac{{g{q_2}}}{{QR}}\left( {\frac{1}{{{\rho _2}}} - \frac{1}{{{\rho _1}}}} \right)\frac{{\partial {q_1}}}{{\partial \phi }}, \end{array} $ |
| $ \begin{array}{l} {R_U} = \frac{1}{Q}\sum\limits_{k = 1}^2 {{q_k}} \left( {\frac{{{u_k}}}{{R\cos \phi }}\frac{{\partial {u_k}}}{{\partial \lambda }} + \frac{{{v_k}}}{R}\frac{{\partial {u_k}}}{{\partial \phi }}-\frac{{{u_k}{v_k}\tan \phi }}{R}} \right)-\\ \frac{{{A_h}}}{Q}\sum\limits_{k = 1}^2 {{q_k}\Delta {u_k}}-\sum\limits_{k = 1}^2 {{u_k}} \frac{\partial }{{\partial t}}\left( {\frac{{{q_k}}}{Q}} \right), \end{array} $ |
| $ \begin{array}{l} {R_V} = \frac{1}{Q}\sum\limits_{k = 1}^2 {{q_k}} \left( {\frac{{{u_k}}}{{R\cos \phi }}\frac{{\partial {v_k}}}{{\partial \lambda }} + \frac{{{v_k}}}{R}\frac{{\partial {v_k}}}{{\partial \phi }} + \frac{{u_k^2\tan \phi }}{R}} \right)-\\ \frac{{{A_h}}}{Q}\sum\limits_{k = 1}^2 {{q_k}\Delta {v_k}}-\sum\limits_{k = 1}^2 {{v_k}} \frac{\partial }{{\partial t}}\left( {\frac{{{q_k}}}{Q}} \right)。\end{array} $ |
其中:h=h1+h2为静水深;
构造代价函数:
| $ J(q,u,v;p)=\\ \frac{1}{2}\int {_\Sigma } \left[{{K_u}\sum\limits_{k = 1}^2 {{{\left( {{u_k}-{{\hat u}_k}} \right)}^2} + {K_v}\sum\limits_{k = 1}^2 {{{\left( {{v_k}-{{\hat v}_k}} \right)}^2}} } } \right]{\rm{d}}\sigma 。$ | (4) |
其中:k为内模态变量的层数指标;∑为模式的时空计算区域;p代表模型参数;u和v代表状态变量;uk和vk均为第k层模式模拟的结果;
构造Lagrangian函数如下:
| $ \begin{array}{l} L\left( {q, u, v;{q_a}, {u_a}, {v_a};p} \right) = J\left( {q, u, v;p} \right) + \int {_\Sigma } [{q_{a1}} \cdot \\ Eq.\left( {1a} \right) + {u_{a1}}{q_1} \cdot Eq.\left( {1b} \right) + {v_{a1}}{q_1} \cdot Eq.\left( {1c} \right)]{\rm{d}}\sigma {\rm{ + }}\\ \int {_\Sigma } [{q_{a2}} \cdot Eq.\left( {2a} \right) + {u_{a2}}{q_2} \cdot Eq.\left( {2b} \right) + {v_{a2}}{q_2} \cdot Eq.\left( {2c} \right)]{\rm{d}}\sigma 。\end{array} $ | (5) |
其中:伴随变量qak,uak和vak分别为状态变量qk,uk和vk的伴随算子;Δ为Laplace算子。
在满足控制方程及其初边值条件的限制下,使代价函数达到最小的模型控制参数。为此,令:
| $ \frac{{\partial L}}{{\partial {q_{ak}}}} = 0, \frac{\partial }{{\partial {u_{ak}}}} = 0, \frac{{\partial L}}{{\partial {v_{ak}}}} = 0, $ | (6) |
| $ \frac{{\partial L}}{{\partial {q_k}}} = 0, \frac{{\partial L}}{{\partial {u_k}}} = 0, \frac{{\partial L}}{{\partial {v_k}}} = 0, $ | (7) |
| $ \frac{{\partial L}}{{\partial p}} = 0。$ | (8) |
方程组(6)即是原来的控制方程(1a)~(2c),方程组(7)为导出伴随方程,而方程组(8)则给出了代价函数关于控制参数的梯度,由此可得到控制参数的校正关系式。伴随模型同样分为内外两种模态,文献[11]给出了这两种模态的细节以及公式。
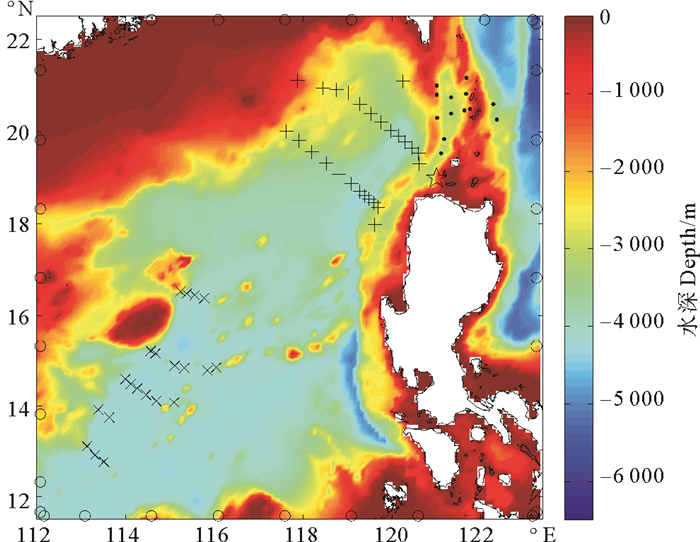
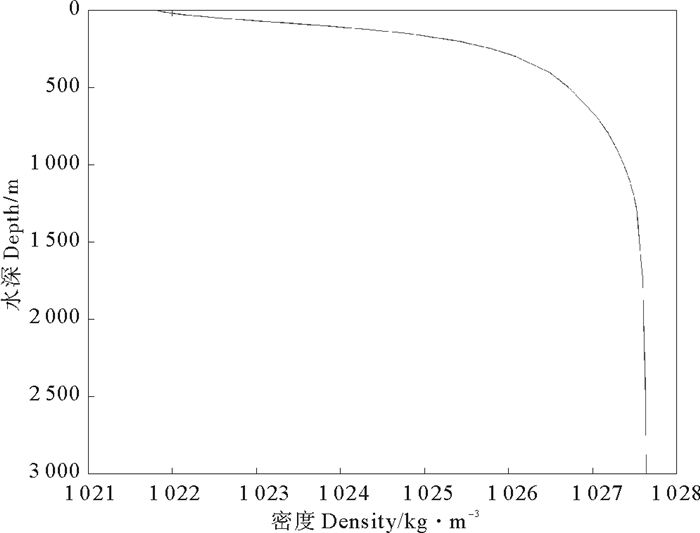
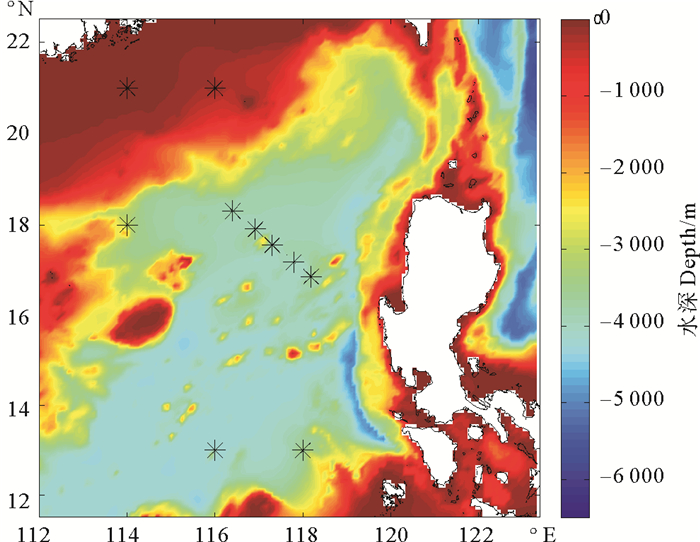
2 实验设置如图 1所示,实验区域选取为南海东北部,包含吕宋海峡(112°E~123.4°E,11.5°N~22.5°N),水平分辨率为5′×5′,水平方向共有137×133个计算网格,垂向分为2层,分层界面深度位于500 m处。科氏力参数选取当地值,仅对M2分潮进行研究,该潮波的角频率为1.405 078 902 5×10-4s-1。时间步长选取为7.453 min(M2分潮周期的1/100)。计算区域中的垂向密度结构采用图 1中符号“☆”所在位置(121°E,19°N)的实测值,该点位势密度的垂向结构如图 2所示, 可见密度在500 m之后变化较小,故将500 m设置为初始分层界面,上下两层密度分别为1 025.24和1 027.48 kg/m3。
|
(“o”表示独立点位置;符号“?”表示第1组观测站点的位置;“+”表示第2组观测站点的位置;“×”表示第3组观测站点的位置;“☆”为垂向密度结构的位置。‘o’ are independent points position; ’?’, ‘+’, ’×’ represent observation points of No.1, No.2 and No.3 group respectively; ‘☆’ is the position of vertical density structure.) 图 1 实验海域深度图 Fig. 1 Depth map of experimental area |
|
图 2 实验海域图 1中“☆”位置的位势密度 Fig. 2 The potential density of experimental area on the position '☆'in Fig. 1. |
本研究考察观测站点的分布位置对开边界条件反演结果的影响。首先,通过同化该海域的T/P资料以获得实验所需的模型参数,其中,层间摩擦系数为0.02 m2/s,底摩擦系数为0.003,上下两层的水平涡动粘性系数分别为2 478和1 981 m2/s。第二步将得到的模型参数及开边界条件代入模型中进行理想实验,具体步骤如下:
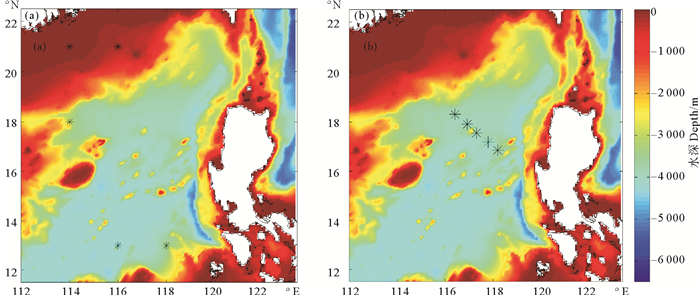
如图 1所示,将南海60个观测站点根据其分布位置分为3组,其中吕宋海峡内的13个站点为第1组,吕宋海峡西侧的26个站点为第2组,在计算区域西南部的21个站点为第3组。从三组观测站点中选出部分站点作为待同化的观测数据的获取位置,并利用理想实验考察观测站点的分布位置对开边界条件反演结果的影响,共进行6个理想实验。实验1:同化第1组和第2组观测站点的数据;实验2:同化第1组和第3组观测站点的数据;实验3:同化第2组和第3组观测站点的数据;实验4:同时同化三个组观测站点的数据;实验5和实验6是基于实验4的基础上,在计算区域合理增加观测点进行实验(增加站点位置如图 3所示)。实验所同化的观测资料均为上层的流速数据,是将模型参数和给定的开边界条件代入正向模型进行数值模拟得到。在同化实验中,首先将开边界条件设置为0,其他模型参数保持不变,再利用伴随方法通过不断优化开边界条件,逐步对观测数据进行同化。优化开边界条件过程中采用了独立点方案,独立点的设置如图 1所示。
|
(“*”表示新增观测点位置。‘*’represent new added observation position.) 图 3 实验5(a)与6(b)海域深度图 Fig. 3 Depth on experimental ara of test 5(a)and 6(b) |
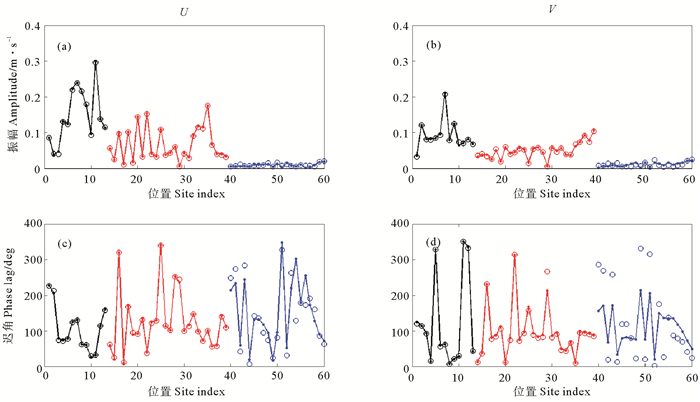
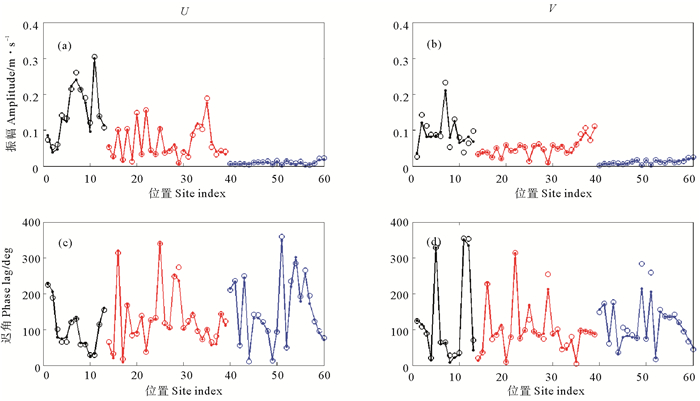
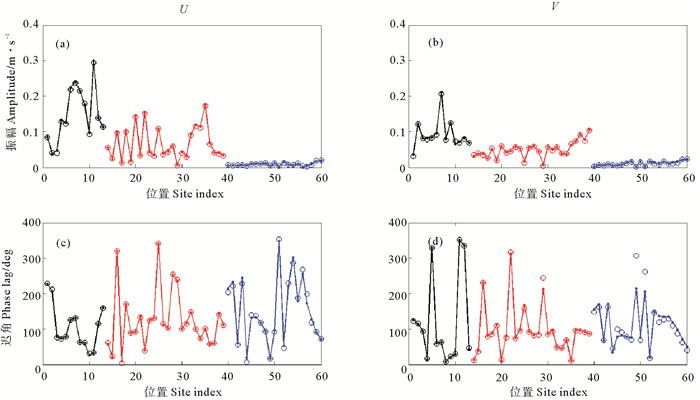
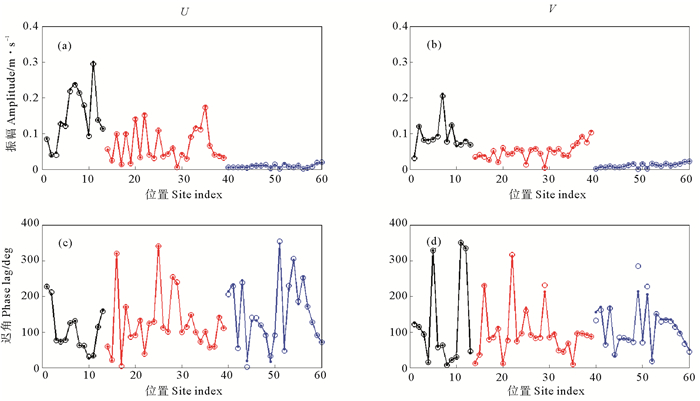
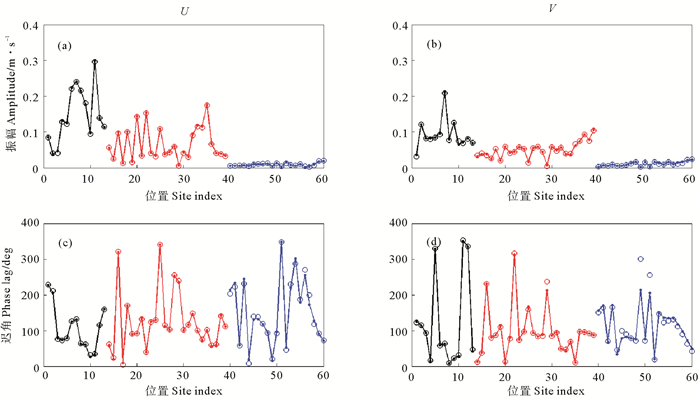
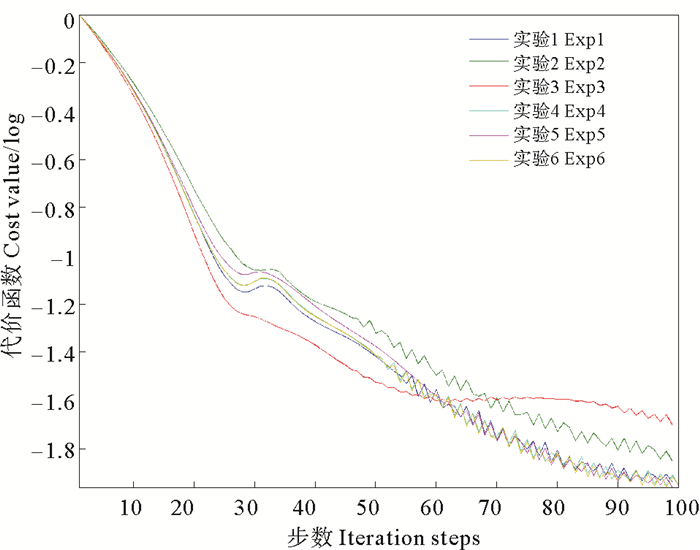
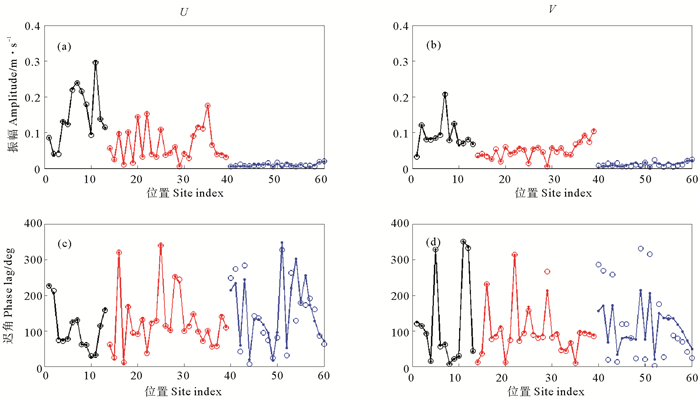
同化过程中代价函数的变化如图 4所示,可发现6个实验的代价函数均下降到接近初始值的百分之一。6个实验的模拟结果与60个站点的观测数据的对比如图 5~10所示,每个图像的四幅图中,(a)图表示纬向流速U的振幅,(c)图为其迟角;(b)图表示经向流速V的振幅,(d)图为其迟角;每幅图中,圆圈代表观测数据,圆点代表模拟结果。为方便区分不同分组的站点,分别用黑色、蓝色、红色代表第1、2、3组站点的数据,并且同一分组的数据用直线进行连接。
|
图 4 同化过程中代价函数的变化情况 Fig. 4 The variation of cost value during assimilation process |
|
(圆点和圆圈代表观测数据和模拟结果;黑色、红色、蓝色分别代表第1、2、3组站点的相关数据和模拟结果。Points and circles represent observation data and simulated results respectively. Black, red, blue represent data and simulated result of No.1, No.2, No.3 station respectively.) 图 5 实验1的模拟结果 Fig. 5 Simulated result of test |
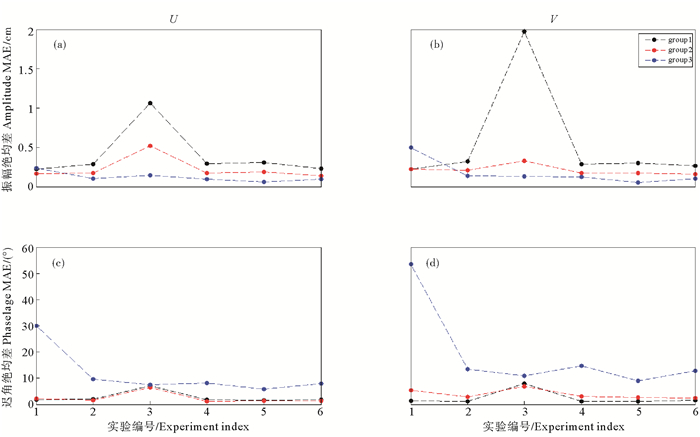
图 11给出了4个实验对各组站点数据的模拟误差的统计结果,其中(a)图表示纬向流速U振幅的模拟相对均方差,(c)图为迟角;(b)图表示经向流速V振幅的模拟相对均方差,(d)图表示迟角;黑色、蓝色、红色分别表示第1、2、3组站点数据的相关结果。
|
(黑色、红色、蓝色分别代表第1、2、3组站点;(a)图表示纬向流速U的振幅,(c)为其迟角;(b)图表示经向流速V的振幅,(d)其为迟角。Black, red, blue represent No.1, 2, 3 station respectively (a) and (c) represent amplitude and phase lag of U, respectively;(b) and (d) represent amplitude and phase lag of V, respectively.) 图 11 实验1~6模拟结果的绝对平均误差对比 Fig. 11 Mean absolute errors of Simulated result from test 1~6 |
从实验结果可以看出:
(1) 由图 5~8中的观测数据以及南海潮汐潮流的传播特点可以推断出潮波从东边界(太平洋)由吕宋海峡向西进入南海,首先进入第1组站点所在的海域,因而第一组站点的潮流最强。此后一部分潮波继续向西传播至第2组站点所在的海域,潮流强度稍有减弱,另一部分潮波向西南方向传播一段距离后进入第3组站点所在的海域,此时潮流强度已经大幅度减弱。此外还有一部分波动转向西北大陆架方向传播。另一方面,考虑整个南海的地理环境,南海四面大部分被陆地环绕,其南、西、北三个方向的陆地对潮波有一定的反射作用,因而模拟区域的这三个方向的开边界条件值可以认为主要是由陆地对潮波的反射作用所致,尤其在北边界,大陆坡对潮波的反射作用再加上由台湾海峡向南传入计算区域的潮波,使得第1、2组站点的经向流动也很强。
(2) 由计算区域的潮波传播特点以及整个计算海域的模拟情况可以推断出:第1组站点携带了更重要的开边界信息,其次是第2组站点,第3组站点对开边界条件的反演作用明显小于前两组站点。因而在该区域的内潮模拟中东边界和北边界的开边界条件是两个重要的控制变量。
3.2 增加站点后的实验从实验结果可以看出:
(1) 东边界是该海域潮波驱动力的主要来源,第1组站点最靠近东边界,其携带更多的东边界的潮汐强迫信息,因而有第1组观测数据参与的同化实验模拟结果都比较理想,只有实验3未同化第1组站点的观测数据,其总体的模拟结果最差(见表 1、2)。
|
|
表 1 实验1~6模拟结果振幅的绝对平均误差对比 Table 1 Mean absolute errors of simulated results from test 1-6 |
|
|
表 2 实验1~6模拟结果振幅的相对平均误差对比 Table 2 Relative mean errors of simulated results from test 1-6 |
(2) 第3组站点所在海域的潮波模拟的影响因素比较复杂,一方面要考虑由吕宋海峡传播而来的波动,另一方面还要考虑来自陆地的反射波动。该组站点纬向流的模拟情况与其他两组站点的模拟情况一致,都是有第1组观测数据参与的同化实验的模拟误差较小。对于均同化第3组站点的实验2(同化第1、3组站点)与3(同化第2、3组站点)来说,实验3未同化第1组站点的观测数据,对纬向流的模拟误差是最大的,这说明该组站点的纬向流信息的主要来源是由吕宋海峡经过第1组站点传播而来的信息。相比之下,第3组站点的经向流的模拟情况则大不相同。只有实验1未同化该组站点的观测数据,其经向流的模拟误差最大,其他实验经向流的模拟结果都明显优于实验1的结果,这说明该组站点经向流信息的主要来源已经不是由吕宋海峡经过第1组站点区域传播而来的波动,而是来自南边界方向的波动。
(3) 针对增加站点后的实验5与6可以发现,在人为的增加5个站点后,通过表 1可以发现三组站点的绝对平均误差均有一定程度的减小,实验6的误差总体上是最小的,而通过表 2的相对平均误差也可以得到相同的结论从而可以推断在计算区域中部放置呈断面状的站点可以更为有效的提高模拟结果的精度。
3.3 对比实验 3.3.1 增加站点数量将实验5与6相结合,即在实验区域共增加10个观测站点(见实验7),以研究增加站点数量对站位优化的影响。图 12给出了增加的站点位置。
|
(“*”为增加站点的位置。‘*’are new added observation positions.) 图 12 实验7的站点位置图 Fig. 12 Station position of test 7 |
通过表 3和4可以发现,当增加站点为10个时,并不能大幅度提高模拟精度,并且部分站点的模拟效果实验6要更优于实验7,所以综合考虑,实验6的站点布放方式即呈断面式布放要更优于其它方式,并且站点的数量增多并不能起到大幅度提高模拟精度的作用。
|
|
表 3 实验7与实验6模拟结果的绝对平均误差 Table 3 Mean absolute errors of simulated results of test 7 and 6 |
|
|
表 4 实验7与实验6模拟结果的相对平均误差 Table 4 Relative mean errors of simulated results of test 7 and 6 |
通过上述试验5~7可以发现实验6的布放位置为最优方案。为了进一步对布放位置进行优化研究,现基于实验6的布放方式即在实验区域放置呈断面状的站点,而将布放位置由随机在实验区域中部更改为在地形变化剧烈的区域增加观测数据(数量仍为5个,实验8增加观测站点位置如图 13所示)。
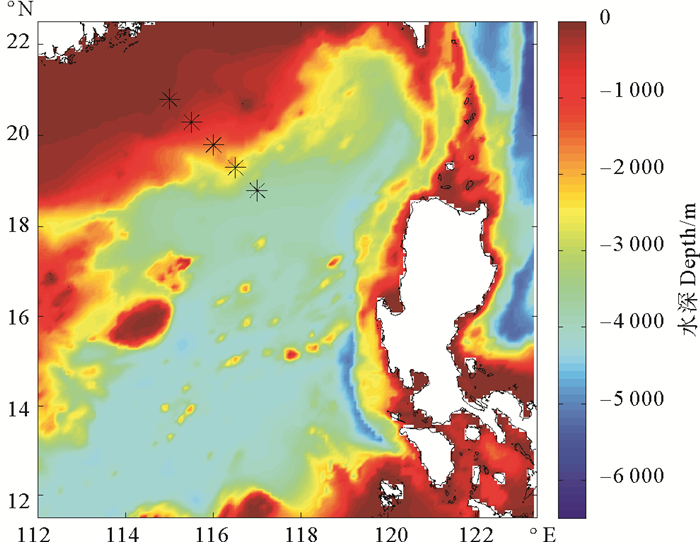
|
(“*”为增加站点的位置。‘*’are new added observation positions.) 图 13 实验8的站点位置图 Fig. 13 Station position of test 7 |
通过表 5和6可以发现,当合理改变站点时,可以在一定程度上减小模拟结果的误差。综上所述,选取地形变化较为剧烈的区域,呈断面式布放站点可以较好的提高该区域内潮的模拟精度。
|
|
表 5 实验6与实验8模拟结果的绝对平均误差 Table 5 Mean absolute errors of simulated results of test 6 and 8 |
|
|
表 6 实验6与实验8模拟结果的相对平均误差 Table 6 Relative mean errors of simulated results of test 6 and 8 |
在海洋观测中,合理规划潜标的布放位置有利于充分发挥每套潜标的作用,使获取的实测数据能够更加准确、更加全面地包含海洋物理过程的主要信息,从而提高海洋观测的效率和质量。基于南海现有的潜标布放位置,利用伴随同化方法对潜标布放位置进行优化,将南海现有的60个观测站点分为3组。由观测数据可知,第1组站点处的潮流最强,第2组次之,第3组最弱。通过该区域的潮波传播特点可知,东、北两个边界处的开边界条件对于该区域的内潮的数值模拟最为关键,因此从位置上可以看出,第1组站点携带了更多与开边界条件相关的信息,第2组次之,第3组最少。数值实验的结果表明,东开边界条件在全海域的纬向流速、北部海域的径向流速模拟中起着主导作用;第3组站点处的纬向流速信息主要是由吕宋海峡传播而来,经向流速信息来自南边界;基于现有的60个站点反演开边界,还不能准确模拟该区域的内潮,实验结果表明:在人为的增加5个站点后,3组站点的绝对平均误差均有一定程度的减小,并且增加一定数量的站点并不能大幅度减小模拟误差。实验8的误差总体上是最小的,从而可以推断,选取地形变化较为剧烈的区域,放置呈断面状的站点可以大幅度提高所有站点处的模拟结果,从而提高了该区域内潮的模拟精度。
| [1] |
方欣华, 杜涛. 海洋内波基础和中国海内波[M]. 青岛: 中国海洋大学出版社, 2005. Fang Xinhua, Du Tao. Fundamentals of Oceanic Internal Waves and Internal Waves in the China Seas[M]. Qingdao: Press of Ocean University of China, 2005. (  0) 0) |
| [2] |
Miao Chunbao, Chen Haibo, Lv Xianqing. An isopycnic-coordinate internal tide model and its application to the South China Sea[J]. Chin J Oceano Limno, 2011, 29(6): 1339-1356. DOI:10.1007/s00343-011-1023-5
(  0) 0) |
| [3] |
Wang X, Peng S, Liu Z, et al. Tidal mixing in the South China Sea: An estimate based on the internal tide energetics[J]. J Phys Oceanor, 2016, 46: 107-124. DOI:10.1175/JPO-D-15-0082.1
(  0) 0) |
| [4] |
张继才. 三维正压潮汐潮流伴随同化模型数值建模及应用研究[D]. 青岛: 中国海洋大学, 2008. Zhang Jicai. Development and Application of A Three-Dimensional Numerical Barotropic Adjoint Assimilation Tidal Model [D]. Qingdao: Ocean University of China, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10423-2008176302.htm (  0) 0) |
| [5] |
Kurapov A L, Egbert G D, Allen J S, et al. The M2 internal tide off oregon: Inferences from data assimilation[J]. J Phys Oceanogr, 2003, 33: 1733-1757. DOI:10.1175/1520-0485(2003)033<1733:TMITOO>2.0.CO;2
(  0) 0) |
| [6] |
Muccino J C, Arango H G, Bennett A F, et al. The inverse ocean modeling system. Part Ⅱ: Applications[J]. J Atmos Oceanic Tech, 2008, 25(9): 1623-1637. DOI:10.1175/2008JTECHO522.1
(  0) 0) |
| [7] |
Zaron E D, Chavanne C, Egbert G D, et al. Baroclinic tidal generation in the Kauai Channel inferred from high-frequency radio Doppler current meters[J]. Dynam Atmos Oceans, 2009, 48: 93-120. DOI:10.1016/j.dynatmoce.2009.03.002
(  0) 0) |
| [8] |
Chen H B, Miao C B, Lv X Q. A 3-D numerical internal tidal model involving adjoint method[J]. Int J Num Method Flu, 2011. DOI:10.1002/fld.2650
(  0) 0) |
| [9] |
Pinkel R, Munk W, Worcester P, et al. Ocean mixing studied near Hawaiian Ridge[J]. EOS, Transactions American Geophysical Union, 2000, 81(46): 545-553.
(  0) 0) |
| [10] |
陈海波. 一个等密度坐标内潮伴随同化模型的数值建模及其应用研究[D]. 青岛: 中国海洋大学, 2012. Chen Haibo, Development and Application of an Isopycnic-Coordinate Numerical Model for Simulation of Internal Tides with Adjoint Assimilation Method [D]. Qingdao: Ocean University of China, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012505857.htm (  0) 0) |
| [11] |
Chen Haibo, Cao Anzhou, Zhang Jicai, et al. Estimation of spatially varying open boundary conditions for a numerical internal tidal model with adjoint method[J]. Mathematics and Computers in Simulation, 2014, 97: 14-38. DOI:10.1016/j.matcom.2013.08.005
(  0) 0) |
2. Institute of Oceanography Chinese Academy of Sciences, Qingdao 266100, China
 2018, Vol. 48
2018, Vol. 48