2. 中国海洋大学山东省海洋环境地质工程重点实验室,山东 青岛 266100;
3. 中国海洋大学环境科学与工程学院,山东 青岛 266100
发生于海底的滑坡会释放大量的泥沙,其形成的含沙浑水体在平缓的坡度上(0.5°~3°)会运行长达数百公里,并且对固定平台,海底电缆、管线等造成严重损害[1]。1929年在Grand Band发生的7.2级地震引发的浊流,导致了12根海底电缆损坏[2]。2009年8月强台风导致台湾高屏溪入海处的悬沙浓度增高,形成异重流,随后多条通讯电缆有顺序地遭受不同程度的破坏[3-4]。在河口、水库中,悬浮于水体中黏粒也会形成具有异重流特征的浑水,能携带泥沙流动很远的距离[5]。研究水下含沙浑水体的物理力学特征对海底结构物的安全设计、沿程的侵蚀、最终的沉积体都具有重要意义。
在考虑海底构筑物所受浑水体作用力时,作用力可以被分解为三个正交的分力,其中垂直于轴线的拖曳力是最主要的破坏力[6]。Zakeri给出了不同含沙量、不同流速浑水体对管线作用时拖曳力系数的数值模拟结果[6-7],庞启秀等通过试验推导出含有块体形状影响的拖曳力计算公式[8],吕楚岫等测定了不同浓度浑水体的流变特性,当含沙量高于400 g/L时为宾汉流体,且浓度不同,流动的宏观表现不同[9]。对于浑水体对结构物的拖曳力,通常通过拖曳力系数(Cd=F/(ρU2RL)来分析[10],而拖曳力系数是弗劳德数Fr与雷诺数Re的函数[6];对于大部分流体,不考虑重力的影响,则Fr是无关紧要的,拖曳力系数只是Re的函数,而Re与液体的黏度有关[11]。含沙浑水体因为其内部黏粒及各粒径泥沙的存在,可能不应被视为牛顿流体。浑水体的浓度不同其流变特性不同,黏度与含沙量有关[9]。测量非牛顿流体的黏度常用方法有毛细管黏度测量法、落球法、旋转流变仪法及振动法[12]。落球法是在无涡旋的相对静态的情况下测量黏度的经典方法。旋转流变仪法是用旋转式黏度计进行黏度测量,使用便捷,测量准确,但其转子剪切速率的提高,会使得测量环境的动力条件与落球法不同。由于浑水体的黏度参数是计算浑水体运动及对结构物作用的重要参数,本文运用落球法和流变仪测试法,测定不同含沙量浑水体的黏度,并比较在两种情况下测得的黏度的区别,分析其原因及其在工程上的应用。
1 试验方法采用落球试验得到不同浓度浑水体的表观黏度;利用流变仪测试试验得到不同浓度浑水体的起始表观黏度,以及浑水剪切稀化后的稳定表观黏度。对比两次试验中得到的黏度,对起始黏度与稳定黏度进行比较分析。
1.1 试验仪器与样品流变测试试验中所用仪器为R/S+流变仪(Brookfield工程实验室公司生产),使用同轴转子测试(型号为MK3-CC40-DIN)。落球法试验中所用玻璃小球直径1.59 cm,质量5.20 g,表面光滑。玻璃球通过高强度的鱼线与反射板相连挂于滑轮上。反射板为直径2 cm的白纸片,用于激光测距仪的光反射。SICK激光位移传感器(型号为DX35,精度1‰)连接到DEWSoft瞬态数据采集仪(型号为DEWE-43,精度1‰),以100 Hz频率采集位移信息。落球法装置见图 1。试验中所用浑水体均由高岭土和清水配成,样品温度为14 ℃,所用高岭土平均粒径约为3.7 μm,属黏土。

|
图 1 落球试验装置图 Fig. 1 Schematic diagram of falling ball test |
取不同质量高岭土,分别配成浓度为280、300、360、380、400、450、500 g/L的7组浑水样品,每组平行测试三次,每个浓度的样品一次性制备足够量,每次测试时充分搅拌后倒入流变仪的样品杯中开始测试。测量模式为CSR(控制输入剪切速率,得到相应的剪切应力和黏度),设置测量时间为300 s,测试点共300个。测试完成后,生成黏度随剪切率变化的曲线与剪切应力随剪切率变化的曲线。
1.2.2 落球法试验配制与流变试验中相同浓度的样品,每个浓度的样品配制一次,通过三次测量来完成平行组的试验,每次测量前充分搅拌,静置10 s左右,水体稳定下来后立刻释放小球进行测量。小球自样品液面处由静止释放,用激光位移传感器与瞬态数据采集仪记录小球的位移与时间,传感器频率为100 Hz,在不同浓度组浑水样品落球试验前,先使小球和反射板系统在滑轮上自由下落,测得加速度,用以计算反射板、滑轮等在小球下落过程中产生的阻力。通过其位移与时间图像,计算得到小球在浑水样品中匀速沉降段的速度,进而计算得到各浓度组样品的黏度,黏度计算公式为:
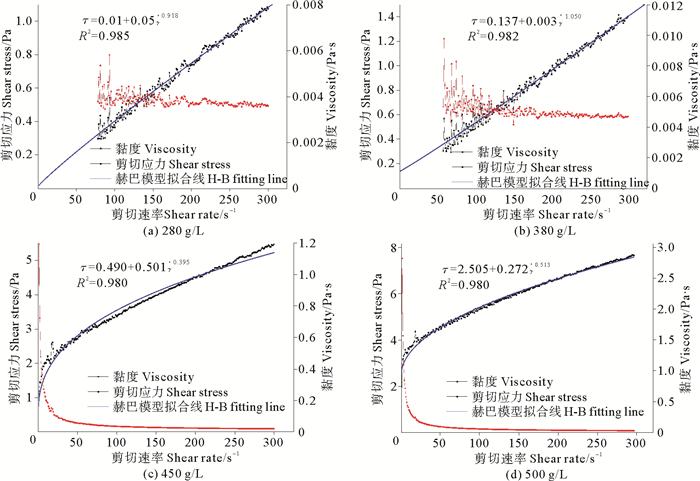
根据流变试验结果,绘制剪切速率-剪切应力和剪切速率-黏度的关系曲线,图 2给出浓度280、380、450、500 g/L的浑水样品的测试结果。
|
图 2 流变试验结果图 Fig. 2 Rheological experiment results |
在所有浓度组的测试过程中,黏度与剪切应力随剪切率的变化趋势一致,试验开始转子启动后,黏度迅速降低,随着剪切速率的增大,黏度趋于稳定;剪切应力则随剪切速率的增大而增大,大部分富含黏土的浑水体可以用赫巴模型描述[13],对剪切应力-剪切速率曲线进行赫巴模型拟合,相关性较强,R2均大于0.9,其中τ为剪切应力,
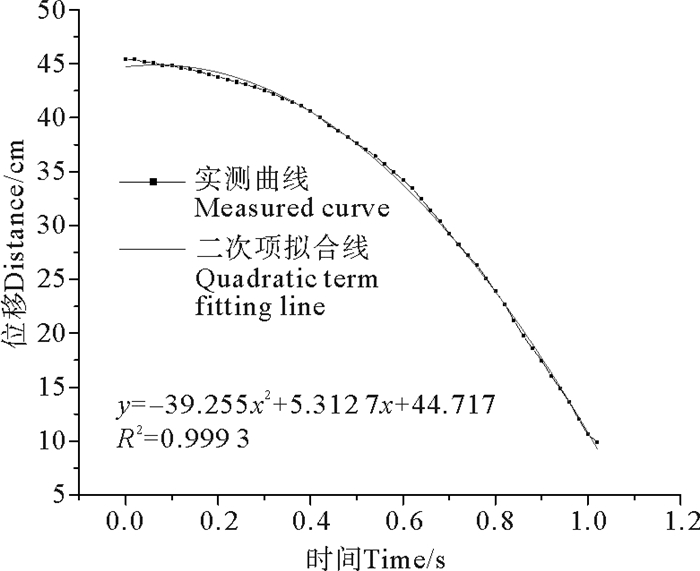
在玻璃球自由下落的空白试验中,对其位移和时间数据作图后进行二次项拟合(见图 3),其相关系数为0.999 3,可以视为匀加速直线运动,阻力在其下落过程中基本稳定,加速度约为78.81 cm/s2。
|
图 3 空白组位移曲线 Fig. 3 Displacement curve of blank group |
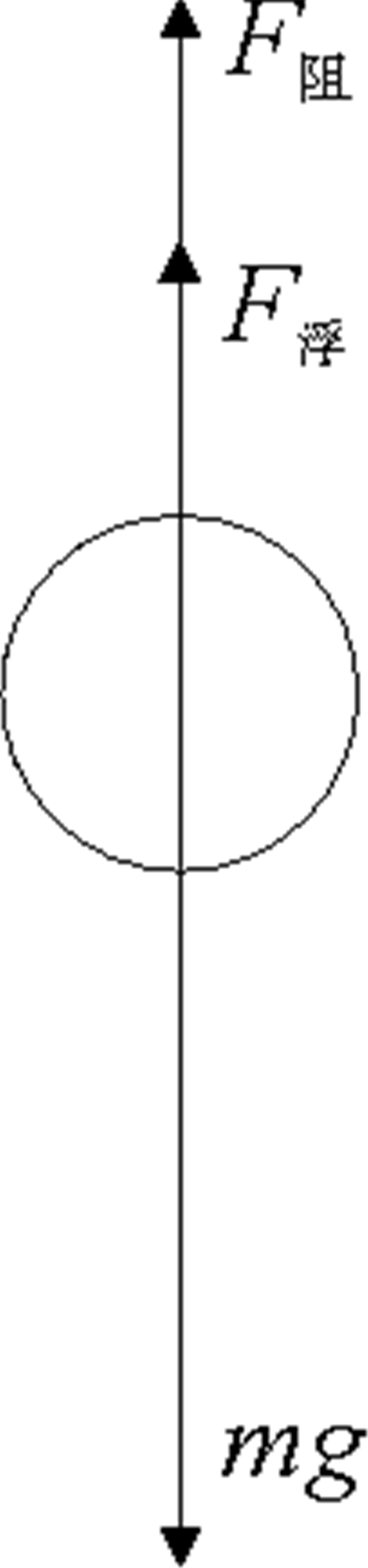
由于小球在下降过程中,小球重力减去所受浮力和阻力后向下合力较小,进入浑水体后的加速度段不明显,小球下落过程中的受力图如图 4所示,根据斯托克斯公式
| $ mg-{{F}_{阻}}-{{F}_{浮}}=6\pi rv\eta, $ |
|
图 4 落球受力分析图 Fig. 4 Force analysis diagram of glass ball |
反射板重力,滑轮摩擦力等阻力合计为方向向上的阻力。对其位移和时间数据进行分析计算,截取相同的位移起点,降落相同的时间,得到位移-时间图像如图 5。对玻璃球的位移与时间关系进行线性拟合,其相关系数均R2均大于0.9,整个下落过程均可视为匀速下降。且浓度越低,其位移-时间曲线斜率越大,即小球下落速度越快。空白试验所测得的加速度与小球质量乘积即为mg-F阻,代入斯托克斯公式,可得测试样品的黏度。

|
图 5 各浓度组小球位移曲线 Fig. 5 The displacement curves of different concentration groups |
流变仪试验中所测得的黏度,随剪切速率的增大,开始下降明显,最后趋于平缓。根据数据结果,取测试结束前,剪切速率为250~300 s-1时间段内的平均黏度为稳定黏度,测试开始时测得的最大黏度为起始黏度,与落球试验计算所得黏度整理比较(见图 6)。

|
图 6 浑水体浓度与黏度关系图 Fig. 6 Relationship between concentration and viscosity |
将浑水体利用落球法试验和流变仪试验得到的黏度整理在表 1中。落球法试验所得黏度与流变仪测得的起始黏度量级相同,且随含沙量变化的趋势相同,但是与流变仪试验得到的稳定黏度差距较大,相差达两个数量级。且当浓度超过400 g/L时,黏度增幅显著变大。
|
|
表 1 落球法与流变仪测试的浑水体黏度值表 Table 1 Test viscosity of turbid water in drop ball test and rheometer test |
在根据斯托克斯公式计算流体黏度时,需满足待测流体样品是无限广深且无涡流的假设前提。试验中所用小球直径为1.59 cm,盛放样品水槽尺寸21 cm×20 cm×40 cm,相对于玻璃球可以认为无限广深,且小球下落位置为水槽中心,远离边壁。在小球下落过程中,由于自身质量较轻,减去反射板重力及滑轮阻力后,其在浑水中下落速度较慢。在浓度为280 g/L的浑水体中下落最快,为3 cm/s,在低速下落过程中,未见光滑小球四周产生涡流,因此,落球法试验计算得到的低速层流状态下的黏度值具有可靠性。
流变仪试验测得的起始黏度,与落球法测度数据在同一个量级,但是表 1中给出的数据普遍小于落球法的测值。原因在于流变仪在转子在开始低速转动中,剪切速率低于50 s-1时,测试含沙量低于400 g/L的浑水体时剪切应力过小,仪器未能有效记录数据,从而难以获得最起始运动状态下的黏度数据。由此对低速运动状态下的浑水体黏度测量,宜采用落球法,或者使用更高测试精度的流变仪。
钱宁等指出,当水流中有大量粒径小于0.01 mm颗粒时,此时不能把这种含沙水体继续当作牛顿流体来看待[14]。吕楚岫等通过测定不同浓度的高岭土浑水体,指出当含沙浑水体浓度低于340 g/L时,仍可视为牛顿流体[8]。在本文试验中,配制的280和300 g/L的浑水体浓度低于340 g/L,试验发现存在一定的剪切稀化现象,如图 2所示可以用赫巴模型描述[15]。但是小于340 g/L浓度的两个样品在用赫巴模型描述时,其拟合线与剪切应力坐标轴存在较小的截距,约为0.01 Pa量级,若精度要求不高,浓度为280和300 g/L的浑水体也可视为牛顿流体。在落球法试验与流变仪测试试验中,起始黏度与稳定黏度在各浓度组中均存在较大差异,稳定黏度比起始黏度小得多,差百倍量级。在落球试验中,由于小球表面光滑,落速较慢,其周围的流体以层流的形式运动,这与流变试验中,转子刚开始启动时情况一致,转子刚启动时,剪切速率接近0,转子周围流体做层流运动。在有速度梯度的流场中会产生流动阻力,通常把这种阻止流体运动的性质就叫做黏度[16],流体的黏度是一种内摩擦阻力。流变仪测试在开始启动时,转子在这种阻力的作用下,带动周围的液体运动,这时所测得的黏度最大,当剪切速率变大,转子相对于液体的速度差越来越大,流体的层流状态被破坏,黏度迅速降低,且随着剪切速率的增大,黏度的降低越来越缓慢。
在实际的工程中,要评估海底构筑所受浑水流的拖曳力,需考虑浑水流的黏度,而浑水流的状态不同,其黏度的参考标准也不一样。对于速度较慢,以层流的形式绕流的浑水流,可使用起始黏度计算拖曳力系数,评估构筑物的稳定性,而对于流速较快的浑水流,层流状态已被破坏,则应用稳定黏度。
对于牛顿流体,常用雷诺数来判断其流态,Re临界值约为2 000~2 100。而对于非牛顿流体,其雷诺数是其流变参数的函数。有研究给出非牛顿流体在不同的流变函数情况下的临界雷诺数,可以通过临界雷诺数推测浑水体的流动状态,进而确定在计算时所需的黏度种类[17-18]。海岸风暴浪、海底滑坡、地震等作用形成的海底浑水体,往往运动速度较快,据推测,水下碎屑流最快时速可达30 m/s[19],在这样的浑水体内部,湍流剧烈,内部有充分的动力作用,在计算其对构筑物的作用力时,可以用稳定黏度。而例如航道落淤形成的浮泥层,强风浪结束后落淤形成的浮泥层的流动,其含沙量较高,速度较慢,多为层流[20],在计算这种浑水体对构筑物的作用力时,则要根据实际情况,确定选择层流条件下的起始黏度还是动力作用下的稳定黏度。
4 结论本文通过落球法与流变仪试验,测定了不同含沙量浑水体的黏度,将浑水体的黏度分为层流状态下的起始黏度与动力作用后的稳定黏度,落球法试验得到的黏度为起始黏度,流变仪测试得到的黏度在测试开始后出现的黏度最大值为起始黏度,黏度趋于平稳后的值为稳定黏度。对于含沙量不同的浑水体,两种试验方法得到的起始黏度数值与变化趋势相近。试验给出如下结果:
(1) 含沙浑水体浓度不同,黏度不同,随浓度的增大,黏度增大;当浓度大于400 g/L时,黏度增幅变大,落球试验与流变仪测试试验的结果一致。
(2) 所测400~500 g/L浓度范围内的含沙浑水体均为非牛顿流体,浓度低于400 g/L浓含沙浑水体在低精度要求时可视为牛顿流体。将剪切应力-剪切速率曲线与赫巴模型曲线进行拟合,相关系数均大于0.9,在计算其对构筑物作用力及浑水体流动特征时,不能按照牛顿流体来计算。
(3) 含沙浑水体有起始黏度与稳定黏度两种黏度值,浓度大于400 g/L的浑水体,起始黏度约为动力作用后的稳定黏度的100倍。在计算浑水体对构筑物的作用力时,需考虑浑水体的具体流态来确定使用的黏度种类,动力作用较强的如高速的浊流碎屑流等,应使用稳定黏度;动力作用较弱的如慢速运动的浮泥层等,应使用起始黏度。
| [1] |
Nadim F. Risk Assessment for Earthquake-Induced Submarine Slides[M]. Berlin: Submarine Mass Movements and Their Consequences, 2012: 15-27.
(  0) 0) |
| [2] |
Fine I V, Rabinovich A B, Bornhold B D, et al. The grand banks landslide-generated tsunami of November 18, 1929: preliminary analysis and numerical modeling[J]. Marine Geology, 2005, 215(1-2): 45-57. DOI:10.1016/j.margeo.2004.11.007
(  0) 0) |
| [3] |
Carter L, Milliman J D, Talling P J, et al. Near-synchronous and delayed initiation of long run-out submarine sediment flows from a record-breaking river flood, offshore Taiwan[J]. Geophysical Research Letters, 2012, 39(12): 12603.
(  0) 0) |
| [4] |
徐景平. 海底浊流研究百年回顾[J]. 中国海洋大学学报(自然科学版), 2014, 44(10): 98-105. Xu J P. Turbidity current research in the past century: an overview[J]. Periodical of Ocean University of China, 2014, 44(10): 98-105. (  0) 0) |
| [5] |
王燕.黄河口高浓度泥沙异重流过程-现场观测与数值模拟[D].青岛: 中国海洋大学, 2012. Wang Yan. Process of Higha-Concentrated Sediment Hyperpycnal Flow at the Huanghe River Mouth: In-Situ Observations and Numerical Simulation[D]. Qingdao: Ocean University of China, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012506611.htm (  0) 0) |
| [6] |
Zakeri A, Høeg K, Nadim F. Submarine debris flow impact on pipelines-Part Ⅰ: Experimental investigation[J]. Coastal Engineering, 2008, 55(12): 1209-1218. DOI:10.1016/j.coastaleng.2008.06.003
(  0) 0) |
| [7] |
Zakeri A, Høeg K, Nadim F. Submarine debris flow impact on pipelines-Part Ⅱ: Numerical analysis[J]. Coastal Engineering, 2009, 56(1): 1-10. DOI:10.1016/j.coastaleng.2008.06.005
(  0) 0) |
| [8] |
庞启秀.水流作用下块体受力试验研究[D].南京: 河海大学, 2005. Pang Qi-xiu. Experimental Study of the Hydrodynamic Forces on the Square-Section Cylinder[D]. Nanjing: Hehai University, 2005. http://cdmd.cnki.com.cn/article/cdmd-10294-2005042692.htm (  0) 0) |
| [9] |
吕楚岫, 许国辉, 任宇鹏, 等.不同含沙量浑水体流变特性试验研究[J].中国海洋大学学报(自然科学版), 2017, 47(1): 43-51. Lv Chu-xiu. Experimental Study on the Rheological Properties of Turbid Water in Different Concentrations[J]. Periodical of Ocean University of China, 2017, 47(1): 43-51. http://qdhy.cbpt.cnki.net/WKD/WebPublication/paperDigest.aspx?paperID=091668e5-d94f-4f21-b3da-bc8696db5b76 (  0) 0) |
| [10] |
White F M. Viscous Fluid Flow[M]. Boston: Mc Graw-Hill Higher Education, 2006: 548-550.
(  0) 0) |
| [11] |
Kundu P K. Fluid mechanics[J]. Fluid Mechanics, 2002, 46(10): 346-369.
(  0) 0) |
| [12] |
施庆珊, 王计伟, 欧阳友生, 等.非牛顿流体粘度测定方法研究进展[J].发酵科技通讯, 2011, 40(2): 42-45. Shi Qing-shan. Progress in the study of non Newtonian fluid viscosity measurement[J]. Fermenting Science and Technology Communication, 2011, 40(2): 42-45. http://www.cnki.com.cn/Article/CJFDTotal-FJKJ201102017.htm (  0) 0) |
| [13] |
Locat J. Normalized Rheological Behaviour of Fine Muds and Their Flow Properties in a Pseudoplastic Regime[C]. San Francisco: ASCE First International Conference, 1997: 260-269.
(  0) 0) |
| [14] |
钱宁, 万兆惠.泥沙运动力学[M].北京: 科学出版社, 2003. Qian Ning. Mechanics of Sediment Transport[M]. Beijing: Science Press, 2003. (  0) 0) |
| [15] |
张仲寅, 乔志德编著.粘性流体力学[M].北京: 国防工业出版社, 1989. Zhang Zhong-yin, Qiao Zhi-dei. Viscous Fluid Mechanics[M]. Beijing: National Defense Industry Press, 1989. (  0) 0) |
| [16] |
巴勒斯.流变学导引[M].北京:中国石化出版社, 1992. Barnes. Rheology Guidance[M]. Beijing: Sinopec Press, 1992. (  0) 0) |
| [17] |
岳湘安, 陈家琅.非牛顿流体流动的稳定性参数Y及其应用[J].水动力学研究与进展, 1987(3): 114-122. Yue Xiang-an. The stability parameter Y of non Newtonian fluid flow and its application[J]. Research and Development of Hydrodynamics, 1987(3): 114-122. http://www.cnki.com.cn/Article/CJFDTotal-SDLJ198703011.htm (  0) 0) |
| [18] |
侯卓识, 周宇鹏, 任照照, 等.赫巴流体在圆管中流动状态的转变[J].科学技术与工程, 2012, 12(11): 2521-2524. Hou Zhuo-shi. Change the present flow state of HB fluid in circular pipe[J]. Science and Technology and Engineering, 2012, 12(11): 2521-2524. http://www.cnki.com.cn/Article/CJFDTotal-KXJS201211004.htm (  0) 0) |
| [19] |
Blasio F V D, Elverhøi A, Issler D, et al. Flow models of natural debris flows originating from overconsolidated clay materials[J]. Marine Geology, 2004, 213(1-4): 439-455. DOI:10.1016/j.margeo.2004.10.018
(  0) 0) |
| [20] |
杨小宸, 张庆河, 赵洪波, 等. 浮泥沿航道流动的数值模拟[J]. 泥沙研究, 2013(4): 13-20. Yang xiaohuan, Zhang qinghei, Zhao hongbo, et al. Numerical simulation of the flow of floating mud along the channel[J]. Sediment Research, 2013(4): 13-20. DOI:10.3969/j.issn.0468-155X.2013.04.003 (  0) 0) |
2. Ocean University of China, Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering, Qingdao 266100, China;
3. Ocean University of China, College of Environmental Science and Engineering, Qingdao 266100, China
 2019, Vol. 49
2019, Vol. 49


