海洋立管作为海面浮式装置和海底井口的主要连接件,是海洋油气开发中的重要结构物之一。由于深海立管细长柔性和只在两端有支撑的特点,海面波浪、海流和内波等对立管的作用会对立管的工作效率和安全性有较大影响,因此必须对海洋环境下立管的动力特性进行研究。涡激振动是立管的一种重要流固耦合形式,其周期性振动和锁振时的大振幅震荡是立管疲劳损伤的重要原因。因此研究涡激振动对海洋立管结构设计和安全评估具有重要意义。
海洋内波是一种在密度稳定层化的海水内部所产生的波动,在全世界海域中内波很常见。有大量的观测资料表明中国南海海域内波活动频繁,分布范围广,振幅大。由于内波密度跃层上下流速方向相反,处于内波流场中的柱体绕流、漩涡脱落和结构与流场的耦合作用更加复杂,立管的响应也更加复杂。
对于内波和海洋立管之间的相互作用,蔡树群等[1]引入Morison公式并采用模态分析法计算孤立子内波对圆柱形桩柱作用力,发现孤立子内波对桩柱的作用力和力矩远大于表面波; 程友良[2]和叶春生[3]相继采用Morison公式计算了内波作用于小直径圆柱体的作用力,得出内波在两层流体之间产生的作用力方向相反的结论,并指出最大作用力和力矩与内波振幅相关。谢皆烁等[4]用MCC理论和KdV两种理论对比分析了两层流体中大振幅、强非线性内孤立波对小直径圆柱体的作用力和力矩。徐肇廷等[5]通过试验研究了内波与水平桩柱之间的作用。谢皆烁等[6]还基于连续分层理论,结合Morison公式计算了内孤立波和潮汐流共同作用下小尺度桩柱的受力,发现无论内孤立波的传播方向与潮汐流方向一致或相反,考虑内孤立波后桩柱的受力将远大于仅考虑潮汐流的受力。李巍等[7]采用CFD方法建立内孤立波数值水槽,用ABAQUS软件模拟管道,分析了内孤立波与立管的相互作用,发现内孤立波不仅会对深海立管产生突发性剪切荷载作用,还会使立管产生大幅度变形现象。蒋武杰等[8]用振型叠加法研究了顶张力立管在内孤立波与非均匀海流共同作用下的多模态振动,发现在非均匀海流下深海张力立管会发生大振幅多模态横向组合涡激共振。袁玉堂等[9]基于半潜式海洋平台基本结构参数和南海海洋环境条件参数,分别模拟得出波长、波高和密度跃层位置等对周期内波载荷的影响及作用力特点,并分析了相位差的影响。郭海燕等[10-11]采用数值与试验结合的方法, 对两层流体中内孤立波对不同水深竖直圆柱体水平作用力进行了分析,并通过数值模拟的方法分析了潜体所受垂向力及力矩在内波流场中不同位置处的时历变化。陈伟民等[12]基于模态能量理论的多模态锁频计算方法,并结合改进的尾流振子模型对内波、海流等不同流场下立管涡激振动进行了响应分析。
目前对于内波流场与立管相互作用研究多为顶张力立管,对于内波流场中悬链线立管的振动研究较少,而且均为顺流向。内孤立波的稳定传播是非线性效应和频散效应动力学平衡的结果,根据MICHALLET H[13]和黄文昊等[14]的研究,本文内孤立波选用eKdv理论描述。本文基于内波流场的eKdv理论并结合尾流振子模型和挠性立管的非线性振动方程建立内波流场中悬链线立管的运动模型,分析了内波流场对悬链线立管升力方向涡激振动的影响,并分析了不同内波波高和不同密度跃层位置对悬链线立管涡激振动响应的影响。
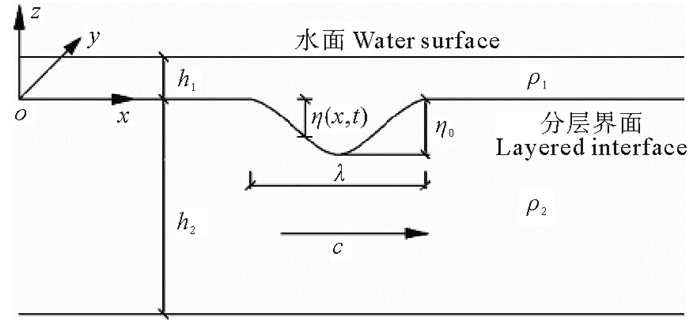
1 数值方法 1.1 内波理论(见图 1)
|
图 1 内孤立波及其参数 Fig. 1 Internal solitary waves and their parameters |
设内孤立波振幅为η0,自由面为刚盖的情况下,eKdv理论的波面方程为:
| $ \eta(x, t)=\frac{\eta_{0}}{B+(1-B) \cosh ^{2}\left[\frac{x-c_{e k d v} t}{\lambda_{ {ekdv }}}\right]}, $ | (1) |
其中:
| $ B=\frac{-\eta_{0} c_{3}}{2 c_{1}+c_{3} \eta_{0}}, $ | (2) |
| $ c_{e k d v}=c_{0}+\frac{\eta_{0}}{3}\left(c_{1}+\frac{1}{2} c_{3} \eta_{0}\right), $ | (3) |
| $ \lambda_{e k d v}=\sqrt{\frac{12 c_{2}}{\left(c_{1}+\frac{1}{2} c_{3} \eta_{0}\right) \eta_{0}}}, $ | (4) |
| $ c_{0}=\sqrt{\frac{g\left(\rho_{2}-\rho_{1}\right) h_{1} h_{2}}{\rho_{1} h_{2}+\rho_{2} h_{1}}}, $ | (5) |
| $ \begin{aligned} c_{1} &=\frac{3}{2} \frac{c_{0}}{h_{1} h_{2}} \frac{\rho_{2} h_{1}^{2}-\rho_{1} h_{2}^{2}}{\rho_{2} h_{1}+\rho_{1} h_{2}}, \\ c_{2} &=\frac{c_{0} h_{1} h_{2}}{6} \frac{\rho_{1} h_{1}+\rho_{2} h_{2}}{\rho_{2} h_{1}+\rho_{1} h_{2}}, \\ c_{3} &=\frac{3 c_{0}}{h_{1}^{2} h_{2}^{2}}\left[\frac{7}{8}\left(\frac{\rho_{1} h_{2}^{2}-\rho_{2} h_{1}^{2}}{\rho_{1} h_{2}+\rho_{2} h_{1}}\right)^{2}-\frac{\rho_{1} h_{2}^{3}+\rho_{2} h_{1}^{3}}{\rho_{1} h_{2}+\rho_{2} h_{1}}\right]。\end{aligned} $ | (6) |
式中:h1为上层流体深度; h2为下层流体深度; ρ1为上层流体密度; ρ2为下层流体密度; λ为内孤立波特征波长; cekdv为内孤立波相速度。
波面方程已知后,可由水动力学和流体连续方程内孤立波引起的流场水平方向的速度和加速度。
其中eKdv理论适合振幅与水深比大于0.1的情况,并且存在极限振幅为:
| $ \left|\eta_{\text {0lim }}^{e k d v}\right|=\left| \frac{4 h_{1} h_{2}\left(h_{1}-h_{2}\right)}{h_{1}^{2}+h_{2}^{2}+6 h_{1} h_{2}} \right|。$ | (7) |
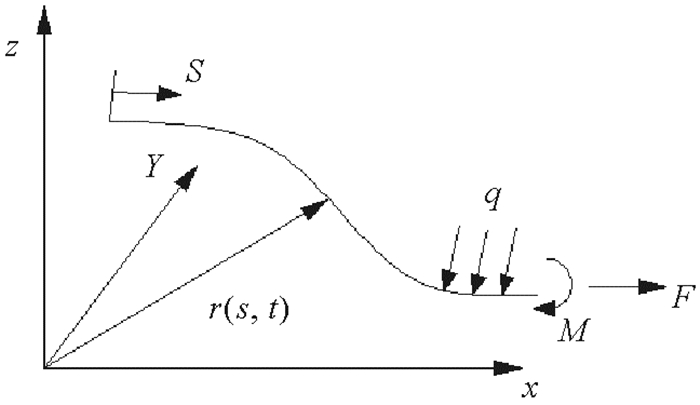
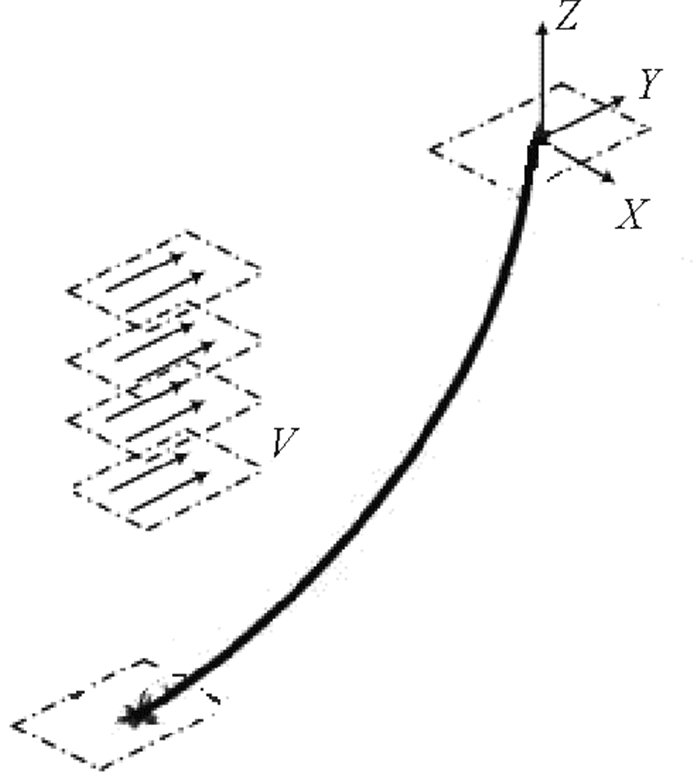
本文基于柔性杆模型(见图 2)建立了刚悬链线立管(见图 3)的运动方程,图 2为柔性立管模型示意图。在三维笛卡尔坐标系中,将柔性杆变形后的空间曲线r(s, t)表示为弧长s和时间t的函数。忽略转动惯量和剪切变形的影响,根据动量守恒和动量矩守恒可得:
| $ \boldsymbol{F}^{\prime}+\boldsymbol{Q}=\rho \ddot{\boldsymbol{r}}+\rho_{f} \frac{D^{2} \boldsymbol{r}}{D t^{2}}, $ | (8) |
| $ \boldsymbol{M}^{\prime}+\boldsymbol{r}^{\prime} \times \boldsymbol{F}+\boldsymbol{m}=0。$ | (9) |
|
图 2 柔性杆模型 Fig. 2 Flexible rod model |
|
图 3 钢悬链线立管 Fig. 3 Steel catenary riser |
其中:F为作用在立管轴线上的合力; Q为立管单位长度所受的外力(包括立管单位长度的重力、周围海水的水静力荷载和水动力荷载); ρ为立管的密度; ρf为内流密度; M为作用于单位长度立管轴线上的内力矩; m为施加于单位长度立管上的外力矩,式中符号右上角撇号表示变量对空间变量求偏导数; 变量正上方圆点代表变量对时间变量求偏导数(下同)。
内力矩由弯矩和扭矩两部分构成,由立管刚度的轴对称性和欧拉-伯努利梁理论可得:
| $ \boldsymbol{M}=\boldsymbol{r}^{\prime} \times E I \boldsymbol{r}^{\prime \prime}+\boldsymbol{H} r^{\prime}。$ | (10) |
式中: EI为立管弯曲刚度; H为扭矩。一般立管上没有均布扭矩和分布外力矩的作用,因此H=0, m=0。
将(10)代入(9)中,并联立(8)(9)得到立管的运动方程为:
| $ \left(\rho+\rho_{f}\right) \ddot{\boldsymbol{r}}+2 \rho_{f} V_{f} \dot{\boldsymbol{r}}^{\prime}+\left(E I \boldsymbol{r}^{\prime \prime}\right)^{\prime \prime}-\left(\bar{\lambda} \boldsymbol{r}^{\prime}\right)^{\prime}=\boldsymbol{Q}。$ | (11) |
式中:
假定上述推导过程中立管伸长量为小量,变形条件满足
本文采用Facchinetti[15]推荐的尾流振子模型,模拟流体对立管的涡激升力,该模型采用经典模拟振子运动的Van Der Pol方程表达漩涡脱落的振动特性,仅考虑结构与流体的线性耦合项,相比其他振子模型简单有效,其振动方程为:
| $ \ddot{q}+\varepsilon \omega_{f}\left(q^{2}-1\right) \dot{q}+\omega_{f}^{2} q=F_{q}。$ | (12) |
其中:q为升力振子系数; ε为非线性项的小参数,一般ε=0.3,ωf=2πStUc/D为漩涡脱落频率; Uc表示立管外部流体速度; St为Strouhal数,取为0.2;Fq=
如图 2所示,立管所在平面为YOZ,当外流沿Y轴正方向流动时,立管会在XOZ平面内产生的横向涡激振动。由于漩涡脱落引起的涡激升力为:
| $ F_{L}=\frac{1}{2} \rho_{w} D_{0} C_{L}\left(U_{c}-\dot{y}\right)^{2}-\frac{1}{2} \rho_{w} D_{0} C_{\mathrm{D}} V_{r} \dot{x}。$ | (13) |
式中:D0为立管外径; Uc为立管外部流体速度; Vr为立管和流体相对速度; CD和CL分别为立管拖曳力系数和升力系数,CD取0.7,
采用有限元的方法,把立管沿轴向离散成若干长度为L单元,将单元内部的变量
| $ r_{i}(s, t)=A_{l}(s) U_{i l}(t), $ | (14) |
| $ \bar{\lambda}(s, t)=P_{m}(s) \bar{\lambda}_{m}(t)。$ | (15) |
其中Al和Pm分别为三次和二次Hermite插值函数。
将(11)式和变形条件分别乘以δri然后沿单元全长积分,可以得到每个立管单元矩阵形式的运动微分方程和变形协调方程:
| $ \begin{aligned} &\left(\boldsymbol{M}_{i j l k}+\boldsymbol{M}_{i j l k}^{a}\right) \ddot{U}_{j k}+\boldsymbol{C}_{i j l k}^{f} \dot{U}_{j k}+\left(\boldsymbol{K}_{i j l k}^{1}+\bar{\lambda}_{n} \boldsymbol{K}_{n j l k}^{2}\right) U_{j k}-\\ F_{i l}=& 0, \end{aligned} $ | (16) |
| $ \boldsymbol{G}_{m}=\boldsymbol{A}_{m i l} U_{k i} U_{k l}-\boldsymbol{B}_{m}-\boldsymbol{C}_{m n} \bar{\lambda}_{n}+\boldsymbol{C}_{m n} h_{n}=0。$ | (17) |
式(16)中:Mijlk为质量矩阵; Mijlka为附加质量矩阵; Cijlkf为因内流柯氏力而引起的阻尼矩阵; Kijlk1为与材料抗弯刚度EI相关的刚度矩阵; Knijlk2为由立管内部张力和曲率引起的刚度矩阵。式(17)中:
| $ A_{m i l}=\frac{1}{2} \int_{0}^{L} P_{m} A^{\prime}{ }_{i} A^{\prime}{}_{l} \mathrm{d} s ; $ |
| $ B_{m}=\frac{1}{2} \int_{0}^{L} P_{m} \mathrm{~d} s; $ |
| $ C_{m}=\frac{1}{E A} \int_{0}^{L} P_{m} P_{n} \mathrm{~d} s ; $ |
| $ h_{n}=A_{D} P_{D n}-A_{d} P_{d n}。$ |
其中:E为立管弹性模量; A、AD和Ad分别为管截面面积、外直径面积和内直径截面面积; PDk和Pdk(k=1, 2, 3)分别为立管每单元两端点和终点位置处的管内外静水压强。本文探讨的是三维问题,其中i, j=1, 2, 3;下标l, k, m, n为Hermite插值函数各项的编号。
同样用三次Hermite插值函数对尾流振子模型进行离散得到矩阵形式的单元运动方程:
| $ \left[\boldsymbol{M}_{e q x}\right]\left\{\ddot{q}_{x}\right\}+\left[\boldsymbol{C}_{e q x}\right]\left\{\dot{q_{x}}\right\}+\left[\boldsymbol{K}_{e q x}\right]\left\{q_{x}\right\}=\left\{\boldsymbol{F}_{e q x}\right\}。$ | (18) |
将钢悬链线立管的单元耦合振动方程组(16)(17)(18)分别集合得到整体耦合方程组的矩阵表达式之后,采用Newmark-β算法求解尾流振子模型涡激力作用下钢悬链线立管的涡激振动响应。在此基础上采用振型叠加法对钢悬链线立管的位移振动响应结果进行分析,得到钢悬链线立管的各阶涡激振动模态权重时程变化,并讨论钢悬链线立管的涡激振动特性。
3 模型验证Larsen等[16]比较了7种柔性立管涡激振动数值模型,发现各种数值模型的计算结果之间差别较大,并且与实际工程还有一定的差距,还需改进计算模型。为了验证本计算模型的有效性,将表 1中悬链线立管计算结果与Zhu H[17]试验结果进行对比,如图 4所示,模拟结果和实验结果对比发现立管涡激振动响应振幅大小有一定的差别,但响应频率和响应变化趋势基本相同,可以说明本文计算结果的有效性。
|
|
表 1 立管模型参数 Table 1 Riser model parameters |
|
(细实线为数值模拟结果,带标记点实线为实验结果。The red line is the numerical simulation result, and the blue line is the experimental result. ) 图 4 数值模型与实验结果对比 Fig. 4 Comparison between numerical models and experimental results |
参考蔡树群等[1]在南海北部一次内孤立波的实测资料,所采用下凹型内孤立波参数如下:上层水深h1=60 m,下层水深h2=412 m,上层水密度为ρ1=1.025 kg/m3,下层水密度为ρ2=1.028 kg/m3,这里内孤立波波幅取为η0=-62.5 m,内孤立波的传播方向与悬链线立管所处空间位置的面平行,如图 2中所示。且初始时刻内孤立波波谷距悬链线底端水平距离取为600 m。在计算中立管长度取为L=600 m,外径D=0.812 m,壁厚为δ=0.027 6 m,弹性模量E=2.1×1011 N/m2,立管密度ρr=7 850 kg/m3,泊松比υ=0.3,本文中未考虑管道内部流体的作用。
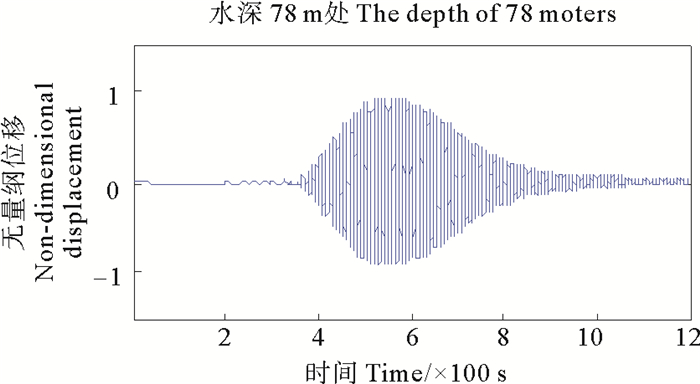
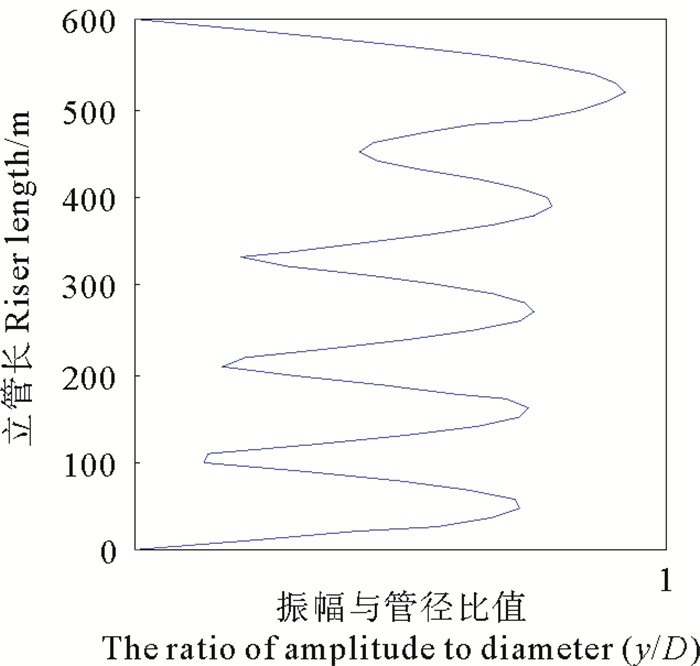
图 5为悬链线立管水深78 m位置处单元升力方向涡激振动位移时程曲线,其中78 m水深较为接近密度跃层位置。可以看出前400 s内立管的位移很小,这是因为初始时刻内孤立波距离立管距离较远,在立管位置处所形成的流场还很小; 400~800 s立管升力方向发生剧烈的涡激振动现象,并且随时间的变化涡激振动幅值先增大后减小,这种现象是因为400~800 s之间内孤立波经过立管,流场流速突发性增大,涡激荷载突然增大导致涡激振动位移大小变化,并且立管周围所形成的内波流场流速随时间先增加后减小,和袁玉堂等[10]中结论较为吻合。图 6为沿立管长度方向涡激振动无量纲位移包络图,可以看出在密度跃层附近立管升力方向的涡激振动振幅比立管其他位置处的振幅稍大。
|
图 5 悬链线立管单元涡激振动时程曲线 Fig. 5 Time-history curve of vortex-induced vibration of catenary riser unit |
|
图 6 沿立管长度方向涡激振动无量纲位移包络图 Fig. 6 Dimensionless displacement envelope of vortex-induced vibration along the length of the riser |
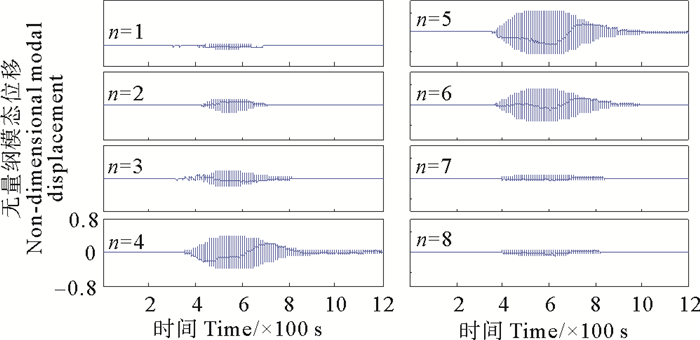
对内孤立波流场中悬链线立管的涡激振动进行模态分析,图 7所示为前8阶模态权重时程变化曲线,可以发现在内孤立波经过悬链线立管时,其中四、五、六阶模态权重逐渐变大并占主导。
|
图 7 前八阶振型权重时程变化 Fig. 7 The first eight modes of mode weight time history changes |
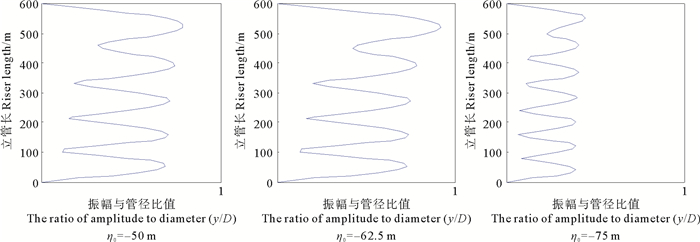
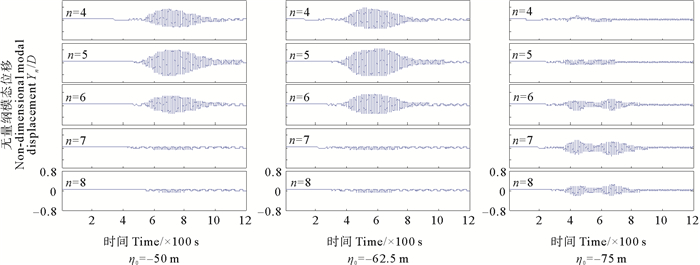
本文考虑了3种不同波幅内波对悬链线立管横向运动的影响。3种内波波幅分别为:-50、-62.5、-75 m,其他条件不变,3种波幅均适用于eKdv理论。
由图 8和图 9发现:内波波高由50 m变化到62.5 m时,悬链线立管涡激振动位移变化不太明显,对应的振动模态变化也很小,当波高增加到75 m时,内波流场激起了悬链线立管振动模态逐渐从四、五、六阶转变为了六、七、八阶占主导,从而导致其涡激振动位移明显变小。说明悬链线立管的振动主导模态未发生变化时,内孤立波波高对涡激振动响应的影响较小,若立管振动模态发生转换,则内波波高对涡激振动幅值影响较为明显。
|
图 8 三种波幅内孤立波流场下悬链线立管横流向涡激振动位移包络图 Fig. 8 Displacement diagram of vortex-induced vibration displacement of catenary riser under three amplitudes internal wave flow field |
|
图 9 3种波幅内孤立波流场下悬链线立管横流向振动模态权重 Fig. 9 Transverse modal modal weights of catenary risers under three amplitudes internal wave flow field |
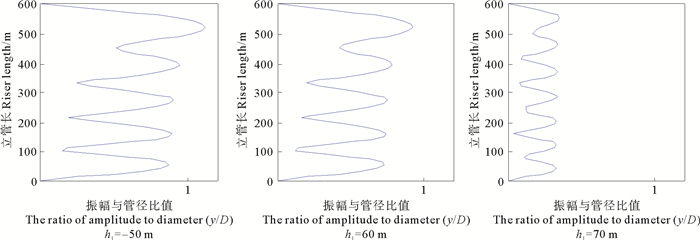
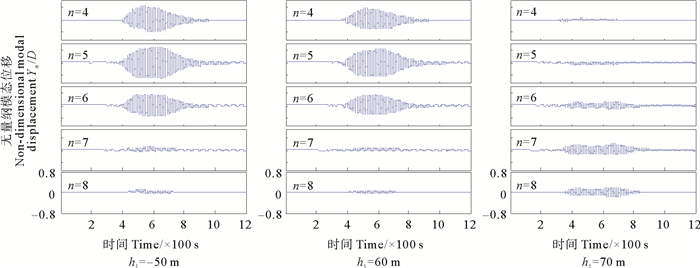
海水密度跃层位置依次为50 m水深、60 m水深和70 m水深,波高(-62.5 m)保持不变。图 10所示为3种密度跃层内孤立波流场下悬链线立管涡激振动位移包络图,图 11所示为3种密度跃层内孤立波流场下悬链线立管升力方向振动模态权重。分析可知:随着密度跃层位置的加深,悬链线立管涡激振动位移明显减小,对应的悬链线立管的横流向振动逐渐变为更高阶主导。所以,密度跃层位置较接近水面的内孤立波对悬链线立管横向位移振动影响较大。
|
图 10 3种密度跃层内孤立波流场下悬链线立管横流向涡激振动位移包络图 Fig. 10 Displacement diagram of vortex-induced vibration displacement of catenary riser under internal wave flow field in three density hop position |
|
图 11 3种密度跃层内孤立波流场下悬链线立管横流向振动模态权重 Fig. 11 Transverse modal modal weights of catenary risers in internal wave flow fields in three density hop position |
本文研究了悬链线立管在内孤立波流场中的横流向运动响应,并分析了不同内波波高和不同密度跃层位置对悬链线立管横向运动响应的影响,可以得到如下结论:
(1) 内孤立波经过悬链线立管时,在升力方向会引起悬链线立管突然增大的涡激振动,并以高阶模态振动为主,其中立管振动位移最大值发生于流体密度跃层位置附近;
(2) 随着内孤立波波幅增大悬链线立管逐渐转变为更高阶模态振动,涡激振动位移相应减小;
(3) 随着流体密度跃层位置变深,悬链线立管涡激振动明显减小,振动逐渐变为更高阶模态占主导,说明密度跃层接近水面的内孤立波对悬链线立管安全性影响较大。
| [1] |
Cai S Q, Long X M, Gan Z J. A method to estimate the forces exerted by internal solitons on cylindrical piles[J]. Ocean Engineering, 2003, 30(5): 673-689. DOI:10.1016/S0029-8018(02)00038-0
(  0) 0) |
| [2] |
Cheng Y L, Li J C, An L S, et al. The Induced Flow Field by Internal Solitary Wave and Its Action on Cylindrical Piles in the Stratified Ocean[C]. Dalian: Proceeding of the 4th International Conference on Fluid Mechanics, 2004.
(  0) 0) |
| [3] |
叶春生, 沈国光. 海洋内波对小尺度圆柱体作用力的分析与计算[J]. 天津大学学报, 2005, 38(2): 102-108. Ye C S, Shen G G. Numerical calculation and analysis about internal waves force on smal1-scale cylinder[J]. Journal of Tianjin University, 2005, 38(2): 102-108. (  0) 0) |
| [4] |
Xie J, Jian Y, Yang L. Strongly nonlinear internal soliton load on a small vertical circular cylinder in two-layer fluids[J]. Applied Mathematical Modelling, 2010, 34(8): 2089-2101. DOI:10.1016/j.apm.2009.10.021
(  0) 0) |
| [5] |
徐肇廷, 陈旭, 吕红民, 等. 内波场中水平桩柱波阻的实验研究[J]. 中国海洋大学学报(自然科学版), 2007, 37(1): 1-6. Xu Z T, Chen X, Lv H M, et al. An experimental study of wave resistance of honrizontal cylinder in internal waves[J]. Periodical of Ocean University of China, 2007, 37(1): 1-6. (  0) 0) |
| [6] |
Xie J, Jian Y, Yang L. Strongly nonlinear internal soliton load on a small vertical circular cylinder in two-layer fluids[J]. Applied Mathematical Modelling, 2010, 34(8): 2089-2101. DOI:10.1016/j.apm.2009.10.021
(  0) 0) |
| [7] |
刘碧涛, 李巍, 尤云祥, 等. 内孤立波与深海立管相互作用数值模拟[J]. 海洋工程, 2011, 29(4): 1-7, 50. Liu B T, LI W, You Y X, et al. Numerical simulation of interaction of internal solitary waves with deep-sea risers[J]. The Ocean Engineering, 2011, 29(4): 1-7, 50. (  0) 0) |
| [8] |
蒋武杰, 林忠义, 尤云祥, 等. 内孤立波与非均匀海流共同作用下顶张立管动力特性[J]. 水动力学研究与进展(A辑), 2012, 27(4): 424-435. Jang W J, Lin Z Y, You Y X, et al. Dynamic characteristics of a top tension riser under combined internal solitary wave and non-uniform current[J]. Chinese Journal of Hydrodynamics, 2012, 27(4): 424-435. (  0) 0) |
| [9] |
袁玉堂, 牟永春, 李冰. 半潜式海洋平台的周期内波载荷分析[J]. 船海工程, 2012, 41(4): 142-146. Yuan Y T, Mou Y C, Li B. Periodical internal wave load analysis for the semi-submersible platform[J]. Ship and Ocean Engineering, 2012, 41(4): 142-146. (  0) 0) |
| [10] |
殷文明, 郭海燕, 廖发林, 等. 内孤立波对不同水深竖直圆柱体水平作用力分析[J]. 中国海洋大学学报(自然科学版), 2018, 48(9): 125-131. Yin W M, Guo H Y, Liao F L, et al. Analysis of honrizontal forces on vertical cylinders under internal solitary waves in different depth[J]. Periodical of Ocean University of China, 2018, 48(9): 125-131. (  0) 0) |
| [11] |
殷文明, 郭海燕, 吴凯锋, 等. 内孤立波对水平圆柱潜体作用力的计算[J]. 浙江大学学报(工学版), 2016, 50(7): 1252-1257, 1275. Yin W M, Guo H Y, Wu K F, et al. Calculation of internal solitary wave force on horizontal submerged circular cylinder[J]. Journal of Zhejiang University(Engineering Science), 2016, 50(7): 1252-1257, 1275. (  0) 0) |
| [12] |
陈伟民, 郑仲钦, 张立武, 等. 内波致剪切流作用下深海立管的涡激振动[J]. 工程力学, 2011, 28(12): 250-256. Chen W M, Zheng Z Q, Zhang L W, et al. Vortex-induced vibration of deepwater flexible riser experencing internal-wave-induced shear flow[J]. Engineering Mechanics, 2011, 28(11): 250-256. (  0) 0) |
| [13] |
Michallet H, Barthelemy E. Experimental study of large interfacial solitary waves[J]. Journal of Fluid Mechanics, 1998, 366: 159-177.
(  0) 0) |
| [14] |
黄文昊, 尤云祥, 王旭, 等. 有限深两层流体中内孤立波造波实验及其理论模型[J]. 物理学报, 2013, 62(8): 354-367. Huang W H, YouY X, Wang X, et al. Wave-making experiments and theoretical models for internal solitary waves in a two-layer fluid of finite depth[J]. Acta Phys Sin, 2013, 62(8): 354-367. (  0) 0) |
| [15] |
Facchinetti M L, Langre E D, Biolley F. Coupling of structure and wake oscillators in vortex-induced vibrations[J]. Journal of Fluids and Structures, 2004, 19(2): 123-140.
(  0) 0) |
| [16] |
Carl M Larsen, Karl H Halse. Comparison of models for vortex induced vibration of slender structures[J]. Marine Structures, 1997, 10: 413-441.
(  0) 0) |
| [17] |
Zhu H, Lin P, Gao Y. Vortex-induced vibration and mode transition of a curved flexible free-hanging cylinder in exponential shear flows[J]. Journal of Fluids and Structures, 2019, 84: 56-76.
(  0) 0) |
 2021, Vol. 51
2021, Vol. 51


