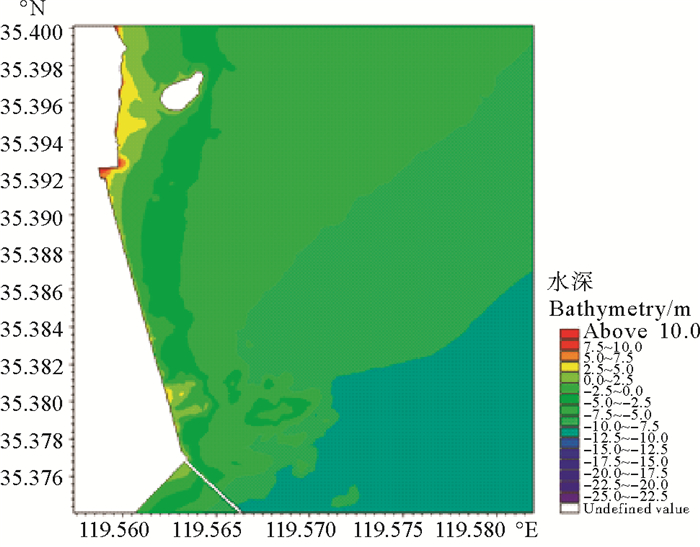
沙质岸滩是海岸带中重要的地貌单元,在人为活动造成的负面环境影响和全球气候变暖的共同作用下,沙质岸滩侵蚀严重[1-2]。对于沙质岸滩侵蚀的修复防护技术,近年来,越来越多的研究者从硬防护转向软防护和软硬结合的防护技术[3-7],人工沙滩与潜堤结合的防护方式就属于软硬结合的防护技术。山东日照月亮湾在1980年代,因为港口建设需要,向海推移数百米建成煤堆场浆砌石直立护岸和3.5 t扭王字块护面斜坡护岸,自然沙滩不复存在,其现状地形如图 1所示。近年来,随着石臼港的搬迁和煤堆场的腾空,新的规划将重新修复月亮湾沙质岸滩,在先期人造、后期自然淤积的共同作用下,逐渐修复形成自然沙滩。
本文针对山东日照石臼港北侧月亮湾沙滩修复工程,采用人工沙滩与潜堤结合的岸滩防护技术,应用XBeach水沙运动数值模型进行岸滩防护剖面演变数值分析[8],研究如何将人工沙滩与潜堤相结合,以达到良好的沙滩防护效果。
1 数值计算原理本文采用XBeach模型进行数值分析,XBeach模型是由荷兰的代尔福特理工大学(TU Delft)和代尔夫特三角洲研究中心(Deltares Institute)联合开发,基于结构化Fortran 77/90架构的开放源码的二维平面海岸动力学数值模型[9]。
|
图 1 日照月亮湾现状地形 Fig. 1 Current topography of Rizhao Moon Bay |
浅水动量方程的波浪作用由基于时间的波能平衡方程得到。考虑能量密度的方向分布,由单一代表频率表示频谱,波能平衡方程为:
| $ \frac{{\partial A}}{{\partial t}} + \frac{{\partial {c_x}A}}{{\partial x}} + \frac{{\partial {c_y}A}}{{\partial y}} + \frac{{\partial {c_\theta }A}}{{\partial \theta }} = - \frac{{{D_{\rm{w}}}}}{\sigma }。$ | (1) |
波作用为:
| $ A\left( {x, y, t.\theta } \right) = \frac{{{S_{\rm{w}}}\left( {x, y, t, \theta } \right)}}{{\sigma (x, y, t)}}。$ | (2) |
其中:θ表示入射波相对x轴的夹角; Sw表示每个方向的能量密度; σ为波浪固有频率。
1.2 浅水方程对于低频波和平均流,采用浅水方程,为考虑波浪引起的质量通量和回流,选用水深平均的广义拉格朗日平均浅水方程(GLM)[10-11]:
| $ \begin{array}{l} \frac{{\partial {u^L}}}{{\partial t}} + {u^L}\frac{{\partial {u^L}}}{{\partial x}} + {v^L}\frac{{\partial {u^L}}}{{\partial y}} - \\ {\rm{ }}f{v^L} - {\nu _h}\left( {\frac{{{\partial ^2}{u^L}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u^L}}}{{\partial {y^2}}}} \right) = \\ \frac{{{\tau _{sx}}}}{{\rho h}} - \frac{{\tau _{_{bx}}^E}}{{\rho h}} - g\frac{{\partial \eta }}{{\partial x}} + \frac{{{F_x}}}{{\rho h}}, \end{array} $ | (3) |
| $ \begin{array}{l} \frac{{\partial {v^L}}}{{\partial t}} + {u^L}\frac{{\partial {v^L}}}{{\partial x}} + {v^L}\frac{{\partial {v^L}}}{{\partial y}} - \\ {\rm{ }}f{u^L} - {\nu _h}\left( {\frac{{{\partial ^2}{v^L}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v^L}}}{{\partial {y^2}}}} \right) = \\ \frac{{{\tau _{sx}}}}{{\rho h}} - \frac{{\tau _{_{by}}^E}}{{\rho h}} - g\frac{{\partial \eta }}{{\partial x}} + \frac{{{F_x}}}{{\rho h}}, \end{array} $ | (4) |
| $ \frac{{\partial \eta }}{{\partial t}} + \frac{{\partial h{u^L}}}{{\partial x}} + \frac{{\partial h{v^L}}}{{\partial y}} = 0。$ | (5) |
其中:τsx和τsy是风引起的剪切应力;τbx和τby是床面剪切应力;η是水位;Fx和Fy是波浪引起的剪切应力;νh是水平黏滞系数;f是科氏力系数。
1.3 泥沙及地形动力控制方程二维沿水深平均的对流扩散方程[12]:
| $ \begin{array}{l} \frac{{\partial hC}}{{\partial t}} + \frac{{\partial hC{u^E}}}{{\partial x}} + \frac{{\partial hC{v^E}}}{{\partial y}} + {\rm{ }}\\ \frac{\partial }{{\partial x}}\left[ {{D_{\rm{h}}}h\frac{{\partial C}}{{\partial x}}} \right] + \frac{\partial }{{\partial y}}\left[ {{D_{\rm{h}}}h\frac{{\partial C}}{{\partial y}}} \right] = \\ {\rm{ }}\frac{{h{C_{{\rm{eq}}}} - hC}}{{{T_{\rm{s}}}}}。\end{array} $ | (6) |
式中:C代表波包时间尺度上水深平均的泥沙浓度;Dh是泥沙扩散参数;挟沙适应时间Ts可以由水深h和泥沙沉降速度ωs简单估计:
| $ {T_s} = {\rm{max}}\left( {0.05\frac{h}{{{\omega _{\rm{s}}}}}, 0.2} \right)s。$ | (7) |
其中当Ts值很小时就可以近似表示瞬时泥沙响应。
基于泥沙输移的梯度,底床高度的改变可以表示为:
| $ \frac{{\partial {Z_{\rm{b}}}}}{{\partial t}} + \frac{{{f_{{\rm{mor}}}}}}{{\left( {1 - p} \right)}}\left( {\frac{{\partial {q_x}}}{{\partial x}} + \frac{{\partial {q_y}}}{{\partial y}}} \right) = 0。$ | (8) |
其中:p是孔隙率,fmor是地形加速系数[12-17];qx和qy为在x和y方向上的泥沙输移率:
| $ {q_x}\left( {x, y, t} \right) = \left[ {\frac{{\partial hC{u^E}}}{{\partial x}}} \right] + \left[ {\frac{\partial }{{\partial x}}\left[ {{D_{\rm{h}}}h\frac{{\partial C}}{{\partial x}}} \right]} \right] $ | (9) |
| $ {q_y}\left( {x, y, t} \right) = \left[ {\frac{{\partial hC{v^E}}}{{\partial y}}} \right] + \left[ {\frac{\partial }{{\partial y}}\left[ {{D_{\rm{h}}}h\frac{{\partial C}}{{\partial y}}} \right]} \right] $ | (10) |
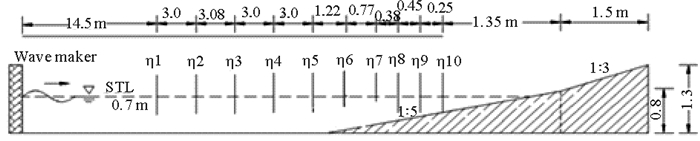
在中国海洋大学山东省海洋工程重点实验室长60 m、宽3 m、高1.5 m的波流水槽中进行物理模型试验,作为数值模型的验证模型。试验装置配置如图 2所示,沙质粒径0.6 mm,岸滩坡度1/5,水位0.7 m,波高0.2 m,周期2.1 s,整个水槽波浪区域范围内布置10个电容式波高仪(见图 2中η1~10)波浪持续作用时间为60 min。
|
图 2 试验装置配置图 Fig. 2 Sketch of the experiment setup |
根据此物理模型工况,应用XBeach建立数值模型,模型网格空间分辨率s为0.03 m,开边界波浪条件为波高0.2 m、周期1.2 s的规则波时间序列,持续计算时间为60 min。
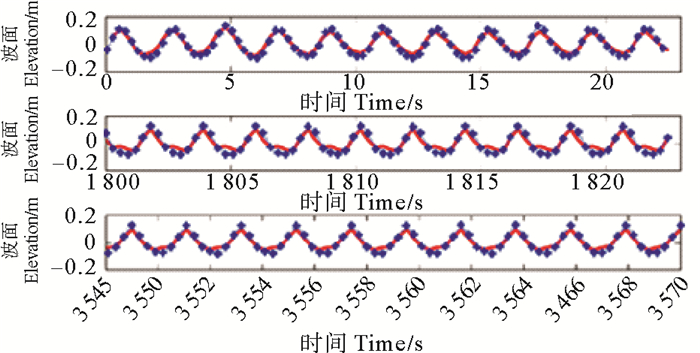
2.2 计算结果比较选取前部(η1)、中部(η5)和后部(η9)3个测点的测试结果与XBeach数值模拟计算结果进行比较,如图 3~5所示。
|
(蓝色测试结果,红色数模结果。Blue line represents simulated data, red line represents measured data. ) 图 3 η1测试结果与数模结果比较 Fig. 3 Comparison of measured data and simulated data of η1 |
|
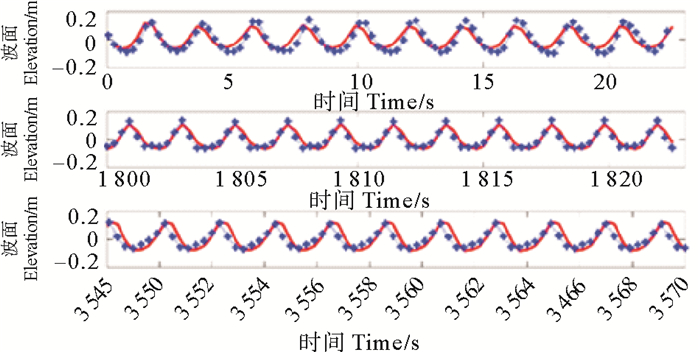
(蓝色测试结果,红色数模结果。Blue line represents simulated data, red line represents measured data. ) 图 4 η5测试结果与数模结果比较 Fig. 4 Comparison of measured data and simulated data of η5 |

|
(蓝色测试结果,红色数模结果。Blue line represents simulated data, red line represents measured data. ) 图 5 η9测试结果与数模结果比较 Fig. 5 Comparison of measured data and simulated data of η9 |
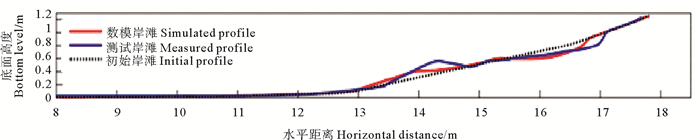
由图 3~5可以看出,红色的数值模拟计算结果与蓝色的物理模型试验测试结果吻合得比较好。图 6进一步给出最终岸滩形态的数模结果与测试结果比较,可以看出数模结果与测试结果的岸滩侵蚀与淤积的位置范围基本一致,但侵蚀与淤积的大小略有差别,最终岸滩形态的吻合效果较波浪差一些。
|
图 6 最终岸滩形态测试结果与数模结果比较 Fig. 6 Comparison of measured data and simulated data of final beach profile |
采用Brier SkillScore (BSS)值来检验数值模拟的准确性和有效性,BSS值是一种常用的检验数值模型有效性的标准[13-15]。BSS表达式如下所示:
| $ BSS = 1 - \left[ {\frac{{\left[ {{{\left| {{x_{\rm{p}}} - {x_{\rm{m}}}} \right|}^2}} \right]}}{{\left[ {{{\left| {{x_{\rm{b}}} - {x_{\rm{m}}}} \right|}^2}} \right]}}} \right]。$ | (11) |
其中:xp是数值模拟计算结果;xm是物理模型测试结果;xb是原始数据。通常BSS值在0.6~0.8之间时,表明此数值模型是有效的[14],而上述XBeach数值模拟的BSS值是0.653,因此,本文采用的数值模拟方法——XBeach模型是有效的、可信赖的。
3 工程数值分析对日照月亮湾进行沙滩修复,在工程海域建设人工沙滩,考虑在后期达到自然维护的效果,采用人工沙滩与潜堤组合的岸滩防护技术。应用XBeach建立其岸滩剖面数值模型,对风暴海况波浪作用下,工程区域无潜堤、有潜堤以及潜堤的不同位置和不同高度进行岸滩剖面演变数值分析。
3.1 计算工况人工沙滩设计坡度为1/30,上部滩肩坡度为1/60;考虑工程海域界限水深,潜堤设置于界限水深之外,在离岸230 m以外,堤脚加强;波浪条件为工程所在海域十年一遇波况:有效波高Hs=3.0 m,平均波周期T=7.8 s;模型水位变化见图 7。设置计算工况见表 1。

|
图 7 模型水位时程变化图 Fig. 7 Water level variation with time of the numerical model |
|
|
表 1 计算工况 Table 1 Calculating case |
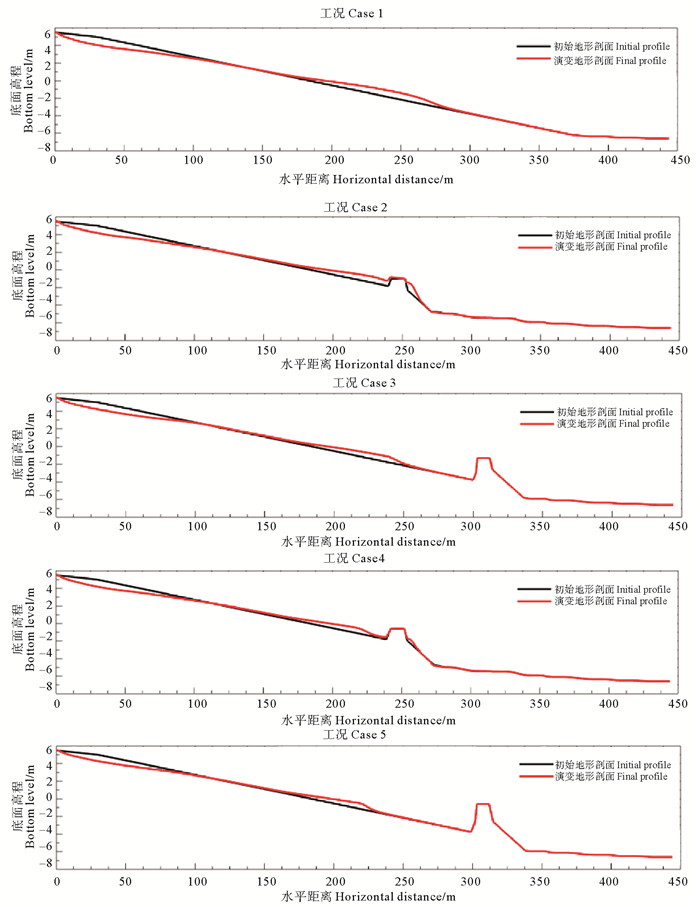
5个计算工况分别计算25 h,其岸滩剖面演变结果如图 8所示。各个计算工况的滩肩坡度、宽度和人工沙滩坡度相同,而潜堤的设置位置和高度不同,由图 8可以看出,各工况均在沙滩上部,即冲泄区区域发生侵蚀;在沙滩下部,即距离岸线200 m附近区域发生淤积,但侵蚀的厚度各不相同。
|
图 8 各工况岸滩剖面演变计算结果 Fig. 8 Calculated beach profile of all cases |
由于侵蚀区域主要在沙滩上部冲泄区处,因此对各工况上部0~150 m侵蚀区的侵蚀情况进行数值分析。图 9为各工况侵蚀区的侵蚀厚度,可以看出,有无潜堤以及潜堤位置和高度的不同都会影响侵蚀厚度,对工程的防护效果不同。潜堤的设置可以有效的提高工程的岸滩防护效果,沙滩侵蚀均有不同程度的减轻或范围缩小;而在所有设置潜堤的工况中,工况5的防护效果是最优的。

|
图 9 各工况侵蚀厚度 Fig. 9 Eroded sands thickness of all cases |
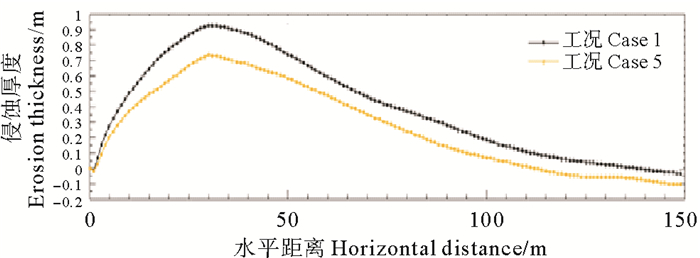
工况1为仅铺设人工沙滩,无潜堤的情况,其侵蚀厚度是最大的。图 10、11为工况1与防护效果最优的工况5侵蚀厚度的对比图和侵蚀厚度差,潜堤的设置使沙滩侵蚀的范围缩小、厚度减小。工况1侵蚀厚度最大为0.93 m,工况5侵蚀厚度最大为0.73 m,侵蚀厚度可减小22%以上,可见潜堤与人工沙滩相结合,对沙滩的防护具有良好的效果。
|
图 10 工况1和工况5侵蚀厚度对比图 Fig. 10 Eroded sands thickness comparison of case 1 and case |

|
图 11 工况1和工况5侵蚀厚度差 Fig. 11 Eroded sands thickness difference of case 1 and case 5 |
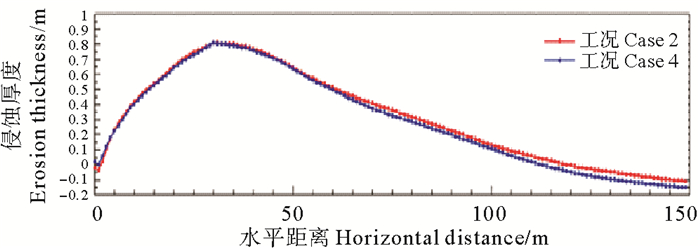
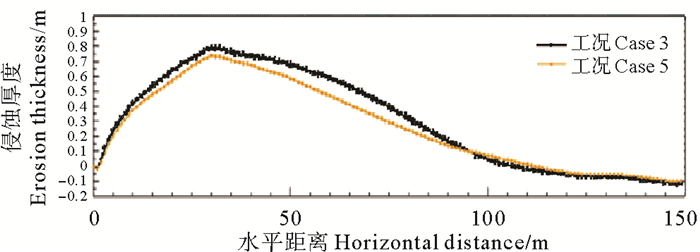
工况2与工况3的潜堤高度均为使潜堤处波浪破碎的高度,而工况3的潜堤较工况2后移60 m,由图 12可以看出,潜堤后移使侵蚀最大处的侵蚀量减小,侵蚀较大区域向离岸方向后移。工况2与工况4的潜堤位置相同,而工况4的潜堤高度较工况2升高0.4m,由图 13可以看出,潜堤升高使整个侵蚀区域的侵蚀量减小;工况3与工况5也是类似情况,潜堤位置相同,而高度相差0.7 m,由于工况3和工况5的潜堤高度差较大,由图 14可以看出,潜堤升高使侵蚀区域的侵蚀量明显减小。工况5与工况2对比,潜堤的位置后移并且高度升高,由图 15看出,工况5的侵蚀量较工况2明显减小,侵蚀较大区域向离岸方向略有后移,这是由于潜堤的位置后移和高度升高都会加快波浪的浅水变形,使波浪更早的破碎,冲泄区下移,从而减少对上部沙滩的侵蚀,对人工沙滩的防护效果更好。

|
图 12 工况2和工况3侵蚀厚度对比图 Fig. 12 Eroded sands thickness comparison of case 2 and case 3 |
|
图 13 工况2和工况4侵蚀厚度对比图 Fig. 13 Eroded sands thickness comparison of case 2 and case 4 |
|
图 14 工况3和工况5侵蚀厚度对比图 Fig. 14 Eroded sands thicknesscomparison of case 3 and case 5 |

|
图 15 工况2和工况5侵蚀厚度对比图 Fig. 15 Eroded sands thickness comparison of case 2 and case 5 |
本文应用XBeach水沙运动数值模型,对月亮湾沙滩修复工程人工沙滩与潜堤相结合的岸滩防护技术,进行岸滩防护剖面演变数值分析。首先利用实验室物模试验结果对XBeach数值模型进行了有效性检验,得出BSS值是0.653,XBeach模型是有效的、可信赖的。然后采用该模型对风暴海况波浪作用下,该工程有、无潜堤以及潜堤的不同位置和不同高度的5个工况进行岸滩剖面演变数值计算。通过对数值计算结果的分析,得出如下结论:潜堤的设置,可以使沙滩侵蚀有不同程度的减轻或范围缩小,对人工沙滩的防护具有良好的效果;潜堤的位置和高度影响其对沙质岸滩防护效果,潜堤的位置后移和高度升高都会使波浪的冲泄区下移,从而减少对上部沙滩的侵蚀,对人工沙滩的防护效果更好。
| [1] |
蔡锋, 苏贤泽, 刘建辉, 等. 全球气候变化背景下我国海岸侵蚀问题及防范对策[J]. 自然科学进展, 2008, 18(10): 1093-1103. Cai Feng, Su Xianze, Liu Jianhui, et al. Problems and countermeasures of coastal erosion in China under the background of global climate change[J]. Progress in Natural Science, 2008, 18(10): 1093-1103. DOI:10.3321/j.issn:1002-008X.2008.10.002 (  0) 0) |
| [2] |
孙杰, 詹文欢, 姚衍桃, 等. 广东省海岸侵蚀现状及影响因素分析[J]. 海洋学报, 2015, 37(7): 142-152. Sun Jie, Zhan Wenhuan, Yao Yantao, et al. Current situation and influence factors of coastal erosion in Guangdong[J]. Acta Oceanologica Sinica, 2015, 37(7): 142-152. DOI:10.3969/j.issn.0253-4193.2015.07.014 (  0) 0) |
| [3] |
Dean R G. Beach Nourishment Theory and Practice[M].[S.l.]: World Scientific Publishing, 2002.
(  0) 0) |
| [4] |
张华, 韩广轩, 王德, 等. 基于生态工程的海岸带全球变化适应性防护策略[J]. 地球科学进展, 2015, 30(9): 996-1005. Zhang Hua, Han Guangxuan, Wang De, et al. Ecological engineering based adaptive coastal defense strategy to global change[J]. Advances in Earth Science, 2015, 30(9): 996-1005. (  0) 0) |
| [5] |
Omran F, Essam D. Erosion chain reaction at El Alamein Resorts on the western Mediterranean coast of Egypt[J]. Coastal Engineering, 2012(69): 12-18.
(  0) 0) |
| [6] |
庄振业, 王永红, 包敏, 等. 海滩养护过程和工程技术[J]. 中国海洋大学学报(自然科学版), 2009, 39(5): 1019-1024. Zhuang Zhen-Ye, Wang Yong-Hong, Bao Min, et al. Beach nourishment process and engineering technology[J]. Periodical of Ocean University of China, 2009, 39(5): 1019-1024. (  0) 0) |
| [7] |
Elko N A, Holman R A, Gelfenbaum G. Quantifying the rapid evolution of a nourishment project with video imagery[J]. Journal of Coastal Research, 2005, 21(4): 633-645.
(  0) 0) |
| [8] |
Jamal M H, Simmonds D J, Magar V. Modelling gravel beach dynamics with XBeach[J]. Coastal Engineering, 2014(89): 20-29.
(  0) 0) |
| [9] |
Dano Roelvink, Reniers Ad, Van Dongeren A R. XBeach Model Descrption and Manual: Unesco-IHE[M]. Delft: Deltares and Delft University of Technology, 2010.
(  0) 0) |
| [10] |
Andrews D G, McIntyre M E. An exact theory of nonlinear waves on aLagrangian-mean flow[J]. JFluid Mech, 1978, 89(4): 609-646. DOI:10.1017/S0022112078002773
(  0) 0) |
| [11] |
Walstra D J, Roelvink J A, Groeneweg J. 3D calculation of wave-driven cross shorecurrents[C]//Proceedings 27th International Conference on Coastal Engineering. Sydney: ICCE, 2000.
(  0) 0) |
| [12] |
Galappatti R, Vreugdenhil C B. A depth integrated model for suspendedtransport[J]. J Hydraul Res, 1985, 23(4): 359-377. DOI:10.1080/00221688509499345
(  0) 0) |
| [13] |
Sutherland J, Peet A H, Soulsby R L. Evaluating the performance of morphologicalmodels[J]. Coastal Engineering, 2004(51): 917-939.
(  0) 0) |
| [14] |
Van Rijn L C, Walstra, DJ R, Grasmeijer B, et al. Thepredictability of cross-shore bed evolution of sandy beaches at the time scale ofstorms and seasons using process-based profile models[J]. Coastal Engineering, 2003(47): 295-327.
(  0) 0) |
| [15] |
Williams J J, de Alegría-Arzaburu A R, Mccall R T, et al. Modellinggravel barrier profile response to combined waves and tides using XBeach: Laboratoryand field results[J]. Coastal Engineering, 2012(63): 62-80.
(  0) 0) |
 2019, Vol. 49
2019, Vol. 49


