2. 中国海洋大学海底科学与探测技术教育部重点实验室, 山东 青岛 266100;
3. 青岛海洋地质研究所,山东 青岛 266071;
4. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237
近年来,以海洋大地电磁法(Marine Magnetotellurics)为代表的海洋电磁探测技术,常用于获得深部地层的电性结构,并且具有对海底以下低阻层反应灵敏的特点。电磁波不受高阻地层屏蔽影响,能够穿透高阻覆盖层,这对海底致密岩层以下的结构探测是非常有利的。因此,在海洋地球物理勘探中,海洋MT探测常作为地震勘探方法的有效补充,在国际上得到了快速发展和应用[1-2]。由于海洋MT以天然电磁场为场源,如太阳风、雷电等产生的感应电磁场,工作频段一般为10-4~103Hz[3],该方法在具备较大穿透深度的同时,其探测的空间分辨能力也受到了一定制约,对地层的分层能力不足[4]。因此,海洋MT对地层的空间分辨能力有待进一步提高。海底地震仪(Ocean Bottom Seismometer,OBS)探测是目前海洋深部地震探测的主要方法之一,是在海底深部地质构造调查、天然地震活动性和地震预报等研究中广泛应用的方法[5]。主动源OBS探测以人工激发震源为场源,主要应用于油气资源勘探或者海底壳幔速度结构研究等,对地下结构的垂向分层能力相对较强。当海底以下地层地震波波阻抗差较小时,海洋地震勘探对地层的识别会存在一些困难[6]。不同海洋地球物理勘探方法基于不同的岩石物性参数,考虑到海洋地球物理场的复杂性,在研究中,综合利用多种地球物理场的信息进行分析可以减少单一方法的多解性。将海洋OBS探测资料提供的速度结构信息引入海洋MT反演中,并获得更理想的解释结果是一项有重要意义的研究。
在构造大地电磁反演目标函数时,可以选择不同的模型稳定泛函为反演问题的解提供合适的模型空间类型,如基于模型参数梯度算子的最平缓模型稳定泛函、基于模型参数Laplace算子的最光滑稳定泛函等可以构造出光滑的模型解,反演结果总体呈现光滑渐变,但是无法生成较为清晰的地质体界面[7]。为解决这个问题,Last等提出“聚焦”反演的思想,以最小支撑(Minimum Support,MS)稳定泛函对目标函数中的正则化项施加约束[8]。Portniaguine等在此基础上做出改进,提出最小梯度支撑稳定泛函(Minimum Gradient Support,MGS),通过引入梯度支撑的概念,对模型参数发生变化的位置进行最小化处理,以减小模型的平滑效果,使反演得到的模型电性界面更清晰[9-10]。根据岩石物理关系,地震速度结构和地下电阻率结构的边界在深度上具有结构相似性,地层的结构或边界能够被两种不同的地球物理方法分辨出来[11-13],可以在大地电磁反演目标函数的模型稳定泛函中添加其他物性参数,如地震、钻井等先验信息,对反演结果起到有益的约束作用[14]。Yan等、Corbo等利用过MT测线的钻孔数据约束MT二维反演,验证电阻率测井先验信息可以对MT电阻率成像起到明显的改善效果[15-16];Ichiki等利用已有的俯冲板块信息建立约束模型,添加到MT反演的目标函数中,获得了更准确的俯冲带三维电阻率模型[17];Kieu等基于模糊聚类方法,在反演中添加结构和岩石物理方面的先验信息,对地质体边界进行约束,实现了更好的模型电阻率解释效果[18]。基于此,本文提出一种速度约束的海洋大地电磁反演方法,由主动源OBS探测获得的二维速度结构提取一维速度模型,该模型包含了重要的地层界面信息。以速度结构信息构建大地电磁模型约束泛函,约束反演迭代过程中,电阻率模型的层位更倾向于出现在速度梯度发生变化的位置[19],旨在发挥两种海洋地球物理探测方法的优势,使海洋MT反演的电阻率模型具有较好的地层分辨能力和更接近真实模型的电阻率值估计。
1 速度约束的海洋大地电磁聚焦反演方法考虑到海洋大地电磁反演主要针对于深部构造信息,在此采用拟线性反演算法中计算速度较快的Gauss-Newton最优化方法开展本项研究。在进行常规MT反演时,采用的目标函数如式所示[20-21]:
| $ \begin{gathered} \phi(\boldsymbol{m})=\phi_d(\boldsymbol{m})+\lambda \phi_m(\boldsymbol{m})= \\ \left\|\boldsymbol{W}_{\mathrm{d}}\left(\boldsymbol{d}^{\text {obs }}-F(\boldsymbol{m})\right)\right\|^2+\lambda\left\|\boldsymbol{W}_m \boldsymbol{m}\right\|^2 。\end{gathered} $ | (1) |
式中:ϕd(m) 为观测数据拟合泛函;ϕm(m) 为模型约束稳定泛函;m为M维模型参数向量;λ为正则化因子,用于平衡数据拟合项和模型约束项之间的权重;dobs为观测数据,F(m) 为正演响应;Wd和Wm分别为数据加权矩阵和模型加权矩阵。
反演过程中模型参数数量的限制以及噪声干扰等因素都会导致反演问题出现多解性情况,因此需要引入其他的约束信息对模型结构进行约束,即模型约束稳定泛函ϕm(m),其主要目的是在先验信息的指导下,为反演问题的解选择适当的模型类型[22],表达式如式所示:
| $\phi_\boldsymbol{m}(\boldsymbol{m})=\left\|\boldsymbol{W}_m\left(\boldsymbol{m}-\boldsymbol{m}_{r e f}\right)\right\|^2 。$ | (2) |
式中:mref为参考模型,一般包含有先验信息;Wm为M×M阶的模型加权矩阵,不同的Wm可以定义不同的模型约束泛函ϕm(m),从而获得不同模型约束下的反演结果。常见的模型约束泛函形式有最小模型稳定泛函(MM)、最平缓模型稳定泛函(FM)、最光滑模型稳定泛函(SM)等[23],其模型加权矩阵Wm的形式如式所示:
| $ \begin{aligned} \boldsymbol{W}_{M M} & =\left(\begin{array}{llll} 1 & & & \\ & \ddots & & \\ & & 1 & \end{array}\right)_{M \times M}, \\ \boldsymbol{W}_{F M} & =\left(\begin{array}{cccc} 0 & 0 & & \\ -1 & 1 & & \\ & \ddots & \ddots & \\ & & -1 & 1 \end{array}\right)_{M \times M} , \\ \boldsymbol{W}_{S M} & =\left(\begin{array}{ccccc} -1 & 1 & & & \\ 1 & -2 & 1 & & \\ & \ddots & \ddots & \ddots & \\ & & 1 & -2 & 1 \\ & & & 1 & -1 \end{array}\right)_{M \times M}。\end{aligned} $ | (3) |
众所周知,最小模型稳定泛函反演结果中容易出现冗余的突变结构;最平缓模型稳定泛函以及最光滑模型稳定泛函倾向于得到电阻率参数光滑渐变的模型结构。以上三种模型稳定泛函在大地电磁反演中的应用比较广泛,但是许多情况下不能准确描述地下真实的块状地质构造[24]。为了使反演得到的模型参数在地层界面位置发生明显的变化,可以使用基于聚焦反演思想的最小梯度支撑稳定泛函(MGS),以减小模型的“平滑”效果。该方法原理是对模型参数变化剧烈或者不连续的区域进行面积最小化,因其具有保留突变结构且可以移除虚假震荡的优势,有助于使目标地层边界更加清晰,并能提高对块状地质结构的分辨能力[25]。最小梯度支撑稳定泛函(MGS)的形式为[10]:
| $ \phi_{M G S}(\boldsymbol{m})=\sum\limits_{i=1}^N\left(\frac{\nabla\left(m^{(i)}-m_{\mathrm{apr}}^{(i)}\right)}{\sqrt{\left(\nabla\left(m^{(i)}-m_{\mathrm{apr}}^{(i)}\right)\right)^2+\beta^2}}\right)^2 。$ | (4) |
式中,β为聚焦参数,影响聚焦面积最小化的效果,取值一般为[10-6, 10-3]内的常数,可避免在零值处的奇异性,保持模型约束泛函的稳定性。在一维反演计算中,可以将空间梯度计算近似为相邻两层之间的一阶差分[19, 23]。
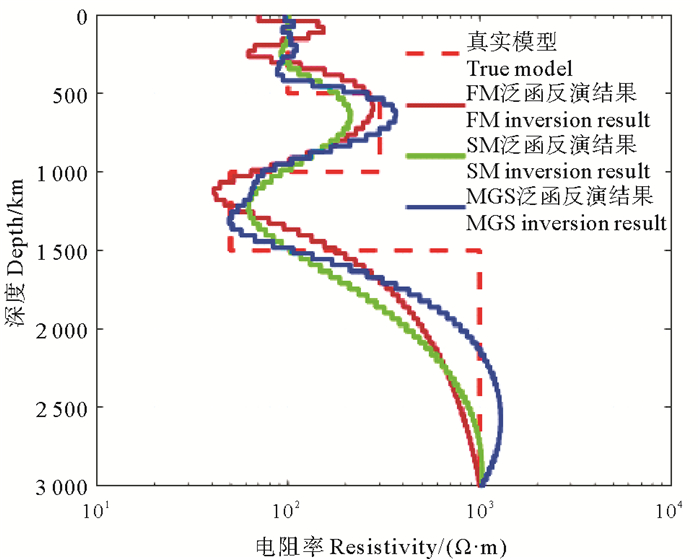
为了分析MGS模型稳定泛函的聚焦效果,设计如表 1所示的四层地电模型,用于测试光滑稳定泛函(FM与SM稳定泛函)与最小梯度支撑稳定泛函(MGS)的反演结果对比效果,三种模型稳定泛函的反演结果如图 1所示。结果表明,在达到RMS最小的情况下,相较于光滑稳定泛函,MGS稳定泛函反演结果反映的电阻率值更准确,更加突出地层的边界和层状结构,明显体现出其“聚焦”的效果,且浅部不会出现冗余电阻率异常。随着迭代次数的增加,相较于光滑稳定泛函,MGS稳定泛函不会出现过拟合现象。
|
|
表 1 四层地电模型电阻率-层厚参数 Table 1 The parameters of four-layer geoelectric model |
|
图 1 MGS稳定泛函与光滑稳定泛函反演结果对比 Fig. 1 The inversion results of MGS and smooth stabilizing functional |
根据电磁波的传播特性,海洋大地电磁法作为频率域电磁测深方法,反演结果对电阻率和层厚的乘积比较敏感,若仅采用MGS稳定泛函而未添加其他地球物理参数的先验信息的约束,其结果仍会受到电磁反演等值性的影响,这对反演的电阻率模型进行定量解释是极为不利的[26]。因此,本文提出了一个基于地震速度资料的大地电磁反演模型约束泛函,基于电阻率模型与速度模型具有结构相似性的前提,定义了如式所示的速度约束稳定泛函:
| $ \begin{gathered} \phi_{v {\rm{M G S}}}(\boldsymbol{m})=\left\|\frac{\beta \nabla \boldsymbol{m}}{\sqrt{(\nabla \boldsymbol{v})^2+\beta^2}}\right\|^2= \\ \sum\limits_{i=1}^N\left(\frac{\beta \nabla\left(m^{(i)}-m_{\mathrm{apr}}^{(i)}\right)}{\sqrt{\left(\nabla v^{(i)}\right)^2+\beta^2}}\right)^2。\end{gathered} $ | (5) |
式中:v(i)为模型第i层的地震速度参数;β为聚焦算子,这里既可以避免在0值处的奇异性,也可以对速度参数做归一化处理,避免与电阻率数值差异太大引起反演算法不稳定。在一维层状介质情况下,速度空间梯度可以近似为模型空间相邻两层之间的差分。因此其模型加权矩阵Wv为:
| $ \boldsymbol{W}_v= {diag}\left(\frac{\beta}{\sqrt{\left((\nabla v)^2+\beta^2\right)}}\right) \cdot \nabla \boldsymbol{m} \text { 。} $ | (6) |
式中,▽m为模型约束泛函ϕvMGS的核函数。对于模型空间m=[m1, m2, …, mN],核函数▽m可以写成梯度矩阵的形式:
| $\nabla \boldsymbol{m}=\left(\begin{array}{cccc} 0 & 0 & & \\ -1 & 1 & & \\ & \ddots & \ddots & \\ & & -1 & 1 \end{array}\right)_{N \times N}。$ | (7) |
式中,N为反演过程中模型空间划分的层数。由于模型的权重来自于地震波速度信息,而地震速度模型具有更高的深度分辨率,所以,相较于ϕMGS(m) 而言,ϕvMGS(m) 可以在地电结构反演中更清晰地反映出地层差异特征,这有助于反演得到更准确的电阻率值估计。
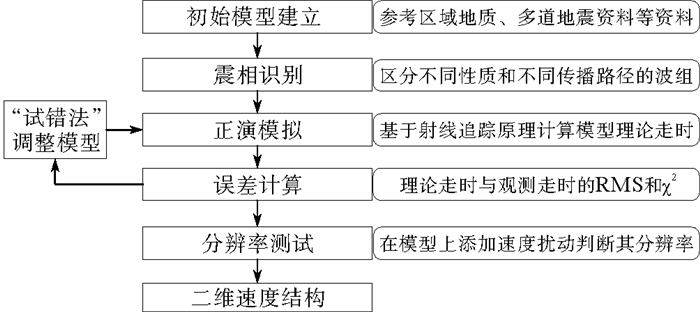
为了获取高质量的速度约束信息,在应用主动源海洋地震探测时,可采用低主频、大容量气枪震源,多支气枪枪阵以及大排列间距的方式增加地震波的穿透性和传播距离,获得质量更高的深部地震波场信息,使得主动源OBS探测深度可达莫霍面,且对主要层位识别比较准确[27-29]。OBS方法进行速度结构成像的基本流程一般如图 2所示[30]。本次研究中采用纵波速度模型作为速度约束先验信息。在获得二维速度结构基础上,根据海洋MT测点位置提取相应点位海底以下一维速度结构,作为先验信息添加到海洋大地电磁反演的目标函数中,可构建基于速度梯度的模型约束泛函ϕvMGS(m),对不同地层的模型更新量进行加权,达到约束效果,引导反演的迭代方向,提高海洋MT反演的分辨能力。
|
图 2 OBS资料速度结构成像基本流程 Fig. 2 Basic flow of velocity structure imaging of OBS Data |
由式(1)、式(5)和式(6),得到地震速度信息约束的大地电磁反演目标函数为:
| $ \begin{array}{r} \phi(\boldsymbol{m})=\phi_d(\boldsymbol{m})+\lambda \phi_{v M G S}(\boldsymbol{m})= \\ \left\|\boldsymbol{W}_d\left(\boldsymbol{d}^{o b s}-F(\boldsymbol{m})\right)\right\|^2+\lambda\left\|\boldsymbol{W}_v \boldsymbol{m}\right\|^2 。\end{array} $ | (8) |
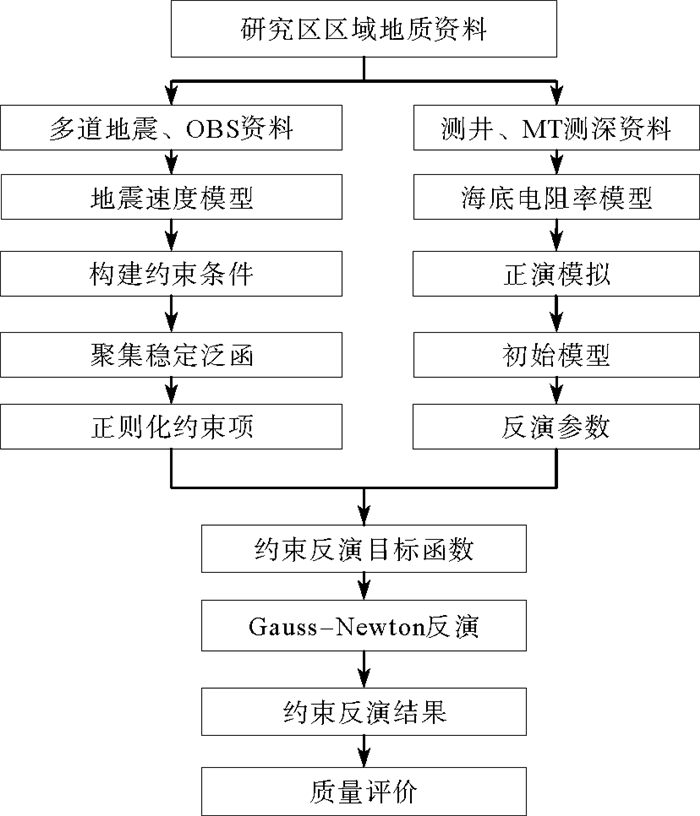
综上,本文研究方法的技术路线如图 3所示。
|
图 3 速度约束的大地电磁反演算法技术路线 Fig. 3 Technical route of velocity-constrained MT inversion |
为了验证本文研究速度约束的海洋大地电磁反演方法,并测试其在出现速度倒转、波阻抗差异较小地层深部结构研究应用的效果,以我国南黄海千里岩隆起区地层结构构建地电模型进行反演计算。众所周知,我国南黄海海域广泛分布中古生界海相碳酸盐岩层[31],新生代低速陆相沉积碎屑岩覆盖在高速海相碳酸盐岩地层之上,而在南黄海千里岩隆起区,根据地震资料可以判断该隆起区存在逆冲推覆构造,前震旦系变质岩高速推覆体覆盖在中-古生界海相沉积层之上,并且该推覆体的厚度也比较大,可达3~7 km,推覆体底界面最大深度可达10 km[32-33]。海相沉积层相较于变质岩推覆体速度较低,因此会出现速度倒转现象,但其速度反转程度并不明显。推覆构造的速度、电阻率性质表现为前震旦系变质岩的岩石物理性质。根据千里岩隆起海区露头—千里岩岛出露,变质岩类型主要为:榴辉岩、片麻岩、超镁铁质岩、花岗质片麻岩等[34],呈现高速度、高电阻率的岩石物理特性。推覆体的速度一般为6.3~6.9 km/s;根据苏北盆地测井信息可得,前震旦系变质岩电阻率一般在200~500 Ω·m[35-36]。变质岩推覆体呈现高速度和高电阻率特性,因此可以发挥电磁波不受高阻层屏蔽的优势,利用海洋大地电磁法研究推覆构造以下地质构造特点及电性特征。
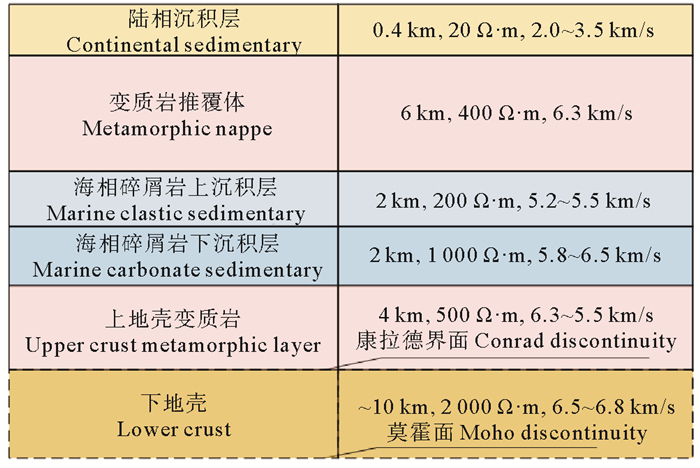
参考区域地质资料构建如图 4所示的速度-电阻率模型。根据南黄海千里岩隆起区OBS二维速度结构剖面[32],将该地区地壳及上部地层速度结构划分为6层,这里的海相沉积层速度参考表 2 “南黄海地区地层速度表”[37-38],上地壳与下地壳速度参考OBS探测速度资料[39]。模型中陆相沉积层厚度为400 m,高阻的变质岩推覆体厚度为6 km,推覆体以下为海相沉积层。基于该模型进行海洋大地电磁反演测试,分析该反演方法在发挥电磁波不受高阻层屏蔽优势及提高地层分辨率方面的效果。
|
图 4 速度-电阻率参考模型 Fig. 4 Velocity-resistivity reference model |
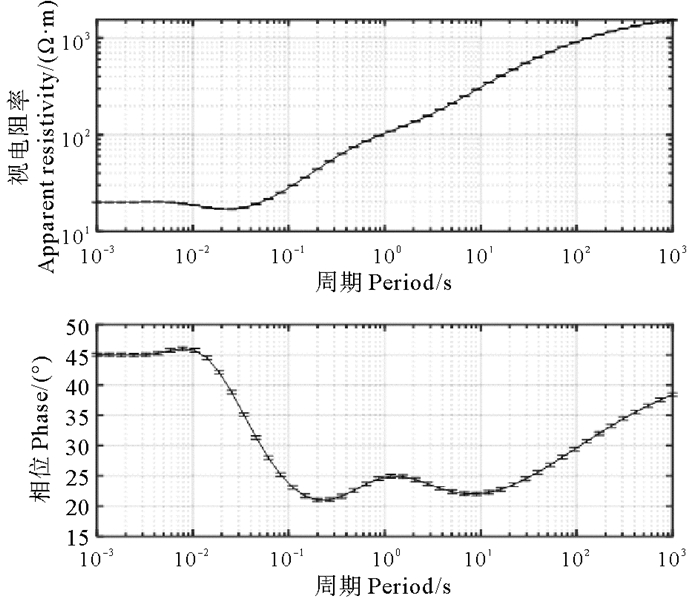
首先,以电阻率模型为基础进行大地电磁正演模拟,在周期10-3~103 s范围内选取48个等对数间隔分布的频点数据,加入1%的随机噪声。其正演模拟结果如图 5所示。在该区域海洋MT正演资料基础上,分别开展无速度约束和有速度约束的大地电磁聚焦反演,并测试不同的速度模型对约束反演的影响。
|
图 5 参考电阻率模型正演结果 Fig. 5 Forward modeling results of reference resistivity model |
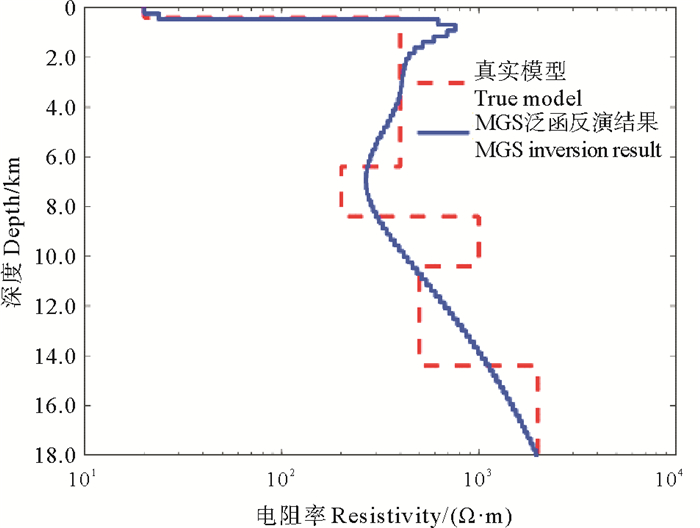
采用Gauss-Newton反演算法,将反演模型空间均匀划分为80层,初始模型设定为100 Ω·m的均匀半空间模型。根据模型加权矩阵形式,采用式(4)中模型稳定泛函ϕMGS的进行聚焦反演,反演经过17次迭代达到RMS最小(RMS=0.76),反演结果如图 6所示。
|
图 6 基于MGS稳定泛函MT聚焦反演结果 Fig. 6 MT focusing inversion result based on MGS stabilizing functional |
从整体来看,反演结果可以反映出电阻率的变化趋势,厚度为0.4 km的低阻陆相沉积层的深度和电阻率值可以准确得到;在深度6.4~8.4 km的范围可以看到呈现相对低阻特性的海相碎屑岩层,这已较好地解决了上覆高速层对速度结构成像造成的不利影响;深度8.4 km以下的反演结果可以反映下部地层电阻率变化的整体趋势;得到的各层位中心位置反演电阻率值相对误差由浅至深依次为:0.15%、0.59%、34.42%、58.8%、48.54%和25.39%。
由区域地质资料可知,海相沉积层可进一步分为相对低阻(< 200 Ω·m)的海相碎屑岩沉积层和相对高阻(200~1 000 Ω·m)的海相碳酸盐岩层,基于最小梯度支撑(MGS)稳定泛函大地电磁聚焦反演对参考模型中两种沉积层的界面(深度8.4 km处)反映并不清楚。受到海洋大地电磁反演分层能力不足的限制,深部地层的结构划分不明显,很难准确描述电性层位变化的位置。
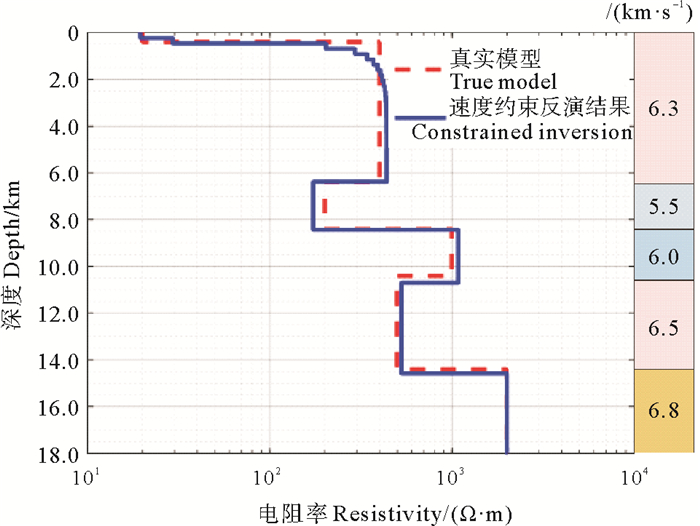
2.2 准确速度信息约束的海洋大地电磁反演为了进一步改善反演效果,需进行速度约束的大地电磁反演。假设在理想情况下,与海洋MT勘探深度匹配的主动源OBS资料可以提供准确的地层速度信息,则可利用层位信息较为准确的速度资料对海洋大地电磁反演进行约束。在图 4电阻率模型的基础上,添加各层位的速度约束信息,如图 7右侧条带所示。电阻率模型空间仍均匀划分为80层,保持正则化因子选取策略、电阻率值上下限约束、反演收敛条件等参数不变。该条件下速度约束大地电磁反演在第11次迭代达到RMS最小(RMS=0.98),反演结果如图 7所示。
|
图 7 基于MGS聚焦稳定泛函的速度约束MT反演结果 Fig. 7 Velocity constrained MT inversion result based on MGS focusing stabilizing functional |
与无速度约束的海洋MT聚焦反演结果相比,添加速度信息约束后,由低阻陆相沉积层向高阻推覆体突变位置(深度0.4 km处)的虚假电性异常得到了压制。
海相沉积层界面在添加了速度约束以后,可以准确地反映相对低阻层和相对高阻层的电性界面。更为重要的是,海相下构造碳酸盐岩层与上地壳在常规的MT反演中无法分辨出,在添加速度约束后可以较好地反映两层的电阻率值差异;各层位中心位置反演电阻率值相对误差由浅至深依次为:0.87%、8.41%、13.42%、8.25%、5.55%和0.42%,相较于无约束反演结果,误差大幅减小。
总体上,理想情况下,引入准确的速度信息约束不仅可以提高常规MT反演的分层能力,在速度梯度信息的约束下,电阻率值反演结果也接近真实模型。
2.3 速度模型扰动对约束反演的影响海洋OBS探测相较于海洋MT探测而言具有层位分辨能力高的优势,但实际探测中存在的诸多影响因素可能会造成所获得的速度信息存在误差,速度数值扰动会在计算约束反演模型加权矩阵Wv时发生速度梯度变化,因此有必要测试模型速度具体数值扰动对约束反演算法的影响。
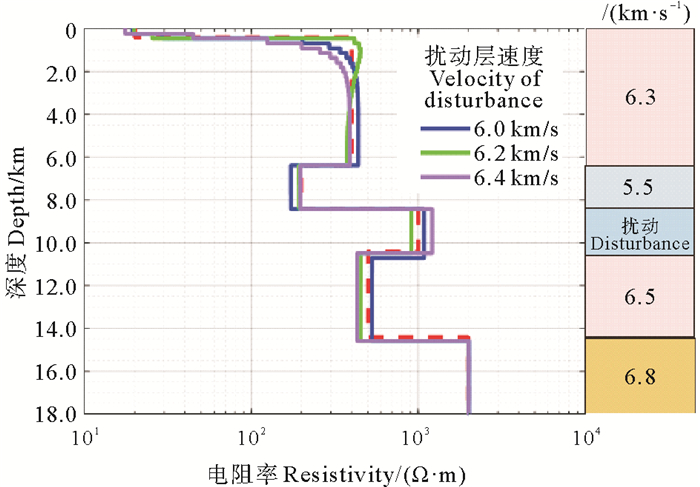
就如图 4所示的速度-电阻率模型而言,海相酸盐岩沉积层埋深较大,且呈现高速特性,与下部上地壳变质岩层的地震波波阻抗接近,速度结构获取过程中易受影响而产生误差。考虑存在速度误差的情况,对8.4~10.4 km的海相碳酸盐岩高速层的速度值进行扰动变化,即对约束模型中8.4~10.4 km段的速度值在6.0 km/s的基础上,逐次递增0.2 km/s,向上地壳变质岩层速度6.5 km/s逼近,赋值分别为6.0、6.2和6.4 km/s,基于这三种速度模型约束的海洋MT反演结果如图 8所示,结果表明:速度数值的变化会对反演结果产生一定的影响,但总体上比较小;三种情况下的各层电阻率值与真实模型均比较接近,这是因为在利用速度资料构建模型加权矩阵时计算的是各层的速度梯度,即电阻率模型在迭代过程中倾向于在速度梯度变化的位置生成电阻率界面,而当速度值在一定范围内发生变化时,模型约束泛函ϕvMGS中的聚焦稳定因子β可以对速度梯度做归一化处理,反演达到RMS最小时的迭代总次数会发生变化,但是反演结果保持稳定。所以,当速度约束模型的某层速度值存在一定范围内的扰动时,该约束反演方法仍可表现出较好稳定性。
|
图 8 海相碳酸盐岩层速度变化约束反演结果 Fig. 8 Constrained inversion results of velocity variation in marine carbonate sedimentary layer |
进行震相拟合时,随着深度增加,在获得深部其他层位速度值时也可能会产生误差。为了分析这种条件下的反演效果,在图 7速度约束模型的基础上,对高速层以下(深度6.4 km以下)每一层的速度值分别添加±0.2 km/s的扰动,以此构建约束条件并进行约束反演,得到各层中心位置相对误差,如表 3所示。结果表明:对速度模型不同层位分别予以速度值扰动而构建的约束条件对MT约束反演所得到的电阻率值会产生一定的影响,但对总体结构特征影响不大,产生的电阻率误差与图 7反演结果接近。
|
|
表 3 层位速度扰动对反演各层电阻率的影响 Table 3 Effects of velocity perturbation on the resistivity of each layer in the inversion |
当考虑高速推覆体对速度资料获取的影响时,高速层以下会出现速度倒转的情况,当相邻地层之间的地震波波阻抗差异较小时,也会影响对下伏地层的精准识别,此时以地震方法获得的速度约束模型可能存在结构不完整的情况,模拟分析速度约束结构与电阻率模型结构不匹配对约束反演的影响是有实际意义的。
仍以南黄海千里岩隆起区为例,根据图 4所示的电阻率模型,参考区域地质资料,由OBS走时拟合的速度结果可知,在6.4 km以深的区域总体上的速度平均为6.5 km/s[32]。假设高速变质岩推覆体以下难以由OBS速度资料获得准确的低速层(深度为6.4~8.4 km)速度信息,则将速度模型的高速层以下区域(深度为6.4~18.0 km)的速度约束值均设定为6.5 km/s,以此速度模型对海洋大地电磁反演进行约束,模型空间层位划分情况及反演策略与上文保持一致。
图 9所示的反演结果表明:相较于无速度约束MT聚焦反演结果(见图 6),虽然OBS资料提供的高速层以下区域均以6.5 km/s的速度进行约束,仅在界面(6.4 km)处提供了速度梯度信息,但速度约束后的MT聚焦反演得到的陆相沉积层和高速推覆体的深度和电阻率更加接近真实模型,无速度约束反演中0.4 km深度处出现的浅部电阻率突变造成的虚假异常得到了一定程度的压制,0.4~6.4 km深度内高速推覆体的电阻率变化更加平稳;更重要的是,6.4~8.4 km深度的低阻异常也得到了较好的恢复,电阻率值接近真实模型,8.4 km深度以下电阻率结果仍可反映电性变化的整体趋势。

|
图 9 高速推覆体对速度约束大地电磁反演的影响 Fig. 9 The influence of high-speed nappe on velocity constrained MT inversion |
海洋大地电磁法是研究海底深部电性结构的重要手段,但其对地层的空间分辨能力有待进一步提高。将以地震速度信息构建的模型稳定泛函引入大地电磁聚焦反演的目标函数中,实现了速度约束的大地电磁反演。通过模型测试可知:
(1) 本文研究方法是以地质构造本身电性差异为基础,基于MGS聚焦稳定泛函的大地电磁模型反演结果可以反映出高阻地层以下的低电阻率异常,在海底地层地震波波阻抗接近或者存在高速覆盖层的海域可以作为海洋地震探测方法的有效补充,取得良好的应用效果。
(2) 通过引入速度约束泛函,在准确的速度结构约束下,可以进一步压制虚假异常,增强海洋大地电磁反演的分层能力,大幅提高对地电界面深度的确定精度,电阻率反演结果更接近真实模型,各层电阻率误差均大幅减小,且与无速度约束的MGS稳定泛函反演结果相比,添加约束信息后,反演收敛速度更快。即使在约束反演采用的速度模型存在一定的误差或速度结构信息不完整的情况下,添加约束后相应的层位反演结果也可以得到显著改善,仍能刻画出电性变化的整体趋势。
在获得多站OBS速度结构资料的同时,进一步探测获得更多站位的海洋大地电磁数据,则可利用速度约束的二维海洋大地电磁反演进一步提高对深部岩层的解释精度。
| [1] |
柳建新, 郭天宇, 王博琛, 等. 油气勘探中海洋电磁技术的研究进展[J]. 石油物探, 2021, 60(4): 527-538. Liu J X, Guo T Y, Wang B C, et al. Review of marine electromagnetic methods for hydrocarbon exploration[J]. Geophysical Prospecting For Petroleum, 2021, 60(4): 527-538. DOI:10.3969/j.issn.1000-1441.2021.04.001 (  0) 0) |
| [2] |
Duan S, Li Y, Pei J, et al. Carbonate imaging with magnetotellurics in a shallow-water environment, South Yellow Sea, China[J]. Journal of Applied Geophysics, 2020, 178: 104076. DOI:10.1016/j.jappgeo.2020.104076 (  0) 0) |
| [3] |
魏文博, 邓明, 谭捍东, 等. 我国海底大地电磁探测技术研究的进展[J]. 地震地质, 2001(2): 131-137. Wei W B, Deng M, Tan H D, et al. Development of marine magnetotelluric prospecting technique in China[J]. Seismology and Geology, 2001(2): 131-137. (  0) 0) |
| [4] |
Zhdanov M S. 地球物理电磁理论与方法[M]. 北京: 科学出版社, 2015: 373-378. Zhdanov M S. Geophysical Electromagnetic Theory and Methods[M]. Beijing: Science China Press, 2015: 373-378. (  0) 0) |
| [5] |
阮爱国, 李家彪, 冯占英, 等. 海底地震仪及其国内外发展现状[J]. 东海海洋, 2004(2): 19-27. Ruan A G, Li J B, Feng Z Y, et al. Ocean bottom seismometer and its development in the world[J]. Donghai Marine Science, 2004(2): 19-27. (  0) 0) |
| [6] |
张训华, 郭兴伟, 吴志强, 等. 南黄海盆地中部隆起CSDP-2井初步成果及其地质意义[J]. 地球物理学报, 2019, 62(1): 197-218. Zhang X H, Guo X W, Wu Z Q, et al. Preliminary results and geological significance of Well CSDP-2 in the Central Uplift of South Yellow Sea Basin[J]. Chinese Journal of Geophysics, 2019, 62(1): 197-218. (  0) 0) |
| [7] |
陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005(4): 937-946. Chen X B, Zhao G Z, Tang J, et al. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005(4): 937-946. DOI:10.3321/j.issn:0001-5733.2005.04.029 (  0) 0) |
| [8] |
Last B J. Compact gravity inversion[J]. Geophysics, 2012, 48(6): 713. (  0) 0) |
| [9] |
Portniaguine O, Zhdanov M S. Focusing geophysical inversion images[J]. Geophysics, 1999, 64(3): 874-887. DOI:10.1190/1.1444596 (  0) 0) |
| [10] |
Portniaguine O, Zhdanov M S. 3-D magnetic inversion with data compression and image focusing[J]. Geophysics, 2002, 67(5): 1532-1541. DOI:10.1190/1.1512749 (  0) 0) |
| [11] |
Gallardo L A, Meju M A. Structure-coupled multiphysics imaging in geophysical sciences[J]. Reviews of Geophysics, 2011, 49(1): 1003. (  0) 0) |
| [12] |
彭国民, 刘展. 电磁和地震联合反演研究现状及发展趋势[J]. 石油地球物理勘探, 2020, 55(2): 465-474. Peng G M, Liu Z. An overview of joint electromagnetic-seismic inversion and its future development[J]. Oil Geophysical Prospecting, 2020, 55(2): 465-474. (  0) 0) |
| [13] |
Moorkamp M, Roberts A W, Jegen M, et al. Verification of velocity-resistivity relationships derived from structural joint inversion with borehole data[J]. Geophysical Research Letters, 2013, 40(14): 3596-3601. DOI:10.1002/grl.50696 (  0) 0) |
| [14] |
吴萍萍, 丁志峰, 谭捍东, 等. 基于V_P/V_S波速比模型约束的张渤地震带深部电性结构研究[J]. 地球物理学报, 2021, 64(8): 2716-2732. Wu P P, Ding Z F, Tan H D, et al. Inversion MT data for the electrical structure beneath the Zhangbo seismic belt based on constraint of the VP/VS model[J]. Chinese Journal of Geophysics, 2021, 64(8): 2716-2732. (  0) 0) |
| [15] |
Yan P, Garcia Juanatey M A, Kalscheuer T, et al. A magnetotelluric investigation of the Scandinavian Caledonides in western Jämtland, Sweden, using the COSC borehole logs as prior information[J]. Geophysical Journal International, 2016, 208(3): 1465-1489. (  0) 0) |
| [16] |
Corbo F, Arzate J, Oleaga A. Structure of the Guarani Aquifer in the surroundings of the Uruguay River from magnetotelluric soundings[J]. Geofísica Internacional, 2012, 51(1): 17-37. (  0) 0) |
| [17] |
Ichiki M, Ogawa Y, Kaida T, et al. Electrical image of subduction zone beneath northeastern Japan[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(12): 7937-7965. DOI:10.1002/2015JB012028 (  0) 0) |
| [18] |
Kieu D T, Kepic A, Pethick A M, et al. Inversion of magnetotelluric data with fuzzy cluster petrophysical and boundary constraints[J]. ASEG Extended Abstracts, 2016(1): 1-6. (  0) 0) |
| [19] |
Brown V, Key K, Singh S. Seismically regularized controlled-source electromagnetic inversion[J]. Geophysics, 2012, 77(1): 57-65. (  0) 0) |
| [20] |
Li G, Cai H, Li C. Alternating joint inversion of controlled-source electromagnetic and seismic data using the joint total variation constraint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(8): 5914-5922. DOI:10.1109/TGRS.2019.2903043 (  0) 0) |
| [21] |
Rodi W, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 66(1): 174-187. DOI:10.1190/1.1444893 (  0) 0) |
| [22] |
Zhdanov M S. Chapter 2-Ill-Posed Problems and the Methods of Their Solution[M]. Inverse Theory and Applications in Geophysics(Second Edition), Oxford: Elsevier, 2015: 33-61.
(  0) 0) |
| [23] |
Rao L, Wu X, Guo R, et al. A comparative study of different stabilizers for retrieving geoelectric structure based on a unified framework[J]. Journal of Applied Geophysics, 2020, 175: 104001. (  0) 0) |
| [24] |
白宁波, 周君君, 胡祥云. 优化策略的二维大地电磁光滑聚焦反演研究[J]. 石油地球物理勘探, 2021, 56(4): 902-909. Bai N B, Zhou J J, Hu X Y. Two-dimensional magnetotelluric smooth focusing inversion based on optimization strategy[J]. Oil Geophysical Prospecting, 2021, 56(4): 902-909. (  0) 0) |
| [25] |
Xiang Y, Yu P, Zhang L, et al. Regularized magnetotelluric inversion based on a minimum support gradient stabilizing functional[J]. Earth, Planets and Space, 2017, 69(1): 158. (  0) 0) |
| [26] |
朱宇启, 裴建新, 段双敏, 等. 测井约束的海洋CSEM反演及其在南黄海中部隆起区勘探应用[J]. 中国海洋大学学报(自然科学版), 2021, 51(6): 70-77. Zhu Y Q, Pei J X, Duan S M, et al. Marine CSEM inversion with well logging constraints and its application in the central uplift of the South Yellow Sea[J]. Periodical of Ocean University of China, 2021, 51(6): 70-77. (  0) 0) |
| [27] |
祁江豪, 吴志强, 郭兴伟, 等. 大容量气枪震源在南黄海海相高速屏蔽层下VSP资料采集中的应用——以大陆架科学钻探CSDP-2井为例[J]. 地球物理学进展, 2019, 34(4): 1661-1670. Qi J H, Wu Z Q, Guo X W, et al. Application of large capacity air gun source in VSP data acquisition under marine high speed shielding layer in South Yellow Sea: Illustrated by the example of well CSDP(Continental Shelf Drilling Program)-2[J]. Progress in Geophysics, 2019, 34(4): 1661-1670. (  0) 0) |
| [28] |
林建民, 王宝善, 葛洪魁, 等. 大容量气枪震源特征及地震波传播的震相分析[J]. 地球物理学报, 2008(1): 206-212. Lin J M, Wang B S, Ge H K, et al. Study on large volume airgun source characteristics and seismic phase analysis[J]. Chinese Journal of Geophysics, 2008(1): 206-212. (  0) 0) |
| [29] |
赵明辉, 丘学林, 夏少红, 等. 大容量气枪震源及其波形特征[J]. 地球物理学报, 2008(2): 558-565. Zhao M H, Qiu X L, Xia S H, et al. Large volume air-gun sources and its seismic waveform characters[J]. Chinese Journal of Geophysics, 2008(2): 558-565. (  0) 0) |
| [30] |
阮爱国, 等. 海底地震勘测理论与应用[M]. 北京: 科学出版社, 2020: 106-112. Ruan A G. Ocean Bottom Seismic Theory and Application[M]. Beijing: Science Press, 2020: 106-112. (  0) 0) |
| [31] |
吴志强, 曾天玖, 肖国林, 等. 南黄海低信噪比地震资料处理技术探索[J]. 物探与化探. Wu Z Q, Zeng T J, Xiao G L, et al. A tentative discussion on low SNR seismic data processing technique for marine carbonate in the South Yellow Sea area[J]. Geophysical and Geochemical Exploration. DOI:10.11720/wtyht.2014.5.28 (  0) 0) |
| [32] |
祁江豪. 南黄海地区地壳速度结构研究[D]. 北京: 中国地质大学, 2015. Qi J H. Research on the Crustal Velocity Structure in the Southern Yellow Sea[D]. Beijing: China University of Geosciences, 2015. (  0) 0) |
| [33] |
姚蓉, 罗开平, 杨长清. 南黄海北部地区逆冲推覆构造特征[J]. 石油实验地质, 2011, 33(3): 282-284. Yao R, Luo K P, Yang C Q. Features of thrust nappe structure in northern South Yellow Sea[J]. Petroleum Geology and Experiment, 2011, 33(3): 282-284. (  0) 0) |
| [34] |
韩宗珠, 肖莹, 于航, 等. 南黄海千里岩岛榴辉岩的矿物化学及成因探讨[J]. 海洋湖沼通报, 2007(1): 83-87. Han Z Z, Xiao Y, Yu H, et al. A study on the mineralchemistgry and genesis of the eclogite from Qianliyan island, the Southern Huanghai sea[J]. Transactions of Oceanology and Limnology, 2007(1): 83-87. (  0) 0) |
| [35] |
吴健生, 王家林, 于鹏, 等. 苏北及邻区前志留基础层的综合地球物理研究[J]. 勘探地球物理进展, 2006(2): 109-114. Wu J S, Wang J L, Yu P, et al. Integrated geophysical studies of the Pre-Silurian bedrock strata in north Jiangsu area and adjacent regions[J]. Progress in Exploration Geophysics, 2006(2): 109-114. (  0) 0) |
| [36] |
杨子建. 下扬子北部地区电性参数分析[J]. 石油物探, 1996, 35(2): 114-122. Yang Z J. The analysis of the electric parameters in the northern Xiayangzi[J]. Geophysical Prospecting For Petrole, 1996, 35(2): 114-122. (  0) 0) |
| [37] |
吴志强, 骆迪, 曾天玖, 等. 南黄海海相油气地震勘探难点分析与对策建议[J]. 海相油气地质, 2014, 19(3): 8-17. Wu Z Q, Luo D, Ceng T J, et al. Technical difficulties and countermeasures of petroleum seismic exploration in the South Yellow Sea Basin[J]. Marine Origin Petroleum Geology, 2014, 19(3): 8-17. (  0) 0) |
| [38] |
吴志强, 陆凯. 南黄海沉积层纵波速度与地震反射特征[J]. 海洋地质与第四纪地质, 2011, 31(2): 73-77. Wu Z Q, Lu K. Characteristics of p-wave velocity and seismic reflection of the sedimentary layer in the South Yellow Sea[J]. Marine Geology & Quaternary Geology, 2011, 31(2): 73-77. (  0) 0) |
| [39] |
祁江豪, 张训华, 吴志强, 等. 南黄海OBS 2013海陆联合深地震探测初步成果[J]. 热带海洋学报, 2015, 34(2): 76-84. Qi J H, Zhang X H, Wu Z Q, et al. Preliminary results of the South Yellow Sea OBS 2013 onshore-offshore joint deep seismic survey[J]. Journal of Tropical Oceanography, 2015, 34(2): 76-84. (  0) 0) |
2. The Key Laboratorg of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Ocean University of China, Qingdao 266100, China;
3. Qingdao Institute of Marine Geology, Qingdao 266071, China;
4. The Laboratory for Marine Mineral Resources, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China
 2023, Vol. 53
2023, Vol. 53


