2. 国家海洋局第一海洋研究所, 山东 青岛 266061
高频地波雷达(HFSWR)利用高频段(3~30 MHz)垂直极化电磁波沿海面绕射的特性,实现对海面运动目标和低空飞行目标的超视距探测[1],作用距离可达到数百公里。地波雷达能够探测目标的距离、方位、速度等参数信息[2],其中目标的距离参数对目标的跟踪起着至关重要的作用。为了实现对目标的连续跟踪和精确探测,必须进行精确的目标距离参数估计。高频地波雷达在探测目标时,可以从目标回波谱中得到目标的距离信息[3-4],但是受距离分辨率的影响,目标距离总是离散的,即地波雷达测距处理后只能确定目标所在的距离单元。当目标实际距离不是距离分辨率的整数倍时,就会带来较大的测距误差。此外,采用线性调频连续波(LFMCW)作为发射信号的雷达系统会存在距离与速度耦合的问题,会使得目标的径向距离谱产生模糊[5-6],这些因素都影响雷达的目标测距精度,进而影响目标参数估计及后续的航迹跟踪精度。
为了提高地波雷达的目标距离参数探测精度,国内外学者进行了大量的研究。陈祝明等[7]提出了逐点插值法和二分插值法,可以在增加计算量不多的情况下来保证雷达的测距精度,但是,目前只有仿真实验,未有实测验证。耿籍等[8-9]提出了一种扩展比值插值法来提高地波雷达的测距精度,这种算法可以较好的改善测距精度,但是比较复杂。石阳升等[4]则提出了基于实测数据的三元加权插值方法,该方法原理简单,易于实现。对于在测距过程中的距离-速度耦合问题,也有学者通过分析线性调频连续波雷达回波差拍信号的频谱特点,提出了距离-速度配对的去耦合方法[10-11],以此来减小测距误差;Bruno和胡红军等人则对线性调频地波雷达回波信号中的距离多普勒耦合现象进行了分析,提出利用补偿系数[12-14]来修正产生的测距误差,从而提高高频地波雷达的目标探测精度。
为了实现对高频地波雷达目标距离的准确估计,提高地波雷达的目标探测精度,本文结合地波雷达实测数据,给出了地波雷达目标参数估计处理流程,分析了在处理过程中各种因素对雷达测距误差的影响情况,最后将实测的高频地波雷达数据和船舶自动识别系统(AIS)数据进行对比,统计分析了补偿处理前后的距离误差。
1 地波雷达目标距离参数估计与修正方法高频地波雷达在探测目标时,其发射信号被目标反射回到接收天线,接收信号经射频放大、混频、低通滤波可以得到基带信号,再对其作傅里叶变换可以得到幅度谱,进而就可以得到所需要的距离信息。根据地波雷达的测距原理,图 1给出了本文中地波雷达目标距离估计及修正的处理流程。其处理过程主要分为三步:第一步是目标距离初步估计,第二步是目标距离精细估计,第三步是目标距离最终确定。
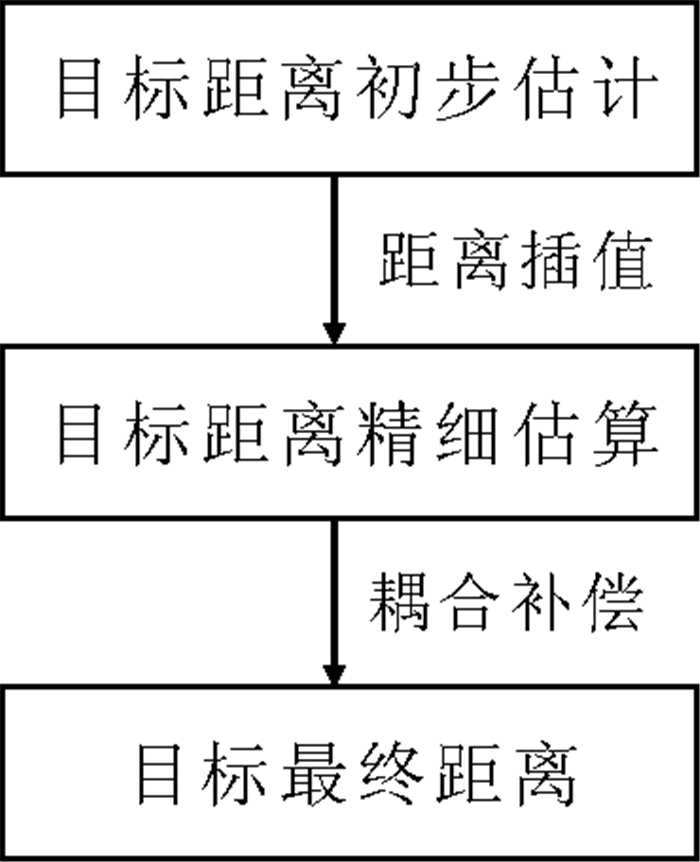
|
图 1 目标测距修正流程图 Fig. 1 Target location and correction flowchart |
目标的初步估计结果主要是基于恒虚警检测方法(CFAR检测)得到的。经典的曲线拟合CFAR检测方法是选用拟合曲线的方式对距离向和多普勒向分别进行处理,然后把距离向和多普勒向的目标检测结果进行“与”运算,便得到目标的最终检测结果,这样能够消除杂波、噪声或其他因素的影响,提高目标的检测性能[15-16]。本文利用CFAR检测得到目标在距离-多普勒谱(R-D谱)中的位置,给出目标峰值点所在的距离单元格,然后根据公式(1)就初步确定了目标的距离信息。
| $ R = N \cdot \Delta R。$ | (1) |
式中:N为目标CFAR得到的峰值点所在的距离单元格;ΔR为地波雷达的距离分辨率。
1.2 目标距离精细估计CFAR检测结果仅给出了目标所在的距离单元格,但不是精确的目标距离信息。目标的运动会导致目标回波信号峰值在距离向上的展宽,出现一个目标占据多个距离单元格的情况。因此应充分利用在距离向的多个单元格,结合CFAR结果做距离插值,以获得更准确的距离信息。三元加权方法原理简单,易于实现,为地波雷达目标参数估计提供了一种适用的估计方法。三元加权插值法是指目标采样点及其相邻的两个采样点,利用三者的幅值将它们对应的离散距离作加权平均,作为最后的估计距离[4]。在存在偏差的情况下,两个相邻采样点与峰值点的幅度比反映了偏离的程度,如图 2所示,因此,可以通过这一点得到目标距离的精细估计。
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;R' = \frac{a}{{a + b + c}}\left( {M - 1} \right) \cdot \Delta R + \\ \frac{b}{{a + b + c}}M \cdot \Delta R + \frac{c}{{a + b + c}}\left( {M + 1} \right) \cdot \Delta R = \\ M \cdot \Delta R + \frac{{c - a}}{{a + b + c}} \cdot \Delta R。\end{array} $ | (2) |
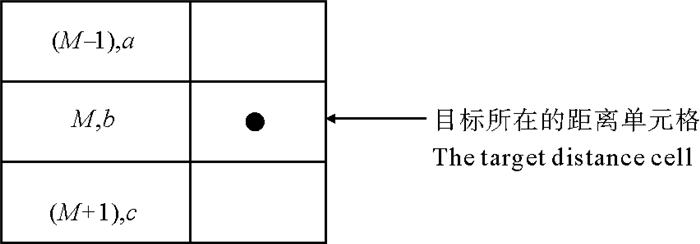
|
图 2 三元加权插值 Fig. 2 Ternary weighted interpolation |
式中:M为目标所在距离元;采样幅值为b;M-1和M+1距离元的采样幅值分别为a和c。
1.3 目标距离最终确定对于采用线性调频信号的高频地波雷达,运动目标会受距离多普勒耦合的影响,这种耦合现象会使地波雷达的径向速度在回波信号中产生多普勒频移,导致雷达测得的目标距离在经过接收机的匹配滤波器后会额外增加一个与线性调频信号参数有关的时间延迟,使得距离和速度之间存在相应的耦合[17-19],从而引起目标的测距误差。因此,为减小雷达的测距误差,需要用耦合补偿处理的方法进行修正,修正之后得到目标的距离R为:
| $ \begin{array}{l} \;\;\;R = \frac{c}{2}{t_0} - \frac{c}{2}\frac{{t{f_0}}}{{{f_2} - {f_1}}} + \frac{{t{f_0}}}{{{f_2} - {f_1}}}v = \\ R' + \frac{{t{f_0}}}{{{f_2} - {f_1}}}v。\end{array} $ | (3) |
式中:当线性调频信号采用上调频信号时,f1<f2;当线性调频信号采用下调频信号时,f1>f2;t是脉冲重复周期;t0是初始延迟时间;f0是中心带宽频率;v是目标的速度。
对于耦合补偿过程中的影响因素主要有目标运动状态和雷达参数:
目标运动状态的影响主要是速度的大小和正负。对于上调频信号,当目标朝向雷达运动时(规定速度大于0),地波雷达测得的距离比实际距离小,误差补偿为正值,反之,目标远离雷达运动的时候误差补偿为负值,且雷达测得距离相对于实际距离偏大。对于下调频信号,当目标朝向雷达运动的时候,地波雷达测得的距离比实际距离大,误差补偿为负值,反之,目标远离雷达运动的时候误差补偿为正值,且雷达测得距离相对于实际距离偏小。
雷达参数的影响主要有(1)调频斜率。由中心频率的计算公式fb=μτ0-fd可知,同一目标对于不同的调频斜率μ,频率偏移均是fd,根据这一特点,可以由不同的调频斜率求出目标的距离和速度,这样有利于对目标的距离进行更准确的估计。(2)频偏。在实际应用中,通常目标距离R远远大于距离分辨率ΔR,将公式(3)进行整理化简可得R=fdTΔR,由该公式可以看出,当雷达的信号时宽T一定的时候,频偏fd越大,产生的测距误差越大,需要的补偿也越多。(3)信号时宽。引起线性调频信号雷达的距离速度耦合的根本原因是信号时宽T较大,并且信号时宽T越大,产生的测距误差越大,对测距精度的影响也越大。
2 实验数据处理与分析 2.1 实验数据及处理结果本次实验采用的是某一岸基高频地波雷达系统,该系统采用等间距八阵元线性接收阵,两个相邻天线阵元之间的间距为14.5 m,频率为4.7 MHz,带宽为60 kHz,线性调频信号的持续时间为0.128 s。同时,本次实验还获取了实时的AIS数据,能给出海面船只目标的实际分布情况,可以利用同步的AIS信息评价地波雷达的目标探测结果[20]。
图 3给出了地波雷达的距离-多普勒谱及CFAR检测结果。从图 3中可以看出,CFAR结果中仅给出了目标所在的距离单元格,不是精确的目标距离信息,测距误差很大,会影响到后续目标航迹关联的探测精度,因此我们进行了距离插值和耦合补偿处理,并统计分析了处理前后目标的距离误差。
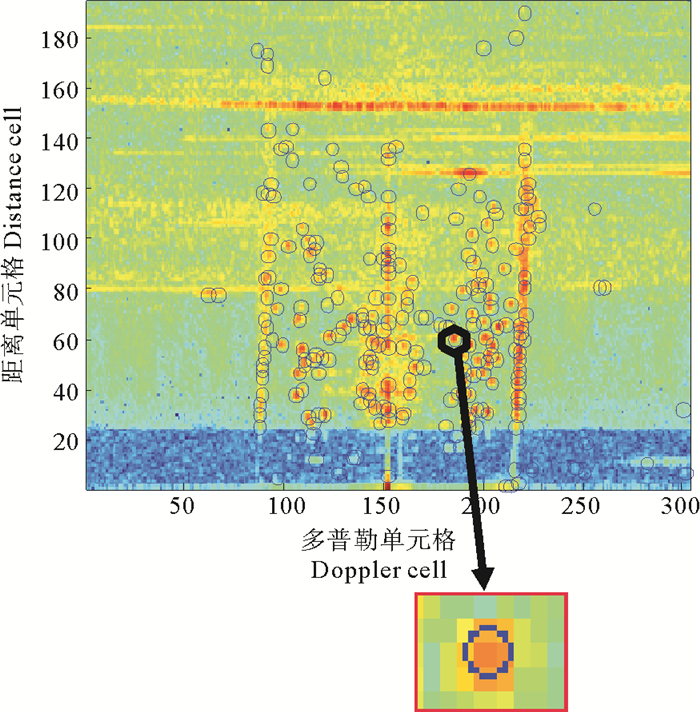
|
图 3 CFAR检测结果 Fig. 3 Detection result of CFAR |
根据实验数据,在将高频地波雷达数据与AIS数据进行匹配之后,给出了该批数据目标航迹的距离误差比较示意图,如图 4所示。图 4(a)为目标径向距离在处理前后的误差均值柱状图,图 4(b)则给出了目标在距离插值和耦合补偿前后的均方根误差比较情况。根据图中的统计结果发现目标的距离误差大部分在2 km附近,测距误差较大,从进行距离插值和耦合补偿之后的统计误差中可以看到原先比较分散的数据经过处理之后基本集中在±0.5 km以内,经过统计计算,该批数据的距离误差均值由原来的由2.25 km减小到了0.52 km,而均方根误差也由1.73 km减小到了0.32 km,雷达的测距精度得到了显著提高。此外,由于地波雷达的发射信号与理想的线性调频信号达不到完全一致,会存在一定的差别,导致目标的测距并不准确,引起补偿后的过补偿现象,从而使得目标的距离在补偿处理之后出现偏差增大的情况。
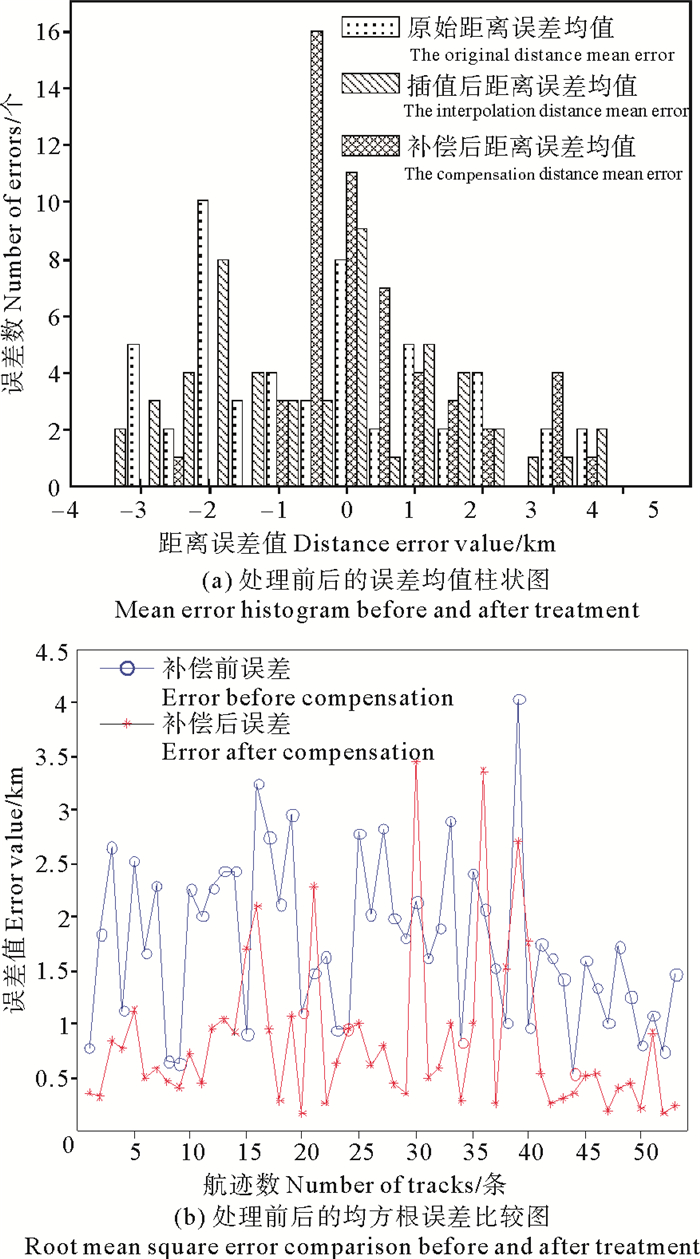
|
图 4 处理前后误差比较图 Fig. 4 Error comparison before and after treatment |
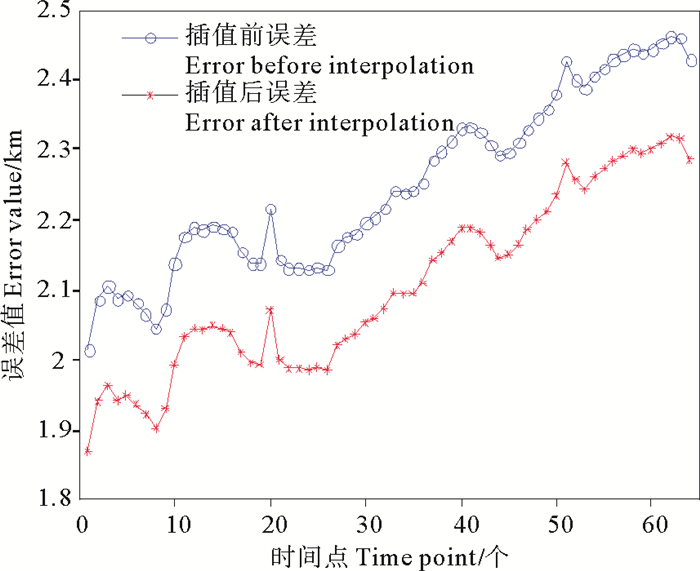
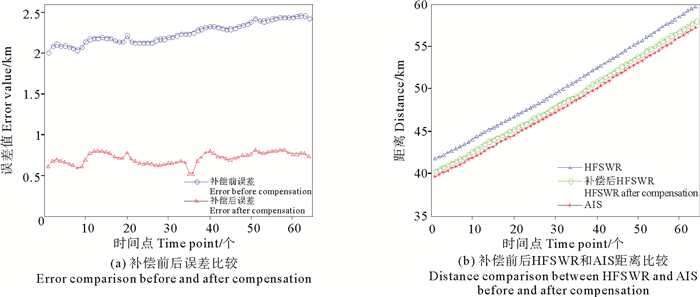
从经过匹配之后的高频地波雷达与AIS的匹配分布图中取出一条航迹进行个例分析,给出了该条航迹经过距离插值和耦合补偿处理之后的误差对比情况,分别如图 5、6所示,并对处理前后的误差进行了统计分析。图 5给出了本次实验中某条航迹在插值前后的误差比较情况,图 6是该条航迹在耦合补偿之后的距离误差比较图以及距离修正图。
|
图 5 插值前后的误差比较 Fig. 5 Error comparison before and after interpolation |
|
图 6 目标补偿前后的对比 Fig. 6 Comparison before and after compensation |
在图 5中,由高频地波雷达和AIS数据统计得到了该条航迹在距离插值之前的距离均方根误差为2.25 km,经过三元加权插值之后的距离均方根误差为2.11 km,误差减小了0.14 km,可以看出虽然目标的测距误差有所减小,但是减小的幅度很小,为了进一步提高地波雷达的测距精度,本文又采用距离-速度耦合补偿的方法进行处理,图 6(a)为距离插值和耦合补偿处理前后的误差比较情况,经统计分析后得到了目标径向距离在理论修正之后的均方根误差为0.52 km,相对插值之后误差又减小了1.59 km,显著提高了地波雷达的探测精度。而且,由图 6(b)的目标距离修正情况也可以看出高频地波雷达测得的目标距离在经过距离插值和耦合补偿处理之后,与AIS测得的实际距离之间的差异明显减小。
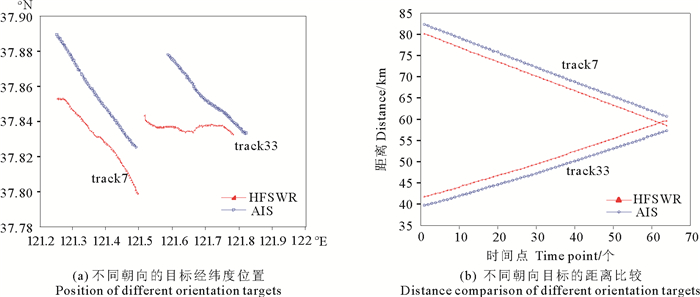
另外,根据匹配图本文选取了两条航迹对目标航向与距离补偿关系进行个例分析。图 7给出了不同朝向的两个目标对地波雷达测距的影响情况,可以看出,对于正调频信号,目标1(即图中track33)朝远离雷达站的方向运动,地波雷达测得的距离为41.74 km,比实际距离39.72 km大,而目标2(即图中track7)朝接近雷达站的方向运动,地波雷达测得的距离为80.17 km,比实际距离82.30 km小。此外,对于目标1,其向远离雷达的方向运动,所得到的误差补偿大小为-1.83 km,其值为负,同样对于朝向雷达运动的目标2,其误差补偿是正值。因此,距离补偿大小和正负与目标速度大小和方向密切相关。
|
图 7 不同朝向目标的分析 Fig. 7 Analysis of different targets oriented |
本文结合高频地波雷达目标探测过程,给出了地波雷达目标距离参数估计的处理流程,通过将实测地波雷达数据与AIS信息进行比对,统计分析了距离插值和耦合补偿前后的误差。从实验数据的分析中可以看出,目标距离的误差均值和均方根误差经过处理之后,均值误差由2.25 km减小到0.52 km,均方根误差由1.73 km减小到0.32 km,雷达的测距精度得到了显著提高。另外,本文还给出了实验中某一条航迹在修正前后高频地波雷达得到的距离和AIS得到的距离对比情况,同时通过两个目标的实测数据分析得出了雷达所需距离误差补偿的大小和正负与目标的速度大小和方向密切相关。
| [1] |
李波. T/R-R高频地波雷达探测范围分析及目标配对算法研究[D].哈尔滨: 哈尔滨工业大学, 2010. Li Bo. T/R-R High Frequency Surface Wave Radar Detection Range Analysis and Matching Algorithms Reaearch[D]. Harbin: Harbin Institute of Technology, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D268206 (  0) 0) |
| [2] |
丁剑飞. FMICW信号性能分析[D].哈尔滨: 哈尔滨工业大学, 2006. Ding Jianfei. FMICW Signal Performance Analysis[D]. Harbin: Harbin Institute of Technology, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10213-2006171565.htm (  0) 0) |
| [3] |
Roarty H J, Smith M, Glenn S M, et al. Expanding maritime domain awareness capabilities in the arctic: High Frequency radar vessel-tracking[C]. Ottawa, Canada: Radar Conference IEEE, 2013: 1-5. https://www.researchgate.net/publication/261278089_Expanding_maritime_domain_awareness_capabilities_in_the_arctic_High_Frequency_radar_vessel-tracking
(  0) 0) |
| [4] |
石阳升, 文必洋, 杨静, 等. 基于旁瓣信息的高频地波雷达高精度测距方法[J]. 中北大学学报(自然科学版), 2015(2): 219-224. Shi Yangsheng, Wen Biyang, Yang Jing, et al. High frequency surface wave radar high precision ranging method based on the sidelobe information[J]. Journal of North Central University: Natural Science Edition, 2015(2): 219-224. DOI:10.3969/j.issn.1673-3193.2015.02.025 (  0) 0) |
| [5] |
吴礼, 彭树生, 肖泽龙, 等. 一种LFMCW雷达距离速度去耦合方法[J]. 现代雷达, 2008, 30(11): 48-51. Wu Li, Peng Shusheng, Xiao Zelong, et al. A LFMCW radar distance speed decoupling method[J]. Modern Radar, 2008, 30(11): 48-51. DOI:10.3969/j.issn.1004-7859.2008.11.012 (  0) 0) |
| [6] |
杜雨洺, 张容权, 杨建宇. 毫米波LFMCW雷达加速运动目标回波检测与加速度-速度估计[J]. 红外与毫米波学报, 2005, 24(5): 348-351. Du Yuming, Zhang Rongquan, Yang Jianyu. Millimeter wave LFMCW radar accelerated motion target echo detection and acceleration-velocity estimation[J]. Journal of Infrared Millimeter Waves, 2005, 24(5): 348-351. DOI:10.3321/j.issn:1001-9014.2005.05.008 (  0) 0) |
| [7] |
陈祝明, 丁义元, 向敬成. 提高线性调频连续波雷达测距精度的最大值估值算法[J]. 系统工程与电子技术, 1999, 21(6): 39-42. Chen Zhuming, Ding Yiyuan, Xiang Jingcheng. The maximum value algorithm of improving the linear frequency modulated continuous wave radar ranging accuracy[J]. Systems Engineering and Electronics, 1999, 21(6): 39-42. DOI:10.3321/j.issn:1001-506X.1999.06.010 (  0) 0) |
| [8] |
林茂庸. 雷达信号理论[M]. 北京: 国防工业出版社, 1984. Lin Maoyong. Radar Signal Theory[M]. Beijing: National Defence Industry Press, 1984. (  0) 0) |
| [9] |
耿籍. 扩展比值插值算法的雷达测距、测速精度分析[J]. 现代防御技术, 2010, 38(5): 107-109. Geng Ji. The radar ranging and speed measuring precision analysis of the extension ratio interpolation algorithm[J]. Modern Defence Technology, 2010, 38(5): 107-109. (  0) 0) |
| [10] |
潘勇先, 朱子平. 一种调频连续波距离-速度配对处理方法[J]. 雷达与对抗, 2011(4): 21-23. Pan Yongxian, Zhu Ziping. A frequency modulated continuous wave distance and velocity matching processing method[J]. Radar and Countermeasure, 2011(4): 21-23. (  0) 0) |
| [11] |
肖汉, 杨建宇, 熊金涛. LFMCW雷达多目标MTD-速度配对法[J]. 电波科学学报, 2005, 20(6): 712-715. Xiao Han, Yang Jianyu, Xiong Jintao. LFMCW radar multi-target MTD- speed matching method[J]. Journal of Radio Science, Journal of Radio Science, 2005, 20(6): 712-715. DOI:10.3969/j.issn.1005-0388.2005.06.004 (  0) 0) |
| [12] |
Fitzgerald R J. Effects of range-doppler coupling on chirp radar tracking accuracy[J]. IEEE Transactions on Aerospace & Electronic Systems, 1974, 10(4): 528-532.
(  0) 0) |
| [13] |
Bruno L, Braca P, Horstmann J, et al. Experimental Evaluation of the Range-Doppler Coupling on HF Surface Wave Radars[J]. Geoscience & Remote Sensing Letters IEEE, 2013, 10(4): 850-854.
(  0) 0) |
| [14] |
胡红军. 脉冲压缩雷达距离多普勒耦合对测距影响分析[J]. 现代雷达, 2011, 33(12): 47-50. Hu Hongjun. The pulse compression radar range Doppler coupling influence analysis on ranging[J]. Modern Radar, 2011, 33(12): 47-50. DOI:10.3969/j.issn.1004-7859.2011.12.013 (  0) 0) |
| [15] |
黄晓静.多频高频地波雷达目标检测与跟踪技术研究[D].武汉: 武汉大学, 2010. Huang Xiaojing. Multiple Frequency High Frequency Surface Wave Radar Target Detection and Tracking Technology Research[D]. Wuhan: Wuhan University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10486-1011065911.htm (  0) 0) |
| [16] |
梁建.高频地波雷达目标二维CFAR检测及软件实现[D].青岛: 中国海洋大学, 2014. Liang Jian. High Frequency Surface Wave Radar Target Two-Dimensional CFAR Detection and the Software Implementation[D]. Qingdao: Ocean University of China, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D546578 (  0) 0) |
| [17] |
Bar-Shalom Y. Negative Correlation and Optimal Tracking with Doppler Measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(3): 1117-1120. DOI:10.1109/7.953264
(  0) 0) |
| [18] |
Niu R, Willett P, Bar-Shalom Y. Tracking considerations in selectionof radar waveform for range and range-rate measurements[J]. Proceedings IEEE Conference on Industrial Automation and Control Emerging Technology Applications, 2002, 38(2): 467-487.
(  0) 0) |
| [19] |
李政. LFMCW雷达目标检测与参数估计方法研究[D].成都: 电子科技大学, 2006. Li Zheng. LFMCW Radar Target Detection and Parameter Estimation Method Research[D]. Chengdu: University of Electronic Science and Technology, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10614-2006111385.htm (  0) 0) |
| [20] |
王祎鸣, 张杰, 纪永刚, 等. 基于AIS距离-多普勒投影的地波雷达CFAR检测验证方法[J]. 海洋学报, 2015(4): 76-82. Wang Yiming, Zhang Jie, Ji Yonggang, et al. The surface wave radar CFAR detection validation method based on AIS range- Doppler projection[J]. Marine Journal, 2015(4): 76-82. DOI:10.3969/j.issn.0253-4193.2015.04.007 (  0) 0) |
2. The First Institute of Oceanography, SOA, Qingdao 266061, China
 2019, Vol. 49
2019, Vol. 49


