2. 河北省气象台,河北 石家庄 050021;
3. 海门市亚森网络有限公司,江苏 南通 226100
大气水平能见度(简称能见度)是反映大气透明度的一个指标[1]。低能见度天气对于陆运、航海、航空的顺利进行都会造成严重的影响,甚至导致社会生产及军事活动无法进行[2]。低能见度事件如雾霾、雾等的产生是由地理环境差异、物理化学作用等共同导致的。这些过程往往与大气内部的运动、大气与地面及海气间的相互作用有关。由于这些过程都是瞬息万变的,因此预报难度相对较大[3]。随着改革开放及现代进程的加快,近年来中国出现了越来越多的雾霾天气,针对低能见度天气的预报被社会各界广泛关注重视。由此,对于大气能见度研究,特别是关于大气低能见度的相关研究工作也陆续开展起来[4-6]。
河北省东部面向渤海,西部与太行山接壤,将北京和天津紧紧环绕,是一个集多种地理环境于一身的省份。近年来,河北省东部及中部地区低能见度事件频发[7]。因此,研发一个针对河北省地区能见度预报方法是有必要的。
人工神经网络可以通过内部神经元实现复杂的算法计算,作为统计模型的一种,人工神经网络对于随时间变化的过程有强大的学习能力[8]。20世纪80年代以来,神经网络方法便被广泛运用到气象学中的各个领域[9-11]。李法然等[9]利用神经网络方法,对浙江湖州地区的雾建立了计算模型并预报。李沛等[1]针对北京地区的能见度进行了研究,利用神经网络算法建立了该地区的能见度模型。徐志鹏等[12]使用BP神经网络对青岛海岸附近站点建立了能见度预报模型。李昕蓓等[13]分析了影响福州地区能见度的气象要素,并采用循环神经网络,对福州单站建立了能见度短临预报模型。由上可见,神经网络预报方法在能见度预报方面是有一定进展和成效的。但前人研究均集中于相同地区,而能见度具有很强的局地性,低能见度事件如雾的产生是物理、化学、辐射过程在不同空间和时间尺度上活动的结果,这些过程受到局部地形条件如不规则地形、海陆边界、海面条件影响[3]。因此沿海与内陆地区影响能见度的主要气象要素可能是不同的,挑选出各自适合的气象要素作为神经网络的特征值,从而得到适合各自的能见度计算模型是有必要的。
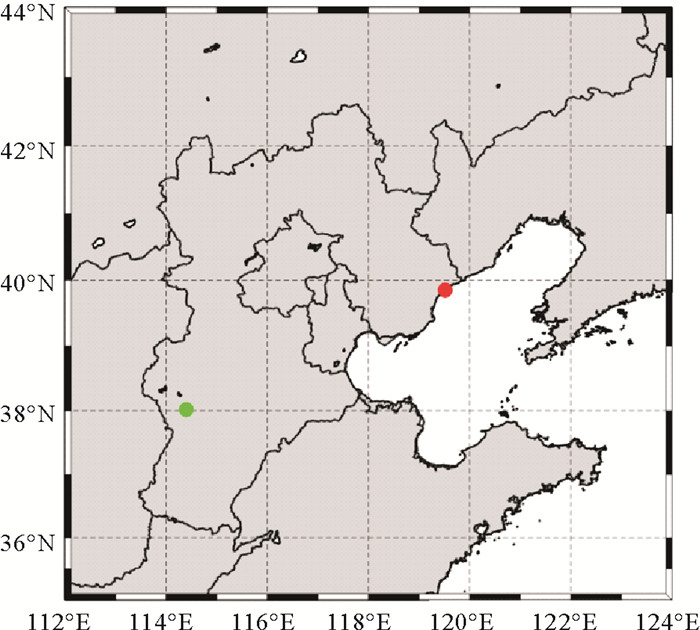
石家庄位于河北省中部,是河北省的政治、文化、人口的中心;秦皇岛位于河北东北部,面朝渤海,是河北经济强市。对两站能见度建立计算模型对整个河北地区具有较好的地区代表意义及经济价值。本文采用循环神经网络方法,将石家庄站(114.39°E,38.01°N) 和秦皇岛站(119.51°E,39.85°N)(见图 1)作为河北省的内陆和沿海的代表站,对比分析两站基本气象要素与能见度的关系,进而建立单站能见度计算模型,并用多种评判方法检验模型效果,探究循环神经网络在能见度预报上的可行性。
|
(红色点代表秦皇岛站,绿色点代表石家庄站。Red dot represents Qinhuangdao station; Green dot represents Shijiazhuang station.) 图 1 自动气象站位置 Fig. 1 Location of automatic weather station |
本文使用资料为河北省石家庄和秦皇岛自动气象站2017—2018年逐小时地面观测资料,随机挑选其中70%的资料用于建立能见度计算模型,剩余的资料用于检验。自动气象站测量资料包括风速、降水量、温度、相对湿度和逐分钟能见度。
前人研究指出,风、相对湿度是影响能见度变化的重要因子[14], 高湿度(RH≥80%)、小风速和雾是造成低能见度的主要气象条件[15]。而在雾出现的阶段,往往伴随着增湿降温的过程。为了反映这个过程,计算得出了1、2和3 h的相对湿度变化量、绝对湿度变化量以及温度变化量,并定义和计算出了1、2和3 h有效降温量(i小时有效降温=Txi=T-Tdi,其中:T为当前温度;Tdi为i小时前露点温度)。降水会导致能见度天气的产生,为了排除这种情况,在统计完所有样本后,剔除掉有降水的样本,本文主要关注能见度较低的事件,因此剔除了能见度大于10 km的样本。
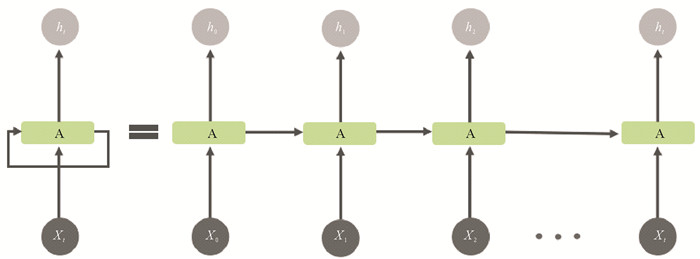
1.2 循环神经网络方法如图 2所示,一个典型的循环神经网络(Recurrent Neural Network,RNN)是由一个输入Xt,一个输出ht以及神经网络单元A所构成。与常见的BP神经网络不同的是,循环神经网络的神经网络单元A不仅与输入和输出存在联系,其自身内部也存在一个回路。将这个自身回路展开便可展示为等号右边的形式。循环神经网络中最初始的输入值为X0,输出值为h0,同时该时刻网络神经元的状态会保存在神经单元A中,当下一个时刻到来后,此时网络神经元的状态不仅仅会由于下一时刻的输入X1产生变化,也会由此时刻的神经元状态A所决定。以此类推,直到时间序列的末尾时刻。基于这种结构,循环神经网络可以理解并记忆随时间变化的气象要素,较BP神经网络将各要素当做离散的数字,该方法在处理能见度数据时能够提取其中更多的特征变化规律。
|
图 2 循环神经网络结构图 Fig. 2 Structure of RNN |
参考中国气象局制定的能见度等级划分标准(即能见度小于1 km为低能见度,能见度大于10 km为高能见度),并考虑到神经网络模型的计算能力及气象局的实际业务运用,本文将能见度划分为0~1 km,1~5 km,5~10 km三个级别,本研究主要关注1级别(0~1 km)和2级别(1~5 km)两个级别能见度的征兆评分(Threat Score,TS)及样本的准确率。
1.4 评分方法气象中常用TS(Threat Score)评分判断单项目标的预报准确性;ACC(Accuracy)评分判断总体目标的预报准确性,ACC又称为准确率。
| $ T S=\frac{T P}{T P+F N+F P}, $ | (1) |
| $ A C C=\frac{T P+T N}{T P+F N+F P+T N} \text { 。} $ | (2) |
式中:TP称为命中,即实测为低能见度,预报为低能见度;FP称为漏报,即实测为低能见度,预报为高能见度;FN称为空报,即实测为高能见度,预报为低能见度。TN称为正确否定,即实测为高能见度,预报为高能见度。
2 石家庄站与秦皇岛站气象要素与其能见度的关系 2.1 石家庄站与秦皇岛站气象要素与分级后能见度的频率分布特征为找到与低能见度有关的基本气象要素,本文分别统计了秦皇岛站和石家庄站基本气象要素在三个级别能见度区间内的频率分布。频率计算方法如下:
i节点频率
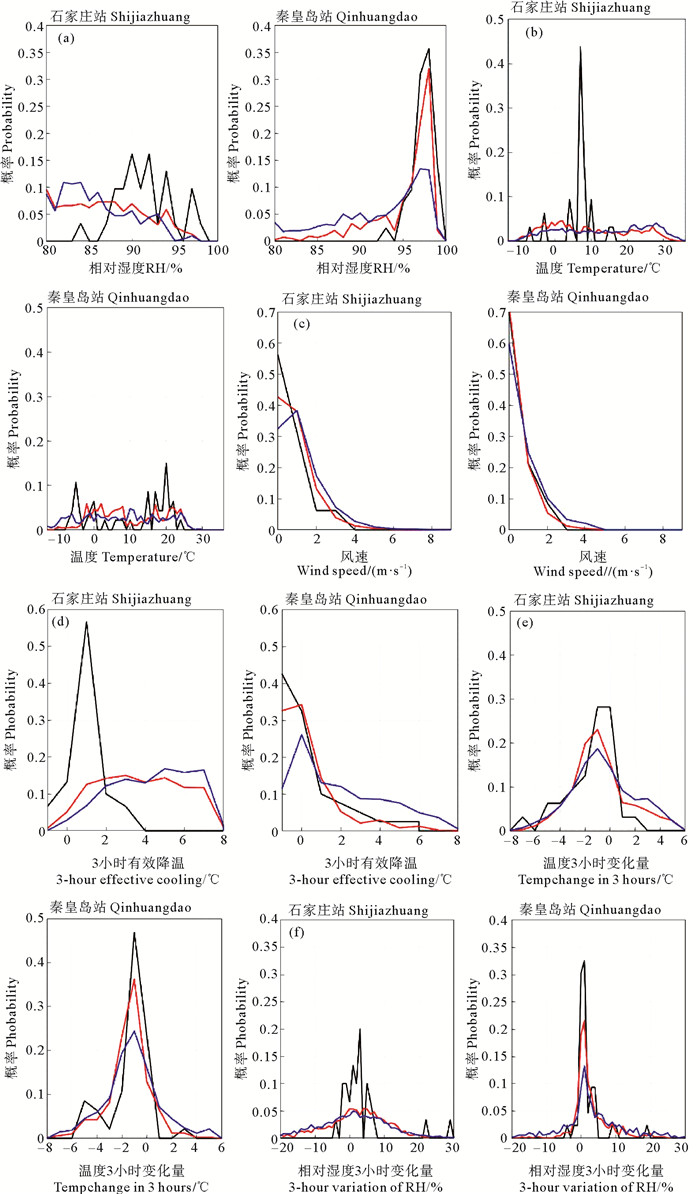
从图 3(a)可以发现,石家庄站相对湿度在1级能见度下的频率呈多峰分布,秦皇岛站相对湿度在各级能见度下的频率均呈单峰分布,故相对湿度可能不适合作为两站能见度计算因子。从图 3(b)中可知,石家庄站温度在1级别能见度下的频率呈单峰分布,而在2、3级别能见度下的频率呈多峰分布,故温度可能适合作为该站能见度计算因子。秦皇岛站温度在各级能见度下的频率均呈多峰分布,故温度可能不适合作为该站能见度计算因子。观察图 3(c)可以发现,两站都符合风速越大,低能见度出现概率越低的规律。但对于石家庄站而言,当风速为0 m/s时,1级能见度发生的概率最大,为0.55,且风速小于2 m/s时,1级能见度发生的概率很大,因此风速可能适合作为该站能见度计算因子。由图 3(d)可知,石家庄站3小时有效降温在1级能见度下的频率呈单峰分布,因此3小时有效降温可能适合作为该站能见度计算因子。观察图 3(e)及3(f)可知,石家庄站与秦皇岛站温度3小时变化在各级能见度下的频率均呈单峰分布,故温度3小时变化可能不适合作为两站能见度计算因子。秦皇岛站相对湿度3小时变化在各级能见度下的频率均呈单峰分布,故相对湿度3小时变化可能不适合作为两站能见度计算因子。
|
(黑线为1级能见度,红线代表 2级,蓝线代表 3级。The black line is visibility of 0~1 km; The red line is visibility of 1~5 km; The blue line is visibility of 5~10 km.) 图 3 2017年1月—2018年12月不同能见度条件下石家庄站和秦皇岛站部分气象要素频率折线图 Fig. 3 Frequency broken line chart of some meteorological elements at Shijiazhuang station and Qinhuangdao station under different visibility conditions from January 2017 to December, 2018 |
为了定量的分析各气象要素与分级后能见度的相关性,计算出了各级能见度与各气象要素的相关系数。表 1中展示部分特征较为明显的要素。
|
|
表 1 基本气象要素与能见度的同期相关系数(2017年1月—2018年12月) Table 1 Correlation coefficient of basic meteorological element and visibility in the same period (January 2017—December 2018) |
表中使用RH、TEMP、AH、V、EC分别代表相对湿度、温度、绝对湿度、风速和有效降温,其中1、2和3 h分别代表 1、2、3小时改变量。通过观察表 1可以发现,当能见度为1级时,石家庄站的相对湿度、温度2、3小时改变量、绝对湿度改变量以及有效降温与能见度的相关性较强, 通过了显著水平0.01的检验,且有效降温与能见度的相关系数最大;秦皇岛站相对湿度以及3、2、1小时有效降温均通过了显著性水平为0.01显著性检验,风速通过了显著性水平为0.05的显著性检验,相对湿度与能见度的相关系数绝对值最大。这可能是由于内陆地区出现低能见度天气主要以辐射雾为主,而沿海地区以平流雾居多。
当考虑所有样本时,石家庄站的相对湿度、1小时有效降温、风速通过了显著性检验,且除了相对湿度和有效降温以及风速外,其他要素相关系数绝对值均小于0.1。秦皇岛站各项要素中,风速、相对湿度以及1、2、3小时有效降温通过了显著水平0.01的检验,其中相对湿度、有效降温的相关系数绝对值大于0.3。两站相对湿度的相关系数绝对值均大于0.2,是较为理想的计算因子。
3 基于循环神经网络建立石家庄站和秦皇岛站能见度模型并检验通过第2节的统计分析,排除与能见度相关性较小的相对湿度改变量,随机挑选70%的样本数据,选用不同气象要素建立能见度计算模型。利用剩余30%数据对模型进行检验,检验结果如表 2。
|
|
表 2 检验样本的能见度计算的单因子TS评分结果(2017年1月—2018年12月) Table 2 TS score results of visibility forecast from January 2017 to December 2018 |
观察表 2可以发现,对使用单一因子建立的两站能见度模型进行检验,结果都是比较稳定的。随着计算因子不断增多,检验结果就会变得复杂起来。选取相对湿度、有效降温及温度改变量这三项作为石家庄站能见度模型的计算因子时,该站1级别能见度的TS评分以及准确率是最高的。继续增加因子反而会降低这1级别能见度的TS评分。观察秦皇岛站的结果可知,选取相对湿度、有效降温这两项作为秦皇岛站能见度模型的计算因子时,该站1级别能见度的TS评分最高,达到了0.3,准确率达到了55%。继续增加计算因子,反而会导致该站准确率降低。由此可见,挑选关键因子建立能见度模型是必要的。
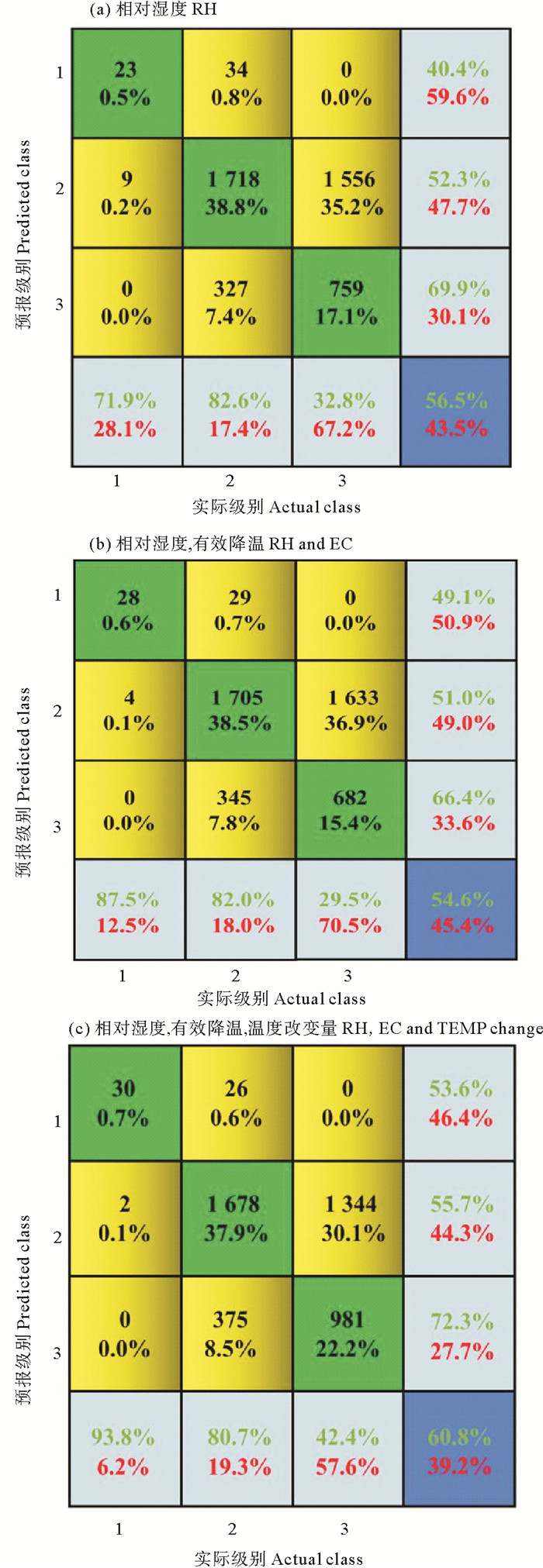
接下来分别使用相对湿度,相对湿度和有效降温,相对湿度、有效降温和温度改变量,作为神经网络输入因子,进而得到石家庄站三种能见度计算模型并检验(见图 4)。图中横坐标为实际级别,即对历史观测的能见度进行分级。纵坐标为预报级别,即对模型计算所得的能见度进行分级。图中绿色方框内数字代表模型计算的能见度与历史观测的能见度级别相同的个数,下方百分数代表该样本数占总样本数的百分比。黄色方框内数字代表模型计算的能见度与历史观测的能见度级别不同的个数。浅蓝色方块中绿色及红色百分数分别代表方块所在级别正确样本百分比和错误样本百分比。深蓝色方块内的百分数代表准确率。
|
图 4 石家庄站能见度计算结果检验 Fig. 4 Visibility forecast result verification at Shijiazhuang Station |
观察图 4(a)可以发现,当选取相对湿度作为石家庄站能见度模型的计算因子时,1级别能见度的空报率(即第一行中黄色方块内的数值之和除以第一行中绿色方块与黄色方块中数值总和,也就是第一行浅蓝色方块中的红色百分数)为59.6%,该模型会将属于2级别能见度的34个样本计算为1级别;漏报率(即第一列中黄色方块内的数值之和除以第一列中绿色方块与黄色方块内的数值总和,即第一列浅蓝色方块中的红色百分数)为28.1%;该模型算计1级别的TS评分为0.35。2级别的空报率为47.7%,该模型将3级别样本中很大一部分计算为了2级别样本,漏报率为17.4%。相比于1级别,该模型计算得出的2级别漏报率及空报率明显较低,准确率为56.5%;图 4(b)中,当选取相对湿度、有效降温作为石家庄站能见度模型的计算因子时,相较于上一个计算模型,该模型对1级别能见度的空报率降低为50.9%,同时漏报率下降到12.5%,对于低能见度事件预报,提升效果是显著的。2级别的空报率及漏报率略有增加,且仍将大量的3级别样本计算为2级别事件;准确率下降为54.6%;图 4(c)当选取相对湿度、有效降温、温度改变量作为石家庄站能见度模型的计算因子时,该模型对1级别能见度的漏报率下降为6.2%,同时其空报率也下降为46.4%,相比上面两个模型,三项计算因子得到的算法模型使得2级别空报率显著下降,同时准确率显著增大,达到了60.8%。总结发现,随着计算因子的不断增加,石家庄站能见度计算模型对于2级别能见度预报的倾向会减小,由此提升了模型的准确率。
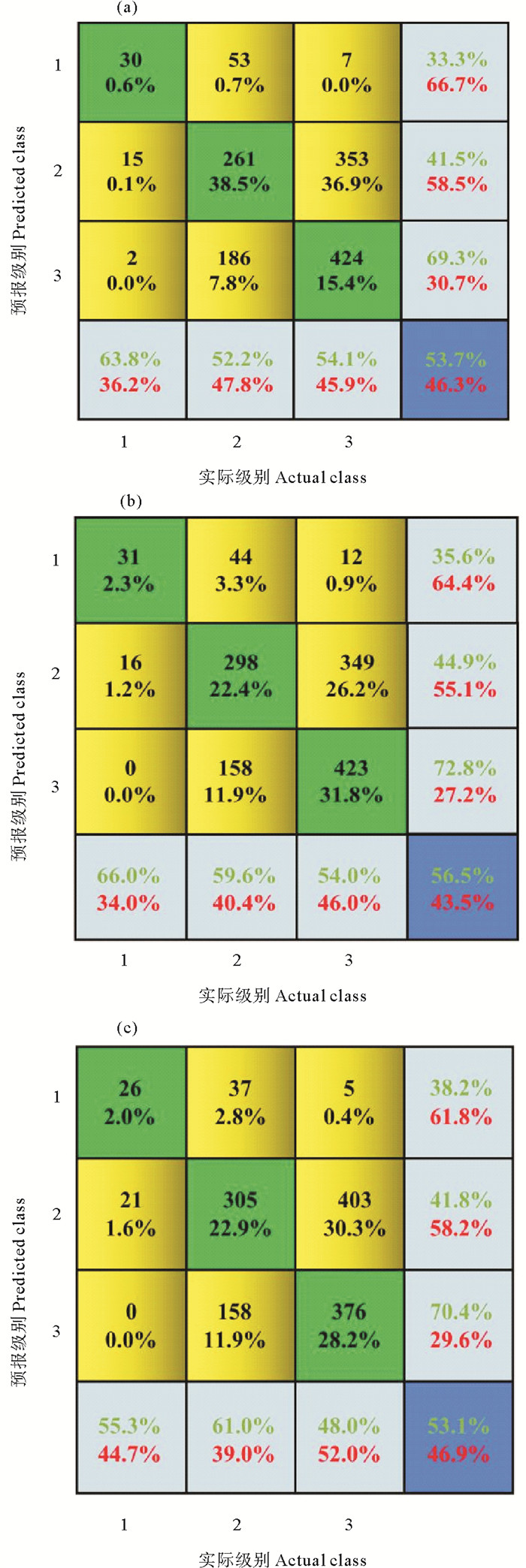
观察图 5(a)可以发现,当选取相对湿度作为秦皇岛站能见度模型计算因子时,该模型对1级别能见度的空报率为66.7%,漏报率为36.2%,对1级别能见度的TS评分为0.28。对2级别能见度的空报率为58.5%,漏报率为47.8%,将近大量3级别能见度样本计算为2级别能见度;图 5(b)中,当选取相对湿度、有效降温作为秦皇岛站能见度模型计算因子时,该模型较仅适用相对湿度建立的能见度模型,对1级别能见度的空报率及漏报率有所降低,这反映出模型对于1级别事件计算能力提升了,同时模型对1级别能见度的TS评分达到了0.3。同时该模型对2级别能见度的空报率及漏报率显著降低,同时准确率达到了56.5%;图 5(c)当选取相对湿度、有效降温和温度改变量作为秦皇岛站能见度模型计算因子时,得到的能见度模型对于各级别能见度预报能力下降。由此可知,挑选关键因子建立的能见度模型,预报效果更佳。
|
图 5 秦皇岛站能见度计算结果检验 Fig. 5 Visibility forecast result verification at Qinhuangdao Station |
通过对石家庄站和秦皇岛站两个自动气象站2017年1月—2018年12月逐小时观测资料进行分析,分布挑选两站能见度影响因子。随机挑选70%的样本数据,利用神经网络方法建立能见度计算模型,并利用剩余30%数据进行检验,得到如下结论:
(1) 大气能见度与气象要素的频率分布特征在石家庄站和秦皇岛站有明显不同。当石家庄站温度在20 ℃、相对湿度为90%;秦皇岛站温度在7 ℃,相对湿度为98%时,出现1级能见度概率最大。
(2) 通过分析气象要素和能见度的相关性可以发现,两站均显示相对湿度和有效降温与能见度的相关性较强。1级能见度时,秦皇岛站相对湿度与能见度的负相关系数最大,而石家庄站则是有效降温和温度改变量与能见度的相关性最好。这可能是由于内陆地区出现低能见度天气主要以辐射雾为主,而沿海地区以平流雾居多。
(3) 通过使用循环神经网络来建立基本要素和能见度的计算模型发现,基于单一因子建立的计算模型TS评分较低,但随着计算因子的不断增多,计算的效果也不一定会变得更好。秦皇岛站采用相对湿度和有效降温作为计算因子时,1、2级别能见度的TS评分最高,准确率达56%。石家庄站采用相对湿度、有效降温和温度改变量作为计算因子时,1、2级别能见度的TS评分最高。
使用循环神经网络方法建立的能见度模型,对于低能见度事件的空报率较高,可能与建模时低能见度样本较少有关。今后工作将用更多自动气象站资料,对不同地理环境的站点进行更细致分区,筛选出适合各分区的能见度影响因子,最终利用业务预报模式中的要素,由点及面,得到河北省格点能见度预报。
致谢: 本文所用的观测数据由河北省气象局提供,作者对此表示诚挚谢意。
| [1] |
李沛, 王式功, 尚可政, 等. 基于神经网络逐级分类建模的北京地区能见度预报[J]. 兰州大学学报(自然科学版), 2012, 48(3): 52-57. Li P, Wang S G, Shang K Z, et al. Visibility forecasting in Beijing based on neural network level-by-level classification modeling[J]. Journal of Lanzhou University (Natural Science Edition), 2012, 48(3): 52-57. (  0) 0) |
| [2] |
王淑英, 张小玲, 徐晓峰. 北京地区大气能见度变化规律及影响因子统计分析[J]. 气象科技, 2003, 31(2): 109-114. Wang S Y, Zhang X L, Xu X F. Statistical analysis of atmospheric visibility variation patterns and influencing factors in Beijing[J]. Meteorological Science and Technology, 2003, 31(2): 109-114. DOI:10.3969/j.issn.1671-6345.2003.02.009 (  0) 0) |
| [3] |
Baguskas S A, Peterson S H, Bookhagen B, et al. Evaluating spatial patterns of drought-induced tree mortality in a coastal California pine forest[J]. Forest Ecol Manag, 2014(315): 43-53. (  0) 0) |
| [4] |
Qiu Jinhuan, Yang Liquan. Variation characteristics of atmospheric aerosol optical depths and visibility in North China during 1980—1994[J]. Atmospheric Environment, 2000, 34(4): 603-609. DOI:10.1016/S1352-2310(99)00173-9 (  0) 0) |
| [5] |
袁成松, 梁敬东, 焦圣明, 等. 低能见度浓雾监测、临近预报的实例分析与认识[J]. 气象科学, 2007, 27(6): 661-665. Yuan C S, Liang J D, Jiao S M, et al. Example analysis and understanding of low-visibility dense fog monitoring and proximity forecasting[J]. Meteorological Science, 2007, 27(6): 661-665. (  0) 0) |
| [6] |
王继志, 徐祥德, 杨元琴. 北京城市能见度及雾特征分析[J]. 应用气象学报, 2002, 13(S1): 160-169. Wang J Z, Xu X D, Yang Y Q. Analysis of visibility and fog characteristics in Beijing city[J]. Journal of Applied Meteorology, 2002, 13(S1): 160-169. (  0) 0) |
| [7] |
田跃思, 张军科, 王莉莉, 等. 京津冀区域大气霾污染研究意义、现状及展望[J]. 地球科学进展, 2014(3): 388-389. Tian Y S, Zhang J K, Wang L L, et al. The significance, status and outlook of research on atmospheric haze pollution in the Beijing-Tianjin-Hebei region[J]. Advances in Earth Sciences, 2014(3): 388-389. (  0) 0) |
| [8] |
章国材. 中国雾的业务预报和应用[J]. 气象科技进展, 2016, 6(2): 42-48. Zhang G C. Operational forecasting and application of fog in China[J]. Progress in Meteorological Science and Technology, 2016, 6(2): 42-48. (  0) 0) |
| [9] |
李法然, 周之栩, 陈卫锋, 等. 湖州市大雾天气的成因分析及预报研究[J]. 应用气象学报, 2005, 16(6): 794-803. Li F R, Zhou Z X, Chen W F, et al. Analysis of the causes and forecasting of foggy weather in Huzhou[J]. Journal of Applied Meteorology, 2005, 16(6): 794-803. (  0) 0) |
| [10] |
张承福. 人工神经网络在天气预报中的应用研究[J]. 气象, 2008, 20(6): 43-47. Zhang C F. Research on the application of artificial neural networks in weather forecasting[J]. Meteorology, 2008, 20(6): 43-47. (  0) 0) |
| [11] |
金龙, 陈宁. 基于人工神经网络的集成预报方法研究和比较[J]. 气象学报, 1999, 57(2): 798-807. Jin L, Chen N. Research and comparison of integrated forecasting methods based on artificial neural networks[J]. Journal of Meteorology, 1999, 57(2): 798-807. (  0) 0) |
| [12] |
徐志鹏, 张苏平, 衣立, 等. 青岛近岸能见度逐小时分级预报模型初探[J]. 海洋湖沼通报, 2018(1): 19-17. Xu Z P, Zhang S P, Yi L, et al. A preliminary investigation of hour-by-hour classification forecast model for nearshore visibility in Qingdao[J]. Marine Lake and Marsh Bulletin, 2018(1): 19-17. (  0) 0) |
| [13] |
李昕蓓, 张苏平, 衣立, 等. 基于循环神经网络的单站能见度短临预报试验[J]. 海洋气象学报, 2019, 39(2): 76-83. Li X B, Zhang S P, Yi L, et al. Experiments on single-station visibility short prognosis based on recurrent neural network[J]. Journal of Marine Meteorology, 2019, 39(2): 76-83. (  0) 0) |
| [14] |
王晓丽, 张苏平, 张晓梅, 等. 青岛市水平能见度变化特征及气象影响因子分析[J]. 气象科学, 2008, 28(S1): 31-36. Wang X L, Zhang S P, Zhang X M, et al. Analysis of horizontal visibility variation characteristics and meteorological impact factors in Qingdao[J]. Meteorological Science, 2008, 28(S1): 31-36. (  0) 0) |
| [15] |
王淑英, 张小玲, 徐晓峰. 北京地区大气能见度变化规律及影响因子统计分析[J]. 气象科技, 2003(2): 109-114. Wang S Y, Zhang X L, Xu X F. Statistical analysis of atmospheric visibility variation and influencing factors in Beijing[J]. Meteorological Science and Technology, 2003(2): 109-114. (  0) 0) |
2. Hebei Meteorological Station, Shijiazhuang 050021, China;
3. Haimen Yasen Network Co., Ltd, Nantong 226100, China
 2022, Vol. 52
2022, Vol. 52


