在实际应用中,几乎所有的控制系统都会受到来自外部的扰动信号。系统的外部扰动往往使得控制系统的性能明显减弱,甚至使闭环系统无法正常工作。在实际系统中,具有正弦特性或周期性特性的扰动是很常见的扰动形式,如飞机飞行振动控制系统[1]、海洋平台振动实时控制系统[2]、工业噪声减振控制、汽车振动减振控制系统等都是在具有正弦特性或周期性特性的扰动下工作的。因此,研究如何减弱或者抑制外部扰动信号对控制系统性能的影响,对实际工程实践有重要的意义。
对于受扰系统的扰动抑制问题,通常前馈反馈算法较经典的反馈控制有更好的扰动抑制效果,例如文献[3]针对正弦扰动的控制系统,给出了一种前馈反馈的扰动抑制算法。前馈控制的缺点是需要增加扰动传感器实时测量扰动信号。对于已知频率、未知振幅和初相角的不可测量的正弦扰动,或其它不可测量的恒值扰动,比较有效的扰动抑制控制方案包括自适应控制[4-5]和预测控制[6-7]等,这些方法对于具有持续扰动(如正弦扰动)的抑制在一定范围内都会存在不同程度的静差。基于内模原理的控制器设计可以保证闭环系统实现无静差扰动抑制,目前利用内模原理主要是针对扰动的不稳定模态设计扰动抑制控制器[8-9]。文献[10]利用内模原理设计了一种受正弦扰动的系统的无静差扰动抑制控制器,这种控制器要求正弦扰动是可测量的,控制器中包含了前馈控制的分量。
本文针对受外部持续正弦扰动的n阶线性系统,提出了一种设计无静差扰动抑制控制器的设计方法。设计的动态状态反馈控制器具有二阶动态特性。通过设计控制器中的n+2个参数,可以使闭环系统的极点任意配置,从而保证了闭环系统的指数渐近稳定性。利用内模原理,通过在控制器中嵌入正弦扰动的模态矩阵,保证了闭环系统的无静差扰动抑制。
1 问题描述考虑受正弦扰动的线性系统
| $ \begin{aligned} \dot{\boldsymbol{x}}(t)=\boldsymbol{A} \boldsymbol{x}(t) &+\boldsymbol{B u}(t)+\boldsymbol{B} w(t), \\ & \boldsymbol{x}(0)=\boldsymbol{x}_{0}。\end{aligned} $ | (1) |
式中:x∈Rn、u∈R、w∈R分别是状态向量、控制输入和扰动输入;x0是初始状态向量;A, B为适当维数的常量矩阵,假设矩阵对(A, B)是完全能控的。不失一般性,可将系统(1)描述为能控规范型形式,即
| $ \boldsymbol{A}=\left[\begin{array}{ccccc}{0} & {1} & {0} & {\cdots} & {0} \\ {0} & {0} & {1} & {\cdots} & {0} \\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {0} & {0} & {0} & {\cdots} & {1} \\ {a_{1}} & {a_{2}} & {a_{3}} & {\cdots} & {a_{n}}\end{array}\right], \boldsymbol{B}=\left[\begin{array}{c}{0} \\ {0} \\ {\vdots} \\ {0} \\ {1}\end{array}\right]。$ | (2) |
假设外部扰动w(t)为正弦特性:
| $ w(t)=a \sin (\omega t+b)。$ | (3) |
式中:频率ω是已知的,振幅a和初相位b是未知的。并假设外部扰动w(t)是物理不可测量的。
在实际系统中,由公式(3)描述的外部扰动是普遍存在的,如工业生产过程中,来自50 Hz工频干扰的电压信号,其频率是已知的,但初相位和干扰的振幅是未知的。
本文的研究目的是对于由公式(1)描述的线性系统,如何设计反馈控制律,实现对正弦扰动公式(3)的无静差扰动抑制。
2 无静差控制律的设计为了实现对外部持续扰动公式(3)的无静差抑制,现将扰动公式(3)改为向量微分方程描述。令v1(t)=
| $ \begin{aligned} \dot{\boldsymbol{v}}(t) &=\boldsymbol{G} \boldsymbol{v}(t), \\ w(t) &=v_{1}(t), \\ \boldsymbol{v}(0) &=\left[\begin{array}{cc}{a \sin b} & {a \omega \cos b}\end{array}\right]^{\mathrm{T}}。\end{aligned} $ | (4) |
式中
| $ \boldsymbol{v}(t)=\left[\begin{array}{c}{v_{1}(t)} \\ {v_{2}(t)}\end{array}\right], \boldsymbol{G}=\left[\begin{array}{cc}{0} & {1} \\ {-\omega^{2}} & {0}\end{array}\right]。$ | (5) |
对于传统的内模原理设计方法,总是考虑在闭环系统内嵌入系统扰动或系统参考输入的不稳定的模态,其目的是抵消系统外部输入的不稳定模态引起的闭环系统的稳态误差。基于内模原理的设计方法,本文试图在闭环系统中嵌入纯虚数极点模态,并提出设计镇定控制器的设计方法。
我们设计如下动态控制律:
| $ \begin{aligned} \dot{\boldsymbol{z}}(t) &=\boldsymbol{G z}(t)-\boldsymbol{H x}(t), \\ \boldsymbol{u}(t) &=-\boldsymbol{k x}(t)+\boldsymbol{z}_{1}(t)。\end{aligned} $ | (6) |
式中z(t)=[z1(t), z2(t)]T为控制器(6)的状态向量,H为待定的2×n矩阵,k为待定的n阶行向量。
将动态控制律(6)代入系统(1),得到系统(1)的闭环系统:
| $ \begin{aligned} \dot{\boldsymbol{x}}(t) &=(\boldsymbol{A}-\boldsymbol{B k}) \boldsymbol{x}(t)+\boldsymbol{B} \bf{z}_{1}(t)+\boldsymbol{B} \boldsymbol{w}(t), \\ \dot{\boldsymbol{z}}(t) &=-\boldsymbol{H} \boldsymbol{x}(t)+\boldsymbol{G z}(t)。\end{aligned} $ | (7) |
图 1示出了闭环系统(7)的结构图。
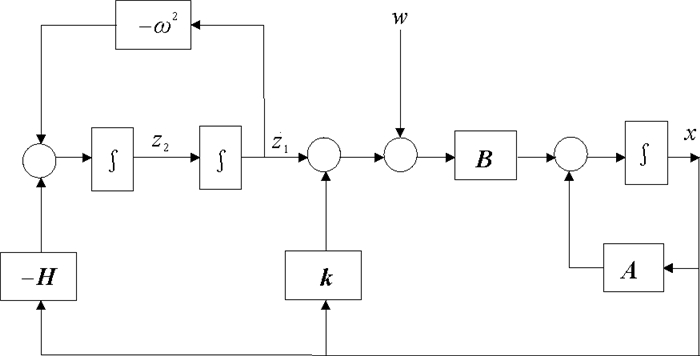
|
图 1 系统结构图 Fig. 1 System structure diagram |
我们的目的是设计2×n矩阵H和n阶行向量k使得:
(Ⅰ)闭环系统(7)的极点可以任意配置,即可使闭环系统(7)渐近稳定,且当扰动w(t)≡0时,状态向量x(t)可以以任意预先给定的指数速率趋向于0。
(Ⅱ)当扰动w(t)由(3)描述时,闭环系统(7)可以实现无静差扰动抑制,即:状态向量x(t)满足:
| $ \mathop {\lim }\limits_{t \to \infty } \mathit{\boldsymbol{x}}(t) = 0。$ | (8) |
由公式(7)可知,闭环系统是一个(n+2)阶系统。我们知道,要使闭环系统(7)的极点可以任意配置,在控制律公式(6)的2×n矩阵H和n阶行向量k中,至少要有(n+2)个自由分量可供我们设计。又要使控制律(6)的结构尽量简单,我们希望控制律公式(6)的2×n矩阵H和n阶行向量k中分量可供我们设计的自由分量个数越少越好。依据这一设计原则,我们选择2×n矩阵H和n阶行向量k的结构为:
| $ \begin{array}{c} \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{l}} 0\\ \mathit{\boldsymbol{h}} \end{array}} \right], \\ \mathit{\boldsymbol{h}} = \left[ {\begin{array}{*{20}{l}} {{h_1}}&{{h_2}}& \cdots &{{h_n}} \end{array}} \right], \\ \mathit{\boldsymbol{k}} = \left[ {\begin{array}{*{20}{l}} 0& \cdots &0&{{k_1}}&{{k_2}} \end{array}} \right]。\end{array} $ | (9) |
k1, k2和hi(i=1, 2, …, n)为待定的常数。
我们先给出主要结果:
定理1 设计受正弦扰动(3)的线性系统(1)的动态反馈控制律公式(6)。适当选择控制器参数k1, k2和hi(i=1, 2, …, n),闭环系统公式(7)的极点可以任意配置。
证明 令s(t)=[xT(t) z1(t) z2(t)]T, 则闭环系统(7)可以写为:
| $ \dot{\boldsymbol{s}}(t)=\overline{\boldsymbol{A}} s(t)+\overline{\boldsymbol{B}}\boldsymbol{w}(t)。$ | (10) |
式中,
| $ \overline{\boldsymbol{A}}=\left[\begin{array}{ccc}{\boldsymbol{A}-\boldsymbol{B} \boldsymbol{k}} & {\boldsymbol{B}} & {0} \\ {0} & {0} & {1} \\ {-\boldsymbol{h}} & {-\boldsymbol{\omega}^{2}} & {0}\end{array}\right]=\\ \left[\begin{array}{ccccccc}{0} & {1} & {\cdots} & {0} & {0} & {0} & {0} \\ {0} & {0} & {\cdots} & {0} & {0} & {0} & {0} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ {0} & {0} & {\cdots} & {0} & {1} & {0} & {0} \\ {a_{1}} & {a_{2}} & {\cdots} & {a_{n-1}-k_{1}} & {a_{n}-k_{2}} & {1} & {0} \\ {0} & {0} & {\cdots} & {0} & {0} & {0} & {1} \\ {-h_{1}} & {-h_{2}} & {\cdots} & {-h_{n-1}} & {-h_{n}} & {-\omega^{2}} & {0}\end{array}\right] 。$ | (11) |
即闭环系统(10)的极点即为矩阵A的特征值。矩阵A的特征多项式为:
| $ \operatorname{det}(\lambda \boldsymbol{I}-\overline{\boldsymbol{A}})=\\ \det \left[ {\begin{array}{*{20}{c}} \lambda &{ - 1}&0& \cdots &0&0&0\\ 0&\lambda &{ - 1}& \cdots &0&0&0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0&0&0& \vdots &{ - 1}&0&0\\ { - {a_1}}&{ - {a_2}}& \cdots &{{k_1} - {a_{n - 1}}}&{\lambda + {k_2} - {a_n}}&{ - 1}&0\\ 0&0& \cdots &0&0&\lambda &{ - 1}\\ {{h_1}}&{{h_2}}& \cdots &{{h_{n - 1}}}&{{h_n}}&{{\omega ^2}}&\lambda \end{array}} \right]=\\ \lambda^{n+2}+\left(k_{2}-a_{n}\right) \lambda^{n+1}+\left(\omega^{2}+k_{1}-a_{n-1}\right) \lambda^{n}+\\ \left[h_{n}+\omega^{2}\left(k_{2}-a_{n}\right)-a_{n-2}\right] \lambda^{n-1}+\\ \left[h_{n-1}+\omega^{2}\left(k_{1}-a_{n-1}\right)-a_{n-3}\right] \lambda^{n-2}+\\ \left( {{h_{n - 2}} - {\omega ^2}{a_{n - 2}} - {a_{n - 4}}} \right){\lambda ^{n - 3}} + \cdots + \left( {{h_3} - {\omega ^2}{a_3} - {a_1}} \right){\lambda ^2} + \\ \left(h_{2}-\omega^{2} a_{2}\right) \lambda+\left(h_{1}-\omega^{2} a_{1}\right) 。$ | (12) |
预先给定闭环系统公式(10)的(n+2)个极点λi(i=1, 2, …, n+2),则有:
| $ \begin{array}{l}{\operatorname{det}(\lambda \boldsymbol{I}-\overline{\boldsymbol{A}})=} \\ {\lambda^{n+2}+\beta_{n+1} \lambda^{n+1}+\beta_{n} \lambda^{n}+\beta_{n-1} \lambda^{n-1}+\cdots+\beta_{1} \lambda+\beta_{0}}。\end{array} $ | (13) |
其中:
| $ \begin{array}{l} {\beta _0} = {( - 1)^{n + 2}}\prod\limits_{i = 1}^{n + 2} {{\lambda _i}} , \\ {\beta _1} = {( - 1)^{n + 1}}\sum\limits_{j = 1}^{n + 2} {\left( {\frac{1}{{{\lambda _j}}}\prod\limits_{i = 1}^{n + 2} {{\lambda _i}} } \right)} , \\ {\beta _2} = {( - 1)^n}\sum\limits_{k = 2}^{n + 2} {\sum\limits_{j = 1}^{k - 1} {\left( {\frac{1}{{{\lambda _j}{\lambda _k}}}\prod\limits_{i = 1}^{n + 2} {{\lambda _i}} } \right)} } , \\ \cdots \\ {\beta _{n - 1}} = {( - 1)^3}\left( {\sum\limits_{k = 3}^{n + 2} {\sum\limits_{j = 2}^{k - 1} {\sum\limits_{i = 1}^{j - 1} {{\lambda _i}} } } {\lambda _j}{\lambda _k}} \right), \\ {\beta _n} = {( - 1)^2}\left( {\sum\limits_{j = 2}^{n + 2} {\sum\limits_{i = 1}^{j - 1} {{\lambda _i}} } {\lambda _j}} \right), \\ {\beta _{n + 1}} = ( - 1)\left( {\sum\limits_{i = 1}^{n + 2} {{\lambda _i}} } \right)。\end{array} $ | (14) |
比较公式(12)和(13)等号右边λ的同次幂系数,得到:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{h_n} + {\omega ^2}\left( {{k_2} - {a_n}} \right) - {a_{n - 2}} = {\beta _{n - 1}}, }\\ {{h_{n - 1}} + {\omega ^2}\left( {{k_1} - {a_{n - 1}}} \right) - {a_{n - 3}} = {\beta _{n - 2}}, }\\ {{h_{n - 2}} - {\omega ^2}{a_{n - 2}} - {a_{n - 4}} = {\beta _{n - 3}}, }\\ \ldots \\ {{h_3} - {\omega ^2}{a_3} - {a_1} = {\beta _2}, }\\ {{h_2} - {\omega ^2}{a_2} = {\beta _1}, }\\ {{h_1} - {\omega ^2}{a_1} = {\beta _0}, }\\ {{k_2} - {a_n} = {\beta _{n + 1}}, }\\ {{\omega ^2} + {k_1} - {a_{n - 1}} = {\beta _n}}。\end{array} \end{array} $ | (15) |
求解(15)得:
| $ \begin{array}{*{20}{l}} {{h_n} = {a_{n - 2}} - {\omega ^2}{\beta _{n + 1}} + {\beta _{n - 1}}, }\\ {{h_{n - 1}} = {a_{n - 3}} + {\omega ^2}\left( {{\omega ^2} - {\beta _n}} \right) + {\beta _{n - 2}}, }\\ {{h_{n - 2}} = {a_{n - 4}} + {\omega ^2}{a_{n - 2}} + {\beta _{n - 3}}, }\\ \cdots \\ {{h_3} = {a_1} + {\omega ^2}{a_3} + {\beta _2}, }\\ \begin{array}{l} {h_2} = {a^2}{a_1} + {\beta _0}, \\ {h_1} = {\omega ^2}{a_1} + {\beta _0}, \end{array}\\ {{h_2} = {a_n} + {\beta _{n + 1}}, }\\ {{k_1} = {a_{n - 1}} - {\omega ^2} + {\beta _n}}。\end{array} $ | (16) |
综上分析,只要按(16)选取控制器参数k1, k2和hi(i=1, 2, …, n),则闭环系统(10)的极点可以任意配置。
推论1 设计受正弦扰动(3)的线性系统(1)的动态反馈控制律(6)。适当选择控制器参数k1, k2和hi(i=1, 2, …, n),如果系统扰动w(t)≡0,闭环系统(7)可以是指数渐近稳定的,且状态向量x(t)可以以任意预先给定的指数速率趋向于0。
证明 令系统扰动w(t)≡0,则闭环系统(10)可以写为:
| $ \dot{\boldsymbol{s}}(t)=\overline{\boldsymbol{A}} s(t)。$ | (17) |
类似于定理1的证明,预先给定闭环系统(17)的(n+2)个具有负实部极点λi(i=1, 2, …, n+2),按(16)设计控制器参数k1, k2和hi(i=1, 2, …, n),则闭环系统(7)是指数渐近稳定的。不妨令
| $ \mathop {\min }\limits_i \left( {{\mathop{\rm Re}\nolimits} \left( {{\lambda _i}} \right), i = 1, 2, \cdots , n + 2} \right) = {\mathop{\rm Re}\nolimits} \left( {{\lambda _1}} \right)。$ | (18) |
显然,闭环系统(17)的解满足:
| $ \|\boldsymbol{x}(t)\| \leqslant\|\boldsymbol{s}(t)\| \leqslant M \cdot \exp \left(\operatorname{Re}\left(\lambda_{1}\right) t\right)。$ | (19) |
式中M是足够大的正常数。又由于是任意给定的具有负实部的常数,所以且状态向量x(t)可以以任意预先给定的指数速率趋向于0。
注1:定理1的证明不仅证明了闭环系统(10)的极点可任意配置,而且给出了动态反馈控制律公式(6)的参数k1, k2和hi(i=1, 2, …, n)的选取公式(16)。
定理2 设计受正弦扰动(3)的线性系统(1)的动态反馈控制律公式(6)。按公式(16)选取控制器参数k1, k2和hi(i=1, 2, …, n),则闭环系统公式(7)关于状态向量x(t)是渐近稳定的,从而实现对系统公式(1)的无静差扰动抑制,即公式(8)成立。
证明 令
| $ \boldsymbol{e}_{i}(t)=\boldsymbol{v}_{i}(t)+\boldsymbol{z}_{i}(t), i=1, 2。$ | (20) |
由(4)和(7)得:
| $ \begin{array}{c}{\dot{\boldsymbol{x}}(t)=(\boldsymbol{A}-\boldsymbol{B k}) \boldsymbol{x}(t)+\boldsymbol{Be} _{1}(t)} \\ {\dot{\boldsymbol{e}}(t)=\boldsymbol{G e}(t)-\boldsymbol{H} \boldsymbol{x}(t)}。\end{array} $ | (21) |
令r(t)=[xT(t) eT(t)]T, 则闭环系统(21)可以写为:
| $ \dot{\boldsymbol{r}}(t)=\overline{\boldsymbol{A}} \boldsymbol{r}(t)。$ | (22) |
其中A由公式(11)确定。与定理1的证明过程类似,预先给定闭环系统公式(22)的(n+2)个具有负实部极点λi(i=1, 2, …, n+2),按公式(16)选取控制器参数k1, k2和hi(i=1, 2, …, n),则闭环系统公式(22)是渐近稳定的。这说明,在正弦扰动公式(3)下,闭环系统公式(7)关于状态向量x(t)是渐近稳定的,从而实现对系统公式(1)的无静差扰动抑制,即公式(8)成立。
注2:由定理2不仅说明了利用受正弦扰动(3)的线性系统(1)的动态反馈控制律公式(6)可以实现无静差扰动抑制,而且给出了动态反馈控制律公式(6)的参数k1, k2和hi(i=1, 2, …, n)的选取公式(16)。
3 示例仿真考虑受正弦扰动(3)的3阶线性系统(1),其中:
| $ \boldsymbol{A}=\left[\begin{array}{ccc}{0} & {1} & {0} \\ {0} & {0} & {1} \\ {-2} & {1} & {-1}\end{array}\right], \boldsymbol{B}=\left[\begin{array}{l}{0} \\ {0} \\ {1}\end{array}\right]。$ |
假设系统的输出为y(t)=x1(t)。系统的初始条件为:
| $ \begin{array}{l}{x_{1}(0)=x_{2}(0)=x_{3}(0)=0} \\ {a=2, b=0}。\end{array} $ |
以下作者利用本文提出的动态控制律算法公式(6)与状态反馈控制律对该系统的控制效果进行比较。在两种控制律控制效果的讨论中,假设选择状态反馈控制闭环系统的极点为:
s1=-1+j, s2=-1-j, s3=-2。
状态反馈控制律及设计过程从略。
设计动态控制律公式(6),由公式(11)得闭环系统公式(7)的系数矩阵为:
| $ \overline{\boldsymbol{A}}=\left[\begin{array}{ccccc}{0} & {1} & {0} & {0} & {0} \\ {0} & {0} & {1} & {0} & {0} \\ {-2} & {1-k_{1}} & {-1-k_{2}} & {1} & {0} \\ {0} & {0} & {0} & {0} & {1} \\ {-h_{1}} & {-h_{2}} & {-h_{3}} & {-\omega^{2}} & {0}\end{array}\right]。$ |
本文分2种情形讨论动态控制律公式(6)的控制效果。
给定闭环系统公式(7)的(n+2)=5个极点:
s1=-1+j, s2=-1-j, s3=-2, s4=-3, s5=-4。
则由公式(12)、(13)和(14)得:
β0=48, β1=100, β2=94, β3=46, β4=11。
再由公式(16)得到控制器参数:
| $ \begin{array}{*{20}{l}} {{h_3} = 92 - 11{\omega ^2}, }\\ {{h_2} = {\omega ^2}\left( {{\omega ^2} - 46} \right) + 100, }\\ {{h_1} = - 2{\omega ^2} + 48, }\\ {{k_2} = 10, }\\ {{k_1} = - {\omega ^2} + 47}。\end{array} $ |
图 2示出了ω=0.5π时的系统仿真曲线。
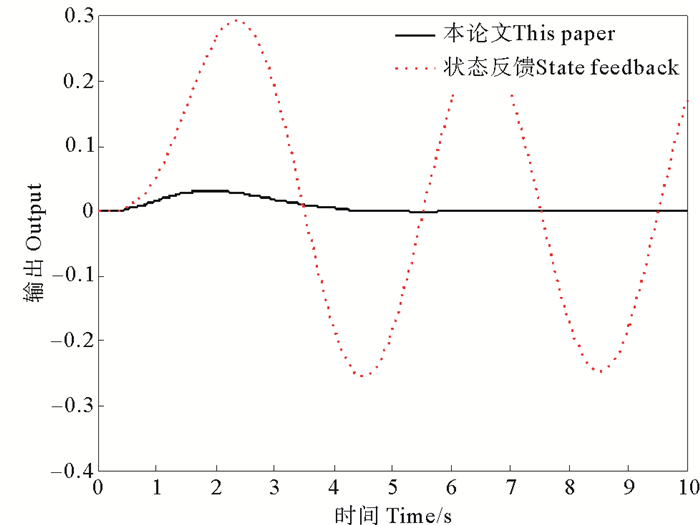
|
图 2 ω=0.5π时的系统仿真曲线 Fig. 2 Simulation curves of the system when ω=0.5π |
图 3示出了ω=π时的系统仿真曲线。
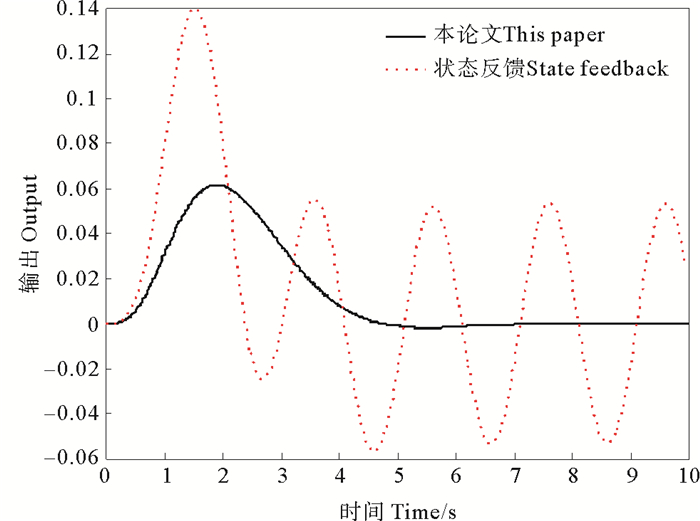
|
图 3 ω=π时的系统仿真曲线 Fig. 3 Simulation curves of the system when ω=π |
图 4示出了ω=1.5π时的系统仿真曲线。
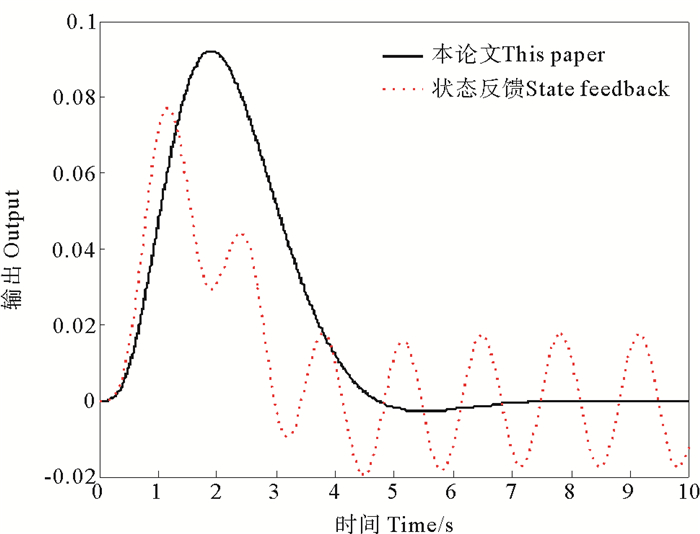
|
图 4 ω=1.5π时的系统仿真曲线 Fig. 4 Simulation curves of the system when ω=1.5π |
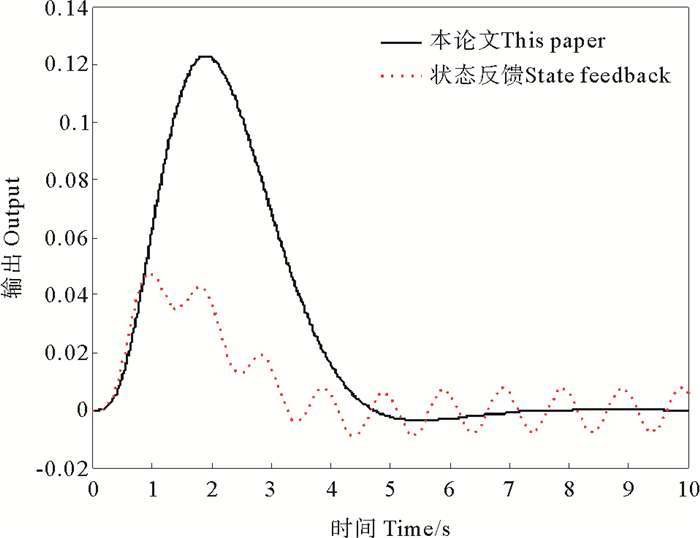
图 5示出了ω=2π时的系统仿真曲线。
|
图 5 ω=2π时的系统仿真曲线 Fig. 5 Simulation curves of the system when ω=2π |
从图 2~5中可以看到,不论外部正弦扰动信号的频率如何,利用本文提出的控制器算法,都能使闭环系统的响应逐渐趋于0。正弦扰动信号的频率越低,控制效果越好。但是利用本文设计的控制律,闭环系统的响应曲线的超调量会随着正弦扰动信号频率的增加而增加。在列举的仿真例子中,当正弦扰动信号频率ω>1.5π时,闭环系统的响应曲线的超调量会迅速增大。而仅利用状态反馈控制律,闭环系统的响应曲线都不能使闭环系统的响应逐渐趋于0。但会随着正弦扰动信号频率的增加而增加,闭环系统的响应曲线的振荡幅值越来越小,这说明利用状态反馈控制的闭环系统有低通滤波的特性。
综上分析表明,本文设计的扰动抑制控制律能使闭环系统指数渐近稳定,而且在正弦扰动下能够实现无静差扰动抑制。本文的控制器设计方法特别适合于具有较低振荡频率的正弦扰动的系统。
4 结语本文基于内模原理研究了输出反馈扰动抑制控制律的设计问题。本文设计的扰动抑制控制律能使闭环系统指数渐近稳定,而且在正弦扰动下能够实现无静差扰动抑制。仿真结果表明,本文的控制器设计方法仅适用于具有较低振荡频率的正弦扰动的系统,正弦扰动的振荡频率越低,闭环系统的动态性能越好。
| [1] |
Chen Z, Huang J. Attitude tracking of rigid spacecraft subject to disturbances of unknown frequencies[J]. International Journal of Robust and Nonlinear Control, 2014, 24(16): 2231-2242. DOI:10.1002/rnc.v24.16
(  0) 0) |
| [2] |
Ma H, Tang G Y, Zhao Y D. Feedforward and feedback optimal control for off shore structures subjected to irregular wave forces[J]. Ocean Engineering, 2006, 33(7): 1105-1117.
(  0) 0) |
| [3] |
Tang G Y, Gao D X. Approximation design of optimal controllers for nonlinear systems with sinusoidal disturbances[J]. Nonlinear Analysis, Theory, Methods and Applications, 2007, 66(2): 403-414. DOI:10.1016/j.na.2005.11.035
(  0) 0) |
| [4] |
Basturk H I, Krstic M. Adaptive sinusoidal disturbance cancellation for unknown LTI systems despite input delay[J]. Automatica, 2015, 58: 131-138. DOI:10.1016/j.automatica.2015.05.013
(  0) 0) |
| [5] |
Kim H, Shim H, Jo N H. Adaptive add-on output regulator for rejection of sinusoidal disturbances and application to optical disc drives[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5490-5499. DOI:10.1109/TIE.2014.2304920
(  0) 0) |
| [6] |
Maeder U, Morari M. Offset-free reference tracking with model predictive control[J]. Automatica, 2010, 46(9): 1469-1476. DOI:10.1016/j.automatica.2010.05.023
(  0) 0) |
| [7] |
Kumar C, Mishra M K. Predictive voltage control of transformerless dynamic voltage restorer[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2693-2697. DOI:10.1109/TIE.2014.2365753
(  0) 0) |
| [8] |
Marino R, Tomei P. Output regulation for linear systems via adaptive internal model[J]. IEEE Transactions on Automatic Control, 2003, 48(12): 2199-2202. DOI:10.1109/TAC.2003.820143
(  0) 0) |
| [9] |
Richard R, George W. Internal model based tracking and disturbance rejection for stable well-posed systems[J]. Automatica, 2003, 39(9): 1555-1569. DOI:10.1016/S0005-1098(03)00192-4
(  0) 0) |
| [10] |
Tang G Y, Zhang S M, Zhang B L. Optimal tracking control with zero steady-state error for time-delay systems with sinusoidal disturbances[J]. Journal of Sound and Vibration, 2007, 299(3): 633-644. DOI:10.1016/j.jsv.2006.07.020
(  0) 0) |
 2019, Vol. 49
2019, Vol. 49


