2. 中国海洋大学 山东省海洋环境地质工程重点实验室,山东 青岛 266100;
3. 中国海洋大学 环境科学与工程学院,山东 青岛 266100
海底沉积物流是世界上最重要的泥沙搬运方式之一,是陆源碎屑沉积物和其他颗粒物质由陆地向深海运输的重要通道[1],通过世界上的主要河流及其入海口,沉积物流将大量的泥沙由大陆架输送到深海盆地中[2]。由海底滑坡、高含沙量流体入海或风暴潮等触发形成的沉积物流[3-5],会对海底线缆及其他海底结构物产生很强的冲击力,使其受到严重损害,造成巨大经济损失,甚至引发生态灾害。如1929年GrandBanks处7.2级地震触发的浊流,造成了数根海底电缆依次发生断裂,由此反推出浊流的最大速度达到28 m/s[6-8]。此外,我国台湾海域是海底浊流的高发区域,近些年来,发生了多次由浊流引发的线缆断裂事故,对东南亚及全球通讯造成重大影响[2, 9-10]。
鉴于水下沉积物流对结构物有如此强大的破坏力,为保证海底线缆的安全,国内外的学者针对水下沉积物流冲击海底结构物(以海底管线为主)在理论分析、模型试验和数值模拟方面开展了大量的研究。位于海底的结构物会受来自任意方向的沉积物流的冲击,可将其分解为三个正交分量:沿流方向垂直于结构物轴线的力、平行于结构物轴线的纵向力和垂直于轴线可使结构物上提、下推或振荡的力。沿流方向垂直于结构物轴线的力(包括拖曳力与惯性力),通常被认为是结构物破坏的主要因素[11]。
Pazwash等首先基于流体力学和流变学原理研究了非牛顿流体绕物体流动时所产生的拖曳力[12]。Bea等也使用流体动力学方法分析了Pazwash等[12]的实验数据,但发现其提出的方法估计的拖曳力要比他们试验中测量的低[13]。Det Norske Veritas为了计算含沙浑水体作用在管道上的作用力,对作用在管道上的稳态流采用拖曳力系数分析的方法,用专门的公式对其轴向力和法向力进行了计算,为海底管道的铺设打下了理论基础[14];Zakeri等通过多次的水槽试验研究了水下沉积物流对海底结构物的冲击作用,对不同粒径级配的沉积物流冲击结构物所产生的拖曳力进行了分析研究,通过公式计算得到了沉积物流冲击作用下结构物的拖曳力系数,并通过计算流体动力学(CFD)软件进行了数值模拟反演分析,分析结果与试验结果有较好的吻合度,于是提出了用赫巴模型描述海底沉积物流冲击悬跨管道时,非牛顿流体雷诺数的表达式,并提出了用该雷诺数表达的拖曳力系数的经验公式[11, 15-17]。刘君等[18-19]在Zakeri研究的基础上,采用Power-Law流变模型,引入土力学方法与流体力学方法形成对比,进一步修正了拖曳力系数与雷诺数的关系表达式。
目前,针对水下沉积物流对结构物所受拖曳力、拖曳力系数等多个方面研究广泛。但是,研究过多的关注了结构物本身的性质,而忽略了流体性质的影响。由于深海沉积物流的粘粒含量极高[20],而目前针对粘土组分的水下沉积物流速度变化特征及对结构物的拖曳力还鲜有研究。故本文采用自主设计的可调节坡度平直水槽,对不同浓度的粘土组分的水下沉积物流在多个坡度下的速度变化特征与结构物所受拖曳力进行研究,分析其速度、拖曳力与浓度、坡度之间的关系,并给出沉积物流速度、密度与拖曳力之间的关系表达式。
1 试验方法研究水下沉积物流速度特征及对海底结构物的作用力,其根本在于沉积物流的运动能力,而沉积物流的运动又会受到其流变特性的影响。由此也需要关注沉积物流流变特征发生变化的浓度界限。本文在开展不同浓度沉积物流冲击试验的同时,取其沉积物流样品进行沉积物流流变测试。
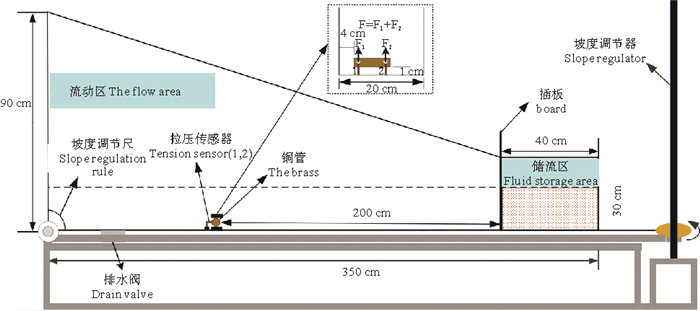
1.1 试验仪器与样品沉积物流冲击试验在实验室中利用自主设计的可调坡度平直水槽进行结构物受力测量试验,试验装置的布局和尺寸(长350 cm、宽20 cm)如图 1所示。平直水槽分为储流区(用来盛放沉积物流)和流动区(盛放清水),储流区和流动区之间设置一个可上下抽动的插板,试验中采用抽板法制造沉积物流。在水槽中距离插板2.0 m处放置结构物(本试验中用长80 mm、外径20 mm、壁厚1 mm的铜管模拟结构物),在结构物后方两端分别放置一个拉压传感器(型号CZL-1012,额定荷载10N,精确度等级0.3,编号为1、2),用来实时测量结构物所受拖曳力,采样频率为100 Hz。在试验过程中,储流区和流动区的水深始终是相同的。同时,为了便于得到沉积物流运动至结构物处的实时速度,采用摄像机对放置结构物区域进行录像监测。
|
( F.拖曳力Drag force F1、F2;拉压传感器1、2所受拖曳力。Drag force on the tension sensor1、2. ) 图 1 平直水槽 Fig. 1 Straight flume |
流变测试所用仪器为美国BrookfieLd工程实验室公司所生产的R/S+流变仪。测试时所用转子为型号MK3-CC40-DIN的同轴转子及配套样品杯。流变仪通过端口连接计算机,可实时查看测试数据和流变曲线。
本次试验用土为高岭土。其平均粒径3.7 μm。
1.2 试验过程 1.2.1 水槽冲击试验本次试验根据沉积物流质量体积浓度不同,取不同质量高岭土,由低到高分别配制了9个浓度,分别为280、340、400、460、500、560、600、660和700 g/L。每个浓度都在四个坡度下(0°、3°、6°、9°)进行,坡度可通过水槽的支架旋转来调节。
试验过程中,首先将沉积物流在容器中利用搅拌器搅拌均匀,而后将清水导入水槽流动区至指定高度处并静置,待水面无波动后,将配置好的沉积物流导入储流区与流动区水面平行并再次充分搅拌,待搅拌结束十秒后,迅速抽出插板,沉积物流冲入水槽流动区对结构物产生冲击。
试验过程中使用30帧/s的摄像机记录结构物受冲击段过程,位置与结构物平齐。试验结束后利用视频回放软件进行逐帧分析沉积物流头部到达结构物处的流动速度。使用DEWESoftX软件来采集结构物受力数据,并实时监测结构物受力情况。
1.2.2 流变测试流变测试样品与水槽冲击试验所用沉积物流样品同时配置,共9组。测试前,将样品倒入小烧杯中用玻璃棒搅拌均匀,随后倒入样品杯,将其安装并固定在流变仪上。测试时,采用等剪切率测试程序[21](CSR模式,即控制剪切速率随时间线性增加),测试时间300 s,测试点100个。对每一个样品,均进行3次平行测试,在3次测试结果具有一致性的情况下,选取其中1次的曲线进行结果分析。
2 试验结果 2.1 水槽冲击试验结果试验采用抽板法制造沉积物流,试验过程中,抽出插板,不同浓度的沉积物流流动至结构物处对其产生冲击。图 2给出一个浓度(以660 g/L为例)沉积物流在四个坡度下的的结构物前流动状态。可以清晰的看到沉积物流头部尖锐,并在同一浓度下,随着坡度的增加,沉积物流的头部高度是呈现不断增大的趋势。

|
图 2 沉积物流结构物前流动状态 Fig. 2 Flow state in front of typical sediment flow structure |
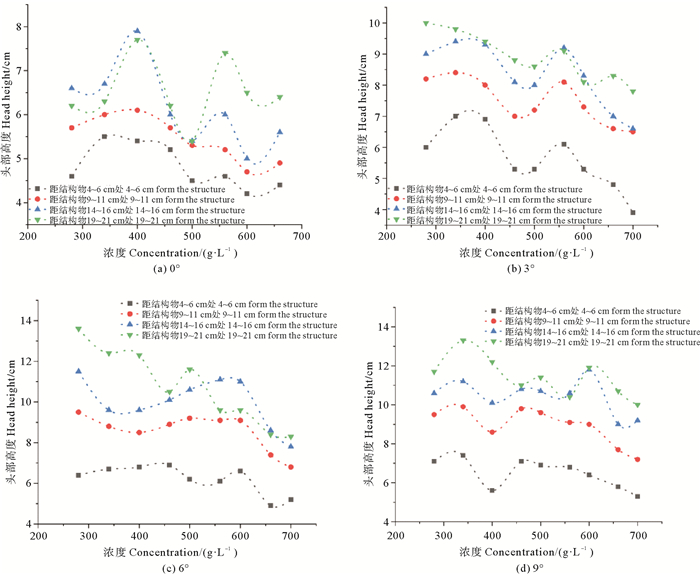
通过试验录像回放,在图像处理软件中利用槽身上的尺寸对沉积物流结构物前头部高度进行同比例测量。图 3所示为在不同坡度下,结构物前沉积物流头部高度随浓度变化关系图,结合试验现象,可以发现当头部刚刚到达并接触结构物时,在结构物前15~25 cm的距离区间内,沉积物流头部高度达到了最大值。同时,在结构物前0~20 cm区间内,低浓度的沉积物流头部高度普遍要比高浓度的大。在试验录像中可以看出,在结构物前25 cm的距离内沉积物流头部的速度没有显著变化(以560 g/L、6°坡为例,结构物前25、15、5 cm处速度均为50 cm/s),故采用此区间内的平均速度来表征沉积物流对结构物产生冲击时的速度。
|
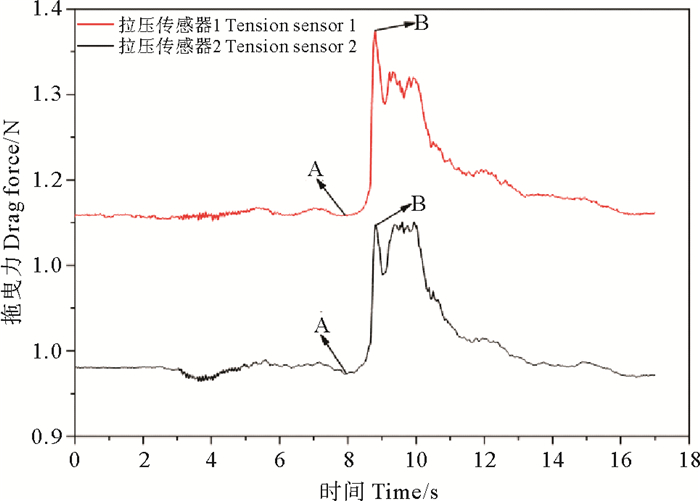
图 3 拖曳力响应曲线 Fig. 3 Drag force response curve |
图 4所示为试验过程中结构物拖曳力响应曲线(以600 g/L、6°坡为例),拉压传感器1、2相加即为结构物所受拖曳力。图中,A点为沉积物流头部最前端刚刚作用于结构物,可以看到在沉积物流接触结构物后产生拖曳力出现第一个峰值(B点),而在其后,再次出现了峰值,这种现象应是由于沉积物流接触结构物后产生了循环和涡流,从而再次对结构物产生了作用力,其影响较小,故在本次试验后续分析中,只考虑第一个峰值的大小。
|
图 4 不同坡度下沉积物流头部高度随浓度变化 Fig. 4 The head height of sediment flow varies with concentration under different slopes |
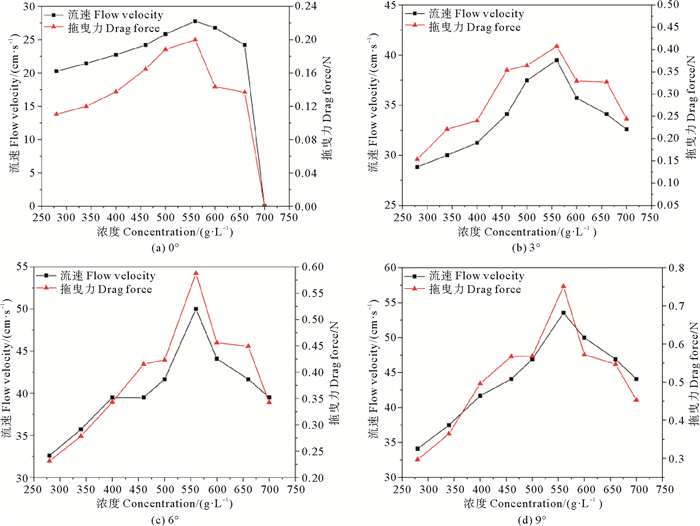
本文对在不同坡度下,沉积物流结构物前流速与结构物所受拖曳力随浓度变化进行了分析(见图 5)。
|
图 5 不同坡度下浓度与速度、拖曳力关系曲线 Fig. 5 Curve of concentration versus velocity and dragforce at different slopes |
图中可以看出,在0°、3°、6°、9°坡上,随浓度增大,速度都呈现一个先增后减的趋势。本次试验的九个浓度,在相应坡上对应速度达到最大值的浓度都为560 g/L,对应的最大速度分别为27.778、39.494、50和53.533 cm/s。拖曳力变化曲线与速度变化曲线呈现了良好的一致性,其在相应的浓度下对应的最大拖曳力分别为0.2、0.4、0.58和0.75 N。由此可见,速度与拖曳力曲线都呈现了相同的趋势,即在试验的四个坡度下,存在一个对应沉积物流最大速度与最大拖曳力的浓度,在本文中将之称为临界沉积物流浓度。
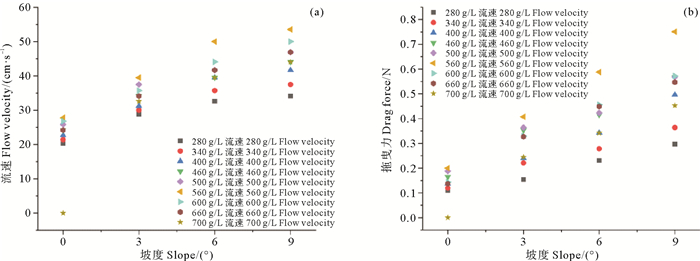
2.1.2 不同浓度下坡度与速度、拖曳力的关系图 6所示为沉积物流结构物前流速与结构物所受拖曳力随坡度变化的曲线图。可以看到,流速与拖曳力随坡度的增大而增大,且变化幅度较大。值得注意的是,当沉积物流的浓度为700 g/L时,在0°坡下结构物前流速与拖曳力为0(700 g/L的沉积物流在结构物前30 cm处停止运动),而在增加坡度后,运动能力发生了很大的变化,其速度达到了32.595、39.499和44.092 cm/s,对应的拖曳力为0.24、0.34和0.45 N。说明坡度是水下沉积物流运动状态及对结构物冲击的重要影响因素之一。
|
图 6 坡度与速度(a)、拖曳力关系(b) Fig. 6 Relationship of slope to speed(a) and drag force(b) |
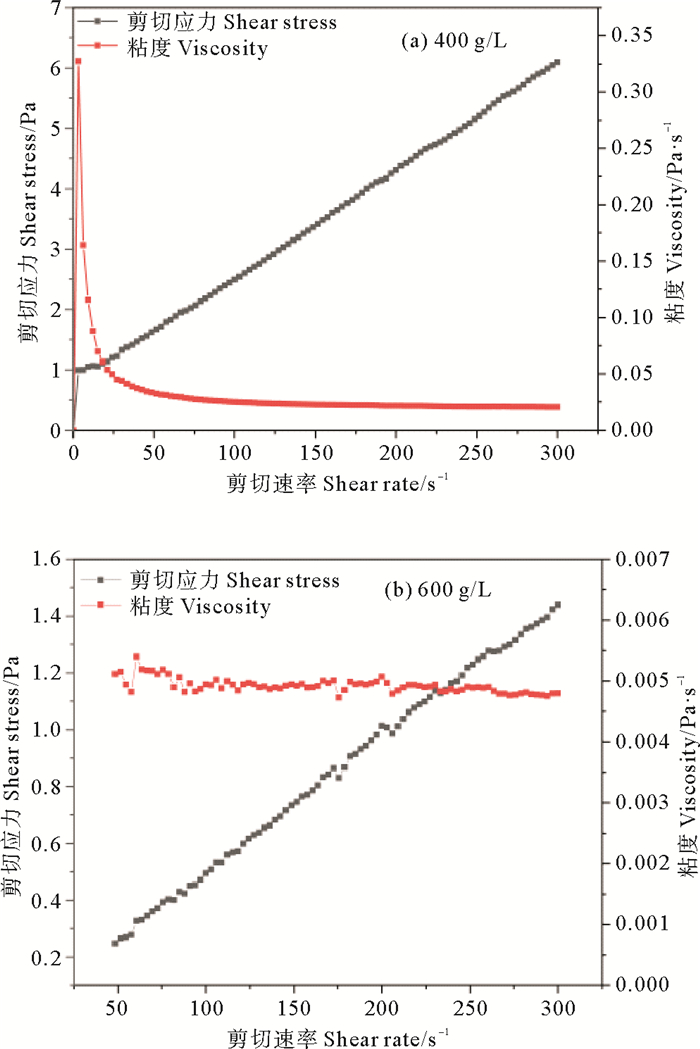
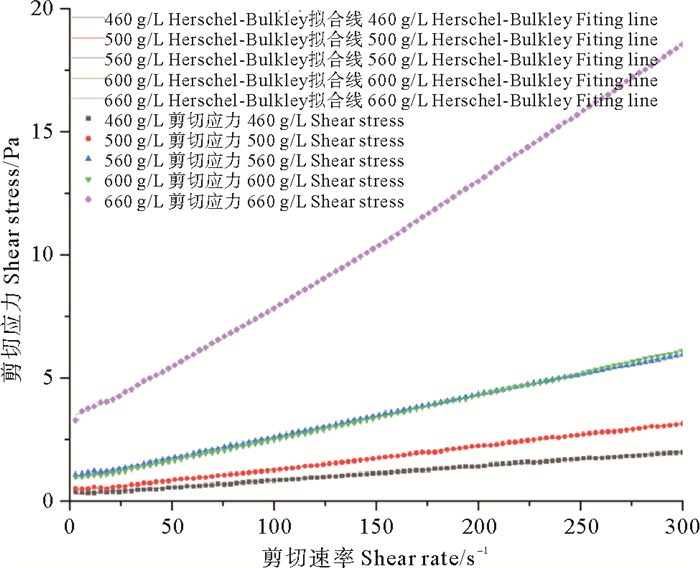
水下沉积物流的运动能力会受到沉积物流流变特性的影响,由此也需要关注沉积物流流变特征发生变化的浓度界限。通过对沉积物流样品的流变测试,发现3组低浓度(280、340和400 g/L)样品在剪切速率达到一定阈值时才可以测到剪切应力和粘度,其粘度在一定值附近保持相对稳定并伴随一定波动,将其与流变模型特征曲线比较,符合牛顿流体特征。其余6组较高浓度的沉积物流在初始剪切率下就存在可测量的剪切应力和粘度,其剪切应力则随剪切速率的增大而增大,粘度在初始剪切率时达到最大,随着剪切速率的增大而不断降低并趋于平稳,可用赫巴模型来描述。图 7给出两个典型浓度(400、600 g/L)的流变曲线。图 8所示为5个浓度(460、500、560、600和660 g/L)的沉积物流流变模型拟合。表 1给出了流变模型拟合公式及R2值,可以看到,R2均大于0.99,相关性很强,故用赫巴模型来描述本试验上述5个浓度的沉积物流非常适合,其中τ为剪切应力,γ为剪切速率。
|
图 7 典型浓度流变曲线 Fig. 7 Typical concentrationrheological curve |
|
图 8 流变数据和模型拟合 Fig. 8 Rheological data and model fitting |
|
|
表 1 流变模型拟合公式 Table 1 Fitting formula of rheological model |
图 3所示为沉积物流头部高度曲线。当坡度一定时,在结构物前0~10 cm的区间内,沉积物流头部高度有显著的增大;在结构物前10~15 cm与15~20 cm的区间内,曲线中沉积物流头部高度呈现一个交替的状态。说明沉积物流在接触结构物时,头部在结构物前0~10 cm呈现缓慢增高,直到在10~20 cm处达到头部最高处,其形态呈现为一种“火车头”状。当浓度一定时,在试验所处坡度下,沉积物流头部高度呈现一个随坡度增大而增大的规律。
3.1 浓度、坡度对沉积物流速度影响当浓度一定时(见图 6),速度随坡度增大而明显增大,说明坡度是速度变化的重要影响因素之一。当坡度一定时(见图 5),随浓度增大,速度会出现先增后减的趋势,即存在一个临界沉积物流浓度。沉积物流在水下运动时,其动力来源为重力驱动(由沉积物流与水体之间的密度差导致的密度驱动),在沉积物流浓度小于临界沉积物流浓度时,由于其与流动区水体密度差较小,抽板后流动的驱动力较小,流动速度较低,随着浓度的增加,速度不断增大,直至达到临界沉积物流浓度对应的最大速度;在沉积物流浓度大于临界沉积物浓度时,抽板后虽然沉积物流流动的驱动力较大,但由于沉积物流本身粘性增加,流动能力下降,故随着浓度的不断增大,速度明显降低(在沉积物流700 g/L、0°坡时,沉积物流在结构物前30 cm处就停止了流动)。
3.2 浓度、坡度对拖曳力影响图 4所示为结构物所受拖曳力变化曲线,A点为沉积物流头部最前端刚刚到达时,B点为沉积物流头部最厚处到达时。可知,拖曳力并不是一个瞬时变化的值,而是沉积物流接触结构物并围绕结构物流动,在短时间内(A点—B点,约0.15~0.3 s,取决于头部速度)随时间逐渐递增的过程,这与Zakeri等在室内试验的结果曲线具有一致性[11]。结合试验现象与数据进行分析,在拖曳力逐渐增加的这段过程中,沉积物流的流动距离约为10~20 cm。
本次试验中,结构物所受拖曳力的变化与沉积物流速度变化呈现了良好的一致性(见图 5),当坡度一定时,随浓度增大,拖曳力同样会出现先增后减的趋势,在达到临界沉积物浓度时,拖曳力同时达到了最大值。由上可知,在达到临界沉积物流浓度时,沉积物流有一个较强的流动能力,此时对结构物的拖曳力最大。
3.3 拖曳力与沉积物流密度之间的关系如图 5所示,沉积物流速度与结构物所受拖曳力都会在临界沉积物流浓度时达到一个峰值,在试验条件下,不同的沉积物流浓度对应不同的密度,分析可知,沉积物流密度是影响其速度与结构物受力的重要因素。表 2所示为各个浓度沉积物流所对应的密度。
|
|
表 2 不同浓度沉积物流密度表 Table 2 Density table of sediment flow with different concentrations |
在流体动力学中,采用以下公式来计算拖曳力:
| $ {F_D} = \frac{1}{2}\rho {C_D}{U_\infty }^2A。$ | (1) |
式中:FD表示结构物所受拖曳力;ρ为密度;CD为拖曳力系数;U∞为结构物前流速;A为结构物的特征面积,在本试验中即铜管截面的面积。
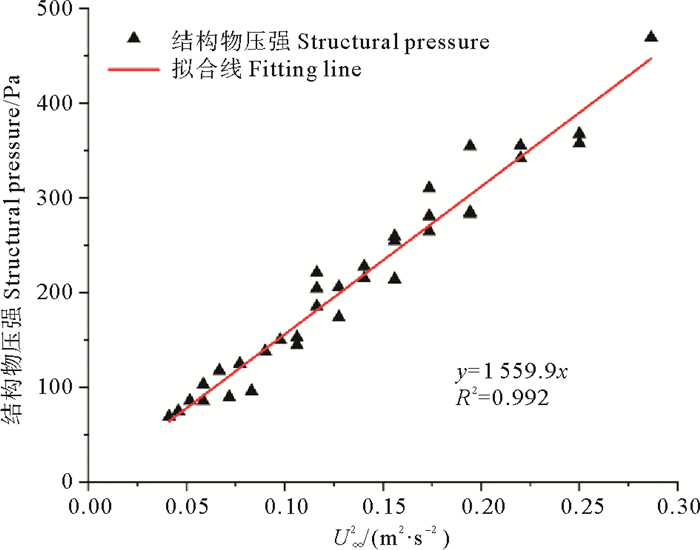
图 9所示为结构物所受压强与速度平方之间的关系。关系式如下:
| $ {P_D} = 1\;559.9{U_\infty }^2。$ | (2) |
|
图 9 压强与速度平方关系图 Fig. 9 Pressure and velocity squared diagram |
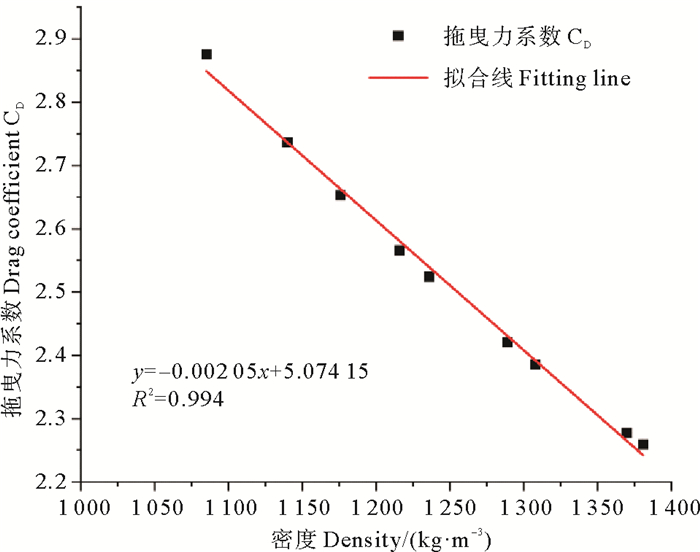
式中:PD为结构物所受压强;U∞为结构物前流速。可得,压强与速度平方有良好的线性关系。将式(2)中速度平方项前系数带入式(1),可得到在试验实测值情况下拖曳力系数与密度之间的关系,如图 10所示。可得,试验情况下拖曳力系数与密度的关系为:
| $ {C_D} = - 0.002\;05\rho + 5.074\;15。$ | (3) |
|
图 10 拖曳力系数与密度关系图 Fig. 10 Relationship between drag coefficient and density |
式中:CD为拖曳力系数;ρ为密度。
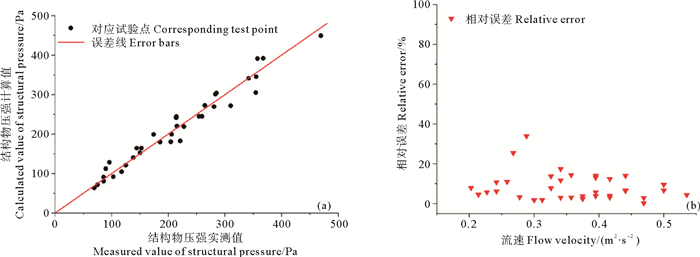
将利用式(3)所得的拖曳力系数代入式(1),可得到本次所有试验结构物受力的计算值,将其与实测值进行误差分析。图 11(a)所示为结构物压强计算值与实测值误差图,图 11(b)所示为在试验中不同速度下的误差范围。可知,计算值与实测值相对误差基本都在20%以内,说明在本次试验条件下,采用上述方法来计算分析结构物受力情况是可行的。
|
图 11 计算值与实测值对比 Fig. 11 Comparison of calculated and measured values |
Zakeri等通过计算流体动力学的数值模拟手段(CFD)研究了水下沉积物流对管线冲击荷载,同时对室内试验结果进行了反演分析(室内试验采用高岭土和砂来配制沉积物流,管壁前速度范围为0.5~1.4 m/s),提出了赫巴模型描述水下沉积物流时,用雷诺数来表达的拖曳力系数的经验公式[11, 15]:
| $ {C_D} = 1.4 + \frac{{17.5}}{{\mathit{Re}_{non - newtonian}^{1.25}}}。$ | (4) |
式中,Renon-newtonian是非牛顿流体的雷诺数。
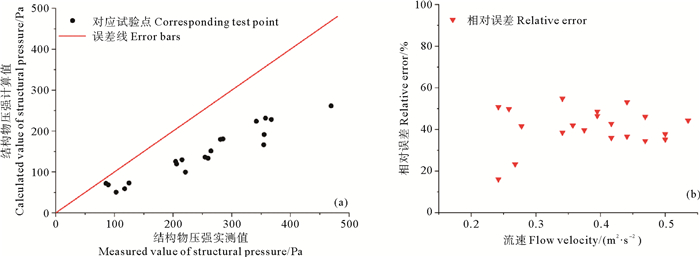
利用式(1)、(4)得到本次试验中非牛顿流体(460~660 g/L)所对应的结构物压强,并与实测值进行对比。图 12(a)所示为结构物压强计算值与实测值误差图,图 12(b)所示为在试验中不同速度下的误差范围。
|
图 12 由Zakeri所提公式计算值与实测值对比 Fig. 12 Comparison between the calculated value and the measured value by zakeri's formula |
由图 12可知,利用Zakeri等提出的方法来得到的结构物压强计算值小于试验实测值,相对误差普遍在20%~50%范围内。由此可得,对于280~700 g/L浓度范围内的纯粘土组分的沉积物流在速度较低(0.2~0.6 m/s)时,此方法并不适用。
综上分析, 在试验浓度范围内(280~700 g/L),对于纯粘土组分沉积物流速度较低(0.2~0.6 m/s)时,可建立结构物所受拖曳力与沉积物流速度、密度之间的关系表达式:
| $ {F_D} = \frac{1}{2}\rho \left( {5.074\;15 - 0.002\;05\rho } \right){U_\infty }^2A。$ | (5) |
式中:FD表示结构物所受拖曳力;ρ为密度;U∞为结构物前流速;A为结构物的特征面积。
4 结论本文基于自主设计的可调坡度平直水槽上,针对不同浓度粘土组分的水下沉积物流,在不同的坡度下进行了对结构物冲击试验,并对所配制的沉积物流进行流变测试,给出了速度、拖曳力与浓度、坡度之间的关系,通过对试验数据的分析讨论,得出如下结论:
(1) 低浓度粘土组分的沉积物流(280~400 g/L)为牛顿流体,高浓度(460~700 g/L)为非牛顿流体,符合赫巴流变模型。
(2) 在一定的浓度下,沉积物流速度与结构物所受拖曳力会随坡度的增大而增大;在一定的坡度下,随着沉积物流浓度不断增大,沉积物流速度与结构物所受拖曳力呈现先增后减的趋势(存在临界沉积物流浓度),本次试验条件下,在0°、3°、6°、9°四个坡度下所得临界沉积物流浓度为560 g/L。
(3) 在试验浓度范围内(280~700 g/L),对于纯粘土组分沉积物流速度较低(0.2~0.6 m/s)时,得到了结构物所受拖曳力与沉积物流速度、密度三者之间的关系表达式:FD=1/2ρ(5.074 15-0.002 05ρ)· U∞2A。
| [1] |
Stetson H C, Smith J F. Behavior of suspension currents and mud slides on the continental slope[J]. American Journal of Science, 1938, 35(205): 1-13.
(  0) 0) |
| [2] |
徐景平. 海底浊流研究百年回顾[J]. 中国海洋大学学报(自然科学版), 2014, 44(10): 98-105. Xu Jing-Ping. Turbidity current research in the past century: An overview[J]. Periodical of Ocean University of China, 2014, 44(10): 98-105. (  0) 0) |
| [3] |
Talling, Peter J. On the triggers, resulting flow typesand frequencies of subaqueous sediment density flows in different settings[J]. Marine Geology, 2014, 352: 155-182. DOI:10.1016/j.margeo.2014.02.006
(  0) 0) |
| [4] |
Wang F, Dai Z, Nakahara Y, et al. Experimental study on impact behavior of submarine landslides on undersea communication cables[J]. Ocean Engineering, 2018, 148: 530-537. DOI:10.1016/j.oceaneng.2017.11.050
(  0) 0) |
| [5] |
Pirmez C, Imran J. Reconstruction of turbidity currents in Amazon Channel[J]. Marine & Petroleum Geology, 2003, 20(6-8): 849.
(  0) 0) |
| [6] |
Bruce C. Heezen, Maurice Ewing.Turbidity currents and submarine slumps, and the 1929 Grand Banks earthquake[J]. American Journal of Science, 1952, 250(12): 849-873. DOI:10.2475/ajs.250.12.849
(  0) 0) |
| [7] |
Bruce C Heezen, Ericson D B, Maurice Ewing. Further evidence for a turbidity current following the 1929 Grand Banks earthquake[J]. Deep Sea Research(1953), 1954, 1(4): 193-202.
(  0) 0) |
| [8] |
Kuenen P H. Estimated size of the Grand Banks[Newfoundland] turbidity current[J]. American Journal of Science, 1952, 250(12): 874-884. DOI:10.2475/ajs.250.12.874
(  0) 0) |
| [9] |
Hsu S K, Kuo J, Lo C L, et al. Turbidity currents, submarine landslides and the 2006 Pingtung earthquake off SW Taiwan. Terrestrial atmospheric and ocean[J]. Science, 2008, 19: 767-772.
(  0) 0) |
| [10] |
Carter L, Milliman J D, Talling P J, et al. Near-synchronous and delayed initiation of long run-out submarine sediment flows from a record-breaking river flood, offshore Taiwan[J]. Geophysical Research Letters, 2012, 39(12): L12603.
(  0) 0) |
| [11] |
Zakeri A, Høeg K, Nadim F. Submarine debris flow impact on pipelines-Part Ⅰ: Experimental investigation[J]. Coastal Engineering, 2008, 55(12): 1209-1218. DOI:10.1016/j.coastaleng.2008.06.003
(  0) 0) |
| [12] |
Pazwash H, Robertson J M. Forces on bodies in Bingham fluids[J]. Journal of Hydraulic Research, 1975, 13(1): 35-55. DOI:10.1080/00221687509499719
(  0) 0) |
| [13] |
Bea R G, Aurora R P. Design of pipelines in mudslide areas[J]. Journal of Petroleum Technology, 1983, 35(11): 1985-1995. DOI:10.2118/12343-PA
(  0) 0) |
| [14] |
Det Norske Veritas. Rules for the design, construction and inspection of submarine pipelines and pipeline risers[M]. [s.l.]: Det Norske Veritas, 1976.
(  0) 0) |
| [15] |
Zakeri A, Høeg K, Nadim F. Submarine debris flow impact on pipelines-Part Ⅱ: Numerical analysis[J]. Coastal Engineering, 2009, 56(1): 1-10. DOI:10.1016/j.coastaleng.2008.06.005
(  0) 0) |
| [16] |
Zakeri A. Submarine debris flow impact on suspended (free-span) pipelines: Normal and longitudinal drag forces[J]. Ocean Engineering, 2009, 36(6): 489-499.
(  0) 0) |
| [17] |
Zakeri A, Hawlader B. Drag forces caused by submarine glide block or out-runner block impact on suspended (free-span) pipelines-Numerical analysis[J]. Ocean Engineering, 2013, 67: 89-99. DOI:10.1016/j.oceaneng.2013.03.007
(  0) 0) |
| [18] |
Liu J, Tian J, Yi P. Impact forces of submarine landslides on offshore pipelines[J]. Ocean Engineering, 2015, 95(1): 116-127.
(  0) 0) |
| [19] |
Jun Liu, Jianlong Tian. Impact forces of submarine landslides on free-span pipelines[C]//Asme International Conference on Ocean. [s. l. ]: American Society of Mechanical Engineers, 2014, 6(B).
(  0) 0) |
| [20] |
Maier K L, Gales J A, Paull C K, et al. Linking direct measurements of turbidity currents to submarine canyon-floor deposits[J]. Frontiers in Earth Science, 2019, 7: 104. DOI:10.3389/feart.2019.00104
(  0) 0) |
| [21] |
吕楚岫, 许国辉, 任宇鹏, 等. 不同含沙量浑水体流变特性试验研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(1): 43-51. LV Chu-Xiu, XU Guo-Hui, REN Yu-Peng, et al. Experimental study on the rheological properties of turbid water in different concentrations[J]. Periodical of Ocean University of China, 2017, 47(1): 43-51. (  0) 0) |
2. Ocean University of China Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering, Qingdao 266100, China;
3. Ocean University of China College of Environmental Science and Engineering, Qingdao 266100, China
 2021, Vol. 51
2021, Vol. 51


