2. 大连理工大学海岸与近海工程国家重点实验室,辽宁 大连 116023
钢悬链线立管(Steel catenary riser, SCR)是连接海上浮式平台和海底管道的重要系统[1]。浮式平台在海流波浪等海洋环境作用下会产生剧烈的运动,从而牵引立管触地段运动。悬链线立管与海床土体接触的临界点为触地点(Touchdown point, TDP),在触地点附近,海洋立管和海床均会产生一定的变形,管道压入海床使海床形成沟槽,再逐渐上升到海底表面,这一管段称为海洋立管的触地段(Touchdown zone, TDZ),触地段是管道结构设计的关键部位。针对触地段的研究主要有实验方法和数值方法,Bridge[2-3]和Hodder[4]分别开展了管土相互作用的全尺寸试验和模型试验,量化了立管性能,为研究立管与海床相互作用和数值模型的验证评估奠定了基础。针对管土相互作用,不同学者对管-土接触模型做了不同的简化,Palmer[5]基于刚塑性海床假设通过数值分析得出管道在沉陷过程中会产生较大的应力。杜金鑫[6]和黄维平[7]利用等效弹簧单元模拟土体,基于大挠度曲线梁模型和弹性地基梁理论,研究了管-土相互作用的模拟方法。郭海燕[8]和任艳荣[9]利用接触单元模拟分析了钢悬链线立管与海床土体的接触问题。不少学者对触地段管道的动力载荷也做了评估,Bridge[10-11]根据试验数据拟合得到海床的动刚度及其对管道结构的影响。Pesce[12]考虑立管触地段管道抗弯刚度以及管土相互作用,分析触地段管道动力响应的非线性特征值问题。Bai等[13-14]研究了在正弦升沉位移载荷下管道与海床相互作用的动态行为。
针对触地段,国内外学者所做的大量研究基本立足于完好管道。但是管道在服役过程中,由于管形弯曲,管内流体流经触地段时对管道的冲蚀作用强烈,加之管内油气含有H2S、CO2等酸性腐蚀性物质导致金属管道腐蚀[15],形成体积缺陷。在缺陷区域结构刚度骤减,结构局部变柔,产生较大的应变集中和应力集中,不仅降低了立管的承载力,而且还改变管道的动力学性能,增加了管道的动力放大系数。目前国内外对于损伤管道的研究基本集中于平铺管道。其中,陈严飞[16]预测腐蚀管道的剩余强度,研究海底腐蚀管道在工作荷载以及环境荷载作用下的极限荷载和破坏机理。李昕[17]和孙丽[18]分别研究了完好平铺管道和损伤平铺管道在悬跨状态下的动力响应问题。然而,在触地段损伤海底管道的动力特性方面研究十分有限,因此,本文运用实体单元与土弹簧-阻尼单元相互作用的模型,开展触地段损伤管道在复杂载荷作用下的动力响应研究。
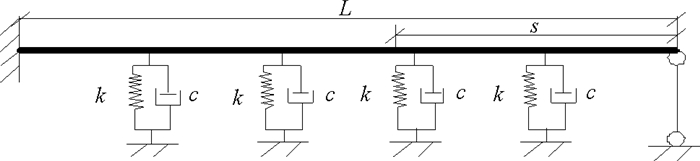
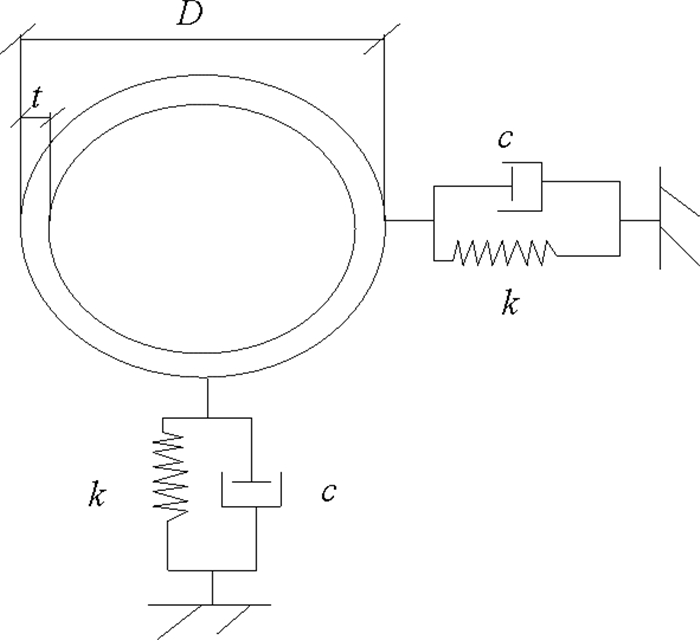
1 钢悬连线立管触地段的动力学模型管道简化为一端固定、一端竖向约束的管道模型(见图 1)。图中L为计算管道的长度,在管道的流线端(见图 1左端)采用水平、轴向两向全约束,对管道提升端(见图 1右端)在竖方向施加1个竖直向上的位移u,水平向约束,轴向不约束,可自由伸缩。考虑管道内外流体介质对管道结构动力响应的影响,为精确计算损伤管道的动力特性,在数值模拟过程中管道采用实体单元来模拟,管土相互作用的截面图如图 2所示。D为圆管道横截面外径,t为管道壁厚。
|
图 1 触地段管道的计算模型 Fig. 1 Simplified computation model of damaged pipe in TDZ |
|
图 2 海底管道的横截面图 Fig. 2 Cross section of pipeline TDZ |
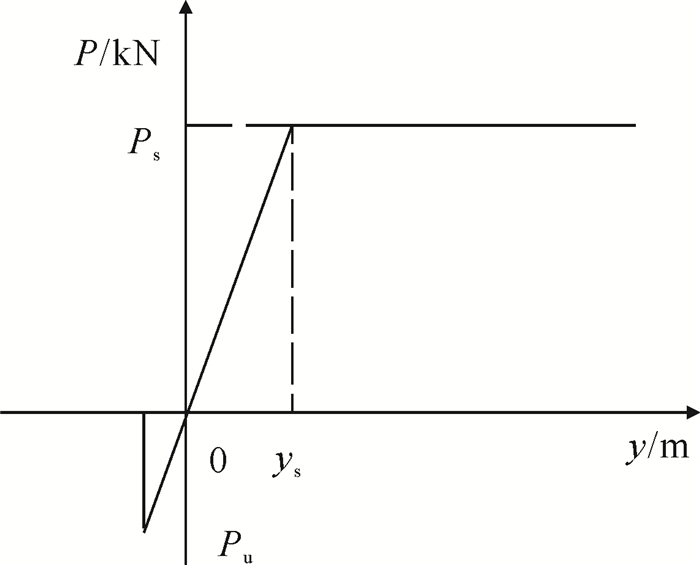
由于海床土体大多是软黏土,考虑海床与管线的相互作用效应和动力荷载作用下土体性能的退化效应,即土体的非线性特性,海床土体简化为一系列的弹塑性受压阻尼土弹簧,沿管轴方向均匀排列,土弹簧的刚度为k,阻尼为c。同时,管道从土体中拔出的过程中管道还会受到一定的土吸力。单位管长所受的土壤阻力随管道竖向位移的变化曲线,即土弹簧的P-y曲线见图 3,Ps表示土弹簧在受压过程中的屈服极限,ys表示相应的弹性变形,Pu表示最大土吸力。利用土弹簧模拟海床土体的非线性特性可以较好的反映海床土体在与管道作用的过程中刚度的变化以及海床对管道运动的影响。
|
图 3 等效海床竖向土弹簧的P-y曲线 Fig. 3 Equivalent P-y curve of seabed soil spring |
据有限单元法的理论[19],将管道结构离散成实体单元,在每个单元内,采用节点位移向量X的插值函数表示实体单元位移的空间变化,则管道结构的动力方程可以表示为式(1)[20]
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M\ddot X}}\left( t \right) + \mathit{\boldsymbol{C\dot X}}\left( t \right) + \mathit{\boldsymbol{KX}}\left( t \right) = }\\ { - \mathit{\boldsymbol{KA}}{{\left( {2{\rm{ \mathit{ π} }}f} \right)}^2}\sin \left( {2{\rm{ \mathit{ π} }}ft} \right)。} \end{array} $ | (1) |
式中,M为管道模型的N×N阶质量矩阵,N为结构单元的自由度的个数。K为管道模型的N×N阶刚度矩阵,X(t)为管道模型随时间t变化的位移向量,
| $ \mathit{\boldsymbol{C}} = {\alpha _{\rm{d}}}\mathit{\boldsymbol{M}} + {\beta _{\rm{d}}}\mathit{\boldsymbol{K}}, $ | (2) |
| $ {\alpha _{\rm{d}}} = \frac{{2\xi {\omega _1}{\omega _3}}}{{{\omega _1} + {\omega _3}}},{\beta _{\rm{d}}} = \frac{{2\xi }}{{{\omega _1} + {\omega _3}}}。$ | (3) |
将式(2)代入式(1)可以转化为式(4)
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M\ddot X}}\left( t \right) + \left[ {{\alpha _d}\mathit{\boldsymbol{M}} + {\beta _d}\mathit{\boldsymbol{K}}} \right]\mathit{\mathit{\boldsymbol{\dot X}}}\left( t \right) + \mathit{\boldsymbol{KX}}\left( t \right) = }\\ { - \mathit{\boldsymbol{KA}}{{\left( {2{\rm{ \mathit{ π} }}f} \right)}^2}\sin \left( {2{\rm{ \mathit{ π} }}ft} \right)。} \end{array} $ | (4) |
根据结构体系的频率方程式(5)可以求出结构的自振频率向量ω。
| $ \left\| {\mathit{\boldsymbol{K}} - {\mathit{\boldsymbol{\omega }}^2}\mathit{\boldsymbol{M}}} \right\| = 0。$ | (5) |
其中ω2代表结构的自振频率的平方;由式(5)可以得出ω的N个解ωn,n=1, 2, 3, …, N,分别称为结构的第n阶固有频率,全部振型频率按顺序排列组成向量ω代表结构的频率向量。第n阶固有频率ωn所对应的结构振型φn可以由式(6)求出。
| $ \left[ {\mathit{\boldsymbol{K}} - \omega _n^2\mathit{\boldsymbol{M}}} \right]{\phi _n} = 0。$ | (6) |
使用正规坐标变换把N个耦合的运动方程式(4)转化为N个非耦合的方程,相当于N个独立的单自由度方程(见式(7))。
| $ \begin{array}{*{20}{c}} {{M_n}{{\ddot X}_n}\left( t \right) + \left[ {{\alpha _d}{M_n} + {\beta _d}{K_n}} \right]{{\dot X}_n}\left( t \right) + {K_n}{X_n}\left( t \right) = {P_n}\left( t \right),}\\ {n = 1,2,3, \cdots ,N。} \end{array} $ | (7) |
其中Xn(t)分别表示结构第n阶振型向量φn随时间变化的振型幅值,
| $ \begin{array}{*{20}{c}} {{M_n} = \phi _n^{\rm{T}}\mathit{\boldsymbol{M}}{\phi _n},{K_n} = \phi _n^{\rm{T}}\mathit{\boldsymbol{K}}{\phi _n},}\\ {{P_n}\left( t \right) = {{\left( {2{\rm{ \mathit{ π} }}f} \right)}^2}\phi _n^{\rm{T}}\mathit{\boldsymbol{KA}}\sin \left( {2{\rm{ \mathit{ π} }}ft} \right)。} \end{array} $ | (8) |
根据式(8)分别求出每一阶振型随时间变化的响应幅值Xn(t),则总的位移响应X(t)为式(9):
| $ X\left( t \right) = \sum {{\phi _n}} {X_n}\left( t \right)。$ | (9) |
结构的动力放大系数(Dynamic amplification factor, DIF)能够有效表示结构动力响应的程度,定义结构位移响应的动力放大系数DIFu为当结构振动达到稳态的时候,结构位移响应的振幅与静载荷-KAsin(2πft)所引起静位移的比值,其表达式为式(10):
| $ DI{F_u} = \frac{{\max \left( {X\left( t \right)} \right)}}{A}。$ | (10) |
同理,定义结构应力响应的应力放大系数DIFσ表示当结构振动达到稳态的时候,结构单元有效应力的最大值max(σ(t))与静载荷-KAsin(2πft)所引起单元静应力σm的比值,其表达式为式(11):
| $ DI{F_\sigma } = \frac{{\max \left( {\sigma \left( t \right)} \right)}}{{{\sigma _{\rm{m}}}}}。$ | (11) |
在有限元计算过程中,钢材采用X65型号钢,本构模型为线弹性模型,其详细的力学参数及其管道的几何尺寸见表 1。管道的缺陷为管道外环形体积损伤,其详细的损伤尺寸见表 1。非线性接地弹簧约束的参数见表 2。
|
|
表 1 损伤管道结构参数表 Table 1 Parameters list of damaged pipe structure |
|
|
表 2 土弹簧的参数表 Table 2 Parameters list of soil spring |
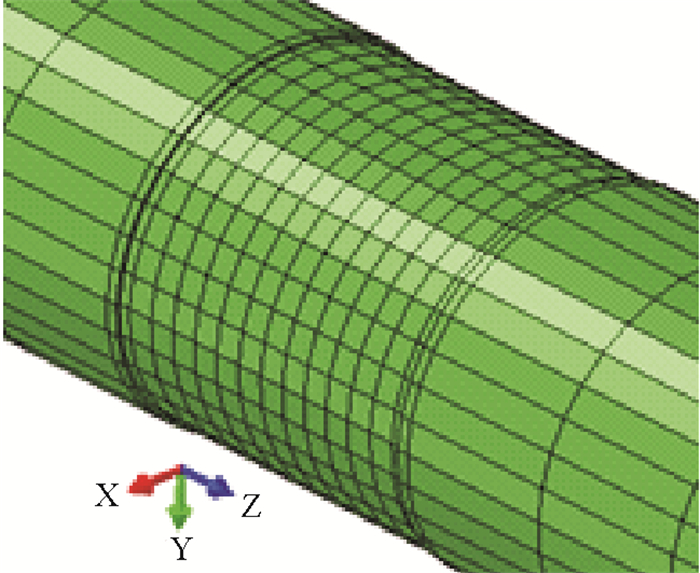
本模型采用大型有限元软件ABAQUS进行了分析,重点研究三维的体积损伤管道,对于三维问题,六面体单元可以用最小的计算代价给出最好的结果,因此选择的单元类型为一次单元C3D8I,该单元在每一节点处都有3个平动自由度1、2和3,分别代表x,y和z方向上的线位移。管道损伤部位的模型在笛卡尔坐标系中见图 4。
|
图 4 海底管道体积损伤部位的完整模型 Fig. 4 Model of completed damaged pipe body |
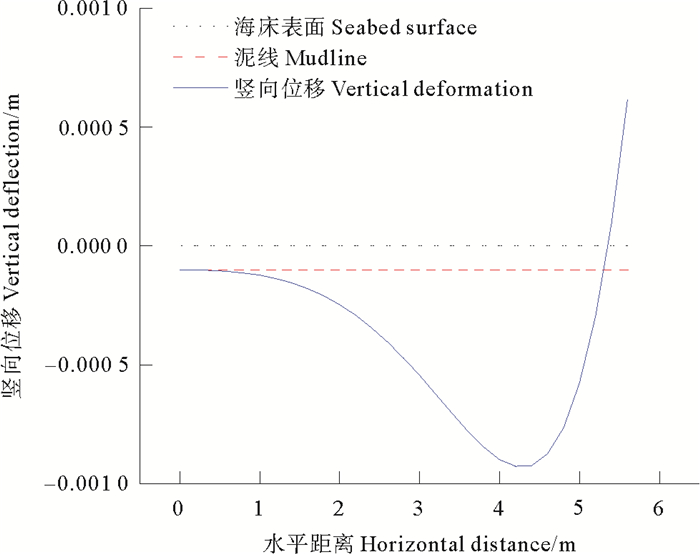
触地段管道与海床相互作用,会形成具有一定深度的沟槽,管道产生了相应的变形(见图 5),管道在触地段的变形是根据完好管道与海底土弹簧的接触模型而得出,图中水平点线表示海床表面的高度,水平虚线表示管道平铺于海床上由于重力作用而具有一定的入土深度,称为泥线[5],实线表示在管道提升端(右端)受到竖直向上的位移载荷后,管道在触地段形成的竖向变形。虽然触地段管道变形较大,但是较光滑平坦,管道的提升端具有一定的转角,管道流线端(左端)的竖向位移逐渐趋向平铺管道的入土深度,与平铺管道的变形相吻合,而在触地点附近管道挠度达到最大。
|
图 5 沿着管道轴向触地段完好海底管道的竖向位移 Fig. 5 Vertical deflection of intact pipeline along pipeline in TDZ |
为研究体积缺陷所处的位置对管道动力特性的影响,体积缺陷由距管道提升端5 m的位置沿着管道轴向以1 m的梯度变化到距离管道提升端15 m的位置,共11种损伤管道模型,以损伤位置距离提升端的距离s来表示(见图 1),损伤管结构的参数列于表 3。
|
|
表 3 损伤管结构及其载荷工况参数表 Table 3 Parameters list of damaged pipe and loading conditions |
立管触地段一般工作于几百米甚至上千米水深的深海环境下,在运行过程中承受着复杂的静力和动力载荷,包括管道内压、环境外压、提升端的提升载荷,以及平台的牵引。研究表明[2, 21-23],平台的垂荡运动对触地段交变应力的影响最大,引起触地点的交变循环应力,成为触地段的主要动力载荷[5],大大降低了立管在触地段的载荷寿命。在管道提升端施加10周的动力循环位移载荷后,海床和管道的相互作用会达到稳定状态[12],动力响应趋于稳定,因此动力载荷的循环次数z为10。管道所受静力、动力载荷列于表 3。
3.3.2 加载与分析过程根据触地段的工作环境确定合理的载荷路径,研究管道损伤位于触地段的不同位置时,损伤管道的动力响应。作为一种细长型结构,管道在提升端受到位移载荷时,使管道部分悬空,会产生大变形,后续的应力求解须建立在变形后的结构构型上,本文考虑管道大变形所产生的几何非线性、海床土体的材料非线性以及管土相互作用的接触非线性,采用增量法对有限元模型进行计算,其加载及分析过程如下:
(1) 首先,加载重力,重力加速度g=9.8 m/s2;
(2) 其次,加载外压Pe;
(3) 再次,加载内压Pi;
(4) 第四,加载竖向位移提升载荷u;
(5) 第五,模态分析,得出管结构的固有频率;
(6) 最后,加载位移动力载荷,平台竖向运动为简谐运动Xu=A sin(2πft)。
4 结果分析针对触地段管道的几何构型,沿管道不同的轴向位置引入相同尺寸的体积损伤,研究内压、外压、提升高度以及动力载荷频率等载荷因素对管道动力特性及动力响应的影响,基于大量的工况得到不同载荷条件下各损伤管道的动力特性及其动力响应,并计算各因素对结构特征节点动力放大系数(DIF)的影响。
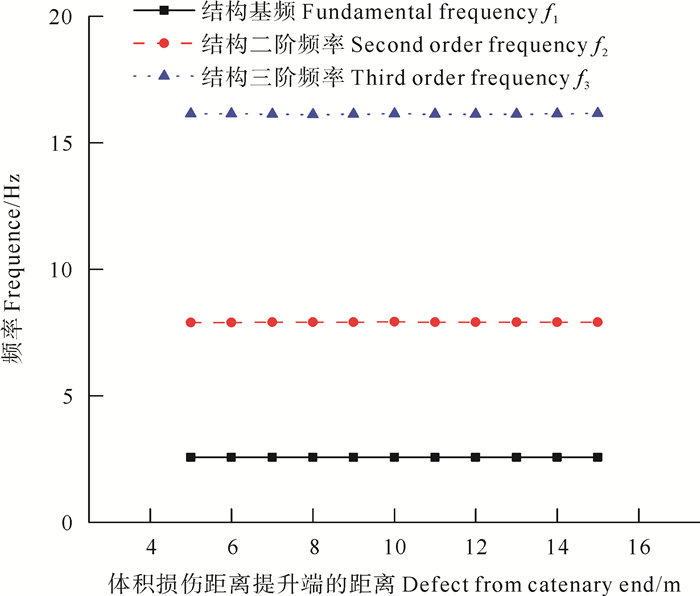
4.1 损伤位置对结构动力特性的影响 4.1.1 损伤位置对自振频率的影响选择外载:重力加速度(g=9.8 m/s2),外压(Pe=5 MPa),内压(Pi=5 MPa),管道提升端的位移载荷(u=0.36 m),静力载荷达到稳定后进行模态分析,计算出各损伤结构的前三阶自振频率(见图 6)。当相同尺寸的体积损伤沿着管道轴向由s=5 m以1 m的梯度变为s=15 m的过程中,不同的损伤结构对应的各阶自振频率几乎分别相等,只有微小的波动,这说明损伤位置对结构自振频率的影响不大。
|
图 6 各损伤管结构的自振频率与完好管道的比较 Fig. 6 Frequencies of damaged and intact pipeline structures |
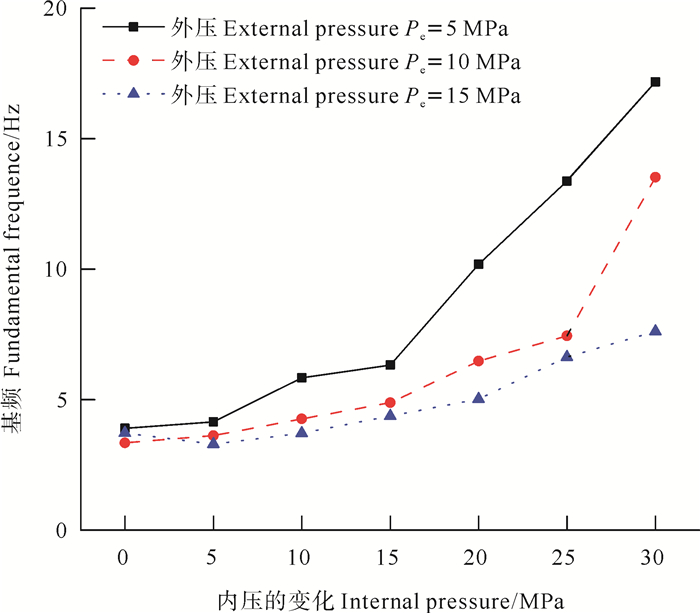
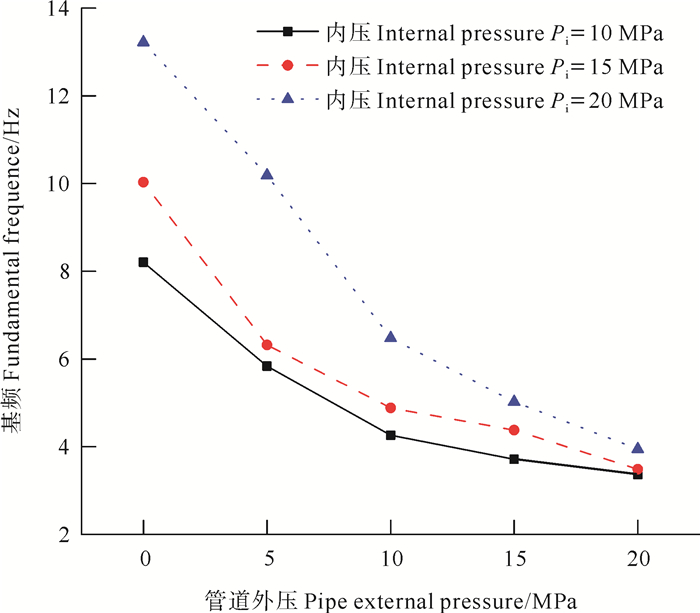
选择损伤管道(s=10 m),依次加载重力(g=9.8 m/s2),外压Pe,内压Pi,管道提升端的位移载荷(u=0.12 m)后,对管结构进行模态分析。结构的前三阶固有频率与所受内压、外压之间的关系分别如图 7、8所示。图 7表示,在一定的外压作用下,随着管道所受内压的升高,结构自振频率显著升高,当外压Pe=5 MPa时,结构基频由3 Hz升高到17 Hz左右,这是由于管道内压增加了管道的弯曲刚度,从而使其自振频率升高。当管道内压较低甚至不受内压的情况下,管道外压对结构基频的影响较小,基频在4 Hz附近变化。图 8表示外压的作用与内压相反,在一定的内压作用下,随着管道所受外压的升高,结构自振频率越来越低,低至3.5 Hz左右。这是由于管道外压增大了管道的柔度,从而使其自振频率降低。随着管道外压的增大,管道内压对结构动力参数的影响变得越小,使结构的基频局限于一个较小的区间,大约是3~4 Hz。
|
图 7 管道结构的基频随内压的变化 Fig. 7 Fundamental frequency of pipe under different internal pressure |
|
图 8 管结构基频随外压的变化 Fig. 8 Fundamental frequency of pipe under different external pressure |
结构所受内压与外压对结构的动力响应共同作用,相互影响,当内压远大于外压的时候,结构的自振频率较高,相反,当结构外压远大于内压时,结构基频会显著降低,可能使结构基频接近外载频率,从而产生共振现象,使结构的动力响应急剧变大,导致结构损坏。因此为了避免管结构的共振破坏,要使结构的自振频率,尤其是结构基频,远离环境载荷的激励频率。
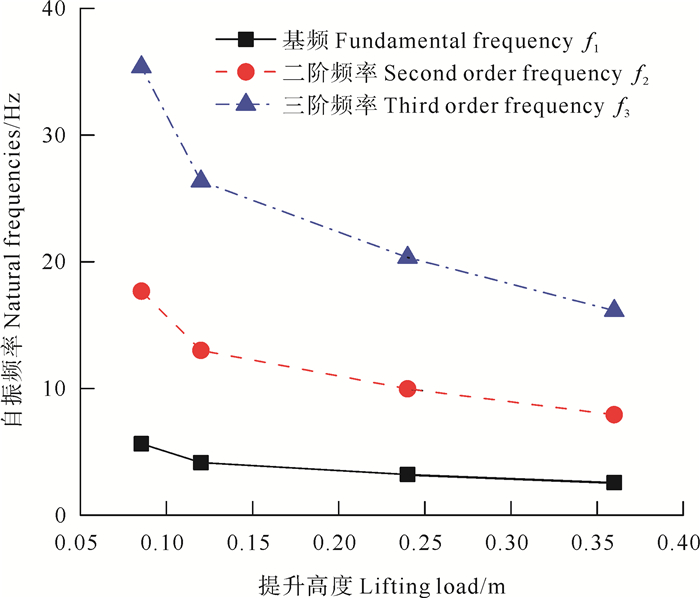
4.1.3 管道提升端位移载荷对其动力特性的影响选择损伤管道(s=10 m),依次加载重力(g=9.8 m/s2),管道提升端的位移载荷u,外压(Pe=5 MPa),内压(Pi=5 MPa)后,对管结构进行模态分析研究其结构的自振频率与所受位移载荷的关系。如图 9所示,在一定的内外压作用下,随着管道提升端位移载荷的增大,结构自振频逐渐降低,管道基频由6 Hz低至3 Hz左右。这是由于当管道提升端受到竖直向上的位移载荷后,部分管段与海床分离,海床减少了对管道的约束,因此位移载荷越大,管道所受海床的约束越小,从而降低了结构刚度,增加了管道的柔度,使其自振频率降低。同时发现,当管道提升端位移较小的时候,结构的基频显著降低,随着管道提升端位移的增大,结构基频的变化趋缓,说明越是远离管道提升端,管道的约束情况对结构的动力参数影响越小。
|
图 9 管结构基频随管结构提升端提升高度的变化 Fig. 9 Fundamental frequency of pipe under different uplift loading |
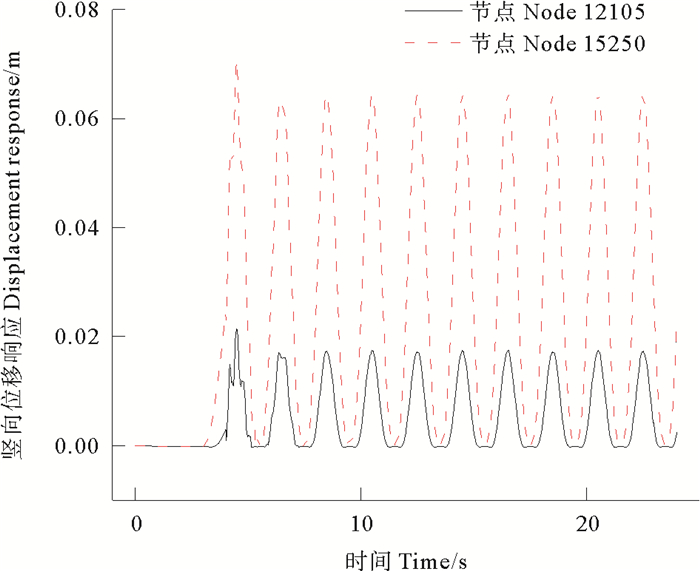
选择损伤管道(s=10 m),依次加载重力加速度(g=9.8 m/s2),外压(Pe=5 MPa),内压(Pi=5 MPa),管道提升端的位移载荷(u=0.12 m),动力载荷(f=0.5 Hz,A= 0.1 m),载荷循环次数为10次,即20 s的动力时程,绘制体积损伤部位的节点12105以及悬垂段节点15205的竖向位移时程曲线(见图 10)。由两节点的时程图可知,在4 s时刻,突然加载竖向动力载荷,导致管道产生较剧烈的抖动,出现多个峰值点,位移响应达到最大,节点12105与节点15205的峰值响应分别达到0.021 4和0.070 6 m。随着动力载荷的继续,结构位移响应趋于平稳,动力响应进入稳态,结构的稳态响应是动力研究的重点,两点的最大响应分别稳定在0.017 2和0.064 3 m。两节点的位移响应在其平衡位置附近根据载荷频率以一定的幅值振动。当节点由触地点靠近管道的提升端时,节点振幅变大,位移响应变得更强烈。
|
图 10 节点12105和15250的竖向位移的时程曲线 Fig. 10 Vertical displacement time history at node 12105 and 15250 |
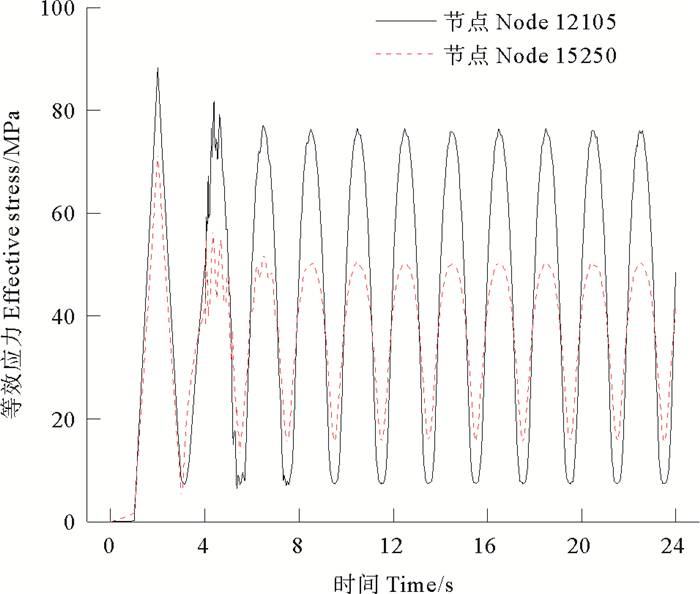
图 11给出了两节点等效应力的时程曲线,节点应力时程曲线的变化规律与位移响应的变化规律类似,两节点的应力分别在加载动力载荷的初始阶段达到最大值,分别为81.8和56.6 MPa,在后续的响应中,逐渐进入到稳态响应阶段,最大应力响应分别稳定于76.0和50.4 MPa。虽然损伤区节点12105的位移响应较小,但是其最大应力和应力变化幅值均远大于节点15205的应力,说明管道的体积损伤不仅降低了管道损伤区的承载力,而且损伤区的应力响应峰值已经达到最大,幅值变化大,响应剧烈,成为管道结构的薄弱部位。
|
图 11 节点12105和15250的有效应力的时程曲线 Fig. 11 Effective stress time history at node 12105 and 15250 |
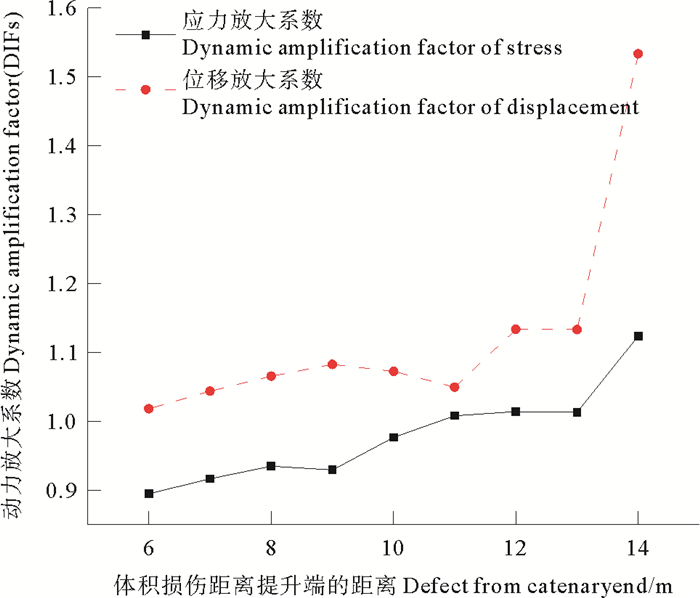
选择外载:重力加速度(g=9.8 m/s2),外压(Pe=5 MPa),内压(Pi=5 MPa),管道提升端位移载荷(u=0.12 m),动力循环载荷(f=0.5 Hz,A=0.1 m),计算结构的损伤区域中特征点的动力响应,包括相应点的竖向位移响应与Mises有效应力响应。其次再求解静位移载荷所引起的静位移及静应力,此时结构所受的竖向位移载荷为初始竖向位移u与动力载荷的最大位移幅值A之和,u+A。根据以上动力计算结果和静力结算结果计算结构特征点的动力放大系数(包括位移放大系数DIFu和应力放大系数DIFσ),结果见图 12。随着体积损伤距离管道提升端的距离越来越远,也就是损伤部位距离管道的触地点越来越近,损伤单元的竖向位移的放大系数与有效应力放大系数都不断增大,结构位移响应的放大系数DIFu始终大于1,且高于结构的应力放大系数DIFσ,说明距离触地点越近,管道的变形越大,应力变化越复杂,并且管道的位移变化相对管道的应力变化幅度更大。
|
图 12 不同损伤管道结构的动力放大系数 Fig. 12 DIFs indifferent damaged pipeline structure |
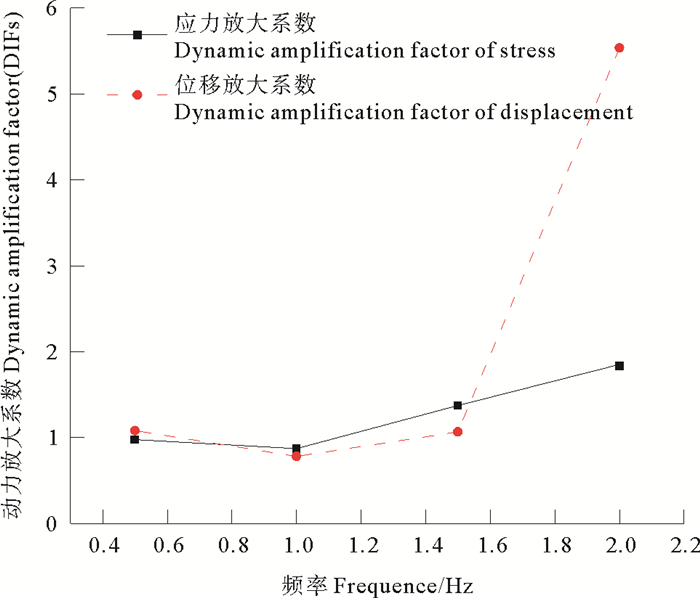
结构的动力放大系数与其自振频率以及所受的动力载荷频率相关,当载荷频率与结构的自振频率越接近,结构的动力响应越强烈,动力放大系数越大。选择损伤管道(s=10 m),依次加载重力,外压(Pe=5 MPa),内压(Pi=5 MPa),提升端位移载荷(u=0.12 m),动力载荷(A= 0.1 m),其动力载荷的频率由f=0.5 Hz以0.5 Hz的梯度变化到2 Hz,共四个工况,载荷循环次数为10次。在不同的频率载荷下,结构动力放大系数的数值模拟结果见图 13。载荷频率由0.5 Hz变化到2 Hz的过程中,始终低于结构基频,随着载荷频率的增大,越来越接近于结构的固有频率,管道的动力响应越来越强烈,动力放大系数与频率呈非线性变化的关系,当载荷频率远离结构基频时,动力放大系数变化缓慢,当载荷频率靠近结构基频的时候,动力放大系数急剧增大,而且结构的竖向位移响应的动力放大系数DIFu较有效应力放大系数DIFσ变化更明显。
|
图 13 结构的动力放大系数随载荷频率的变化 Fig. 13 DIFs under different frequencies |
本文以大型有限元软件ABAQUS为平台,运用实体单元与弹簧阻尼器单元来模拟管-土相互作用,在立管触地段的不同部位引入相同尺寸的体积损伤,研究不同的损伤结构在复杂载荷作用下的动力特性及动力响应,该模型不仅可以模拟管道所受的内压、外压等复杂载荷,还有效模拟了海床的刚度和阻尼,更加符合工程实际,分析结果表明:
(1) 一定尺寸的损伤位于管道的不同位置时,管道的整体刚度基本相同,但是在相同的载荷下,不同管道上损伤单元的动力响应不同,随着损伤远离管道的提升端,损伤单元的应力放大系数和竖向位移响应的放大系数都会升高。
(2) 内压和外压对管结构刚度及其自振频率影响很大,管道内压增加了管道的刚度,增大了管结构的基频,外压的效应与内压的相反,管道的固有频率随外压的增大而减小,对于深海工程,应当校核外压对海底管道动力性能的影响,保证管道稳定运行。
(3) 管道提升端的竖向位移会导致部分管段与海床分离,减弱了海床对管道的约束,降低了结构刚度,降低结构自振频率,且海床约束距离管道提升端越远,位移载荷对管道动力特性的影响越小。
(4) 当外载频率低于结构基频时,随着载荷频率的增大,管结构的响应越来越强烈,动力放大系数DIF先缓慢增长后急剧变大,呈非线性变化的趋势,而且结构的位移放大系数DIFu较应力放大系数DIFσ对频率的反应更加敏感。
| [1] |
Xia J, Purnendu K D, Karunakaran D. A parametric design study for a semi/SCR system in Northern North Sea[J]. Ocean Engineering, 2008, 35(17): 1686-1699.
(  0) 0) |
| [2] |
Bridge C, Willis N. Steel Catenary Risers-results and Conclusions from Large Scale Simulations of Seabed Interaction[C]. New Orleans, Louisiana: Proc, IntConf on Deep Offshore Technology, 2002: 1-10.
(  0) 0) |
| [3] |
Bridge C, Howells H. Observations and Modelling of Steel Catenary Risers Trenches[C]. Lisbon, Portugal: Proceedings of the 17th International Offshore and Polar Engineering Conference, 2007: 803-813.
(  0) 0) |
| [4] |
Hodder M S, Byrne B W. 3D experiments investigating the interaction of a model SCR with the seabed[J]. Applied Ocean Research, 2010, 32(2): 146-157. DOI:10.1016/j.apor.2009.09.004
(  0) 0) |
| [5] |
Palmer A. Touchdown indentation of the seabed[J]. Applied Ocean Research, 2008, 30(3): 235-238. DOI:10.1016/j.apor.2008.09.004
(  0) 0) |
| [6] |
杜金新, Low Y M. 海洋立管一海床土体接触作用数值分析[J]. 工程地质计算机应用, 2008, 52(4): 6-11. Du J X, Low Y M. numerical analysis the interaction of risers and seabed[J]. Calculating Machine Application on Engineering and Geology, 2008, 52(4): 6-11. (  0) 0) |
| [7] |
黄维平, 孟庆飞, 白兴兰. 钢悬链式立管与海床相互作用模拟方法研究[J]. 工程力学, 2013, 30(2): 14-18. Huang W P, Meng Q F, Bai X L. The simulation methods of the interaction of steel catenary risers and soil in touchdown down zone[J]. Engineering Mechanics, 2013, 30(2): 14-18. (  0) 0) |
| [8] |
郭海燕, 高秦岭, 王小东. 钢悬链线立管与海床土体接触问题的ANSYS有限元分析[J]. 中国海洋大学学报(自然科学版), 2009, 39(3): 521-525. Guo H Y, Gao Q L, Wang X D. Finite element analysis of steel catenary riser-soil contact problem by ANSYS[J]. Periodical of Ocean University of China, 2009, 39(3): 521-525. (  0) 0) |
| [9] |
任艳荣, 刘玉标, 顾小芸. 弹塑性海床上的管土相互作用分析[J]. 工程力学, 2004, 21(2): 83-87. Ren Y R, Liu Y B, Gu X Y. Analysis of pipe-soil interaction on elastic-placticseabed[J]. Engineering Mechanics, 2004, 21(2): 83-87. (  0) 0) |
| [10] |
Bridge C, Laver K, Clukey E, et al. Steel Catenary Riser Touchdown Point Vertical Interaction Model[C]. Houston Texas: Offshore Technology Conference, 2004: 1-9.
(  0) 0) |
| [11] |
Bridge C. Effects of Seabed Interaction on Steel Catenary Risers[D]. Guildford: University of Surrey, 2005.
(  0) 0) |
| [12] |
Pesce C P, Martins C A. Riser-soil interaction: Local Dynamics at TDP and a Discussion on the Eigenvalue Problem[C]. Vancouver: Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, 2004: 583-594.
(  0) 0) |
| [13] |
Bai X L, Huang W P, Murilo A V, et al. Riser-soil interaction model effects on the dynamic behavior of a steel catenary riser[J]. Marine Structures, 2015, 41: 53-76. DOI:10.1016/j.marstruc.2014.12.003
(  0) 0) |
| [14] |
白兴兰, 黄维平, 高若沉. 海床土刚度对钢悬链线立管触地点动力响应的影响分析[J]. 工程力学, 2011, 28(S1): 211-216. Bai X L, Huang W P, Gao R C. Effect of seabed soil stiffness on dynamic research of a steel catenary riser at touchdown point[J]. Engineering Mechanics, 2011, 28(S1): 211-216. (  0) 0) |
| [15] |
Benjamin A C, Freire J L F, Vieira R D. Analysis of pipeline containing interacting corrosion defects[J]. Experimental Techniques, 2007, 31(3): 74-82. DOI:10.1111/j.1747-1567.2007.00190.x
(  0) 0) |
| [16] |
陈严飞.海底腐蚀管道破坏机理和极限承载力研究[D].大连: 大连理工大学, 2009. Chen Y F. Study on Failure Mechanism and Ultimate Load Capacity of Corroded Submarine Pipeline[D]. Dalian: Dalian University of Technology, 2009. (  0) 0) |
| [17] |
李昕, 刘亚坤, 周晶, 等. 海底悬跨管道动力响应的试验研究和数值模拟[J]. 工程力学, 2003, 20(2): 21-25. Li X, Liu Y K, Zhou J, et al. Dynamic research of suspended subsea pipeline based on experimental study and numerical simulation[J]. Engineering Mechanics, 2003, 20(2): 21-25. DOI:10.3969/j.issn.1000-4750.2003.02.005 (  0) 0) |
| [18] |
孙丽, 张新收, 张美真. 腐蚀海底管线悬跨段的地震响应分析[J]. 工程力学, 2013, 30(S1): 343-346, 352. Sun L, Zhang X S, Zhang M Z. The seismic response analysis of corrosive submarine pipeline suspend span segment[J]. Engineering Mechanics, 2013, 30(S1): 343-346, 352. (  0) 0) |
| [19] |
姜礼尚. 有限元方法及其理论基础[M]. 北京: 人民教育出版社, 1979. Jiang L S. Finite Element Method and Basic Theory[M]. Beijing: People's Education Press, 1979. (  0) 0) |
| [20] |
Clough R W, Penzien J. Dynamics of Structures[M]. New York: McGraw-Hill, 1975.
(  0) 0) |
| [21] |
Nakhaee A, Zhang J. Trenching effects on dynamic behavior of a steel catenary riser[J]. Ocean Engineering, 2010, 37: 277-288. DOI:10.1016/j.oceaneng.2009.10.005
(  0) 0) |
| [22] |
Shiri H, Randolph M. The influence of seabed response on fatigue performance of steel catenary risers in touchdown zone[C]. //Proceedings of the ASME 2010 29th International Conference on Ocean. Shanghai: Offshore and Arctic Engineering, 2010: 1-10.
(  0) 0) |
| [23] |
Bridge C, Laver K, Clukey E, etc. Steel catenary riser touch down point vertical interaction models[C]. //Proceedings of the Offshore Technology Conference. Houston, Texas: [s.n.]. 2004: 1-9.
(  0) 0) |
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116023, China
 2020, Vol. 50
2020, Vol. 50


