2. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室, 山东 青岛 266237;
3. 海底科学与探测技术教育部重点实验室, 山东 青岛 266100
随着油气勘探开发的不断深入,新的油气藏愈发隐蔽,人们对油气勘探能力提出了更加苛刻的要求。地震资料叠前深度偏移能够对复杂构造成像,是解决隐蔽油气藏勘探的有力手段。目前叠前深度偏移方法主要分为射线类偏移与波动方程类偏移两种,其中射线类偏移以克希霍夫积分法偏移为代表。克希霍夫积分法叠前深度偏移具有占用计算机硬件资源小、成像精度较高且方法灵活的优点,是目前实际资料处理中最为常用的方法,但是当地下构造非常复杂时,常规的克希霍夫积分偏移难以获得高质量的成像[1]。波动方程类偏移以逆时偏移为代表,其能够对复杂构造精确成像,但是运算量巨大,难以应用于生产实践[2-5]。
2001年Hill将高斯束方法应用于叠前深度偏移,其综合应用高斯束运动学射线追踪(即求取中心射线的旅行时和路径)与复值动力学射线追踪(即求取高斯束能量以及形态)的信息,将经倾角叠加后的局部平面地震信息映射到成像点处,不仅解决了常规射线法在焦散区失效问题,还避免了两点射线追踪的走时单一与射线丢失等问题,提高了在复杂构造区域成像的精度[6]。针对Hill所提出高斯束叠前偏移方法仅仅能够适用共偏移距道集的问题,Nowack与Gray分别将高斯束深度偏移方法应用至炮集记录,其中Gray所提出的方法可以看作是将Hill的高斯束深度偏移方法对炮集记录的扩展[7-8]。为了解决传统的高斯束偏移方法对振幅相位校正系数计算不精确的问题,Gray等基于广义真振幅偏移理论,通过重新计算高斯束的振幅项,实现了保幅高斯束偏移[9]。目前,高斯束偏移方法可被认为是一种在计算精度与效率上均介于克希霍夫积分偏移与波动方程逆时偏移之间的成像方法,被视为是深度域克希霍夫积分类偏移的有效补充而受到高度重视,并在实际生产中得到一定的应用[10-12]。
高斯束的运动学与动力学射线追踪过程,从物理上讲是一个典型的动力学过程。辛几何算法是专门针对动力学过程设计的算法,可以提高动力学问题求解的精度与效率[13]。在应用辛几何算法进行运动学射线追踪方面,诸多学者已进行过探索:陈景波与秦孟兆将辛几何算法应用于运动学射线追踪中,并将辛几何算法与Maslov方法结合,提出了能够适应焦散区的射线追踪方法[14]。高亮应用二阶欧拉型辛差分格式进行运动学射线追踪,并将结果与四阶经典Runge-Kutta(RK)方法比较,认为在精度差异不大的情况下,二阶辛方法具有效率上的优势[15]。李川等将二维三次卷积模型插值算法与四阶辛Partitioned-Runge-Kutta(PRK)法结合,进行了运动学射线追踪方法研究,并认为相较于常规数值方法,辛几何算法可以提高运动学射线追踪的精度与效率[16]。
虽然前人应用辛几何算法进行了运动学射线追踪的研究,并一致认为相较于常规算法,辛几何算法在求解运动学射线追踪方程组时具有一定优势,但是目前辛几何算法尚未被应用于高斯束动力学射线追踪方程组的求解,也未实现基于辛几何算法的高斯束偏移像。本文将基于辛几何算法的运动学射线追踪引入高斯束叠前深度偏移中,并在推导高斯束动力学射线追踪方程组的三级四阶辛RKN格式的基础上实现基于辛几何算法的高斯束叠前深度偏移。
1 高斯束偏移成像公式本文选用炮集高斯束偏移“全波场算法”进行成像值的求取[17]。Zhang等给出了二维频率域保幅互相关成像条件[18]
| $ I = - {\rm{i}}\int {{P_U}} \left( \omega \right)P_D^ * \left( \omega \right)sgn\left( \omega \right)d\omega 。$ | (1) |
其中,
| $ \left\{ \begin{array}{l} {P_U} = - 2\int d {x_r}{P_U}\left( {{x_r},{x_s},\omega } \right) \times {p_{rz}}i\omega {G^ * }\left( {x,{x_r},\omega } \right)\\ P_D^ * = 2{p_{sz}}i\omega {G^ * }\left( {x,{x_s},\omega } \right) \end{array} \right.。$ | (2) |
在式(2)中,psz与prz分别表示震源射线与检波点射线在z方向上的慢度分量,G(x, xs, ω)与G(x, xr, ω)分别表示震源与检波点波场的格林函数。将式代入式可得
| $ \begin{array}{*{20}{c}} {I = - 4\int d \omega i\omega \left| \omega \right|{\rho _{sz}}{G^ * }\left( {x,{x_s},\omega } \right) \cdot }\\ {\int d {x_r}{P_U}\left( {x,{x_s},\omega } \right){p_{rz}}{G^ * }\left( {x,{x_r},\omega } \right)。} \end{array} $ | (3) |
在二维介质中,用高斯束叠加积分合成格林函数的公式为
| $ G\left( {x,x',\omega } \right) = \frac{i}{{4{\rm{ \mathsf{ π} }}}}\int {\frac{{d{p_{x'x}}}}{{{p_{x'z}}}}{u_{GB}}} 。$ | (4) |
其中px′x与px′z分别表示点x′出射的高斯束水平和竖直慢度分量,uGB为高斯束表达式
| $ {u_{GB}} = {A_{GB}}\exp \left( { - i\omega {T_{GB}}} \right)。$ | (5) |
其中
| $ {A_{GB}} = {A_{GB}}\left( {{s_0}} \right)\sqrt {\frac{{det{Q_0}v\left( s \right)}}{{det{Q_s}v\left( {{s_0}} \right)}}} 。$ | (6) |
为高斯束振幅,而在全局直角坐标系中
| $ {T_{GB}} = t\left( s \right) + {{\hat x}^{\rm{T}}}p + \frac{1}{2}{{\hat x}^{\rm{T}}}{P_s}Q_s^{ - 1}\hat x。$ | (7) |
表示高斯束旅行时。在式与式中AGB(s0)为初始高斯束振幅,v(s0)与v(s)为高斯束中心射线上地震波传播速度的初始值以及成像点在中心射线上的对应点s上的值,t(s)表示中心射线s处的旅行时,
| $ \begin{array}{*{20}{c}} {I = \frac{1}{{4{{\text{\pi }}^2}}}\int d {x_r}\iint d{p_{sx}}d{p_{rx}}\int d \omega i\omega {P_U}\left( {x,{x_s},\omega } \right)} \\ {A_{GBS}^ * A_{GBR}^ * \exp \left( { - i\omega \left( {T_{GBS}^ * + T_{GBR}^ * } \right)} \right)。} \end{array} $ | (8) |
其中,uGB(x, xs, ω)=AGBSexp (-iωTGBS)表示震源高斯束,AGBS与TGBS为震源处高斯束的振幅以及旅行时;而检波点处的高斯束用uGB(x, xr, ω)=AGBRexp(-iωTGBR)表示,AGBR与TGBR为检波点高斯束的振幅与旅行时。
由高斯束偏移成像公式可知,实现高斯束偏移成像的关键是中心射线上点s坐标值、走时t(s)、慢度p、以及动力学参数Ps与Qs的求取,其中中心射线上点s坐标值、走时t(s)以及慢度p的求取过程被称为运动学射线追踪,而高斯束动力学参数Ps与Qs的求取过程被称为动力学射线追踪。
2 基于辛几何算法的运动学射线追踪高斯束偏移成像需通过运动学射线追踪获得高斯束心射线上点s坐标值、走时t(s)和慢度p,在网格模型中,上述参数一般通过数值求解相应的常微分方程组完成。射线追踪的过程是一个动力学过程,在使用常规数值方法(例如龙格库塔法等)求解时,难免会有人为耗散等歪曲动力学体系原特征的缺陷而影响计算精度与效率[13]。为提高运动学射线追踪的精度与效率,本文应用辛几何算法求解高斯束运动学射线追踪方程组。
2.1 运动学射线追踪方程组的三级四阶辛RKN格式运动学射线追踪方程组可写为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{d{x_i}}}{{d\mu }} = {p_i}} \\ {\frac{{d{p_i}}}{{d\mu }} = \frac{\partial }{{\partial {x_i}}}\left( {\frac{1}{{{v^2}}}} \right)} \end{array},i = 1,2,3} \right.。$ | (9) |
其中:xi表示中心射线上点的坐标;pi表示中心射线的慢度;v为纵波速度;μ为任意射线参数。因为运动学射线追踪方程组,满足辛Runge-Kutta-Nyström(RKN)方法的求解条件,而四阶格式精度较高,其能够满足运动学与动力学射线追踪的精度要求[19],与此同时,在相同阶精度的格式中,显式格式一般比隐式格式具有更高的效率,所以本文推导了针对运动学射线追踪方程组的三级四阶显式辛RKN格式。
对于形如
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{d{p_i}}}{{d\mu }} = f\left( {{x_i}} \right)}\\ {\frac{{d{x_i}}}{{d\mu }} = {p_i}} \end{array},i = 1,2,3} \right.。$ | (10) |
的正则方程组,多级RKN方法具有如下格式
| $ \left\{ \begin{array}{l} {{\hat x}_i} = {x_n} + h{c_i}{p_n} + {h^2}\sum\limits_{j = 1}^s {{a_{ij}}} f\left( {{{\hat x}_j}} \right)\\ {x_{n + 1}} = {x_n} + h{p_n} + {h^2}\sum\limits_{j = 1}^s {{{\bar b}_j}} f\left( {{{\hat x}_j}} \right)\\ {p_{n + 1}} = {p_n} + h\sum\limits_{j = 1}^s {{b_j}} f\left( {{{\hat x}_j}} \right) \end{array} \right.,i,j = 1,2,3, \cdots s。$ | (11) |
其中
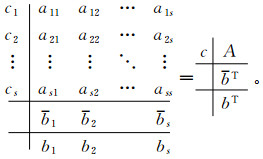
|
(12) |
只有当式中的f(xi)为标量函数的梯度且式中的系数满足如下关系时,式才为辛格式。
| $ \left\{ {\begin{array}{*{20}{l}} {{{\bar b}_i} = {b_i}\left( {1 - {c_i}} \right),}\\ {{b_i}\left( {{{\bar b}_j} - {a_{ij}}} \right) = {b_j}\left( {{{\bar b}_i} - {a_{ij}}} \right)} \end{array},i,j = 1} \right., \cdots s。$ | (13) |
更进一步,若式还满足i≤j时aij=0,则式为一个显式辛RKN格式[13]。
本文使用四阶显式算法求取运动学射线追踪方程组。在所有四阶显式辛RKN格式中,被广泛使用的是三级四阶显式辛RKN格式,其Butcher表为
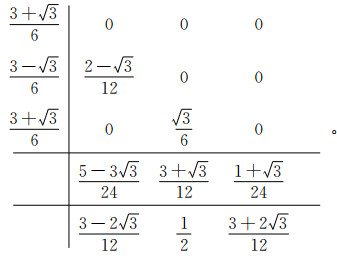
|
(14) |
将代入可导出针对运动学射线追踪方程组的三级四阶显式辛RKN差分格式为
| $ \left\{ \begin{array}{l} {{\hat x}_{i1}} = {x_{in}} + \frac{{3 + \sqrt 3 }}{6}h{p_{in}}\\ {{\hat x}_{i2}} = {x_{in}} + \frac{{3 - \sqrt 3 }}{6}h{p_{in}} + \\ \;\;\;\;\;\;\;{\left. {\frac{{{h^2}\left( {2 - \sqrt 3 } \right)}}{{24}}\frac{\partial }{{\partial x}}\left( {\frac{1}{{{V^2}}}} \right)} \right|_{\hat x1}}\\ {{\hat x}_{i3}} = {x_{in}} + \frac{{3 + \sqrt 3 }}{6}h{p_{in}} + {\left. {\frac{{{h^2}\sqrt 3 }}{{12}}\frac{\partial }{{\partial x}}\left( {\frac{1}{{{V^2}}}} \right)} \right|_{\hat x2}}\\ {p_{in + 1}} = {x_{in}} + h{p_{in}} + {\left. {\frac{{\left( {5 - 3\sqrt 3 } \right){h^2}}}{{48}}\frac{\partial }{{\partial x}}\left( {\frac{1}{{{V^2}}}} \right)} \right|_{\hat x1}} + \\ \;\;\;\;\;\;\;\;{\left. {\frac{{\left( {3 + \sqrt 3 } \right){h^2}}}{{24}}\frac{\partial }{{\partial x}}\left( {\frac{1}{{{V^2}}}} \right)} \right|_{\hat x2}} + {\left. {\frac{{\left( {1 + \sqrt 3 } \right){h^2}}}{{48}}\frac{\partial }{{\partial x}}\left( {\frac{1}{{{V^2}}}} \right)} \right|_{\hat x3}}\\ {x_{in + 1}} = {x_{in}} + {\left. {\frac{{\left( {3 - 2\sqrt 3 } \right)h}}{{24}}\frac{\partial }{{\partial x}}\left( {\frac{1}{{{V^2}}}} \right)} \right|_{\hat x1}} + {\left. {\frac{h}{4}\frac{\partial }{{\partial x}}\left( {\frac{1}{{{V^2}}}} \right)} \right|_{\hat x2}} + \\ \;\;\;\;\;\;\;\;\;{\left. {\frac{{\left( {3 + 2\sqrt 3 } \right)h}}{{24}}\frac{\partial }{{\partial x}}\left( {\frac{1}{{{V^2}}}} \right)} \right|_{\hat x3}} \end{array} \right.。$ | (15) |
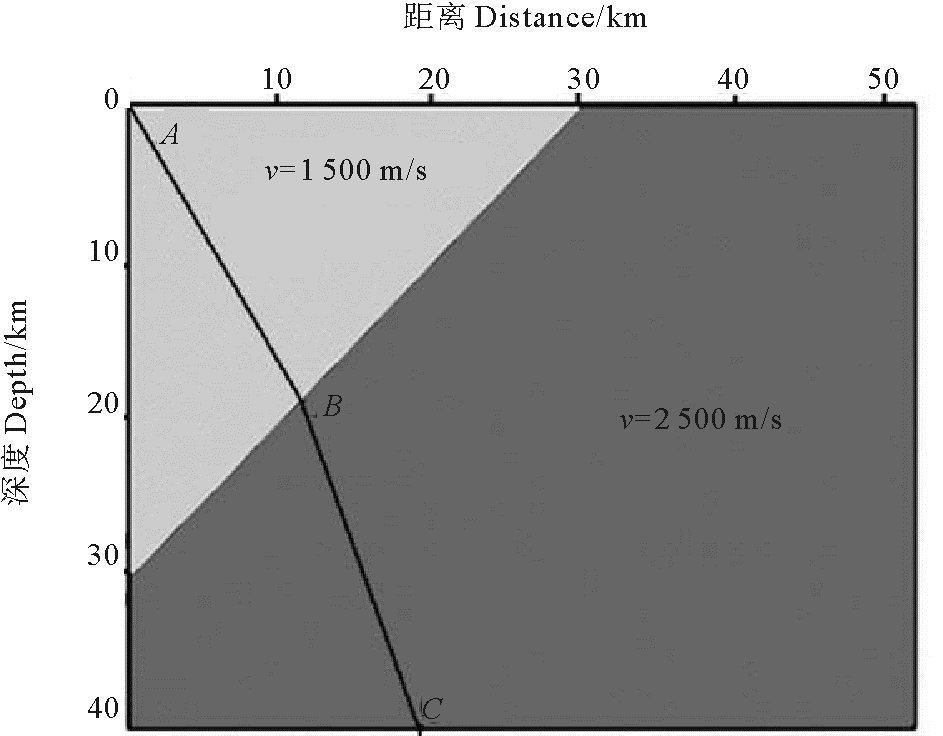
如图 1所示,运动学射线追踪精度测试所使用的网格速度模型分为两个速度层,其纵波速度分别为v1=1 500 m/s和v2=2 500 m/s,速度层分界面倾角为45°且与模型左边界相交于30 000 m处,模型最大深度为40 000 m,网格间距为5 m×5 m。
|
图 1 运动学射线追踪精度测试模型 Fig. 1 Test model of kinematic ray tracing accuracy |
测试射线以30°出射角由图 1中的点A(0, 10)出射,由几何关系可得,该射线与界面相交于点B(10 977.1, 19 022.9),由Snell定律可以计算透射射线的出射角度并最终可得射线与底边之间的交点C的坐标为(18 383.1, 40 000.0),射线总旅行时为tsnell=23.535 s。在运动学射线追踪试算中,所有追踪格式步长均设为h=4 000 m2/s(注:若设Δs与v分别为空间步长与相应速度,则h=vΔs,即在数学上相当于将空间步长Δs放大了v倍,实际计算时由于h为定值,则Δs将随v的不同而变化)。在应用数值方法获得射线终点坐标的基础上,求取终点横向位置以及旅行时的误差率
| $ \left\{ \begin{array}{l} {\sigma _x} = \left( {\frac{{\left| {{x_{trace}} - {x_{snell}}} \right|}}{{{x_{snell}}}} \times 100} \right)\% \\ {\sigma _t} = \left( {\frac{{\left| {{t_{trace}} - {t_{snell}}} \right|}}{{{t_{snell}}}} \times 100} \right)\% \end{array} \right.。$ | (16) |
保留五位有效数字可得射线终点水平位置误差率表(见表 1)。
|
|
表 1 不同运动学射线追踪方法误差率 Table 1 Error rate of kinematic ray tracing |
分析表 1可知,通过三级四阶辛RKN算法获得的射线路径与走时误差都是最低的,而经典四阶RK方法误差最大,Adams预报校正法的求解精度介于二者之间。
针对运动学射线追踪效率进行测试时,仍然选用如图 1所示的网格模型,震源位置仍设置为(0, 10),运动学射线追踪步长为h=4 000 m2/s,计算每种运动学射线追踪方法从20°~70°以0.01°为间隔的5 001根射线的总CPU耗时(运行程序的CPU平台为主频2.33 GHz的Intel Xeon E5410,测试时用C++语言编写串行程序,编译器版本为G++ 4.4.7,所有程序都使用O2级别优化编译,CPU耗时精确到毫秒)。所得运动学射线追踪耗时见表 2。
|
|
表 2 运动学射线追踪方法耗时
Table 2 Time-consuming of Kinematic ray tracing method |
从表 2中可以看出,辛几何算法的计算效率要高于两种常规算法,而在常规方法中,Adams预报校正法的效率高于经典四阶RK方法。
3 基于辛几何算法的动力学射线追踪高斯束偏移成像还需通过动力学射线追踪求取高斯束动力学参数Ps与Qs。动力学射线追踪的过程实际上是在已知中心射线的基础上求解动力学射线追踪方程组。在笛卡尔坐标系中,动力学射线追踪方程组与运动学射线追踪方程组具有相似的形式,因此理论上辛几何算法同样可以更好地针对动力学射线追踪方程组进行数值求解。根据2.2节的数值实验结果可以看出,三级四阶辛RKN格式在精度与效率上都要优于常规格式,因此本文选用三级四阶辛RKN算法求解高斯束动力学射线追踪方程组。
高斯束动力学参数为Ps与Qs满足
| $ \left\{ \begin{array}{l} {Q_{ij}} = \frac{{\partial {x_i}}}{{\partial {\gamma _j}}}\\ {P_{ij}} = \frac{{\partial {x_i}}}{{\partial {\gamma _j}}} \end{array} \right.,i,j = 1,2,3。$ | (17) |
设在笛卡尔坐标系下程函方程哈密尔顿函数形式为
| $ {H^{\left( x \right)}}\left( {{x_i},p_i^{\left( x \right)}} \right) = 0,i,j = 1,2,3。$ | (18) |
由其可得以下正则方程组
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{x_i}}}{{{\rm{d}}\mu }} = \frac{{\partial {H^{\left( x \right)}}}}{{\partial p_i^{\left( x \right)}}}}\\ {\frac{{{\rm{d}}{p_i}}}{{{\rm{d}}\mu }} = \frac{{\partial {H^{\left( x \right)}}}}{{\partial {x_i}}}} \end{array},\;\;\;\;i = 1,2,3} \right.。$ | (19) |
对正则方程组两边同时对γ求取偏导数,并注意到∂/∂γ与d/dμ微分次序可调换,得
| $ \left\{ \begin{array}{l} \frac{{dQ_{ij}^{\left( x \right)}}}{{d\mu }} = A_{ij}^{\left( x \right)}Q_i^{\left( x \right)} + B_{ij}^{\left( x \right)}P_j^{\left( x \right)},Q_0^{\left( x \right)} = {A_0}\\ \frac{{dP_{ij}^{\left( x \right)}}}{{d\mu }} = - C_{ij}^{\left( x \right)}Q_i^{\left( x \right)} - D_{ij}^{\left( x \right)}P_j^{\left( x \right)},P_0^{\left( x \right)} = M_0^{\left( x \right)}{A_0}\\ M_0^{\left( x \right)} = {\mathop{\rm Re}\nolimits} M_0^{\left( x \right)} + {\rm{lm}}M_0^{\left( x \right)}\\ i,j = 1,2,3 \end{array} \right.。$ | (20) |
其中M0(x)为初始Hessian矩阵,ReM0(x)与lmM0(x)分别为其实部和虚部。在地震勘探中一般选取ReM0(x)=0,而μ表示射线参数,Aij(x)、Bij(x)、Cij(x)和Dij(x)可由以下公式求得
| $ \left\{ \begin{array}{l} A_{ij}^{\left( x \right)} = \frac{{{\partial ^2}{H^{\left( x \right)}}}}{{\partial p_i^{\left( x \right)}\partial {x_j}}}\;\;\;\;B_{ij}^{\left( x \right)} = \frac{{{\partial ^2}{H^{\left( x \right)}}}}{{\partial p_i^{\left( x \right)}\partial p_j^{\left( x \right)}}}\\ c_{ij}^{\left( x \right)} = \frac{{{\partial ^2}{H^{\left( x \right)}}}}{{\partial {x_i}\partial {x_j}}}\quad D_{ij}^{\left( x \right)} = \frac{{{\partial ^2}{H^{\left( x \right)}}}}{{\partial {x_i}\partial p_j^{\left( x \right)}}}\\ i,j = 1,2,3 \end{array} \right.。$ | (21) |
针对声波方程,式中的各参数为
| $ \left\{ \begin{array}{l} A_{ij}^{\left( x \right)} = 0\;\;\;\;B_{ij}^{\left( x \right)} = 1\\ C_{ij}^{\left( x \right)} = 0\;\;\;\;D_{ij}^{\left( x \right)} = - \frac{1}{2}\frac{{{\partial ^2}}}{{\partial x_i^2}}\left( {\frac{1}{{{v^2}}}} \right)\\ i,j = 1,2,3 \end{array} \right.。$ | (22) |
将式代入式,可得在全局直角坐标系下的动力学射线追踪方程组
| $ \left\{ \begin{array}{l} \frac{{dQ_i^{\left( x \right)}}}{{d\mu }} = P_j^{\left( x \right)}\\ \frac{{dP_i^{\left( x \right)}}}{{d\mu }} = \frac{1}{2}\frac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)Q_j^{\left( x \right)} \end{array} \right.,i,j = 1,2,3。$ | (23) |
动力学射线追踪方程组满足辛RKN方法的应用条件,因此可以应用三级四阶辛RKN算法求解,将式与式代入式可得动力学射线追踪方程组的差分格式为
| $ \left\{ \begin{array}{l} \hat Q_{i1}^{\left( x \right)} = {Q_{in}} + \frac{{3 + \sqrt 3 }}{6}h{P_{in}}\\ \hat Q_{i2}^{\left( x \right)} = {Q_{in}} + \frac{{3 - \sqrt 3 }}{6}h{P_{in}} + {\left. {\frac{{{h^2}\left( {2 - \sqrt 3 } \right)}}{{24}}{Q_{jn}}\frac{\partial }{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)} \right|_{\hat x1}}\\ \hat Q_{i3}^{\left( x \right)} = {Q_{in}} + \frac{{3 + \sqrt 3 }}{6}h{P_{in}} + {\left. {\frac{{{h^2}\sqrt 3 }}{{12}}{Q_{jn}}\frac{\partial }{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)} \right|_{\hat x2}}\\ {p_{n + 1}} = {p_n} + h{P_{in}} + {\left. {\frac{{{h^2}\left( {5 - 3\sqrt 3 } \right)}}{{48}}{Q_{jn}}\frac{\partial }{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)} \right|_{\hat x1}} + \\ {\left. {\frac{{{h^2}\left( {3 + \sqrt 3 } \right)}}{{24}}{Q_{jn}}\frac{\partial }{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)} \right|_{\hat x2}} + {\left. {\frac{{{h^2}\left( {1 + \sqrt 3 } \right)}}{{48}}{Q_{jn}}\frac{\partial }{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)} \right|_{\hat x3}}\\ {Q_{in + 1}} = {Q_{in}} + {\left. {\frac{{h\left( {3 - 2\sqrt 3 } \right)}}{{24}}{Q_{jn}}\frac{\partial }{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)} \right|_{{{\hat x}_1}}} + \\ {\left. {\frac{h}{4}{Q_{jn}}\frac{\partial }{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)} \right|_{\hat x2}} + {\left. {\frac{{h\left( {3 + 2\sqrt 3 } \right)}}{{24}}{Q_{jn}}\frac{\partial }{{\partial {x_i}\partial {x_j}}}\left( {\frac{1}{{{v^2}}}} \right)} \right|_{\hat x3}}\\ i,j = 1,2,3 \end{array} \right.。$ | (24) |
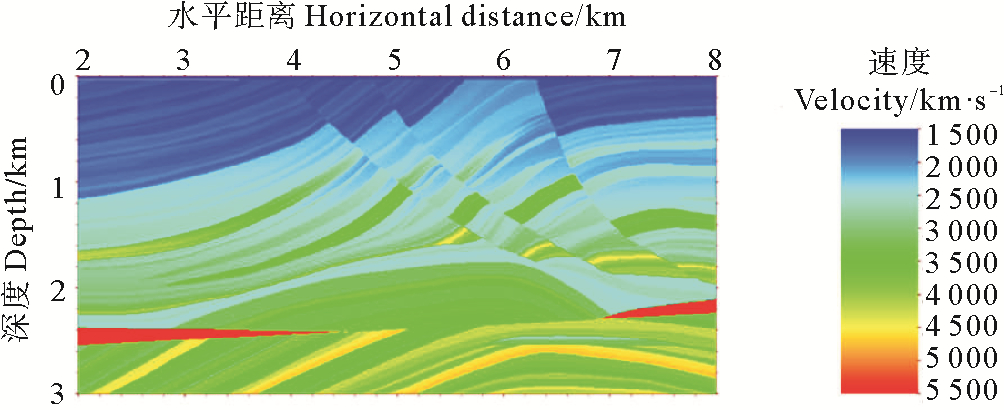
本实验应用国际上使用的行业标准模型─Marmousi模型(见图 2)进行高斯束叠前深度偏移试算的数值实验。Marmousi模型包含陡倾角断层以及大量速度剧烈变化的复杂地层,其横向网格间隔为5 m,总长度为9 200 m,纵向网格间隔为4 m,总深度为3 000 m;实验中采用右边放炮左边接收的观测系统,自2 575 m处开始放炮,炮点向右移动,炮间距为25 m,共265炮;最小偏移距为0 m,道间距为25 m,每炮104道;使用主频为30 Hz的零相位雷克子波,应用声波方程有限差分法进行地震记录正演模拟,记录总长度为3 000 ms。成像点横纵向间隔均为5 m。应用全波场高斯束偏移方法,从震源和检波点均以0.5°为间隔出射-75°~75°之间的301条高斯束,并选取高斯束初始宽度为w0=300,参考角频率为ωr=10π进行高斯束偏移波场计算,所得叠前深度偏移剖面如图 3所示。
|
图 2 Marmousi网格速度模型 Fig. 2 Marmousi velocity model |

|
图 3 与Marmousi模型对应的基于辛几何算法的高斯束偏移剖面 Fig. 3 Symplectic algorithm based Gaussian beam migration profile corresponding to Marmousi model |
由图 3可以看出,基于辛几何算法的高斯束叠前深度偏移剖面,波组特征明显,断层归位精确,同相轴连续性较好。由此说明,基于辛几何算法的高斯束叠前深度偏移具有对复杂模型精确成像的能力。
5 结论本文将基于辛几何算法的运动学射线追踪引入高斯束叠前深度偏移中,在推导了动力学射线追踪方程组的辛差分格式基础上,实现了基于辛几何算法的高斯束叠前深度偏移。模型实验表明:
(1) 基于辛几何算法的运动学射线追踪,其效率与精度相比常规算法都具有一定优势,能够满足高斯束成像的运动学射线追踪要求。
(2) 基于辛几何运动学射线追踪与动力学射线追踪算法的高斯束叠前深度偏移方法可适合于复杂构造模型的精确成像。
| [1] |
孙建国. Kirchhoff型偏移理论的研究历史、研究现状与发展趋势展望——与光学绕射理论的类比、若干新结果、新认识以及若干有待于解决的问题[J]. 吉林大学学报(地球科学版), 2012, 42(5): 1521-1552. Sun J. The history, the state of the art and the future trend of the research of Kirchhoff-type migration theory: A comparison with optical diffraction theory, some new results and new understanding, and some problems to be solved[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(5): 1521-1552. (  0) 0) |
| [2] |
He B, Mou H, Hu N. P-and S-wave angle-domain common-image gathers (ADCIGs) based on elastic-wave reverse-time migration[J]. Geological Journal, 2016, 51(S1): 669-679.
(  0) 0) |
| [3] |
郭鹏, 何兵寿, 郭敏. 基于坡印亭矢量的声波方程叠前逆时偏移成像条件[J]. 煤炭学报, 2011, 36(8): 1290-1295. Guo P, He B, Guo M. Acoustic equation pre-stack reverse-time migration imaging condition based on Poynting vector[J]. Journal of the China Coal Society, 2011, 36(8): 1290-1295. (  0) 0) |
| [4] |
Yang J, He B, Zhang J. Multicomponent seismic forward modeling of gas hydrates beneath the seafloor[J]. Applied Geophysics, 2014, 11(4): 418-428. DOI:10.1007/s11770-014-0465-x
(  0) 0) |
| [5] |
李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1-21. Li Z. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. (  0) 0) |
| [6] |
Hill N R. Prestack Gaussian-beam depth migration[J]. Geophysics, 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071
(  0) 0) |
| [7] |
Nowack R L, Sen M K, Stoffa P L. Gaussian beam migration for sparse common-shot and common-receiver data[C]. //SEG Int. Exposition and 73rd Annual Meeting.[s.l.]: Society of Exploration Geophysicists, 2003: 1114-1117.
(  0) 0) |
| [8] |
Gray S H. Gaussian beam migration of common-shot records[J]. Geophysics, 2005, 70(4): 71-77. DOI:10.1190/1.1988186
(  0) 0) |
| [9] |
Gray S H, Bleistein N. True-amplitude Gaussian-beam migration[J]. Geophysics, 2009, 74(2): 11-23. DOI:10.1190/1.3052116
(  0) 0) |
| [10] |
段新意, 李振春, 黄建平, 等. 各向异性介质共炮域高斯束叠前深度偏移[J]. 石油物探, 2014, 53(5): 579-586. Duan X, Li Z, Huang J, et al. A prestack Gaussian beam depth migration in common-shot domain for anisotropic media[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 579-586. DOI:10.3969/j.issn.1000-1441.2014.05.011 (  0) 0) |
| [11] |
李振春, 刘强, 韩文功, 等. VTI介质角度域转换波高斯束偏移成像方法研究[J]. 地球物理学报, 2018(4): 1471-1481. Li Z, Liu Q, Han W, et al. Angle domain converted wave Gaussian beam migration in VTI media[J]. Chinese Journal of Geophysics, 2018(4): 1471-1481. (  0) 0) |
| [12] |
Zhu T, Krishnasamy T, Trad D. Beam migration of canadian foothills datasets[J]. CSEG Convention, Expanded Abstracts, 2009, 685-688.
(  0) 0) |
| [13] |
冯康.哈密尔顿系统的辛几何算法[M].杭州: 浙江科技出版社, 2003. Feng K, Qin M, Symplectic Geometric Algorithms for Hamiltonian Systems[M]. Hangzhou: Zhejiang Sciencs & Technology Press, 2003. (  0) 0) |
| [14] |
秦孟兆, 陈景波. Maslov渐近理论与辛几何算法[J]. 地球物理学报, 2000, 43(4): 522-533. Qin M, Chen J. Maslov asymptotic theory and symplectic algorithm[J]. Chinese Journal of Geophysics, 2000, 43(4): 522-533. DOI:10.3321/j.issn:0001-5733.2000.04.013 (  0) 0) |
| [15] |
高亮, 李幼铭, 陈旭荣, 等.地震射线辛几何算法初探[J].地球物理学报, 2000, 43(3): 402-410. Gao L, Li Y. An attempt to seismic ray tracing with symplectic algorithm[J]. Chinese Journal of Geophysics, 2000, 43(3): 402-410. http://www.cnki.com.cn/Article/CJFDTotal-DQWX200003013.htm (  0) 0) |
| [16] |
李川, 王有学, 何晓玲, 等. 基于二维三次卷积插值算法的辛几何射线追踪[J]. 地球物理学报, 2014, 57(4): 1235-1240. Li C, Wang Y, Li X. Symplectic ray-tracing based upon the bi-cubic convolution interpolation method[J]. Chinese Journal of Geophysics, 2014, 57(4): 1235-1240. (  0) 0) |
| [17] |
岳玉波.复杂介质高斯束偏移成像方法研究[D].青岛: 中国石油大学(华东), 2011. Yue Y. Study on Gaussian Beam Migration Methods in Complex Medium[D]. Qingdao: China University of Petroleum, 2011. (  0) 0) |
| [18] |
Zhang Y, Xu S, Bleistein N, et al. True-amplitude, angle-domain, common-image gathers from one-way wave-equation migrations[J]. Geophysics, 2007, 72(1): S49-S58. DOI:10.1190/1.2399371
(  0) 0) |
| [19] |
韩复兴.论波前构建法中的几个计算问题[D].长春: 吉林大学, 2009. Han F. On Some Computational Problems in Wavefront Construction Method[D]. Changchun: Jilin University, 2009. (  0) 0) |
2. Laboratory for Marine Mineral Resource, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China;
3. Key Laboratory of Submarine Geosciences and Prospecting Techniques Ministry of Education, Qingdao 266100, China
 2020, Vol. 50
2020, Vol. 50