海冰占海洋总面积约12%,覆盖地球表面积约7%,主要分布在北极和南极大陆周围的海洋区域[1]。近些年海冰的范围逐渐退缩,同时海冰存在明显的季节变化特征。在北半球,海冰的覆盖面积通常在3~9月期间缩小,9月~次年3月覆盖面积扩大。中国的海冰主要集中在渤海地区,同时渤海地区也是我国的经济重心,海上交通发达,经济活动频繁。海冰的存在对于海上波浪的情况会产生重要的影响。随着海冰范围的缩减,包括航运和海上建设在内的经济发展也在持续增加,这需要可靠的波浪和海冰预测来应对这种不断变化的环境,同时对经济活动影响最重大的海冰边缘区的波浪模拟变得越来越重要。
当波浪穿过海冰边缘区时,它们的传播和衰减与开放水域中的波浪传播不同。先前的实地观测研究表明,波幅随着距海冰边缘的距离呈指数衰减,衰减率随着频率的增加而增加[2]。目前已经提出了几种理论模型来描述通过冰盖的波浪的散射和衰减。实地观测和实验室的结果可以在Squire[3]的综述中找到,在Mosig等[4]的研究中可以找到更多最新的研究成果。由于对波浪模拟的准确性的需求日益增加,特别是在北极地区,通过冰盖的波浪传播成为海冰研究领域的热点[5-7]。目前最新版本的全球波浪模型WAVEWATCH III®(WW3,version 5.16)[8]提供了多个海冰的模块可供研究。
冰-浪相互作用的建模极具挑战性,一种常见的方法是将异质冰场假设为漂浮在水面上的连续层。通过采用本构方程来描述该层,可以推导出该层的频散关系。通过假设不同类型冰的不同流变特性,已经推导出了几种模型,例如薄弹性板模型[9-10]、粘性层模型[11-12]和粘弹性模型[13-14]。
对于如此多的理论模型,选择一个合适的模型对于结果的准确性至关重要。在本研究使用的模型工具为WAVEWATCH III®(以下称WW3),WW3提供了若干个海冰模型。本文将使用WW3进行针对渤海海域的海冰覆盖海域的波浪情况进行模拟。
1 不同海冰模型介绍海洋表面的波浪模型用于描述由风产生的海浪能量的演变,并通过各种运输和源/汇机制进行修改。这些模型考虑了大气风强迫、非线性波相互作用和耗散。它们输出描述区域海洋或全球海洋的波高、周期和传播方向的统计数据。这种波浪模拟和波浪预测对于航运和海上建设,沿海管理以及短期或长期的生态和环境评估极为重要。本文采用的研究工具为WAVEWATCH III®,现在应用广泛的波浪模型还有SWAN,但是SWAN并没有提供任何海冰模型,因此SWAN没有在海冰覆盖海域预报波浪的能力。
对于WW3,位于海冰覆盖海域时的控制方程如下:
| $ \begin{array}{l} \frac{{\partial F\left( {f, \theta } \right)}}{{\partial t}} + {\nabla _x} \cdot {\mathit{\boldsymbol{c}}_g}F\left( {f, \theta } \right) = \left( {1 - C} \right)\left( {{S_{in}} + {S_{ds}}} \right) + \\ {S_{nl}} + C{S_{ice}} \circ \end{array} $ | (1) |
上式中忽略了其他无关源项。F(f, θ)为谱密度;cg为群速度;C为海冰密集度;Snl为不同频率的非线性传递项;Sin是风能输入项;Sds是由于波浪破碎造成的耗散;Sice是海冰项。本文主要研究目标为Sice海冰项模块,即由冰盖所造成的衰减。
在目前的WW3版本中,海冰模块是众多研究人员的持续研究工作的结果,而并非是模型内部可以完全建模的。针对不同类型的海域和海冰类型,WW3提供了多组模型可供选择,同时还有多种经验公式可供使用,但是并没有一个通用的海冰模型可以使用在所有的海域,因此模型还需要使用者自行甄别模拟海域所适用的模型。WW3主要提供了四种理论海冰模型可供选择,分别是IC0,IC1,IC2,IC3。
根据复波数理论,对于沿着x方向传播的,周期为T,波数为k的小振幅简谐波,可以表示为:
| $ \eta = A{{\rm{e}}^{i \left( {kx - \sigma t} \right)}} \circ $ | (2) |
式中:η为自由表面和水冰交界面的起伏;A为波动的振幅,σ=2π/T为角频率,t为时间。复波数定义为:
| $ k = {k_r} + {\rm{i}}{k_i} \circ $ | (3) |
式中波数的实部kr确定波速;而波数的虚部ki确定振幅衰减。在WW3模型中除了IC0外,其余模型均是通过模型给出衰减率,即ki。
在IC0中,海冰覆盖的海域被认为是“陆地”,在计算的过程中,海冰覆盖的位置会与陆地使用相同的计算条件,所有的边界条件均与岸线的边界条件相同。IC1并没有提供一个物理模型来计算衰减率,而是使用用户定义的衰减率。该值并不随着频率发生变化,而是一个常数因此IC1并无法很好的适用于各种冰场与海域,仅仅适用于风场和海浪相对单一的情况下。
IC2和IC3使用特定模型来计算ki。IC2有两个版本。一个基于Liu和Mollo-Christensen等[15-16]的论文,它使用恒定的涡粘度来参数化边界层耗散。Ardhuin等[17]发展了该理论,以区分层流和湍流。本文采用的为Liu的方法,它是由假设消散是由冰下边界层的摩擦引起的,该模型假设冰盖为连续的薄弹性板。其控制方程如下:
| $ {\sigma ^2} = \frac{{g{k_r} + Bk_r^5}}{{\coth \left( {{k_r}{h_w}} \right) + {k_r}M}}, $ | (4) |
| $ {C_g} = \frac{{g + (5 + 4{k_r}M)Bk_r^5}}{{2\sigma {{(1{ + _{kr}}M)}^2}}}, $ | (5) |
| $ {k_i} = \frac{{\sqrt {{r_\sigma }{k_r}} }}{{{C_g}\sqrt 2 (1 + {k_r}M)}} \circ $ | (6) |
式中:hw为水深;B和M为量化的海冰的弯曲和惯性的影响,它们都是海冰厚度的函数。该模型假设边界层总是层流,使用的参数为涡流粘度ν。同时IC2给出了新的频散关系,这意味着当海浪传播进入海冰覆盖海域时,其波数等物理性质会发生改变,这与之前的模型是截然不同的,但是在WW3目前的版本中,并没有使用IC2的波数。
IC3代表了基于Wang和Shen[14]的粘弹性理论的冰浪相互作用模型。该模型需要两个参数,即有效剪切模量G和粘度ν,其控制方程如下:
| $ {\sigma ^2} - {Q_c}gk\tanh kH = 0, $ | (7) |
| $ \begin{array}{l} {Q_c} = 1 + \frac{{{\rho _{ice}}}}{{{\rho _{water}}}} \cdot \\ \frac{{{g^2}{k^2}{S_k}{C_\alpha } - \left( {{N^4} + 16{k^6}{\alpha ^2}v_e^4} \right){S_k}{S_\alpha } - 8{k^3}\alpha v_e^2{N^2}\left( {{C_k}{C_\alpha } - 1} \right)}}{{gk\left( {4{k^3}\alpha v_e^2{S_k}{C_\alpha } + {N^2}{S_\alpha }{C_k} - gk{S_k}{S_\alpha }} \right)}} \circ \end{array} $ | (8) |
式中:H为水深;Sk=sinhkh;Sα=sinhαh;Ck=coshkh;Cα=coshαh;N=σ+2ik2νe;
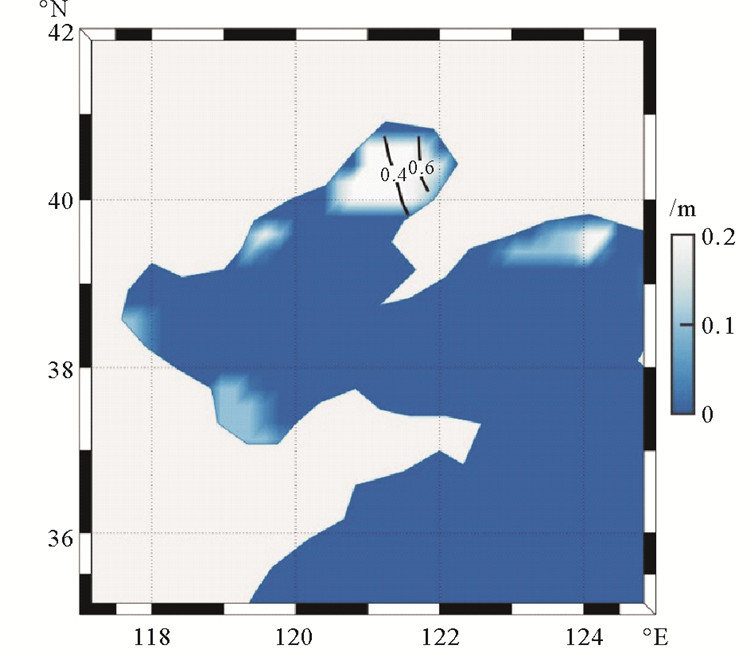
这里使用的波浪模型为WW3最新的版本5.16。图 1显示了用于模拟的计算区域,其计算范围是35°N~42°N,117°E~125°E,网格的分辨率为0.1°。计算区域包含了完整的渤海海域。使用扩大后的区域(30°N~47°N,112°E~130°E)进行实验后可得相同的结果,证明实验结果对边界的改变敏感性较低。同时在渤海区域周围存在大范围的岛屿与陆地,其它大洋的长波是无法传入。对于模型的初始条件,本文选用了常见的冷启动做法,即初始的风场和浪场均设定为0。计算的时间为2019年1月15日0点~28日0点,选取该时间的原因在于该时间段内渤海海冰覆盖面积较大,此时比较不同模型的波浪结果较为明显。为了验证计算时间是否足够,我们延长了计算时间,但是结果并没有差异,因此,可以确定计算时间是足够的。
|
(白色代表了海冰覆盖区域的海冰厚度,黑色等值线为海冰密集度。The white represents the thickness of sea ice in the sea ice covered area; The black lines are the sea ice concentration. ) 图 1 模拟的计算区域 Fig. 1 The hindcast design area |
WW3提供的四个模型中,IC0不需要提供任何参数,而其他模型均需要由用户提供参数。IC1需要提供衰减系数,IC2需要提供涡流粘度系数,IC3需要提供有效剪切模量和粘度。本文使用的所有参数均来自于前人的研究成果。
模型的运转需要提供风场和冰场信息。本文使用的风场和海冰厚度来自于NCEP的CFSv2数据(https://rda.ucar.edu/datasets/ds094.1/),海冰密集度数据来自于NOAA OI SST V2高分辨率数据集(https://www.esrl.noaa.gov/psd/data/gridded/data.noaa.oisst.v2.highres.html)。这些数据集的空间分辨率为15 km,时间分辨率为6 h。这些数据将会在WW3中通过线性插值到和网格相同的空间和时间分辨率上。
模拟将使用WW3提供的全部理论海冰模型。除冰场相关的模型外,其他的模型全部为默认设置(见表 1)。
|
|
表 1 其余模型和参数 Table 1 Other models and parameters |
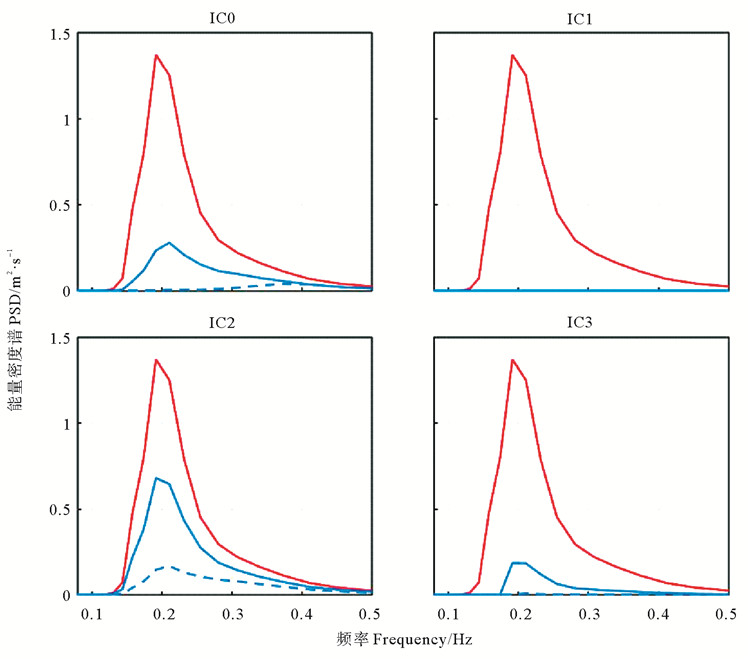
在WW3输出的结果中,本文选择了三个位置作为观测点,这三个点的位置分别位于开阔水域、海冰边缘区和海冰中部区,输出时间为2019年1月27日0点。图 2的结果为不同海冰模型的海浪能量密度谱(PSD)的结果。
|
(红实线为开阔水域的PSD(121.3°E,40.4°N),蓝色实线为海冰边缘区域的PSD(121.5°E,40.5°N),蓝色虚线为海冰中部区域的PSD(121.7°E,40.6°N)。The red solid line is PSD (121.3°E, 40.4°N) in open water; The blue solid line is PSD (121.5°E, 40.5°N) in the marginal area of sea ice; The blue dashed line is PSD (121.7°E, 40.6°N) in the central area of sea ice. ) 图 2 不同海冰模型的海浪能量密度谱(2019年1月27日0点) Fig. 2 Wave power spectrum density of different sea ice models |
不同的海冰模型的结果差异很大,因此针对海冰区域的海浪模拟,海冰模型的选取至关重要。在海冰区域除了关注PSD外,更为重要的一个物理量为α,即海冰造成的波浪衰减率。其定义如下:
| $ \alpha = - \frac{{\mathit{ln}\left( {\sqrt {{P_2}/{P_1}} } \right)}}{D} \circ $ | (9) |
其中:α是海浪波幅衰减系数;P2和P1是同一频率下两个点的PSD值;D是两点之间的距离。它反映了由海冰造成的能量的衰减大小。它与副波数ki的关系为:
| $ \alpha = C{k_i} \circ $ | (10) |
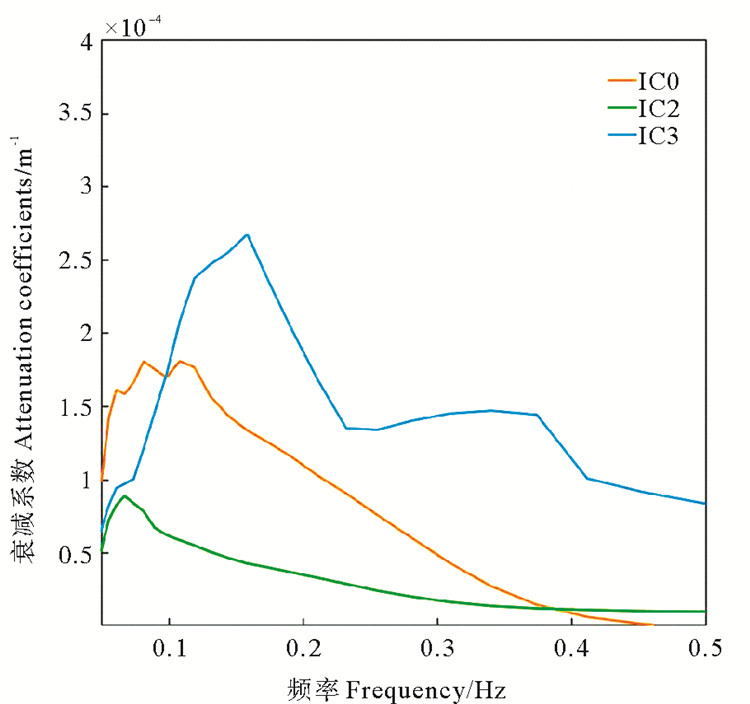
式中:C为海冰密集度;衰减系数α是根据能量的结果算出的;而ki则是由海冰模型计算得到的理论值。图 3的结果为海冰边缘区和海冰中部区之间的衰减值。
|
图 3 不同海冰模型的衰减系数(通过PSD计算) Fig. 3 Attenuation coefficients of different sea ice models (calculated by PSD) |
在图 3结果中,不同模型的结果差异明显。因为IC0并非真实的海冰模型,在IC0中海冰被当作陆地处理。在上述结果中,当波浪传入海冰中部区域后,其低频的波浪消失,而高频的能量并没有得到有效衰减。低频率的波动为较大尺度的长波,这些长波在进入冰盖后不容易被衰减,而高频的波动则对应着小尺度的毛细波等,这些短波则很容易被海冰衰减掉。而IC0则是在低频部分PSD很小,而在高频部分则比较高,这与实际情况是不相符的。究其原因是由于IC0并不是一个实际的物理模型,把海冰当作陆地并不能很好地模拟实际情况下波浪传播进入。同时PSD较小的原因在于IC0将海冰作为陆地处理,而在海冰边缘区域,其海冰的物理性质与陆地完全不同,并不会产生特别大的衰减。尽管IC0无法提供一个很好的结果,但是IC0第一次将海冰的处理引入了WW3中,还是具有非常大的进步意义。
图 3中IC1的结果并未显示,因为IC1的PSD能量在海冰中部地区已衰减殆尽,无法计算衰减系数。同时IC1与IC0不同,IC1是根据用户提供的海冰衰减率进行计算而后输出结果。本文是用的IC1的衰减率是10-5m-1,该值取自于其它模型的平均结果。在IC1中,用户提供的衰减率不随着频率变化,是一个常数。但是真实的衰减率并非如此,在低频区域较小,而在高频区域则比较大。而使用同一个海冰衰减率来应对全部频率显然是不合理的,而且在海冰密集度较小的地方,使用和海冰密集度较高的地方使用相同的衰减率也是不合理的,因此IC1仅仅适用于某些特殊情况。对于IC0和IC1的不好的结果,作者是可以预见的,因为仅仅使用简单的模型或者一个定常的衰减系数来模拟复杂的冰浪相互作用是不现实的,因此下文不会就IC0和IC1做更多的讨论。
IC2是一个完整的物理模型,它是建立于Greenhill[21]和Wadhams[22]的理论之上,在该理论中,海冰覆盖海域的冰盖被看作是弹性材料,这种假设不同于IC0,IC0将每个计算点单独考虑,而IC2将冰盖认为是一个连续的整体,在这个模型中厚度并不是最重要的,厚度相对于波长的比例非常小。但是在实际的模型中也存在一些厚度超过1 m的海冰,尽管这部分海冰所占的比例很小。该模型需要提供一个涡流粘度系数,本文使用的值为10-4 m2·s-1,该值取自于IC2开发组给出的参数范围。在实验结果中,IC2的结果要好于IC0与IC1。根据Liu和Mollo-Christensen[15-16]的理论假设,海浪在冰盖下传播会产生额外的能量衰减,而能量衰减的原因是冰盖粗糙度,因此需要考虑冰盖下的粘性,即涡流基于冰-水界面粗糙度产生的湍流漩涡的论证,并引入了一个新的参数涡流粘度υ,而涡流粘度是由冰盖的粘性所引起的。由于冰盖的摩擦引起的粘性,会使得在冰盖下的水体产生湍流。在开阔水域中,WW3模型的海浪的恢复力为重力,然而在粘性模型中,重力被忽略,此时的恢复力为粘性,所以在实际模型中为弯曲重力波。IC2成功的捕获了重要的物理过程,即海冰造成的湍流会引起一定能量的损失,因此IC2的结果更为贴近实际情况。
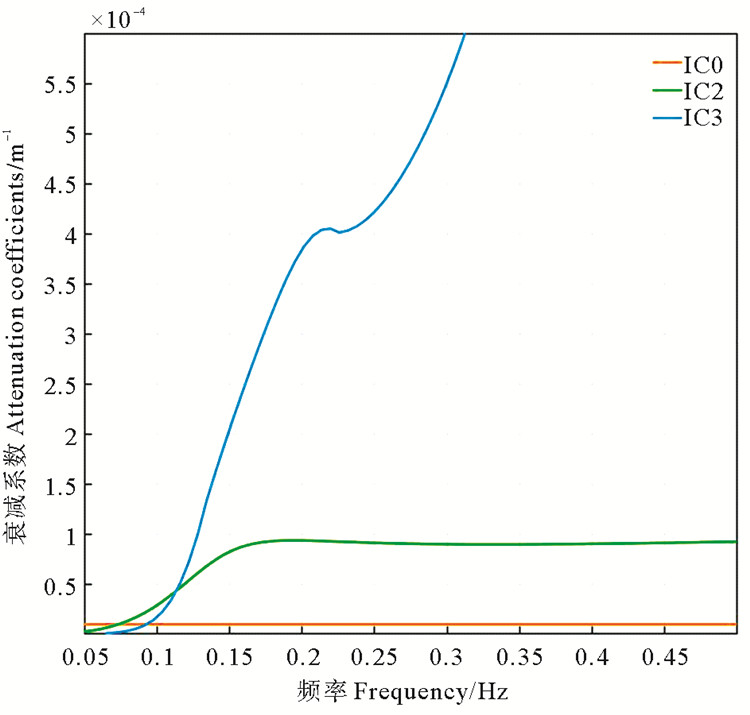
IC3为粘弹性模型,是根据Wang和Shen[14]提出的理论开发的。粘弹性模型不仅仅考虑由于冰盖的粘性所造成的弹性,同时考虑了由于冰盖的弹性也会存储一部分能量。粘弹性模型主要预测的是在双层冰-水系统中生成的波动。粘弹性模型结合了薄弹性板模型和粘性模型。粘弹性模型需要输入海冰的密集度、厚度、密度、冰层的有效剪切模量G和有效运动粘度ν。本文使用的G和ν的值为0.3 m2/s与20 000 Pa。在计算频散关系时不需要用到海冰密集度,海冰密集度作为缩放系数将确定耗散的大小。在有效剪切模量G为0的情况下,粘弹性模型与Keller[19]提出的方案完全相同。在实验结果中IC3的结果要偏小一些,这与参数的选取有一定的关系。但是IC3结果的趋势更贴近于其他研究中真实测量的结果,其衰减率在中低频部分随频率的增加而增大,这符合真实海洋下波浪的衰减情况。在模型输出的结果中,不仅仅受到海冰衰减的影响,同时还会有其他源项的影响,因此,我们输出了纯理论模型的结果(见图 4)。
|
图 4 不同海冰模型的衰减系数(理论值) Fig. 4 Attenuation coefficients of different sea ice models (theoretical value) |
为了进一步比较不同模型衰减率的差异,本文直接通过理论模型计算输出了衰减系数(见图 4)。该衰减率不同于图 3的结果,图 3的结果是通过PSD计算得到,而图 4则是直接由理论模型输出,其差异在于通过PSD计算得到的结果还会受到其他模块的影响,比如风和地形等影响。通过该图可以直观地看到不同模型衰减率的差异,IC1是由用户直接提供的衰减率,其不随着频率变化,除IC1外,其他模型都是衰减率随着频率的上升而增大。IC2与IC3在高频部分要显著高于IC1,这是因为高频部分对应着波长较小的波浪,其更容易被海冰衰减,而在低频部分则低于IC1,因为在冰下长波的衰减率要更小,但是在IC1中,长波依然与短波处于相同的衰减率中,这会导致在IC1的长波被快速衰减,使其能量远小于真实范围。IC2与IC3则可以根据频率变换衰减率,使其衰减率处于合理的范围之内。在低频部分,IC2与IC3衰减率范围比较接近,但是在高频部分,IC3的衰减率迅速增加,对于IC2与IC3的结果,需要更多的数据进行比较才能发现哪种模型更适合在渤海海域使用。
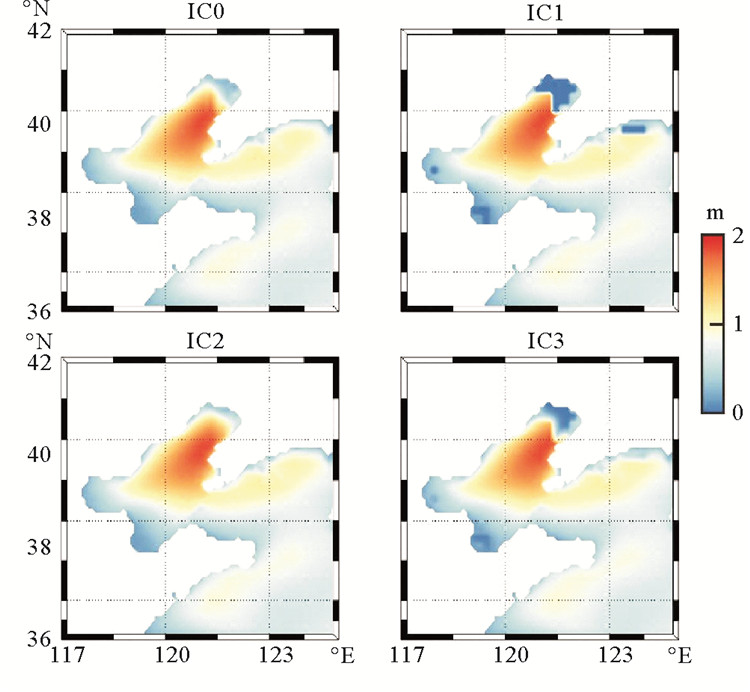
图 5给出了区域的有效波高结果。在区域场的海冰范围中,不同模型差别也非常明显。由于,IC0与IC1是非理论模型,其不具备大规模的海冰覆盖海域波浪模拟能力。IC2的结果明显高于IC3的结果,在IC3中,可以明显地观察到由于海冰造成的能量衰减。根据现有资料,尽管IC2与IC3的结果存在差异,但是无法明确判断哪种更贴近真实情况,同时不同的模型也对应着不同的冰情,这也需要根据实际的海冰情况选择不同的理论模型。
|
图 5 不同海冰模型的有效波高(2019年1月27日0点) Fig. 5 Significant wave heights for different sea ice models |
本文使用WW3针对冬季渤海的海冰覆盖海域做出了海浪的模拟。研究发现,不同海冰模型的结果差异很大。其中IC0为简单的衰减模型,其仅根据海冰密集度的不同来对波浪能量进行衰减,同时对于高海冰密集度的会关闭该计算网格,将其视为陆地处理,因此其结果是不可靠的。IC1为用户提供一个衰减参数,该参数不随频率变化,仅仅是一个常数。将一个常数应用于全部频率段的海浪谱是不合理的,因为在该高频区域的海浪的衰减要明显高于低频区域的海浪,因此IC1的结果仅仅适用于某些特定区域,而无法进行区域模拟。IC2和IC3为理论模型,需要提供参数。其中IC2需要提供涡流粘度,IC3需要提供有效剪切模量和粘度。不同理论模型的结果差异很大,IC2与IC3的衰减率随着频率变化,其可以对高频部分进行有效的衰减,同时在低频区域的衰减率也处于合理的范围,而IC0与IC1则无法做到。对于IC2与IC3,其在低频部分衰减率较为接近,说明对于长波,两种理论的结果较为接近,但是在高频部分,IC3的衰减率快速增大,因此说明IC3对于短波的衰减更强。但是IC2与IC3的模型结果均要好于IC0与IC1。因此针对海冰覆盖海域的海浪模拟应该首选IC2或IC3,同时根据实地海冰的情况来确定参数。
本研究还存在一定的局限性,目前缺乏足够的观测数据来分析对比IC2与IC3哪一个更适合在渤海海域使用,同时本文使用的风场与冰场数据分辨率偏低,因此,对于渤海海域的海冰模型差异研究还有待进一步进行。
| [1] |
Shokr M, Sinha N. Sea ice:Physics and remote sensing[J]. John Wiley & Sons, 2015. DOI:10.1002/9781119028000
(  0) 0) |
| [2] |
Wadhams P, Squire V A, Goodman D J, et al. The attenuation rates of ocean waves in the marginal ice zone[J]. Journal of Geophysical Research:Oceans, 1988, 93(C6): 6799-6818. DOI:10.1029/JC093iC06p06799
(  0) 0) |
| [3] |
Squire V A. Review of ocean waves and sea-ice revisited[J]. Cold Regions Science and Technology, 2007, 49(2): 110-133. DOI:10.1016/j.coldregions.2007.04.007
(  0) 0) |
| [4] |
Mosig J E, Montiel F, Squire V A. Comparison of viscoelastic-type models for ocean wave attenuation in ice-covered seas[J]. Journal of Geophysical Research:Oceans, 2015, 120(9): 6072-6090. DOI:10.1002/2015JC010881
(  0) 0) |
| [5] |
Meylan M H, Bennetts L G, Mosig J E M, et al. Dispersion relations, power laws, and energy loss for waves in the marginal ice zone[J]. Journal of Geophysical Research:Oceans, 2018, 123(5): 3322-3335. DOI:10.1002/2018JC013776
(  0) 0) |
| [6] |
Montiel F, Squire V A, Doble M, et al. Attenuation and directional spreading of ocean waves during a storm event in the autumn Beaufort Sea marginal ice zone[J]. Journal of Geophysical Research:Oceans, 2018, 123(8): 5912-5932. DOI:10.1029/2018JC013763
(  0) 0) |
| [7] |
Rogers W E, Posey P, Li L, et al. Forecasting and Hindcasting Waves In and Near the Marginal Ice Zone: Wave Modeling and the ONR Sea State Field Experiment No. NRL/MR/7320-18-9786[R]. United States: Naval Research Lab Stennis Detachment Stennis Space Center Ms Stennis Space Center, 2018.
(  0) 0) |
| [8] |
Tolman H L, the WAVEWATCH III® Development Group, User manual and system documentation of WAVEWATCH III® version5.16, NOAA Technical Note[R].USA: MMAB Contribution No. 329, 2016.
(  0) 0) |
| [9] |
Wadhams P. The Seasonal Ice Zone[M]. US: The Geophysics of Sea Ice. Springer 1986: 825-991.
(  0) 0) |
| [10] |
Fox C, Squire V A. Reflection and transmission characteristics at the edge of shore fast sea ice[J]. Journal of Geophysical Research:Oceans, 1990, 95(C7): 11629-11639. DOI:10.1029/JC095iC07p11629
(  0) 0) |
| [11] |
Keller J B. Gravity waves on ice-covered water[J]. Journal of Geophysical Research:Oceans, 1998, 103(C4): 7663-7669. DOI:10.1029/97JC02966
(  0) 0) |
| [12] |
De Carolis G, Desiderio D. Dispersion and attenuation of gravity waves in ice:A two-layer viscous fluid model with experimental data validation[J]. Physical Letters A, 2002, 305: 399-412. DOI:10.1016/S0375-9601(02)01503-7
(  0) 0) |
| [13] |
Fox C, Squire V A. On the oblique reflexion and transmission of ocean waves at shore fast sea ice[J]. Philosophical Transactions of Royal Society of London A, 1994, 347: 185-218. DOI:10.1098/rsta.1994.0044
(  0) 0) |
| [14] |
Wang R, Shen H H. Gravity waves propagating into an ice-covered ocean:A viscoelastic model[J]. Journal of Geophysical Research:Oceans, 2010, 115(C6). DOI:10.1029/2009JC005591
(  0) 0) |
| [15] |
Liu A K, Mollo-Christensen E. Wave propagation in a solid ice pack[J]. Journal of Physical Oceanography, 1988, 18(11): 1702-1712. DOI:10.1175/1520-0485(1988)018<1702:WPIASI>2.0.CO;2
(  0) 0) |
| [16] |
Liu A K, Holt B, Vachon P W. Wave propagation in the marginal ice zone:Model predictions and comparisons with buoy and synthetic aperture radar data[J]. Journal of Geophysical Research:Oceans, 1991, 96(C3): 4605-4621. DOI:10.1029/90JC02267
(  0) 0) |
| [17] |
Ardhuin F. Semiempirical dissipation source functions for ocean waves[J]. Journal of Physical Oceanography, 2010, 40(9): 1917-1941. DOI:10.1175/2010JPO4324.1
(  0) 0) |
| [18] |
Peters A S. The effect of a floating mat on water waves[J]. Communications on Pure and Applied Mathematics, 1950, 3: 319-354. DOI:10.1002/cpa.3160030402
(  0) 0) |
| [19] |
Keller J B. Gravity waves on ice-covered water[J]. Journal of Geophysical Research:Oceans, 1998, 103(C4): 7663-7669. DOI:10.1029/97JC02966
(  0) 0) |
| [20] |
Fox C, Squire V A. On the oblique reflexion and transmission of ocean waves at shore fast sea ice[J]. Philosophical Transactions of Royal Society of London A, 1994, 347: 185-218. DOI:10.1098/rsta.1994.0044
(  0) 0) |
| [21] |
Greenhill A G. Wave motion in hydrodynamics (continued)[J]. American Journal of Mathematics, 1887, 97-112.
(  0) 0) |
| [22] |
Wadhams P. Attenuation of swell by sea ice[J]. Journal of Geophysical Research, 1973, 78(18): 3552-3563. DOI:10.1029/JC078i018p03552
(  0) 0) |
 2020, Vol. 50
2020, Vol. 50


