2. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237
由于地下介质分布的非均匀性,常规的地震信号在时间域和空间域往往表现为非平稳性。时频分析技术将输入的地震信号从一维时域变换到二维时-频域,为研究数据中的隐藏信息提供了新的分析维度,在分析地震数据的频率非平稳变化方面发挥着重要作用。常规地震属性由于地震主频的约束,在地震数据分析上存在很大的局限,已不满足愈发复杂油气勘探的需求。近年来,基于谱分解的地震时频属性技术在储层预测[1-2]、沉积研究[3-4]、地质体识别[5-6]等领域广泛应用。
在储层预测方面,常用的线性时频技术有短时傅里叶变换(Short-Time Fourier Transform,STFT)[7]、连续小波变换(Continues Wavelet Transform,CWT)[8]、S变换(S-Transform,ST)[9],此外还有非线性的Wigner-Ville时频分布[10]、Cohen类时频分布[11]以及基于稀疏脉冲反演原理的匹配追踪算法[12]等。S变换是Stockwell于1996年在STFT和CWT的基础上,提出的一种具有高时-频域分辨率的时频分析理论[13]。对于S变换,可以通过频率时窗函数来控制分辨率,即低频时有高的频率分辨率,高频时有高的时间分辨率。但是其窗函数为高斯函数,无法对时宽和频宽进行调节,导致低频时时间分辨率变差,高频时频率分辨率变差。此后众多研究学者从改进窗口函数和小波基方面来优化时频分辨率。Mcfadden等[14]提出了一种基于非对称窗函数的广义S变换,应用更加灵活。高静怀等[15]提出用待定参数的调幅简谐波代替小波基,在薄层分析方面取得显著效果。陈学华等[16]则提出可根据地震信号自适应调整时宽的广义S变换,将其应用到储层分析。Sejdic等[17]通过优化窗函数宽度,解决了S变换在时频域能量集中的问题。Li和Catsagna[18]提出含有两个参数的修正S变换(Modified S-Transform,MST),其窗函数选择更加灵活,可以得到更高的时频分辨率;之后,Li等详细讨论了MST时窗参数的选择问题并将其应到烃类直接检测中,证明MST是一种具有鲁棒性的、灵活性的可用于地震勘探中的时频分析方法[19]。后来,Liu等[20]进一步对S变换的窗函数进行了改进,提出一种三参数S变换(Three Parameters S-Transform,TPST),并通过实际数据证明TPST对河道的刻画优于ST和MST,本文尝试将其用于储层预测中。
地震波穿过含油气储层时会发生明显的高频衰减现象。Mitchell等[21]提出了一种用于计算高频衰减的能量吸收分析(Energy Absorption Analysis,EAA)技术,利用高频部分的指数衰减系数来表征衰减程度,从而识别油气藏的存在。之后,毕研斌等[22]和张固澜等[23]分别基于小波变换和广义S变换提取了地震波的频率衰减梯度属性进行油气藏的识别,见到了一定的效果。为提高频率衰减梯度属性的求取精度,学者们从提高时频变换的分辨率和频率衰减梯度属性的求取两个方面进行。熊晓军等[24]利用比常规短时傅立叶变换时频分辨率更高的时频三参数小波变换对信号进行时频分析,并采用非线性拟合方式求取信号的频率衰减梯度,取得比常规方法更高的计算精度;李延等[25]基于S变换利用二次多项式拟合求取频率衰减梯度属性,并进行了天然气水合物的检测,取得一定的效果。为了更稳定地计算频率衰减梯度,潘晓等[26]改进了常规的频率衰减梯度属性只利用占地震总能量的65%及85%的两点所对应的频率及能量值求取梯度的方法,他们基于同步挤压小波变换利用信号的多级重心求取了地震波的频率衰减梯度属性,使求得的频率衰减梯度属性更稳定。
鉴于TPST的优势及多级重心频率衰减梯度属性的稳定性,本文在前人研究的基础上,提出利用TPST求取信号的多级重心频率衰减梯度属性的方法并将其应用于储层预测,利用模型数据和实际资料验证方法的有效性。通过与基于TPST的常规频率衰减梯度属性及基于STFT和CWT的多级重心频率衰减梯度属性对比,证明了基于TPST的多级重心频率衰减梯度属性具有更高的精度,能更准确地刻画储层的衰减特征,实现储层的精确定位。
1 方法原理 1.1 三参数S变换三参数S变换(TPST)是在S变换的基础上改进的新型时频分析方法。对于连续时间信号h(t)∈L2(R),其S变换为
| $ \begin{array}{*{20}{c}} {S(\tau, f)=\int\limits_{-\infty}^{+\infty} h(t) w(\tau-t, f) \mathrm{e}^{-i 2 \pi f t} \mathrm{~d} t=}\\ {\int\limits_{-\infty}^{+\infty} h(t) \frac{|f|}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{(t-t)^2 f^2}{2}} \mathrm{e}^{-i 2 \pi f t} \mathrm{~d} t。} \end{array} $ | (1) |
其中,τ和f分别为时间变量和频率变量,
S变换的窗函数可随频率变化,克服了短时傅里叶变换固定窗的缺陷。但由于窗函数形态是固定的,窗口宽度不能灵活调节,在实际应用中受到限制,因此需要对窗函数加以改进。
TPST利用一个非线性频率函数δ(f)=
| $ w(\tau-t, f)=\frac{\left|k f^p+m\right|}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{(\tau-t)^2\left(k f^p+m\right)^2}{2}} 。$ | (2) |
将(2)式代入(1)式即可得到TPST的完整表达式:
| $ \begin{gathered} \operatorname{TPST}(\tau, f)= \\ \int\limits_{-\infty}^{+\infty} h(t) \frac{\left|k f^p+m\right|}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{(\tau-t)^2\left(k f^p+m\right)^2}{2}} \mathrm{e}^{-i 2 \pi f t} \mathrm{~d} t。\end{gathered} $ | (3) |
图 1显示了时间域中的窗函数,其中图 1(a)—(d)分别对应窗函数中心频率fc为10、20、30和40 Hz的情况。在每一个中心频率下,TPST的窗函数调节参数设置了三种情况,三种情况下均是(k=1.5, m=3),不同的是p取值为0.5、1.5和1(相当于MST)的情况。从图中可以看出,在不同中心频率下,ST的时窗宽度只与频率相关,而TPST的时窗宽度还可以通过参数(k, p, m)灵活调节。结合TPST的高斯窗函数表达式可知,时窗参数的选择影响时频分析结果的时频分辨率:

|
((a)中心频率fc = 10 Hz; (b) fc = 20 Hz; (c) fc = 30 Hz; (d) fc = 40 Hz。(a) Center frequency fc = 10 Hz; (b) fc = 20 Hz; (c) fc = 30 Hz; (d) fc = 40 Hz.) 图 1 不同频率下TPST和ST的高斯窗对比 Fig. 1 Gaussian window comparison of TPST and ST at different frequencies |
(1) 当(k=1, p=1, m=0) 时,TPST退化为标准的S变换,时频分辨率与S变换保持一致。
(2) 当(k≠0, p=1, m≠0) 时,TPST相当于MST的情况,时窗宽度可以根据k和m的取值较为灵活地调节。
(3) 以(k=1.5, m=3)为例,当p>1时,TPST的时窗宽度相比于ST和MST变小,时间分辨率提高,频率分辨率降低;当p < 1时,TPST的时窗宽度变大,时间分辨率降低,频率分辨率提高;参数p起到随频率变化调节时窗宽度变化速率的作用。
对于实际地震信号,可根据信号的特点及需求设置不同的参数便可以获得较高的时频分辨率。
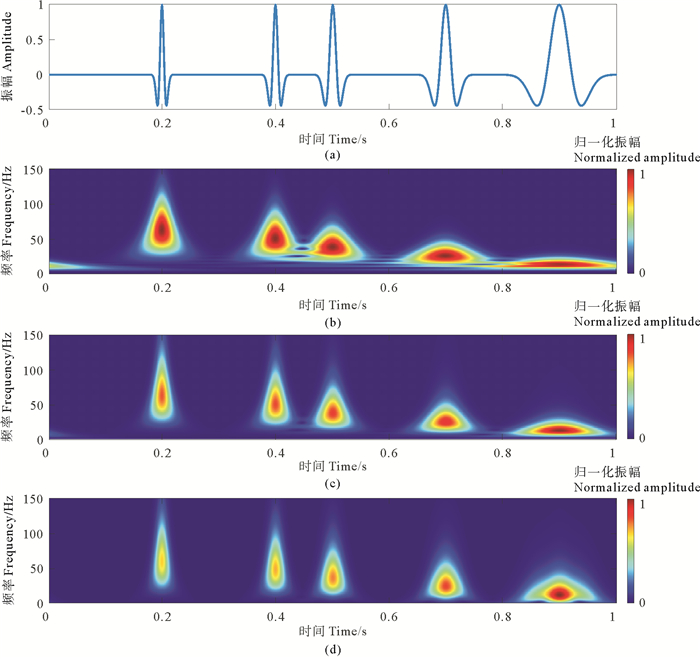
为更好地说明TPST多分辨率的优势,将主频为10~50 Hz的Ricker信号合成为一个信号,信号总长度为1 s,如图 2(a)所示。分别采用ST、MST(k=1.5, m=10)和TPST(k=5, p=0.75, m=30)对信号进行时频分析,结果如图 2(b)—(d)所示。从图 2(b)可以看出,ST的时频谱在0.45 s处和0.8 s处出现了频率混叠现象,此时分别对应信号的30~40 Hz及10~20 Hz频率成分,可见,ST在低频时存在时间分辨率不足的局限性。图 2(c)和(d)中MST和TPST时频谱能够有效区分信号在0.45 s处和0.8 s处10~40 Hz的频率成分,消除了ST中的频率混叠现象对信号时频谱的影响,具有很好的时间分辨率。对比MST结果和TPST结果,发现TPST的时频谱上的能量团比MST时频谱上的能量团更集中,说明其具有更好的时频分辨率,更适合描述地震勘探频带内的非平稳信号。
|
((a) 合成信号; (b) ST; (c) MST; (d) TPST。(a) The signal; (b) Spectrum of ST; (c) Spectrum of MST; (d) Spectrum of TPST.) 图 2 Ricker合成信号不同变换时频谱 Fig. 2 The spectra of Ricker wavelet synthetic signal using different transforms |
吸收衰减属性是频谱分析中一项重要的属性特征。当地层中含有油气时,吸收系数会随着频率的增大而增大[27],高频部分的能量衰减变快。因此可以利用地震波的衰减属性差异来识别储层的含油气性。
Mitchell等提出能量吸收分析(EAA)技术来计算地震信号的能量衰减,其本质是用一系列小时窗(如高斯时窗)截取地震数据作频谱分析,对得到的瞬时振幅谱的高频部分进行指数拟合求得衰减系数,而进行线性拟合可得到衰减梯度属性,两种衰减属性都可以检测由于油气引起的地震频谱中高频成分的衰减异常。
传统的频率衰减梯度属性是利用信号的两个频率点所对应的能量值求取。即:对于单道地震信号x(t),经时频变换后的时频谱为P(t, f),在t=tm时刻的总幅值能量E为该时刻所有频率对应的幅值之和,即
| $ E=\sum\limits_n P\left(t_m, f_n\right) 。$ | (5) |
将幅值能量最大时对应的频率fmax作为初始衰减频率,累积能量达到65%和85%时所对应的频率分别为fM和fN,则频率衰减梯度g的计算公式为:
| $ g=\frac{65 \% E-85 \% E}{f_M-f_N} 。$ | (6) |
仅用两个设定能量范围的频率点的值求取频率衰减梯度属性容易受到偶然因素的影响,致使求取的频率衰减梯度属性值不准确。为获得更稳定的频率衰减梯度值,本文采用潘晓等提出的利用信号的多级重心求取频率衰减梯度的方法。重心频率能够描述信号频谱中分量较大的信号成分的频率,反映信号功率谱的分布情况,即使有噪声的干扰,重心频率的变化也相对稳定[28]。以信号的重心将信号分段,在每部分按照信号重心的定义计算分段信号的重心得到二级重心频率,依此类推可以得到信号的多级重心频率。
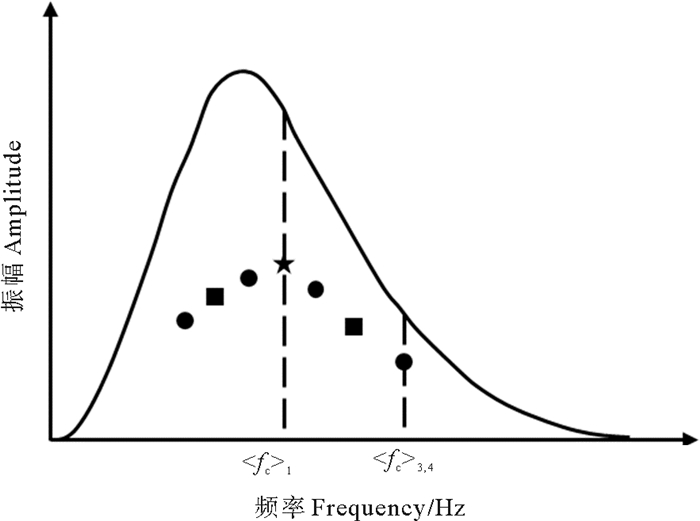
如图 3所示,信号的多级重心频率计算如下:
|
图 3 信号的多级重心示意图 Fig. 3 The multi-level barycenter of signal |
一级重心频率(星号)
| $ \left\langle f_c\right\rangle_1=\frac{\int_{-\infty}^{\infty} f\left|P\left(t_m, f\right)\right| \mathrm{d} f}{\int_{-\infty}^{\infty}\left|P\left(t_m, f\right)\right| \mathrm{d} f} 。$ | (7) |
二级重心频率(正方形)
| $ \begin{aligned} & \left\langle f_c\right\rangle_{2, 1}=\frac{\int_{-\infty}^{\left\langle f_c\right\rangle_1} f\left|P\left(t_m, f\right)\right| \mathrm{d} f}{\int_{-\infty}^{\left\langle f_c\right\rangle_1}\left|P\left(t_m, f\right)\right| \mathrm{d} f}, \\ & \left\langle f_c\right\rangle_{2, 2}=\frac{\int_{\left\langle f_c\right\rangle_1}^{\infty} f\left|P\left(t_m, f\right)\right| \mathrm{d} f}{\int_{\left\langle f_c\right\rangle_1}^{\infty}\left|P\left(t_m, f\right)\right| \mathrm{d} f} 。\\ & \end{aligned} $ | (8) |
三级重心频率(圆点)
| $ \begin{aligned} \left\langle f_c\right\rangle_{3, 1} & =\frac{\int_{-\infty}^{\left\langle f_c\right\rangle_{2, 1}} f\left|P\left(t_m, f\right)\right| \mathrm{d} f}{\int_{-\infty}^{\left\langle f_c\right\rangle_{2, 1}}\left|P\left(t_m, f\right)\right| \mathrm{d} f}, \\ \left\langle f_c\right\rangle_{3,2} & =\frac{\int_{\left\langle f_c\right\rangle_{2,1}}^{\left\langle f_c\right\rangle_1} f\left|P\left(t_m, f\right)\right| \mathrm{d} f}{\int_{\left\langle f_c\right\rangle_{2,1}}^{\left\langle f_c\right\rangle_1}\left|P\left(t_m, f\right)\right| \mathrm{d} f}, \\ \left\langle f_c\right\rangle_{3,3} & =\frac{\int_{\left\langle f_c\right\rangle_1}^{\left\langle f_c\right\rangle_{2,2}} f\left|P\left(t_m, f\right)\right| \mathrm{d} f}{\int_{\left\langle f_c\right\rangle_1}^{\left\langle f_c\right\rangle_{2,2}}\left|P\left(t_m, f\right)\right| \mathrm{d} f}, \\ \left\langle f_c\right\rangle_{3, 4} & =\frac{\int_{\left\langle f_c\right\rangle 2, 2}^{\infty} f\left|P\left(t_m, f\right)\right| \mathrm{d} f}{\int_{\left\langle f_c\right\rangle_{2, 2}}^{\infty}\left|P\left(t_m, f\right)\right| \mathrm{d} f} 。\end{aligned} $ | (9) |
一般而言,三级重心频率范围为信号的主频带,本文采用一级重心频率和三级重心频率之间的频率范围(〈fc〉1~〈fc〉3, 4)作为频率衰减梯度的计算频段。根据一级重心和三级重心所对应的频率(〈fc〉1, 〈fc〉3, 4)和累积能量(E1, E2)计算频率衰减梯度。
| $ g=\frac{E_1-E_2}{\left\langle f_c\right\rangle_1-\left\langle f_c\right\rangle_{3, 4}} 。$ | (10) |
为了验证基于TPST计算频率衰减梯度的可行性和效果,采用部分Marmousi2模型数据进行模拟实验。如图 4所示,该模型数据包含了一个透镜状的含气砂岩(CDP 400~600之间的1.3~1.4 s处)。

|
图 4 部分Marmousi2模型数据 Fig. 4 Part of Marmousi2 model data |
比较式(6)和式(10)两种频率衰减梯度属性的差异,采用TPST时频分析方法(k=1.5, p=1.2, m=3)分别对部分Marmousi2模型数据剖面进行频率衰减梯度属性的提取,并对计算结果进行归一化处理。为了简化表示,将利用65%和85%累积能量的频率点计算频率衰减梯度的方法记为方法1;将利用信号多级重心计算频率衰减梯度的方法记为方法2。
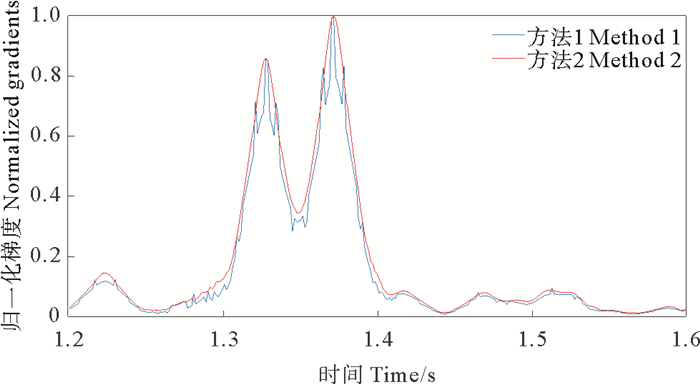
抽取图 4中红线位置处(CDP 500)的单道地震数据进行频率衰减梯度计算,结果如图 5所示。从图中可以看出,在含气区域,频率衰减梯度明显变大,这与Marmousi2模型的实际含气性情况一致。但方法1求取的频率衰减梯度曲线锯齿现象严重,而方法2求取的频率衰减梯度曲线较为光滑,有效消除了常规方法的锯齿现象。对比两种方法求取的率衰减梯度属性,可以看出信号的多级重心频率衰减梯度要比常规方法的更加精确,能更好地刻画储层。
|
图 5 基于TPST的单道频率衰减梯度计算对比 Fig. 5 The comparison of frequency attenuation gradients of single trace based on TPST |
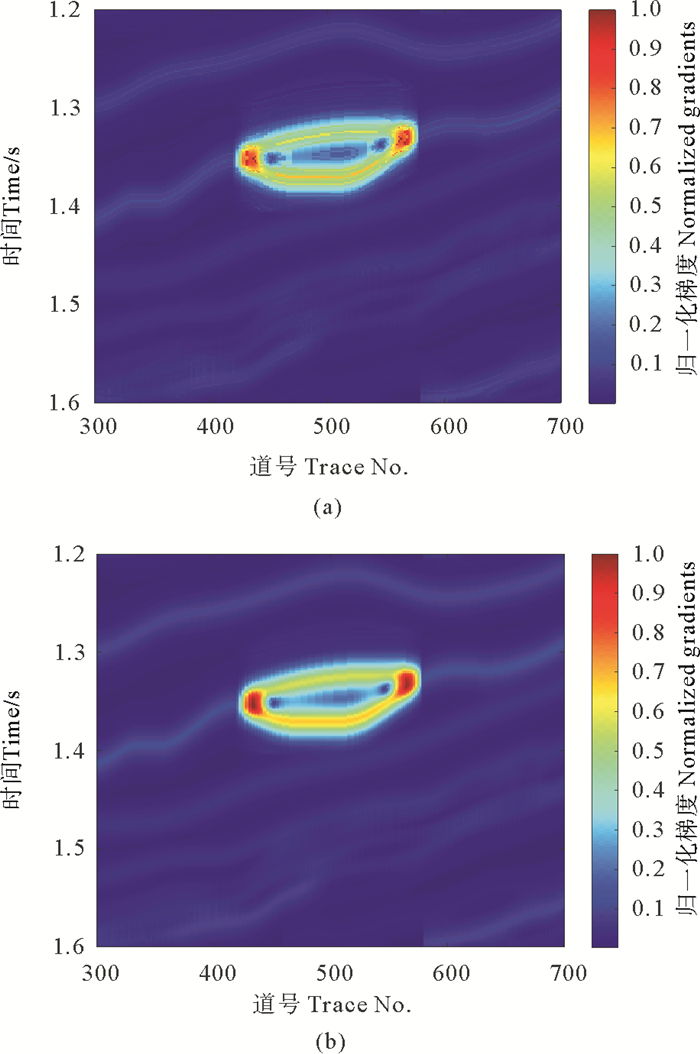
对整个模型剖面进行频率衰减梯度计算的结果如图 6所示,从图中可以看出,方法2多级重心频率衰减梯度属性(见图 6(b))比方法1求取的频率衰减梯度属性(见图 6(a))连续性和光滑性更好,与储层边界能更好地对应,因此多级重心频率衰减梯度属性更适合油气储层的识别。
|
((a)方法1; (b)方法2。(a) Method 1; (b) Method 2.) 图 6 部分Marmousi2模型数据的频率衰减梯度 Fig. 6 The frequency attenuation gradients of part of Marmousi2 model data |
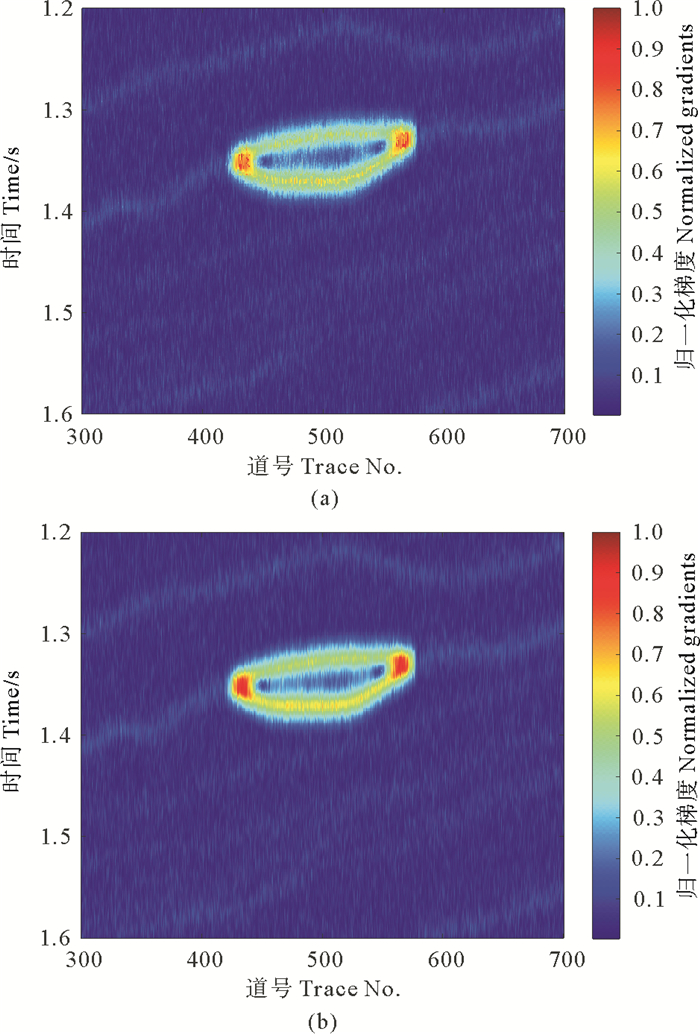
为进一步说明多级重心频率衰减梯度属性的稳定性,将图 4的部分Marmousi2模型数据添加SNR= 2 dB的高斯噪声,分别利用方法1和方法2求取模型数据的频率衰减梯度属性,结果如图 7所示。从图中可以看出,当存在噪声干扰时,方法2求取的频率衰减梯度属性仍然比方法1求取的频率衰减梯度属性清晰,连续性好。因此,多级重心频率衰减梯度属性具有很好的稳定性,比传统频率衰减梯度属性具有优势。
|
((a)方法1; (b)方法2。(a) Method 1; (b) Method.) 图 7 含噪剖面的频率衰减梯度 Fig. 7 The frequency attenuation gradients of part of Marmousi2 model data with noise |
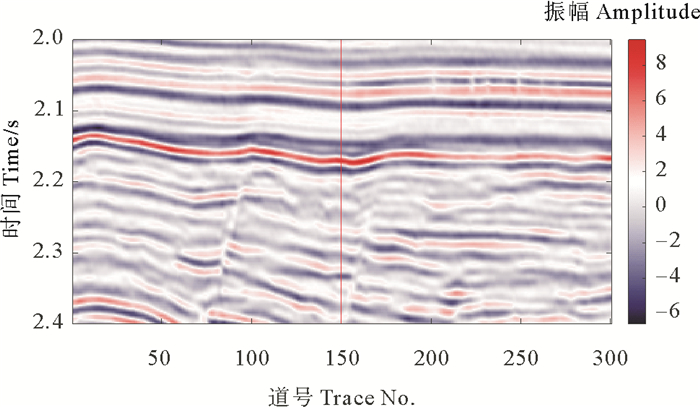
为进一步验证本文提出的基于TPST的多级重心频率衰减梯度属性的有效性,对南海某工区过井叠后地震剖面数据进行频率衰减属性计算。图 8为实际过井地震剖面,井位于CDP 150处,如图中红线所示。根据井资料得知该井在2.17 s附近存在油层,以辫状河三角洲砂体沉积为主,是潜在的含油气储层。为准确获得过井剖面的含油储层位置,采取的TPST时窗参数为(k=5, p=0.75, m=30)。
|
图 8 实际地震数据 Fig. 8 The field seismic data |
首先对过井道数据进行频率衰减梯度计算,结果如图 9所示。图 9(a)为过井道地震记录,图 9(b)—9(d)分别为TPST时频谱及基于TPST的频率衰减梯度。从时频谱上可以看出,井旁地震记录中主要频率成分为40 Hz,利用TPST得到的时频谱具有很好的能量聚集性和时频分辨率。对比图 9(c)和图 9(d)可以看出,在2.17 s附近,两种梯度属性均出现了大值异常,说明此处存在有利储层,但利用方法2提取的多级重心频率衰减梯度属性比方法1提取的频率衰减梯度曲线更平滑,峰值更突出(2.17 s附近),说明多级重心的引入使得频率衰减梯度属性的抗干扰性更强,能更真实地反映地下储层的含油气性分布。因此,基于TPST的多级重心频率衰减梯度属性在油气区域更敏感,能更好地刻画储层。

|
((a)过井道地震信号; (b)TPST时频谱; (c)方法1衰减梯度; (d) 方法2衰减梯度。(a) The seismic trace of crossing well; (b) The spectrum based on TPST; (c) The gradient using method 1; (d) The gradient using method 2.) 图 9 过井道地震数据时频谱及频率衰减梯度 Fig. 9 The spectrum and frequency attenuation gradients of seismic data crossing well |
图 10是整个地震剖面的频率衰减梯度属性提取结果,其中图 10(a)和图 10(b)分别是基于TPST的利用方法1和方法2提取的频率衰减梯度属性。图 10(c)和图 10(d)分别是基于STFT和CWT利用方法2求取的频率衰减梯度属性。从图中可以看出,在过井处四种方法提取的频率衰减梯度属性在2.17 s附近均显示频率衰减异常,表示有油气存在,与井的实际含油气情况吻合。对比图 10(a)—(d),基于STFT的多级重心频率衰减梯度属性(见图 10(c))横向连续性差,时间分辨率低;基于CWT的多级重心频率衰减梯度属性(见图 10(d))横向连续性和时间分辨率均有所改善,但精度均不如用基于TPST提取的频率衰减梯度属性;对比基于TPST提取的常规频率衰减梯度属性(见图 10(a))和多级重心频率衰减梯度属性(见图 10(b)),可以看出,基于TPST的多级重心频率衰减梯度属性横向连续性最好,对储层的边界刻画最清晰,具有比其他三种方法更高的精度和分辨率。

|
((a)基于TPST的方法1提取的属性; (b)基于TPST的方法2提取的属性; (c) 基于STFT的方法2提取的属性; (d) 基于CWT的方法2提取的属性。(a) Method 1 based on TPST; (b) Method 2 based on TPST; (c) Method 2 based on STFT; (d) Method 2 based on CWT.) 图 10 过井剖面的频率衰减梯度属性 Fig. 10 The frequency attenuation gradients of the crossing well profile |
地震波在地下介质中传播时的能量衰减是介质的内在属性,穿过含油气地层时尤为明显,可以利用地震波的衰减梯度属性进行储层含油气识别。精度高的时频分析方法有利于频率衰减梯度属性的提取。利用信号的多级重心求取频率衰减梯度值可以增加属性的稳定性。TPST参数选择更加灵活,可获得具有更高时频分辨率的时频谱,因此,本文提出一种基于TPST的多级重心频率衰减梯度属性。理论模型测试和实际数据应用表明,基于TPST的多级重心频率衰减梯度属性更加光滑和稳定,可更准确地展示储层特征与衰减属性的对应,可以更好地描述储层的能量衰减情况,为高精度储层含油气性检测提供了一种途径。由于TPST有三个参数可调,可以使之具有较高的时频分辨率,同时也带来一个最佳参数不容易调节的问题,下一步的工作应是在减少参数的前提下研究提高时频分辨率的方法。
| [1] |
Zhang Y, Wen X, Jiang L, et al. Prediction of high-quality reservoirs using the reservoir fluid mobility attribute computed from seismic data[J]. Journal of Petroleum Science and Engineering, 2020, 190: 107007. DOI:10.1016/j.petrol.2020.107007 (  0) 0) |
| [2] |
武迪, 宋维琪, 刘军, 等. 变分模态分解与包络导数算子结合的时频分析方法及溶洞储层预测[J]. 石油地球物理勘探, 2021, 56(2): 346-355. Wu D, Song W Q, Liu J, et al. Seismic time-frequency analysis based on VMD and envelope derivative operator for fractured-vuggy reservoir prediction[J]. Oil Geophysical Prospecting, 2021, 56(2): 346-355. (  0) 0) |
| [3] |
陈珊, 徐兴友, 罗晓玲, 等. 基于改进匹配追踪算法的时频属性在薄储层沉积微相研究中的应用[J]. 物探与化探, 2018, 42(5): 1006-1012. Chen S, Xu X Y, Luo X L, et al. Time-frequency attribute based on modified matching pursuit algorithm and its application to sedimentary microfacies of thin reservoir area[J]. Geophysical and Geochemical Exploration, 2018, 42(5): 1006-1012. (  0) 0) |
| [4] |
杨应, 杨巍, 朱仕军. 基于EEMD的高分辨率层序地层划分方法[J]. 岩性油气藏, 2018, 30(5): 59-67. Yang Y, Yang W, Zhu S J. Method for high-resolution sequence stratigraphy division based on Ensemble Empirical Mode Decomposition[J]. Lithologic Reservoirs, 2018, 30(5): 59-67. (  0) 0) |
| [5] |
Yuan S Y, Yang S, Wang T Y, et al. Inverse spectral decomposition using an lp-norm constraint for the detection of close geological anomalies[J]. Petroleum Science, 2020, 17(6): 1463-1477. DOI:10.1007/s12182-020-00490-6 (  0) 0) |
| [6] |
高静怀, 刘乃豪, 吕奇, 等. 薄互层型油气储层同步挤压变换域分析方法[J]. 石油物探, 2018, 57(4): 512-521. Gao J H, Liu N H, Lv Q, et al. Characterization of thin interbedded reservoir using synchrosqueezing transform[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 512-521. DOI:10.3969/j.issn.1000-1441.2018.04.003 (  0) 0) |
| [7] |
严海滔, 龚齐森, 周怀来, 等. 基于同步挤压改进短时傅里叶变换的谱分解应用[J]. 大庆石油地质与开发, 2019, 38(3): 122-131. Yan H T, Gong Q S, Zhou H L, et al. Application of the spectral decomposition based on the improved short-time Fourier transform by synchronous extrusion[J]. Progress in Geophysics, 2019, 38(3): 122-131. (  0) 0) |
| [8] |
张国印, 王志章, 林承焰, 等. 基于小波变换和卷积神经网络的地震储层预测方法及应用[J]. 中国石油大学学报(自然科学版), 2016, 55(4): 83-93. Zhang G Y, Wang Z Z, Lin C Y, et al. Seismic reservoir prediction method based on wavelet transform and convolutional neural network and its application[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016, 55(3): 433-440. (  0) 0) |
| [9] |
Wu L, Castagna J. S-transform and Fourier transform frequency spectra of broadband seismic signals[J]. Geophysics, 2017, 82(5): 71-81. (  0) 0) |
| [10] |
李思源, 徐天吉. 基于Wigner-Ville分布与Chrip-Z变换的高分辨时频分析方法[J]. 石油地球物理勘探, 2022, 57(1): 168-175. Li S Y, Xu T J. A new high-resolution time-frequency analysis method based on Wigner-Ville distribution and Chrip-Z transform[J]. Oil Geophysical Prospecting, 2022, 57(1): 168-175. (  0) 0) |
| [11] |
李雪英, 田亚军, 程云, 等. 基于仿射类平滑伪Wigner分布的厚度有序递变型薄互层时频特征分析[J]. 石油地球物理勘探, 2019, 54(5): 1094-1105. Li X Y, Tian Y J, Cheng Y, et al. Time-frequency characteristics analysis of orderly thickness-graded thin inter-beds based on affine smoothed pseudo-Wigner distribution[J]. Oil Geophysical Prospecting, 2019, 54(5): 1094-1105. (  0) 0) |
| [12] |
潘辉, 印兴耀, 李坤, 等. 基于经验模态分解字典的自适应匹配追踪谱分解方法及其在油气检测中的应用[J]. 石油地球物理勘探, 2021, 56(5): 1117-1129. Pan H, Yin X Y, LI K, et al. Spectral decomposition method of adaptive matching pursuit based on empirical mode decomposition dictionary and its application in oil and gas detection[J]. Oil Geophysical Prospecting, 2021, 56(5): 1117-1129. (  0) 0) |
| [13] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: The S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. (  0) 0) |
| [14] |
Mcfadden P D, Cook J G, Forster L M. Decomposition of gear vibration signals by the generalized S transform[J]. Mechanical Systems and Signal Processing, 1999, 13(5): 691-707. (  0) 0) |
| [15] |
高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析[J]. 地球物理学报, 2003(4): 526-532. GAO J H, CHEN W C, LI Y M, et al. Generalized s transform and seismic response analysis of thin interbeds[J]. Chinese Journal of Geophysics, 2003(4): 526-532. (  0) 0) |
| [16] |
陈学华, 贺振华, 黄德济. 基于广义S变换的地震资料高效时频谱分解[J]. 石油地球物理勘探, 2008(5): 530-534. Chen X H, He Z H, Huang D J. High-efficient time-frequency spectrum decomposition of seismic data based on generalized S transform[J]. Oil Geophysical Prospecting, 2008(5): 530-534. (  0) 0) |
| [17] |
Sejdié E, Djurovié I, Jiang J. A window width optimized S-transform[J]. EURASIP Journal on Advances in Signal Processing, 2008, 1-13. (  0) 0) |
| [18] |
Li D, Castagna J. Modified S-transform in Time-frequency Analysis of Seismic Data[C]. [s. 1. ]: SEG Technical Program Expanded Abstracts, 2013: 4629-4634.
(  0) 0) |
| [19] |
Li D, Castagna J, Goloshubin G. Investigation of generalized S-transform analysis windows for time-frequency analysis of seismic reflection data[J]. Geophysics, 2016, 81(3): 235-247. (  0) 0) |
| [20] |
Liu N, Gao J, Zhang B, et al. Time-frequency analysis of seismic data using a three parameters S transform[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(1): 142-146. (  0) 0) |
| [21] |
Mitchell J T, Derzhi N, Lichman E, et al. Energy Absorption Analysis: A Case Study[C]. [s. 1. ]: SEG Technical Program Expanded Abstracts, 1996: 1785-1788.
(  0) 0) |
| [22] |
毕研斌, 龙胜祥, 郭彤楼, 等. 应用频率衰减属性预测TNB地区储层含气性[J]. 石油与天然气地质, 2007(1): 116-120. Bi Y B, Long S X, Guo T L, et al. Prediction of gas distribution with frequency attenuation attribute in TNB area[J]. Oil & Gas Geology, 2007(1): 116-120. (  0) 0) |
| [23] |
张固澜, 贺振华, 李家金, 等. 基于广义S变换的吸收衰减梯度检测[J]. 石油地球物理勘探, 2011, 46(6): 905-910. Zhang G L, He Z H, Li J J, et al. Absorption attenuation gradient detection based on generalized S transform[J]. Oil Geophysical Prospecting, 2011, 46(6): 905-910. (  0) 0) |
| [24] |
熊晓军, 王飞, 米鸿, 等. 基于时频三参数小波变换的频率衰减梯度分析[J]. 石油地球物理勘探, 2015, 50(4): 699-705. Xiong X J, Wang F, Mi H, et al. Frequency attenuation analysis based on time-frequency three-parameter wavelet transform[J]. Oil Geophysical Prospecting, 2015, 50(4): 699-705. (  0) 0) |
| [25] |
李延, 文鹏飞, 张宝金, 等. 频率衰减梯度属性在南海北部神狐海域天然气水合物检测中的应用[J]. 海洋地质前沿, 2019, 35(7): 1-7. Li Y, Wen P F, Zhang B J, et al. Application of frequency attenuation gradient to gas hydrate prediction: A case from shenhu area, northern south China sea[J]. Marine Geology Frontiers, 2019, 35(7): 1-7. (  0) 0) |
| [26] |
潘晓, 曹思远, 徐彦凯, 等. 基于同步挤压小波变换的烃类识别技术[J]. 地球物理学报, 2020, 63(11): 4176-4187. Pan X, Cao S Y, Xu Y K, et al. The hydrocarbon detection technology based on synchrosqueezing wavelet transform[J]. Chinese Journal of Geophysics, 2020, 63(11): 4176-4187. (  0) 0) |
| [27] |
张会星, 何兵寿, 姜效典, 等. 利用地震波在双相介质中的衰减特性检测油气[J]. 石油地球物理勘探, 2010, 45(3): 343-349. Zhang H X, He B S, Jiang X D, et al. Utilizing attenuation characteristic of seismic wave in dual-phase medium to detect oil and gas[J]. Oil Geophysical Prospecting, 2010, 45(3): 343-349. (  0) 0) |
| [28] |
丁向辉, 李平, 孟晓辉. 结合信号重心与ASDF估计超声窄带信号时延[J]. 数据采集与处理, 2011, 26(6): 718-722. Ding X H, Li P, Meng X H. Time delay estimation using ASDF and center of gravity for narrowband ultrasonic signals[J]. Journal of Data Acquisition and Processing, 2011, 26(6): 718-722. (  0) 0) |
2. Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China
 2023, Vol. 53
2023, Vol. 53


