本文所提到的亚纯函数是指在整个复平面上的亚纯函数.设f与g是复平面内2个非常数的亚纯函数,并假定读者熟悉Nevanlinna理论的基本概念[1],例如T(r, f),m(r, f),N(r, f),(r, f)和δ(a, f)等。另外,本文用E⊂(0, ∞)表示线性测度有穷的集合,并且在本文中每次出现时可以不同。我们用S(r, f)表示满足S(r, f)=o(T(r, f))(r∉E, r→∞)的量。设a是1个有穷复数,如果f-a与g-a具有相同的零点且每个零点的重数相同,则称f与gCM分担a。如果f-a与g-a具有相同的零点且不考虑重数,则称f与gIM分担a。如果1/f与1/gCM分担0,则称f与gCM分担∞。如果1/f与1/gIM分担0,则称f与gIM分担∞[2]。我们称亚纯函数b为f的小函数,如果T(r, b)=S(r, f)。另外,我们用
| $ M\left[ f \right] = b{f^{{n_0}}}{\left( {f'} \right)^{{n_1}}} \cdots {\left( {{f^{\left( k \right)}}} \right)^{{n_k}}} $ |
和
| $ M\left( {z,f} \right) = bf{\left( z \right)^{{n_0}}}{\left( {f\left( {z + {\eta _1}} \right)} \right)^{{n_1}}} \cdots {\left( {f\left( {z + {\eta _k}} \right)} \right)^{{n_k}}} $ |
分别表示f的微分单项式和差分单项式,其中, b为f的小函数,n0, n1, …, nk是非负整数,η1, η2, …, ηk为k个相互判别的非零复常数,并用
| $ {\gamma _{M\left[ f \right]}} = {n_0} + {n_1} + \cdots + {n_k} $ |
和
| $ {\gamma _{M\left[ {z,f} \right]}} = {n_0} + {n_1} + \cdots + {n_k} $ |
分别表示M[f]和M(z, f)的次数,用
| $ {\Gamma _{M\left[ f \right]}} = {n_0} + 2{n_1} + \cdots + \left( {k + 1} \right){n_k} $ |
表示M[f]的权。假设,M1[f], M2[f], …, Ml[f]为f的l个微分单项式,则称
| $ P\left[ f \right] = {M_1}\left[ f \right] + {M_2}\left[ f \right] + \cdots + {M_l}\left[ f \right] $ |
是次数为
| $ \deg \left( {P\left[ f \right]} \right) = \max \left\{ {{\gamma _{{M_j}\left[ f \right]}}:1 \le j \le l} \right\}, $ |
权为
| $ {\Gamma _{P\left[ f \right]}} = \max \left\{ {{\Gamma _{{M_j}\left[ f \right]}}:1 \le j \le l} \right\} $ |
的微分多项式[3]。假设
| $ {M_1}\left( {z,f} \right),{M_2}\left( {z,f} \right) + \cdots + {M_l}\left( {z,f} \right) $ |
为f的l个差分单项式,则称
| $ P\left( {z,f} \right) = {M_1}\left( {z,f} \right) + {M_2}\left( {z,f} \right) + \cdots + {M_l}\left( {z,f} \right) $ |
是次数为
| $ \deg \left( {P\left( {z,f} \right)} \right) = \max \left\{ {{\gamma _{{M_j}\left( {z,f} \right)}}:1 \le j \le l} \right\} $ |
的差分多项式[4]。另外,本文还需要下述定义:
定义1[5] 设p是1个正整数,并且a∈C∪{∞}。以下用
| $ \begin{array}{l} {N_k}\left( {r,\frac{1}{{f - a}}} \right) = \bar N\left( {r,\frac{1}{{f - a}}} \right) + {{\bar N}_{\left( 2 \right.}}\left( {f,\frac{1}{{f - a}}} \right) + \\ \cdots + {{\bar N}_{\left( k \right.}}\left( {r,\frac{1}{{f - a}}} \right)。\end{array} $ |
并定义
| $ {\delta _k}\left( {a,f} \right) = 1 - \mathop {\lim }\limits_{r \to \infty } \sup \frac{{{N_k}\left( {r,\frac{1}{f}} \right)}}{{T\left( {r,f} \right)}}。$ |
显然
| $ \begin{array}{l} 0 \le {\delta _k}\left( {a,f} \right) \le {\delta _{k - 1}}\left( {a,f} \right) \le \cdots \le {\delta _2}\left( {a,f} \right) \le \\ {\delta _1}\left( {a,f} \right) = \Theta \left( {a,f} \right) \le 1。\end{array} $ |
1959年,Hayman[6]开始了亚纯函数的微分多项式的值分布理论的研究,证明了下述定理:
定理A[6] 假设f是1个非常数的整函数,n≥3是1个正整数,a≠0是1个复常数,那么f′-afn取任意1个有限值无穷多次。
后来,杨重骏[7]在一定条件下研究了1类更一般的微分多项式的值分布问题,证明了下述定理:
定理B[7] 假设f是1个非常数的亚纯函数,且满足
| $ N\left( {r,f} \right) + N\left( {r,\frac{1}{f}} \right) = S\left( {r,f} \right)。$ | (1) |
再设
| $ \mathit{\Psi }\left( f \right) = \sum {b{f^{{l_0}}}{{\left( {f'} \right)}^{{l_1}}} \cdots {{\left( {{f^{\left( k \right)}}} \right)}^{{l_k}}}} $ |
是1个次数为n的微分多项式,其中Ψ(f)的每一项的次数l0+l1+…+lk≥2,并且Ψ(f)不是关于f的齐次微分多项式,那么对任意有穷复数a,我们有
| $ \delta \left( {a,\mathit{\Psi }} \right) \le 1 - \frac{1}{{2n}}。$ |
近几年来,Halburd-Korhone-Tohge[8]及冯绍继与蒋翼迈[9]分别独立地建立了差分Nevanlinna理论,Laine-Yang[10]得到了涉及差分多项式的Clunie引理。应用这些理论,一些芬兰学者和中国学者开始了差分多项式的值分布理论的研究[10]和差分唯一性理论的研究[11]。
2007年,Laine-Yang[12]证明了下述定理:
定理C[12] 假设f是1个非常数的亚纯函数,并且其增长级满足ρ(f)=ρ<∞。如果
| $ N\left( {r,f} \right) + N\left( {r,\frac{1}{f}} \right) = O\left( {{r^{\rho - 1}}} \right) + S\left( {r,f} \right), $ |
那么
| $ N\left( {r,\frac{1}{G}} \right) \ne O\left( {{r^{\rho - 1}}} \right) + S\left( {r,f} \right), $ |
这里
| $ G\left( z \right) = \sum\limits_{\lambda \in J} {{b_\lambda }\left( z \right)} \prod\limits_{j = 1}^{{\tau _\lambda }} {f{{\left( {z + {\delta _{\lambda ,j}}} \right)}^{{\mu _{\lambda ,j}}}}} $ |
是关于f(z)及其移动算子的差分多项式,其次数deg(G)=n为正整数,δλ, j为复常数,并且至少有1个δλ, j不等于零。
本文将利用差分Nevanlinna理论,研究1类差分多项式的值分布问题,证明了下述定理,该定理推广了定理C。
定理1 设f是1个超级小于1的非常数的亚纯函数,满足(1),设
| $ \begin{array}{l} \mathit{\Psi }\left( {f\left( z \right)} \right) = \sum {b\left( z \right)f{{\left( z \right)}^{{l_0}}}{{\left( {f\left( {z + {\eta _1}} \right)} \right)}^{{l_1}}} \cdots } \\ {\left( {f\left( {z + {\eta _k}} \right)} \right)^{{l_k}}} \end{array} $ |
是关于f的1个次数为n的差分多项式,其中,η1, η2, …, ηk是k个判别的有限非零复常数,再设Ψ(f)是每一项的系数为f的小函数的差分多项式,并且Ψ(f)的每一项的次数l0+l1+…+lk≥2。若Ψ(f)不是关于f的齐次差分多项式,那么对任意的有限复值a,有
1997年,Lahiri[13]提出了下述问题:
问题1[13] 如果2个非常数的亚纯函数的非线性微分多项式CM分担1,那么这2个亚纯函数的关系如何?
1997年,Yang-Hua[14]研究了问题1,证明了下述定理:
定理D[14] 假设f与g是2个非常数的亚纯函数,n是1个正整数且满足n≥11。如果fnf′与fnf′CM分担1,那么f与g满足下述2种情形之一:
(ⅰ) f=tg, 其中t是一个常数,且满足tn=1;
(ⅱ) f=c1ecz, g=c2e-cz, 其中,c, c1和c2是非零常数,且满足(c1c2)n+1c2=-1。
2002年,方明亮[15]在整函数条件下研究了问题1,证明了下述定理:
定理E[15] 假设f与g是2个非常数的整函数,n, k是2个正整数且满足n≥2k+8。如果(fn(f-1))(k)与(gn(g-1))(k)CM分担1,那么f=g。
本文继续研究问题1,证明下述定理:
定理2 假设f和g是2个非常数的亚纯函数,且满足(1)和
| $ N\left( {r,g} \right) + N\left( {r,\frac{1}{g}} \right) = S\left( {r,g} \right)。$ | (2) |
再设
| $ {\mathit{\Psi }_1}\left( f \right) = {f^n}\left( {{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right), $ |
其中,P1[f]和P2[f]是关于f的微分多项式,使得Ψ1(f)为关于f的非齐次微分多项式,其中n是正整数且满足
| $ n > \deg \left( {{P_1}\left[ f \right]} \right) > \deg \left( {{P_2}\left[ f \right]} \right), $ |
这里deg(P1[f])和deg(P2[f]分别表示P1[f]和P2[f]的次数。如果Ψ1(f)与Ψ1(g)CM分担1,那么f=tg,其中t是1个常数,且满足tn+deg(P1(f))=1。
应用定理2的证明方法,由引理1和引理2可得下述定理:
定理3 假设f和g是2个有穷级非常数的亚纯函数,且满足(1)和(2)。再设
| $ {\mathit{\Psi }_2}\left( {f\left( z \right)} \right) = f{\left( z \right)^n}\left( {{P_1}\left( {z,f} \right) + {P_2}\left( {z,f} \right)} \right) $ |
是关于f的非齐次差分多项式,其中P1(z, f)和P2(z, f)是2个差分多项式,且满足
| $ n > \deg \left( {{P_1}\left( {z,f} \right)} \right) > \deg \left( {{P_2}\left( {z,f} \right)} \right), $ |
这里deg(P1(z, f))和deg(P2(z, f))分别表示P1(z, f)和P2(z, f)的次数。如果Ψ2(f)与Ψ2(g)CM分担1,那么f=tg,其中t是1个常数,且满足tn+deg(P1(z, f))=1。
由定理3可得下述推论:
推论1 假设f是1个非常数的有穷级亚纯函数,且满足(1)。再设
| $ {\mathit{\Psi }_2}\left( f \right) = f{\left( z \right)^n}\left( {{P_1}\left( {z,f} \right) + {P_2}\left( {z,f} \right)} \right) $ |
是关于f的非齐次差分多项式,其中P1(z, f)和P2(z, f)是2个差分多项式,且满足
| $ n > \deg \left( {{P_1}\left( {z,f} \right)} \right) > \deg \left( {{P_2}\left( {z,f} \right)} \right), $ |
这里deg(P1(z, f))和deg(P2(z, f))分别表示P1(z, f)和P2(z, f)的次数。如果Ψ2(f(z))与Ψ2(f(z+η))CM分担1,其中η是一个非零复常数,那么f(z)=tf(z+η),这里t是1个常数,且满足tn+deg(P1(z, f))=1。
1 几个引理引理1[8] 设f是1个非常数的亚纯函数,且η是一个非零复数。若f是有穷级,则对任意ε>0,存在一个线性测度有穷的集合
| $ E = E\left( {f,\varepsilon } \right) \subset \left( {0,\infty } \right), $ |
满足
| $ \mathop {\lim }\limits_{r \to \infty } \sup \frac{{\int_{EI\left[ {1,r} \right)} {\frac{{{\rm{d}}t}}{t}} }}{{\log r}} \le \varepsilon , $ |
即E的对数密度至多为ε,使得当r→∞, r∉E时,有
| $ m\left( {r,\frac{{f\left( {z + c} \right)}}{{f\left( z \right)}}} \right) = O\left( {\frac{{\log r}}{r}T\left( {r,f} \right)} \right)。$ |
若f的超级
| $ ϛ\left( f \right) = \mathop {\lim }\limits_{r \to \infty } \sup \frac{{\log \log T\left( {r,f} \right)}}{{\log r}} = \zeta < 1, $ |
则对任意ε>0,使得当r→∞, r∉E时,有
| $ m\left( {r,\frac{{f\left( {z + c} \right)}}{{f\left( z \right)}}} \right) = o\left( {\frac{{T\left( {r,f} \right)}}{{{r^{1 - ϛ - \varepsilon }}}}} \right)。$ |
其中,E是一个对数测度有穷的集合。
引理2[8] 设T:[0, +∞)→[0, +∞)是1个非减的连续函数,s∈[0, +∞)。若T的超级小于1,即
| $ \mathop {\lim }\limits_{r \to \infty } \sup \frac{{\log \log T\left( r \right)}}{{\log r}} = ϛ < 1, $ |
则对任意δ∈(0, 1-ς),有
| $ T\left( {r + s} \right) = T\left( r \right) + o\left( {\frac{{T\left( r \right)}}{{{r^\delta }}}} \right)\left( {r \to \infty ,r \notin E} \right), $ |
其中,E是一个对数测度有穷的集合。
引理3[7] 假设
| $ P\left( f \right) = {b_n}{f^n} + {b_{n - 1}}{f^{n - 1}} + \cdots + {b_2}{f^2} + {b_1}f + {b_0}, $ | (3) |
其中,f是1个超越亚纯函数,b0, b1, …, bn是n+1个亚纯函数,并且满足bn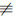
| $ T\left( {r,{b_j}} \right) = S\left( {r,f} \right),0 \le j \le n, $ |
则
| $ T\left( {r,P\left( f \right)} \right) = nT\left( {r,f} \right) + S\left( {r,f} \right)。$ |
引理4[1] 设f是1个超越亚纯函数,且fnP(f)=Q(f),其中,P(f)和Q(f)是f的微分多项式。如果Q(f)的次数≤n,则m(r, P(f))=S(r, f)。
注:当P(f)和Q(f)的系数b满足m(r, b)=S(r, f)时,引理4的结论也成立[1]。
引理5[14] 假设F与G是2个非常数的亚纯函数,并且F与GCM分担1,那么下述情形之一成立:
(ⅰ) T(r,f)≤N2(r,f)+N2(r,G)+
(ⅱ) FG=1;
(ⅲ) F=G。
引理6[16] 假设f是1个非常数的亚纯函数,再设
| $ {\mathit{\Psi }_3}\left( f \right) = {a_n}{f^n} + {a_{n - 1}}{f^{n - 1}} + \cdots + {a_1}f + {a_0} $ |
是关于f的n≥1次多项式,其中,an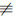
如果
| $ \bar N\left( {r,\frac{1}{{{\mathit{\Psi }_3}\left( f \right)}}} \right) + \bar N\left( {r,f} \right) = S\left( {r,f} \right), $ |
那么
| $ {\mathit{\Psi }_3}\left( f \right) = {a_n}{\left( {f + \frac{{{a_{n - 1}}}}{{n{a_n}}}} \right)^n}。$ |
定理1的证明:由于
| $ f\left( {z + {\eta _j}} \right) = \frac{{f\left( {z + {\eta _j}} \right)}}{{f\left( z \right)}} \cdot f\left( z \right)\left( {j = 1,2, \cdots ,k} \right), $ |
所以
| $ \begin{array}{l} \mathit{\Psi }\left( {f\left( z \right)} \right) = \sum {b\left( z \right)f{{\left( z \right)}^{{l_0}}}{{\left( {f\left( {z + {\eta _1}} \right)} \right)}^{{l_1}}} \cdots } \\ {\left( {f\left( {z + {\eta _k}} \right)} \right)^{{l_k}}} \end{array} $ |
转化成关于f的微分多项式如下:
| $ \begin{array}{l} \mathit{\Psi }\left( {f\left( z \right)} \right) = \sum {b\left( z \right)f{{\left( z \right)}^{{l_0}}}{{\left( {\frac{{f\left( {z + {\eta _1}} \right)}}{{f\left( z \right)}} \cdot f\left( z \right)} \right)}^{{l_1}}} \cdot } \\ \cdots \cdot {\left( {\frac{{f\left( {z + {\eta _k}} \right)}}{{f\left( z \right)}} \cdot f\left( z \right)} \right)^{{l_k}}} = \sum {\hat b\left( z \right)f{{\left( z \right)}^{{l_0} + {l_1} + {\rm{L + }}{l_k}}}} , \end{array} $ | (4) |
其中,
| $ \hat b\left( z \right) = b\left( z \right)\prod\limits_{j = 1}^k {\frac{{f\left( {z + {\eta _j}} \right)}}{{f\left( z \right)}}} 。$ | (5) |
由于Ψ(f)是非齐次的,且每一项的次数至少是2,因此
| $ \mathit{\Psi }\left( f \right) = {{\hat b}_n}{f^n} + {{\hat b}_{n - 1}}{f^{n - 1}} + \cdots + {{\hat b}_2}{f^2}。$ | (6) |
由引理1,对于j=1, 2, …, k,当r→∞, r∉E时,有
| $ m\left( {r,\frac{{f\left( {z + {\eta _j}} \right)}}{{f\left( z \right)}}} \right) = o\left( {\frac{{T\left( {r,f} \right)}}{{{r^{1 - ϛ - \varepsilon }}}}} \right)。$ | (7) |
由引理2,对于j=1, 2, …, k,当r→∞, r∉E时,有
| $ \begin{array}{*{20}{c}} {N\left( {r,\frac{{f\left( {z + {\eta _j}} \right)}}{{f\left( z \right)}}} \right) \le N\left( {r,\frac{1}{{f\left( z \right)}}} \right) + }\\ {N\left( {r,f\left( {z + {\eta _j}} \right)} \right) \le N\left( {r,\frac{1}{{f\left( z \right)}}} \right) + N\left( {r,f\left( z \right)} \right) + }\\ {o\left( {\frac{{N\left( {r,f\left( z \right)} \right)}}{{{r^\delta }}}} \right) = o\left( {\frac{{N\left( {r,f\left( z \right)} \right)}}{{{r^\delta }}}} \right) + S\left( {r,f} \right)。} \end{array} $ | (8) |
因此
| $ T\left( {r,\frac{{f\left( {z + {\eta _j}} \right)}}{{f\left( z \right)}}} \right) = o\left( {T\left( {r,f} \right)} \right),\left( {r \to \infty ,r \notin E} \right)。$ | (9) |
于是对于i=2, 3, …, n,有
| $ T\left( {r,{{\hat b}_i}} \right) = S\left( {r,f} \right)\left( {r \to \infty ,r \notin E} \right)。$ | (10) |
往证:Ψ(f)退化成单项式,从而与定理假设矛盾。事实上,现在假设Ψ(f)是项数大于等于2的多项式,则对于i≠j,一定有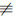
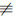
| $ \mathit{\Psi }\left( f \right) = {{\hat b}_k}{f^k} + {{\hat b}_{k - 1}}{f^{k - 1}} + \cdots + {{\hat b}_2}{f^2}。$ | (11) |
对任意有限复值a,设
| $ g = \frac{{\mathit{\Psi }\left( f \right) - a}}{{{{\hat b}_k}}} $ | (12) |
和
| $ f = H - \frac{1}{k}\frac{{{{\hat b}_{k - 1}}}}{{{{\hat b}_k}}}。$ | (13) |
将(13)代入(11),并结合(12),可得
| $ g = {H^k} + {T_{k - 2}}\left( H \right), $ | (14) |
其中,Tk-2(H)是H的1个微分多项式,且其次数至多是k-2。由(14)两边求导可得
| $ g' = k{H^{k - 1}}H' + {\left( {{T_{k - 2}}\left( H \right)} \right)^\prime }。$ | (15) |
(15) 两边同时乘以
| $ {H^{k - 1}}\left( {kH' - \frac{{g'}}{g}H} \right) = {P_{k - 2}}\left( H \right), $ | (16) |
其中,Pk-2(H)是H和H′的1个微分多项式,其次数至多是k-2,系数a满足m(r, a)=S(r, f)。
在引理4中分别令
| $ P\left( f \right) \equiv kH' - \frac{{g'}}{g}H $ |
和
| $ P\left( f \right) \equiv H\left( {kH' - \frac{{g'}}{g}H} \right), $ |
由引理4的结论可得
| $ m\left( {r,kH' - \frac{{g'}}{g}H} \right) = S\left( {r,f} \right) $ | (17) |
和
| $ m\left( {r,H\left( {kH' - \frac{{g'}}{g}H} \right)} \right) = S\left( {r,f} \right)。$ | (18) |
从而
| $ \begin{array}{l} T\left( {r,kH' - \frac{{g'}}{g}H} \right) = m\left( {r,kH' - \frac{{g'}}{g}H} \right) + \\ N\left( {r,kH' - \frac{{g'}}{g}H} \right) \le \bar N\left( {r,\frac{1}{g}} \right) + N\left( {r,f} \right) + S\left( {r,f} \right) = \\ \bar N\left( {r,\frac{1}{g}} \right) + S\left( {r,f} \right)。\end{array} $ | (19) |
同理
| $ T\left( {r,H\left( {kH' - \frac{{g'}}{g}H} \right)} \right) \le \bar N\left( {r,\frac{1}{g}} \right) + S\left( {r,f} \right)。$ | (20) |
以下用反证法完成定理1的证明。
假设
| $ \delta \left( {a,\mathit{\Psi }\left( f \right)} \right) > 1 - \frac{1}{{2n}}, $ | (21) |
则由(12)可知
| $ \delta \left( {0,g} \right) > 1 - \frac{1}{{2n}}。$ | (22) |
往证:
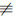
| $ \begin{array}{*{20}{c}} {T\left( {r,H} \right) \le T\left( {r,H\left( {kH' - \frac{{g'}}{g}H} \right)} \right) + }\\ {T\left( {r,\frac{1}{{kH' - \frac{{g'}}{g}H}}} \right) \le 2\bar N\left( {r,\frac{1}{g}} \right) + S\left( {r,f} \right)。} \end{array} $ | (23) |
另一方面,由(21)得
| $ \mathop {\lim }\limits_{r \to \infty } \sup \frac{{N\left( {r,\frac{1}{g}} \right)}}{{T\left( {r,g} \right)}} < \frac{1}{{2n}}。$ | (24) |
(23) 两边同时乘以k,可得
| $ kT\left( {r,H} \right) \le 2k\bar N\left( {r,\frac{1}{g}} \right) + S\left( {r,f} \right), $ | (25) |
因此
| $ \frac{1}{{2k}} \le \mathop {\lim }\limits_{r \to \infty } \sup \frac{{N\left( {r,\frac{1}{g}} \right)}}{{kT\left( {r,H} \right)}}。$ | (26) |
由(14)和引理3可得
| $ T\left( {r,g} \right) = kT\left( {r,H} \right) + S\left( {r,H} \right), $ |
因此
| $ \frac{1}{{2k}} \le \mathop {\lim }\limits_{r \to \infty } \sup \frac{{N\left( {r,\frac{1}{g}} \right)}}{{T\left( {r,g} \right)}}。$ | (27) |
由(24)与(27)可得矛盾。
于是
| $ kH' - \frac{{g'}}{g}H = 0, $ | (28) |
所以
| $ g\left( z \right) = c{\left( {H\left( z \right)} \right)^k}, $ | (29) |
其中,c为常数。于是(14)变为
| $ \left( {1 - c} \right){H^k} + {T_{k - 2}}\left( H \right) = 0。$ | (30) |
以下分两种情形讨论:
情形1 假设c≠1,由引理4可得
| $ m\left( {r,\left( {1 - c} \right)H} \right) = S\left( {r,H} \right)。$ | (31) |
由于
| $ \begin{array}{l} N\left( {r,\left( {1 - c} \right)H} \right) \le N\left( {r,f} \right) + \\ S\left( {r,f} \right) \le S\left( {r,f} \right), \end{array} $ | (32) |
所以
| $ T\left( {r,\left( {1 - c} \right)H} \right) = S\left( {r,f} \right)。$ | (33) |
由(13)和(33)可得矛盾。
情形2 假设c=1。首先设
| $ g\left( z \right) = {H^k}\left( z \right)。$ | (34) |
由(12)和(13),
| $ g = \frac{{\mathit{\Psi }\left( f \right) - a}}{{{{\hat b}_k}}} = {\left( {f + \frac{1}{k}\frac{{{{\hat b}_{k - 1}}}}{{{{\hat b}_k}}}} \right)^k}, $ | (35) |
即
| $ \mathit{\Psi }\left( f \right) - a - {{\hat b}_k}{\left( {f + \frac{1}{k}\frac{{{{\hat b}_{k - 1}}}}{{{{\hat b}_k}}}} \right)^k} = 0。$ | (36) |
由于(36)左边是1个形如引理3中形如(3)的系数是小函数的f的多项式, 因此
| $ {\left( {\frac{1}{k}\frac{{{{\hat b}_{k - 1}}}}{{{{\hat b}_k}}}} \right)^{k - 1}} = 0。$ | (37) |
和
| $ {{\hat b}_k}{\left( {\frac{1}{k}\frac{{{{\hat b}_{k - 1}}}}{{{{\hat b}_k}}}} \right)^k} = a。$ | (38) |
于是
定理2的证明:首先由(1),(2)和
| $ {\mathit{\Psi }_1}\left( f \right) = {f^n}\left( {{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right) $ |
可得
| $ \begin{array}{l} {N_2}\left( {r,{\mathit{\Psi }_1}\left( f \right)} \right) \le 2\bar N\left( {r,f} \right) + \\ S\left( {r,f} \right) = S\left( {r,f} \right) \end{array} $ | (39) |
和
| $ {N_2}\left( {r,{\mathit{\Psi }_1}\left( g \right)} \right) = s\left( {r,g} \right)。$ | (40) |
再由条件
| $ {\mathit{\Psi }_1}\left( f \right) = {f^n}\left( {{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right), $ |
n>deg(P1[f])>deg(P2[f]),条件(1)和引理3可得
| $ \begin{array}{l} {N_2}\left( {r,\frac{1}{{{\mathit{\Psi }_1}\left( f \right)}}} \right) \le 2\bar N\left( {r,\frac{1}{f}} \right) + \\ N\left( {r,\frac{1}{{{P_1}\left[ f \right] + {P_2}\left[ f \right]}}} \right) \le T\left( {r,{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right) + \\ S\left( {r,f} \right) \le m\left( {r,{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right) + S\left( {r,f} \right) = \\ \deg \left( {{P_1}\left[ f \right]} \right)m\left( {r,f} \right) + S\left( {r,f} \right)。\end{array} $ | (41) |
同理,由(2)可得
| $ {N_2}\left( {r,\frac{1}{{{\mathit{\Psi }_1}\left( g \right)}}} \right) \le \deg \left( {{P_1}\left[ g \right]} \right)m\left( {r,g} \right) + S\left( {r,g} \right)。$ | (42) |
由(1),(2)和引理3可得
| $ \begin{array}{l} T\left( {r,{\mathit{\Psi }_1}\left( f \right)} \right) = T\left( {r,{f^n}\left( {{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right)} \right) = \\ m\left( {r,{f^n}\left( {{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right)} \right) + N\left( {r,{f^n}\left( {{P_1}\left[ f \right] + } \right.} \right.\\ \left. {\left. {{P_2}\left[ f \right]} \right)} \right) = \left( {n + \deg \left( {{P_1}\left[ f \right]} \right)} \right)m\left( {r,f} \right) + S\left( {r,f} \right)。\end{array} $ | (43) |
和
| $ T\left( {r,{\mathit{\Psi }_1}\left( f \right)} \right) = \left( {n + \deg \left( {{P_1}\left[ g \right]} \right)} \right)m\left( {r,g} \right) + S\left( {r,g} \right)。$ | (44) |
由引理5,以下分3种情形讨论:
情形1 假设Ψ1(f)Ψ1g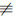
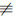
| $ \begin{array}{l} T\left( {r,{\mathit{\Psi }_1}\left( f \right)} \right) + T\left( {r,{\mathit{\Psi }_1}\left( g \right)} \right) \le \\ 2{N_2}\left( {r,{\mathit{\Psi }_1}\left( f \right)} \right) + 2{N_2}\left( {r,{\mathit{\Psi }_1}\left( g \right)} \right) + 2{N_2}\\ \left( {r,\frac{1}{{{\mathit{\Psi }_1}\left( f \right)}}} \right) + 2{N_2}\left( {r,\frac{1}{{{\mathit{\Psi }_1}\left( g \right)}}} \right) + S\left( {r,{\mathit{\Psi }_1}\left( f \right)} \right) + S\left( {r,{\mathit{\Psi }_1}\left( g \right)} \right)。\end{array} $ | (45) |
由于deg(P1[f])=deg(P1[g]),由(39)~(45)可知
| $ \begin{array}{l} \left( {n + \deg \left( {{P_1}\left[ f \right]} \right)} \right)\left( {m\left( {r,f} \right) + } \right.\\ \left. {m\left( {r,g} \right)} \right)2\deg \left( {{P_1}\left[ g \right]} \right)m\left( {r,f} \right) + \\ 2\deg \left( {{P_1}\left[ f \right]} \right)m\left( {r,g} \right) + S\left( {r,f} \right) + \\ S\left( {r,g} \right) = 2\deg \left( {{P_1}\left[ f \right]} \right)\left( {m\left( {r,f} \right)} \right) + \left. {m\left( {r,g} \right)} \right) + \\ S\left( {r,f} \right) + S\left( {r,g} \right), \end{array} $ | (46) |
由此可得n≤deg(P1[f]),这与条件n>deg(P1[f])矛盾。
情形2 假设Ψ1(f)Ψ1(g)=1,那么
| $ \left( {{f^n}\left( {{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right)} \right)\left( {{g^n}\left( {{P_1}\left[ g \right] + {P_2}\left[ g \right]} \right)} \right) = 1。$ | (47) |
由(47)和(2)可知
| $ \begin{array}{l} N\left( {r,\frac{1}{{{f^n}\left( {{P_1}\left[ g \right] + {P_2}\left[ g \right]} \right)}}} \right) = \\ N\left( {r,{g^n}\left( {{P_1}\left[ g \right] + {P_2}\left[ g \right]} \right)} \right) \le \\ \left( {n + {\Gamma _{{P_1}\left[ f \right]}} + {\Gamma _{{P_2}\left[ f \right]}}} \right)N\left( {r,g} \right) = S\left( {r,g} \right)。\end{array} $ | (48) |
再由Ψ1(f)Ψ1(g)=1可知,Ψ1(f)与Ψ1(g)CM分担1和-1,结合(1)和(2)可得
| $ \begin{array}{l} \left( {n + \deg \left( {{P_1}\left[ f \right]} \right)} \right)m\left( {r,f} \right) = \\ \left( {n + \deg \left( {{P_1}\left[ f \right]} \right)} \right)T\left( {r,f} \right) + S\left( {r,f} \right) = \\ T\left( {r,{\mathit{\Psi }_1}\left( f \right)} \right) + S\left( {r,f} \right) \le \bar N\left( {r,{\mathit{\Psi }_1}\left( f \right)} \right) + \\ \bar N\left( {r,\frac{1}{{{\mathit{\Psi }_1}\left( f \right) - 1}}} \right) + \bar N\left( {r,\frac{1}{{{\mathit{\Psi }_1}\left( f \right) + 1}}} \right) + \\ S\left( {r,f} \right) \le \bar N\left( {r,\frac{1}{{{\mathit{\Psi }_1}\left( g \right) - 1}}} \right) + \bar N\left( {r,\frac{1}{{{\mathit{\Psi }_1}\left( g \right) + 1}}} \right) + \\ S\left( {r,f} \right) \le 2T\left( {r,{\mathit{\Psi }_1}\left( g \right)} \right) + S\left( {r,f} \right) = 2m\left( {r,{\mathit{\Psi }_1}\left( g \right)} \right) + \\ S\left( {r,f} \right) + S\left( {r,g} \right) = 2\left( {n + \deg \left( {{P_1}\left[ g \right]} \right)} \right)T\left( {r,g} \right) + \\ S\left( {r,f} \right) + S\left( {r,g} \right)。\end{array} $ | (49) |
和
| $ \begin{array}{l} \left( {n + \deg \left( {{P_1}\left[ g \right]} \right)} \right)T\left( {r,g} \right) + S\left( {r,g} \right) = \\ T\left( {r,{\mathit{\Psi }_1}\left( g \right)} \right) + S\left( {r,g} \right) \le 2\left( {n + } \right.\\ \left. {\deg \left( {{P_1}\left[ f \right]} \right)} \right)T\left( {r,f} \right) + S\left( {r,f} \right) + S\left( {r,g} \right)。\end{array} $ | (50) |
由(49)和(50)可得S(r, g)=S(r, f),结合(1)和(48)可得
| $ N\left( {r,f} \right) + N\left( {r,\frac{1}{{f{{\left( z \right)}^n}\left( {{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right)}}} \right) = S\left( {r,f} \right)。$ | (51) |
和
| $ {P_1}\left[ f \right] + {P_2}\left[ f \right] = {a_{{n_1}}}{f^{{n_1}}} + {a_{{n_1} - 1}}{f^{{n_1} - 1}} + \cdots + {a_0}, $ | (52) |
其中
| $ \deg \left( {{P_1}\left[ f \right]} \right) = {n_1} \ge 1。$ |
由(1)和(52)可知an1, an1-1, …, a1, a0的特征函数满足T(r, aj)=S(r, f), 0≤j≤n1。
由(51),(52)和引理6可得
| $ {P_1}\left[ f \right] + {P_2}\left[ f \right] = {a_n}{\left( {f + \frac{{{a_{{n_1} - 1}}}}{{{n_1}{a_{{n_1}}}}}} \right)^{{n_1}}}。$ | (53) |
注意到P1[f]+P2[f]不是关于f的齐次微分多项式,由(53)可知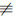
| $ N\left( {r,1/\left( {f + {a_{{n_1} - 1}}/\left( {{n_1}{a_{{n_1}}}} \right)} \right)} \right) = S\left( {r,f} \right)。$ | (54) |
由(1),(54)和三密度不等式[2]可得
| $ \begin{array}{l} T\left( {r,f} \right) \le N\left( {r,f} \right) + N\left( {r,1/f} \right) + \\ N\left( {r,1/\left( {f + {a_{{n_1} - 1}}/\left( {{n_1}{a_{{n_1}}}} \right)} \right)} \right) = S\left( {r,f} \right), \end{array} $ |
该式表明f是1个常数,这是不可能的。
情形3 假设Ψ1(f)=Ψ1(g),
则有
| $ {f^n}\left( {{P_1}\left[ f \right] + {P_2}\left[ f \right]} \right) = {g^n}\left( {{P_1}\left[ g \right] + {P_2}\left[ g \right]} \right)。$ | (55) |
设(52),则由(52)和(55)可得
| $ \begin{array}{*{20}{c}} {{a_{{n_1}}}\left( z \right)\left( {1 - {{\left( {\frac{{g\left( z \right)}}{{f\left( z \right)}}} \right)}^{n + {n_1}}}} \right)f{{\left( z \right)}^{n + {n_1}}} + }\\ {{a_{{n_1} - 1}}\left( z \right)\left( {1 - {{\left( {\frac{{g\left( z \right)}}{{f\left( z \right)}}} \right)}^{n + {n_1} - 1}}} \right)f{{\left( z \right)}^{n + {n_1} - 1}} + \cdots + }\\ {{a_1}\left( z \right)\left( {1 - {{\left( {\frac{{g\left( z \right)}}{{f\left( z \right)}}} \right)}^{n + 1}}} \right)f{{\left( z \right)}^{n + 1}} + }\\ {{a_0}\left( z \right)\left( {1 - {{\left( {\frac{{g\left( z \right)}}{{f\left( z \right)}}} \right)}^n}} \right)f{{\left( z \right)}^n} = 0。} \end{array} $ | (56) |
类似于情形2可得(49)和(50)。再由(1),(2),(49)和(50)可得
| $ T\left( {r,{a_j}\left( z \right)\left( {1 - {{\left( {\frac{{g\left( z \right)}}{{f\left( z \right)}}} \right)}^{n + j}}} \right)} \right) = S\left( {r,f} \right),0 \le j \le {n_1}。$ |
由(56)和引理3可得
| [1] |
Hayman W K. Meromorphic Functions[M]. Oxford: The Claredon, 1964.
(  0) 0) |
| [2] |
仪洪勋, 杨重骏. 亚纯函数的唯一性理论[M]. 北京: 科学出版社, 1995. Yi H X, Yang C C. Uniqueness Theory of Meromorphic Functions[M]. Beijing: Science Press, 1995. (  0) 0) |
| [3] |
Yi H X. On a Theorem of Tumura and Clunie for a Differential Polynomial[J]. Bull London Math Soc, 1988, 20(6): 593-596. DOI:10.1112/blms/20.6.593
(  0) 0) |
| [4] |
Laine I, Yang C C. Value distribution of difference polynomials[J]. Proc Japan Acad Ser A Math Sci, 2007, 83(8): 148-151.
(  0) 0) |
| [5] |
Lahiri I. Weighted sharing of three values and uniqueness of meromorphic functions[J]. Kodai Math J, 2001, 24(3): 421-435. DOI:10.2996/kmj/1106168813
(  0) 0) |
| [6] |
Hayman W K. Picard values of meromorphic functions and their derivatives[J]. Ann Math, 1959, 70(2): 9-42.
(  0) 0) |
| [7] |
Yang C C. On deficiencies of differential polynomials Ⅱ[J]. Math Z, 1972, 125(2): 107-112. DOI:10.1007/BF01110921
(  0) 0) |
| [8] |
Halburd R, Korhonen R, Tohge K. Holomorphic curves with shift-invariant hyperplane preimages[J]. Trans Amer Math Soc, 2014, 366: 4267-4298. DOI:10.1090/tran/2014-366-08
(  0) 0) |
| [9] |
Chiang Y M, Feng S J. On the Nevanlinna characteristic of f(z+η) and difference equations in the complex plane[J]. Ramanujan J, 2008, 16: 105-129. DOI:10.1007/s11139-007-9101-1
(  0) 0) |
| [10] |
Laine I, Yang C C. Clunie theorems for difference and q-difference polynomials[J]. J London Math Soc, 2007, 76: 556-566. DOI:10.1112/jlms/jdm073
(  0) 0) |
| [11] |
Heittokangas J, Korhonen R, Laine I, et al. Value sharing results for shifts of meromorphic functions and sufficient conditions for periodicity[J]. J Math Anal Appl, 2009, 355: 352-363. DOI:10.1016/j.jmaa.2009.01.053
(  0) 0) |
| [12] |
Laine I, Yang C C. Value distribution of difference polynomials[J]. Proc Japan Acad Ser A Math Sci, 2007, 83(8): 148-151. DOI:10.3792/pjaa.83.148
(  0) 0) |
| [13] |
Lahiri I. Uniqueness of meromorphic functions as governed by their differential polynomials[J]. Yokohama Math J, 1997, 44: 147-156.
(  0) 0) |
| [14] |
Yang C C, Hua X H. Uniqueness and value-sharing of meromorphic functions[J]. Ann Acad Sci Fenn Math, 1997, 22: 95-406.
(  0) 0) |
| [15] |
Fang M L. Uniqueness and value sharing of entire functions[J]. Comput Math Appl, 2002, 44: 823-831. DOI:10.1016/S0898-1221(02)00194-3
(  0) 0) |
| [16] |
Mues E, Steinmetz N. The theorem of Tumura-Clunie for meromorphic functions[J]. J London Math Soc, 1981, 23(2): 113-122.
(  0) 0) |
 2019, Vol. 49
2019, Vol. 49

