2. 中国海洋石油湛江分公司, 广东 湛江 524057;
3. 中国海洋大学海洋地球科学学院, 山东 青岛 266100;
4. 中国海洋大学海底科学与探测技术教育部重点实验室, 山东 青岛 266100;
5. 中海油服物探事业部特普公司, 广东 湛江 524057
三维地震勘探工区位于珠三拗陷中部文昌A凹陷,主要发育文昌组、恩平组两套四种类型的烃源岩[1],并具有中新统珠江组海相砂岩储集层与海侵泥岩盖层[2],从而形成良好的生、储、盖成藏组合。该区域还发育一系列背斜、断背斜及断块构造等圈闭[1],构成了“下生上储,陆生海储”的古近-新近系含油气系统及油气聚集区。文昌A凹陷低压构造脊带呈北东向展布,形成了多个局部构造,其中存在低幅度小背斜和异常体。该区三维地震资料分别为三个年度采集,部分年度的数据质量差、信噪比低,导致常规地震处理结果为圈闭落实、有利目标评价带来极大困难。
在海洋地震勘探中,需将震源和检波器放置于海平面以下一定深度。气枪震源激发的能量其中一部分直接向上传播到海面,然后发生反射并向地下深部传播,遇到地下界面再反射回来被电缆检波器所接收,形成尾随于一次反射波之后的震源鬼波;与此类似,震源激发后能量向下传播,遇到地下界面后反射回海面,再发生下行反射后被电缆检波器所接收,同样会形成位于一次反射波之后的电缆鬼波[3]。由于鬼波的波形、频率、视速度等均与一次反射波接近,其不但导致地震资料出现陷频,还造成地震资料出现多轴、多相位现象,从而严重影响局部构造解释——尤其会误导针对低幅度小背斜、异常体的识别分析。
为了实现鬼波的压制处理,进而获得具有较宽频带的地震资料,国内外的地球物理学家提出了联合反褶积鬼波压制[4-7]、基于格林定理的鬼波压制[8-13]以及基于逆散射级数法的鬼波压制[14-17]等多类方法。上述各类方法中,联合反褶积具有明显的效率优势,当虚反射与一次波时差较小(譬如海上常规拖缆地震)时,若能够求出较为准确的虚反射时间延迟量,可获得理想的鬼波压制效果。在频率——空间域联合反褶积鬼波压制方法[18-19]的基础上,Wang等[20-21]提出了在F-K域、τ-p域进行的联合反褶积鬼波压制算法,将入射角引入到鬼波延迟时估算而减小了误差,从而在实际地震处理中获得了更优的效果。
在浅水区域文昌A凹陷的三维地震资料鬼波压制中,由于边缆的纵向偏移距较大,相应单缆记录的二维τ-p变换结果出现了严重的空间假频,致使基于二维τ-p变换的鬼波剔除遇到了困难。为此,本文实现了基于三维τ-p变换的鬼波压制技术,然后对工区三个年度的三维地震资料进行了鬼波压制处理,其最终偏移数据体中紧随一次波信号的鬼波同相轴旁瓣得到明显压制,地层反射更加清晰、信噪比显著提高,从而验证了三维τ-p域鬼波压制技术的有效性。
1 三维τ-p域鬼波压制的基本原理τ-p域鬼波压制方法首先将偏移距域地震数据变换到τ-p域,即实现地震数据的平面波分解,然后对每个平面波分量进行鬼波压制。若已知震源(或检波器)沉放深度与海水的地震波速,鬼波延迟时可视为波场入射(或出射)角度的函数。因此,在τ-p域可根据射线参数(水平慢度)p估计出具有不同入射(或出射)角度平面波分量的鬼波延迟时,据此实现震源(或检波器)鬼波的精准压制。
1.1 三维τ-p变换的基本原理三维离散空间——时间域的τ-p正、反变换的计算公式[22]分别为
| $ \left\{ {\begin{array}{*{20}{l}} {u({p_x},{p_y},\tau ) = \sum\limits_x {\sum\limits_y d } (x,y,t = \tau + {p_x}x + {p_y}y)}\\ {{d^\prime }(x,y,t) = \sum\limits_{px} {\sum\limits_{py} u } ({p_x},{p_y},\tau = t - {p_x}x - {p_y}y)} \end{array}} \right.。$ | (1) |
式中:d(x, y, t)为偏移距域数据;u(px, py, τ)为τ-p变换的结果;d′(x, y, t)为τ-p反变换的地震记录;t为双程旅行时,τ为双程零偏移距旅行时;x、y分别为x、y方向的偏移距;px、py分别为x、y方向的射线参数(水平慢度)。
为了保证τ-p变换过程的稳定性,令输入记录d(x, y, t)与反变换结果d′(x, y, t)的误差平方和最小,从而导出频率域的最小平方三维τ-p正、反变换的表达式[23-24]:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}} = {{({\mathit{\boldsymbol{L}}^{{\rm{T*}}}}\mathit{\boldsymbol{L}} + \beta \mathit{\boldsymbol{I}})}^{ - 1}}{\mathit{\boldsymbol{L}}^{{\rm{T*}}}}d}\\ {{\mathit{\boldsymbol{d}}^\prime } = \mathit{\boldsymbol{Lu}}} \end{array}} \right.。$ | (2) |
式中:d、u分别表示偏移距域、(2)τ-p域的单频数据矩阵;d′为τ-p反变换的结果;β为常数,I表示单位矩阵;上标T表示矩阵转置;*表示复共轭。
根据偏移距信息(x, y)与射线参数(px, py)确定复矩阵L,即
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{L}} = \\ \left| {\begin{array}{*{20}{c}} {{e^{ - i\omega (p_x^1{x_1} + p_y^1{y_1})}}}&{{e^{ - i\omega (p_x^2{x_1} + p_y^2{y_1})}}}& \cdots &{{e^{ - i\omega (p_x^n{x_1} + p_y^n{y_1})}}}\\ {{e^{ - i\omega (p_x^1{x_2} + p_y^1{y_2})}}}&{{e^{ - i\omega (p_x^2{x_2} + p_y^2{y_2})}}}& \cdots &{{e^{ - i\omega (p_x^n{x_2} + p_y^n{y_2})}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{e^{ - i\omega (p_x^1{x_m} + p_y^1{y_m})}}}&{{e^{ - i\omega (p_x^2{x_m} + p_y^2{y_m})}}}& \cdots &{{e^{ - i\omega (p_x^n{x_m} + p_y^n{y_m})}}} \end{array}} \right| \end{array}。$ | (3) |
式中:ω表示角频率;(x1, y1)、(x2, y2)、…、(xm, ym)表示各道数据在X、Y方向的偏移距;m为输入道数;(px1, py1)、(px2, py2)、…、(pxn, pyn)表示τ-p域各道数据的射线参数;n为τ-p域数据的道数。
在公式(2)中,复矩阵LT*为L的共轭转置矩阵,因此有
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{L}}^{{\rm{T}} * }} = \\ \left| {\begin{array}{*{20}{c}} {{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^1{{\rm{x}}_1} + {\rm{p}}_{\rm{y}}^1{{\rm{y}}_1})}}}&{{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^1{{\rm{x}}_2} + {\rm{p}}_{\rm{y}}^1{{\rm{y}}_2})}}}& \cdots &{{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^1{x_{\rm{m}}} + {\rm{p}}_{\rm{y}}^1{{\rm{y}}_{\rm{m}}})}}}\\ {{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^2{{\rm{x}}_1} + {\rm{p}}_{\rm{y}}^2{{\rm{y}}_1})}}}&{{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^2{{\rm{x}}_2} + {\rm{p}}_{\rm{y}}^2{{\rm{y}}_2})}}}& \cdots &{{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^2{x_{\rm{m}}} + {\rm{p}}_{\rm{y}}^2{{\rm{y}}_{\rm{m}}})}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^{\rm{n}}{{\rm{x}}_{\rm{1}}} + {\rm{p}}_{\rm{y}}^{\rm{n}}{{\rm{y}}_{\rm{1}}})}}}&{{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^{\rm{n}}{{\rm{x}}_{\rm{m}}} + {\rm{p}}_{\rm{y}}^{\rm{n}}{{\rm{y}}_{\rm{m}}})}}}& \cdots &{{e^{ - {\rm{i \mathsf{ ω} }}({\rm{p}}_{\rm{x}}^{\rm{n}}{x_{\rm{m}}} + {\rm{p}}_{\rm{y}}^{\rm{n}}{{\rm{y}}_{\rm{m}}})}}} \end{array}} \right| \end{array}。$ | (4) |
对于三维τ-p变换而言,由于射线参数P(px, py)的规模极为庞大,而输入记录与待求解的τ-p域数据中均存在大量零值,因此利用公式中第1个方程求取u的过程属于大规模稀疏矩阵的线性方程组求解问题,通常采用共轭梯度法进行迭代计算。
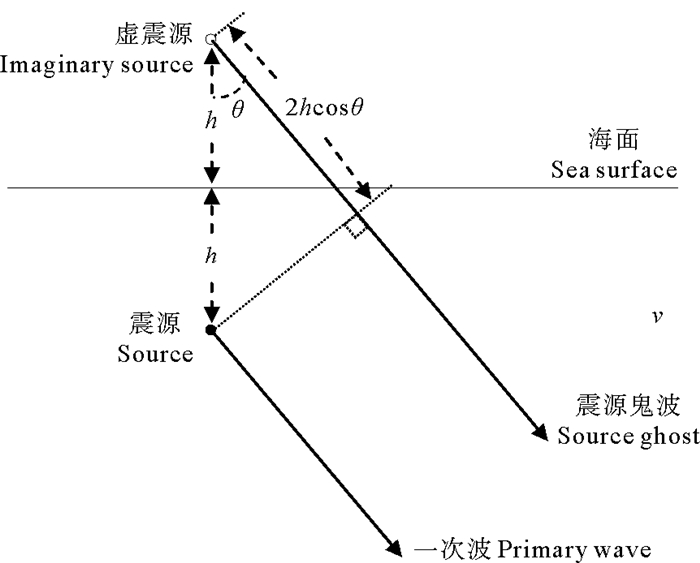
1.2 基于三维τ-p变换的鬼波压制在假设地震波的传播满足平面波的前提条件下,鬼波延迟时Δt(鬼波与一次波的旅行时差)仅与震源(或拖缆检波器)沉放深度、地震波入射(或出射)角度有关。在图 1所示一次波与鬼波的传播过程示意图中,设震源的沉放深度为h,平面波的入射(或出射)角度为θ,则鬼波的延迟时Δt为
| $ \Delta t = \frac{{2h{\kern 1pt} {\kern 1pt} {\rm{cos}}\theta }}{v}。$ | (5) |
|
图 1 平面波假设条件下的震源鬼波传播过程示意图 Fig. 1 Schematic diagram of the propagation of source ghost under the assumption of plane wave |
式中:h为震源(或拖缆检波器)深度;v为地震波在水中传播的速度。
在τ-p域中,射线参数p与地震波入射(或出射)角度θ存在以下关系
| $ p = \frac{{{\rm{sin}}\theta }}{v}。$ | (6) |
将式(6)代入到式(5)中,可得
| $ \Delta t = \frac{{2h\sqrt {1 - {p^2}{v^2}} }}{v}。$ | (7) |
在三维情况下,射线参数p可表示为
| $ p = \sqrt {{{({p_x})}^2} + {{({p_y})}^2}}。$ | (8) |
因此,三维情况下的鬼波延迟时Δt为
| $ \Delta t = \frac{{2h\sqrt {1 - [{{({p_x})}^2} + {{({p_y})}^2}]{v^2}} }}{v}。$ | (9) |
根据波场延拓理论,鬼波可视为一次波波场在海面发生下行反射所形成的下行波场,即
| $ g({p_x},{p_y},\omega ) = R({p_x},{p_y},\omega ){u^\prime }({p_x},{p_y},\omega ){e^{ - i\omega \Delta t}}。$ | (10) |
式中,g表示下行的鬼波波场;u′表示一次波波场;R为鬼波入射到平界面的反射系数,可基于Zoeppritz方程组予以求解,由于海面为自由界面,R通常取-1。因此,总波场u为
| $ \begin{array}{*{20}{l}} {u({p_x},{p_y},\omega ) = {u^\prime }({p_x},{p_y},\omega ) + g({p_x},{p_y},\omega ) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {u^\prime }({p_x},{p_y},\omega ) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R({p_x},{p_y},\omega ){u^\prime }({p_x},{p_y},\omega ){e^{ - i\omega \Delta t}}}。\end{array} $ | (11) |
利用式可求出一次波波场,即消除鬼波后的结果
| $ {u^\prime }({p_x},{p_y},\omega ) = \frac{{u({p_x},{p_y},\omega )}}{{1 + R({p_x},{p_y},\omega ){e^{ - i\omega \Delta t}}}}。$ | (12) |
为简便起见,通常利用鬼波算子G来描述形成鬼波的波场延拓过程,即
| $ G({p_x},{p_y},\omega ) = 1 + R({p_x},{p_y},\omega ){e^{ - i\omega \Delta t}}。$ | (13) |
因此,式(12)所描述的鬼波压制过程可简单地表示为
| $ {u^\prime }({p_x},{p_y},\omega ) = \frac{{u({p_x},{p_y},\omega )}}{{G({p_x},{p_y},\omega ) + \varepsilon }}。$ | (14) |
其中ε为保证分母不为0的阻尼因子。
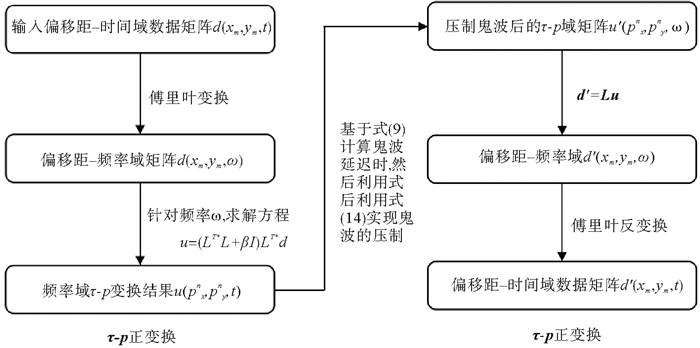
图 2展示了鬼波压制的详细流程,主要包括以下步骤:
|
图 2 τ-p域鬼波压制流程图 Fig. 2 The processing flow chart of τ-p domain deghosting |
① 将包含多缆数据的三维炮集记录由时间域变换到频率域,针对每个频率成分ω解方程u=(LT*L+βI)·LT*d(见公式(2)),即可获得频率域的τ-p域记录。
② 根据每一组射线参数(pxi, pyi)利用公式(9)计算相应平面波分量的鬼波延迟时Δti,据此构建鬼波算子,然后通过公式(14)实现鬼波压制。
③ 基于τ-p反变换将压制鬼波后的频率域记录u′(pxn, pyn, ω)变换回偏移距域。
2 文昌A凹陷区域三维鬼波压制分析目标工区具有三个时期采集的地震数据,其采集时间分别为1997、2006和2014年,且野外观测参数具有明显差异(见表 1)。为了获得较优的成像效果,需要基于工区内的三批数据进行地震联片处理。
|
|
表 1 与鬼波压制有关的野外采集参数 Table 1 Acquisition parameters are related of deghosting |
输入衰减多次波后的炮记录,基于图 2所示的处理流程进行鬼波压制。为保证三维τ-p变换的精度,需采用较大的px、py值范围与较小的px、py值间隔,通常根据主要反射同相轴在最大偏移距道中的时移量γ来描述τ-p变换参数:
| $ \begin{array}{*{20}{c}} {X{\rm{(主测线)方向 }}:\gamma _x^{{\rm{min}}} = - 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 000{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ms}},}\\ \ \ \ \ {\gamma _x^{{\rm{max}}} = 4{\kern 1pt} {\kern 1pt} {\kern 1pt} 000{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ms}},d{\gamma _x} = 4{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ms}}}\\ {{\rm{ }}Y{\rm{(联络测线)方向 }}:\gamma _y^{{\rm{min}}} = - 160{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ms}},}\\ \ \ \ \ {\gamma _y^{{\rm{max}}} = 160{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ms}},d{\gamma _y} = 8{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ms}}}。\end{array} $ |
其中,γx、γy分别为反射同相轴在X、Y方向最大偏移距道中的最大时移量,据此可求出射线参数p。
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {p_x} = \frac{{{\gamma _x}}}{{{x_{{\rm{max}}}}}},}\\ {{p_y} = \frac{{{\gamma _y}}}{{{y_{{\rm{max}}}}}}}。\end{array} $ | (15) |
因此,根据表 1中的野外观测参数可计算出px、py的范围与间隔。此外,在基于公式(14)进行鬼波压制时,为保证公式中分母不为0,设阻尼因子ε为0.01。
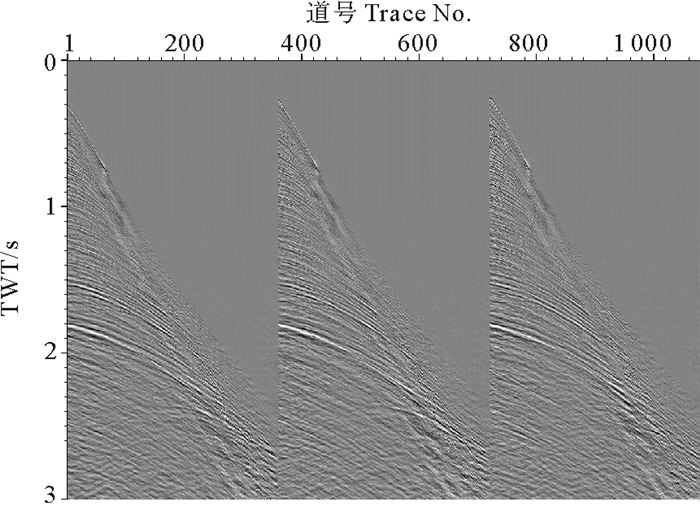
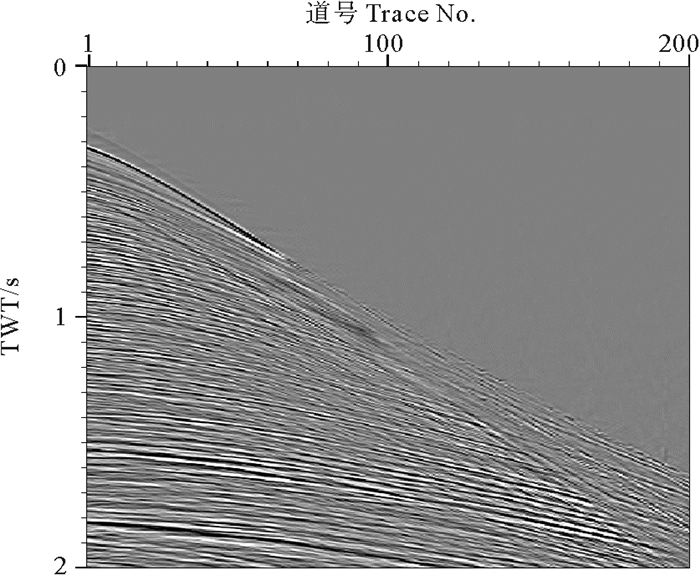
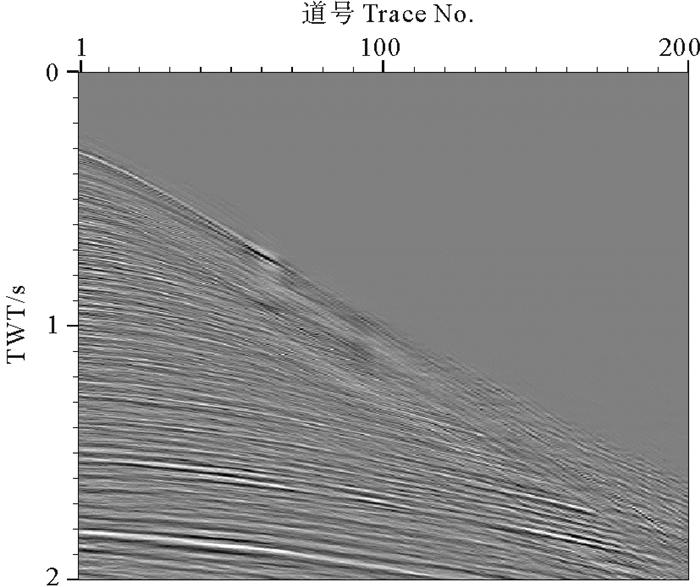
采用上述参数进行三维τ-p域的鬼波压制处理,图 2、3分别展示了鬼波压制前、后的一组炮集记录对比。为清晰起见,对图 3、4中所示数据的局部记录(道号范围:1~200,时间范围:0~2 s)进行放大显示,分别见图 5、6。通过对比可知,输入炮记录中紧随一次波信号的鬼波旁瓣得到明显压制,地震数据的信噪比显著提高。抽取同震源炮集的第11道与第101道组成共检波器道集,压制鬼波前、后的共检波器道集分别如图 7、8所示,因震源鬼波与检波器鬼波叠加所形成的同相轴旁瓣已被去除,两剖面中的强反射同相轴处于“反相”状态,并且由原来的多相位变成单相位。创建图 7、8所示道集的自相关谱,所得结果分别如图 9、10所示,其中箭头指向的一次波与鬼波旁瓣相关所形成的能量已被完全消除。

|
( 2006年采集,1~3缆。Acquisition in 2006, 1~3 Cable. ) 图 3 鬼波压制前的炮集记录示例 Fig. 3 Shot record before deghosting |
|
( 2006年采集,1~3缆。Acquisition in 2006, 1~3 Cable. ) 图 4 鬼波压制后的炮集记录示例 Fig. 4 Shot record after deghosting |
|
(道号范围:1~200,时窗范围:0~2 s。Trace number: 1~200, Time window: 0~2 s. ) 图 5 图 3所示记录的局部放大显示 Fig. 5 Enlarged part of the record as shown in Fig. 3 |
|
(道号范围:1~200,时窗范围:0~2 s。Trace number: 1~200, Time window: 0~2 s. ) 图 6 图 4所示记录的局部放大显示 Fig. 6 Enlarged part of the record as shown in Fig. 4 |

|
图 7 压制鬼波前的共检波器道集 Fig. 7 Common receiver gathers before deghosting |

|
图 8 压制鬼波后的共检波器道集 Fig. 8 Common receiver gathers after deghosting |

|
图 9 压制鬼波前共检波器道集的自相关谱 Fig. 9 Autocorrelation spectrum of commonreceiver gathers before deghosting |

|
图 10 压制鬼波后共检波器道集的自相关谱 Fig. 10 Autocorrelation spectrum of commonreceiver gathers after deghosting |
图 11、12展示了压制鬼波前、后的叠前时间偏移剖面。在原始成像剖面中,时差较小的鬼波信号尾随于一次波之后,且叠加在一起形成了同相轴旁瓣,导致剖面中的反射层位处于多相位状态,这对后续的解释分析是非常不利的。在图 12所示去除鬼波的偏移剖面中,紧随一次波信号的鬼波旁瓣得到明显压制,地层反射更加清晰,中深层低频能量增强,信噪比显著提高。

|
图 11 鬼波压制前的偏移剖面示例 Fig. 11 Example of the migration profile before deghosting |

|
图 12 鬼波压制后的偏移剖面示例 Fig. 12 Example of the migration profile after deghosting |
本文首先实现了基于三维τ-p变换的鬼波压制技术,并对浅水区文昌A凹陷工区进行了鬼波压制处理,其最终偏移数据体中紧随一次波信号的鬼波旁瓣得到明显压制,地下反射界面更加清晰、信噪比显著提高,从而证明了三维τ-p域鬼波压制技术的有效性。
| [1] |
尤丽, 李才, 张迎朝, 等. 珠江口盆地文昌A凹陷珠海组储层碳酸盐胶结物分布规律及成因机制[J]. 石油与天然气地质, 2012, 33(6): 883-890. You Li, Li Cai, Zhng Yingzhao, et al. Distribution and genetic mechanism of carbonate cements in the Zhuhai Formation reservoirs in Wenchang-A sag, Pear River Mouth Basin[J]. Oil & Gas Geology, 2012, 33(6): 883-890. (  0) 0) |
| [2] |
王柯, 张洋, 黄胜兵, 等. 文昌A凹陷地温-地压系统与油气成藏的关系[J]. 特种油气藏, 2017, 24(2): 63-68. Wang K, Zhang Y, Huang S B, et al. Geothermal-geopressure system in the Wenchang A sag and its relationship with hydrocarbon Accumulation[J]. Special Oil and Gas Reservoir, 2017, 24(2): 63-68. DOI:10.3969/j.issn.1006-6535.2017.02.012 (  0) 0) |
| [3] |
陈宝书, 陶杰, 李松康, 等. 基于确定性子波处理的鬼波压制方法[J]. 中国海上油气, 2017, 29(1): 39-45. Chen B S, Tao J, Li S K, et al. Deghosting method based on deterministic wavelet processing[J]. China Offshore Oil and Gas, 2017, 29(1): 39-45. (  0) 0) |
| [4] |
Lindsey J P. Elimination of seismic ghost reflections by means of a linear filter[J]. Geophysics, 1960, 25(1): 130-140.
(  0) 0) |
| [5] |
Schneider W A, Larner K L, Burg J P, et al. A new data processing technique for the elimination of ghost arrivals on reflection seismograms[J]. Geophysics, 1964, 29(5): 783-805. DOI:10.1190/1.1439419
(  0) 0) |
| [6] |
Dushan B J. Ghosting and marine signature deconvolution: A prerequisite for detailed seismic interpretation[J]. Geophysics, 1983, 48(11): 1468-1485. DOI:10.1190/1.1441431
(  0) 0) |
| [7] |
Ghosh S K. Deconvolving the ghost effect of water surface in marine seismics[J]. Geophysics, 2000, 65(6): 1831-1836. DOI:10.1190/1.1444866
(  0) 0) |
| [8] |
Weglein A B, Shaw S A, Matson K H, et al. New Approaches to Deghosting Towed-Streamer and Ocean-Bottom Pressure Measurements[C].[s.1.]: 72nd SEG Abstract, 2002: 1016-1019.
(  0) 0) |
| [9] |
Zhang J F, Weglein A B. Application of Extinction Theorem Deghosting Methodon Ocean Bottom Data[C]. [s.1.]: 76th SEG Expanded Abstracts, 2006: 2674-2678.
(  0) 0) |
| [10] |
Adriana C R, Weglein A B. The Role of the Direct Wave and green's theorem in Seismic Interferometry and Spurious Multiples[C].[s.1.]: 77th SEG Expanded Abstracts, 2007: 2471-2475.
(  0) 0) |
| [11] |
Adriana C R, Weglein A B. Deriving, Explicating, and Extending Interferometric Methods Using Green's Theorem[C].[s.1.]: 78th SEG Expanded Abstracts, 2008: 2917-2921.
(  0) 0) |
| [12] |
Adriana C R, Weglein A B. Green's theorem as a comprehensive framework for data reconstruction, regularization, wavefield separation, seismic interferometry, and wavelet estimation: A tutorial[J]. Geophysics, 2009, 74(6): 35-62.
(  0) 0) |
| [13] |
James D M, Weglein A B. First application of Green's theorem derived source and receiver deghosting on deep water Gulf of Mexico synthetic (SEAM) and field data[J]. Geophysics, 2013, 78(2): WA77-WA89.
(  0) 0) |
| [14] |
Weglein A B, Gasparotto F A, Carvalho P M, et al. An inverse-scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298
(  0) 0) |
| [15] |
Weglein A B, Araujo F V, Carvalho P M, et al. Inverse scattering series and seismic exploration[J]. Inverse Problems, 2003, 19(6): R27-R83. DOI:10.1088/0266-5611/19/6/R01
(  0) 0) |
| [16] |
Ikelle L T. Using even terms of the scattering series for deghosting and multiple attenuation of ocean-bottom cable data[J]. Geophysics, 1999, 64(2): 579-592. DOI:10.1190/1.1444565
(  0) 0) |
| [17] |
王芳芳, 李景叶, 陈小宏. 基于逆散射级数法的鬼波压制方法[J]. 地球物理学报, 2013, 56(5): 1628-1636. Wang F F, Li J Y, Chen X H. Deghosting method based on inverse scattering series[J]. Chinese J Geophys, 2013, 56(5): 1628-1636. (  0) 0) |
| [18] |
Aytun K. The footsteps of the receiver ghost in the f-k domain[J]. Geophysics, 1999, 64(5): 1618-1626. DOI:10.1190/1.1444666
(  0) 0) |
| [19] |
Fang Y F. The method of eliminating marine seismic ghost reflections in f-k domain[J]. World Geology, 1999, 18(1): 75-77.
(  0) 0) |
| [20] |
Wang P, Peng C. Premigration Deghosting for Marine Towed Streamer Data Using a Bootstrap Approach[C]. [s.1.]: 82th SEG Expanded Abstracts, 2012: 1-5.
(  0) 0) |
| [21] |
Wang P, Ray S, Peng C, et al. Premigration Deghosting for Marine Streamer Data Using a Bootstrap Approach in Tau-p Domain[C]. [s.1.]: 83th SEG Expanded Abstracts, 2013: 4221-4225.
(  0) 0) |
| [22] |
Wang P, Nimsaila K. Fast Progressive Sparse Tau-P Transform for Regularization of Spatially Aiased Seismic Data[C]. [s.1.]: 84th SEG Expanded Abstracts, 2014: 3589-3593.
(  0) 0) |
| [23] |
Thorson J R, Claerbout J F. Velocity-stack and slant-stack stochastic inversion[J]. Geophysics, 1985, 50(12): 2727-2741. DOI:10.1190/1.1441893
(  0) 0) |
| [24] |
Hampson D. Inverse velocity stacking for multiple elimination[J]. Journal of the Canadian Society of Exploration Geophysicists, 1986, 22(1): 44-55.
(  0) 0) |
2. China National Offshore Oil Corporation, Zhanjiang Company Limited, Zhanjiang 524057, China;
3. College of Marine Geosciences, Ocean University of China, Qingdao 266100, China;
4. The Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Ocean University of China, Qingdao 266100, China;
5. Data Processing Company of Geophysical-China Oilfield Services Limited, Zhanjiang 524057, China
 2020, Vol. 50
2020, Vol. 50


