2. 中国海洋大学山东省海洋工程重点实验室,山东 青岛 266100
波浪滑翔机是一种海洋无人航行器,通过将波浪垂荡转化为航行器的前进动力,实现长时间、远距离的自主巡航和海上观测作业,具有续航长、零排放、经济性等明显优势。当前波浪滑翔机在海洋科学考察、渔业资源调查、国防安全等多个领域得到了应用,取得了较好的应用效果[1-2]。
国内外学者对波浪滑翔机进行了大量研究。在系统动力学建模方面,Kraus等[3-4]提出了一种用于波浪滑翔机位置估算的二维简化动力学模型,并基于船舶空间运动的建模方法将模型进一步拓展到了六自由度。Wang等[5]运用牛顿-欧拉法建立了波浪滑翔机在不规则波中的四自由度动力学模型,探讨了各运动参数对浪流的敏感性。Tian等[6-7]结合D-H法与拉格朗日法,给出了波浪滑翔机纵剖面的动力学模型,完成了典型海况下的运动仿真。Qi等[8]、Zhou等[9]、常宗瑜等[10]利用凯恩方法建立了波浪驱动推进装置的动力学模型,通过仿真与实验分析了波浪参数、水翼倾角对装置推进速度的影响。Li等[11]、Wang等[12]针对缆索张紧、松弛状态建立了波浪滑翔机动力学模型,得到了波浪滑翔机各部分间的运动关系。
在水动力学研究方面,Politis等[13]分析了翼片随机升沉和主动控制俯仰运动的水动力学性能,提出了具有高推进性能的翼片转角主动控制方法。Silva等[14]对二维振荡翼片的水动力学行为进行了模拟与分析,研究了波浪和翼片运动相位差、遭遇波频率和航行速度等参数对推进效率的影响。刘芬等[15]通过仿真柔性水翼主动升沉运动下的被动变形过程,重点分析了俯仰运动参数和斯特劳哈尔数对水翼推进性能的影响。Liu等[16]研究了异步扑翼的水下推进性能,发现了多翼由于翼间涡流的影响可以产生比单翼更大的推进力。Yang等[17]采用流体力学方法对六列串联翼片进行了分析与优化,总结了翼片扭簧刚度与推进性能间的变化规律。胡峰等[18]采用CFD技术对波浪滑翔机多自由度耦合运动进行了三维模拟,探究了波浪参数和翼片结构参数对其推进性能的影响。
目前为止,对波浪滑翔机推进性能的相关研究一般是在规则波的作用下开展的,但实际的波浪具有随机性,其作用下的波浪滑翔机动力学响应会产生显著变化[19]。因此本文对波浪滑翔机在随机波浪激励下运动过程进行了研究。首先,基于JONSWAP谱及浮体的幅值响应算子(Response Amplitude Operator,RAO),给浮体以随机的垂荡激励;其次,建立了波浪滑翔机的动力学模型;最后,利用多体动力学软件对其运动过程进行了仿真,分析了波浪滑翔机的动态响应,进一步分析了影响其推进性能的因素。
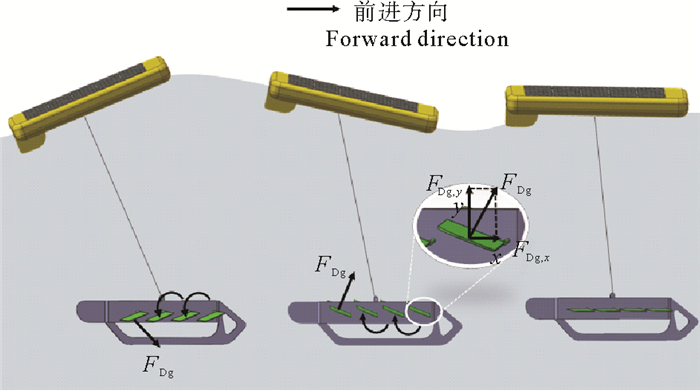
1 随机波浪下波浪滑翔机动力学分析波浪滑翔机由水面浮体、水下推进机构以及连接缆索组成由图 1所示。水面浮体在波浪的作用下产生复杂刚体运动,简化模型仅考虑浮体的垂荡,并带动水下推进机构产生垂荡。这种垂荡运动会使推进机构翼片在水动力的作用下发生摆动,同时,翼片的水动力具有一个向前推进力分量,推动水下推进机构以及水面浮体向前运动。
|
图 1 波浪滑翔机工作原理 Fig. 1 Operational mechanism of wave glider |
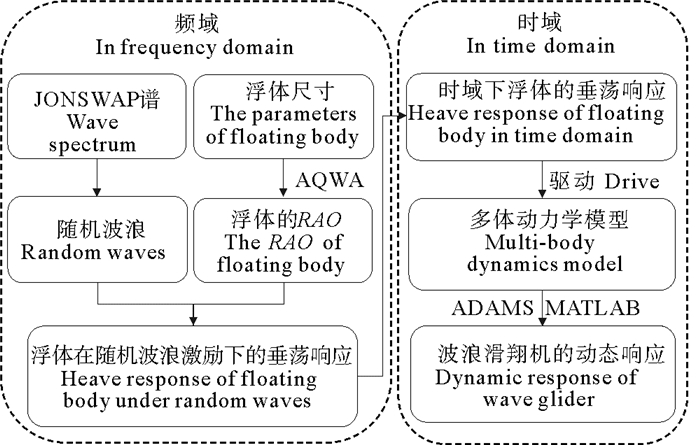
在随机波浪情况下滑翔机动力学分析过程如图 2所示。首先,选取适当参数根据JONSWAP谱生成所需随机波浪,根据浮体船型尺寸获得浮体的RAO,得到浮体在随机波浪下的频谱响应。其次,利用线性波浪叠加法将具有随机相位的多个频率响应叠加得到水面浮体的时域响应,并将其作为水面浮体或水下推进机构的激励运动。最后,根据莫里森方程定义波浪滑翔机运动过程中所受水动力,进而建立多体动力学模型;利用ADAMS仿真并分析波浪滑翔机在随机波浪下的动态响应情况,进一步分析影响其推进性能的因素。
|
图 2 波浪滑翔机动力学分析框图 Fig. 2 Dynamic analysis flow chart of wave glider |
采用JONSWAP谱作为波浪条件求得浮体的垂荡响应,其改进后的波能谱能量密度函数S(ω)如下:
| $ \left.S(\omega)=\alpha^* H_{\mathrm{S}}^2 \frac{\omega_{\mathrm{m}}^4}{\omega^5} \exp \left[-\frac{5}{4}\left(\frac{\omega_{\mathrm{m}}}{\omega}\right)^4\right] \gamma^{\exp \left[-\frac{\left(\omega-\omega_{\mathrm{m}}\right)^2}{2 \sigma^2 \omega_{\mathrm{m}}^2}\right.}\right] 。$ | (1) |
式中:α*为谱峰升高因子相关系数;HS为有义波高;ωm为谱峰频率;γ为谱峰升高因子;σ为峰形系数。
波浪激励到浮体运动的传递函数可以用RAO表示,其可在水动力软件AQWA中根据浮体结构参数(见表 1)计算得出。频域下随机波浪激励下浮体的垂荡响应可由下式表示[20]。
| $ S_Y(\omega)=R A O^2(\omega) \cdot S(\omega) 。$ | (2) |
|
|
表 1 水面浮体主要参数 Table 1 Main parameters of floating body |
随机波浪激励下浮体的响应具有不规则的随机性,可将其视为多个幅值、周期、初相位不同的余弦波叠加,根据式(3)将频域下的垂荡响应转化到时域[21]:
| $ x_y(t)=\sum\limits_{i=1}^{\infty} a_i \cos \left(\omega_i t+\varphi_i\right) 。$ | (3) |
式中:ai、ωi、φi分别为第i个余弦波的幅值、圆频率、初相位。其中,初相位φi是均布于[0, 2π]间的随机值,幅值
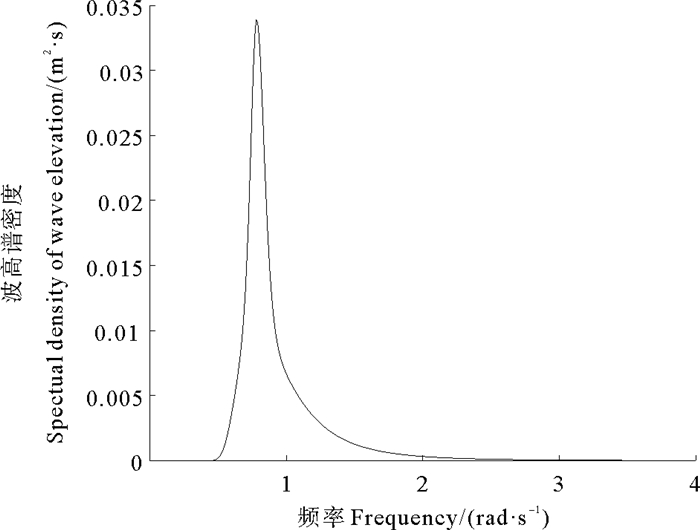
选定波浪参数:γ=3.3、TP=2π/ω=7.5 s、HS=0.6 m,计算得到如图 3所示的JONSWAP谱,进一步根据浮体RAO求得浮体的垂荡位移并将其转化至时域。
|
图 3 JONSWAP谱 Fig. 3 JONSWAP wave spectrum |
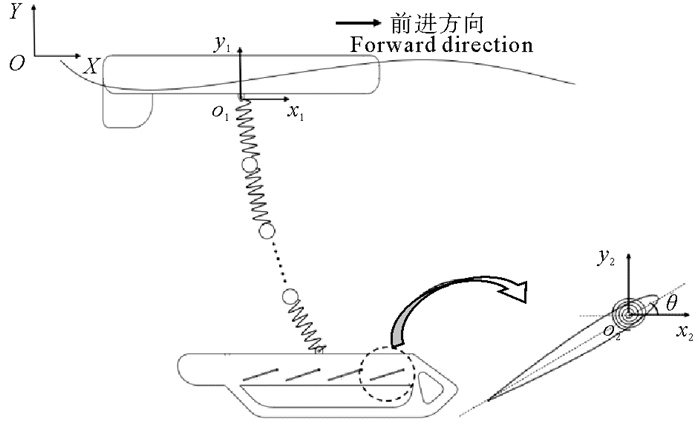
波浪滑翔机简化模型如图 4所示,为简化计算,本文做出了以下假设:
|
图 4 波浪滑翔机简化模型 Fig. 4 Simplified model of wave glider |
(1) 只考虑波浪滑翔机在XY平面中的运动,其他方向运动忽略不计。
(2) 将翼片表面受到的力集中到翼片质心处。
(3) 翼片因转动而产生的涡流和尾流忽略不计。
为描述波浪滑翔机的运动,建立了坐标系(见图 4):绝对坐标系O-XY,相对坐标系o1-x1y1和o2-x2y2。其中绝对坐标系与大地相连,相对坐标系原点o1为水面浮体与缆索铰接点,o2位于翼片转轴处。翼片对于坐标系o2-x2y2转过的角度表示为θ。
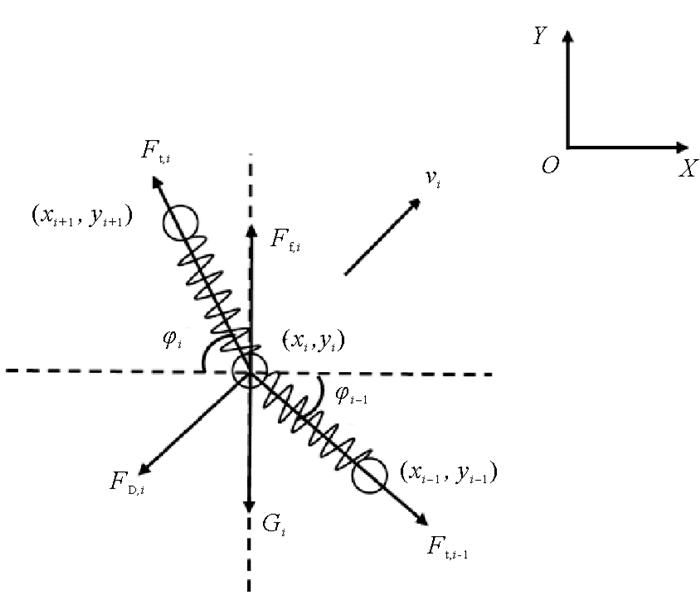
3.2 缆索的受力分析将缆索视作若干个集中质量点与无质量弹簧构成的微单元的集合(见图 5),将作用在缆索上的力离散到各微单元的集中质量点上。其中,质量点所受的水阻力FD,i可通过莫里森方程得出,质量点间的相互作用力Ft,i可根据缆索状态计算得出:
| $ F_{\mathrm{t}, i}=\left\{\begin{array}{l} k_l\left(l_i-l_{i 0}\right), l_i>l_{i 0} \\ 0, l_i \leqslant l_{i 0} \end{array}\right. \text { 。} $ | (4) |
|
图 5 缆索受力示意图 Fig. 5 Force analysis diagram of the cable |
式中:kl为微元段弹簧的刚度;li0为第i段微元段弹簧的初始长度;li为弹簧当前状态长度。
假设质量点重力Gi与浮力Ff,i相等,则第i个集中质量点所受的合力Fsection, i可以表示为:
| $ F_{\text {section }, i}=\left[\begin{array}{l} F_{\mathrm{t}, i-1} \cos \varphi_{i-1}-F_{\mathrm{t}, i} \cos \varphi_i-F_{\mathrm{D}, i x} \\ F_{\mathrm{t}, i} \sin \varphi_i-F_{\mathrm{D}, i y}-F_{\mathrm{t}, i-1} \sin \varphi_{i-1} \end{array}\right] 。$ | (5) |
式中:φi为第i根无质量弹簧与水平方向的夹角,FD,ix和FD,iy分别为水阻力FD,i在水平和竖直方向的分量。
将缆索总张紧力Ft近似看作:
| $ F_{\mathrm{t}}=k_1\left(l_1-l_\mathrm{l0}\right) \text { 。} $ | (6) |
式中:ll0为缆索初始总长度;ll为缆索当前状态总长度,定义为
| $ l_1=\sqrt{\left(x_2-x_1\right)^2+\left(y_1-y_2\right)^2} \text { 。} $ | (7) |
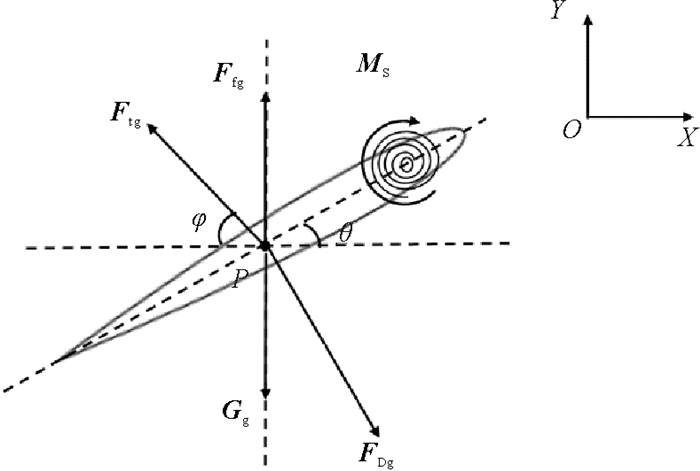
翼片受力如图 6所示,在波浪滑翔机运行过程中,翼片受到水动力的切向分量要远小于法向分量,因此可以忽略切向分量,只考虑垂直于翼片的水动力FDg,其定义为:
| $ \begin{array}{l} \;\;\;\;\;\;\;F_{\mathrm{Dg}}= \\ -\frac{1}{2} C_{\mathrm{d} \rho} S\left[\begin{array}{l} \left(\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right)\left|\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right| \sin \theta \\ -\left(\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right)\left|\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right| \cos \theta \end{array}\right] 。\end{array} $ | (8) |
|
图 6 翼片受力示意图 Fig. 6 Force analysis diagram of hydrofoil |
式中:Cd为翼片水动力系数;ρ为海水密度;S为翼片垂直于入射水流方向截面面积;
弹簧恢复力矩MS同翼片转动方向相反,其大小可以表示为:
| $ M_{\mathrm{S}}=k_{\mathrm{g}} \theta+c_{\mathrm{g}} \dot{\theta}。$ | (9) |
式中:kg为控制翼片转动的弹簧刚度;cg为其阻尼常数。
缆索对推进装置的拉力Ftg定义为:
| $ F_{\mathrm{tg}}=\left[\begin{array}{c} -F_{\mathrm{t}} \frac{x_2-x_1}{l_1} \\ F_{\mathrm{t}} \frac{y_1-y_2}{l_{\mathrm{l}}} \end{array}\right] 。$ | (10) |
式中:x1为浮体水平方向的位移;x2为翼片水平方向的位移;y1为浮体竖直方向的位移;y2为翼片竖直方向的位移。
假设翼片浮力Ffg与重力Gg相等,则翼片所受合力可以表示为:
| $ F_{\text {glider }}=\left[\begin{array}{l} F_{\mathrm{Dg} x}+F_{\mathrm{tg} x} \\ F_{\mathrm{Dg} y}+F_{\mathrm{tg} y} \end{array}\right] 。$ | (11) |
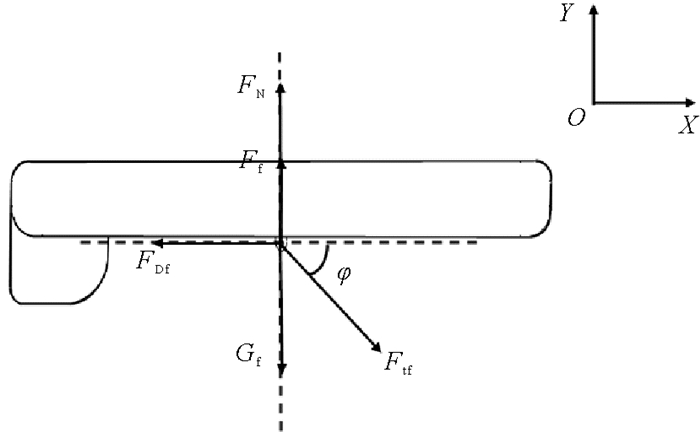
浮体受力如图 7所示,其中水平方向水阻力FDf根据Morison方程定义为:
| $ F_{\mathrm{Df}}=\frac{1}{2} C_x \rho A_y \dot{x}_1\left|\dot{x}_1\right| 。$ | (12) |
|
图 7 浮体受力示意图 Fig. 7 Force analysis diagram of floating body |
式中:Cx为浮体水平方向水阻力系数;ρ为海水密度;Ay为浮体水线以下部分在竖直方向的投影面积;
垂向波浪力FN可表示为:
| $ \begin{array}{l} \;\;\;\;\;\;F_{\mathrm{N}}= \\ -\frac{1}{2} C_y \rho A_x\left(\dot{y}_1-\dot{z}\right)\left|\dot{y}_1-\dot{z}\right|-\rho g A_x\left(y_1-z\right) 。\end{array} $ | (13) |
式中:Cy为浮体竖直方向水阻力系数;Ax为浮体水线以下部分在水平方向的投影面积;z为波浪波高。
浮体所受合外力可以表示为:
| $ \begin{array}{l} \;\;\;\;\;\;F_{\text {float }}= \\ {\left[\begin{array}{c} F_{\mathrm{t}} \frac{x_2-x_1}{l_1}-\frac{1}{2} C_x \rho A_y \dot{x}_1\left|\dot{x}_1\right|-F_{\mathrm{t}} \frac{y_1-y_2}{l_1} \\ -\frac{1}{2} C_y \rho A_x\left(\dot{y}_1-\dot{z}\right)\left|\dot{y}_1-\dot{z}\right|-\rho g A_x\left(y_1-z\right) \end{array}\right] 。} \end{array} $ | (14) |
通过分析,得到波浪滑翔机的动力学方程:
| $ m_{\mathrm{f}} \ddot{x}_1=F_{\mathrm{t}} \frac{x_2-x_1}{l_1}-\frac{1}{2} C_x \rho A_y \dot{x}_1\left|\dot{x}_1\right| \text {, } $ | (15) |
| $ \begin{aligned} & m_{\mathrm{f}} \ddot{y}_1=-\frac{1}{2} C_y \rho A_x\left(\dot{y}_1-\dot{z}\right)\left|\dot{y}_1-\dot{z}\right|- \\ & \rho g A_x\left(y_1-z\right)-F_t \frac{y_1-y_2}{l_1}, \end{aligned} $ | (16) |
| $ \begin{gathered} m_{\mathrm{g}} \ddot{x}_2=-4 C_{\mathrm{d} \rho} S\left(\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right) \cdot \\ \left|\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right| \sin \theta-F_{\mathrm{t}} \frac{x_2-x_1}{l_1}, \end{gathered} $ | (17) |
| $ \begin{gathered} m_{\mathrm{g}} \ddot{y}_2=4 C_{\mathrm{d}} \rho S\left(\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right) \cdot \\ \left|\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right| \cos \theta+F_{\mathrm{t}} \frac{y_1-y_2}{l_1}-G_{\mathrm{p}}, \end{gathered} $ | (18) |
| $ \begin{aligned} & I_{\mathrm{P}} \ddot{\theta}=-\frac{1}{2} C_{\mathrm{d}} \rho S l_{\mathrm{p}}\left(\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right) \cdot \\ & \left|\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right|-k_{\mathrm{g}} \theta-c_{\mathrm{g}} \dot{\theta}。\end{aligned} $ | (19) |
式中:mf为浮体的质量;mg为翼片的质量;Gp为推进机构配重;IP为翼片的转动惯量。
通过对动力学方程进一步分析,可以发现波浪滑翔机的总推力FH主要受翼片水动力的水平分量、浮体水平方向水阻力两部分力影响,因此波浪滑翔机的总推进力FH可近似如下式:
| $ \begin{gathered} F_{\mathrm{H}}=-4 C_{\mathrm{d} \rho} S\left(\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right) \cdot \\ \left|\dot{x}_2 \sin \theta-\dot{y}_2 \cos \theta+l_{\mathrm{p}} \dot{\theta}\right| \sin \theta-\frac{1}{2} C_x \rho A_y \dot{x}_1\left|\dot{x}_1\right| \end{gathered} $ | (20) |
在多体动力学软件中,根据波浪滑翔机水下推进机构参数(见表 2)建立多体动力学模型,对波浪滑翔机进行仿真,分析波浪滑翔机在随机波浪激励下的动态响应特性。为了显示随机波浪和规则波下波浪滑翔机推进性能的差异,本研究计算在波幅为0.3 m、周期为5 s的正弦波浪激励下的,并将得到的响应结果作为对比。
|
|
表 2 波浪滑翔机水下推进机构的参数 Table 2 Main parameters of the glider |
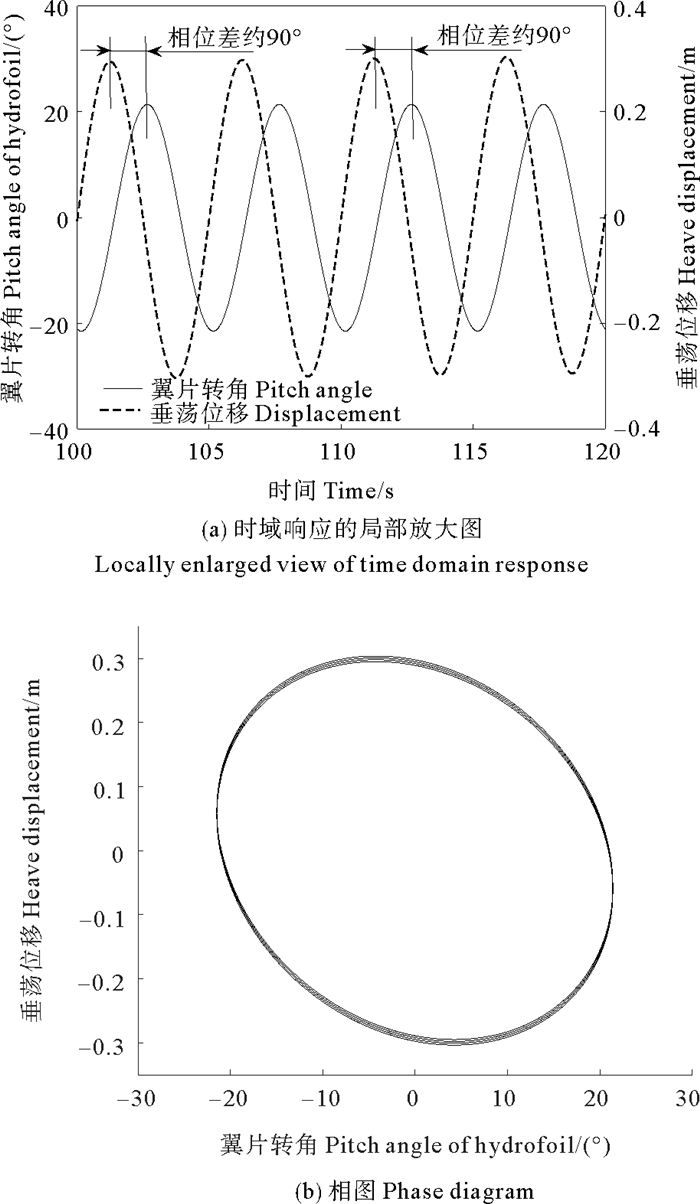
在规则波浪激励下,翼片转角的响应情况如图 11所示。其中图 8(a)给出了翼片转动和水下推进机构垂荡的时域响应,同时翼片转角与垂荡之间的相图如图 8(b)所示。由规则波浪激励下翼片运动情况可以看出,此时翼片的运动具有规律的周期性,翼片转角与浮体垂荡位移的相图为规则的椭圆形,相位差约为90°,即当浮体垂荡到极限位置时,翼片转角接近0°。
|
图 8 规则波浪下翼片转角与垂荡位移关系 Fig. 8 The pitch angle of hydrofoil and the heave displacement of wave glider under regular waves |
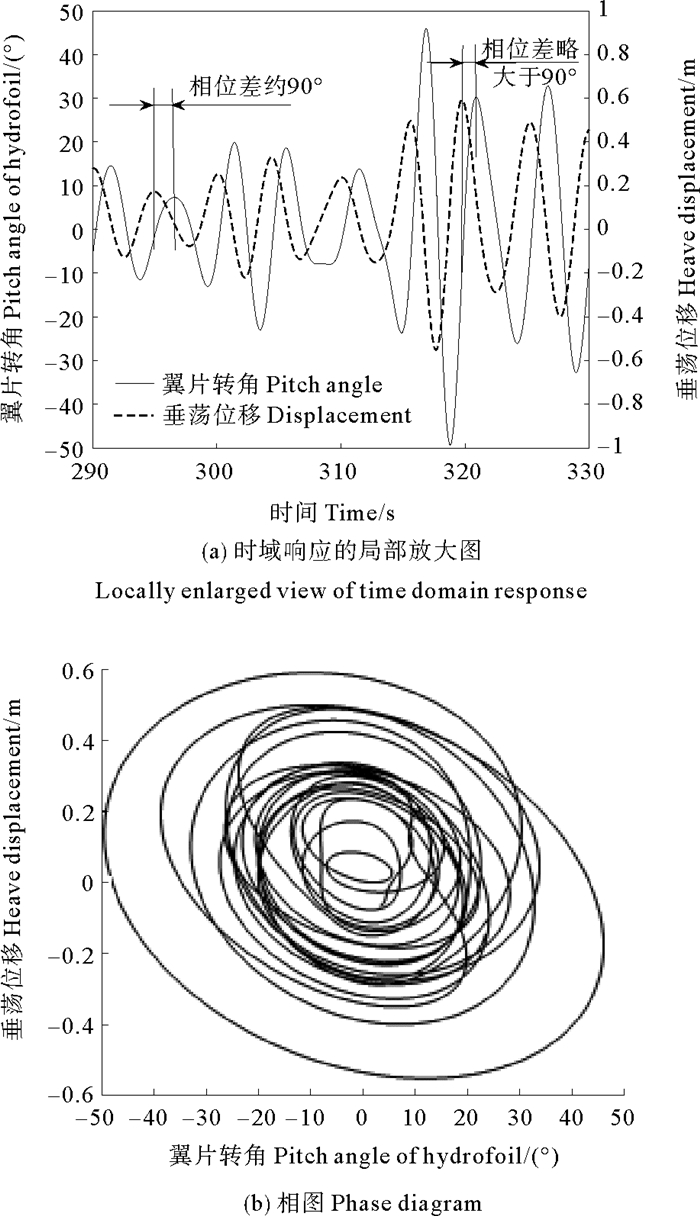
随机波浪激励下,翼片转角的响应情况如图 9所示。可以看出,由于随机波浪被看作由若干波高、周期均不相等的规则简谐波按随机相位叠加而成,故在其激励下,翼片转角变化也不再具有周期性,翼片转角的响应情况更为复杂。翼片转角与浮体垂荡位移的相图由多个大小和形状不同的椭圆轨迹线叠加而成,相位差也随浮体垂荡幅值的变化而变化。在翼片弹簧刚度一定的情况下,浮体垂荡位移越大,翼片转角越大,转角与垂荡位移的相位差也略大于90°,这是由于此时控制翼片转动的弹簧刚度相对较小,提供的恢复力矩不足以带动翼片快速转动复位,翼片在浮体经过垂荡极限位置一段时间后才得以回到初始位置。在此过程中,翼片水动力的水平分量在短时间内可能接近零或为负值,影响波浪滑翔机的推进性能,因此选取适当的弹簧刚度有助于提高波浪滑翔机的推进性能。
|
图 9 随机波浪下翼片转角与垂荡位移关系 Fig. 9 The pitch angle of hydrofoil and the heave displacement of wave glider under random waves |
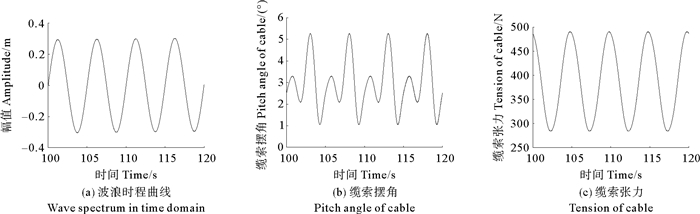
图 10给出了规则波浪激励下缆索的响应情况,其中图 10(a)为规则波浪的时程曲线,图 10(b)为对应波浪时程曲线下缆索摆角变化曲线,图 10(c)为缆索张力变化曲线。分析图 10可以看出,在规则波浪激励下,缆索的动态响应具有规则的周期性。缆索的摆角在1.05°~5.26°范围内变化,装置始终保持正向前进。缆索张力在284~490 N范围内变化,缆索一直处于张紧状态。缆索摆角曲线不同于波浪时程曲线及缆索张力曲线,在每个周期内具有2个不等波峰,其原因在于推进装置增加了配重,因此导致波浪滑翔机下行过程中水平前进速度及缆索摆角均较上行过程有较大波动;而缆索张力主要与翼片水动力的水平分量相关,故其与翼片水动力的变化规律相似。
|
图 10 规则波浪激励下缆索的动态响应 Fig. 10 Dynamic response of the cable under regular waves |
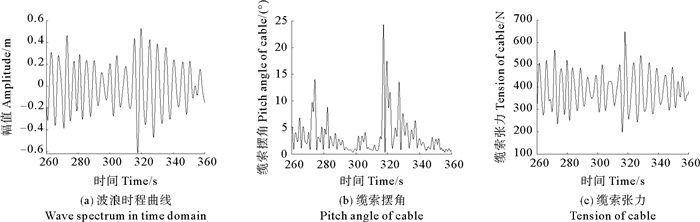
图 11给出了随机波浪下缆索的响应情况。由图可知,随机波浪激励下,缆索摆角及张力的响应失去周期性特征,缆索摆角在0.27°~24.28°范围内波动,张力在198~647 N范围内波动,波动幅度较大。且当波浪波高较大时,摆角及张力变化曲线的波动更为明显,较易产生危险状况,因此应选择合适的推进机构配重,尽量规避缆索张力波动较大或产生松弛的情况。
|
图 11 随机波浪激励下缆索的动态响应 Fig. 11 Dynamic response of the cable under random waves |
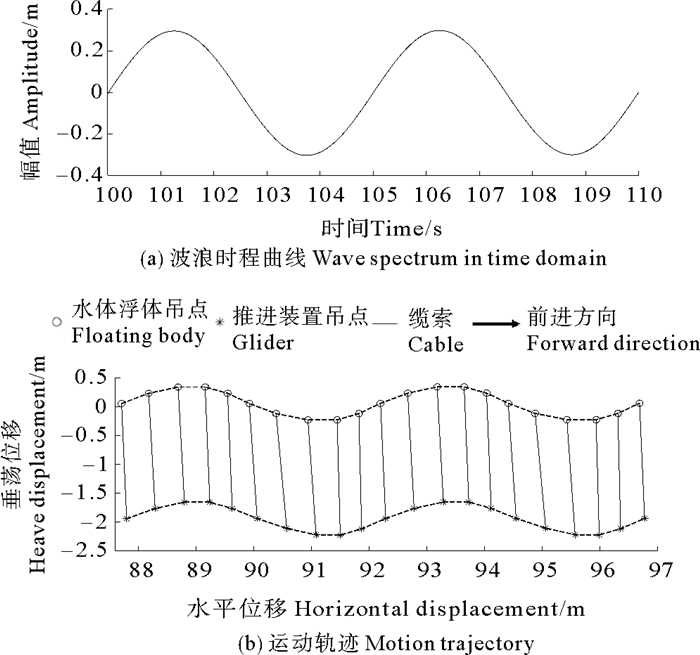
规则波浪激励下,从波浪滑翔机的运动轨迹变化方面对其整体响应进行分析,如图 12所示,其中图 12(a)为规则波浪的部分时程曲线,图 12(b)为对应于波浪时程曲线下的滑翔机运动轨迹,间隔0.5 s取一轨迹来描述波浪滑翔机在该时刻水平、垂荡方向位置。可以看出,在规则波激励下,波浪滑翔机浮体和推进机构运动轨迹基本一致,浮体和推进机构的水平速度、缆索的摆角波动相对较小。
|
图 12 规则波浪激励下波浪滑翔机的运动轨迹 Fig. 12 Motion trajectory of a wave glider under regular waves |
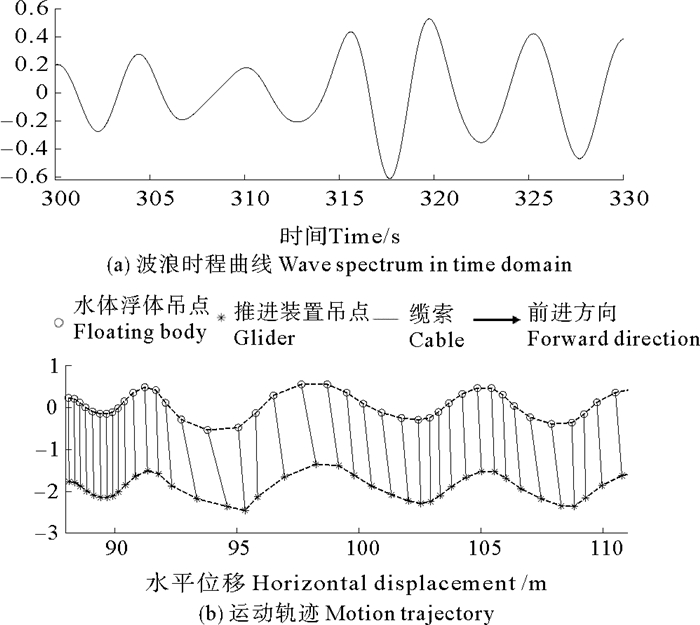
而在随机波浪激励下(见图 13),浮体与推进机构的运动轨迹与规则波下相比差异较大。在波高较大时,推进机构水平速度明显提高,推进机构与浮体的水平间距加大。波高较小、周期较长情况下,各运动参数无显著波动,波浪滑翔机运动轨迹差异较小。
|
图 13 随机波浪激励下波浪滑翔机的运动轨迹 Fig. 13 Motion trajectory of a wave glider under random waves |
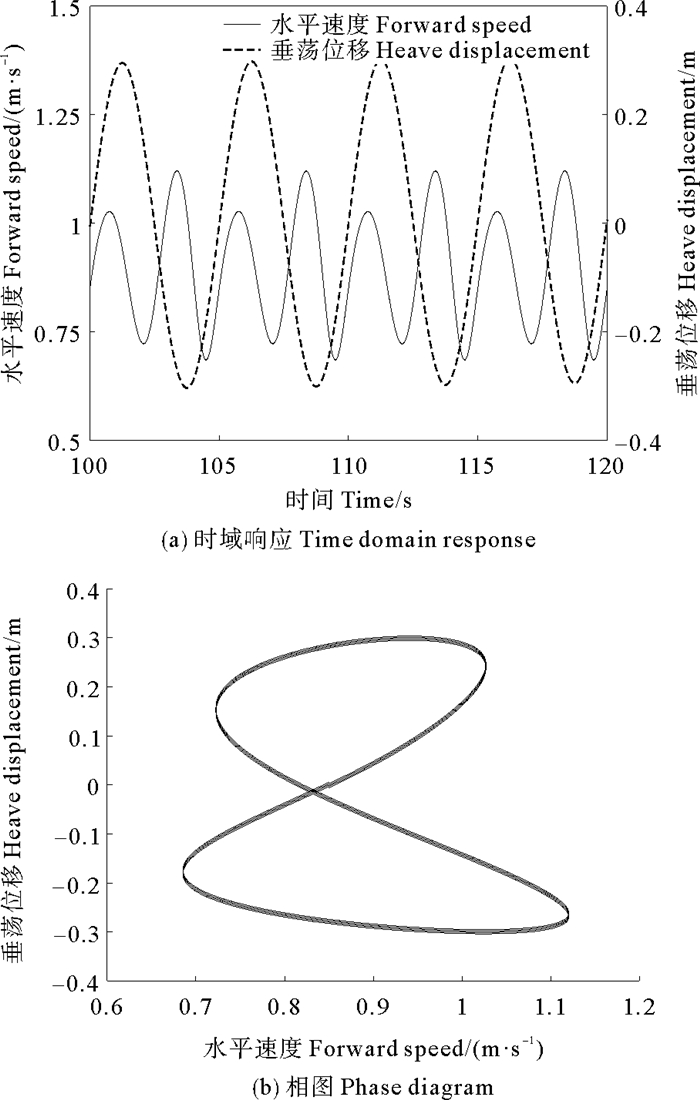
波浪滑翔机水平速度与垂荡位移关系也可反映波浪滑翔机的整体响应情况。如图 14(a)、(b)分别为规则波浪激励下装置的水平速度与垂荡位移的时域响应以及相图。可以看出在规则波浪激励下,水平速度变化具有周期性,水平速度与垂荡位移的相图为规则的8字型,且存在一定的相位差。这是由于浮体受随机波浪激励产生垂荡,至翼片转动,再到推进装置带动浮体前进的一系列运动传递过程存在滞后,其中翼片弹簧刚度的选取也影响翼片水动力与垂荡位移的相位角。
|
图 14 规则波浪下波浪滑翔机水平速度与垂荡位移关系 Fig. 14 The forward speed and the heave displacement of wave glider under regular waves |
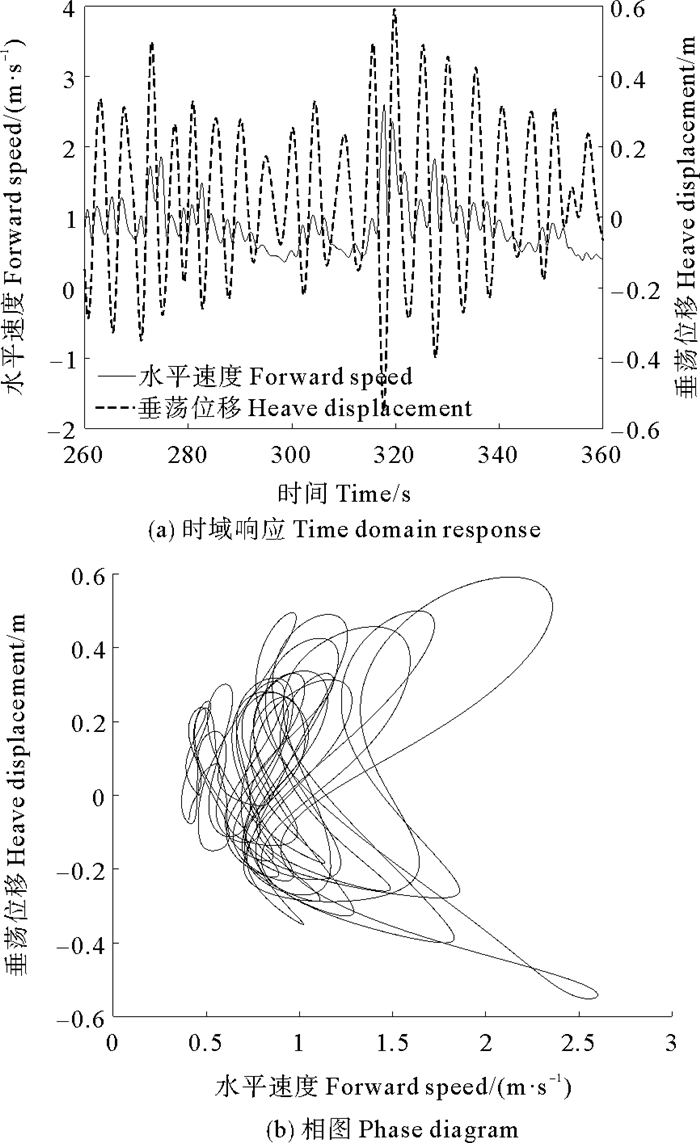
而在随机波浪激励下(见图 15),由于波浪波高、周期、相位均变化,相图表现为若干个8字形轨迹线叠加,呈现明显的不规则性,且当浮体垂荡位移较大时,装置的水平速度波动明显。
|
图 15 随机波浪下波浪滑翔机水平速度与垂荡位移关系 Fig. 15 The forward speed and the heave displacementof wave glider under random waves |
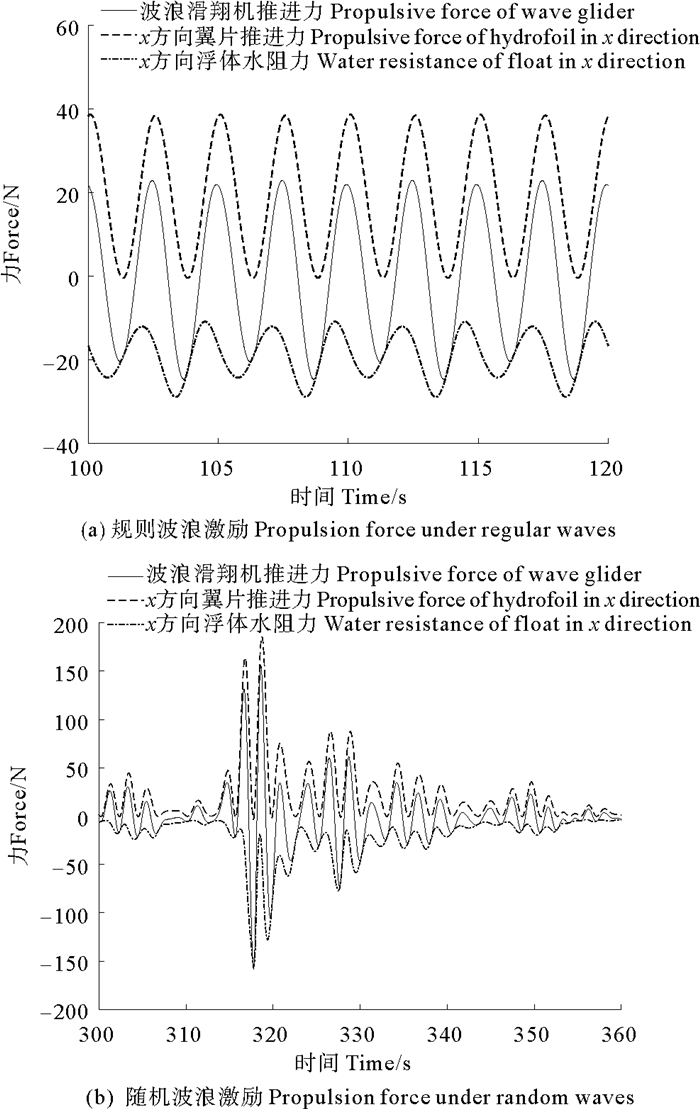
波浪滑翔机的推进力主要受翼片水动力、浮体水阻力两部分力影响,规则波和随机波激励下波浪滑翔机的推进力响应情况分别由图 16(a)、(b)给出。在这两种波浪激励下,翼片推进力基本为正值,浮体水阻力始终为负值,装置总推进力在正负变化,说明波浪滑翔机均可以较为稳定的速度保持正向运动,推进效果显著。翼片推进力相对浮体水阻力变化幅度较大,对波浪滑翔机推进力的波动起主要影响,波浪滑翔机推进力的变化规律与翼片推进力的变化规律相似。浮体水阻力与波浪滑翔机推进力、翼片推进力有明显相位差,分析原因为翼片产生的推进力需经缆索传递至浮体,进而影响浮体的前进速度及水平方向水阻力,此过程存在一定的滞后性。
|
图 16 波浪滑翔机推进力组成 Fig. 16 The propulsion force of wave glider |
在规则波激励下,波浪滑翔机各力呈周期性规则变化,而随机波浪激励下各力变化情况复杂,且与随机波浪波高的变化呈正相关。
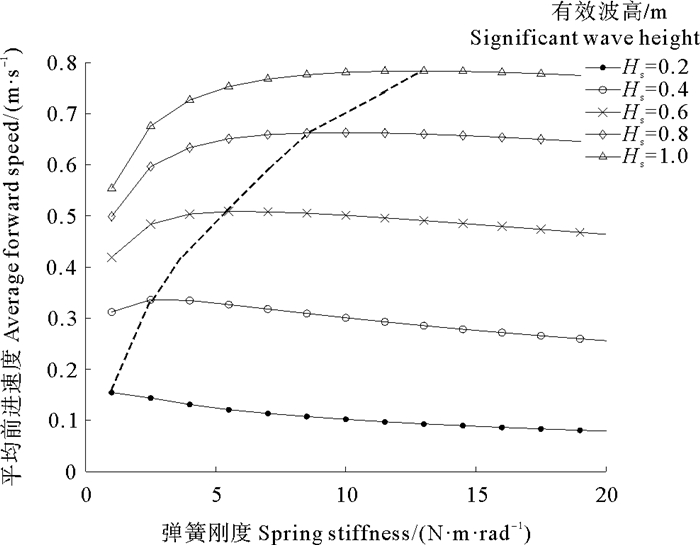
4.4 波浪滑翔机推进性能影响因素分析通过分析随机波浪激励下波浪滑翔机的动态响应情况(见图 9、15),可以看出波浪参数以及控制翼片转动的弹簧刚度均对波浪滑翔机的推进性能有较大影响。根据波浪滑翔机动力学模型,对随机波浪有义波高、弹簧刚度与波浪滑翔机平均前进速度的关系进行分析,如图 17所示。
|
图 17 不同有义波高和弹簧刚度下装置的平均前进速度 Fig. 17 The average forward velocity of the device under different wave heights and spring stiffness |
在波浪周期TP=3.5 s的情况下,随着有义波高的增加,波浪滑翔机的平均前进速度加快。在周期和有义波高一定的情况下,随着翼片弹簧刚度的增加,波浪滑翔机的平均前进速度先增加后减小,存在最优的弹簧刚度,且最优刚度按图 17中虚线规律随有义波高的增大而增大。分析原因:波高较小时,翼片转动适当的角度有利于提高装置推进性能,此时需要的弹簧刚度较小,使翼片在较小波高时可以转动较大的角度;波高较大时,翼片转动过大的角度会使水动力的水平分量迅速减小,对装置的推进产生阻碍,因此需要较大的弹簧刚度限制翼片的转角在适当的范围内。
5 结论本文对随机波浪下波浪滑翔机的动态响应进行了研究。分析了波浪环境对翼片转角、缆索摆角和张力、波浪滑翔机的运动轨迹、水平速度、推进力等要素动态响应的影响。通过分析得到以下结论:
(1) 波浪滑翔机在随机波浪下的响应更加复杂,翼片转角、前进速度与垂荡位移的相图均由多个图形轨迹叠加而成,缆索摆角、推进力等要素的动态响应也不再具有周期性。
(2) 随机波浪下,缆索张力随垂荡位移幅值的增大而显著增加,应合理选择推进机构配重,尽量规避缆索张力波动较大或松弛现象的出现。
(3) 与规则波激励相比,随机波浪作用下,水上浮体与水作用下,推进机构运动轨迹差异较大。在随机波浪波高较大时, 推进机构前进速度显著提高, 推进机构与浮体的水平间距加大。
| [1] |
Hine R, Willcox S, Hine G, et al. The wave glider: A wave-powered autonomous marine vehicle[C]//OCEANS 2009, MTS/IEEE Biloxi-Marine Technology for Our Future: Global and Local Challenges. Biloxi, MS, USA: IEEE, 2009: 1-6.
(  0) 0) |
| [2] |
廖煜雷, 李晔, 刘涛, 等. 波浪滑翔器技术的回顾与展望[J]. 哈尔滨工程大学学报, 2016, 37(9): 1227-1236. Liao Y L, Li Y, Liu T, et al. Unmanned wave glider technology: State of the art and perspective[J]. Journal of Harbin Engineering University, 2016, 37(9): 1227-1236. (  0) 0) |
| [3] |
Kraus N D, Bingham B. Estimation of wave glider dynamics for precise positioning[C]//Proceeding of Oceans 2011 MTS/ IEEE Kona Conference. Kona, USA: IEEE, 2011: 1-9.
(  0) 0) |
| [4] |
Kraus N D. Wave Glider Dynamic Modeling, Parameter Identification and Simulation[D]. Manoa: University of Hawaii, 2012.
(  0) 0) |
| [5] |
Wang P, Tian X L, Lu W Y, et al. Dynamic modeling and simulations of the wave glider[J]. Applied Mathematical Modelling, 2019, 66: 77-96. DOI:10.1016/j.apm.2018.08.027 (  0) 0) |
| [6] |
Tian B Q, Yu J C, Zhang A Q, et al. Dynamics analysis of wave-driven unmanned surface vehicle in longitudinal profile[C]//IEEE/MTS Oceans 2014-Taipei. Taipei: IEEE, 2014: 1-6.
(  0) 0) |
| [7] |
Tian B Q, Yu J C, Zhang A Q. Dynamic modeling of wave driven unmanned surface vehicle in longitudinal profile based on D-H approach[J]. Journal of Central South University, 2015, 22(12): 4578-4584. DOI:10.1007/s11771-015-3008-6 (  0) 0) |
| [8] |
Qi Z F, Liu W X, Jia L J, et al. Dynamic modeling and motion simulation for wave glider[J]. Applied Mechanics & Materials, 2013, 397-400: 285-290. (  0) 0) |
| [9] |
Zhou C L, Wang B X, Zhou H X, et al. Dynamic modeling of a wave glider[J]. Frontiers of Information Technology & Electronic Engineering, 2017, 18(9): 1295-1304. (  0) 0) |
| [10] |
常宗瑜, 于振江, 郑中强, 等. 波浪驱动推进机构的最优水翼倾角的确定[J]. 中国海洋大学学报(自然科学版), 2021, 51(1): 111-116. Chang Z Y, Yu Z J, Zheng Z Q, et al. Selection of optimal angle of hydrofoil of wave driven propel mechanism[J]. Periodical of Ocean University of China, 2021, 51(1): 111-116. (  0) 0) |
| [11] |
Li X T, Liu F, Wang L, et al. Motion analysis of wave glider based on multibody dynamic theory[C]//International Conference on Intelligent Robotics and Applications. Wuhan: Springer, 2017: 721-734.
(  0) 0) |
| [12] |
Wang L F, Li Y, Liao Y L, et al. Dynamics modeling of an unmanned wave glider with flexible umbilical[J]. Ocean Engineering, 2019, 180: 267-278. DOI:10.1016/j.oceaneng.2019.03.047 (  0) 0) |
| [13] |
Politis G, Politis K. Biomimetic propulsion under random heaving conditions, using active pitch control[J]. Journal of Fluids and Structures, 2014, 47: 139-149. DOI:10.1016/j.jfluidstructs.2012.05.004 (  0) 0) |
| [14] |
Silva L W A D, Yamaguchi H. Numerical study on active wave devouring propulsion[J]. Journal of Marine Science and Techno-logy, 2012, 17(3): 261-275. DOI:10.1007/s00773-012-0169-y (  0) 0) |
| [15] |
刘芬, 彭彬, 孙秀军, 等. 波浪滑翔器柔性水翼推进性能数值仿真分析[J]. 水下无人系统学报, 2021, 29(4): 374-382. Liu F, Peng B, Sun X J, et al. Numerical simulation analysis of flexible hydrofoil propulsion performance for wave glider[J]. Journal of Unmanned Undersea Systems, 2021, 29(4): 374-382. (  0) 0) |
| [16] |
Liu P, Su Y M, Liao Y L. Numerical and experimental studies on the propulsion performance of a wave glide propulsor[J]. China Ocean Engineering, 2016(30): 393-406. (  0) 0) |
| [17] |
Yang F M, Shi W C, Wang D Z. Systematic study on propulsive performance of tandem hydrofoils for a wave glider[J]. Ocean Engineering, 2019, 179: 361-370. DOI:10.1016/j.oceaneng.2019.02.030 (  0) 0) |
| [18] |
胡峰, 赵文涛, 黄琰, 等. 三维被动摆动翼片对波浪滑翔机推进动力的性能研究[J]. 机械工程学报, 2020, 56(8): 243-249. Hu F, Zhao W T, Huang Y, et al. Study on propulsion performance of three-dimensional passive swinging hydrofoil on wave glider[J]. Journal of Mechanical Engineering, 2020, 56(8): 243-249. (  0) 0) |
| [19] |
廖煜雷, 李晔, 等. 波浪驱动水面机器人[M]. 北京: 科学出版社, 2020: 142-143. Liao Y L, Li Y, et al. Wave Driven Surface Robot[M]. Beijing: Science Industry Press, 2020: 142-143. (  0) 0) |
| [20] |
杜宇, 胡金雄, 王晨旭. 海上风电浮船分体安装运动响应数值仿真[J]. 船舶工程, 2020, 42(12): 13-17. Du Y, Hu J X, Wang C X. Numerical simulation on motion response of offshore wind turbine components floating installation[J]. Ship Engineering, 2020, 42(12): 13-17. (  0) 0) |
| [21] |
黄柱林, 姚宝恒, 曾铮. 随机波浪下ROV缆索动力响应无因次分析[J]. 舰船科学技术, 2016, 38(15): 43-46. Huang Z L, YAO B H, Zeng Z. Non-dimensional dynamic response of ROV system under excitation of random wave[J]. Ship Science and Technology, 2016, 38(15): 43-46. (  0) 0) |
2. The Key Laboratory of Ocean Engineering of Shandong Province, Ocean University of China, Qingdao 266100, China
 2023, Vol. 53
2023, Vol. 53


