2. 中国海洋大学信息科学与工程学部海洋技术学院, 山东 青岛 266100
海温锋指海水的海表温度变化较大的狭长区域,通常可以用水平梯度来衡量锋面的强度或者判断锋面区域。海温锋所处区域的海表温度变化剧烈,海水之间、海水与大气之间的运动、热量交换、物质交换都较为活跃,会对区域相关天气状况产生作用,乃至影响到海域的长期气候特征。另外,由于海温锋所在海域的运动交换作用较强,影响到海洋中无机盐、叶绿素等物质的分布,对海洋生态、渔业捕捞等相关研究具有重要意义。因此海温锋的研究对天气预测、气候分析、海洋生态保护利用、渔场捕捞业务等生产、生活、科研领域的活动开展都有重要帮助。
梯度能够反映相应变量的变化程度,通过海表温度梯度可以检测海温锋,以梯度为基础的方法包含不同种类,如最大梯度法、以梯度算子为模板的各种边缘检测算法等。最大梯度法将各方向梯度的最大值作为该点最终梯度值,部分克服一般梯度法抗噪性差的缺点。罗琳等[1]基于最大梯度法分析了北部湾的海温锋季节和年际变化特征。邱春华等[2]利用最大梯度法分析了广东沿岸海温锋随着季节变化的规律和产生的原因。以梯度算子为模板的边缘检测算法包括Sobel算法、Canny算法等。Belkin等[3]基于Sobel算子分析了叶绿素锋与海温锋,发现叶绿素锋可以对海温锋的研究起到辅助作用。
Cayula等[4]首次提出直方图分析法,其主要任务在于确定温度分布为单峰还是双峰及分离双峰阈值。后面不断有学者对上述算法进行应用和创新。Cayula等[5]在直方图分析法基础上提出了一种针对多张海表温度图的多图锋面检测算法。Nieto等[6]基于滑动窗口的多重检测对直方图分析法进行了改进,并用数据验证了算法在锋面检测上有较大提升。平博等[7]基于引力算法[8-9]提出引力模型法。随后平博等[10]基于遥感数据证明了引力模型算法识别锋面的有效性和连续性。
Vazquez等[11]基于詹森香农散度提出熵算法,减弱了部分噪音对锋面识别的影响。Shimada等[12]对上述熵算法进行了一定的创新,能够检测不同尺度的锋面。Chang等[13]比较了直方图分析法和上述经改进的熵算法对于海温锋提取的效果,发现两种算法检测的锋面分布非常相似,但薄弱锋面的数量却存在显著差异。李阳东等[14]基于直方图分析和Canny算法中的非极大值抑制对熵算法进行改进,使其在应用噪声较大数据检测大尺度锋面上更具优势。薛存金等[15]根据小波分析对锋面的尺度信息进行分析,能反映海温锋多尺度的信息。陈捷等[16]基于二维连续小波变换对包括海洋锋在内的多种海洋现象进行了检测,并通过试验进行了验证。有学者对多种锋面识别算法进行了对比和总结。黎安舟等[17]对识别海温锋的梯度法、基于引力模型的算法、Canny算法和小波法进行了总结和分析。
与其他锋面检测算法注重提取边缘不同,统计模型检测法以锋面系统本身为研究主体来提取锋面。Hopkins等[18]提出统计模型检测法,利用数学统计模型构建温度场,并通过最大似然原理拟合理想温度场与遥感温度场求解锋面相关的参数,进而提取锋面信息。吴曲然等[19]在此基础上对上述算法稳定性进行了改进。近年来,人工智能算法的发展及应用更加迅速和多样化,应用人工智能解决各类问题受到越来越多行业的重视,相关学者也将人工智能相关算法应用到海温锋识别领域,并取得了不错的效果。曹维东等[20]针对传统海温锋识别算法(梯度法)中阈值选择较为主观、标准不同、单一等问题,提出了结合深度学习的方法,实现对各种类型锋的自适应阈值选择,并对识别结果精度进行量化,提高了识别结果的独立性和完整性。徐慧芳等[21]提出了一种基于Mask R-CNN (Mask region convolutional neural network)的新型海洋锋检测模型,能够克服海洋锋弱边缘且易变的特性,并通过实验证明其对锋面的检测能力有所提升。
检测海温锋即检测海表温度变化超过某一程度的区域,也就是检测温度图像的“边缘”,各种锋面检测算法均以此为目标,但借助的手段有较大不同,以致于各算法在锋面的严格量化定义方面不能统一,因此在检测锋面前对多种不同类型的算法进行对比显得很有必要。前人研究较多的是算法的改进和两种算法的对比,对于多种不同类型的锋面检测算法的对比研究较少。本文综合考虑各算法的特点、发展情况、应用情况等,将五种不同类型的算法进行对比,五种算法分别为Sobel算法、Canny算法、引力模型法、直方图分析法和熵算法。
1 数据与算法 1.1 数据及预处理本文采用美国新一代极轨卫星SNPP/VIIRS(Suomi national polar-orbiting partnership/Visible infrared imaging radiometer suite)遥感Level 2海表温度数据,时间为2015年,区域为0°—25°N,100°E—125°E,覆盖了南海及其邻近海域,数据为nc格式文件,数据处理应用python语言,读取数据时采用0.01°分辨率将数据投影到格点矩阵中,对于一个格点有多个有效数据的情况采用求均值来得到该格点温度值。关于数据的质量控制,本文选取数据自带的质量标签作为筛选标准,质量标签有两种,详见表 1与表 2。
|
|
表 1 质量标签L2p_flags各位数含义 Table 1 Meaning of each number of the quality label L2p_flags |
|
|
表 2 质量标签quality_level各值含义 Table 2 Meaning of each value of the quality label quality_level |
如上表所示,本文基于标签L2p_flags的第10位来区分白天与黑夜数据,单独计算白天与黑夜的锋面信息。基于标签quality_level是否等于4或5来筛选高质量数据,可以去除云及其他低质量数据的影响。
1.2 算法本文将对比Sobel算法、Canny算法、引力模型法、直方图分析法和熵算法的锋面检测结果,Sobel算法应用前需进行中值滤波过滤噪声,Canny算法中的阈值选取经过多次对比实验而得,低阈值采用数据的80%分位数数值,高阈值采用数据的93%分位数数值。
1.2.1 引力模型法引力模型法[7]是基于引力算法提出的,将像素点视为“天体”,将温度看作相应的“质量”,然后应用万有引力定律计算像素点的8邻域点对其的“合力”,最后通过选择合适的阈值来识别锋面。引力模型在应用引力算法前根据数据在锋面识别中的特点对数据进行了预处理,首先进行中值滤波,消除噪声及细小锋面的影响;然后对于温度为0的数据点,因其所受“引力”为0,故将其替换为一个很小的正数,这样可以使温度为0的情况也适用该算法;其次由于万有引力公式是随“质量”增大而增大的,而非随“质量”差异的增大而增大,故对每个窗口内的温度数据进行归一化以消除温度大小对锋面识别的影响;最后对数据进行非线性变换来增强数据的对比度,从而提升锋面识别的效果。
1.2.2 直方图分析法直方图分析法[4]的主体步骤可以概括为三步:
第一步,确定窗口中温度分布是单峰还是双峰以及分离双峰的阈值。首先是窗口大小的选择,窗口既要够大以在窗口内能检测到锋面,又不能太大避免引进其他锋面或云等的干扰。经过对文献[4]中分析的参考以及对不同窗口的测试对比与分析,本文选择窗口大小为64×64。窗口内将温度数据的方差分为类内方差和类间方差,类间方差越大,表示窗口内存在两类温度越明显,因此使类间方差最大的阈值为分离双峰的最优阈值,为此将类间方差占总方差的比例看作一个指标,可用来判断窗口内温度是否为双峰和确定分离双峰的阈值。经过对文献[4]中分析的参考以及测试实验,选取0.7作为该指标区分单双峰的阈值,小于0.7为单峰,不进行后续处理;大于0.7为双峰,计算使该指标达到最大值的阈值,即为划分两类温度的最优阈值,继续后续计算。对于已经判断为存在两类温度的窗口,还需规定每一类温度所占比例应大于等于25%,任一类温度小于25%的窗口不进行后续计算。
第二步,应用凝聚算法进行锋面检验。数据的空间分布信息不容忽视,直方图分析后都需通过温度数据的空间分布来验证结果,云的存在也会导致锋面的误检测。当检测出两类温度后,应用凝聚算法验证每类温度的空间凝聚度,为此建立了凝聚系数指标,凝聚系数越大,表示结果更可靠。参考文献[4]中的设定并经过不同参数的测试对比,本文选取了0.9、0.9和0.92分别作为类一、类二和全集凝聚系数的阈值,低于该阈值的结果被舍弃。最后通过像素点4邻域内是否存在不同温度类像素点来确定锋面像素点,若存在不同温度类像素点则该点为锋面点,否则不是锋面像素点。
第三步,锋面连接算法。通过应用算法前两步发现锋面识别结果较为连续,不存在锋面连接的必要性,因此第三步省略,这也提高了算法的效率。最后加上一步用于去除孤立锋面点:除去8邻域内无锋面点的锋面像素,这样会减少噪声的影响,去除噪声点或伪锋面点。
1.2.3 熵算法本文根据数据及结果的需要在应用熵算法前对数据进行了中值滤波,还进行了其他适当的修改以增强锋面识别效果,修改后的熵算法步骤如下。
熵算法[11]分为三步:
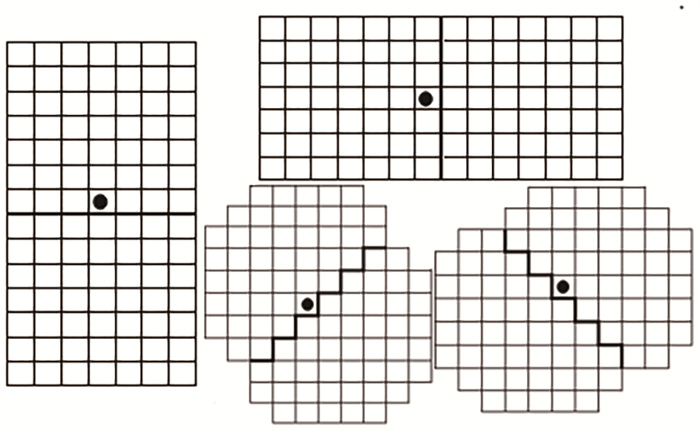
第一步,计算詹森-香农(JS)散度矩阵:将每个滑动窗口划分为两个子窗口,计算两个子窗口在水平、垂直和两个对角线四个方向的詹森-香农散度,其四个方向的最大值作为该点的散度值,最终得到散度矩阵,选择高散度值的像素点作为备选边缘像素;受到Shimada等[12]中散度计算窗口的启发,本文对比了不同规模窗口下的散度计算结果,发现在图 1所示的窗口下,计算散度能够更清晰的识别出边缘信息,故选择该窗口。
|
图 1 熵算法散度计算窗口 Fig. 1 Window for calculating divergence in entropy algorithm |
第二步,确定边缘像素点:原算法使用数次中值滤波器对散度矩阵进行平滑,但因为后面步骤识别出的锋面均为单像素宽度,而中值滤波会影响到数据的分布,进而会对锋面识别的结果产生影响,因此这里去掉中值滤波;然后以备选边缘像素点为中心在水平、垂直和两个对角线四个方向任一方向的奇数一维窗口中选择满足中心像素大于两边像素散度值的像素点作为边缘像素点,这里的边缘检测步骤进行了修改,使得检测出的锋面为单像素宽度;经过对1×3、1×5和1×7的窗口下的锋面识别结果进行比较,发现1×7窗口的结果更抗噪声,能够过滤掉部分噪声点,故一维窗口大小选择为1×7;经过对熵算法的初步测试发现,前两步识别出的锋面连续性很好,并且第三步在提升锋面连续性上的效果与其增加的计算量相比效用较小,故省去第三步。下面简述一下原算法的第三步——边缘连接:首先将每个像素点的散度看作为关于方向的连续函数,以四个已知方向的值为基础,以方向α进行最小二乘二次多项式计算进行方向判断,据此形成整个区域的方向矩阵;然后将与一个或两个边缘点相邻的点定义为端点,端点中满足特定条件的相邻点归为边缘连接点;当一个新的像素被标记为边缘时,其他相邻的像素可能会成为端点,因此算法必须预见这个事件,以便继续搜索边缘连接点。
与直方图分析法相同,最后加一步以去除孤立锋面点:除去8邻域内无锋面点的锋面像素,这样会减少噪声的影响,去除噪声点或伪锋面点。
1.2.4 Sobel算法与引力模型法的调整因Canny算法、直方图分析法和熵算法得到的结果都直接显示锋面的位置信息,而引力模型法与Sobel算法得出的是与锋面信息相关的量的分布结果,为了使各算法效果对比更充分,引力模型法与Sobel算法也进行修改以直接得出锋面分布的结果。有文献对Sobel算法的锋面中心线识别提出了解决办法,如黎安舟等[22]提出了迭代阈值法结合zhang-suen细化算法的思路,不过该方法中的细化算法对锋面位置的确定存在误差。本文受到熵算法中第三步关于边缘提取的启发,发现引力模型法、Sobel算法、熵算法都有类似的中间结果,引力模型法求出了“合力”的分布,Sobel算法求出了梯度的分布,熵算法求出了散度的分布,为了更好的对算法进行对比,可将熵算法的边缘识别步骤应用到另外两个算法上,即选择高值像素点作为备选边缘像素,在备选边缘像素中选择满足一维窗口法的像素作为边缘像素,其中高值像素点的阈值选取图像数据的80%分位数数值,其通过参考文献[7]并经过多种对比实验得出。
2 结果对比分析锋面信息提取取决于每天海表温度数据的分布,由于卫星的速度、数据质量限制等原因,每天的海表温度数据仅能覆盖一小部分海域,按月为时间单位来分析锋面信息可以提高数据的覆盖度,基本能覆盖到整个研究海域,所以本文选择在月度层面上分析锋面的信息,这样对锋面提取的容错率也有所改善,并且月度的锋面信息具有代表性,能够比较稳定、较为全面的反映相关海域的锋面分布。而单日的数据能够精确反映每天的锋面分布细节,可以用来比较各算法的细节差别。
本文选择2015年1月数据作为基础数据,用来比较各算法应用于南海及其邻近海域锋面信息提取的效果。关于月度数据的合成方式,本文对比了两种不同的方法,一种是先求月度温度均值再进行后续处理,另一种是对每天数据进行计算再按均值合成月度结果。结果表明后者的噪声更小,结果更可靠,因此选择后者。由于白天与黑夜在光照、天气方面都存在较大差异,因此白天与黑夜的海表温度数据的覆盖区域、大小等都存在差别,所以决定将白天与黑夜数据分开单独处理,每天都有两个数据集,处理成两个对应的结果,都独立参与合成最终的月度结果,这样既考虑到了白天与黑夜数据的差异,又将白天与黑夜数据融合到一起,提高了结果的稳定性与数据的利用率。
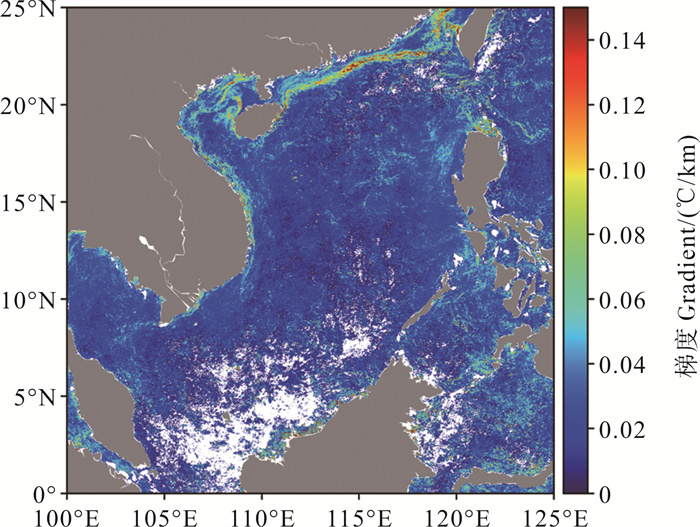
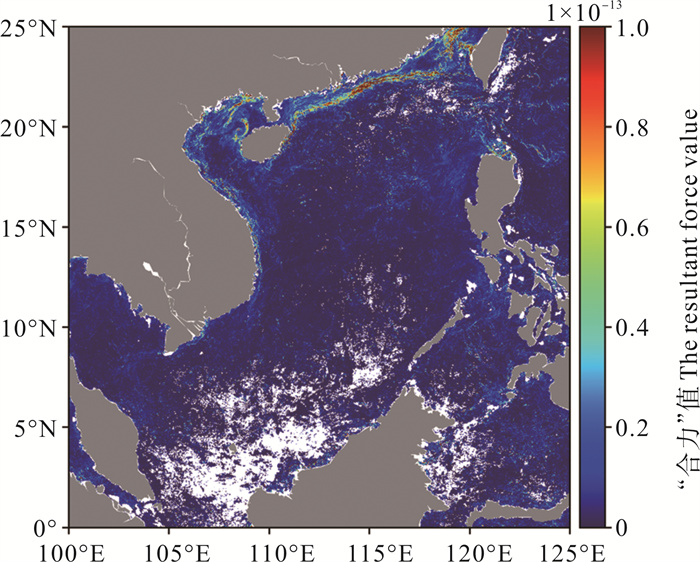
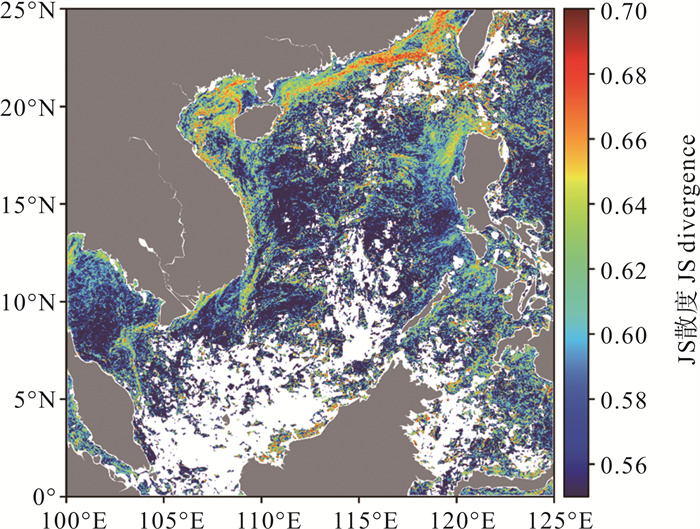
2.1 Sobel算法、引力模型法和熵算法月度中间结果对比分析图 2(a)、2(b)、2(c)分别为2015年1月Sobel算法得出的南海及其邻近海域平均梯度分布、2015年1月引力模型法得出的南海及其邻近海域平均“合力”分布、2015年1月熵算法得出的南海及其邻近海域平均散度分布。三者均为相应算法的月度平均结果,计算方式为用相应算法的指标月度总和除以总有效数据次数,因为白天与黑夜分开计算,所以白天与黑夜的有效数据都单独算一次有效次数,所谓有效是指该点的数据存在且未被质量标签过滤掉。
|
图 2a 2015年1月南海平均梯度分布(Sobel) Fig. 2a Mean gradient distribution in the South China Sea in January, 2015(Sobel) |
|
图 2b 2015年1月南海平均“合力”分布(引力模型法) Fig. 2b Average "resultant force" distribution in the South China Sea in January, 2015 (The gravity model algorithm) |
|
图 2c 2015年1月南海平均散度分布(熵算法) Fig. 2c Mean divergence distribution in the South China Sea in January, 2015 (The entropy algorithm) |
Sobel算法得出的梯度能够衡量温度变化的快慢;引力模型法通过万有引力定律计算不同像元间“引力”的“合力”,周围像素温度差异越大,像元“合力”越大,周围像素温度越均匀,那么不同方向的“引力”相互抵消,“合力”越小,因此“合力”的分布也可衡量温度变化的程度;熵算法通过计算四个方向窗口内两个子窗口中像素间JS散度的最大值得到该点的散度值,而JS散度衡量的是两个样本的概率分布的相似程度,因此像素点的散度值同样可以衡量温度变化的程度。故上述三者具有相似的特点与功能,都可衡量像元间温度变化的程度,具有可比性。像元处三种指标的值越大,表示该点的温度变化越剧烈,则越可能成为锋面像素。通过三者的对比可以初步分析三种算法的特点与差异。
三种指标均能衡量温度变化程度,故观察三种指标值的区域分布能够对锋面信息有一个直观的认识。从辨识性上来看,三种算法的指标分布情况具有一定的相似性与一致性,但三者的对比度有较大差别,对比度越大,区分指标高值区域更容易,对锋面的识别更有帮助,尤其是强锋面。由于引力模型法在数据预处理中对数据进行了局部归一化和对比度增强,因此相对于Sobel算法的梯度分布,引力模型法得出的“合力”分布的对比度更高,即指标值高的更高,指标值低的更低,这会对锋面检测有一定帮助,使锋面检测的噪声减弱,锋面识别得更精准,但可能会丢失部分细小锋面的信息,这在图 2(a)和2(b)的对比中很容易看出。与Sobel算法与引力模型法相比,熵算法的散度分布存在较多差异,散度高值区域即温度变化大的区域更多,比如(115°E—120°E,15°N—20°N)附近海域,因此相对其他两种算法,熵算法可能检测出更多的锋面信息,对弱锋面的检测能力更强,但噪声会更大。此外,因为熵算法的散度计算窗口更大,所以会丢失更多的边缘数据,导致数据覆盖度下降,数据利用率低于另外两种算法。
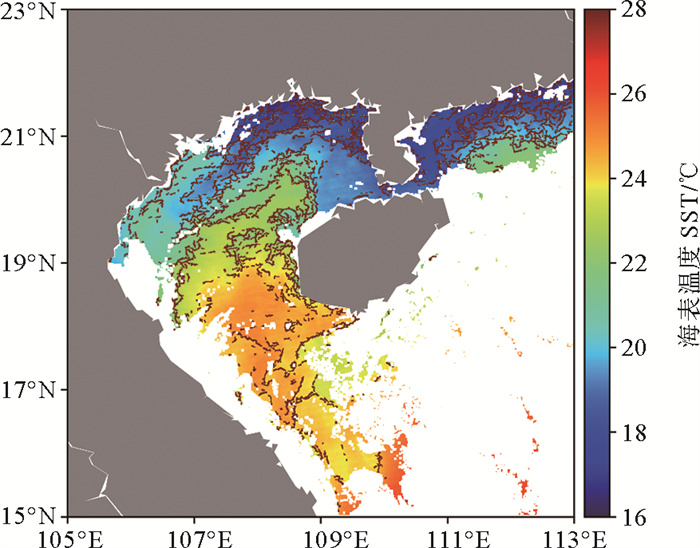
2.2 各算法单日结果对比分析图 3(a)—3(e)依次为2015年1月1日Sobel算法、Canny算法、引力模型法、熵算法和直方图分析法得出的锋面中心线叠加到海表温度分布上的结果,从各算法应用到日锋面检测的结果对比中可以更细致地比较各算法的特点与不同。整体来看,Sobel算法与引力模型法得到的锋面检测结果类似,直方图分析法检测出的锋面更加光滑连续,熵算法识别的锋面更密,Canny算法与上述算法的结果存在较大不同,识别的锋面线密度更小。
|
图 3a 2015年1月1日白天南海海表温度与锋面分布(Sobel) Fig. 3a SST and frontal distribution in the South China Sea during daytime on January 1, 2015 (Sobel) |
|
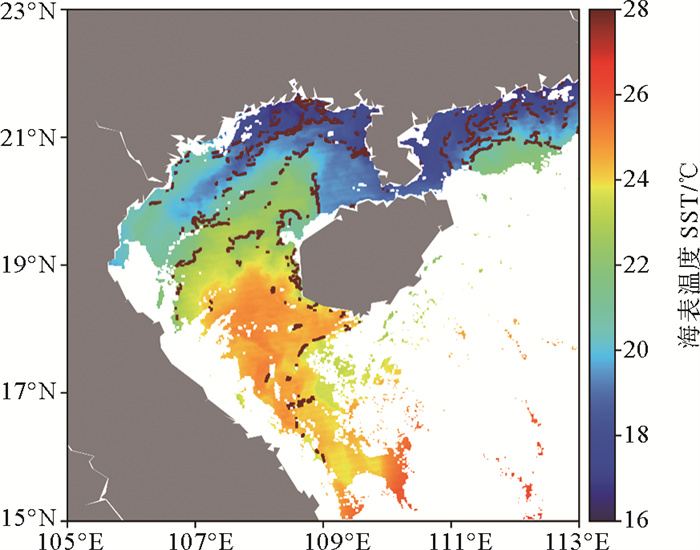
图 3b 2015年1月1日白天南海海表温度与锋面分布(Canny) Fig. 3b SST and frontal distribution in the South China Sea during daytime on January 1, 2015 (Canny) |
|
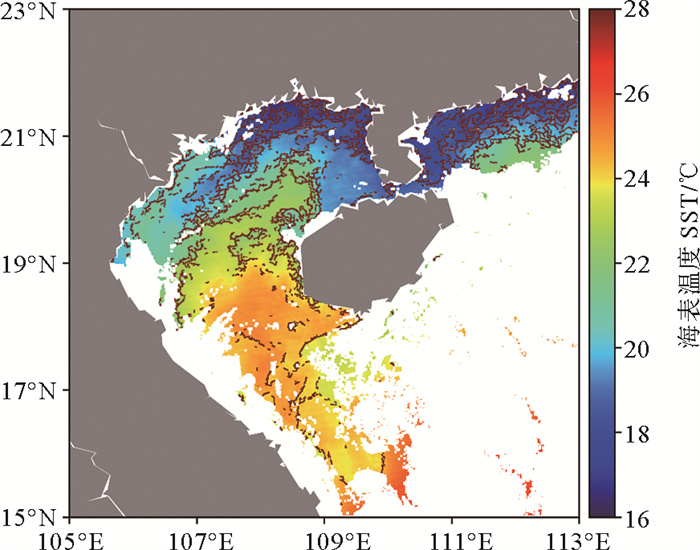
图 3c 2015年1月1日白天南海海表温度与锋面分布(引力模型法) Fig. 3c SST and frontal distribution in the South China Sea during daytime on January 1, 2015 (The gravity model algorithm) |
|
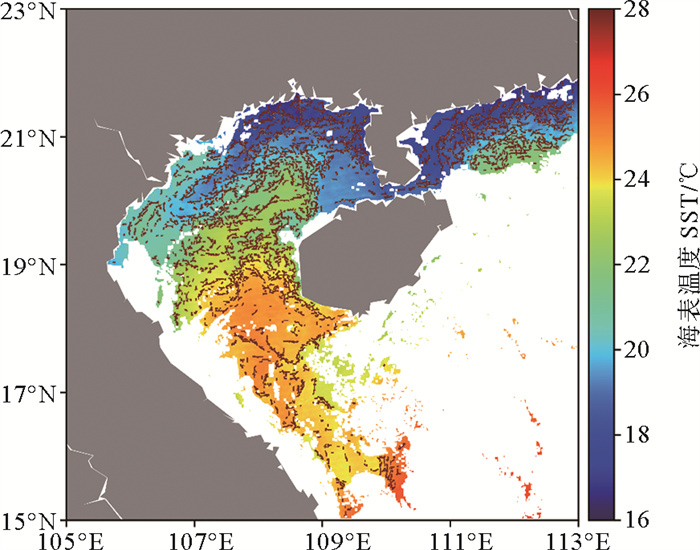
图 3d 2015年1月1日白天南海海表温度与锋面分布(熵算法) Fig. 3d SST and frontal distribution in the South China Sea during daytime on January 1, 2015 (The entropy algorithm) |
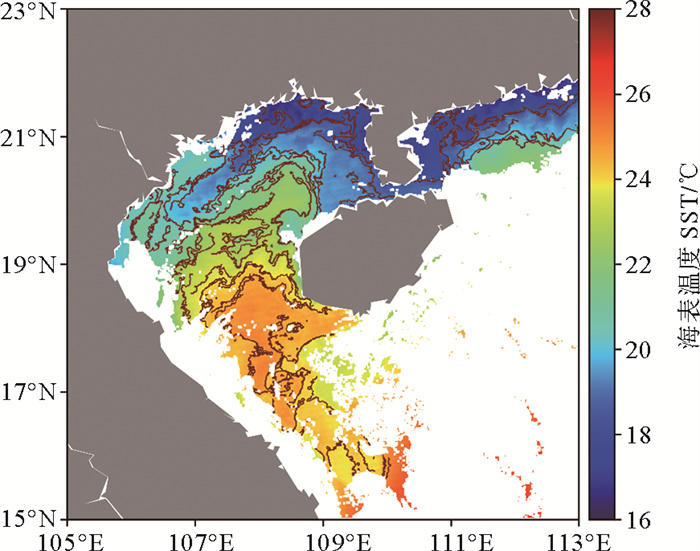
|
图 3e 2015年1月1日白天南海海表温度与锋面分布(直方图分析法) Fig. 3e SST and frontal distribution in the South China Sea during daytime on January 1, 2015 (The histogram analysis algorithm) |
具体来看,与月度数据对比类似,相比Sobel算法,引力模型法由于数据预处理不同,使其在锋面检测中更抗噪声,但可能漏检部分弱锋面,这点在图 3(a)和3(c)的对比中可以发现,两者整体上非常相近,但在大部分海域Sobel算法的锋面检测结果比引力模型法的锋面检测结果多出许多细碎的小锋面,这些细小锋面可能一部分是噪声,一部分是弱锋面,具体还需结合其他手段进行验证。Canny算法的结果与上面两个算法的区别在于其识别的锋面中心线的宽度非单像素而是多像素,这样锋面的辨识性更强,对强锋面的检测效果更好。整体来看,Canny算法识别的锋面点分布在上面两个算法识别的锋面线密集处,锋面的宽度较宽,此外,Canny算法的锋面检测结果中少了一部分细碎锋面。Canny算法锋面分布较少与双阈值检测步骤有关,这与熵算法中边缘检测的一维窗口法相比存在差别。综合来看,上述三种算法的锋面检测结果区别在于对强弱锋面检测的效果以及抗噪声的强弱。总的来说,Sobel算法、引力模型法、Canny算法对强锋面的检测能力依次递增,对弱锋面的检测能力依次递减,抗噪声能力依次递增。
熵算法检测出的锋面相比Sobel算法和引力模型法更密,并且在锋面的位置和连续性上都存在许多差异。在锋面分布上,熵算法检测出了另外两个算法均未测出的锋面,其对弱锋面的检测能力更强。在锋面的连续性上,对于三种算法都检测出的锋面,熵算法的连续性要比另外两个算法差。除此之外,熵算法检测出的锋面呈现突刺状,这可能与算法的特点和噪声干扰有关。整体来看,熵算法识别的锋面连续性一般,抗噪性一般。直方图分析法识别的锋面连续性最好,锋面连贯、清晰且顺滑,从锋面分布上来看,相比其他算法,直方图分析法识别的锋面既有相似之处,也有检测出独有锋面。具体来看,直方图分析法识别出的锋面连接了其他算法检测出的不连续短锋面,但也丢失了部分短锋面的信息,同时也有检测出独有的锋面。造成这些差异的原因不仅关系到算法的特点,还与锋面的定义、特点有关。从算法上来说,直方图分析法注重分析窗口内明显含有两类温度的情况,并对两类温度的占比、空间分布都有限制,这与以梯度计算为基础的Sobel算法和以散度计算为基础的熵算法都有很大不同,也就造成了结果的较大差异。综合来看,熵算法识别的锋面更多更密,检测出的弱海温锋更多,但抗噪性一般。直方图分析法识别的锋面连续性最好,锋面清晰连贯,抗噪性较好。
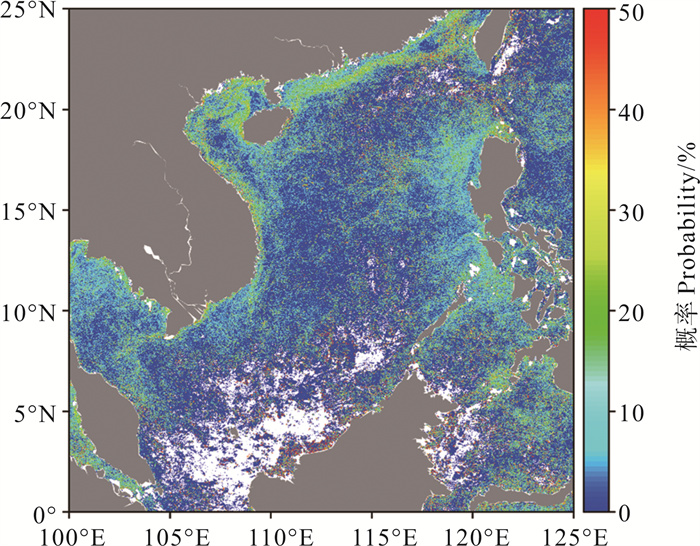
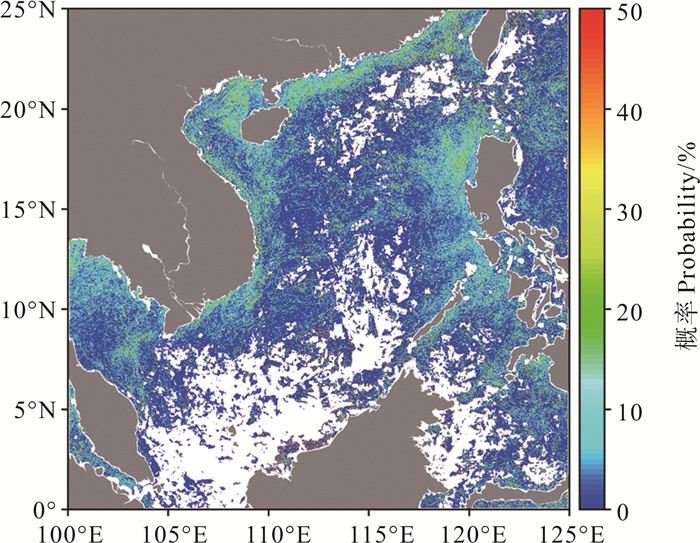
2.3 各算法月度锋面概率对比分析月度锋面概率是计算月份中该像素点被标记为锋面点像素的次数占总有效数据次数的概率,其中白天与黑夜看作是两次独立的数据,图 4(a)—4(e)分别展示了2015年1月Sobel算法、Canny算法、引力模型法、熵算法和直方图分析法得到的月度锋面概率分布图,这里锋面点定义为各算法检测出的锋面中心线像素点。整体来看,Sobel算法、引力模型法和熵算法的月度锋面概率分布相似度较高,另外两种算法的月度概率分布则差别较大。
|
图 4a 2015年1月月度锋面概率分布(Sobel) Fig. 4a Monthly front probability distribution in January, 2015 (Sobel) |
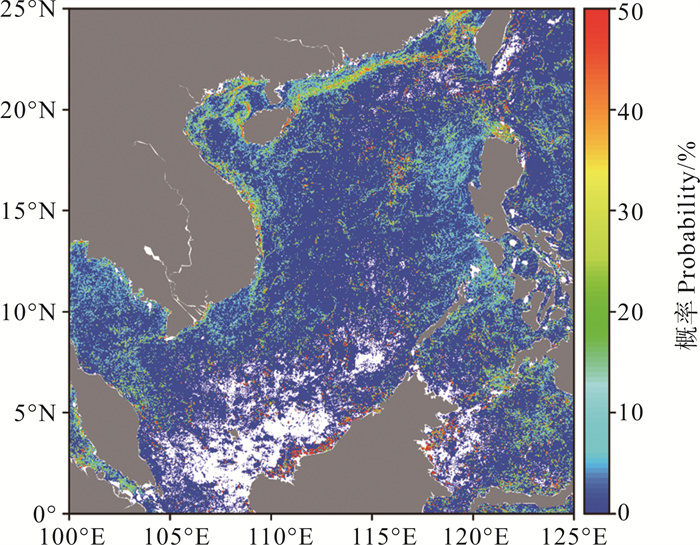
|
图 4b 2015年1月月度锋面概率分布(Canny) Fig. 4b Monthly front probability distribution in January, 2015(Canny) |
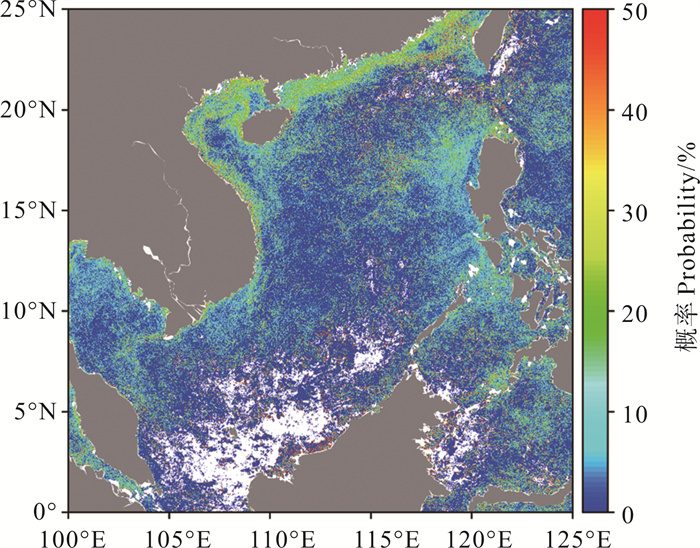
|
图 4c 2015年1月月度锋面概率分布(引力模型法) Fig. 4c Monthly front probability distribution in January, 2015(The gravity model algorithm) |
|
图 4d 2015年1月1日白天南海海表温度与锋面分布(熵算法) Fig. 4d SST and frontal distribution in the South China Sea during daytime on January 1, 2015 (The entropy algorithm) |
|
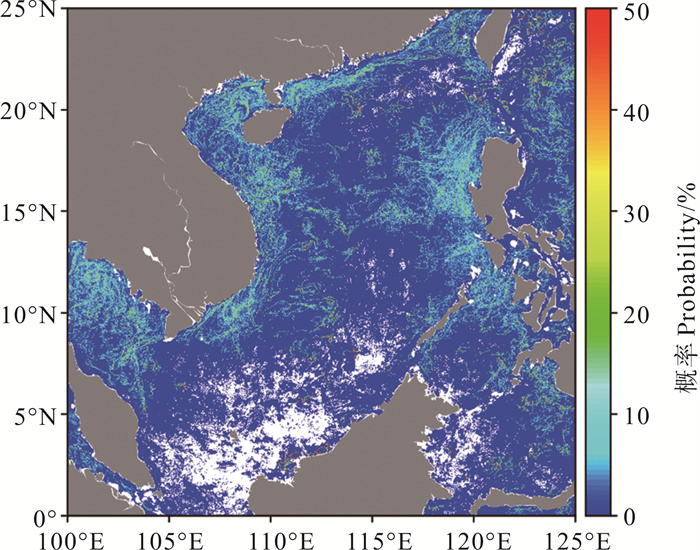
图 4e 2015年1月月度锋面概率分布(直方图分析法) Fig. 4e Monthly front probability distribution in January, 2015(The histogram analysis algorithm) |
引力模型法、Sobel算法和熵算法的锋面概率分布也存在明显区别,三种算法的锋面概率依次减小,且锋面概率大的海域面积有所递减,比如在广东沿岸附近海域,引力模型法、Sobel算法、熵算法的锋面概率依次减小,且锋面概率大的海域面积也减小;但在吕宋岛西部至南海中部海域存在例外,此处熵算法的锋面概率甚至稍大于另外两个算法,这部分反映了熵算法对弱锋面的检测能力更强。因此,在整体上,引力模型法、Sobel算法、熵算法对强锋面的检测能力依次递减,对弱锋面的检测能力依次递增,抗噪性递减。对于Canny算法,其锋面概率高的区域概率更高更集中,锋面概率小的海域面积更小,因此Canny算法对强锋面的检测能力最强,对弱锋面的检测能力最弱,抗噪性最强。
前面分析发现,直方图分析法的锋面连续性最强,但锋面的密度比引力模型法、Sobel算法、熵算法低一些,这也反映在月度概率分布上,直方图分析法的月度锋面概率整体上是小于其他算法的。此外,直方图分析法的月度概率分布在许多锋面的检测中与其他算法差别较大,比如在台湾海峡和越南沿岸海域,其他算法都检测出面积较大且概率较大的锋面,而直方图分析法虽然也检测出了锋面,但概率和面积要小得多。另外,直方图分析法对弱锋面的检测能力强于Canny算法,比如在吕宋岛西部海域和泰国湾海域,直方图分析法的锋面概率都较Canny算法更明显,但与引力模型法、Sobel算法、熵算法也存在明显不同,其他三种算法都表现为吕宋岛西部海域的锋面概率大于泰国湾海域的锋面概率,而直方图分析法中两处海域的锋面概率相似。上面这些不同可能与算法的特点及锋面的定义相关。
3 结语从海温锋的定义、特点来看,各算法的出发点为识别温度变化大的区域,但因各算法的计算方式、侧重点、基础指标的不同,对温度变化大不能进行统一定量的规定,因此不同算法对海温锋的严格量化定义存在差异,这导致不同算法结果出现较大差异。
以梯度计算为基础的Sobel算法或者其他梯度类算法适用于精确计算温度变化程度的应用场景,原因在于梯度具有实际的物理意义,代表了海域内温度变化的程度。Canny算法以Sobel算子为基础计算梯度,不同在于对锋面点识别的规则,Canny算法识别的锋面为多像素宽度,对细小的弱锋面检测较差,因此Canny算法适用于强锋面的研究。引力模型法以万有引力定律为基础计算像素点的“合力”,其本质与Sobel算子类似,独特之处在于数据处理,在计算“合力”前对数据进行局部归一化和对比度增强,使其对强锋面的检测能力和抗噪性更强,因此引力模型法适用于应用噪声较大的数据检测锋面或者强锋面的检测。熵算法以JS散度计算为基础,JS散度代表了两类数据间概率分布的相似程度,故散度大小可以衡量温度变化的强弱,即锋面的强弱,熵算法检测出的锋面多而密,能够检测出其他算法检测不到的锋面信息,这种锋面信息更多偏向为弱锋面,因此熵算法适用于弱锋面的检测。直方图分析法以窗口内温度分布是否能分为两类为突破口,利用直方图分布的单双峰来筛除单峰,只分析双峰分布的窗口,然后通过建立窗口内每类温度的内聚度指标来筛选不满足条件的锋面,这样检测出的锋面表现出较强的连续性,锋面光滑且连贯,因此直方图分析法适合分析连续长锋面。
在应用锋面识别算法分析具体海域的海温锋时空特征时, 要根据海温数据的特点、研究海域的海温锋特点、研究目的及要求等选择合适的算法进行海温锋识别。
| [1] |
罗琳, 王东晓, 刘赟, 等. 北部湾温度锋的季节与年际变化[J]. 热带海洋学报, 2003(4): 60-67. Luo L, Wang D X, Liu Y, et al. Seasonal and interannual variability of thermal fronts in Beibu Gulf, South China Sea[J]. Journal of Tropical Oceanography, 2003(4): 60-67. (  0) 0) |
| [2] |
邱春华, 崔永生, 胡诗琪, 等. 基于融合遥感数据的广东沿岸温度锋面的季节变化研究[J]. 热带海洋学报, 2017(5): 16-23. Qiu C H, Cui Y S, Hu S Q, et al. Seasonal variation of Guangdong coastal thermal front based on merged satellite data[J]. Journal of Tropical Oceanography, 2017(5): 16-23. (  0) 0) |
| [3] |
Belkin I M, O'Reilly J E. An algorithm for oceanic front detection in chlorophyll and SST satellite imagery[J]. Journal of Marine Systems, 2009, 78(3): 319-326. DOI:10.1016/j.jmarsys.2008.11.018 (  0) 0) |
| [4] |
Cayula J, Cornillon P. Edge detection algorithm for SST images[J]. Journal of Atmospheric and Oceanic Technology, 1992(9): 67-80. (  0) 0) |
| [5] |
Cayula J, Cornillon P. Multi-image edge detection for SST images[J]. Journal of Atmospheric and Oceanic Technology, 1995, 12(4): 821-829. DOI:10.1175/1520-0426(1995)012<0821:MIEDFS>2.0.CO;2 (  0) 0) |
| [6] |
Nieto K, Demarcq H, Mcclatchie S. Mesoscale frontal structures in the Canary Upwelling System: New front and filament detection algorithms applied to spatial and temporal patterns[J]. Remote Sensing of Environment, 2012, 123: 339-346. DOI:10.1016/j.rse.2012.03.028 (  0) 0) |
| [7] |
平博, 苏奋振, 杜云艳, 等. 基于引力模型的海洋锋信息提取[J]. 地球信息科学学报, 2013(2): 187-192. Ping B, Su F Z, Du Y Y, et al. Application of the model of universal gravity to oceanic front detection near the Kuroshio front[J]. Journal of Geo-Information Science, 2013(2): 187-192. (  0) 0) |
| [8] |
Sun G, Liu Q, Liu Q, et al. A novel approach for edge detection based on the theory of universal gravity[J]. Pattern Recognition, 2007, 40(10): 2766-2775. DOI:10.1016/j.patcog.2007.01.006 (  0) 0) |
| [9] |
Lopez-Molina C, Bustince H, Fernandez J, et al. A gravitational approach to edge detection based on triangular norms[J]. Pattern Recognition, 2010, 43(11): 3730-3741. DOI:10.1016/j.patcog.2010.05.035 (  0) 0) |
| [10] |
平博, 苏奋振, 杜云艳, 等. 北京一号数据检测渤海海洋锋[J]. 遥感学报, 2014(3): 686-695. Ping B, Su F Z, Du Y Y, et al. Bohai sea front detection using BJ -1 small satellite data[J]. Journal of Remote Sensing, 2014(3): 686-695. (  0) 0) |
| [11] |
Vázquez D, Atae-Allah C, Escamilla P. Entropic approach to edge detection for SST images[J]. Journal of Atmospheric and Oceanic Technology, 1997, 16(7): 970-979. (  0) 0) |
| [12] |
Shimada T, Sakaida F, Kawamura H, et al. Application of an edge detection method to satellite images for distinguishing sea surface temperature fronts near the Japanese coast[J]. Remote Sensing of Environment, 2005, 98(1): 21-34. DOI:10.1016/j.rse.2005.05.018 (  0) 0) |
| [13] |
Chang Y, Cornillon P. A comparison of satellite-derived sea surface temperature fronts using two edge detection algorithms[J]. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 2015, 119: 40-47. DOI:10.1016/j.dsr2.2013.12.001 (  0) 0) |
| [14] |
李阳东, 梁君豪, 笪亨融, 等. 基于直方图分析和Jensen-Shannon散度的海表温度锋检测[J]. 海洋测绘, 2022(4): 60-64. LI Y D, Liang J H, Da H R, et al. Sea surface temperature front detection based on histogram analysis and Jensen-Shannon divergence[J]. Hydrographic Surveying and Charting, 2022(4): 60-64. (  0) 0) |
| [15] |
薛存金, 苏奋振, 周军其. 基于小波分析的海洋锋形态特征提取[J]. 海洋通报, 2007(2): 20-27. Xue C J, Su F Z, Zhou J Q. Extraction of ocean fronts based on wavelet analysis[J]. Marine Bulletin, 2007(2): 20-27. (  0) 0) |
| [16] |
陈捷, 陈标, 许素芹. 基于二维连续小波变换的SAR图像海洋现象特征检测[J]. 电子学报, 2010(9): 2128-2133. Chen J, Chen B, Xu S Q. Detection of ocean features in SAR images with 2D continuous wavelet power spectrum[J]. Acta Electronica Sinica, 2010(9): 2128-2133. (  0) 0) |
| [17] |
黎安舟, 周为峰, 范秀梅. 遥感图像中尺度海洋锋及涡旋提取方法研究进展[J]. 中国图象图形学报, 2017(6): 709-718. Li A Z, Zhou W F, Fan X M. Research progress of methods for the extraction of mesoscale ocean fronts and eddies based on remote sensing data[J]. Journal of Image and Graphics, 2017(6): 709-718. (  0) 0) |
| [18] |
Hopkins J E, Challenor P, Shaw A. A new statistical modeling approach to ocean front detection from SST satellite images[J]. Journal of Atmospheric and Oceanic Technology, 2008, 27(1): 173-191. (  0) 0) |
| [19] |
吴曲然, 胡建宇, 孙振宇, 等. 海洋锋面统计模型检测法的改进与验证[J]. 厦门大学学报: 自然科学版, 2015(2): 199-206. Wu Q R, Hu J Y, Sun Z Y, et al. Improvement and validation of a statistical modeling approach to ocean front detection[J]. Journal of Xiamen University: Natural Science, 2015(2): 199-206. (  0) 0) |
| [20] |
曹维东, 解翠, 韩冰, 等. 融合深度学习的自动化海洋锋精细识别[J]. 计算机工程, 2020(10): 266-274. Cao W D, Xie C, Han B, et al. Automatic fine recognition of ocean front fused with deep learning[J]. Computer Engineering, 2020(10): 266-274. (  0) 0) |
| [21] |
徐慧芳, 黄冬梅, 贺琪, 等. 融合scSE模块的改进Mask R-CNN海洋锋检测方法[J]. 海洋通报, 2022(1): 19-28. Xu H F, Huang D M, He Q, et al. Improved Mask R-CNN ocean front detection method fused with SCSE module[J]. Marine Bulletin, 2022(1): 19-28. (  0) 0) |
| [22] |
黎安舟, 周为峰, 范秀梅. 遥感图像中尺度海洋锋及涡旋提取方法研究进展[J]. 中国图象图形学报, 2017(6): 709-718. Li A Z, Zhou W F, Fan X M. Research progress of methods for the extraction of mesoscale ocean fronts and eddies based on remote sensing data[J]. Journal of Image and Graphics, 2017(6): 709-718. (  0) 0) |
2. College of Marine Technology, Faculty of Information Science and Engineering, Ocean University of China, Qingdao 266100, China
 2024, Vol. 54
2024, Vol. 54


