自动水面航行器(Autonomous surface vehicles)也称为无人水面航行器(Unmanned surface vehicles)[1-2],已迅速发展成为海洋科学技术的一个重要研究领域,对海洋工业具有重要意义。与传统的船舶相比,ASV具有体型小、造价低以及多用途的特点[3],这些特点使它可以独立完成一些特殊任务。尤其是在一些长期任务中,ASV低能耗的特点使它在燃料补给不方便的环境中仍能继续工作。ASV的应用十分广泛[4-5],不仅包括民用领域,还包括科学研究和国防安全。
根据为船提供的动力来源,我们将ASV划分为自动航行船艇和自动航行帆船[6],船艇的动力来源于发动机,而帆船的动力来源于自然的风。在这两者中,自动航行船艇得到了更多研究者的关注,主要是因为船艇具有发动机,所获得的速度更快更稳定; 其次自动航行船艇技术的实际应用范围更加广泛,如小型的游艇、大型的客船甚至战舰。
虽然自动航行船艇具有很多的优势,但是却不适合去完成一些长期远海任务,因为航行所需要的能源补给是一个很大问题。在远海补给困难的情况下,使用自动航行帆船是一个很好的选择。自动航行帆船的动力来源于风,并且不消耗任何化石燃料更加环保。它可长期处于工作状态,随时接受命令执行航行或静止,独立完成一些长期性的远海特殊任务。但是,对帆船的研究相较于船艇来说更加复杂,因为决定帆船航行的因素很多,海上的风为船提供了动力,风的大小和方向决定了船在静水中的速度。而在海面上,海流的速度和方向又会影响着船速。所以最终的帆船速度是由海面环境条件共同决定的。
在帆船的自动导航领域,绝大部分的研究者都只考虑风对自动导航帆船路径规划的影响。其中,图搜索算法应用比较广泛[7-8],该算法将航行地图分成网状格,将地图离散化。图中的每个点都是帆船航行过程的潜在位置,并且每个点都有风速和风向的属性,船在任意点都可以根据帆船的VPP模型[9]获得帆船在此点的速度。当船在两点之间航行时,两点的距离与两点速度的平均值得到时间,最后利用传统寻路算法(如A*和Dijkstra)获得一条所用总时间最小的路径。另一种是基于势能的方法[10-11],研究者将其分为全局势能和局部势能两部分。全局势能是在整张地图上进行分配,将目标点设置为地图中势能最小的位置,而障碍物则具有很大的势能; 局部势能是对帆船自身进行分配,根据风向在船周围划分了顺风禁行区、逆风禁行区以及滞后区,其中滞后区是防止帆船频繁的变换方向而导致倾覆。将势能分配完毕后,帆船将朝向势能最小的方向运动。除此之外,还有以模糊理论控制算法[12]为基础,以先进的高清相机探测[13]为基础的方法来实现自动航行帆船的路径规划。
而在自动船艇的路径规划方面,往往忽略风的作用,更关注海流及障碍物[14]对航行安全的影响。研究者使用了与帆船类似的图搜索法[15]以及基于模糊理论[16]的方法。还有同样强化学习[17-18]、AIS数据[19]、航向移动窗[20]和遗传进化算法[21]。
总的来说,在考虑各种因素下为自动航行帆船找到最优路径是实现帆船自动航行的关键问题。本文提出了基于强化学习的帆船路径规划算法,综合考虑了帆船内在的模型因素以及外在海风、海流以及障碍物的环境影响,为其规划出一条合理的路径。在众多的机器学习方法中,我们将强化学习[22]用在了为帆船规划路径当中。相较于传统的寻路算法,本文算法不需要提前获取全图的路径信息,它通过学习过程中自身输入与环境的相互作用得到反馈,进而确定下一步行动,这更符合实际驾驶帆船航行的情况。
1 自动航行帆船模型众所周知,帆船在海面航行的动力来源于海风和海流,这使得帆船成为蒸汽机之前传统的水上最主要运输工具之一。与其它现代水上交通工具相比,帆船最大的优势正是其航行无需消耗化石燃料,这使得自动航行帆船成为完成长期无间断工作的最佳选择。对于帆船来说,应该优先考虑的主要特征是风和流,因为风和流会代替了在船艇的螺旋桨,成为给帆船提供推进力的主要动力。本章主要对帆船的航行原理,以及本文使用的帆船运动模型进行介绍,以获得一种真实有效的帆船数值模拟方法
1.1 帆船的受力分析帆船主要由船体、桅杆、帆、船舵和中央板五部分组成。如图 1所示,船体是帆船的主要部件,根据帆船型号的不同,船体的大小也不一样; 桅杆的作用是用来固定船帆; 船帆用来接收海上的风,正是因为船帆的受力,才推动帆船前进; 舵的作用相当于汽车的方向盘,用于控制帆船的航行方向; 中央板用于维持帆船的姿态,防止帆船侧翻。
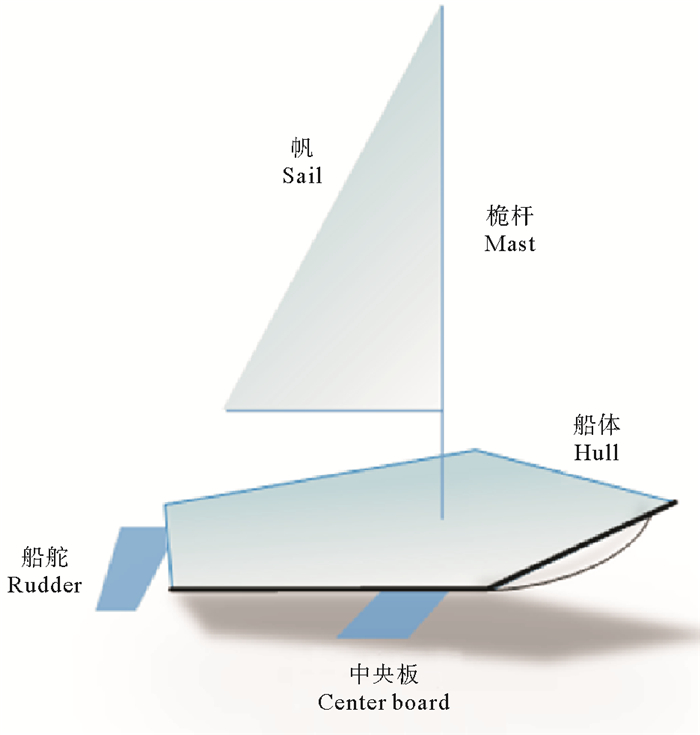
|
图 1 帆船结构图 Fig. 1 The structure of the sailboat |
当风以非垂直方向吹过船帆时,由于船帆产生了一个弧形,船帆两边的气体流动速度出现差异。根据伯努利效应[23],这个风速的差异会在船帆的两侧产生一个压力差,这个压力差产生了对船帆的推力。我们可以把风分为三种,真实风、航行风和相对风。真实风是在陆地测试得到的风速; 航行风的方向与帆船航行方向相反,等于船的航行速度; 相对风是真实风和航行风的矢量合成。帆船受力分析如图 2所示。相对风和航行方向之间的夹角是β。相对风作用于船帆产生了气动升力FL和气动阻力FD两部分,气动阻力FD与相对风的方向相同,而气动升力FL垂直于FD。它们的大小取决于升力系数Cl和阻力系数Cd决定。Cl与船帆周围动态的风压所产生的升力有关; Cd量化了船帆通过风的阻力。气动升力和气动阻力可以由式(1)求得:
| $ \left\{\begin{array}{l} F_{\mathrm{L}}=\frac{1}{2} \rho S C_{1} V_{\mathrm{r}}^{2} \\ F_{\mathrm{D}}=\frac{1}{2} \rho S C_{\mathrm{d}} V_{\mathrm{r}}^{2} \end{array}\right.。$ | (1) |
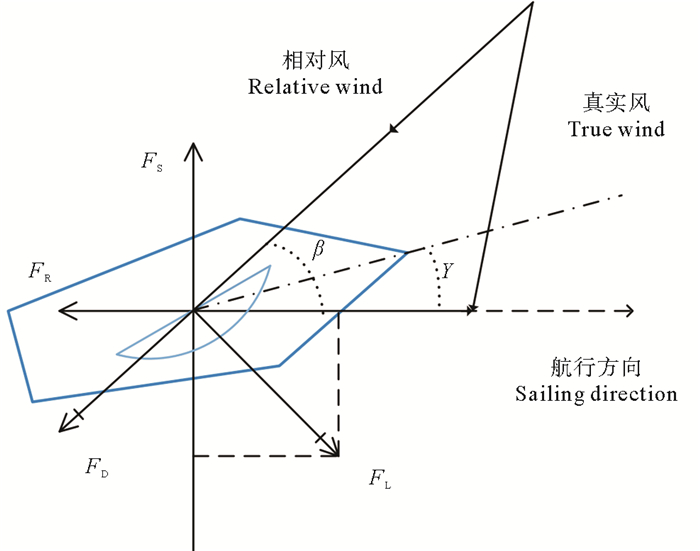
|
图 2 帆船的受力分析 Fig. 2 Force analysis of the sailboat |
式中:ρ是空气密度; S是船帆面积; Vr是相对风的速度。进一步,由气动升力和气动阻力的在船前进方向上的分力得到帆船的推进力:
| $ F=F_{\mathrm{L}} \sin \beta-F_{\mathrm{D}} \cos \beta。$ | (2) |
气动升力和气动阻力在垂直于帆船前进方向的分量的合力构成了侧向力:
| $ F_{\mathrm{S}}=F_{\mathrm{L}} \cos \beta+F_{\mathrm{D}} \sin \beta。$ | (3) |
在逆风行驶时,航行方向与船头的指向是不同的,这个夹角γ称为漂角。同时,由于帆船在水中行驶,水对帆船产生了相对运动方向的力FR和FS。
综上所述,帆船的速度取决于真实风速的大小和方向,当帆船需要沿逆风方向航行时,β趋近于0,推进力F为负值,不能在逆风时直线行驶,所以为了能够顺利地到达目的地,帆船必须要选择“Z”字型路线。
1.2 帆船的运动模型严格来说,一艘在海上运动的船舶在空间当中有6个自由度,其中平移运动3个:纵荡、横荡、垂荡,转动运动3个:横摇、纵摇、艏摇(见图 3)。所以想要完整的表达运动状态下船的状态向量要包括以上6个维度以及船的位置等信息,复杂程度可想而知。
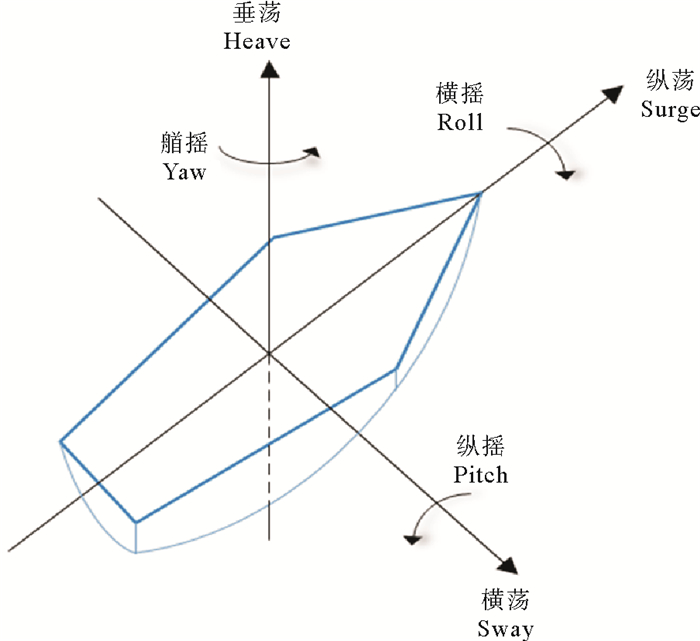
|
图 3 船的6个维度 Fig. 3 Six-degree-of-freedom motion model |
在自动航行船舶的路径规划问题当中,我们更关注的是在船体水平面上发生的运动情况,而船在垂直面上发生的位移变化或摇摆角度变化通常不考虑在内,这主要是为了简化问题,提高算法的效率。所以在研究船舶路径规划问题时,平面运动模型更多的被用到。这样也可以减少船舶的状态向量维数,维数的增加会增加计算复杂度,所以为了再次提高算法效率,式(4)展示了本文在考虑海流影响下的帆船运动公式,在这样的二维平面中研究路径规划问题既有合理性又提高了算法效率。
| $ \left[\begin{array}{l} x \\ y \\ \varPhi \end{array}\right]=\left[\begin{array}{c} V \cos \varphi+V_{\mathrm{c} x}(x, y) \\ V \sin \varphi+V_{\mathrm{c} y}(x, y) \\ \phi \end{array}\right]。$ | (4) |
式中:x和y是船舶在水平面上的位置坐标; V是船舶的航行速度; ϕ是帆船航向与水平x轴的夹角。Vcx(x, y)和Vcy(x, y)分别是海流在座标点(x,y)处沿着x轴和y轴方向的速度。ϕ是船舶在海面上的角速度,代表了船舶航向变化的速率。由于帆船机构中的中央版具有稳定船体抵消横向力的作用,并且在平稳海面中海流速度不大的条件下,与帆船速度方向相垂直的海流速度将被忽略。
帆船不像普通的船舶有发动机提供稳定的速度,其速度来源于海风。在将上述的船舶平面运动模型运用到帆船之前,还需要考虑帆船的运动模型以得到帆船航行速度V。在帆船的运动模型研究中,速度预测程序(Velocity prediction programs, VPP)[9]是主要方式之一。这个程序方式是将帆船进行水池实验,再通过风洞测量将帆船的动力特点参数化,最终可以输出一个极坐标图,用来展示连续变化的真实风速Vw、船速V和航行角度的关系。由于船体模型以及船帆大小的不同,型号不同的帆船具有不同的极坐标。图 4是通过对J24帆船的测试数据所绘制的极坐标图,图中显示了在给定不同的真实风速和风向条件下,船在稳定状态所能达到的最大速度。两侧的浅蓝色区域分别是逆风禁行区和顺风禁行区,在顺风禁行区中理论上是可以航行的,但是出于安全考虑,帆船的航行通常会避开完全顺风的方向。
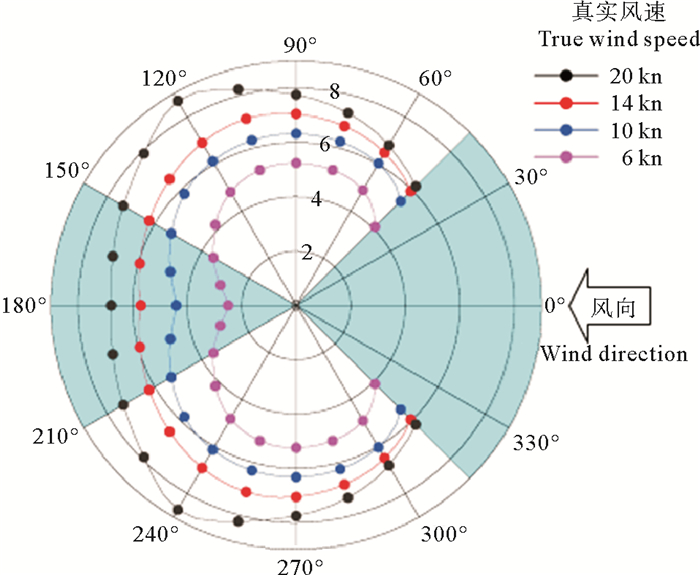
|
图 4 帆船极坐标图 Fig. 4 Polar plot of the sailboat |
根据帆船的极坐标图,船体360°的范围可以分成4个区域(见图 5):(1)有效行驶区; (2)逆风禁行区; (3)滞后区; (4)顺风禁行区。其中滞后区与有效行驶区的极坐标速度曲线是对称的,当船航向位于逆风和顺风区域时,两侧都是有效行驶区。设置滞后区的原因是当需要进行下一步路径选择时,应尽量避免选择这个区域以防止帆船因剧烈的转向而导致发生倾覆等危险情况。
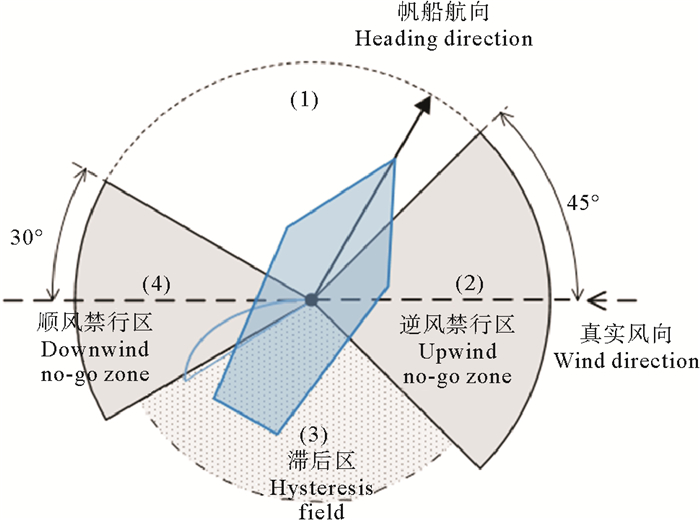
|
图 5 帆船航行区域 Fig. 5 Motion regions of the sailboat |
强化学习(Reinforcement learning,也称为增强学习)是机器学习三大分支之一,它与另外两类监督学习、无监督学习的主要区别在于强化学习是系统与环境进行交互,以使选择的行动获得的奖励最大。强化学习在路径规划领域主要应用在室内机器人[24]。
2.1 强化学习概况强化学习算法主要由智能体(Agent)、状态(State)、环境(Environment)、行动(Action)以及奖励(Reward)组成。智能体也就是实施行动的主体,所决定的行动与环境进行交互。环境是一个与智能体相互独立的系统,它为智能体所实施的行动提供反馈。状态是智能体的内在表达,使智能体可以用参数进行表示。奖励是一个数值,用来表示所选择的行动在环境条件下是利还是弊。图 6展示了强化学习算法的流程图。主体在状态st下选择了行动at,经过环境之后,反馈了奖励值rt+1,同时主体的状态更新为st+1。
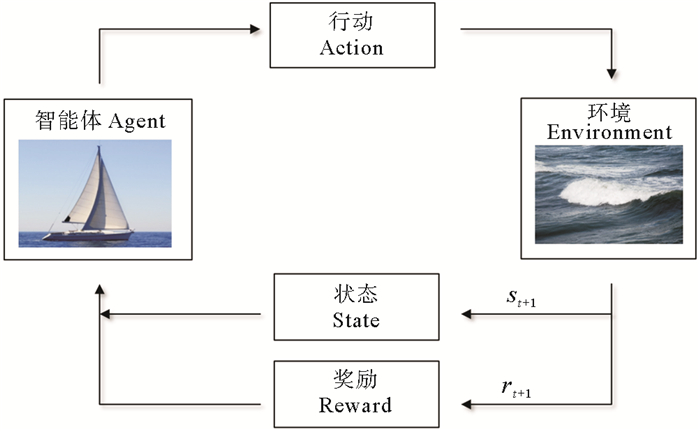
|
图 6 强化学习算法流程图 Fig. 6 Flow diagram of reinforcement learning algorithm |
所以在路径规划问题里,强化学习可以用来找出一条最优路径。当主体选择了一个行动获得了环境反馈的奖励,重复这个过程使得主体选择可以获得最大奖励的行动。强化学习也有很多的分支,本文使用的Q-learning算法属于Off-Policy,其表达式为:
| $ \begin{array}{l} \mathit{\boldsymbol{Q}}(S,A) \leftarrow \mathit{\boldsymbol{Q}}(S,A) + \\ \alpha \left[ {R + \gamma {{\max }_a}\mathit{\boldsymbol{Q}}\left( {{S^\prime },a} \right) - \mathit{\boldsymbol{Q}}(S,A)} \right]。\end{array} $ | (5) |
式中:行动A表示在状态S的所有行动集合; a则表示其中的一个具体动作,它们之间的关系是:a∈A。α为学习率(Learning rate); γ为折扣因子(Discount factor); R是在状态S时实施行动a的奖励值; Q(S, A)是Q-learning的动作价值函数,它是一个矩阵,代表了每个状态下所有行动所对应的逻辑值,本文使用了python编程,其数值是通过Pandas库中的”.loc”计算得到。根据式(5)可以看出,学习速率α越大,保留之前训练的效果就越少。折扣因子γ越大,maxaQ(S′, a)所起到的作用就越大。maxaQ(S′, a)可以看作是智能体记忆中的利益,它是智能体在状态S时选择能获得最大Q值的动作,同时使状态更新到S′。这样智能体再次处于状态S时会选择正确的动作继续进入这个S′。
相较于On-Policy的算法(如Sarsa算法),Q-learning将优化与探索分开考虑。在优化部分,Q-learning在每步选择最大值Q的动作本质来说是一种贪心行为。虽然每步都是得到最优的结果,但是智能体在学习阶段还是需要去探索其他动作,因为如果智能体每次只选择最贪心的动作,那些一开始没有产生最优Q值的动作是永远无法被探索的。所以在探索部分,使用了ε-greedy策略,在概率为ε时随机选择一个非最优的动作而在概率1-ε时选择最优的动作。所以Q-learning可以在保证探索的同时获得最优解。
2.2 问题公式化采用强化学习来解决自动航行帆船的路径规划问题,用帆船的平面运动模型来考虑环境对帆船的影响,需要对问题里的各部分进行公式化。
首先,我们使用图搜索算法有效地将海面上连续空间分割成离散的网状图,将连续的帆船运动状态以及控制行为进行离散化处理。地图的位置变量离散为一个个正方形区域,这些区域包括了目标点位置pgoal,障碍物位置pobsi,每个正方形的中心作为帆船的移动节点,同时也包含了这个位置的海风和海流特性。地图的角分辨率为45°,也就是每个移动节点周围会有8个潜在的移动方向。帆船在每个节点之间航行时不改变方向,只有当帆船到达节点后,才会重新选择方向。
其次,结合Q-learning与路径规划问题。根据上一节介绍的概况,“智能体”代表了帆船,而“环境”就是海洋上的海风速度Vw和海流速度Vc。结合帆船的平面运动模型,帆船的状态由帆船的位置和航向组成,其表达式s为:
| $ s=\left[p_{x}, p_{y}, D_{\text {heading }}\right]。$ | (6) |
式中:px和py是帆船在x和y坐标轴上的坐标; Dheading是帆船此时的朝向。根据1.2节内容,帆船为了在航行时为了保证安全会设置逆风和顺风禁行区以及避免频繁选择滞后区。所以在规划路径时,大部分情况下帆船的行动a会从以下5个之中选择:沿航向直行、左偏45°、右偏45°、左偏90°和右偏90°。
对于帆船路径规划问题,理想的结果是获得一条所用时间最少的路径。所以这里的奖励是一个负面奖励,也就是说这个奖励值越小越好。为了获得时间最少的路径,我们将奖励r定义为帆船通过两个节点间距离所用的时间倒数,其表达式t为:
| $ t=2 d_{i j} /\left(v_{i}+v_{j}\right) ; $ | (7) |
| $ r=1 / t。$ | (8) |
式中:i与j是地图中相邻的两点; dij是它们之间的欧式距离; vi和vj分别是帆船在i点与j点的速度; 其大小是由该点的Vw和Vc决定的:
| $ v_{i}=v_{i}\left(\boldsymbol{V}_{\mathrm{w}}, \boldsymbol{V}_{\mathrm{c}}\right) ; $ | (9) |
| $ v_{j}=v_{j}\left(\boldsymbol{V}_{\mathrm{w}}, \boldsymbol{V}_{\mathrm{c}}\right)。$ | (10) |
当帆船能够完成从起始点到目标点的航行,将此次航行中每段距离所需要的时间和定义为总奖励,于是要获得所用时间最少的路径即是获得最大的总奖励。
在规划最优路径的同时,要考虑对于障碍物的规避。海面上的障碍物主要包括海岛以及礁石,如果船驶入障碍物的范围有发生危险的可能。对于已知位置的障碍物,如果帆船距离障碍物的距离dobstacle满足一定条件,则给予帆船一个负的奖励N作为惩罚。与其相反若dgoal满足一定条件,则给予一个正的奖励M,表示已经到达了目标点。
综上,该算法的奖励表达式为:
| $ R(s, a)=\left\{\begin{array}{ll} N, & \text { if } d_{\text {obstacle }}<d_{1} \\ M, & \text { else if } d_{\text {goal }}<d_{2} \\ r, & \text { o. } \mathrm{w} . \end{array}\right.。$ | (11) |
在这里,将N的值设为-100,代表经过障碍物所给予的惩罚; M值设为+100,代表此处就是目标点。d1和d2是帆船到障碍物和目标点的安全距离。使用Q-learning算法,在考虑海风、海浪以及障碍物的条件下获得一组行动序列,这一组行动可以实现帆船从起始点航行至目标点用时最短,并且满足了对未知路线探索的需要,防止陷入局部最优解。帆船若到达障碍物或者跑出地图边界,路径规划都将停止并重新开始规划。本文设计的帆船的路径规划算法如算法1所示。
|
|
为了验证该算法,本文创建了一个海面环境离散网状图,对海面环境因素就行了仿真,并针对不同海风、海流条件规划J24帆船的航行路线。文献[25]验证了在不同学习率与折扣因子的条件下对路径规划的影响,结果显示学习率和折扣因子的数值较大时,可更快更稳定的找到最佳路径。于是通过对不同参数组合的实验结果进行比较,本次实验将学习率和折扣因子设置为0.6和0.9,ε设置为0.2。本文同时对不同迭代次数的路径规划实验结果进行了比较,由于使用了ε-greedy策略,其路径所用时间与迭代次数的收敛是相对的,智能体总会有ε概率去选择非最优路线。最终发现在本文设置的参数条件下,迭代3 000次之内都能够找到时间最短的路线。
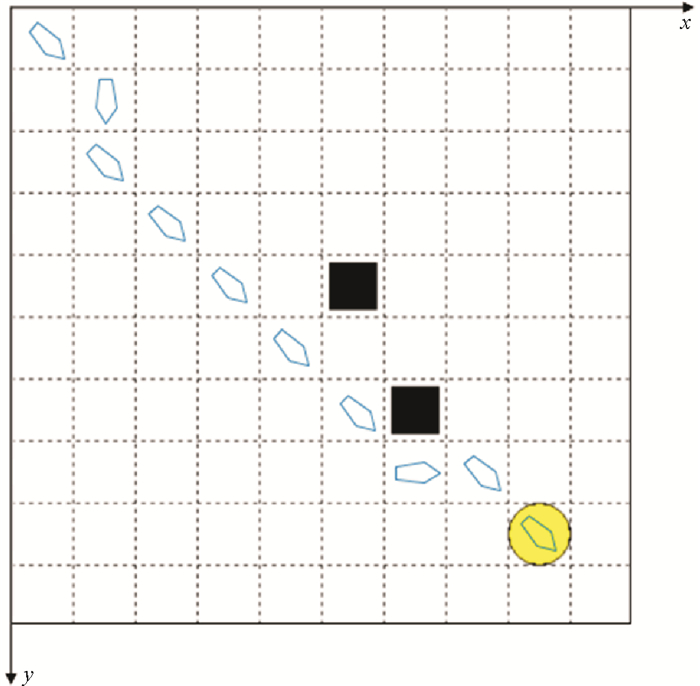
仿真实验地图设置为10×10的网格图,如图 7所示,帆船从左上角出发,黑色方块代表障碍物,黄色圆形代表目标点。图中每一格的宽度L假定为10 n mile,路径节点为每一个网格的中心点,在每一个网格中都包含着海风和海流的矢量速度,考虑到真实情况下风向时刻变化,在船速极坐标图中,风向的范围在±5°之内。
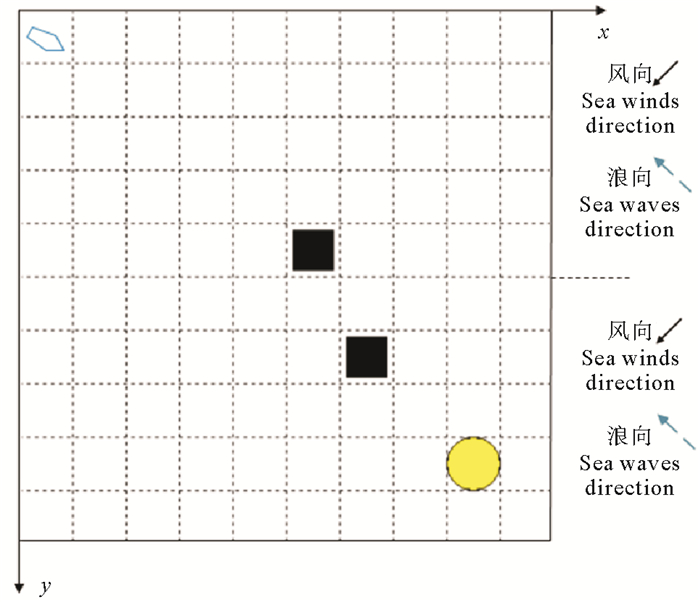
|
图 7 仿真实验地图 Fig. 7 The map of simulation test |
在考虑环境的影响情况下,首先当风向为东北风时,以地图中间为分界线,1≤y≤5的上半部分风速为8 kn,Vcx=Vcy=-1.5;6≤y≤10的下半部分风速为16 kn,Vcx=Vcy=2(见图 7)。使用本文算法所得路线结果见图 8,图中4个结果分别为循环40、1 200、2 400和3 000次所得到的路径,通过这些路径所需要的时间(即分图的标题,下文同)分别为33.74、16.58、14.34和14.30 h。可以看到通过连续学习,帆船在不断的寻找时间最短的最优路线。由于考虑了风向的变化,帆船所获得的速度也在变化,这就造成了结果中在相同路径条件下,时间不同的情况。
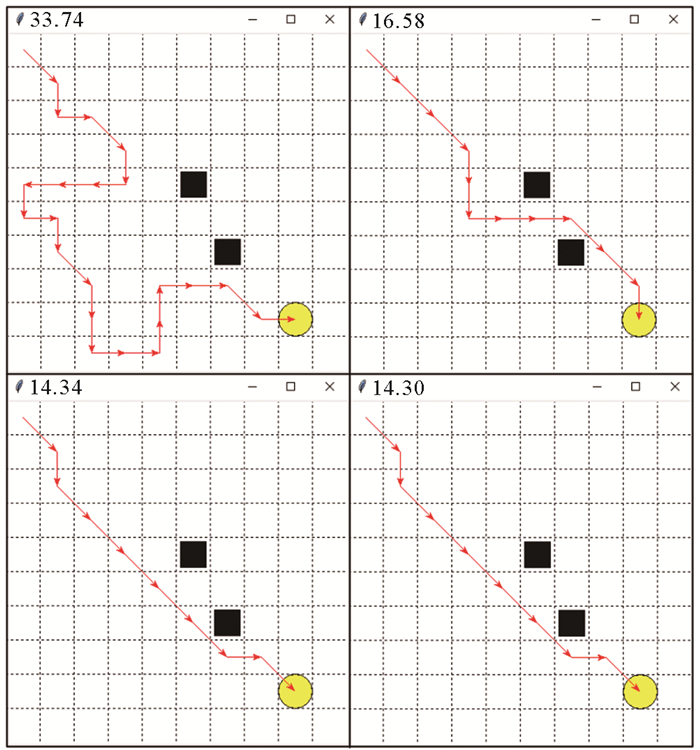
|
图 8 仿真实验结果 Fig. 8 The results of simulation test |
为了证明所获得路线为最优,这里与Dijkstra算法进行比较。但是这类路径规划方法有个弊端,它需要提前获取全图所有路径的权值,再从这些权值中找到权值累加最小的路线,在这里路径的权值即为时间。但是这个权值用在对帆船路径选择时便出现了问题,由于帆船得到的速度与当前航向及风向有关,所以对于图中除起始点外的任意相邻两点xt和xt+1来说,xt+1处的速度可以获得,但是由于无法确定xt-1的位置也就无法知道当时帆船的航向等信息,所以无法确定xt处的速度。为了解决这一问题,在实验中将xt处的速度设置为从所有可到达xt位置方向速度的平均值,以此便可以提前得到仿真地图中所有路线所需的权值。为了与之前实验中条件一致,速度的计算都考虑了海流的影响,风向也同样具有小范围的变化性。最后使用Dijkstra算法找到的路线如图 9所示。起始点为序列“0”点,以此横向计数,目标点序列为“88”。则路线如图 10所示,可以发现与图 8用本文算法找出的路线是一样的,但是由于时间的计算方法有一定的差别,所以总体时间不同。
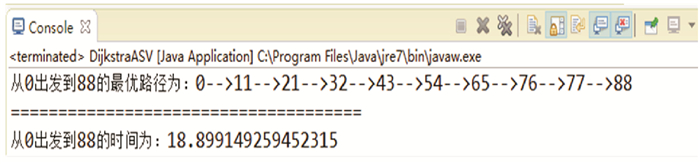
|
图 9 Dijkstra算法路径 Fig. 9 The results of Dijkstra |
|
图 10 Dijkstra算法路径展示 Fig. 10 The path of Dijkstra |
总体上来说,本文的路径规划算法可以为帆船找到最优路线。并且考虑到实际航行情况,特别是帆船的航行更依赖于外界环境,而想要提前得到整个航行海域的环境状态,再使用像Dijkstra这类传统寻路算法进行路径规划是极为困难的。相反,本文提出的基于强化学习的帆船路径规划算法不需要提前获取全地图的信息,通过逐渐学习选择出最佳路线,更符合实际帆船航行情况。
在其它环境条件不变的条件下,改变海流的方向,即上半部分Vcx=Vcy=1.5,下半部分Vcx=Vcy=-2,所规划路径结果如图 11所示,循环次数分别为600、1 200、2 400和3 000次以及时间16.07、15.92、15.12和14.35 h。
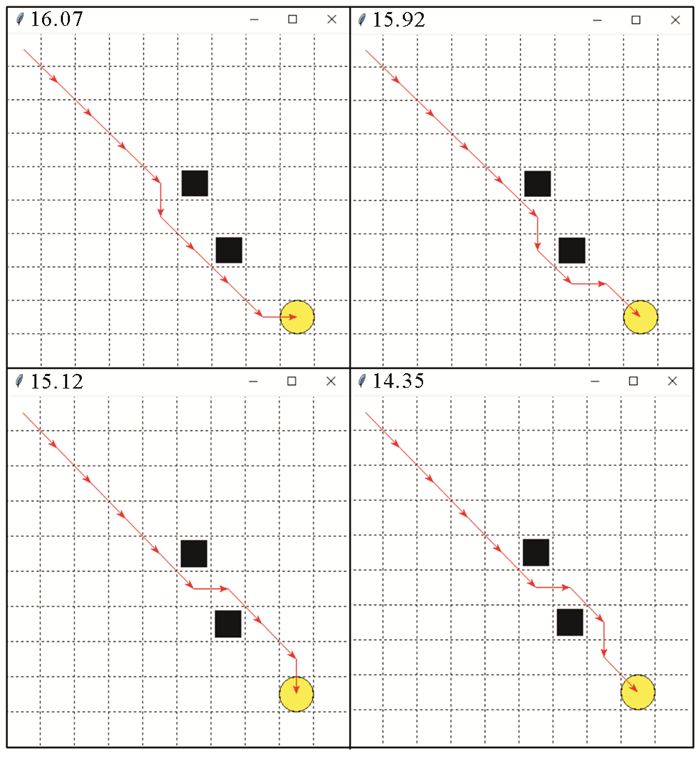
|
图 11 逆向海流仿真实验结果 Fig. 11 The results of inverse direction of sea currents |
为了测试在逆风(东南风)情况下的路径情况,在浪速为0、风向为逆风的情况下在6×6的地图中路径结果见图 12所示,2张结果图的次数分别为50和3 000次,时间为12.66和10.04 h。在逆风条件下,帆船无法直接朝向目标,所以需要选择折线的方式移动。
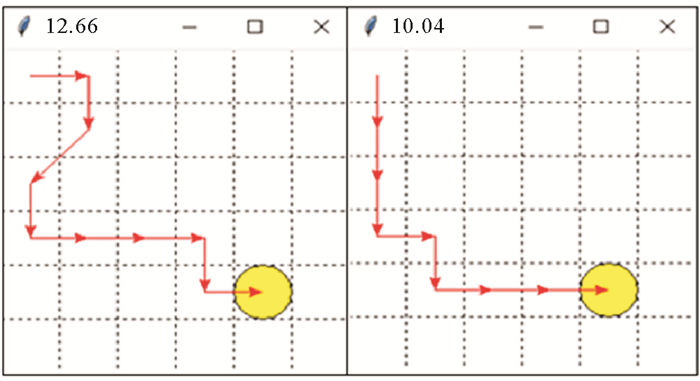
|
图 12 纯逆风情况下实验结果 Fig. 12 The results of upwind direction without sea currents |
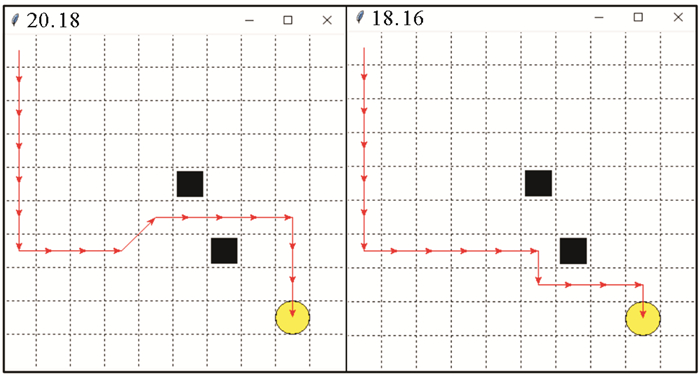
最后,在逆风(东南风)并且海流大小方向与第一个实验相同情况下,对路径进行规划,结果见图 13,循环次数为600和3 000次,时间为20.18和18.16 h。
|
图 13 逆风仿真实验结果 Fig. 13 The results of upwind with sea currents |
从所有实验结果可以发现,随着循环次数的增加,所需要的航行时间都在减小,其航行路线也更加合理。并且根据不同的环境条件,所选择的路线不同,符合帆船运动规律,可以证明本文算法对自动帆船在复杂海面环境中的路径规划是有效的。
4 结语本文针对帆船的自动航行问题进行研究,分析了复杂海面环境与其航行的关系,综合考虑了海风、海流以及海面障碍物对自动帆船路线的影响,同时考虑了帆船的运动模型,最后基于强化学习的方法,对学习过程进行重新定义,通过学习使帆船面对不同环境条件做出最优的选择。最后的仿真结果和对比实验结果也表明该算法可以综合考虑环境因素,为自动航行帆船找到最优路线。综上所述,本文的创新点可归纳为:
(1) 本文将强化学习引入了自动帆船路径规划中,与传统的帆船路径规划算法不同,不需要提前获得全图的信息,而是根据当前状态以及之后状态确定路线,更符合实际情况。
(2) 与基于强化学习自动船艇路径规划不同,帆船所涉及的影响因素更多更复杂,航行速度是由自身模型和环境条件共同决定的,于是本文算法综合参考了帆船运动模型以及船体平面运动模型,更符合帆船海面航行状态。
(3) 相较于其它路径规划方法对于海风、海流、障碍物以及船体模型出现的“顾此失彼”问题,本文算法全面考虑了上述海面环境因素以及帆船自身因素对路径规划的影响。
| [1] |
Bertram V. Unmanned surface vehicles-a survey[J]. Skibsteknisk Selskab Copenhagen Denmark, 2008, 1: 1-14.
(  0) 0) |
| [2] |
Manley J E. Unmanned Surface Vehicles, 15 Years of Development[C]. Kobe, Japan: Oceans IEEE, 2008: 1-4.
(  0) 0) |
| [3] |
Liu Z, Zhang Y, Yu X, et al. Unmanned surface vehicles: An overview of developments and challenges[J]. Annual Reviews in Control, 2016, 41: 71-93. DOI:10.1016/j.arcontrol.2016.04.018
(  0) 0) |
| [4] |
Sarda E I, Bertaska I R, Qu A, et al. Development of a USV Station-Keeping Controller[C]. Genova, Italy: Oceans IEEE, 2015: 1-10.
(  0) 0) |
| [5] |
Wang Y, Liu Y, Guo Z. Three-dimensional ocean sensor networks: A survey[J]. Journal of Ocean University of China, 2012, 11(4): 436-450. DOI:10.1007/s11802-012-2111-7
(  0) 0) |
| [6] |
Cruz N A, Alves J C. Autonomous Sailboats: An Emerging Technology for Ocean Sampling and Surveillance[C]. Bremen, Germany: Oceans IEEE, 2009: 1-6.
(  0) 0) |
| [7] |
Langbein J, Stelzer R, Frühwirth T. A rule-based approach to long-term routing for autonomous sailboats[J]. Robotic Sailing Springer Berlin Heidelberg, 2011, 195-204.
(  0) 0) |
| [8] |
Mannarini G, Lecci R, Coppini G. Introducing Sailboats Into Ship Routing System VISIR[C]. Corfu, Greece: Information, Intelligence, Systems and Applications (ⅡSA), 2015 6th International Conference, 2015: 1-6.
(  0) 0) |
| [9] |
Kerwin J E. A Velocity Prediction Program for Ocean Racing Yachts[M]. [s.l]: Massachusetts Institute of Technology, Department of Ocean Engineering, 1978.
(  0) 0) |
| [10] |
Pêtres C, Romero Ramirez M A, Plumet F, et al. Modeling and Reactive Navigation of an Autonomous Sailboat[C]. San Francisco, USA: Intelligent Robots and Systems (IROS), 2011 IEEE/RSJ International Conference, 2011: 3571-3576.
(  0) 0) |
| [11] |
Plumet F, Pêtrès C, Romero Ramirez M A, et al. Toward an autonomous sailing boat[J]. IEEE Journal of Oceanic Engineering, 2015, 40(2): 397-407. DOI:10.1109/JOE.2014.2321714
(  0) 0) |
| [12] |
Stelzer R, Proll T, John R I. Fuzzy Logic Control System for Autonomous Sailboats[C]. London, UK: IEEE International Fuzzy Systems Conference, 2007: 1-6.
(  0) 0) |
| [13] |
Guo Y, Romero M, Ieng S H, et al. Reactive Path Planning for Autonomous Sailboat Using an Omni-directional Camera for Obstacle Detection[C]. [s.l.]: IEEE International Conference on Mechatronics, 2011: 445-450.
(  0) 0) |
| [14] |
Polvara R, Sharma S, Wan J, et al. Obstacle avoidance approaches for autonomous navigation of unmanned surface vehicles[J]. The Journal of Navigation, 2018, 71(1): 241-256. DOI:10.1017/S0373463317000753
(  0) 0) |
| [15] |
Mannarini G, Coppini G, Oddo P, et al. A prototype of ship routing decision support system for an operational oceanographic service[J]. TransNav, International Journal on Marine Navigation and Safety of Sea Transportation, 2013, 7(1): 53-59.
(  0) 0) |
| [16] |
Perera L P, Carvalho J P, Soares C G. Fuzzy logic based decision making system for collision avoidance of ocean navigation under critical collision conditions[J]. Journal of Marine Science & Technology, 2011, 16(1): 84-99. DOI:10.1007/s00773-010-0106-x
(  0) 0) |
| [17] |
Yoo B, Kim J. Path optimization for marine vehicles in ocean currents using reinforcement learning[J]. Journal of Marine Science and Technology, 2016, 21(2): 334-343. DOI:10.1007/s00773-015-0355-9
(  0) 0) |
| [18] |
王程博, 张新宇, 邹志强, 等. 基于Q-Learning的无人驾驶船舶路径规划[J]. 船海工程, 2018, 47(5): 174-177. WANG Chengbo, ZHANG Xinyu, ZOU Zhiqiang, et al. On path planning of unmanned ship based on Q-Learning[J]. Ship & Ocean Engineering, 2018, 47(5): 174-177. (  0) 0) |
| [19] |
Chen D, Dai C, Wan X, et al. A Research on AIS-Based Embedded System for Ship Collision Avoidance[C]. Wuhan, China: Transportation Information and Safety (ICTIS), 2015 International Conference, 2015: 512-517.
(  0) 0) |
| [20] |
Tang P, Zhang R, Liu D, et al. Research on Near-Field Obstacle Avoidance for Unmanned Surface Vehicle Based on Heading Window[C]. Taiyuan, China: Control and Decision Conference (CCDC), 2012 24th Chinese, 2012: 1262-1267.
(  0) 0) |
| [21] |
Szlapczynski R. Evolutionary sets of safe ship trajectories: A new approach to collision avoidance[J]. The Journal of Navigation, 2011, 64(1): 169-81. DOI:10.1017/S0373463310000238
(  0) 0) |
| [22] |
Sutton R S, Barto A G. Reinforcement Learning: An Introduction[M]. MA, USA: MIT Press, 2018.
(  0) 0) |
| [23] |
Murphy A B, Brusca S. Bernoulli effect[J]. Physics Education, 1986, 21(5): 262-263. DOI:10.1088/0031-9120/21/5/104
(  0) 0) |
| [24] |
Chen Y F, Everett M, Liu M, et al. Socially Aware Motion Planning With Deep Reinforcement Learning[C]. Vancouver, BC, Canada: 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2017: 1343-1350.
(  0) 0) |
| [25] |
刘正萌. 自主移动平台自适应运动规划与学习方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2016. Liu Zhengmeng. Adaptive Motion Planning and Learning Methods for the Study of Autonomous Mobile Platform[D]. Harbin: Harbin Engineering University, 2016. (  0) 0) |
 2021, Vol. 51
2021, Vol. 51

