2. 自然资源部海上丝路海洋资源环境组网观测技术创新中心,山东 青岛 266580
高频地波雷达(High Frequency Surface Wave Radar,HFSWR)作为重要的海上监测手段,其利用高频段电磁波信号沿海面绕射传播的特性,可实现对超视距范围的海洋动力学参数反演与海上船只目标跟踪,具有大范围、全天候、连续探测的优势[1]。船载地波雷达除具备岸基地波雷达的优点外,还可利用船载平台机动灵活的特点,扩展雷达探测范围,具备持续跟踪特定船只目标和探测更远距离的海态信息等优势[2]。
无论是利用地波雷达进行海态参数反演,还是进行海上船只目标探测,海面一阶谱区的精确识别是地波雷达海洋探测与信息提取中的必经环节。对于岸基地波雷达来说,其一阶谱特性已有大量研究[3-4],多种岸基地波雷达一阶谱提取方法也被提出,如信噪比法、基于机器学习的一阶谱识别方法等[5-7]。而对于船载地波雷达,其雷达信号受船载平台运动调制的影响,雷达回波谱会发生频移及展宽现象,并存在一阶回波谱能量降低和一阶谱区信号断裂的问题。此外,展宽后的一阶回波谱,极易被目标信号、地杂波或其他噪声的干扰污染,也增加了展宽一阶谱的提取难度。
近年来,已有学者开始针对船载单基地或天发地收双基地体制地波雷达,进行一阶回波谱展宽特性研究,并发展了相应的展宽一阶谱提取方法。如利用展宽一阶谱区边界处与背景噪声间的强信号差特性,将差谱法直接应用于船载地波雷达一阶谱区提取[8]。但其对一阶谱区信号质量要求较高,当谱区内存在强目标信号干扰时,识别效果下降。此外,有学者利用天地波雷达的一阶谱展宽和距离维上连续的特点,发展了二维信噪比方法[9],实现了展宽一阶谱区提取。但当一阶谱区内出现信号断裂时,仅利用一阶谱展宽特性,不能完全适合于船载地波雷达一阶谱识别。
除此之外,由于船载平台的运动,也会导致目标信号和其他杂波信号的展宽,增大了一阶谱区受其污染的可能性。目前适用于多目标信号、杂波干扰背景下的船载地波雷达展宽一阶谱识别提取研究相对较少,因此,有必要发展适合于此背景下的展宽一阶谱区识别方法。针对船载地波雷达一阶谱位置和范围的不稳定性,本文首先分析了一阶谱的频移及展宽特性,给出了最大检测范围,确保一阶谱区可被检测到;其次,针对船载地波雷达展宽一阶谱区极易被强目标信号污染的问题,研究了船载地波雷达一阶谱的幅度特性,并结合一阶谱在距离域上的分布特性,实现一阶谱区识别。
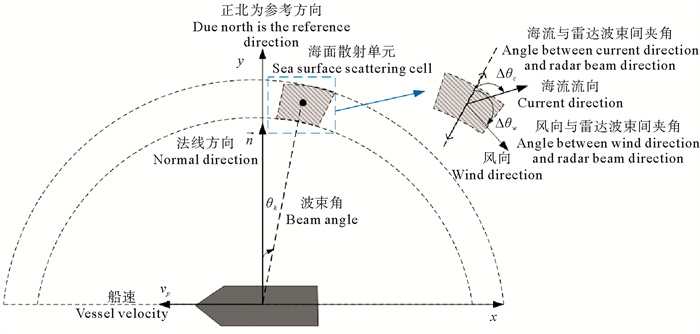
1 船载地波雷达展宽一阶回波谱特性分析为实现船载地波雷达展宽一阶谱区域的识别,需对其频移和幅度特性进行分析,图 1为船载地波雷达接收海面回波示意图。
|
图 1 船载地波雷达接收海面回波信号示意图 Fig. 1 Schematic diagram of receiving sea surface echoe for ship-borne HFSWR |
其中,θk为雷达回波波束方向(本文所有角度参考方向为正北,为分析方便,设船载平台的主轴朝向正北,顺时针为正,θk取值范围为[-90°, 90°])。Δθw为风向与雷达波束方向之间夹角大小,船载地波雷达一阶散射截面积频域公式[10]如下:
| $ \sigma_{\text {sea }}(\omega)=2^6 \pi^2 k_0^4 \sum\limits_{m= \pm 1} S(m \vec{K}) \delta\left(\omega-m \omega_{\mathrm{B}}-\Delta \omega\right)。$ | (1) |
式中:k0表示雷达电磁波波数;m=±1;ωB为发生一阶布拉格(Bragg)后向散射时的角频率;
当不考虑海流时,仅有船速会引起回波多普勒(Doppler)频点的频移,频移值Δω表达式为:
| $ \Delta \omega=\frac{2 \pi}{\lambda}\left(2 v_{\mathrm{s}} \sin \left(\theta_k\right)\right) 。$ | (2) |
式中: vs为船载平台航行速度;λ为电磁波波长。当考虑海流存在时,海流与船速共同引起多普勒频移,此时偏移Δω变为:
| $ \Delta \omega=\frac{2 \pi}{\lambda}\left(2 v_s \sin \left(\theta_k\right)\right)+\frac{2 \pi}{\lambda}\left(2 v_c \cos \left(\Delta \theta_c\right)\right)。$ | (3) |
式中:Δθc=θc-θk表示洋流与雷达波束方向之间夹角大小;vc表示矢量流速大小;θc为矢量流流向。
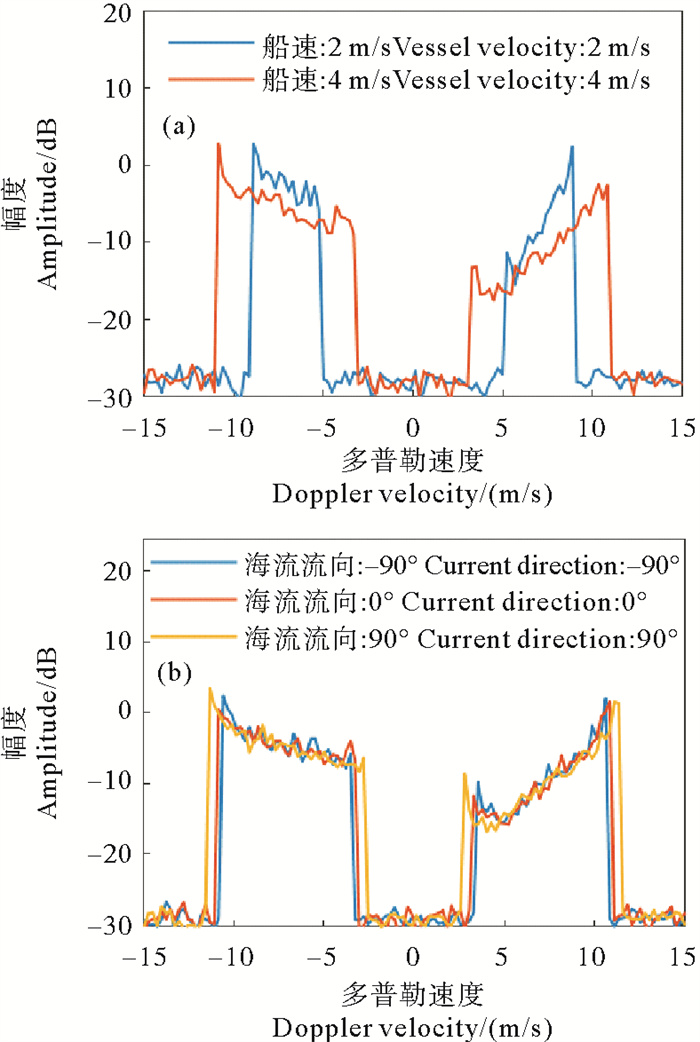
图 2给出了无海流和有海流情况下的船载地波雷达一阶谱仿真结果,为方便观察,本文所有仿真及实测数据谱的x轴以多普勒速度(m/s)为参考单位。
|
( (a)船速分别为2 m/s(蓝色线)和4 m/s(橙色线);(b)船速为4 m/s,流速0.3 m/s,流向分别为-90°(蓝色线)、0°(橙色线)、90°(黄色线)。(a) the velocity of vessels are 2 m/s (blue) and 4 m/s (orange) respectively; (b) the velocity of vessel and current are 4 m/s and 0.3 m/s, the current directions are-90°(blue), 0°(orange), and 90°(yellow), respectively. ) 图 2 船载地波雷达一阶回波谱仿真结果 Fig. 2 Simulation results of the first-order simulation spectrum for ship-borne HFSWR |
图 2(a)可以看出,随着船速的增大,一阶谱展宽范围越大,其左右一阶谱各自展宽约2vs。从图 2(b)中可以看出,展宽幅度与矢量流向与船艏向夹角呈正相关关系,直到矢量流向与船艏向反向(90°)达到最大值,最大展宽范围为:
| $ \left[ \pm f_{\mathrm{B}}-2\left(v_{\mathrm{s}}+v_{\mathrm{c}}\right) / \lambda, \pm f_{\mathrm{B}}+2\left(v_{\mathrm{s}}+v_{\mathrm{c}}\right) / \lambda\right] 。$ | (4) |
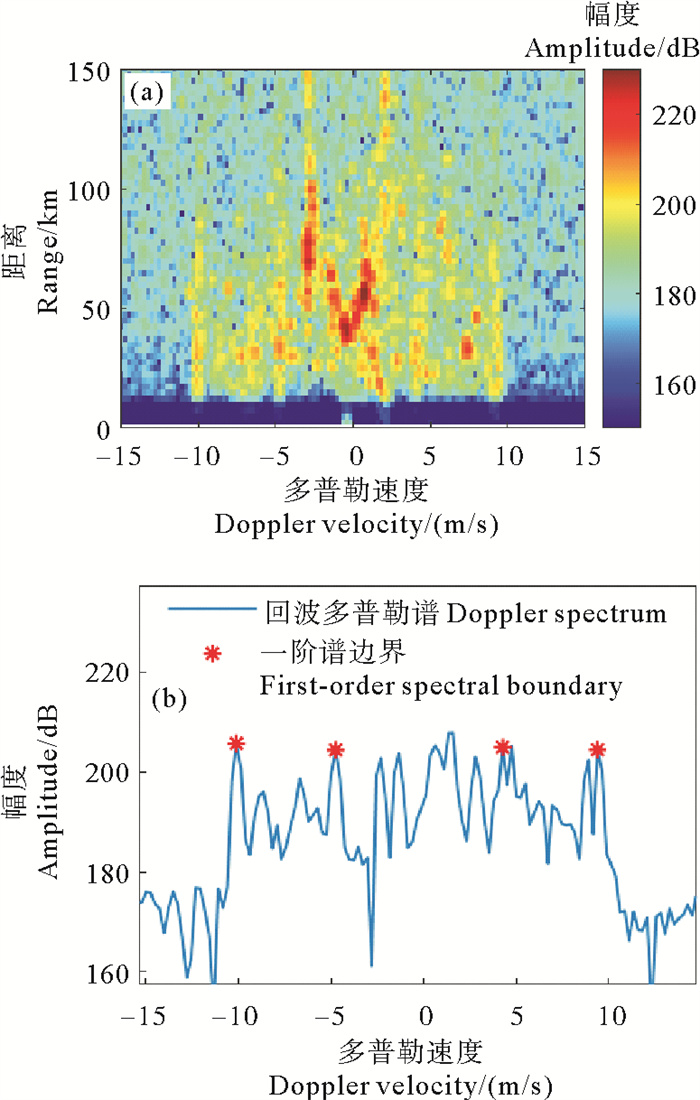
因此,根据公式(4)可进行展宽一阶谱最大检测范围预设,矢量海流选择当前探测海域内的历史最大海流。图 3给出了实测船载地波雷达距离-多普勒(Range-Doppler, RD)谱。
|
( (a)和(b)分别表示了RD谱和25 km处的一维Doppler谱,红色*代表实际边界。(a) and (b) show RD spectrum and the Doppler spectrum at 25 km, respectively. The red * represents the actual boundary. ) 图 3 船载地波雷达实测数据 Fig. 3 Measured data of ship-borne HFSWR |
从图 3(a)中可以看出,船载地波雷达一阶谱即使发生了展宽现象,在二维RD谱上依旧呈连续性分布,此时回波RD谱上的展宽一阶谱区4条边界线将分别出现在多普勒速度大小约为[-10.5, -9.5]、[-5.5, -4.0]、[3.5, 5.0]、[9.0, 10.0]范围内。图 3(b)中给出了25 km处的一维多普勒频谱,其一阶谱大致边界点也是位于上述多普勒速度边界范围内,展宽宽度约为5.3 m/s左右,可以看出,实测雷达回波谱数据中一阶谱展宽范围约等于2vs。这是由于不同距离和方位上存在海流的影响,实际上最大海流速度不会超过1 m/s[11],考虑投影因素,海流对一阶谱展宽的影响明显小于船载平台运动的影响。
以上分析可以看出,航行状态下的船载地波雷达一阶谱的频移及展宽主要受船载平台运动影响。此外,当存在海流的速度投影时,会导致一阶谱发生再次偏移和展宽。因此,需考虑二者共同制约,进行船载地波雷达一阶谱最大检测范围预设,进而提高船载地波雷达一阶谱区识别效果。
1.2 船载地波雷达展宽一阶谱区幅度特性从公式(1)中可以看出,不同回波方位上的一阶回波多普勒谱频点处的幅值大小主要受有向海浪谱的影响,其可表示为无向海浪谱S(k)与风向函数G(φ)乘积,φ为雷达回波方向与海浪方向的夹角,当海面充分发展时认为风向与浪向几乎一致[12]。发生一阶散射时的S(k)值主要与雷达配置、海况环境等因素有关。本文选择修正的余弦函数作为仿真风向模型G(φ)[13]:
| $ G(\varphi)=\frac{\zeta+(1-\zeta) \cos ^4(\varphi / 2)}{2 \pi \zeta+(3 \pi / 4)(1-\zeta)} 。$ | (5) |
其中,ζ为正负一阶频点处的能量比值(通常取经验值ζ=0.04)。对于一维回波多普勒谱,设其频域信号可以用公式表示为X(ω)=Pr(ω)+N(ω),其中N(ω)表示随机噪声。差值曲线上每一频点上的值表示下一频点与当前频点间的多普勒信号幅值差,因此,对于展宽一阶谱区信号来说,相邻频点间的幅值差可表示为:
| $ \begin{aligned} 10 \lg \frac{X\left(\omega_{i+1}\right)}{X\left(\omega_i\right)} & =10 \lg \frac{P_r\left(\omega_{i+1}\right)+N\left(\omega_{i+1}\right)}{P_r\left(\omega_i\right)+N\left(\omega_i\right)} \approx \\ & 10 \lg \frac{P_r\left(\omega_{i+1}\right)}{P_r\left(\omega_i\right)} 。\end{aligned} $ | (6) |
其中,Pr(ωi)为在距离r、方位角θi处的目标散射截面的接收信号功率值。此时,一阶谱区信号占主要地位,噪声影响可被忽略,可将其理解为方位角θi+1与θi间的一阶回波信号幅值差。而在展宽一阶谱的左右边界处,其信号差值分别变为10lg(Pr(ωi+1)+N(ωi+1))/N(ωi)和10lgN(ωi+1)/(Pr(ωi)+N(ωi))。此时,位于展宽一阶谱边界处的差值信号,可以理解为信噪比或噪信比,即会在展宽一阶谱左边界点出现最大正峰值点,在展宽一阶谱右边界点出现最小负峰值点。
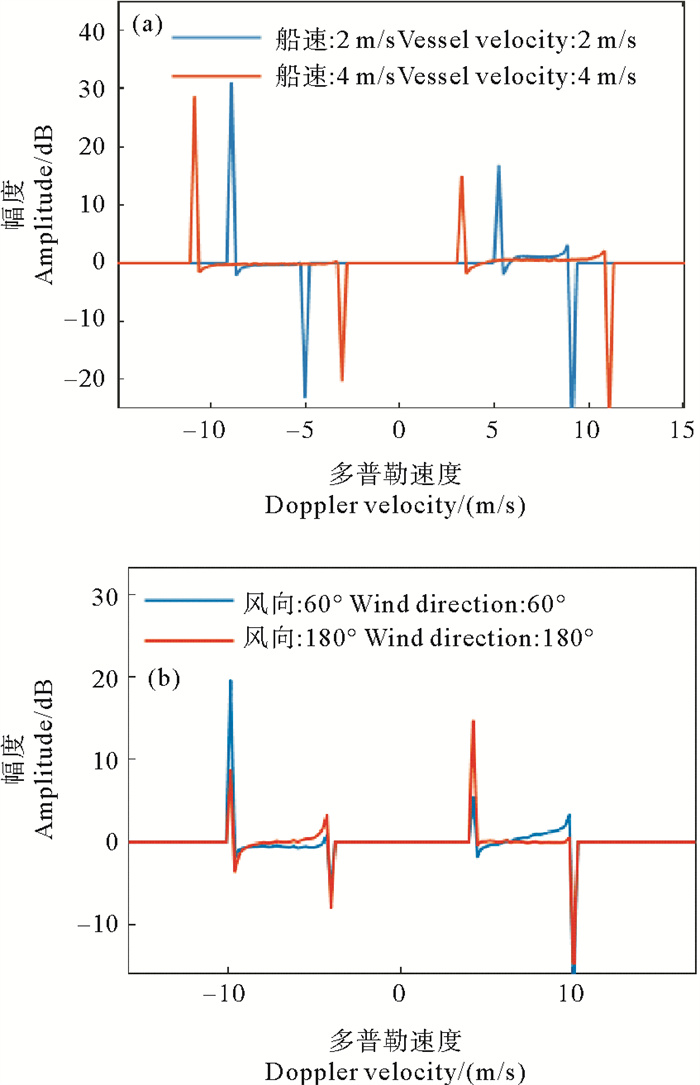
对相邻多普勒频点做信号差,获得如图 4不同船速和风向条件下的船载地波雷达展宽一阶谱多普勒幅值差曲线。
|
( (a)不同船速下;(b)不同风向下。(a) Different vessel velocities; (b) Different wind directions. ) 图 4 不同条件下的船载地波雷达展宽一阶多普勒谱幅值差曲线 Fig. 4 Amplitude difference curve of broaden first-order Doppler spectrum for ship-borne HFSWR in different conditions |
从图 4可以看出,无论仿真条件如何变化,在不考虑噪声影响的情况下,展宽一阶谱在边界点处表现出强信号差特性,且这种特性仅出现在边界处。一阶谱区判断准则[14]为:每一条差值曲线上对应的正、负一阶谱区检测范围内,存在若干极值点,其极大(小)值点中最大(小)值点为一阶谱区左(右)边界。
由于船载平台的运动,一阶Bragg频率发生偏移,原本集中于Bragg峰处的不同回波方位上的谱信号能量分散、降低。当一阶谱区内存在目标信号时,Doppler差值曲线中出现强信号差值点不唯一,图 5为仿真及实测回波多普勒差值曲线。
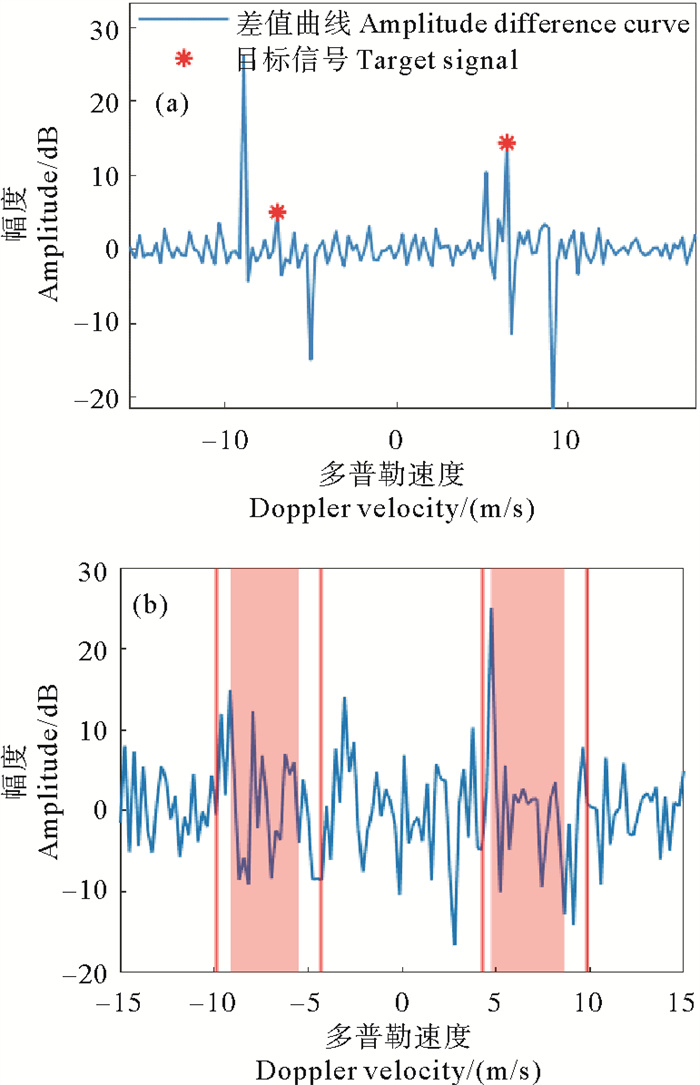
|
( 红色直线为预设的最大检测范围,红色阴影区域为实际一阶谱区,红色*代表目标信号。The red straight line is the pre-set maximum detection range, the red shaded area is the actual first-order spectral and red * represents the target signals. ) 图 5 船速为2 m/s时的多普勒差值曲线仿真结果(a)和实测结果(b) Fig. 5 Doppler spectrum amplitude difference curve at the velocity of vessel is 2 m/s simulation result (a) and measured result (b) |
从图 5的仿真及实测差值曲线可知,即使谱区内存在目标信号,展宽一阶谱区边界点依旧表现出强信号差特性,表现在回波Doppler差值曲线上为某一极值点。因此,可根据此一阶谱区处的强信号差值特性,进行边界点预筛选,进而提高后续检测效率及准确率。
2 方法流程本文根据船载地波雷达一阶谱的频移和幅度特性,提出了一种适用于船载地波雷达展宽一阶谱的差值信噪比(Difference signal-to-noise ratio, DSNR)方法,流程图 6。
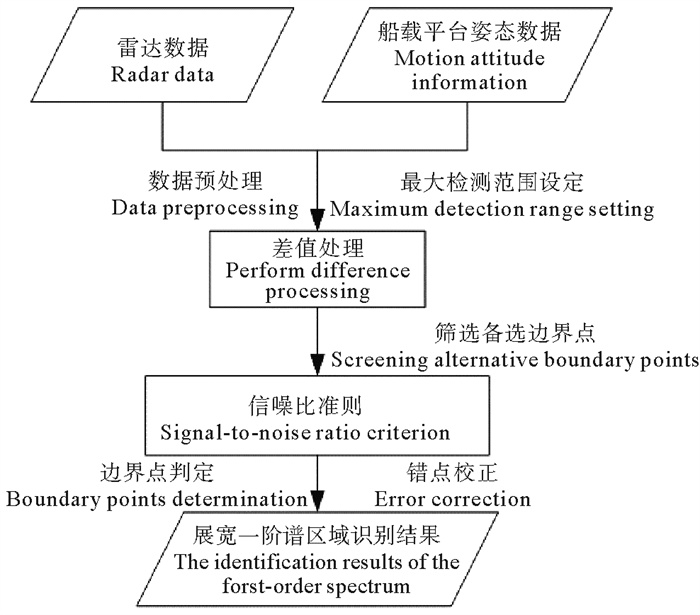
|
图 6 基于DSNR法的船载地波雷达一阶谱区识别流程 Fig. 6 The flow chart of extracting the first-order spectral region based on the DSNR method for ship-borne HFSWR |
受船载平台运动影响,船载地波雷达一阶谱展宽后幅值也随之降低,导致检测困难。通过实验发现,对连续多帧回波谱数据进行累积平均后,可提高信噪比,突出船载地波雷达展宽的一阶谱区及其边界。图 7给出了单帧和十帧累积平均处理后的RD谱。
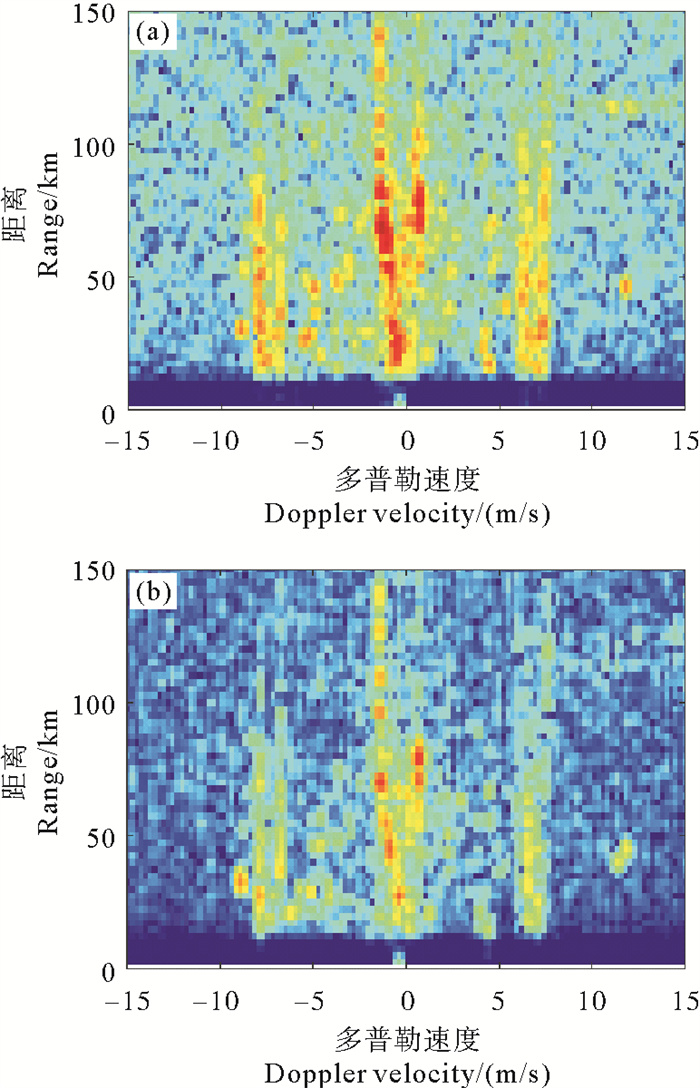
|
图 7 时间序列长度为单帧(a)和十帧(b)累积平均后的船载地波雷达回波RD谱 Fig. 7 The RD spectrum of ship-borne HFSWR after accumulated average with time series of single frame (a) and ten frames (b) |
根据图 7可以看出,随着多帧数据的累积平均后,展宽的一阶谱区域能明显区别于周围背景噪声。通过2.1节对船载地波雷达一阶谱频移及展宽特性分析,可知船速是船载地波雷达一阶谱展宽程度的主要影响因素。因此,不能无限长度进行多帧数据累积平均,需根据船载平台的姿态数据选择最佳时间序列长度,即选择的多帧时间内,船载平台姿态数据变化不能超过1/2个多普勒速度单元分辨单元大小。此外,由于目标及噪声信号干扰,若直接对每一距离维上的多普勒信号进行差值,其曲线中极值点并非总能涵盖真实的一阶谱边界点,会出现边界点漏检问题。因此,将利用展宽一阶谱在距离维上的连续性,在距离维上选择合适的距离窗口进行数据平滑处理,以此降低噪声和一阶谱区附近目标信号对边界点预筛选质量的影响。综上,通过多帧数据累积及距离维平滑处理,完成雷达数据预处理。
2.2 展宽一阶谱备选边界点选取公式(7)从理论上给出了在距离R、方位角θ处的船载地波雷达展宽一阶谱的功率值:
| $ P_r\left(R, \theta_i\right)=\frac{\Gamma \cdot R \cdot \sigma_{\mathrm{sea}}\left(\omega, \theta_i\right)}{L_{r s}(R)} 。$ | (7) |
式中:Γ为雷达系统所确定的参数;Lrs(R)为某距离上的诺顿衰减值,同一距离处的Lrs(R)值默认不变;σsea(ω, θi)为在距离R、方位角θ处的一阶散射截面积。因此将公式(7)、公式(1)带入到公式(6),化简后得:
| $ 10 \lg \frac{P_r\left(R, \theta_{i+1}\right)}{P_r\left(R, \theta_i\right)}=10 \lg G\left(\varphi_{i+1}\right)-10 \lg G\left(\varphi_i\right) 。$ | (8) |
根据公式(8)可知,谱区内相邻频点处的幅值差,可化简为相邻回波方向上风向函数G的幅值差。而谱区边界的信号幅值差,实际上是海面回波信号与噪声信号的幅值差,故表现出强信号差值特性,即一阶谱边界点表现为差值曲线上某一局部极值点。
因此,在获得每一距离维上多普勒谱的幅值差曲线后,分别在预设的正、负一阶谱区最大检测范围内,对差值曲线进行极值检测,获得备选边界点集合如下:
| $ \mathit{Side\_ right}(R, 1: N)=\left[a_1, a_2, \cdots, a_N\right] \text { 。} $ | (9) |
| $ \mathit { Side\_lift }(R, 1: M)=\left[b_1, b_2, \cdots, b_M\right] \text { 。} $ | (10) |
其中:N、M分别为每一距离处正、负一阶谱区内多普勒差值曲线的极值点(备选边界点)个数;a、b为备选边界点对应的多普勒速度(m/s)值。
获得的船载地波雷达展宽一阶谱备选边界点,可能包括真实一阶谱边界点、目标信号、强背景噪声等多种信号点。
2.3 船载地波雷达展宽一阶谱边界识别根据船载地波雷达一阶谱的频移特性可知,随着一阶Bragg频率发生偏移,在一阶谱峰信号会发生分散,分布在展宽一阶谱区域内。且对于上下相邻的距离单元,船载地波雷达展宽一阶谱区存在连续性。因此,选择二维信噪比准则,可以利用距离-多普勒二维区域信噪比最大的特点,对备选边界点进行筛选。
首先,在距离单元R上,选择距离单元窗口大小为win,在正(负)一阶谱区最大检测范围内,选择两个备选边界点,获得相应信号区间的信号均值:SignalR(i, i+n)(SignalL(j, j+m))。其中,i∈[1, N]表示正一阶谱检测区内第i个备选边界点,n∈[i+1, N-i]表示正一阶谱检测区内第i个备选边界点后第n位备选边界点;j∈[1, M]表示负一阶谱检测区内第j个备选边界点,m∈[j+1, M-j]表示负一阶谱检测区内第j个备选边界点后第m位备选边界点。遍历所有备选边界点后,获得正、负一阶谱区的信号均值矩阵SignalR、SignalL。
其次,根据信号区间,选择其左右相邻处的信号区间作为噪声区间,左、右噪声区间长度为信号区间长度的K倍,确定噪声区间的信号均值Noiser(i, i+n)(NoiseL(j, j+m))。完成左、右备选边界点遍历后,获得噪声矩阵NoiseR、NoiseL。
然后,获得正、负一阶谱区二维信噪比矩阵:
| $ \boldsymbol{S N R}_R=\boldsymbol { Signal }_R-\boldsymbol { Noise }_R。$ | (11) |
| $ \boldsymbol{S N R}_L=\boldsymbol { Signal }_L-\boldsymbol { Noise }_L。$ | (12) |
分别对SNRR、SNRL矩阵求得最大值SNRR_max、SNRL_max,并检测其对应的备选边界点,如公式所示:
| $ \boldsymbol{S N R}_{\mathrm{R} \text_{max} }=\boldsymbol{S N R}_R(\mathrm{I}, \mathrm{I}+\mathrm{n}) $ | (13) |
| $ \boldsymbol{S} \boldsymbol{N}\boldsymbol{R}_{\mathrm{L} \text_{ max }}=\boldsymbol{S} \boldsymbol{N} \boldsymbol{R}_L(J, J+m) 。$ | (14) |
此时可得船载地波雷达正、负一阶谱展宽区间分别为[aI, aI+n]、[bJ, bJ+m]。最后,对每一距离维上的多普勒信号重复步骤(2)、(3),可在连续距离单元上获得一系列谱区边界点,连接边界点,获得船载地波雷达二维RD谱的展宽一阶谱区识别结果。
将二维信噪比作为最终的船载地波雷达展宽一阶谱区提取准则,可以排除掉备选点中的目标信号点,提高了识别结果准确度;其次,只对备选边界点进行二维信噪比准则,而非对所有点集进行遍历,提高了检测效率。并且,当展宽一阶谱区内信号断裂时,经过多普勒差值处理的边界点预筛选,可以降低局部区域信噪比突然增大,导致的展宽一阶谱区识别效果下降的问题。
3 方法验证 3.1 仿真数据实验验证船载地波雷达展宽一阶回波RD数据仿真参数如下:雷达频率4.7 MHz;船载平台速度大小为3 m/s、风向120°、风速5 m/s。
图 8依次给出了利用信噪比法、差谱法、DSNR方法的一阶谱提取结果。可以看出,信噪比方法和DSNR法整体检测效果优于差谱法。随着距离的增加,左右一阶谱区信号信噪比降低,且受噪声信号的污染,差谱法检测性能在60 km处开始下降;在130 km内,信噪比方法的检测效果比较平稳,但130 km以上时,正一阶谱区信号较弱时,由于没有对一阶谱范围做约束,导致整体一阶谱区识别效果随之下降;而DSNR法虽然也受到噪声信号的干扰,但依旧能保持良好的识别效果,整体检测效果优于其他两种方法,且识别的一阶谱区也更加平稳连贯。
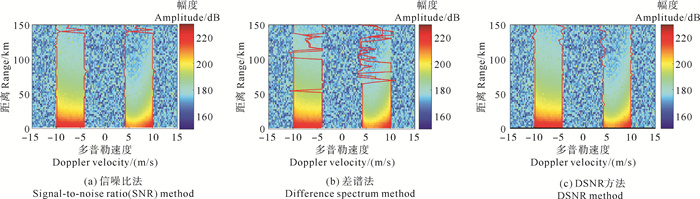
|
( 红色曲线为一阶谱的识别结果。The red curve is the identification results of the first-order spectrum. ) 图 8 不同方法下的船载地波雷达仿真一阶谱区识别结果 Fig. 8 The identification results of the first-order spectrum region for ship-borne HFSWR using different methods |
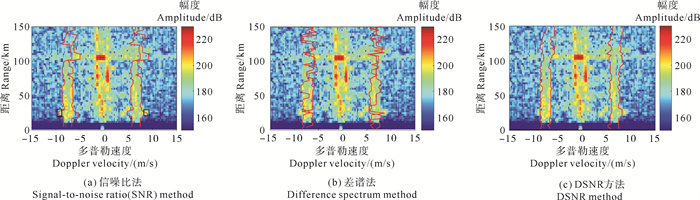
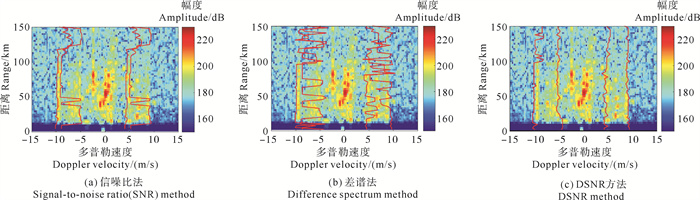
本文选用2021年10月份在青岛附近海域获得的船载地波雷达实测数据进行方法验证。其中,可通过惯导系统从船载地波雷达信号同步的姿态数据,获得船载平台速度信息。图 9、图 10分别给出了船载平台在1.18和2.07 m/s速度时,信噪比、差谱法、DSNR方法的船载地波雷达展宽一阶谱识别结果。
|
( 红色曲线为一阶谱的识别结果,黑色方框内为目标信号。The red curve is the identification results of the first-order spectrum, the black rectangle is the target signal. ) 图 9 船速为1.18 m/s时,不同方法下船载地波雷达实测数据的一阶谱区识别结果 Fig. 9 The identification results of the first-order spectrum with measured data of ship-borne HFSWR using different methods when the vessel velocity is 1.18 m/s |
|
( 红色曲线为一阶谱的识别结果。The red curve is the identification results of the first-order spectrum. ) 图 10 船速为2.07 m/s时,不同方法下船载地波雷达实测数据的一阶谱区识别结果 Fig. 10 The identification results of the first-order spectrum with measured data of ship-borne HFSWR using different methods when the vessel velocity is 2.07 m/s |
从图 9可以看出,当船速较小时,一阶谱区展宽幅度较小,此时一阶谱区信号能量集中。信噪比方法和DSNR方法提取的一阶谱区准确性相对较高,而差谱法检测性能相对下降。从图 9(a)中可以看出,在约25 km处在正、负一阶谱边界两侧存在强目标信号(黑框内信号),使得局部信号能量均值增大,信噪比方法将目标信号错检成一阶谱区内信号,导致局部检测性能下降。但在不存在目标信号干扰时,整体上检测性能比较稳定。图 9(b)的差谱法,受谱区内、外的强目标信号影响,在30 km内其识别效果下降,整体上谱区检测效果存在不稳定性。从图 9(c)中可以看出,DSNR方法在近100 km内整体检测结果不会出现大幅度抖动。虽然在约25 km处正一阶谱右侧谱边界会受到目标信号的干扰,但由于提前进行了最大检测区间预设,相较于其他两种方法误差较小,一定程度上避免了展宽一阶谱区附近目标信号的干扰,整体检测效果优于其他两种算法。
根据图 10分析,当船速较大时,受传播衰减及一阶谱区域展宽加大的影响,一阶谱区域内信号幅值下降,谱区内目标信号显现出来。从图 10(a)可以看出,在约50 km处负一阶谱区内存在局部信号区域断裂,导致局部信噪比增大。因此,在超过30 km后,信噪比方法的识别结果出现集中于某一局部的现象。图 10(b)中,由于差谱法也利用了谱区边界的强信号差值特性,对于负一阶谱区的左边界有较高的识别性能,但由于谱区内目标信号的显现,差谱法极易受到目标信号的干扰,检测性能相对下降。而从图 10(c)可以看出,DSNR方法由于进行了边界点预筛选处理,在捕捉边界点信息的同时,一定程度上降低了谱区内信号断裂和目标信号对谱区识别结果的影响,整体检测效果比较稳定;但在距离约100 km处,负一阶谱左边界出现锯齿状检测结果,这是由于DSNR方法对边界信号有较高的要求,当一阶谱边界信号受传播衰减的影响,逐渐被噪声“淹没”时,强信噪比特性不明显,此时,检测DSNR方法性能受到影响。由此可以看出,DSNR方法对船载展宽一阶谱的边界信号有较高的要求,要求其具备较强的信号差特性。
综上所述,本文所提的DSNR方法的检测性能,与信噪比方法检测性能相近。但当展宽一阶谱区内出现局部信号断裂,或者谱区外存在目标信号时,DSNR法的识别效果会优于信噪比方法,更适合复杂背景下的船载地波雷达展宽一阶谱区识别。
4 结语本文对船载地波雷达展宽一阶谱的展宽范围及幅频特性进行了分析,提出了一种适用于航行状态下的船载地波雷达一阶谱区的差值信噪比(DSNR)识别方法。通过仿真和实测数据实验验证,DSNR法在航行状态下,通过方法中的预筛选处理可获得所有高信噪比频点,进而避免了将目标信号直接错检为一阶谱边界点的问题,保持良好的检测性能。然而,受传播衰减影响,会出现一阶谱区局部信号消失的问题,DSNR法识别性能会受到影响,但其检测效果依旧优于现有方法的识别结果。
然而,在某些探测海域内各海面单元处的海况条件存在差异,各海面单元上接收到的一阶海面回波信号产生差异,此时展宽一阶谱区边界准确识别将遇到新的挑战。此外,当一阶谱边界处存在与边界点信号能量相近的目标信号时,也会影响其检测性能。因此,在后续研究中,将会结合复杂环境条件下的仿真和实测数据,分析更多环境和平台运动条件下的船载地波雷达一阶谱特性,发展适合的一阶谱识别方法,进一步提高船载地波雷达一阶谱的识别效果。
| [1] |
Ponsford A M, Sevgi L, Chan H C. An integrated maritime surveillance system based on high-frequency surface-wave radars 2 Operational status and system performance[J]. IEEE Antennas and Propagation Magazine, 2001, 43(5): 52-63. DOI:10.1109/74.979367 (  0) 0) |
| [2] |
Ji Y G, Liang X, Sun W F, et al. First-order ocean surface cross section for ship-borne bistatic HFSWR derivation and simulation[J]. Journal of Marine Science and Engineering, 2022, 10(5): 649. DOI:10.3390/jmse10050649 (  0) 0) |
| [3] |
Barrick D. First-order theory and analysis of MF/HF/VHF scatter from the sea[J]. IEEE Transactions on Antennas and Propagation, 1972, 20(1): 2-10. DOI:10.1109/TAP.1972.1140123 (  0) 0) |
| [4] |
Silva M T, Huang W M, Gill E W. High-frequency radar cross section of the ocean surface with arbitrary roughness scales: Higher order corrections and general form[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(10): 6723-6738. DOI:10.1109/TAP.2021.3070153 (  0) 0) |
| [5] |
梅晓东, 纪永刚, 王祎鸣, 等. 高频地波雷达海流探测中一阶谱区分离方法[J]. 海洋科学进展, 2014, 32(1): 99-106. Mei X D, Ji Y G, Wang Y M, et al. Separation of first-order spectral region in detecting ocean current with HFSWR[J]. Advances in Marine Science, 2014, 32(1): 99-106. (  0) 0) |
| [6] |
Li Y, Wang X Y, Zhang N, et al. A Machine Learning Based First-Order Sea Clutter Region Extraction Method for HFSWR[C]. USA: Institute of Electrical and Electronics Engineers, 2019: 173-174.
(  0) 0) |
| [7] |
Yao G W, Xie J H, Huang W M. HF radar ocean surface cross section for the case of floating platform incorporating a six-DOF oscillation motion model[J]. IEEE Journal of Oceanic Engineering, 2021, 46(1): 156-171. DOI:10.1109/JOE.2019.2959289 (  0) 0) |
| [8] |
周企豪. 船载高频地波雷达一阶海洋回波分析与处理[D]. 武汉: 武汉大学电子信息学院, 2017. Zhou Q H. Analysis and Processing of the First-order Sea Echo Observed by Ship-Borne HF Surface Wave Radar[D]. Wuhan: School of Electronics and Information, Wuhan University, 2017. (  0) 0) |
| [9] |
纪永刚, 张杰, 王彩玲, 等. 基于信噪比方法的天地波混合体制雷达一阶回波谱提取[J]. 电子与信息学报, 2015, 37(9): 2177-2182. Ji Y G, Zhang J, Wang C L, et al. First-order sea clutter spectrum extraction based on SNR method for HF hybrid sky-surface wave radar[J]. Journal of Electronics & Information Technology, 2015, 37(9): 2177-2182. (  0) 0) |
| [10] |
Xie J H, Sun M L, Ji Z Y. First-order ocean surface cross-section for ship-borne HFSWR[J]. Electronics Letters, 2013, 49(16): 1025-1026. DOI:10.1049/el.2013.1393 (  0) 0) |
| [11] |
张景思, 吴伦宇, 葛建忠, 等. 基于高频地波雷达的多时间尺度海流研究[J]. 海洋学报, 2022, 44(6): 128-139. Zhang J S, Wu L Y, Ge J Z, et al. Study of ocean current at multiple time scales based on the high frequency surface wave radar[J]. Haiyang Xuebao, 2022, 44(6): 128-139. (  0) 0) |
| [12] |
Hasselmann K. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP)[J]. Ergnzungsheft zur Deutschen Hydrographischen Zeitschrift, 1973, 8: 1-95. (  0) 0) |
| [13] |
Shen W, Gurgel K W, Voulgaris G, et al. Wind-speed inversion from HF radar first-order backscatter signal[J]. Ocean Dynamics, 2012, 62(1): 105-121. DOI:10.1007/s10236-011-0465-9 (  0) 0) |
| [14] |
杨绍麟, 柯亨玉, 侯杰昌, 等. MUSIC算法提取海洋表面径向流方位的信号预处理[J]. 现代雷达, 2001, 23(4): 49-54. Yang S L, Ke H Y, Hou J C, et al. Signal preprocessing for bearing determination of ocean surface radial current mapping based on MUSIC[J]. Modern Rada, 2001, 23(4): 49-54. (  0) 0) |
2. Technology Innovation Center for Maritime Silk Road Marine Resources and Environment Networked Observation, Ministry of Natural Resources, Qingdao 266580, China
 2024, Vol. 54
2024, Vol. 54


