2. 自然资源部国家海洋环境预报中心,北京 100081
海浪是最常见的海上自然现象和自然灾害,大风引起的大浪会对船舶航行和海上及近岸建筑物造成非常大的损害,甚至人员伤亡。海浪在近岸破碎形成的沿岸流和离岸流对泥沙输运起着至关重要的作用,其长期效应可引起海岸线的变迁。海浪及其破碎会直接影响海-气界面的动量、热量和物质通量,进而影响海气相互作用强度以及全球气候变化。因此,海浪的准确模拟和预报有非常重要的实际应用和理论研究意义。
目前最为成功的海浪数值预报模式为谱模式,海浪谱S(ω)随着时空的演变由能量平衡方程来表示,即
| $ \frac{\mathrm{d} S(\omega)}{\mathrm{d} t}=S_{\mathrm{in}}+S_{\mathrm{ds}}+S_{\mathrm{nl}}。$ | (1) |
式中: S(ω)为海浪谱; ω为圆频率; 右边各项为源函数项,分别为Sin: 风输入; Sds: 波浪破碎引起的能量耗散; Snl: 非线性波-波相互作用。1988年,以Klaus Hasselmann为首的WAMDI研究团队[1]建立了第一个第三代海浪数值模式——WAM模式,与之前的第二代海浪数值模式不同,WAM模式不需要事先假定海浪谱形,而是通过直接计算风输入、破碎引起的耗散和非线性波-波相互作用等3个源函数项而得到。
在第三代海浪数值模式WAM的基础上,Delft技术大学和美国航空航天局Goddard空间飞行中心分别开发了WAVEWATCH Ⅰ海浪数值模式[2]和WAVEWATCH Ⅱ海浪数值模式[3],美国国家海洋和大气管理局/美国气象环境预报中心(NOAA/NCEP)环境模拟中心海洋模拟小组又开发了WAVEWATCH Ⅲ海浪数值模式[4]。WAVEWATCH Ⅲ第三代海浪数值模式(以后简称WW3模式)考虑波-流相互作用,用波作用量N=S(ω)/ω来代替S(ω)来进行计算,对过去模式的控制方程、程序结构、数值和物理的处理方法等做了改进,有利于采用并行计算技术,从而提高模式的性能和效率。WW3的源代码是公开的,之后很多研究者参与了模式中源函数的改进工作,提供了不同的源函数方案,迄今为止,主要源函数方案有ST2、ST3、ST4和ST6可供选择[5]。
基于卫星和浮标观测数据,Stopa等[5]对上述4种源函数方案进行了评估,认为ST2方案会高估涌浪波高,从而会整体上高估波高。ST3方案的模拟波高比ST2要好,利用其高阶矩计算的Stokes漂流速度和均方波陡与实测大体一致。ST4方案给出的波高具有最小的误差,从全球角度上看,低于5%或30 cm,给出的均方波陡和高阶量与卫星观测一致性很好。ST6方案的表现与ST4方案相似,但ST6会高估高阶量,如Stokes漂流和均方波陡。以飓风Ivan为例,Liu等[6]对上述4种源函数方案进行了评估,发现ST2方案会在整体上低估大浪,其表现较差,而其他3种方案的表现较好,彼此之间没有明显差异。而当浪向和风向不一致时,3种方案会高估波浪能量,得到的波高偏大。在ST6方案中,适当增强涌浪引起的耗散,可以对此有所改善。国内的研究者针对WW3对全球浪场的模拟能力也进行了评估[7]。
基于WW3模式,也有研究者开展了中国东海的海浪数值模拟工作[8-9],从不同角度讨论了WW3在东海的模拟能力。然而,尚缺少对不同源函数方案在东海的全面评估。
本文利用在东海的波浪浮标观测数据,评估ST2、ST4和ST6三种源函数方案在东海的表现,在此基础上,通过改进ST6方案中的拖曳系数计算方法,给出了以波龄和波陡为参数的计算方案,使高风速情形的模拟波高与观测符合得较好,整体提高了WW3模式在东海的波浪模拟能力。
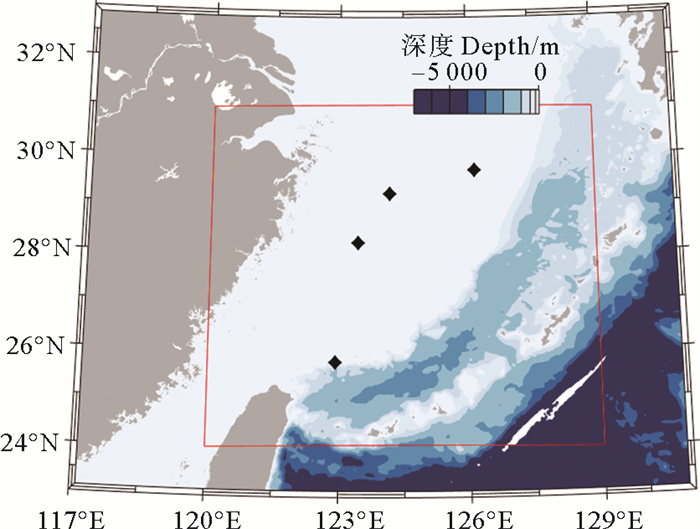
1 数据和模式设置 1.1 所用数据为了对所使用的风场数据和模拟结果进行验证,本文使用了4个波浪浮标观测数据,观测数据包括每小时的风速、风向、有效波高、有效周期、波向、气温和水温等。浮标数据的时间段为2019年1月1日—2020年12月31日,图 1为各个浮标具体位置。
|
(颜色代表水深,自北向南各个浮标对应的水深依次为95、82、85和103 m。Color represents water depth. The corresponding water depths of each buoy from north to South are 95, 82, 85 and 103 m respectively. ) 图 1 位于东海的波浪浮标位置及模式计算区域 Fig. 1 Location of wave buoy in the East China Sea and model calculation area |
下文中所用观测数据为上述4个浮标在2020年8和9月的全部数据。
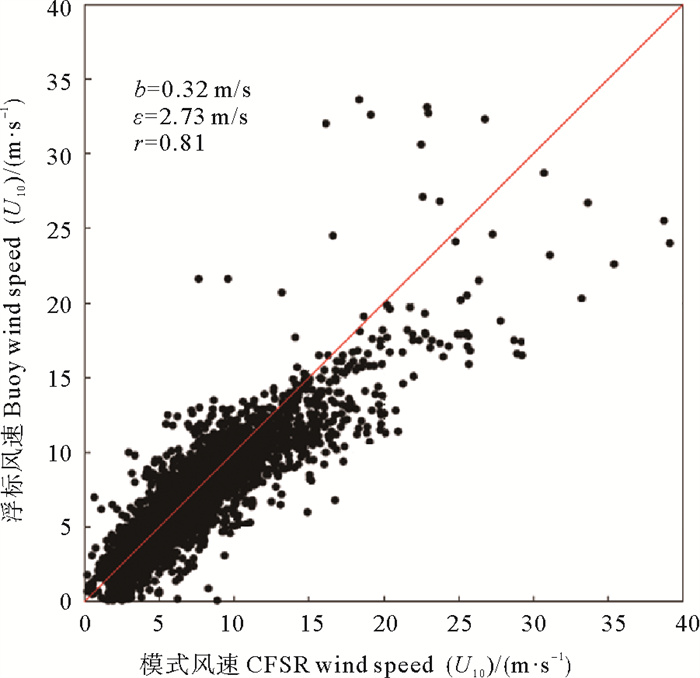
为了驱动海浪模式,所使用的风场为气候预报系统再分析资料(Climate forecast system reanalysis, CFSR)(http://cfs.ncep.noaa.gov),时间分辨率为1 h,空间分辨率为0.2°×0.2°[10]。为了验证CFSP风场数据在东海的适用性,将CFSR风场数据与浮标观测风速U10进行了比较(见图 2),图 2中b为平均偏差,ε为均方根误差,r为相关系数,U10为海面上10 m高度处的风速。从图 2可以看到,两者的相关系数达到了0.81,偏差和均方根误差分别为0.32和2.73 m/s,证明CFSR风场可以用来驱动海浪数值模式。
|
图 2 波浪浮标观测风速与CFSR风速在东海的比较 Fig. 2 Comparison between wave buoy observed wind speed and CFSR wind speed in the East China Sea |
本文所用的WW3为当前最新的V6.07版本,为了保证模拟结果的可靠性,采用了两层嵌套计算方式,大区域的范围为117.0°E—131.0°E,23.0°N—33.0°N,小区域的范围为120.0°E—129.0°E,24.0°N—31.0°N,计算区域如图 1所示,其中红色框内为小区域计算范围。采用规则网格进行计算,所使用的水深数据为etopo2数据,波-波非线性相互作用采用DIA算法,计算大区域的空间分辨率设为0.1°,时间步长为900 s,小区域的空间分辨率设为0.05°,时间步长为600 s,每小时输出一次结果。初始场由JONSWAP-谱提供,对方向谱频率做了35分离散,初始频率为0.037 5 Hz,下一个离散化频率为上一个的1.1倍。计算时间为2020年8、9月的全部天数,模式预热时间为每月第一天,数据从每月的第二天开始输出。之所以选取这两个月份,是因为在此期间均有台风经过研究区域,旨在验证大风情形下模式的模拟能力。
2 不同源函数方案的模拟结果比较 2.1 所用参数化方案针对东海区域,本文将评估WW3模式的ST2、ST4、ST6源函数方案。ST2采用Tolman and Chalikov[11]提出的风输入项Sin和耗散项Sds,ST4采用Ardhuin等[12-13]给出的风输入和耗散项,ST6采用Donelan等[14]、Babanin等[15]、Rogers等[16]和Zieger等[17]改进的方案[18]。
在这些源函数项中,其中最为关键的问题之一就是风应力的计算。作为海-气界面湍流通量的风应力通常采用块体公式进行计算,即
| $ \tau=\rho_{\mathrm{a}} C_{\mathrm{D}} U_{10}^2 \text { 。} $ | (2) |
式中:ρa为空气密度; CD为拖曳系数; 其定义为:
| $ C_{\mathrm{D}}=u_*^2 / U_{10}^2 { 。} $ | (3) |
式中u*为空气摩擦速度。在大气中性稳定条件下,海面上方的不同高度处平均风速U可以表示为对数分布
| $ U=\frac{u_*}{\mathrm{k}} \ln \frac{z}{z_0} 。$ | (4) |
式中:U为海面上方高度z处的平均风速; k=0.4, 为卡曼常数; z0为海面粗糙度,代表海面对风的阻碍效应。显然拖曳系数(CD)与海面粗糙度之间存在一一对应关系,即
| $ C_{\mathrm{D}}=\left(\mathrm{k} / \ln \left(10 / z_0\right)^2\right. 。$ | (5) |
在早期的研究中,由于高风速情形下的条件恶劣和观测困难,几乎所有的观测都是在风速小于20 m/s进行,发现拖曳系数随风速增加而线性增大,并将这一结果推广到高风速情形,直到2003年,Powell等[19]利用飓风情形下的探空气球数据,得到高风速情形下的风速廓形分布,进而得到拖曳系数。发现拖曳系数CD并非随风速增大而单调增大,而是当风速大于临界值30 m/s时,拖曳系数达到饱和,开始随风速增大而减小。之后很多实验室和外海的观测证实了拖曳系数达到饱和的临界风速的存在,但临界风速的变动很大,从20~40 m/s不等。
为了应对这一新发现,避免高风速情形拖曳系数过大,使风输入项增大,造成模拟波高偏大,WW3模式对上述3种方案中的拖曳系数CD做出了上限限制。ST2方案直接将CD上限设置为2.5×10-3,ST4方案通过给海面粗糙度z0设置最大值来防止CD过大。ST6方案采用了由Hwang[20]提出,又经Rogers等[16]对更高风速情形进行了修正的拖曳系数公式:
| $ C_{\mathrm{D}}=\left\{\begin{array}{l} \left(-0.016 U_{10}^2+0.967 U_{10}+8.058\right) \times 10^{-4}, \\ \quad U_{10}<50.33 \mathrm{~m} / \mathrm{s} \\ \left(u_*^C / U_{10}\right)^2, U_{10} \geqslant 50.33 \mathrm{~m} / \mathrm{s} \end{array}\right. 。$ | (6) |
式中u*C=2.206 m/s。根据(6)式,拖曳系数在风速30.2 m/s左右达到最大值2.27×10-3,之后随着风速增大而减小。
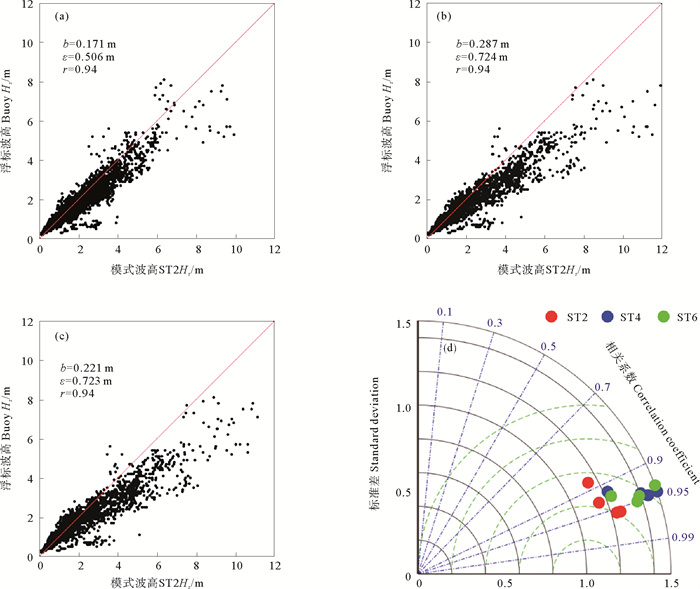
2.2 模拟结果图 3为ST2、ST4和ST6方案模拟的有效波高与浮标观测波高的比较,统计参量包括平均偏差b、均方根误差ε和相关系数r。整体而言,3个方案的模拟结果与观测符合得很好,最大偏差为0.287 m/s,最大的均方误差为0.724 m/s,均为ST4方案的模拟情形。3个方案在东海同时达到最大相关系数0.94,ST2方案整体表现最优。同时由文献[21]可知,3个参数化方案在东海模拟效果整体可观,但还有一定的提升空间。我们还发现,当波高小于3 m,3个方案的模拟结果与观测符合得非常好,没有系统性偏离,当波高大于3 m时,所有的方案均高估了波高,这很可能是高风速情形下,3个方案中的拖曳系数过大所致。
|
((a)ST2结果; (b)ST4结果; (c)ST6结果; (d)整体结果。(a)ST2 results; (b)ST4 results; (c)ST6 results; (d)Overall results. ) 图 3 三个参数化方案有效波高模拟结果 Fig. 3 Simulation results of significant wave height of three parameterized schemes |
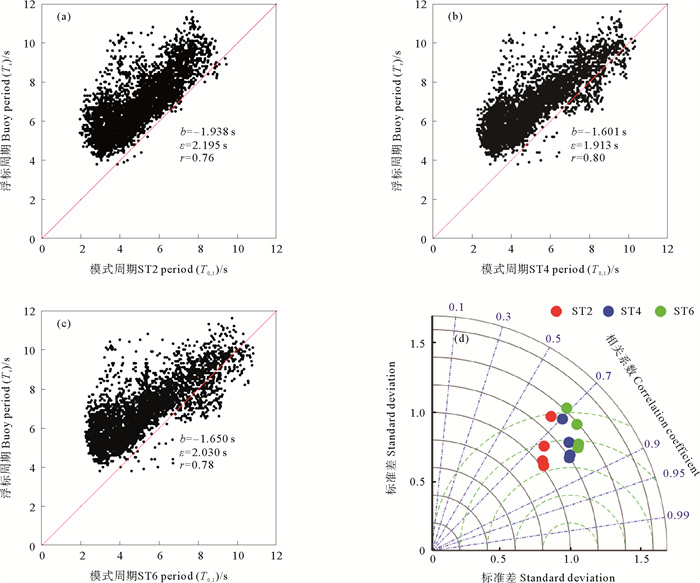
浮标数据仅提供了有效周期Ts,而模式输出的是平均周期(T0, 1、T0, 2)。有研究表明,模式输出的一阶矩周期T0, 1与浮标观测的有效周期Ts较为接近。图 4为3种方案模拟得到的一阶矩周期T0, 1与波浪浮标观测得到的有效周期Ts的比较。因为一阶矩周期T0, 1及二阶矩周期T0, 2更多反映短波的效应,而有效周期Ts则是1/3大波周期的平均,所以一般而言,有效周期Ts要大于一阶矩周期T0, 1及二阶矩周期T0, 2,这一点可以从平均偏差中看到。Taylor图及统计结果均显示3种方案对中国近海周期有较好模拟能力,但是相关性没有有效波高好,这一点有望通过接下来的方案调整得到改善。
|
((a)ST2结果; (b)ST4结果; (c)ST6结果; (d)整体结果。(a)ST2 results; (b)ST4 results; (c)ST6 results; (d)Overall results. ) 图 4 三个参数化方案周期模拟结果 Fig. 4 Simulation results of period of three parameterized schemes |
从上述分析可以看到,ST2方案在东海对有效波高表现最好,ST6方案次之,对周期而言ST2方案模拟效果不如其它两个方案。上文已提及,ST2方案风应力拖曳系数计算方案涉及波龄参量,而ST6风应力拖曳系数是拟合最新观测数据的结果,仅和风速有关,而在台风状况下,只考虑风速的拖曳系数计算方案不能满足模式需求[22-23]。因此有望通过改善ST6方案拖曳系数计算方案来提高WW3数值模式的精度。
3 拖曳系数新参数化方案从上述的分析可以看到,3个参数化方案在东海模拟结果存在一个共同问题,就是高风速时模拟的波高偏大,这显然与风输入项中的拖曳系数公式有关。在ST6方案中,拖曳系数是风速的函数,与波浪状态无关。虽然考虑了拖曳系数饱和现象,但是否适用于东海区域值得商榷。
另一方面,对于拖曳系数饱和或减小的原因,有很多工作对此进行了探讨,但尚没有统一的结论,但所有的工作都认为波浪及其破碎过程有关。如波浪破碎形成白冠覆盖于海面,会使海面“光滑”,产生的海洋飞沫会被风加速而降低风应力效果,海洋飞沫会提高大气边界层的稳定性,从而抑制动量通量,波峰附近发生波流分离会掩盖波谷,导致海面光滑等。
显然所有这些原因均与波浪有关,而描述波浪不同状态最常用的两个量为波龄和波陡。波龄反映了波浪和大气之间的相互作用状态,波龄越小,代表海-气相互作用越强。波陡则反映了波浪自身的稳定性,波陡越大,波浪越不稳定而破碎[24]。
Takagaki等[25]将实验室测得的高风速的结果与外海中低风速的观测数据相结合,认为在风浪情形下,拖曳系数或海面粗糙长度仅与波浪有关,与海上风速没有直接关系,给出了海面粗糙长度(z0)与波高和周期的函数,可表示为波陡和波龄的函数:
| $ z_0=68.35\left(H_{\mathrm{s}} / L_{\mathrm{p}}\right)^4\left(g T_{\mathrm{p}} / 2 \pi U_{10}\right)^2 U_{10}^2 / g 。$ | (7) |
式中:g为重力加速度; Hs/Lp为波陡; Lp为谱峰对应的波长; gTp/(2πU10)为波龄; Tp为谱峰周期。
在通常情况下,波龄和波陡均基于谱峰所对应的波长和周期进行定义,在实际应用中,谱峰有时很难确定,特别是存在混合浪的情形,此时得到的谱峰周期会有非常大的变动,不利于计算的稳定性。与谱峰周期相比,二阶矩周期T0, 2的稳定性较好,因此,用二阶矩周期T0, 2来计算波龄和波陡,以此定义的波龄β和波陡δ分别为:
| $ \beta=\frac{g T_{0, 2}}{2 \pi U_{10}} ; \quad \delta=\frac{2 \pi H_s}{g T_{0, 2}^2} 。$ | (8) |
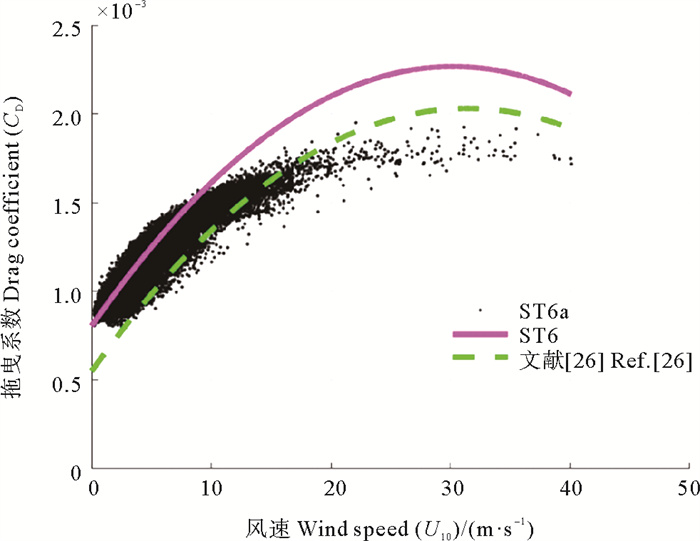
基于前人的工作及(7)式,为了在保证低风速情形模拟精度同时,提高高风速时的模拟精度,作者试图建立类似的适用于东海区域的拖曳系数公式。利用ST6输出的波浪数据(T0, 2及Hs)计算波龄及波陡,通过对公式(9)中参数调整使得其计算的拖曳系数在风速小于15 m/s时,趋势与ST6方案相同,在风速大于15 m/s时,趋势小于ST6方案。将此时的公式替代ST6原始计算方案称为ST6a方案,反复带入模式验证结果,最终得到本文公式(9)中参数。图 5散点为ST6a方案输出的波浪数据计算所得拖曳系数,同时增加了Zijlema等[26]文献资料作为对比,可以发现新拖曳系数方案基本符合以往结果的变化趋势,不同的是,该方案可以自动达到饱和。
| $ \begin{aligned} & C_{\mathrm{D}}=0.65 \times 10^{-3}+\left[\kappa / \ln \left(10 / z_0\right)\right]^2, \\ & z_0=120 \delta^6 \beta^4 U_{10}^2 / g, \beta=\min \left(\frac{g T_{0, 2}}{2 \pi U_{10}}, 0.9\right) 。\end{aligned} $ | (9) |
式中min代表取其后括号内两者的较小值。
|
(图中实线为公式(6)结果,虚线为文献结果对比。The solid line in the figure is the result of formula (6); The dotted line is the literature comparison result. ) 图 5 ST6a方案给出的拖曳系数与公式(6)对比 Fig. 5 Comparison between the drag coefficient given by ST6a scheme and formula (6) |
对于上面的海面粗糙度计算公式,我们仅对波龄做出了限制,因为波龄原则上仅适用于风浪情形,对应的波龄较小,而当波龄很大时,对应的为涌浪情形,此时波龄没有任何意义,不能代表海-气相互作用的强度,因此我们对波龄的上限做出了限制。在实际应用中,也经常用波龄的大小来区分风浪和涌浪。相反,对于波陡没有做限制,由于波浪破碎,波陡自身具有上限值,风浪的波陡通常会大于涌浪波陡。
从图 5还可以看到,以波龄和波陡为参数的拖曳系数会自动达到饱和,即在某一临界风速时,拖曳系数达到最大,之后随着风速继续增大而减小,这也是近年来被很多观测所证实的现象。从图 5中可以看到,该临界风速大约为20 m/s,与ST6原有的公式(6)相比,临界风速明显减少。再次强调的是,对于ST6a方案,本文并没有人为地设定临界风速,而是由于波龄和波陡的变化给出的自然结果。一般而言,随着风速增大,波龄会减小,而波陡由于存在上限不会增大,此时拖曳系数主要随波龄减小而减小。
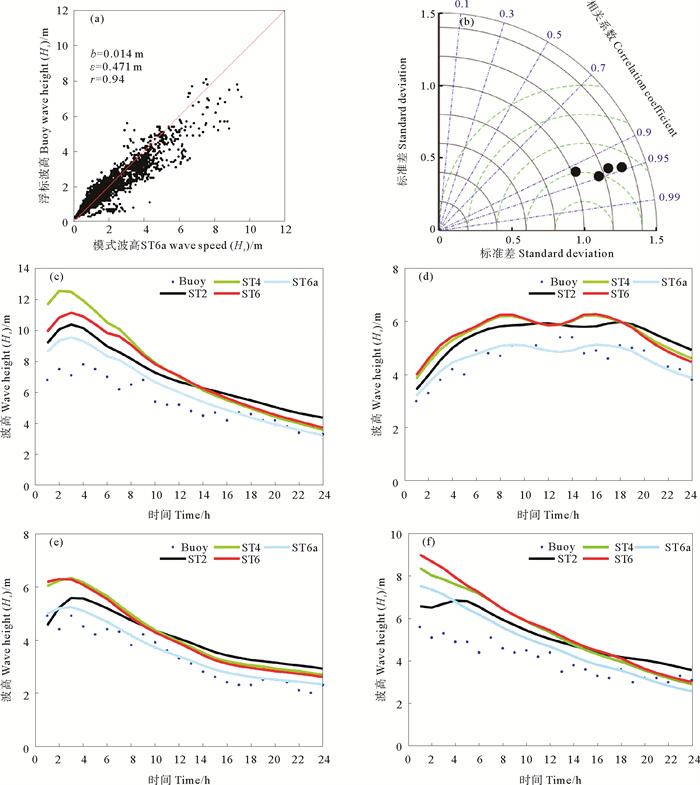
4 新方案的应用图 6为新公式用于ST6源函数方案得到的模拟波高与浮标波高的比较。从图中可以看到,新方案偏差绝对值及均方根误差均有明显降低。图 6同时给出了新方案在东海模拟结果的Taylor图及各个浮标处大波高情形下连续24 h的时间序列图。从图中可以看到,原始方案模拟波高过大的问题得到了改善。具体而言, 相比之前表现最好的ST2方案,ST6a方案的平均偏差绝对值比原始值降低91.8%,相应的均方根误差比原始方案分别降低6.9%,即考虑波龄和波陡对拖曳系数进行参数化,可以得到较好的模拟结果。当然,这需要有更多的数据进行验证。
|
((a~b): ST6a方案整体结果; (c~f): ST6a方案在各个浮标处连续24 h结果; (c)、(d)、(e)、(f)分别为自北向南单个浮标; (c)、(f)时间段为8月27日全天; (d)、(e)时间段为8月2日全天。(a~b): Overall results of ST6a scheme; (c~f): The results of ST6a scheme at each buoy for 24 hours; (c), (d), (e) and (f): A single buoy from North to South; (c), (f): The time range is the whole day of August 27; (d), (e): The time range is the whole day of August 2. ) 图 6 ST6a新参数化方案在东海对有效波高模拟精度状况 Fig. 6 The simulation accuracy of ST6a new parameterized scheme for the significant wave height in the East China Sea |
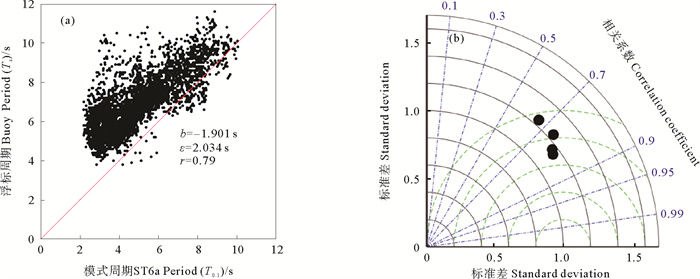
图 7为ST6a新方案模拟得到的一阶矩周期T0, 1与波浪浮标观测得到的有效周期Ts的比较。可以看到,新方案的模拟周期也得到了改善,整体相关性有了提升。
|
((a~b)ST6a方案整体结果。(a~b) overall results of ST6a scheme. ) 图 7 ST6a新参数化方案在东海对周期模拟精度状况 Fig. 7 The simulation accuracy of ST6a new parameterized scheme for the period in the East China Sea |
准确预报中国海的海浪一直是一个非常重要的课题。利用中国东海的波浪浮标观测数据,分析比较了第三代海浪数值模式WW3的三种源函数参数化方案ST2、ST4、ST6在东海的表现。结果表明,对于波高小于3 m的中低风速情形,三种方案的模拟波高与浮标观测波高大体一致,而对于波高大于3 m的高风速情形下,三种方案的模拟波高均明显大于浮标观测波高,即在大风情形下,WW3模拟的波高偏大。为了解决高风速情形下WW3模拟波高偏大问题,本文提出了以波龄和波陡为参数的海面粗糙度计算公式,以此来计算拖曳系数,其重要特征就是拖曳系数随着风速增大自动趋于饱和状态,即当风速达到临界风速20 m/s左右时,拖曳系数达到最大值,之后随风速增大而减小。将上述拖曳系数公式用于ST6源函数方案中,既保证了中低风速时的模拟精度,又有效改善了高风速情形模拟波高偏大的问题。具体而言,相对于ST2方案,有效波高平均偏差降低91.81%,相对于ST4方案,有效波高平均偏差降低95.12%;相对于ST6方案,有效波高平均偏差降低93.66%,同时使模拟周期与附表观测结果相关性更强, 从整体上提高了WW3在中国东海的海浪模拟能力。
| [1] |
WAMDI Group. The WAM model—a third generation ocean wave prediction model[J]. Journal of Physical Oceanography, 1988, 18: 1775-1810. DOI:10.1175/1520-0485(1988)018<1775:TWMTGO>2.0.CO;2 (  0) 0) |
| [2] |
Tolman H L. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents[J]. Journal of Physical Oceanography, 1991, 21(6): 782-797. DOI:10.1175/1520-0485(1991)021<0782:ATGMFW>2.0.CO;2 (  0) 0) |
| [3] |
Tolman H L. Effects of numerics on the physics in a third-generation wind-wave model[J]. Journal of Physical Oceanography, 1992, 22(10): 1095-1111. DOI:10.1175/1520-0485(1992)022<1095:EONOTP>2.0.CO;2 (  0) 0) |
| [4] |
Tolman H L. User Manual and System Documentation of WAVEWATCH Ⅲ Version 1.18[R]. Washington DC: National Oceanic and Atmospheric Administration, 1999: 110.
(  0) 0) |
| [5] |
Stopa J, Ardhuin F, Babanin A, et al. Comparison and validation of physical wave parameterizations in spectral wave models[J]. Ocean Modelling, 2016, 103: 2-17. DOI:10.1016/j.ocemod.2015.09.003 (  0) 0) |
| [6] |
Liu Q, Babanin A V, Fan Y, et al. Numerical simulations of ocean surface waves under hurricane conditions: Assessment of existing model performance[J]. Ocean Modelling, 2017, 118: 73-93. DOI:10.1016/j.ocemod.2017.08.005 (  0) 0) |
| [7] |
吴萌萌, 王毅, 万莉颖, 等. WAVEWATCH Ⅲ模式在全球海域的数值模拟试验及结果分析[J]. 海洋预报, 2016, 33(5): 31-40. Wu M, Wang Y, Wan L, et al. Numerical simulation test and result analysis of WAVEWATCH Ⅲ model in global waters[J]. Ocean Forecast, 2016, 33(5): 31-40. (  0) 0) |
| [8] |
李明悝, 侯一筠. 利用QuikSCAT/NCE混合风场及WAVEWATCH模拟东中国海风浪场[J]. 海洋科学, 2005, 29(6): 9-12. Li M, Hou Y. QuikSCAT /NCE mixed wind field and WAVEWATCH are used to simulate the wind and wave field in the East China Sea[J]. Marine Science, 2005, 29(6): 9-12. (  0) 0) |
| [9] |
徐艳清. 东中国海海浪数值模拟及波候统计分析[D]. 北京: 中国科学院研究生院, 2005. Xu Y. Numerical Simulation and Statistical Analysis of Wave Climate in the East China Sea[D]. Beijing: Graduate School of Chinese Academy of Sciences, 2005. (  0) 0) |
| [10] |
Saha S, Moorthi S, Wu X, et al. The NCEP climate forecast system version 2[J]. Journal of Climate, 2014, 27(6): 2185-2208. DOI:10.1175/JCLI-D-12-00823.1 (  0) 0) |
| [11] |
Tolman H L, Chalikov D. Source terms in a third-generation wind wave model[J]. Journal of Physical Oceanography, 1996, 26: 2497-2518. DOI:10.1175/1520-0485(1996)026<2497:STIATG>2.0.CO;2 (  0) 0) |
| [12] |
Ardhuin F, Chapron B, Collard F. Observation of swell dissipation across oceans[J]. Geophysical Research Letters, 2009, 36: L06607. DOI:10.1029/2008GL037030 (  0) 0) |
| [13] |
Ardhuin F, Rogers E, Babanin A, et al. Semiempirical dissipation source functions for ocean waves, Part Ⅰ, definition, calibration and validation[J]. Journal of Physical Oceanography, 2010, 40(9): 1917-1941. DOI:10.1175/2010JPO4324.1 (  0) 0) |
| [14] |
Donelan M A, Babanin A V, Young I R, et al. Wave-follower field measurements of the wind-input spectral function. Part Ⅱ: Parameterization of the wind input[J]. Journal of Physical Oceanography, 2006, 36: 1672-1689. DOI:10.1175/JPO2933.1 (  0) 0) |
| [15] |
Babanin A V. Breaking and Dissipation of Ocean Surface Waves[M]. Cambridge: Cambridge University Press, 2011: 480.
(  0) 0) |
| [16] |
Rogers W E, Babanin A V, Wang D W. Observation consistent input and whitecapping dissipation in a model for wind-generated surface waves: Description and simple calculations[J]. Journal of Atmospheric and Oceanic Technology, 2012, 29: 1329-1346. DOI:10.1175/JTECH-D-11-00092.1 (  0) 0) |
| [17] |
Zieger S, Babanin A V, Rogers W E, et al. Observation based source terms in the third-generation wave model WAVEWATCH[J]. Ocean Modelling, 2015, 96: 2-25. DOI:10.1016/j.ocemod.2015.07.014 (  0) 0) |
| [18] |
Liu Q, Rogers W E, Babanin A V, et al. Observation-based source terms in the third-generation wave model WAVEWATCH Ⅲ: Updates and verification[J]. Journal of Physical Oceanography, 2019, 49: 489-517. DOI:10.1175/JPO-D-18-0137.1 (  0) 0) |
| [19] |
Powell M D, Vickery P J, Reinhold T A. Reduced drag coefficient for high wind speeds in tropical cyclones[J]. Nature, 2003, 422: 279-283. DOI:10.1038/nature01481 (  0) 0) |
| [20] |
Hwang P A. A note on the ocean surface roughness spectrum[J]. Journal of Atmospheric and Oceanic Technology, 2011, 28(3): 436-443. DOI:10.1175/2010JTECHO812.1 (  0) 0) |
| [21] |
Taylor, Karl E. Summarizing multiple aspects of model performance in a single diagram[J]. Journal of Geophysical Research Atmospheres, 2001, 106(D7): 7183-7192. DOI:10.1029/2000JD900719 (  0) 0) |
| [22] |
Chiang T L, Wu C R, Oey L Y. Typhoon Kai-Tak: An ocean's perfect storm[J]. Journal of Physical Oceanography, 2011, 41: 221-233. DOI:10.1175/2010JPO4518.1 (  0) 0) |
| [23] |
Sanford T B, Price J F, Girton J B, et al. Highly resolved observations and simulations of the ocean response to a hurricane[J]. Geophysical Research Letters, 2007, 34: L13604. (  0) 0) |
| [24] |
Zhao D, Li M. Dependence of wind stress across an air-sea interface on wave states[J]. Journal of Oceanography, 2019, 75(3): 207-223. DOI:10.1007/s10872-018-0494-9 (  0) 0) |
| [25] |
Takagaki N, Komori S, Suzuki N, et al. Strong correlation between the drag coefficient and the shape of the wind sea spectrum over a broad range of wind speeds[J]. Geophysical Research Letters, 2012, 39: L23604. (  0) 0) |
| [26] |
Zijlema M, Vledder G, Holthuijsen L. Bottom friction and wind drag for wave models[J]. Coastal Engineering, 2012, 65: 19-26. DOI:10.1016/j.coastaleng.2012.03.002 (  0) 0) |
2. National Marine Environmental Forecasting Center, Ministry of Natural Resources, Beijing 100081, China
 2023, Vol. 53
2023, Vol. 53


