2. 中国海洋大学数学科学学院,山东 青岛 266100
绝大多数科研成果是由严谨的科学研究得到的,但也有少量的成果是由意外得到的。合成滑动相关系数的发现就是由一项意外引出的重要成果。
在研究两个时间序列相关性随时间变化时,需要使用滑动相关系数(Running correlation coefficient, RCC)。RCC是选择一个小于时间序列长度的数据片段作为时间窗口,将计算一般相关系数的方法用于窗口中的数据,然后移动时间窗口,就可以获得滑动相关系数。我们将其称为局域滑动相关系数(Local running correlation coefficient, LRCC)。
作者用滑动相关系数得到非常有趣的现象,取得了一系列成果。后来发现程序中用的不是标准的LRCC算法。一旦将算法换成LRCC算法,那些重要的现象就消失了。这就有两种可能,一种是因用错了算法得到了错误的结果;还有一种可能就是标准的LRCC算法存在问题。LRCC算法已经用了90多年[1],得到非常广泛的应用,怀疑这种算法是大胆的、极具挑战性的工作。
出于对自己结果的坚信,我们开始寻找这两种算法的差异和联系。经过缜密的推导得出,我们使用的算法实际上是一种与LRCC既有联系又有差别的新算法,给出令人信服的应用结果[2],并进一步证明了SRCC是滑动相关系数的正确表达方式[3]。我们将其命名为合成滑动相关系数(Synthetic running correlation coefficient, SRCC)。本文将综述SRCC方法,展现这种方法的科学价值,推广SRCC方法的应用。
2 两种滑动相关系数的物理差异及其机理为了更好地理解SRCC的作用和价值,我们将其与LRCC算法进行比较,导出二者的关系,以获得对SRCC的认识。对于两个长度为N的等间距时间序列
| $ \begin{array}{l} X = \left\{ {{x_k}:k = 1, 2 \cdots , N} \right\}, \\ Y = \left\{ {{y_k}:k = 1, 2 \cdots , N} \right\}, \end{array} $ |
我们常用的线性相关系数R被称为皮尔逊积矩相关系数(Pearson product-moment correlation coefficient),即[4]:
| $ R = \frac{{\sum\limits_{k = 1}^N {\left( {{x_k} - \bar X} \right)\left( {{y_k} - \bar Y} \right)} }}{{\sqrt {\sum\limits_{k = 1}^N {{{\left( {{x_k} - \bar X} \right)}^2}} } \sqrt {\sum\limits_{k = 1}^N {{{\left( {{y_k} - \bar Y} \right)}^2}} } }}, $ | (1) |
其中,均值定义为
| $ \bar X = \frac{1}{N}\sum\limits_{k = 1}^N {{x_k}, } \bar Y = \frac{1}{N}\sum\limits_{k = 1}^N {{y_k}} 。$ | (2) |
这个算法首先由Francis Galton[5-6]提出,后Karl Pearson进行了推广和应用[7-8]。这里我们将(2)式用全部数据得到的均值称为全局均值(Global mean),将(1)式表达的相关系数R称为全局相关系数(Global correlation coefficient)。
2.1 两种不同的滑动相关系数由于相关系数R只是一个值,人们有时需要了解两个时间序列相关性随时间的变化,开始探索使用滑动相关系数(RCC)[1],即在时间序列中选取一个窗口,将(1)式直接应用到这个窗口之中,得到一个相关系数。然后移动时间窗口,就会得到一个随时间变化的相关系数。设移动的时间窗口i的长度为2n+1,即[i-n, i+n],得到:
| $ \begin{array}{c} {R_r}\left( i \right) = \frac{{\sum\limits_{k = i - n}^{i + n} {\left( {{x_k} - \bar X} \right)\left( {{y_k} - \bar Y} \right)} }}{{\sqrt {\sum\limits_{k = i - n}^{i + n} {{{\left( {{x_k} - {{\bar X}_i}} \right)}^2}} } \sqrt {\sum\limits_{k = i - n}^{i + n} {{{\left( {{y_k} - {{\bar Y}_i}} \right)}^2}} } }}, \\ i = 1 + n, \cdots , N - n, \end{array} $ | (3) |
去掉数据两端的半窗口,滑动相关系数的计算范围为i∈[1+n, N-n],其中均值采用的是时间窗口内数据计算的均值,
| $ \bar X = \frac{1}{{2n + 1}}\sum\limits_{k = i - n}^{i + n} {{x_k}, } \bar Y = \frac{1}{{2n + 1}}\sum\limits_{k = i - n}^{i + n} {{y_k}}。$ | (4) |
这里将(4)式定义的均值称为局域均值(Local means),Rr即LRCC。
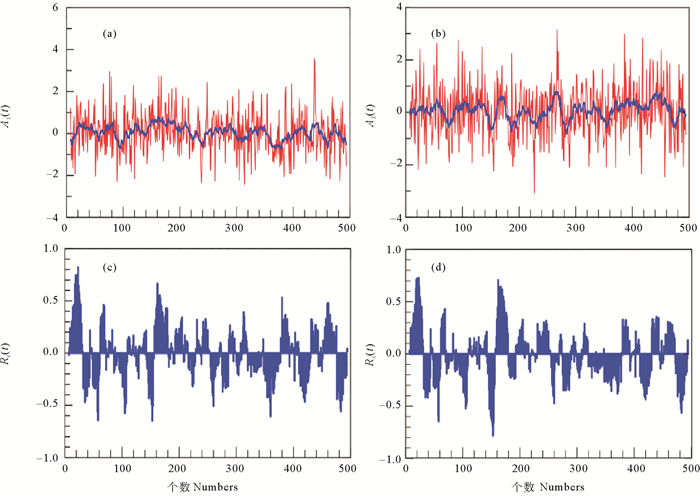
LRCC得到非常广泛的应用[9-15]。然而,LRCC算法隐含了一个假定,即可以将计算全局相关系数的方法直接用于计算LRCC,但是这样做的合理性并未得到理论上的证明。该方法一直沿用至今,从来没有人怀疑它的正确性。然而,用下面一个简单的例子就可以看出LRCC算法可能存在问题。随机生成两个长度为500的白噪声信号,f1(t) 和f2(t),如图 1(a)和(b)表示,二者的全局相关系数趋于零,LRCC(见图 1(c))表现为低于置信度的杂乱无章的值。
|
( ((a)和(b)为两组白噪声时间序列(红线)及其局域均值(蓝线),(c)为LRCC,(d)为SRCC。(a) and (b) two series of the white noise (red lines) and the local means (blue lines); (c) LRCC; (d) SRCC.) ) 图 1 针对白噪声数据两种滑动相关系数的比较(引自文献[2]) Fig. 1 Two running correlation coefficients of the white noise(from reference[2]) |
如果在两个时间序列的150-350处分别加上常数a1和a2,
| $ {A_1}\left( t \right) = {f_1}\left( t \right) + {a_1};{A_2}\left( t \right) = {f_2}\left( t \right) + {a_2}。$ | (5) |
常数取值为:
| $ {a_1} = \left\{ {\begin{array}{*{20}{l}} {3\;\;\;150 \le t \le 350}\\ {0\;\;\;其余部分} \end{array};} \right.{a_2} = \left\{ {\begin{array}{*{20}{l}} {2\;\;\;150 \le t \le 350}\\ {0\;\;\;其余部分} \end{array}} \right.。$ | (6) |
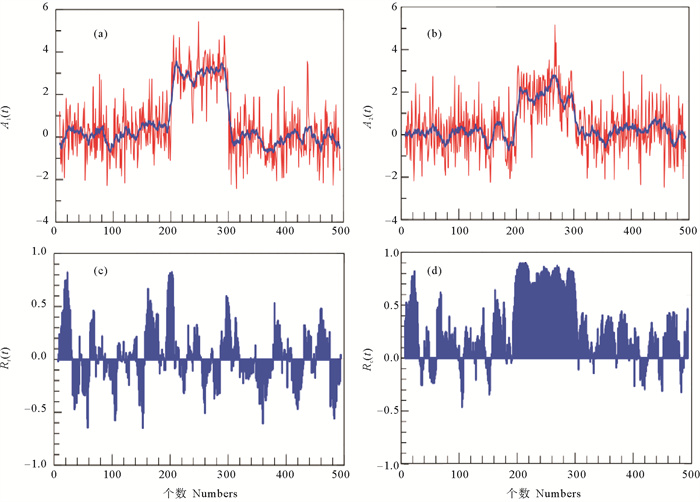
公式(5)式的时间序列示于图 2(a),(b)。我们期待,在加上常数的时间段有比较高的相关性。比如:若时间序列表达的是两地的气温变化,常数都取为正值代表两地在一段时间内气温都出现升高,二者应该体现为正相关。然而,LRCC(见图 2(c))并没有体现这种期待,而是与没有加上常数的结果(见图 1(c))几乎相同。这个不合常理的结果难以解释。
|
( ((a)和(b)为两组加上常数偏差的白噪声时间序列(红线)及其局域均值(蓝线),(c)为LRCC,(d)为SRCC。(a) and (b) two series of the white noise defined by Eq. (5) (red lines) and the local means (blue lines); (c) LRCC; (d) SRCC.) ) 图 2 加常数的白噪声信号两种滑动相关系数的比较(引自文献[2]) Fig. 2 Two kinds of the RCC of the white noise by adding constant deviations(from reference[2]) |
赵等[2]指出,LRCC的问题是:不仅数据本身随时间变化,而且按照(4)式计算的两组局域均值(图 1(a)、(b)和图 2(a)、(b)中的蓝色线)也随时间变化;LRCC反映了数据距平之间的相关性变化,却没能反映均值随时间变化的相关性,因此漏掉了重要的信息。而SRCC算法如(7)式所示[2],即
| $ \begin{array}{l} {R_s}\left( i \right) = \frac{{\sum\limits_{k = i - n}^{i + n} {\left( {{x_k} - \bar X} \right)\left( {{y_k} - \bar Y} \right)} }}{{\sqrt {\sum\limits_{k = i - n}^{i + n} {{{\left( {{x_k} - {{\bar X}_i}} \right)}^2}} } \sqrt {\sum\limits_{k = i - n}^{i + n} {{{\left( {{y_k} - {{\bar Y}_i}} \right)}^2}} } }}, \\ i = 1 + n, \cdots , N - n。\end{array} $ | (7) |
其中使用的均值
虽然文献[2]提出了SRCC算法,并且给出了一些应用实例,但该算法并没有在数学上得到证明。针对这个问题,文献[3]对该算法进行了深入研究,在数学上证实了该算法的正确性和唯一性。数学证明的依据是不同时间段之间滑动相关系数取值应该具有可比性。该文提出,滑动相关系数在任意两个时间段的取值都是应该可以相互比较的,即相关系数相同意味着相关性相同,否则滑动相关系数就失去了意义。
按照比较的定义,需要首先确定比较的标准,比如,南方和北方的城市气温不同,需要有不同的比较标准,才能知道什么时候偏冷或偏暖。在气温的例子中,我们常用的比较标准就是平均气温。在数学上,物理量可以分为标准量和比较量,其中,标准量不参加比较,只有比较量才参加比较[16]。在上例中,两个城市气温的全局均值(
虽然必须用常数作为比较量,但是比较量的选取具有任意性。例如,选择高于或低于均值的量为比较量也是允许的。文献[3]对比较量的选择加了一个限制条件,即不论时间窗口如何选取,其相对于标准量的正偏差和负偏差应该相等,从而证明了全局均值(
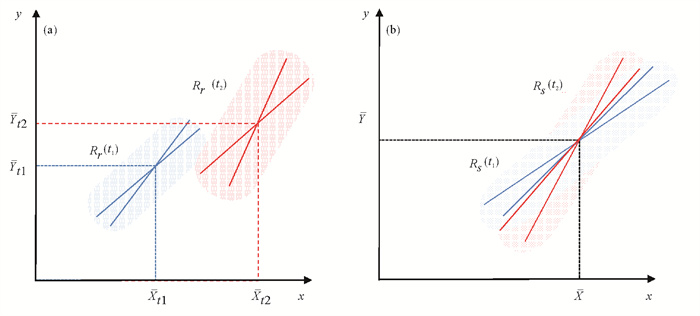
上面证实了采用全局均值是保证滑动相关系数可比性的正确选择,还需要证实SRCC是滑动相关系数的合理形式。文献[3]采用相关系数的基本定义,即最小二乘法确定滑动相关系数,发现只要对LRCC算法加上一个限制条件就可以得出SRCC,即要求所有窗口的相关系数的拟合曲线都通过全局均值(
|
(
图中x轴和y轴为两个时间序列数据的取值,不同颜色的阴影区代表不同窗口的数据散布点。(a) LRCC,带有不同均值( |
文献[2]得出了SRCC和LRCC,也就是Rs(i)和Rr(i)之间的关系,
| $ {R_s}\left( i \right) = {R_r}\left( i \right)\cos {\gamma _x}\cos {\gamma _y} + \sin {\gamma _x}\sin {\gamma _y}。$ | (8) |
其中
| $ \begin{array}{l} \cos {\gamma _x} = \frac{{{\sigma _{rx}}\left( i \right)}}{{\sqrt {\left[ {\sigma _{rx}^2\left( i \right) + {{\left( {{{\bar X}_i} - \bar X} \right)}^2}} \right]} }}, \\ \sin {\gamma _x} = \frac{{{{\bar X}_i} - \bar X}}{{\sqrt {\left[ {\sigma _{rx}^2\left( i \right) + {{\left( {{{\bar X}_i} - \bar X} \right)}^2}} \right]} }}, \\ \cos {\gamma _y} = \frac{{{\sigma _{ry}}\left( i \right)}}{{\sqrt {\left[ {\sigma _{ry}^2\left( i \right) + {{\left( {{{\bar Y}_i} - \bar Y} \right)}^2}} \right]} }}, \\ \sin {\gamma _y} = \frac{{{{\bar Y}_i} - \bar Y}}{{\sqrt {\left[ {\sigma _{ry}^2\left( i \right) + {{\left( {{{\bar Y}_i} - \bar Y} \right)}^2}} \right]} }}。\end{array} $ | (9) |
在一个时间窗口内,两组距平可以计算一个相关系数Rr(i);而均值只有一对,均值之间的相关性不能用相关系数表达。这里,用
| $ \begin{array}{l} \sigma _{rx}^2\left( i \right) = \frac{1}{{2n + 1}}{\sum\limits_{k = i - n}^{i + n} {\left( {{x_k} - {{\bar X_i}}} \right)} ^2}, \\ \sigma _{ry}^2\left( i \right) = \frac{1}{{2n + 1}}{\sum\limits_{k = i - n}^{i + n} {\left( {{y_k} - {{\bar Y_i}}} \right)} ^2}。\end{array} $ | (10) |
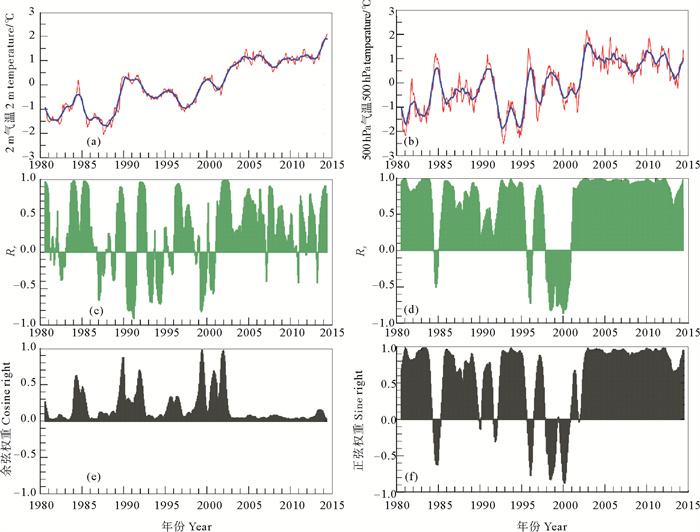
从(8)式可以看出,SRCC实际上是LRCC与1加权的结果,LRCC的权重称为余弦权重,而1的权重称为正弦权重。以2 m气温和500 hPa气温(见图 4(a)、(b))为例,给出了LRCC(见图 4(c))和SRCC(见图 4(d))之间的权重关系。
|
( 2 m和500 hPa气温数据来自NCEP/NCAR Reanalysis 1。(a)2 m气温距平(红线)及其局域均值(蓝线);(b)500 hPa气温距平(红线)及其局域均值(蓝线);(c)LRCC;(d)SRCC; (e)余弦权重cosγxcosγy;(f)正弦权重sinγxsinγy。2 m and 500 hPa air temperature are from NCEP/NCAR Reanalysis 1. (a) 2 m temperature anomalies (red line) and its local mean (blue line); (b) 500 hPa temperature anomalies (red line) and its local mean (blue line); (c)LRCC; (d)SRCC; (e) cosine right cosγxcosγy; (f) sine right sinγxsinγy. ) 图 4 北大西洋2 m和500 hPa气温之间的两种滑动相关系数(引自文献[2]) Fig. 4 The two running correlation coefficients between 2 m and 500 hPa air temperature in North Atlantic Ocean(from referenceis[2]) |
结果表明,两者之间的主导关系是正弦权重(见图 4(f)),因而SRCC在大部分时间的值接近1。而在2000年前后的一段时间,余弦权重占优势(见图 4(e)),SRCC与LRCC更为接近。类似更多的例子见文献[2]。
这个结果的物理意义可以从(9)式看出。正弦权重大表明均值差的贡献大,意味着局域均值与全局均值有比较大的差异,相关系数趋于1;而余弦权重大代表距平的贡献比较大,得到的SRCC与LRCC接近。这个结果进一步表明,如果距平变化强烈,均值差别不大,两个相关系数非常接近;而如果距平变化微小而均值变化很大,则相关系数趋于1;在一般情况下,相关系数是这二者的组合。
2.5 高频信号和低频信号的贡献虽然权重的大小决定了SRCC的取值,但是我们还是更关心其反映的物理意义。如果我们粗略地将信号中时间尺度小于时间窗口的认为是高频信号,大于时间窗口的为低频信号,则正弦权重反映了信号中低频信号所占的相对比重,而余弦权重为高频信号的相对比重。从(8)式可以看出,LRCC主要体现了高频信号之间的相关性,而SRCC既体现了高频信号之间的相关性,也体现了低频信号之间的相关性。也就是说,当信号变化以高频为主时,两个相关系数差别不大(见图 1(c)、(d)),而以低频信号为主时,二者有明显的差别(见图 2(c)、(d))。如果两个时间序列高频信号微弱,而低频信号差异很大,两个相关系数给出的结果有明显差别。
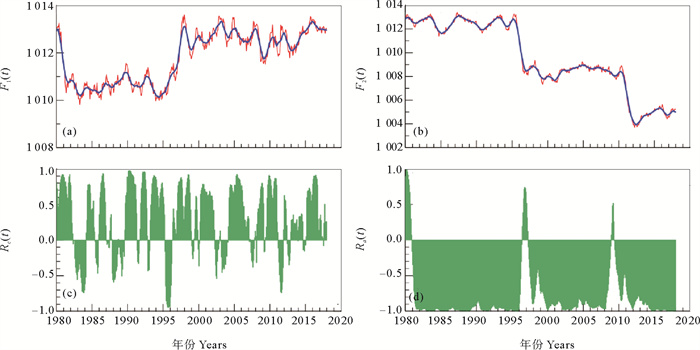
图 5给出北京气压(见图 5(a))与广州气压(见图 5(b))之间的滑动相关系数。在高频成分中,二者体现了相似的变化规律,因而LRCC体现了正相关为主的态势(见图 5(c))。而在低频成分中,二者体现了不同的态势,北京气压在1995—2000年之间发生了阶跃式的升高,而广州的气压却出现了两次阶跃式下降。我们核对了两地的气象站,其间并没有搬迁和移位情况,气压的低频变化应与气候系统的整体变化有关。SRCC体现了二者很高的负相关,很好地展示了这种阶跃式的变化,全局相关系数为-0.755,与SRCC的多年平均值非常一致;而LRCC则并未体现这种负相关的态势,其平均相关系数是正值,与全局相关系数相差甚远。
|
( (a)北京及(b)广州月均气压(红线)及其局域均值(蓝线),单位:hPa。(c)为LRCC,(d)为SRCC。月均气压数据来自中国气象局数据中心。Monthly air pressure (red lines) and its local means (blue lines) in (a) Beijing and (b) Guangzhou with unit hPa; (c) LRCC; (d) SRCC. Monthly air pressure data are from China Meteorological Data Service Center. ) 图 5 低频信号占优势时的滑动相关系数(引自文献[3]) Fig. 5 RCCs dominated by low frequency(from reference[3]) |
上节明确指出了SRCC与LRCC的关系,证实了SRCC是具有可比性要求的RCC,也是全面反映数据中各种频率信号之间合成相关性的RCC。本节将介绍SRCC的主要应用范畴。
3.1 低频变化的长期特征前面2.5节提到,SRCC的一个重要特点就是包含了高频和低频信息。在很多情况下,人们会由于低频信号的持久性而予以更多的关注。尤其是那些低频信号很强的情形,SRCC有特殊的意义。
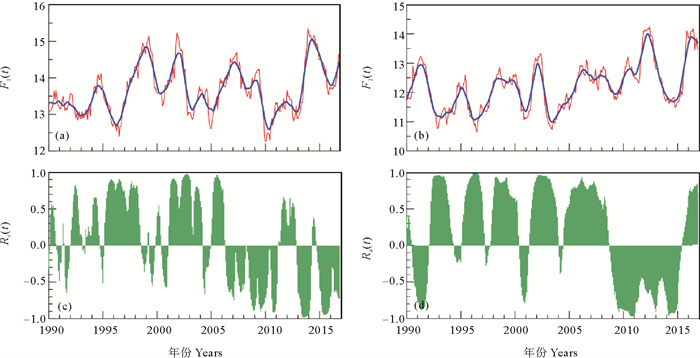
文献[3]给出了一个例子。北京和纽约两个城市的纬度非常接近,都在40°N左右,分处于东西半球。北京(见图 6(a))与纽约(见图 6(b))的气温变化之间相关性由LRCC(见图 6(c))和SRCC(见图 6(d))确定。二者之间有一定的相似性,但在细节上,SRCC更加光滑,体现了低频特性的贡献。首先,2009年之前,SRCC以正相关为主,体现了地球上气温变化及全球变暖的整体一致性。而在2009年突然呈现负相关,我们认为与近些年北极变暖有关[18];产生这种现象的原因是北极变暖条件下大气罗斯贝驻波振幅增大[19],导致冷空气交替从美洲和亚洲流出,东西半球气温呈现跷跷板式的振荡,因而发生负相关。例如,纽约在2009—2013年冬季都发生了极寒天气,而北京在2014—2015年发生极寒天气。第二,即使在2009年之前以正相关为主的期间,SRCC也体现了明显的周期性变化,变化周期为3年左右。这种相关性体现了东西半球之间变化的整体一致性和蕴含的微小差异,需要深入研究。
|
( (a)北京和(b)纽约12点滑动平均的表面气温(℃)(红线)及其局域均值(蓝线);(c) LRCC;(d) SRCC。表面气温数据来自NCEP/NCAR Reanalysis 1。Surface air temperature (unit: ℃) (red lines) and their local means (blue lines) in (a) Beijing and (b) New York with 12-points average; (c) LRCC; (d) SRCC. Surface air temperature data are from NCEP/NCAR Reanalysis 1. ) 图 6 北京与纽约气温之间的滑动相关(引自文献[3]) Fig. 6 Running correlation of the air temperatures in Beijing and New York(from reference[3]) |
类似的例子还有很多,表明SRCC对于揭示低频信号的变化有重要意义。但是,相关的研究还很少[20-22]。按照第1节的介绍,下面引用的两篇文章实际上也是用SRCC完成的[23-24]。
3.2 相关性的空间关系及异常事件前面介绍的都是物理量之间随时间变化的相关性。SRCC在研究空间变化中有特殊的价值。在某一地区发生的变化有可能会影响其周边一定范围的地区,也就是说,其周围一些点的变化与该点的变化具有高度的一致性。按照时空一致性原则,越是低频的现象,发生的时间越长,影响的范围就越大。由于SRCC满足了可比性的要求,可以将不同空间点之间的滑动相关系数进行比较,因此可以计算逐点的SRCC,然后将空间各点同一时间窗口的结果组合起来,体现现象的空间特征,找出某种变化的影响范围。该过程的影响范围之内的点发生的变化应该与该过程有明显的正相关。如果某点出现在中心过程之外,就会表现为没有明显的正相关。如果空间出现明显的涛动现象,就会表现出很强的负相关。
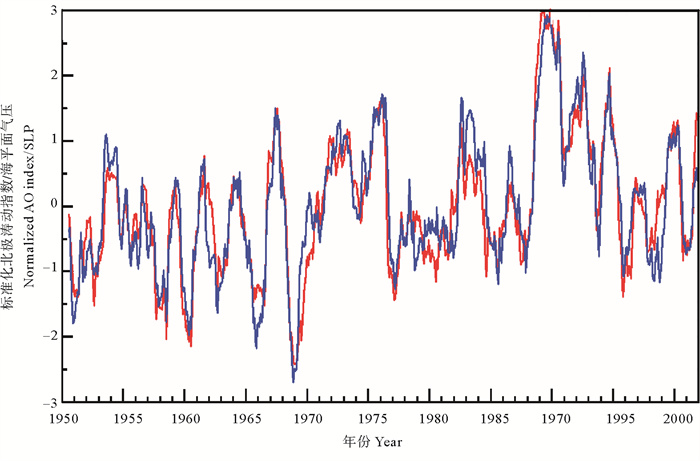
以北极涛动(Arctic oscillation,AO)为例,AO是北半球的重要现象,是对20°N以北海面气压场(Sea level pressure,SLP)进行经验正交分解(Empirical orthogonal function, EOF)得到的第一模态,其时间系数称为北极涛动指数(AOI),与气压变化的符号相反。AOI(见图 7红线)体现了北半球大气环流的整体变化特征,对北半球的很多现象都有影响。我们将北半球各点的SLP与AOI计算滑动相关,以找出AO的影响范围。
|
图 7 北极涛动指数(红线)和北极涛动核心区平均气压的负值(蓝线)(引自文献[23]) Fig. 7 Arctic oscillation index (red line) and average sea level air pressure of the Arctic oscillation core region (blue line)(from reference[23]) |
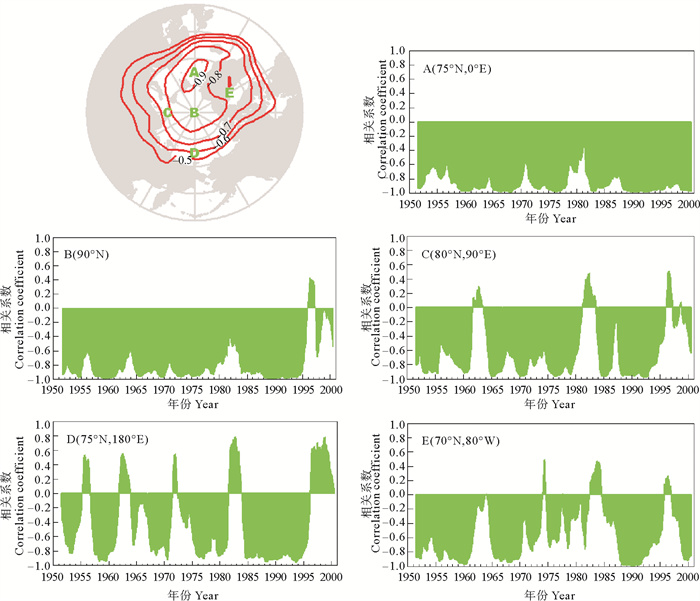
图 8以AOI为参考变量,将北冰洋内的各点SLP(来源:NCEP/NCAR再分析数据)与AOI(来源:NOAA气候预报中心)计算SRCC,其中,位于北欧海内的A点,体现非常完好的负相关。其他点也以负相关为主,体现了AO在北冰洋内有很大的影响范围。
|
图 8 用AOI与各点气压的SRCC表达的AO对北冰洋各个区域的影响(引自文献[23]) Fig. 8 Impact of Arctic oscillation on different regions in the Arctic Ocean by SRCC between AOI and SLP in these points(from reference[23]) |
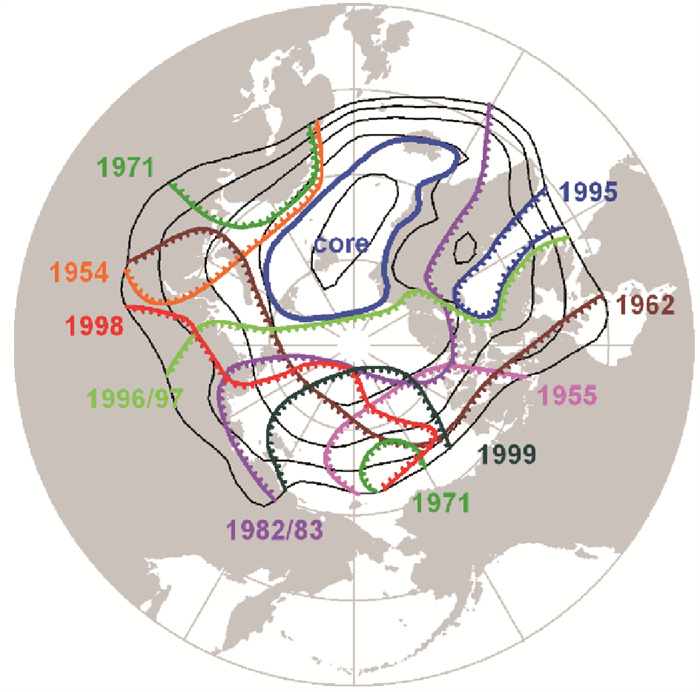
基于我们对SRCC的理解,相关性好固然是体现相关性有意义的结果,相关性不好同样体现了重要的信息。例如,在负相关为主导的区域在有些时间段发生了相关性很差,甚至是正相关的特征,我们将这种与主导相关性不一致的现象称为“异常事件”。对整个北半球所有格点计算滑动相关系数,找出异常事件最靠北的位置,连接起来,得到一个个影响北极的重要事件(见图 9);正是这些异常事件影响北冰洋,导致SLP与AOI的滑动相关特性发生显著变化。图 9表明,大多数异常事件都可以找到原因,1982/1983和1996/1997的异常事件是20世纪最强的两次厄尔尼诺事件,其对遥远的北冰洋有明显影响。其他的异常事件也可以从北太平洋的其他变化中得出[23]。
|
( 图中的锯齿线为发生异常事件的外缘。The dentate lines are the margins of the abnormal events. ) 图 9 北极涛动核心区(用’core’表达)及影响北极地区的异常事件(引自文献[23]) Fig. 9 Arctic oscillation core region (marked with "core") and the abnormal events impacted on Arctic Ocean (from reference[23]) |
图 9还给出,在北欧海附近存在一个特殊的区域,该区域在过去的大半个世纪从来没有发生过异常事件,其中各点的气压变化总是与AOI呈负相关。将该区域所有点的气压进行平均,得到的结果(见图 7蓝线)与AOI的相关系数达到-0.945,二者非常一致,几乎可以相互替换,我们命名这个区域为北极涛动核心区(Arctic oscillation core region,AOCR)。该区域只占北半球面积的0.5%,但是其气压场竟然与AOI高度一致,不能不认为该区域对AO的构成有特别重要的意义。
SRCC能够把时间变化的空间特征找出来,是这个方法的重要用途。主要原因是SRCC充分满足了可比性的要求,而LRCC不能体现与相邻点的关系,因而不同点的LRCC值不具有可比性。因而,LRCC只能用于时间过程的相关性分析,而SRCC可以用于时空变化过程的分析(见下节)。
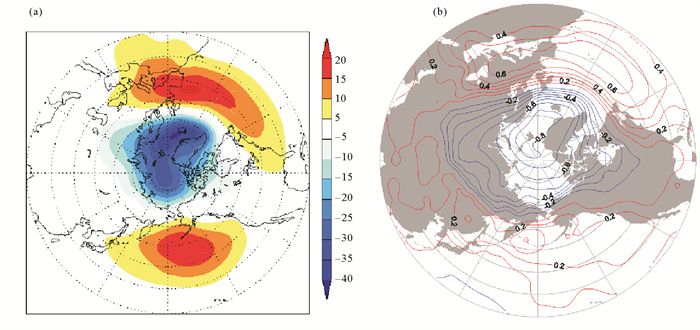
3.3 SRCC与EOF方法联合使用的科学意义地球科学中常用到时空变化的数据(空间二维、时间一维),EOF方法是分析时空变化数据的有效方法[25],得到非常广泛的应用。EOF的结果会得到一个空间结构和一个时间系数[26],空间结构体现为整体的空间分布特征,而时间系数体现了该参数随时间的变化。例如,AO是对北半球20°以北SLP进行EOF分析的结果[27],得到空间结构图(见图 10(a))和时间系数(见图 7红线)。EOF有一个最大的缺点,就是不能体现空间分布随时间的变化,而事实上,气压场的空间结构是随时间变化的。这个问题在EOF的框架下没有办法解决。
|
图 10 (a) 北极涛动的空间结构(填色,引自文献[28])和(b)SRCC多年平均场(引自文献[23]) Fig. 10 (a)Spatial pattern of Arctic oscillation(shaded, from reference[28]) and (b)multiyear average of SRCC(from reference[23]) |
而滑动相关系数SRCC与EOF联合使用就可以解决这个问题,我们采用SRCC计算各点SLP与AOI的相关性,得到逐月的相关系数场。将这些场进行平均,得到的平均相关系数的分布如图 10(b)所示,与AO的空间结构(见图 10(a))非常接近。除此之外,SRCC在每一个时间层都提供了空间结构。图 11是SRCC每年1月相关系数的空间分布,给出了AO的空间变化特征[24]。可见,SRCC给出的相关系数有非常好的低频特性,相关系数的空间分布经常在几年的时间内有很高的一致性,体现了一种持续多年的特征,如1954—1956, 1971—1978, 1989—1995年都体现了长时间的一致性。与此同时,又可以将这些一致的多年特征分成若干历史时期,每个时期的相关系数的空间分布又有所不同。将SRCC与EOF相结合可以得到非常丰富的空间变化信息。

|
图 11 用SRCC空间变化表达的北极涛动空间变化图(引自文献[24]) Fig. 11 Spatially varied patterns of Arctic oscillation by SRCC at different time(from reference[24]) |
本文作为综述性文章介绍了合成滑动相关系数的理论和应用成果。由于对SRCC的认识时间尚短,该方法的深刻内涵尚不为人熟知,我们希望通过本文推广这种方法,有助于数据的分析和科学的发展。
常用的滑动相关系数被称为局域滑动相关系数(LRCC),这种方法将计算相关系数的方法直接应用到一个时间窗口,得到相关系数随时间的变化。LRCC从1928年沿用至今,并未有人怀疑它的正确性。然而,LRCC在一些情况下并没有很好地体现实际的相关性。
LRCC只反映了两个时间序列距平变化之间的相关性,没有体现各个窗口均值变化之间的相关性,因而是一个不完整的滑动相关系数。利用全部长度的数据来计算均值(全局均值),可以得到一个新的滑动相关系数,命名为合成滑动相关系数(SRCC)。SRCC算法背后有深刻的物理内涵:在计算一个窗口的相关系数时,不能认为这个窗口内的数据与其他窗口的数据毫无关联,而全局均值恰恰体现了各个窗口数据之间的联系,各个窗口的数据都以其对全局均值的贡献而进行度量。
对SRCC算法进行了深入的研究认识到,SRCC与LRCC的根本区别在于是否考虑了均值的变化。SRCC实际上是由LRCC和1加权构成的,当距平变化占优势时,SRCC趋于LRCC,而当均值变化占优势时,SRCC趋于1。如果笼统地将数据分为高频变化和低频变化,距平的变化体现了高频变化,LRCC描述了高频信号之间的相关性;而均值的变化体现为低频变化,SRCC对高频变化和低频变化同时进行了描述。结果表明,虽然SRCC全面体现了各种频率现象之间的相关性,但LRCC并非需要淘汰;如果研究人员对于高频变化有兴趣仍可以使用LRCC进行分析。
通过对SRCC算法进行论证,该方法上升到理论的高度,成为一种可信的方法。该方法的数学证明是基于一个基本要求,即不同时间窗口获得的相关系数取值一定要有可比性,即高相关性一定代表了两个时间序列的一致性。从这个基础出发,证实了SRCC是符合可比性要求的滑动相关系数算法。
正是由于可比性得到得了保障,在空间不同位置获得的SRCC都可以相互比较,形成了每一个时间层相关系数的空间分布,成为分析时空三维数据的一种新方法。我们应用这种方法可以通过较高的相关系数找出某物理过程的影响范围,认识该过程在整个空间的分布特征;也可以通过相关性不好的时间段来确定异常事件的发生,深入认识异常事件的影响范围和演化过程,成功地描述了某物理过程的时空变化。
进一步的应用表明,SRCC可以与经验正交分解(EOF)方法联合使用,消除了EOF结果只有一个空间结构分布和一条时间变化曲线的不足,可以对每个时间层给出相关系数的空间分布,清楚地展现其影响范围的演化过程,取得其他方法所无法取得时空变化的分析结果。
由此可见,SRCC的研究揭示了滑动相关系数的实质,在数学上和物理上都与人们的认知一致并得到充分证明,得到的结果全面体现了两个过程的滑动相关特性。滑动相关本来是一个时域的分析算法,而SRCC不仅可以用于时域分析,而且可以拓展到时空变化领域进行应用,揭示了数据中包含的全新过程。相信SRCC将在科学研究中发挥重要作用。
| [1] |
Kuznets S. On moving correlation of time sequences[J]. Journal of the American Statistical Association, 1928, 23(162): 121-136. DOI:10.1080/01621459.1928.10503005
(  0) 0) |
| [2] |
Zhao J P, Cao Y. The physical significance of the synthetic running correlation coefficient and its applications in oceanic and atmospheric studies[J]. Journal of Ocean University of China, 2018, 17(3): 451-460. DOI:10.1007/s11802-018-3798-x
(  0) 0) |
| [3] |
Zhao J P, Cao Y, Shi Y Y, et al. Mathematical proof of the synthetic running correlation coefficient and its ability to reflect temporal variations in correlation[J]. Journal of Ocean University of China, 2021, 20(3): 562-572. DOI:10.1007/s11802-021-4826-9
(  0) 0) |
| [4] |
Pearson K. Mathematical contributions to the theory of evolution——on a form of spurious correlation which may arise when indices are used in the measurement of organs[J]. Proceedings of the Royal Society of London, 1896, 60(3): 489-498.
(  0) 0) |
| [5] |
Galton F. Correlations and the measurements, chiefly from anthropometric data[J]. Proc R Soc Lond, 1888, 45: 135-145.
(  0) 0) |
| [6] |
Galton F. Correlations and their measurement, chiefly from anthropometric data[J]. Nature, 1889, 39: 238. DOI:10.1038/039238a0
(  0) 0) |
| [7] |
Pearson E S. Karl Pearson: An Appreciation of Some Aspects of His Life and Work[M]. Cambridge, U. K: Cambridge Univ. Press, 1938.
(  0) 0) |
| [8] |
Merrington M, Blundell B, Burrough S, et al. A List of the Papers and Correspondence of Karl Pearson[M]. London: Publications Office, University College London, 1983.
(  0) 0) |
| [9] |
Kodera K. Quasi-decadal modulation of the influence of the equatorial Quasi-Biennial Oscillation on the north polar stratospheric temperatures[J]. J Geophys Res, 1993, 98: 7245-7250. DOI:10.1029/92JD02930
(  0) 0) |
| [10] |
Salby M, Callaghan P, Shea D. Interdependence of the tropical and extratropical QBO: Relationship to the solar cycle versus a biennial oscillation in the stratosphere[J]. J Geophys Res, 1997, 102(D25): 29789-29798. DOI:10.1029/97JD02606
(  0) 0) |
| [11] |
Soukhearev B. The sunspot cycle, the QBO, and the total ozone over northeastern Europe: A connection through the dynamics of stratospheric circulation[J]. Ann Geophys, 1997, 15: 1595-1603. DOI:10.1007/s00585-997-1595-8
(  0) 0) |
| [12] |
Elias A G, Zossi de Artigas M. A search for an association between the equatorial stratospheric QBO and solar UV irradiance[J]. Geophys Res Lett, 2003, 30: 1841.
(  0) 0) |
| [13] |
Maurer C, Koch E, Hammerl C, et al. BACCHUS temperature reconstruction for the period 16th to 18th centuries from Viennese and Klosterneuburg grape harvest dates[J]. J Geophys Res, 2009, 114: D22106. DOI:10.1029/2009JD011730
(  0) 0) |
| [14] |
Varotsou E, Jochumsen K, Serra N, et al. Interannual transport variability of upper labrador sea water at flemish Cap[J]. J Geophys Res Oceans, 2015, 120: 5074-5089. DOI:10.1002/2015JC010705
(  0) 0) |
| [15] |
纪旭鹏, 赵进平. 北极中央区海冰密集度与云量相关性分析[J]. 海洋学报, 2015, 37(11): 92-104. Ji X P, Zhao J P. Analysis of correlation between sea ice concentration and cloudiness in the central Arctic[J]. Aita Oceanologica sinica, 2015, 37(11): 92-104. DOI:10.3969/j.issn.0253-4193.2015.11.009 (  0) 0) |
| [16] |
Burdun G D, Markov B N. Osnovy Metrologii(Fundamentals of Metrology)[M]. Moscow: Izd-vo Standartov, 1972.
(  0) 0) |
| [17] |
Schmid Jr J. The relationship between the coefficient of correlation and the angle included between regression lines[J]. The Journal of Educational Research, 1947, 41(4): JSTOR 27528906.
(  0) 0) |
| [18] |
Serreze M C, Francis J A. The Arctic amplification debate[J]. Clim Change, 2006, 76: 241-264. DOI:10.1007/s10584-005-9017-y
(  0) 0) |
| [19] |
Francis J A, Vavrus S J. Evidence linking Arctic amplification to extreme weather in mid-latitudes[J]. Geophys Res Lett, 2012, 39: L06801.
(  0) 0) |
| [20] |
赵进平, Drinkwater K. 北欧海主要海盆海面热通量的多年变化[J]. 中国海洋大学学报(自然科学版), 2014, 44(10): 9-24. Zhao J P, Drinkwater K. The multiyear variation of the surface heat fluxes in the main basins in Nordic Seas[J]. Periodical of Ocean University of China, 2014, 44(10): 9-24. (  0) 0) |
| [21] |
Zhao J P, Drinkwater K, Wang X. Positive and negative feedbacks related to the Arctic oscillation revealed by air-sea heat fluxes[J]. Tellus A: Dynamic Meteorology and Oceanography, 2019, 71(1): 1-21.
(  0) 0) |
| [22] |
Ji X P, Zhao J P. Transition periods between sea ice concentration and sea surface air temperature in the Arctic revealed by an abnormal running correlation[J]. Journal of Ocean University of China, 2019, 18(3): 633-642. DOI:10.1007/s11802-019-3909-3
(  0) 0) |
| [23] |
Zhao J P, Cao Y, Shi J X. Core region of Arctic oscillation and the main atmospheric events impact on the Arctic[J]. Geophys Res Lett, 2006, 33: L22708. DOI:10.1029/2006GL027590
(  0) 0) |
| [24] |
Zhao J P, Cao Y, Shi J X. Spatial variation of the Arctic Oscillation and its long-term change[J]. Tellus, 2010, 62A: 661-672.
(  0) 0) |
| [25] |
Hannachi A, Jolliffe I T, Stephenson D B. Empirical orthogonal functions and related techniques in atmospheric science: a review[J]. Int J Climat, 2007, 27: 1119-1152. DOI:10.1002/joc.1499
(  0) 0) |
| [26] |
Monahan A H, Fyfe J C, Flato G M. A regime view of Northern Hemisphere atmospheric variability and change under global warming[J]. Geophys Res Lett, 2000, 27: 1139-1142. DOI:10.1029/1999GL011111
(  0) 0) |
| [27] |
Thompson D W J, Wallace J M. The Arctic oscillation signature in wintertime geopotential height and temperature fields[J]. Geophys Res Lett, 1998, 25: 1297-1300. DOI:10.1029/98GL00950
(  0) 0) |
| [28] |
NOAA. CPC-Teleconnections: Arctic Oscillation Loading Pattern (noaa. gov)[R]. https://www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/ao.loading.shtml.
(  0) 0) |
2. College of Mathematical Sciences, Ocean University of China, Qingdao 266100, China
 2022, Vol. 52
2022, Vol. 52

