2. 教育部物理海洋重点实验室,山东 青岛 266100
雾是地球低层大气中悬浮的大量水滴或冰晶使得大气水平能见距离降到1 km以下的天气现象[1-2]。雾是重要的大气现象,对交通安全和各种户外作业有较强的影响。
雾的研究一直是气象学的重要内容之一。雾按其形成机制主要分为辐射雾、平流雾、蒸发雾三种[3]。无论产生机制有什么差别,描述雾的物理参数都是相同的,主要有:(1)大气能见度,反映雾引起的大气能见距离衰减;(2)雾滴谱,反映雾滴的大小分布;(3)液态水含量,反映空气中所含液态水的总量,通常是由雾滴谱计算得到的[4-5]。此外,还有用大气化学方法分析得到的雾中的溶解物质[6],有气溶胶探测方法分析雾中的固态物质[7-8]。以上这些参数可帮助人们认识和了解雾的主要物理和化学特性。
在以上各种参数中,大气能见度是描述雾最重要的参数,是指水平方向的可视距离。因为大气能见度直接与人们的能见距离有关,不但便于非专业人士理解,也对人类活动有最直接的影响。实际上,早期的大气能见度不是很精准的物理量,是人们视觉感知的参数,大致表示在雾中的视距[9]。视距不仅与雾有关,而且与人们的视力有关,也与空中的亮度有关,因此估算的误差很大[10]。因而早期的大气能见度一直只能算是粗略定量的物理量。直到大气能见度仪的问世,才将大气能见度变成可以定量观测的物理量。与此同时,大气能见度也不再与人们的视距挂钩,而是一个按照其定义得到的观测结果[11]。
虽然目前的大气能见度测量可以满足对雾研究的需要,但由于大气能见度仪是主动光源的仪器,自重较大,无法用气球带到高空测量,因而迄今为止只有地表大气能见度数据[12]。人们一直希望能探测雾的垂直剖面,但苦于没有合适的仪器而无法实施。本文希望探索用自然光来观测大气能见度的方法,因为探测自然光辐照度的观测系统可以做得很小巧。采用小型的辐照度计,光谱的峰值和带宽都可以非常准确地确定[13-14],有可能用来实现对雾的剖面测量。但是,自然光的测量只能获得垂向光学衰减系数,大气能见度与大气垂直衰减的漫衰减特性之间尚未建立起物理关系。
本文提出了用垂直方向测量的光学数据计算大气能见度的方法,形成了具有理论基础并实际可行的计算方法,使之成为雾光学剖面测量的重要基础,并利用实测数据对提出的算法进行了检验。
1 用光学衰减系数计算雾能见度用光学衰减系数计算大气能见度的研究不多,比较常用的是Koschmieder公式[11],大气能见度V(单位为m)定义为:
| $ V = \frac{{\ln \varepsilon }}{{\beta \left( {{\lambda _{550}}} \right)}}。$ | (1) |
式中:ε为视觉光亮度对比度阈值,它是把人眼能将目标物从背景中区别出来的视觉光亮度对比的最小极限值。在非航空气象领域,通常对于视觉正常的人,白天的视觉光亮度对比度阈值通常为0.02[15];β(λ)为敏感波长的大气消光系数,是水平方向的衰减系数。λ一般选取人眼最敏感的波长,即550 nm。根据大气辐射传输理论,有:
| $ {F_h}\left( {{\lambda _{550}}} \right) = {F_{h0}}\left( {{\lambda _{550}}} \right)\exp \left[ { - \beta \left( {{\lambda _{550}}} \right)L} \right]。$ | (2) |
其中:Fh0为水平方向的源辐照度;Fh为穿过水平距离L的到达辐照度。如果有两台仪器分别测量波长为550 nm的Fh0和Fh,则可得550 nm的消光系数为:
| $ \beta \left( {{\lambda _{550}}} \right) = - \frac{1}{L}\ln \left( {\frac{{{F_h}\left( {{\lambda _{550}}} \right)}}{{{F_{h0}}\left( {{\lambda _{550}}} \right)}}} \right)。$ | (3) |
然后通过Koschmieder公式(1)即可获得大气能见度。这个算法适应早期光学仪器谱段很少的情形。本文中也把这种方法作为参照的方法进行比较。
然而,用Koschmieder公式得到的大气能见度与按照现有大气能见度定义得到的测量结果不具可比性。本文将根据现有大气能见度的定义,构建用光学观测数据计算大气能见度的方法。
1.1 能见度的观测与计算在气象学中,为了排除人视觉因素的影响,大气能见度用气象光学视程(Meteorological optical range,MOR)表示。按照大气能见度的定义,气象光学视程是指白炽灯发出色温为2 700 K的平行光束的光通量,在大气中削弱至初始值的5%所通过的路径长度,单位为m[16]。在航空气象部门,为了保证飞行的安全,在定义能见距离时使用的对比度阈值ε=0.05,与上述定义一致[17]。以下我们将色温为2 700 K的平行光束称为“标准光”。按照比尔定律[18],垂向辐射传输过程中辐射强度的变化为:
| $ {E_r}\left( \lambda \right) = {E_{r0}}\left( \lambda \right)\exp \left[ { - {k_d}\left( \lambda \right)H} \right]。$ | (4) |
其中:Er(λ)和Er0(λ)为标准光的下行谱辐照度;kd(λ)为垂向漫衰减系数的谱分布;H为衰减距离。事实上,按照比尔定律,大气中的衰减并没有特定的方向性,只是与光穿过的距离有关[18],在同样的条件下,水平方向和垂直方向的衰减系数没有区别。因此,比尔定律中的垂向的谱衰减系数同样适用于水平方向,衰减距离H也适用于水平方向。水平与垂直方向衰减特性的一致性也在雾的卫星遥感研究中得到普遍应用[19-20]。根据上述大气能见度的定义,对(4)式两端积分有
| $ \frac{{\int\limits_{400}^{700} {{E_{r0}}\left( \lambda \right)\exp \left[ { - {k_d}\left( \lambda \right)H} \right]{\rm{d}}\mathit{\lambda }} }}{{\int\limits_{400}^{700} {{E_{r0}}\left( \lambda \right){\rm{d}}\mathit{\lambda }} }} = 0.05 = \exp \left( { - {\beta _r}H} \right)。$ | (5) |
公式(5)中的βr是用辐照度的垂向衰减特性确定的全谱段衰减系数。谱衰减系数kd(λ)满足比尔定律,是不随观测距离H变化的物理量,体现了大气的漫衰减特性;而全谱段的衰减系数βr虽然也满足指数衰减律[17],但不满足比尔定律,因为其取值与观测距离有关,因而βr不是大气漫衰减特性,是与测量距离有关的量[21]。公式(5)带给我们两个结果:
第一,如果已知全谱段衰减系数βr,可以导出大气能见度的算法[17]
| $ V = - \frac{1}{{{\beta _r}}}\ln \left( {0.05} \right) \approx \frac{{2.99}}{{{\beta _r}}}。$ | (6) |
从(6)式可见,大气能见度V就是辐照度衰减到初始值5%时所经过的距离H0.05。透射式大气能见度仪就是基于这种观测原理[22]。
第二,如果已知两台仪器之间的距离Hd,就可以计算βr,
| $ {\beta _r} = - \frac{1}{{{H_d}}}\ln \left[ {\frac{{\int\limits_{400}^{700} {{E_{r0}}\left( \lambda \right)\exp \left[ { - {k_d}\left( \lambda \right){H_d}} \right]{\rm{d}}\mathit{\lambda }} }}{{\int\limits_{400}^{700} {{E_{r0}}\left( \lambda \right){\rm{d}}\mathit{\lambda }} }}} \right]。$ | (7) |
公式(7)就是用谱漫衰减系数计算全谱段衰减系数的算法,是符合气象观测规范的算法。需要注意的是,虽然(6)式定义的能见度没有区分引发能见度变化的具体物质,但在(7)式中隐喻了所有可见光谱段没有特殊的吸收带。雾的主要成分是液态水,在可见光谱段没有吸收带,适用于(7)式的算法。但是,霾、火山灰和各种大气气溶胶引起的能见度变化在可见光谱段都有吸收带[18],需要针对吸收带制定特殊的积分方案,不能直接使用(7)式。因此,本文的算法只适用于雾引起的能见度变化,本文将其称为雾能见度(Fog visibility)。
然而,如果利用自然光进行观测,不管是什么形式的辐照度计,测量得到的是自然光的辐照度。按照普朗克黑体辐射定律,黑体辐出度rλ,T可以表达为[23]:
| $ {r_{\lambda , T}}{\rm{d}}\lambda {\rm{ = 2 \mathsf{ π} }}\mathit{h}{\mathit{c}^2}{\lambda ^{ - 5}}\frac{1}{{\exp \left( {\frac{{hc}}{{\lambda kT}}} \right) - 1}}{\rm{d}}\lambda {\rm{。}} $ | (8) |
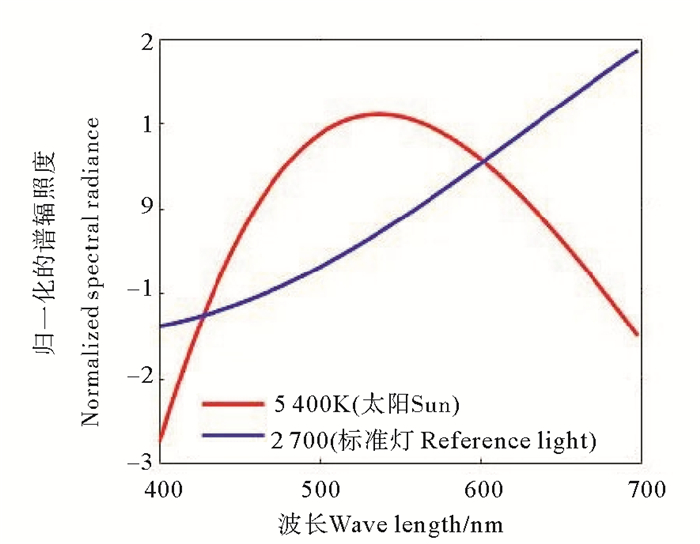
式中:h为普朗克常数;c为光速;k为玻尔兹曼常数;rλ, T为辐出度。(8)式体现了温度导致的谱分布的差异。图 1中用普朗克定律计算了日光和标准光归一化的辐出度。
|
图 1 由普朗克黑体辐射定律计算的归一化的标准光(蓝色)以及日光(红色)辐出度 Fig. 1 Normalized spectral radiance of referencelight (blue) and sunlight (red) based on Planck′s blackbody radiation law |
在图 1中,太阳的辐射温度为5 400 K,光谱分布与2 700 K色温的白炽灯有很大差别,标准光的辐射强度是从紫光到红光递增,而太阳辐射是以蓝绿光为峰值,向紫光和红光递减。因此,需要把自然光的辐照度En(λ)转换为标准光的辐照度Er(λ)才能用以计算雾能见度。由图 1可见,自然光和标准光的辐出度都覆盖了可见光的光谱范围,只是比例不一样,提示我们将自然光各个谱段的谱辐照度都乘以光谱转换系数γ(λ),即:
| $ {E_r}\left( \lambda \right) = \gamma \left( \lambda \right){E_n}\left( \lambda \right)。$ | (9) |
将(9)式代入(7)式,就可以获得标准光的全谱段衰减系数:
| $ {\beta _r} = - \frac{1}{H}\ln \left[ {\frac{{\int\limits_{400}^{700} {\gamma \left( \lambda \right){E_{n0}}\left( \lambda \right)\exp \left[ { - {k_d}\left( \lambda \right)H} \right]{\rm{d}}\mathit{\lambda }} }}{{\int\limits_{400}^{700} {\gamma \left( \lambda \right){E_{n0}}\left( \lambda \right){\rm{d}}\mathit{\lambda }} }}} \right]。$ | (10) |
按照(9)式,γ(λ)可以通过测量标准光和自然光的辐照度来计算,但测量过程很容易带来误差。这里,我们采用普朗克定律计算函数γ(λ)。设太阳的温度T1为5 400 K,标准光的色温T2是2 700 K,按照(8)式,γ(λ)可以表达为:
| $ \gamma \left( \lambda \right) = \frac{{\exp \left( {\frac{{hc}}{{\lambda k{T_1}}}} \right) - 1}}{{\exp \left( {\frac{{hc}}{{\lambda k{T_2}}}} \right) - 1}}。$ | (11) |
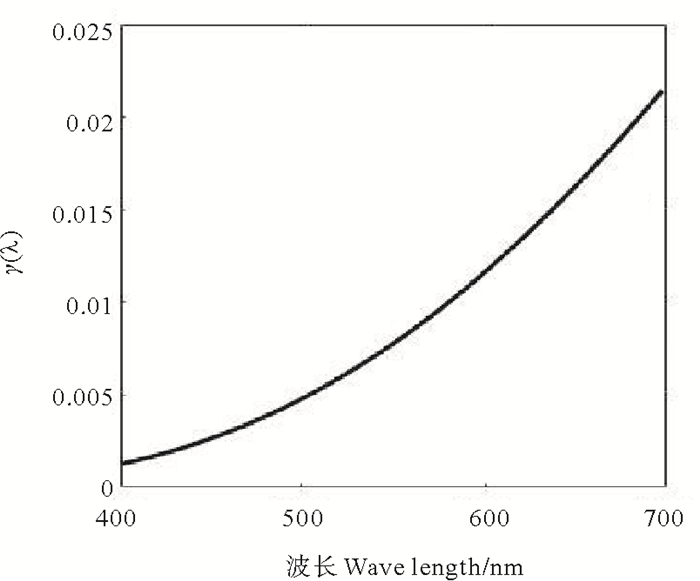
得到的γ(λ)的分布如图 2所示。
|
图 2 光谱转换系数γ(λ) Fig. 2 Transform coefficient of sunlight and lamp γ |
公式(11)用普朗克定律给出的理论算法完全体现了太阳辐射与标准光辐射在可见光谱段的比值,不包含任何观测误差。由于大气在可见光谱段没有明显的吸收带,理论算法不会因大气吸收而产生较大的误差。理论算法完全是按照大气能见度的定义导出的,与大气能见度仪的测量结果具有可比性。
从以上的分析可见,通过对自然光的多光谱观测,采用(11)式和(9)式将自然光谱辐照度转化为标准光谱辐照度,并按照(10)式计算标准光全谱段衰减系数,就可以由(6)式直接计算雾能见度。
1.2 能见度反演的误差分析由上节可见,本文提出的算法没有可以人为调整的经验系数,得出的能见度可信度较高。计算雾能见度只需要全谱段光学衰减系数一个量,各种影响全谱段衰减系数的因素都会影响能见度。从(6)式可以导出能见度的反演误差为:
| $ \frac{{\Delta V}}{V} = - \frac{{\Delta {\beta _r}}}{{{\beta _r}}}, $ | (12) |
也就是说,全谱段衰减系数的误差增大10%,测到的能见度减小10%,导致计算的能见度偏小;反之,如果误差在负方向增大10%,测到的能见度增大10%,导致计算得到的能见度偏大。因此,保证能见度反演精度的方法是控制全谱段光学衰减系数的误差。按照(10)式,导致全谱段衰减系数误差的因素为谱辐照度的观测误差。在计算全谱段衰减系数之前,需要将谱辐照度进行有效的订正,确保计算的精度。实际观测表明,引起谱辐照度误差的原因很多,除了光谱测量误差之外,太阳高度过低、仪器姿态倾斜、时间同步不好、两部仪器偏差较大等都会引起谱辐照度的测量误差。消除这些误差需要在观测环节进行精细安排,要尽可能保证两台光学仪器时间同步,姿态稳定竖直向上,周围没有物体遮挡,并且不使用低太阳高度角的数据。
1.3 由光学数据判断雾的指数如前所述,光学衰减系数的偏差是雾能见度计算的主要误差来源。尤其在轻雾情形,在10余米的垂直范围内,光的衰减很小,衰减系数的微小变化都会影响反演的雾能见度。在实际观测的情形下,尽管已经充分避开了可能造成光污染的因素,还是会有一些因素会影响两部光学仪器数据的一致性,如地面大气湍流过程引起的灰尘、气球上升过程中仪器倾角的变化、人员走动衣服颜色造成的反光、云对上下仪器的遮掩情况不同等等,这些不可避免的因素对两部仪器辐照度的影响都导致计算能见度的误差。这些误差会造成雾的观测虚警,使我们在没有能见度仪同步监测的情况下不知是否真的有雾。为此,我们将光学观测雾分为两个步骤,一是先从光谱数据本身定性地确定是否有雾,二是用(6)式定量计算能见度。
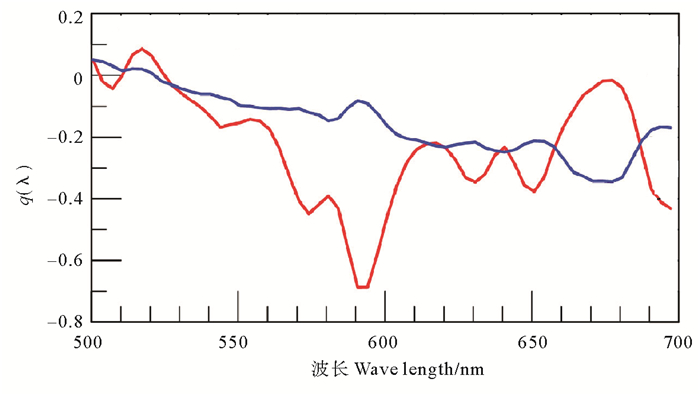
有雾与否的主要差别是:无雾情形以直射光为主,有雾情形以散射光为主,轻雾时直射光和散射光并存。通过对光谱数据的仔细分析,我们发现在直射光和散射光在594和674 nm有光谱强度的特异性变化(见图 3),图中纵坐标为相对光谱
| $ q\left( \lambda \right) = {{\tilde E}_d}\left( \lambda \right) - {{\tilde E}_{d0}}\left( \lambda \right)。$ | (13) |
|
( 蓝线为高能见度时的相对光谱,红线为低能见度时的相对光谱。The relative spectra, q(λ), with high (blue line) and low (red line) visibility. ) 图 3 不同能见度可见光光谱特异性 Fig. 3 Spectral specificity of visible light with different visibility |
其中:
从图 3可见,相对光谱在594和674 nm处有特异表现,二者在轻雾和浓雾时的起伏恰好相反,使我们可以从这两个谱段的差异来判断是否有雾。为此,我们构建了一个光学指数p。
| $ p = q\left( {{\lambda _{594}}} \right) - q\left( {{\lambda _{674}}} \right)。$ | (14) |
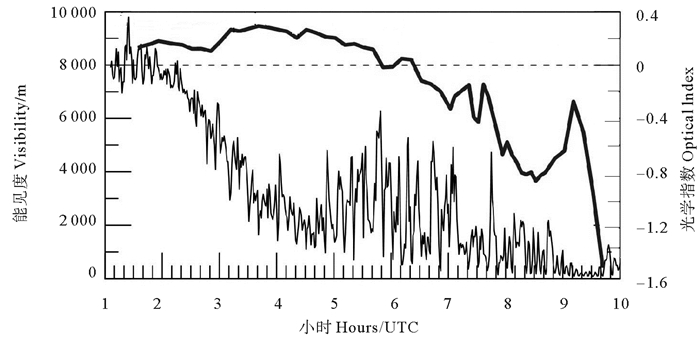
其中:(14)式的指数p用来判断雾能见度是否大于2 000 m;p大于零时为能见度大于2 000 m情形。这个指数很好地体现了在6时之前能见度大于2 000 m的状况及其后来的低能见度状况(见图 4)。其中,4~5时是能见度较低的时间段,但指数p还是给出了其能见度大于2 000 m的特征。因此,我们用指数p定性判断是否有雾,再用本文提出的算法定量计算雾能见度。
|
(定义见公式(14)。Calculated based upon Eq(14). ) 图 4 实测大气能见度(黑线)和光学指数p (蓝色) Fig. 4 Measured atmospheric visibility and the optical index p |
指数p给了我们一个有力的工具,即使用单一光谱仪观测数据就可以定性判断是否有雾,使我们有可能用简单的光学仪器进行大气能见度的长期定性观测。可以设想,不同区域的雾含有的物质不同,其散射光的特性也会有一定的差别。因此,p应该是因地而异的,甚至在不同季节也会不同,需要实际观测来确定。
2 雾能见度反演试验上述反演算法可以通过光学观测计算雾能见度,并同步用能见度仪观测进行检测。为此作者于2016年5月在青岛市八关山山顶(36°4′0″N,120°20′10″E,海拔86 m)的气象台进行了海雾观测。
2.1 试验方法本文采用升降平台来进行观测(见图 5)。升降平台的最低位置为2.7 m,最高位置为10.04和14.8 m两档。在升降平台上,安装了1台Trios光谱仪,获得升降过程中的辐照度数据;并同步安装了芬兰Väisälä公司生产的PWD22型大气能见度仪,其测量范围为10~20 000 m,在10~10 000 m范围内精度为±10%,10 000~20 000 m范围内精度为±15%。在地面,安装了另一台Trios,以获得到达地表的辐照度。Trios的取样频率为0.5 Hz,而大气能见度仪的取样频率为1次/min。平台升降1次的时间约为2 min,然后停留在最低点大约6 min,每8 min完成一个测量周期。

|
图 5 青岛市八关山气象台升降平台和海雾观测现场 Fig. 5 Fog measurement platform at Baguan Hill Observatory in Qingdao City |
虽然组织进行了多次观测,但多数时间雾的持续时间很短,难以获得有效数据。其中,比较理想的数据为2016年5月5日的观测数据。观测从格林威治标准时间(UTC)1时持续到10时(北京时间上午9时到18时),捕捉到一次完整的海雾生成和发展过程,数据完好。其中,上午的雾较轻,大气能见度在2 000 m以上的时间居多;而下午发生了浓雾,大气能见度只有几百米。该观测虽然只有一天,但数据很有代表性,包括了不同浓度的雾,相当于对雾的系列观测。我们用这组数据检验本文提出的算法。
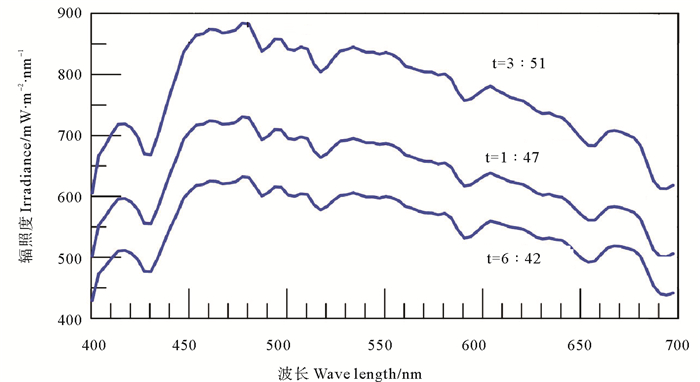
2.2 光学辐照度的测量结果观测获得的辐照度数据如图 6所示,图中给出了任意三个时刻的光谱分布,显示了标准的日光光谱,在430 nm处有极小值,在480 nm处有极大值。不同时刻的光谱结构看起来非常相似,只是强度有较大的差异。实际上,不同时间的光谱结构也有微小的差异,这些差异是计算大气能见度的重要信息。
|
( t为UTC时间。t is in UTC. ) 图 6 光学观测的辐照度数据实例 Fig. 6 Examples of irradiance data from optical observation |
观测期间,共获得有效光学和能见度测量剖面56个,可以分为4种类型:
类型1(9个):实测能见度>2 000 m,计算能见度>2 000 m;
类型2(11个):实测能见度>2 000 m,计算能见度<2 000 m;
类型3(11个):实测能见度<2 000 m,计算能见度>2 000 m;
类型4(25个):实测能见度<2 000 m,计算能见度<2 000 m;
一般大气能见度在1 000 m以下被判定有雾,1 000~2 000 m为薄雾[1, 17],对人类活动有明显影响。这里选取2 000 m以体现算法的适用范畴。2 000 m以上可以认为能见度很高,因而,类型1和类型2的数据可以不用检验。类型3和类型4的实测能见度都小于2 000 m,是我们需要谨慎关注的类型。这两种类型的观测共计36个,占总数的64%,是用来检验雾能见度算法的基础数据。
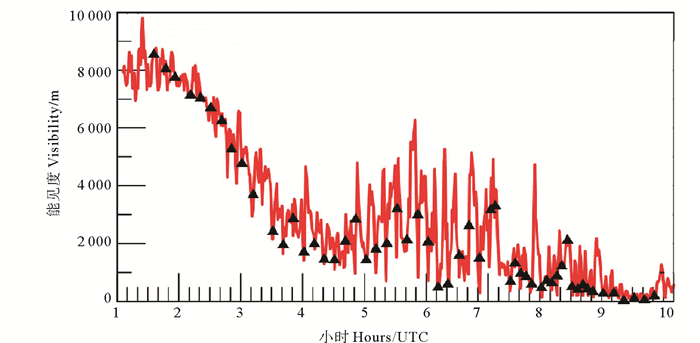
观测期间,雾的发展分为以下几个阶段(见图 7):
|
(红线为能见度仪实测大气能见度;黑色三角为观测上部和下部观测结果的平均值。Red line is atmospheric visibility measured by visibility mete; The black triangle is the average of the upper and lower observations. ) 图 7 利用(15)式得到的用于检验光学计算结果平均能见度 Fig. 7 Measured atmospheric visibility (red lines) and mean visibility (black triangle) calculated based upon Eq.(15) |
第一阶段:能见度2 000~10 000 m阶段。从开始观测到3:30(UTC,下同,加8换算为北京时间),能见度都大于2 000 m,但数值在不断下降,代表了海雾降临过程。其间,雾主要是类型1和类型2。
第二阶段:能见度在2 000 m上下浮动阶段。从3:30~6:00,其中3:30~5:00期间有2 000 m左右的轻雾,5:00~6:00大气能见度较高,主要是类型3和类型4。
第三阶段:能见度小于2 000 m阶段,从6:00~10:00。能见度基本小于2 000 m,属于类型3和类型4。从9:00~10:00的最后4次观测,能见度非常低,同时太阳高度角很低,光学算法误差较大。主要是类型4。
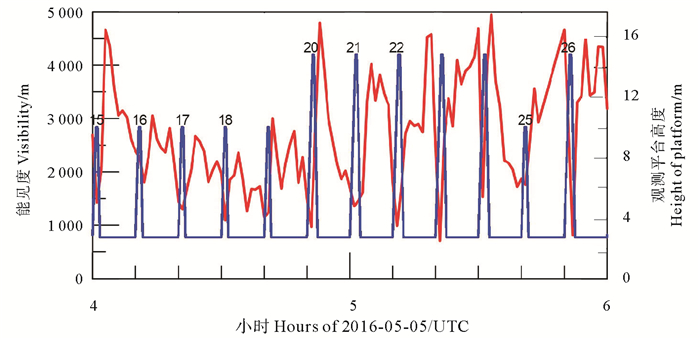
2.3 对能见度计算结果的检验大气能见度随平台的升降呈动态变化,作为例子,图 8给出了4~6时能见度随升降平台高度的变化。图中显示,升降平台在最高点时,即图中蓝色阶梯线达到10.04或14.8 m时,能见度出现极小值;而当升降平台在最低点时,即2.7 m高度上,能见度反而很高,表名发生了雾的上重下轻的现象,这种现象在1天的大部分时间里都存在。本文分析认为是由于太阳辐射导致近地面升温和湍流加强,从而引起地面的雾发生抬升,而在10 m以上的高度雾仍然保持了较高的浓度,这种现象在海雾观测中非常常见[24]。
|
(红线为实测能见度,蓝线为升降平台对应高度。Measured visibility (red line) and height of platform (blue). ) 图 8 实测能见度上重下轻现象 Fig. 8 The fog with low visibility at top and higher visibility at bottom |
能见度的上重下轻现象虽然很正常,但是,这种情形对反演结果的检验带来了困难。上重下轻现象表明,下部的透光特性要好于上部,导致上部和下部的辐照度差别变小,计算得到的衰减系数变小,获得的能见度会大于上部的能见度,小于下部的能见度。为此我们将上下能见度平均,即:
| $ {V_a} = \left( {{V_u} + {V_d}} \right)/2。$ | (15) |
其中:Vu和Vd分别为上部和下部的能见度;Va是平均大气能见度,用来检验光学观测的计算结果,如图 7中的黑色三角形所示。用平均能见度检验上重下轻情形的能见度比单用上部或下部的能见度误差会小一些。而且(14)式对于上下能见度一致的弥漫雾情形也适用。但是计算平均能见度实际上是假定上下能见度呈线性变化的情形,或上下能见度各占一半的情形。实际情况非常复杂,线性近似得到的结果会包含较大的误差,有时偏差达千米以上,成为检验结果方差较大的误差源。
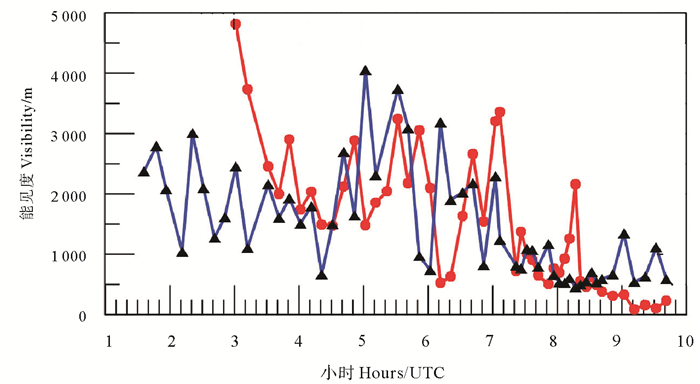
图 9是2016年5月5日全部光学观测结果计算的雾能见度与能见度仪实测能见度的比较。在大气能见度较高的时段,根据指数p,可以不用计算大气能见度,但我们还是把结果放在图中,以了解结果的整体情况。整体上看,光学计算结果与实测能见度有很好的一致性,尤其雾最重的时期,如7:30~9:00,二者的偏差最小。而9:00~10:00因天色已晚,太阳高度角很低,入射光的辐照度也很低,较大的辐照度观测误差导致计算结果和观测结果误差较大,该方法已不适用。
|
(图中红点为平均能见度,黑三角形为根据光学测量得到的雾能见度。Red dots represent averaged visibility and black triangles are retrieved visibility. ) 图 9 能见度的计算结果与能见度仪观测结果的比较 Fig. 9 Comparison of measured (red dot and red line) and calculated (black triangle and blue line) visibility |
使用全部数据(不包括9:00~10:00最后4组数据),1 000 m以内的方均根误差为173和2 000 m以内的方均根误差为471 m。如果按照p判据剔除高能见度数据,1 000 m以内的方均根误差为173和2 000 m以内的方均根误差为323 m。我们也采用(1)式,用550 nm的光学衰减系数计算大气能见度,1 000 m以内的方均根误差为333和2 000 m以内的方均根误差为871 m,其误差大于本文使用的算法。
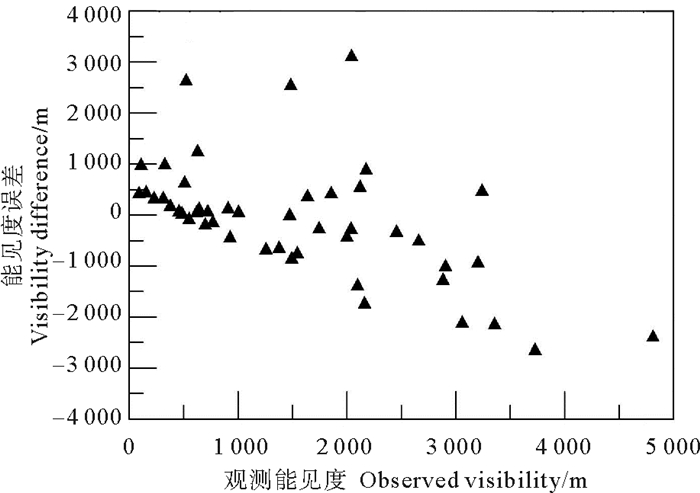
图 10给出了实测能见度与计算能见度的偏差比较,横坐标为观测的大气能见度,纵坐标为实测能见度与计算能见度的差。可以看到,二者的偏差随能见度的增大而增大,能见度越高,离散度越高。在2 000 m以下的能见度,除了个别点之外,凝聚程度较好。对于雾而言, 最为重要的是1 000 m以下的能见度的计算误差,图中可见,能见度小于1 000 m的只有1个异常点发生,表明用光学观测计算的能见度与实测能见度在雾况相对较重的情况下有较高的一致性。图中绝大多数点都发生在纵坐标小于零的情形,表明总体上光学计算的能见度小于实测的能见度,但是,在能见度小于1 000 m的情况下这种差别不大。
|
图 10 实测能见度与计算能见度的偏差 Fig. 10 Deviation between observed and calculated visibilities |
本文提出了用垂直光学辐照度测量计算雾能见度的新方法。文中注重了算法理论上的严谨性和光学数据处理的规范性,并注重误差分析和质量控制,尽量提高可能的测量精度。但由于能见度测量的复杂性,不可避免地存在各种各样的问题,需要在未来的研究中不断完善。
本文的算法是计算雾能见度,需要尽可能避免霾的影响,因而选择了5月进行观测。但我们没有办法辨识观测期间大气中霾的成分,希望在未来的观测中能找到分离霾的方法。在我们观测期间发生了雾的抬升,造成了很大的检验误差,这些误差是不真实的,希望今后能在未发生雾抬升的条件下观测,提高检验的精度。由于检验数据精度限制,我们无法对1 000 m以下的雾进行分级检验,未来应在无雾抬升的条件下进行观测,给出不同能见度下的分析精度,以体现精密光学观测的优势。
3 结论大气能见度是刻画雾的重要物理参数。目前测量大气能见度是采用主动光源测量水平方向的可视距离。由于需要使用主动光源,测量雾的仪器重量较大。人们一直在寻找用自然光源测量雾的手段,例如,使测量自然光辐照度的仪器更加轻便。但是,由于使用自然光源需要垂直方向测量,获得垂直方向的光学衰减系数。大气在水平方向和垂直方向的光学衰减具有相同的原理和表现,只是二者很少被联系起来。或者说,表征大气水平衰减的大气能见度与表征大气垂直衰减的漫衰减系数之间没有建立起物理关系。
本文提出了用垂直方向测量的光学数据计算雾能见度的方法。该方法首先测量两个不同高度上的谱辐照度,获取谱漫衰减系数,然后将自然光转换为标准光,用标准光的全谱段衰减系数计算雾能见度,形成了由垂向光学测量获取水平能见度的合乎规范的理论和实际可行的计算方法。
为了验证这个方法的可行性,采用两台光学辐照度计(Trios)分别安放在地面和可升降高台上,用以计算垂向谱衰减系数,并同步用能见度仪进行大气能见度观测,用于检验由垂向光学观测获得的能见度。在2016年5月5日,进行了9 h的联合观测,获得了一次完整的雾生成和发展过程的数据,可以很好地检验本文中提出的算法。
由于受地面相对高温和湍流加强的影响,地表的雾会出现一定程度的抬升现象,在平台的不同高度测得的能见度差别较大,采用对不同高度观测值进行平均的方法获取检验数据组。由于雾的采样频率是每分钟一次,一分钟内大气能见度可以变化很大,成为检验数据组的又一误差源。文中进行了误差分析,保证了计算结果的精度。
最为重要的问题是,由于受外部环境因素的干扰(如地面的湍流过程、仪器倾角的变化、树木造成的光谱干扰、云遮掩情况不同等),上下两部仪器会发生偏差,而且辐射越强这种偏差会越大,表现为虚报雾的结果。为此,本项研究提出,先从光谱数据本身定性判断是否有雾,再通过本文提出的理论方法计算能见度。根据无雾时以直射光为主,有雾时以散射光为主的光谱特征,发现两种光在594和674 nm的特异性,用这两个谱段归一化光谱之差作为判据,判断是否存在能见度小于2 000 m的雾。实用结果表明,这个判据非常可靠,适用于各种浓度的雾。
通过与实测数据的比较,光学观测的计算结果在大气能见度小于1 000 m的方均根误差为173 m,在能见度小于2 000 m的方均根误差为471 m。与惯常使用的用550 nm单一谱段衰减系数计算能见度的方法比较(方均根误差分别为333和871 m),精度有很大的提高,取得足够可信的能见度计算结果。尤其对于能见度小于2 000 m的情形,与实测能见度有很高的一致性。
本研究的结果表明,用垂向光学辐照度观测结果计算雾能见度是可行的方法。通过控制光学测量的精度,采取有效的算法,可以获得令人满意的结果。本研究为开发轻便精巧的采用光谱观测测量能见度的仪器提供了理论支持。
| [1] |
王彬华. 海雾[M]. 北京: 海洋出版社, 1983: 251-252. Wang Binhua. Sea Fog[M]. Beijing: Ocean Press, 1983: 251-252. (  0) 0) |
| [2] |
李子华. 中国近40年来雾的研究[J]. 气象学报, 2001, 59(5): 616-624. Li Zihua. Studies of fog in China over the past 40 Years[J]. Acta Meteorological Sinica, 2001, 59(5): 616-624. DOI:10.3321/j.issn:0577-6619.2001.05.011 (  0) 0) |
| [3] |
Gultepe I, Tardif R, Michaelides S C, et al. Fog research:A review of past achievements and future perspectives[J]. Pure and Applied Geophysics, 2007, 164(6-7): 1121-1159. DOI:10.1007/s00024-007-0211-x
(  0) 0) |
| [4] |
Kumai M. Arctic fog droplet size distribution and its effect on light attenuation[J]. Journal of the Atmospheric Sciences, 1973, 30(4): 635-643.
(  0) 0) |
| [5] |
Chylek P. Extinction and liquid water content of fogs and clouds[J]. Journal of the Atmospheric Sciences, 1978, 35(2): 296-300. DOI:10.1175/1520-0469(1978)035<0296:EALWCO>2.0.CO;2
(  0) 0) |
| [6] |
Sasakawa M, Uematsu M. Relative contribution of chemical composition to acidification of sea fog (stratus) over the northern North Pacific and its marginal seas[J]. Atmospheric Environment, 2005, 39(7): 1357-1362. DOI:10.1016/j.atmosenv.2004.11.039
(  0) 0) |
| [7] |
Ogiwara S, Okita T. Electron-microscope study of cloud and fog nuclei[J]. Tellus, 1952, 4(3): 233-240. DOI:10.3402/tellusa.v4i3.8685
(  0) 0) |
| [8] |
Rangognio J, Tulet P, Bergot T, et al. Influence of aerosols on the formation and development of radiation fog[J]. Atmospheric Chemistry and Physics Discussions, 2009(5): 17963-18019.
(  0) 0) |
| [9] |
傅刚, 李晓岚, 魏娜. 大气能见度研究[J]. 中国海洋大学学报(自然科学版), 2009, 39(5): 855-862. Fu Gang, Li Xiaolan, Wei Na. Review on the atmospheric visibility research[J]. Periodical of Ocean University of China, 2009, 39(5): 855-862. (  0) 0) |
| [10] |
Blackwell H R. Contrast thresholds of the human eye[J]. JOSA, 1946, 36(11): 624-643. DOI:10.1364/JOSA.36.000624
(  0) 0) |
| [11] |
Koschmieder H. Theorie der horizontalen Sichtweite[J]. Beitrage zur Physik der freien Atmosphare, 1924, 33-53.
(  0) 0) |
| [12] |
林晔, 王庆安, 顾松山, 等. 大气探测学教程[M]. 北京: 气象出版社, 1993: 79-98. Lin Ye, Wang Qingan, Gu Songshan, et al. Atmospheric Observation[M]. Beijing: China Meteorological Press, 1993: 79-98. (  0) 0) |
| [13] |
Hommersom A, Kratzer S, Laanen M, et al. Intercomparison in the field between the new WISP-3 and other radiometers (TriOS Ramses, ASD FieldSpec, and TACCS)[J]. Journal of Applied Remote Sensing, 2012, 6(1): 063615. DOI:10.1117/1.JRS.6.063615
(  0) 0) |
| [14] |
Tveiters J H.Characterization of Hyper Spectral Irradiance and Radiance Sensors[D].Bergen: The University of Bergen, 2013.
(  0) 0) |
| [15] |
麦卡特尼. 大气光学[M]. 北京: 科学出版社, 1988: 45-46. Earl J.McCartney. McCartney.Optics of the Atmosphere[M]. Beijing: Science Press, 1988: 45-46. (  0) 0) |
| [16] |
Jarraud M. Guide to Meteorological Instruments and Methods of Observation (WMO-No.8)[M]. Geneva, Switzerland: World Meteorological Organisation, 2008.
(  0) 0) |
| [17] |
盛裴轩, 毛节泰, 李建国, 等. 大气物理学[M]. 北京: 北京大学出版社, 2003. Sheng Peixuan, Mao jietai, Li Jianguo, et al. Atmospheric Physics[M]. Beijing: Beijing University Press, 2003. (  0) 0) |
| [18] |
饶瑞中. 现代大气光学[M]. 北京: 科学出版社, 2012. Rao Ruizhong. Modern Atmospheric Optics[M]. Beijing: Science Press, 2012. (  0) 0) |
| [19] |
张纪伟, 张苏平, 吴晓京, 等. 基于MODIS的黄海海雾研究--海雾特征量反演[J]. 中国海洋大学学报(自然科学版), 2009(s1): 311-318. Zhang Jiwei, Zhang Suping, Wu Xiaojing, et al. The research on Yellow Sea Fog based on MODIS data:Sea fog properties retrieval and spatial-temporal distribution[J]. Periodical of Ocean University of China, 2009(s1): 311-318. (  0) 0) |
| [20] |
傅刚, 徐杰, 张树钦. 数值模拟和卫星反演大气能见度对比分析[J]. 中国海洋大学学报(自然科学版), 2011, 41(4): 1-10. Fu Gang, Xu Jie, Zhang Shuqin. Comparison of modeling atmospheric visibility with visible satellite imagery[J]. Periodical of Ocean University of China, 2011, 41(4): 1-10. (  0) 0) |
| [21] |
耿彪, 何永强, 武琳, 等. 一种计算某一波段大气平均衰减系数的方法[J]. 红外技术, 2009, 31(6): 323-326. Geng Biao, He Yongqiang, Wu Lin, et al. A method of calculating the coefficient of atmospheric average attenuation for certain spectral waveband[J]. Infrared Technology, 2009, 31(6): 323-326. DOI:10.3969/j.issn.1001-8891.2009.06.004 (  0) 0) |
| [22] |
黄成栋, 李玮, 刘瑞良, 等. 透射式能见度仪校准方法研究[J]. 气象水文海洋仪器, 2018, 35(1): 17-19. Huang Chengdong, Li Wei, Liu Ruiliang, et al. Research on calibration methods of transmission visibility meter[J]. Meteorological, Hydrological and Marine Instruments, 2018, 35(1): 17-19. DOI:10.3969/j.issn.1006-009X.2018.01.005 (  0) 0) |
| [23] |
程守洙, 江之永. 普通物理学, 第三册[M]. 北京: 人民教育出版社, 1998: 314-327. Cheng Shouzhu, Jiang Zhiyong. General Physics, volume 3[M]. Beijing: People's Education Press, 1998: 314-327. (  0) 0) |
| [24] |
Zhang S, Yi L. A comprehensive dynamic threshold algorithm for daytime sea fog retrieval over the Chinese adjacent seas[J]. Pure and Applied Geophysics, 2013, 170(11): 1931-1944. DOI:10.1007/s00024-013-0641-6
(  0) 0) |
2. Key Laboratory of Physical Oceanography, Ministry of Education, Qingdao 266100, China
 2019, Vol. 49
2019, Vol. 49

