重大装备与基础设施在复杂恶劣的海洋环境中长期服役,结构物损伤累积与性能劣化不可避免,装备与设施承受服役载荷能力下降,甚至引发灾难性事故。特别令人关注的是,多次重大事故都源于结构细节的微小损伤,典型案例如导致“亚历山大·基兰”号海洋平台灾难性倾覆,造成严重的人员伤亡、经济损失和环境灾害。开发与保护海洋资源,建设海洋强国,对海上重大工程建设提出了新的迫切需求: 一方面,气候变化导致台风、巨浪和风暴潮等频发,破坏力惊人,传统结构物难以长期抵御复杂严酷的海洋环境载荷;另一方面,由于新型结构物整体尺寸庞大、构件局部构造各异、材料微观组织复杂,使海洋环境下结构-构件-材料跨越多个尺度相互作用所产生的耦合效应更加显著[1-3]。
不同尺度力学过程总存在相互作用或影响,流体、结构、构件、材料分别在水动力学、结构(动)力学、材料力学、固体力学领域发展了适用方法,然而不同尺度基础概念、数学形式、计算方法都存在较大差异。常用传统分析方法中:为描述尺度间的流体-结构相互作用,而产生多种流固耦合方法,但难以耦合精细构件与复杂材料特性;利用广义变分原理可以融合材料、构件、结构的理论与方法,当模型直接包含流体作用下结构至材料全部特性,其表征最小细节取决于基本单元的尺度,即使仅反映材料基本成分(特征尺度约10-3 m),也达到结构尺度(102 m)十万分之一,但是计算单元极多并含奇异性,隐式法收敛难,显式法效率低,因此往往采用“逐级分解”分析模式(水动力方法应用于最上层结构简化模型获得流体载荷,再施加于结构模型得内力分布,所得内力再作为外力施加于下一层细节模型,得到应力应变对照屈服、断裂和稳定性等条件进行设计校核),但是结构出现塑性后各尺度特性都随载荷历史非线性变化,需迭代计算再传递载荷,不同尺度之间极易出现关键变量不连续,计算误差更是难以避免,各类问题相互放大,达到一定程度后将导致认知错误。传统分析都是在单一尺度建立力学模型再实施计算,极大弱化乃至消除各尺度内在力学过程的相互作用,机理误差和繁杂迭代已成为海洋结构物准确高效设计的瓶颈问题,只能通过增大设计余量或降低性能指标以增加安全性。
海洋强国战略下,新能源、新设施、新装备等海上工程快速发展使结构物多尺度耦合更加突显,传统方法严重滞后工程需求,因而难以有效实施结构综合设计优化;如何在结构物分析中构建多个尺度基本理论耦合关系,同时在多个尺度并发同步高效率计算,就成为海上工程建设发展的关键问题。本文针对新型海洋结构物的跨尺度水弹塑性相互作用及其分析方法进行回顾和展望,以期为海洋结构物的优化设计研究与工程实践提供重要参考。
1 跨尺度相互作用及其分析方法考虑基本力学原理[4-6],海洋流体与结构通过流固界面相互作用,宏观结构(特征尺度达102 m)的承载性能由整体关键特征(几何、连接和边界等)与构件力学特性决定,构件的力学特性由其边界、几何(特征尺度约10-1 m)与材料特性决定,材料特性则取决于其组份、构造、缺陷等微观结构(特征尺度可至10-6 m)在应力应变场中的相互作用[7-8],而应力应变则是材料微元在结构体系下对海洋环境载荷的响应。宏观结构的破坏可以归纳为源于局部材料损伤与失效导致的非线性弹塑性及非平衡态崩溃过程,材料的损伤与失效取决于微观缺陷与组份在应力应变场作用下的演化,构件甚至整个结构会随着材料的损伤而逐渐弱化、响应增大、损伤加速[9-10]。由此可见,工程需求是从最高的结构层面提出的,工程设计上需要向下全面分析构件和材料特性,而且失效起源于材料微结构,演化涉及所有尺度且所有尺度间相互作用,因此海洋流体作用下宏观结构-细观构件-微观材料的多尺度相互作用并耦合演化。大型海洋结构物的传统工程设计与分析[11-14],通常是根据规范,通过经验公式估算水动力载荷,再分析校核结构的刚度和强度,由此确定建造材料性能并给出设计值,即“逐级分解”单一尺度分析,但是结构出现塑性后各尺度特性都随载荷历史非线性变化,传统单一尺度方法必须迭代计算再传递载荷,不同尺度间极易出现变形不连续,计算误差更是难以避免,各类问题相互影响,从而导致问题放大,达到一定程度后将导致认知错误,且综合设计优化需考虑结构、构件和材料不同组合,单一尺度方法采用海量试算也只能获得临近尺度之间影响,因此效率低、效果差。
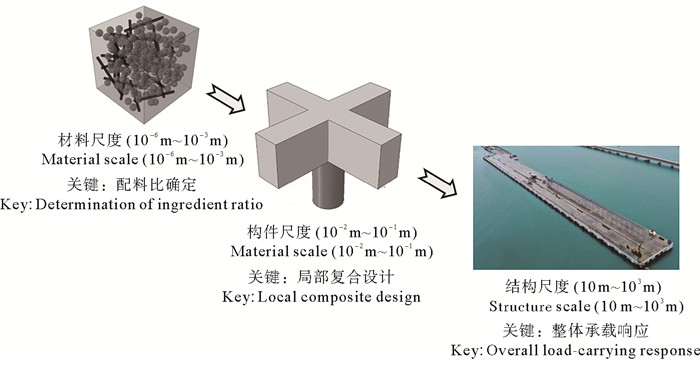
同时,重大装备与工程的设计目标不断创新,特别要求增强结构性能同时提升安全保障,这就需要降低自重的同时提高刚度、强度、阻尼,以增加承载的同时抑制响应。由于钢材与钢混等传统材料的比刚度和比强度较低且阻尼很低,对于结构创新设计的限制十分显著,因此,新型装备与工程研发已更多采用先进的新型复合材料。例如,具有优异的力学性能和耐久性的超高性能混凝土、具有更好的力学性能和加工性的颗粒增强高性能聚合物,在新型海洋结构物中获得重要应用并产生显著的经济社会效益。传统上由新材料出发的结构创新设计需要大量试验来确定材料特性对结构设计的影响机制[15-16],从而使设计、工程与时间三方面成本已成为制约新型海洋结构物发展的重要问题。此外,新型海洋工程材料在不同尺度之间的异质性更加明显,材料(特别是复合材料)组份、配比、体积分数等关键参数的分析难度更大,并且材料密度、弹性、强度和阻尼等本征特性因其微观结构变化而相互影响。但是,传统单一尺度计算中多以力学测试所得标准材料参数为依据,难以充分发挥材料的可设计性,特别是大型海洋结构物的设计分析中,结构特征尺度可达数百米甚至上千米,分层或分级构件和复合材料的微观组分的特征尺度为米~分米级和毫米以下级,如图 1所示。不同几何尺度的水动力特性、结构力学性能和材料组分特征的分析以及后续结构性能的优化,包含了跨越多个尺度的复杂力学过程,传统单一尺度方法难以有效揭示微观材料、细观构件、宏观结构及海洋流体的物理耦合关系,无法实现结构物从结构尺寸到材料组分的全面优化设计,重大工程急需创新跨尺度耦合分析方法支撑新型海洋结构物设计中创新复合材料的分析与应用。
|
图 1 大型海洋结构物的跨尺度问题示意图 Fig. 1 Schematic diagram of the multiple scale problems of large marine structures |
为解决以上问题,学者们致力于在水动力学、结构(动)力学、材料力学和固体力学等领域发展适用方法,然而不同尺度下各领域的基本概念、数学描述和计算方法等都存在较大差异:水动力学分析结构的整体受力与运动[17];结构(动)力学求解自由度响应[18];材料力学得到内力及应力应变[19];固体力学以无量纲微元通过应力应变关系表征材料的本征特性[6]。传统的流固耦合方法结合广义变分原理可以形成耦合流体作用的有限元模型,如果模型直接包含流体、结构、构件和材料的全部特性,则模型的单元数量巨大并包含奇异性,计算收敛难、效率低;如果采用“逐级分解”分析,则结构出现塑性后各尺度特性都随载荷历史非线性变化,需迭代计算再传递载荷,极易出现关键变量不连续,计算误差更是难以避免。为了提高计算效率和精度,研究者发展了结构计算的一致跨尺度分析法[20],将宏观尺度下结构的大部分区域简化为等效的梁、板、壳等单元,在模型的局部构件处采用实体单元描述细节,该类方法有效表征应力热点的材料特征,同时显著提高计算效率,但是未实现细观尺度材料组分与宏观尺度构件乃至结构的耦合计算。为了实现构件与结构耦合,在传统结构自由度耦合原理的基础上,Fang等[21]发展了复杂结构的子结构体元法,并提出虚力模型方法,解决了子结构边界的奇异约束,实现整体结构与特殊构件的双向耦合计算,该子结构体元法为后续多级材料、构件与结构三者间耦合计算提供了一种参考路径。代表性体积元(RVE)方法提供了一种耦合材料细观组分与宏观力学性能的有效均匀化方法。Jin等[2]基于代表性体积元(RVE)方法以及构件-结构耦合计算方法,采用不同尺度模型间的二次桥接技术,明确了大型海洋结构的跨尺度物理耦合机制,发展了相应的计算分析方法,实现了宏细观耦合的等效弹塑性判断以及损伤演化的时域计算,进而实现海洋结构物安全设计的综合优化。该方法的应用对象为码头基础设施、岛礁涉水工程以及海上风电基础等高刚度固定结构,单独计算结构物承受的流体载荷,再通过结构至材料跨尺度耦合分析方法进行了一体化设计。
2 流固耦合与水弹塑性跨尺度分析方法流固耦合作用是海洋结构物设计中需要考虑的重要问题。就大型船舶、浮式桥梁和浮式机场等海洋大型浮式结构而言[22-29],其水平尺度远大于其垂向高度,无法忽略其在外荷载作用下的弹性变形。流体与大型浮式结构的相互作用是非常复杂的流固耦合问题,结构的存在会改变流场,同时流场的变化会使结构产生弹性变形,通常将这类耦合过程称为水弹性问题。以往许多学者针对大型海洋结构物的水弹性响应开展了大量的研究工作[30-42]。早期的研究通常将结构简化为二维弹性梁或三维弹性板,利用水弹性理论研究其动力响应,水弹性分析主要有直接计算和模态展开两种方法。直接计算法是对流场分析得到结构流体力后,利用有限元方法(FEM)计算结构的变形和内力,例如:Hamamoto等[43]建立了大型浮式结构的三维FEM-BEM(边界元方法)耦合模型,将浮式结构简化为Mindlin厚板,板内使用八节点六面体等参单元,固液交界面使用精度相对较高的八节点二次单元;Wang等[44]建立了强耦合形式的高阶FEM-BEM模型,模型中对FEM模型和BEM模型中的节点个数和形函数构造进行了统一,避免了因BEM模型阶数低于FEM模型而导致的短波作用下计算精度较低的问题。模态展开法首先将弹性结构的变形表示为多个振动模态叠加的形式,之后计算各阶模态下结构的变形和流体力,最后将各阶模态的计算结果线性加权叠加,得到结构的总体变形和受力[45]。Lu等[46]针对大型集装箱船的水弹性问题,分析了结构的各阶固有频率和相应振动模态特征。Wang等[47]建立了规则波作用下大型船舶垂向弹性响应的数值计算方法,并进行了试验结果的验证。
随着海洋工程向深远海发展,环境载荷愈加复杂严酷,极端情况下的海洋环境载荷有可能导致结构发生超过材料屈服应力的大变形,造成较大的塑性变形和永久性的累积损伤。对于工程安全设计与综合优化,需要深入了解结构弹性、塑性、损伤至破坏的演化过程,这也是确定新型海洋结构物设计标准和规程的重要依据。针对结构局部进入塑性后整体响应的分析,学者们已开展了相关工作[48-49],已有研究通过将局部塑性区等效为一定刚度的节点,推导了流固耦合界面动力学方程,并进行了试验验证。工程中,结构的局部应力超过弹性极限后,其塑性与损伤成为一个逐渐演化的过程,结构塑性损伤区域有可能扩大,甚至在弹性区域内持续萌生,随着损伤不断累积至临界点,最终在某次载荷下导致整体失效。在流体与弹塑性结构耦合分析中,如果只是将结构塑性区简化为一定刚度的节点,未表征弹塑性损伤的非线性演化过程,则无法准确描述流场与塑性损伤之间的耦合作用,也就难以有效满足新型海洋结构物的设计需求。
前述流固耦合解析方法可以获得结构宏观动态响应的基本规律,但是工程设计需要发展精细高效的数值计算方法。海洋结构数值模拟研究涉及流体力学模拟分析、计算固体力学(CSM)和流固耦合计算方法[50-55],采用流体力学模拟和CSM分区域法可计算流体和固体区域,通过匹配边界条件以实现耦合。分区双向耦合传递的受力和变形信息具有明确的物理意义,可以分析海洋流场与结构变形耦合的非线性细节。传统的水动力-结构响应分析方法[56-57]主要关注结构的宏观物理响应(位移、变形、波浪力等),不能直接反映结构局部空间内力-变形演化和弹塑性响应。Hirdaris等[58]指出结构弹塑性分析是海洋工程结构研究及设计发展的重要组成,工程师需要能够分析结构的非线性动力响应、损伤演化和断裂扩展等问题的技术手段。Iijima等[59]基于Rankine源法和有限元法分别对超大型浮体(VLFS)的动力响应进行模拟,分析了考虑大载荷作用下结构塑性变形的破坏特征,从而发现塑性变形是在弯矩超过临界值后的短时间内形成的,其增加速率会随着弯矩的增大趋于减小。Iijima等[60]基于BEM与FEM耦合方法模拟了VLFS的塑性变形过程,分析了极限弯矩沿着结构物传递后的结构塑性变形和残余变形二者的增加速率。Yu等[61]提出了单向加固面板的动水压力和塑性特征耦合解析模型,讨论了流体-结构非线性响应的无量纲控制参数,并给出了梁和加固面板的设计曲线。
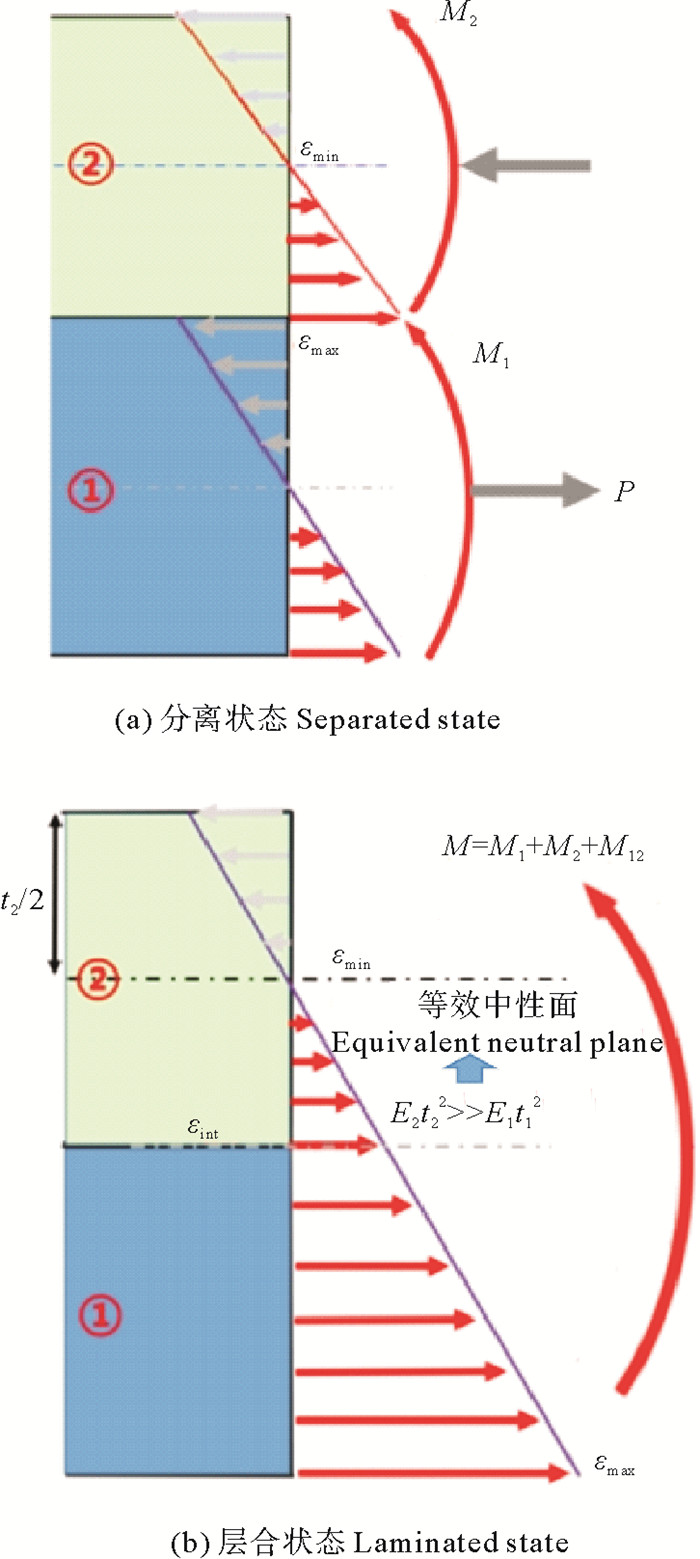
为确保海洋结构物的性能与安全,需要明确海洋环境载荷下结构整体承载、构件局部塑性与材料微观损伤三者间的耦合演化过程,阐明结构承载极限的形成机制,整体上形成流体-结构-构件-材料跨尺度耦合的水弹塑性理论与分析方法,为结构的安全设计与综合优化提供有效的基础理论与技术方法。最近,Fang等[1]发展了大型海洋结构物的跨尺度水弹性分析模式:针对材料至构件层级,构建了三轴复杂应力场下颗粒与纤维增强轻质材料微细观多级代表体元模型;针对结构层级,采用异质截面应变连续和内力平衡条件推导了截面内力分布模式,建立了复合结构的高阶动力学模型,并将该模型作为流固耦合界面建立了波浪作用下超大型复合浮体水弹性响应分析的势流方法,分析了波浪参数、结构宏观尺寸、构件细观特性、材料微观组份与结构响应、构件内力、材料应力的跨尺度耦合关系,提出了相应的结构设计分析方法。Jin等[62]以Fang等[1]提出的跨尺度水弹性分析模式为基础,通过内力平衡的弯矩梯度模型,建立了细观构件材料应变与波浪作用直接耦合的解析模型,提出了超大型浮体跨尺度耦合水弹塑性分析方法,该方法能够描述塑性区域大小和位置与波浪参数和相位的关联关系,即塑性形态模式(见图 2),以此为基础,可以直接通过优化材料组份配比、构件具体尺寸、结构复合特征来消除结构的塑性区域。延续以上思路,Li等[3]提供了一种包含初始结构材料设计、等效水弹性分析和结构塑性分析的浮体结构设计分析方法,采用边界元方法计算浮体水弹性响应,并针对响应最大值分析结构的弹塑性响应特征。
|
( ①:第一层The first layer;②:第二层The second layer;P:层间作用力Interaction forces between the layers;M:总弯矩Total bending moment;M1:第一层所受弯矩Bending moment at the first layer;M2:第二层所受弯矩Bending moment at the second layer;M12:层间作用力所产生弯矩Bending moments from the interaction forces;E1:第一层弹性模量Elastic modulus of the first layer;E2:第二层弹性模量Elastic modulus of the second layer;t1:第一层厚度The first layer thickness;t2:第二层厚度The second layer thickness;:幅值最大应变Strain with maximum amplitude;:幅值最小应变Strain with minimum amplitude;:层间界面应变Interface strain。) 图 2 弯矩作用下双层浮体应变分布[62] Fig. 2 Strain distribution of double-layered floating structures under bending moment[62] |
重大装备与工程要求的不断提高,促使结构设计目标不断提升,特别要求增强结构性能同时提升安全保障,即增加结构承载且抑制响应,就需要同时实现提高比刚度、提高比强度并加大阻尼,由于钢材、混凝土和钢混等传统材料的比刚度和比强度均较低且阻尼极低,对结构创新设计的限制十分显著,此时,复合材料的应用逐渐成为推动新型海洋结构物研发的核心要素之一。各类材料在宏观上表现的力学特性主要取决于微观尺度的材料构造和特征,因此在实际工程中需要从微观特性入手来改善材料的宏观性能,即从微观尺度层面上串联材料配比与细观构件乃至宏观结构的力学性能关系,从而达到需要的工程效果。实现以上目标的关键在于将微观特征与宏观特性相关联,由此学者们开展了大量研究工作,提出了多种均质化理论及解析计算方法(如有效介质理论、Voigt-Reuss-Hill准则以及Mori-Tanaka方法),用于建立材料宏微观之间的耦合关系式[63-67]。理论解析计算在不同尺度之间所建立的耦合桥接关系存在一定的局限性,例如:计算失真度高、耦合比小、假设过多等。随着计算机技术的进步,一些学者通过建立材料微观数值模型,利用数值仿真实现了宏观力学性能与微观组分之间的耦合,计算精度与有效性相比于理论解析具有明显优势[68-71]。
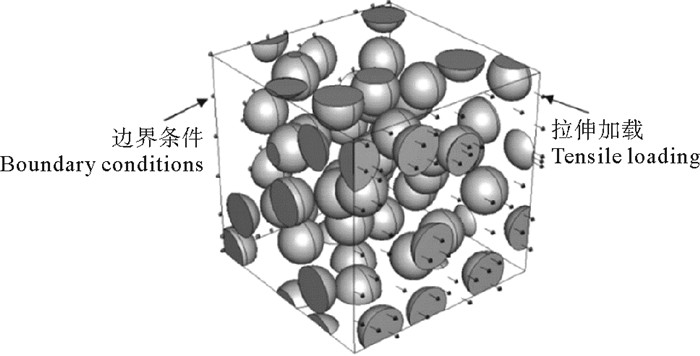
随着机理认识与计算技术的进步,代表体元法(RVE)逐渐成为实现材料微观特征与宏观特性关联建模与分析的一类重要方法。该类方法的提出基于材料细观结构具有统计学周期性的假设,即通过隔离出代表性体积单元(RVE)将整个材料体视为由RVE周期性排列构成[72-74]。当受到远场外载荷作用时,所有RVE单胞的力学行为具有一致性,它们表现出相似的应力应变场,从而可以采用单个RVE模型的应力应变场反映材料的宏观等效应力应变场[7]。不同夹杂物与组分比例的材料宏观力学性能存在明显差异[75-77],而且材料在宏观尺度上表现出均匀性,但是当尺度变小时,材料会表现出明显的异质性[78]。RVE方法将材料在微观尺度下进行分解,通过计算微元特性,实现宏微观物理耦合关系[1-2]。如图 3所示,Sun等[79]应用组分随机分布的代表性体积单元计算了颗粒增强材料的弹性模量和泊松比,比理论解析计算结果更接近试验结果。Su等[80]建立了由钢纤维和混凝土基体组成的二相RVE模型,模拟掺入钢纤维的超高性能混凝土材料,研究了纤维与基体之间的粘结-滑移特征。Borges等[81]建立了双尺度模型来研究混凝土结构加载过程中的力学现象,研究了混凝土梁与混凝土视为三相特征(基体、骨料和两者的界面过渡区(ITZ))的关联关系。Abbes等[82]建立了混凝土结构的弹塑性响应同基体、骨料和孔隙组成的关联关系。如图 4所示,Fang等[1]基于RVE均质化数值分析方法,分层级求解了超高性能混凝土(UHPC)细观组分、孔洞胞元、晶格体元与宏观性能参数(弹性模量、密度)之间的物理耦合关系,通过将参数化公式引入到水弹性模型中,实现了材料-结构的水弹性跨尺度耦合分析。RVE方法揭示了材料微细观组分特征和宏观构件乃至结构力学性能之间的关系,可以根据结构的承载性能并通过耦合计算确定适合不同工程问题的材料微观特征,尤其有利于海洋工程新型材料(例如:超高性能混凝土)的开发与应用。不过,在目前所提出的RVE建模方法中,通常将基体与夹杂物视为弹塑性材料,从而忽略了复杂环境载荷作用下材料至结构的非稳态演化,也就无法获得结构非线性演化与海洋流场的耦合关系。
|
图 3 颗粒增强复合材料代表性体元模型[79] Fig. 3 Representative volume element model of particle-reinforced composites [79] |
海洋结构物的结构性能提升与材料性能优化一体发展是工程研发的重要趋势之一。超高性能复合材料由本质基材、增强颗粒物和增强纤维体构成,具有超高强度、高韧性、高耐久性以及优良耐腐蚀性的特点,使用超高性能复合材料制成的构件具有很高的承载性能、结构延性以及耗能性能,进而可以满足特殊工艺下的高比刚度结构生产。对于海洋环境下结构物的主要承载构件,普通复合材料孔隙较大,容易造成内部构造的严重腐蚀,整体承载性能在结构老化后明显下降。而超高性能复合材料表面密实,能有效防止海洋腐蚀介质侵蚀内部,从而显著提高结构的耐久性[83-84]。另外,复合构件可以充分利用各类材料性能与构件几何特性,也成为结构综合设计优化的关键技术[1]。在利用超高性能复合材料与复合构件进行大型海洋结构物的设计与分析时,必须考虑到整体结构是大规模的,因此除了利用RVE方法进行材料宏细观性能优化外,还需要同时考虑宏观层面上存在的关键局部构件同整体结构之间的耦合作用。
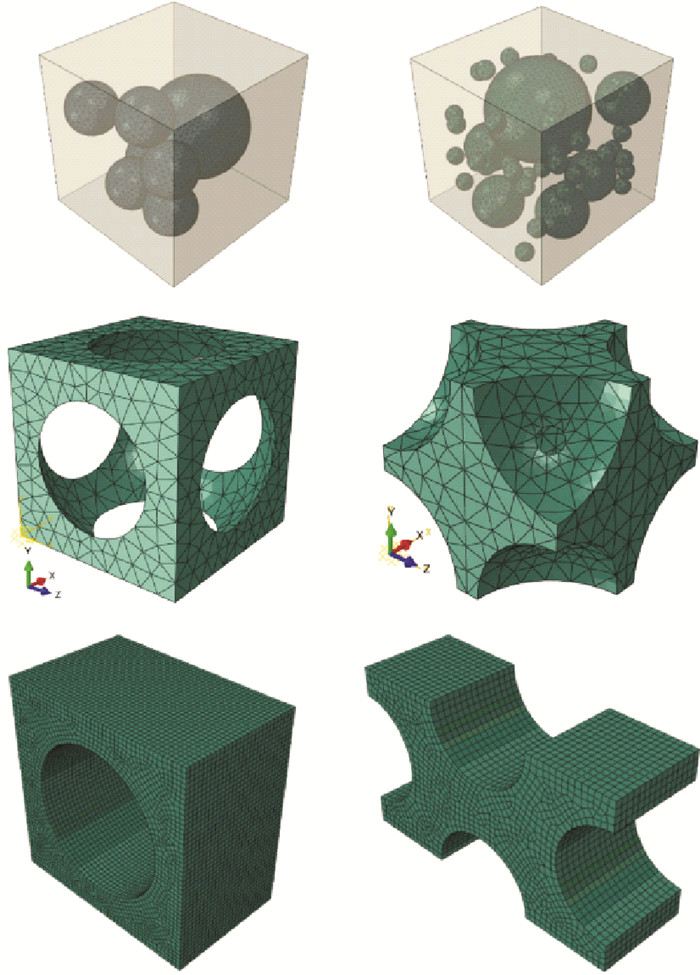
在理论研究方面,Chuang等[85]建立了层合梁的弹性挠曲动力学模型,并基于构件间界面处的变形协调方程与受力平衡方程,提出了层合结构中层间耦合作用的基本假定。Fang等[21]基于异质材料变形协调条件的虚应变等效法,进一步提出了多种材料组成的多层复合构件均匀化等效动力学模型。上述方法为海洋结构物由局部构件到整体结构层级的耦合提供了理论依据。同时,数值模拟逐步成为研究构件-结构跨尺度耦合问题的重要解决手段。海洋工程中,结构物的尺寸数量级往往为几十米、上百米甚至上千米,结构损伤则发生在关键局部构件部位,损伤的范围较小且分散。在计算过程中,尤其是数值模拟中整体结构的精细化建模较为繁琐,构件之间的连接又存在多种方式,不同关键局部构件相应尺寸参数之间的差异容易导致整体建模与分析过程出现界面奇异性。总之,海洋结构物整体模型尺寸庞大,完全精细化建模分析的计算成本高、耗时长、精度与收敛性难以控制。如果采用整体结构简化建模,计算时间会有效缩短且建模较为简单,但是计算精度较低,且无法明确结构弹塑性变形至损伤及破坏的机制,特别是对于采用新型材料的新型结构,难以建立设计必需的标准与规程。一般情况下,由于外荷载作用下的结构破坏部位比较集中,一些学者引入跨尺度数值建模的概念,对宏观尺度上的整体结构和局部构件通过界面模型耦合,研究局部区域的破坏机理以及整体结构的承载演化[2, 86]。Li等[86]通过分析界面耦合约束作用,建立了大跨度桥梁局部构件损伤-整体结构响应的跨尺度数值模型(见图 5),同时分析了焊接构件的局部细观劣化以及局部劣化对桥梁整体结构的影响。Jin等[2]以开孔沉箱为研究对象,基于RVE数值方法,分析了超高性能混凝土(UHPC)纤维体积分数与结构整体承载极限的关联关系,并建立了UHPC组份-开孔前墙-沉箱整体跨尺度数值模型,实现了开孔沉箱的跨尺度耦合优化(见图 6)。
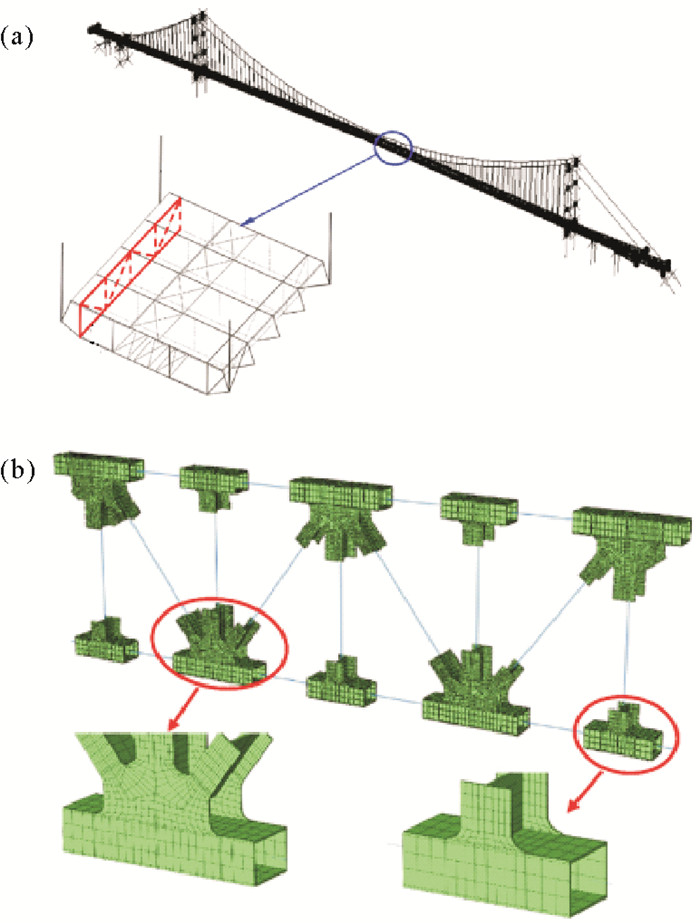
|
( (a) 结构全尺度模型Full-scale structure model; (b) 局部构件模型Local member model. ) 图 5 大跨度桥梁多尺度分析模型[86] Fig. 5 Multiscale models of the large-span bridge[86] |
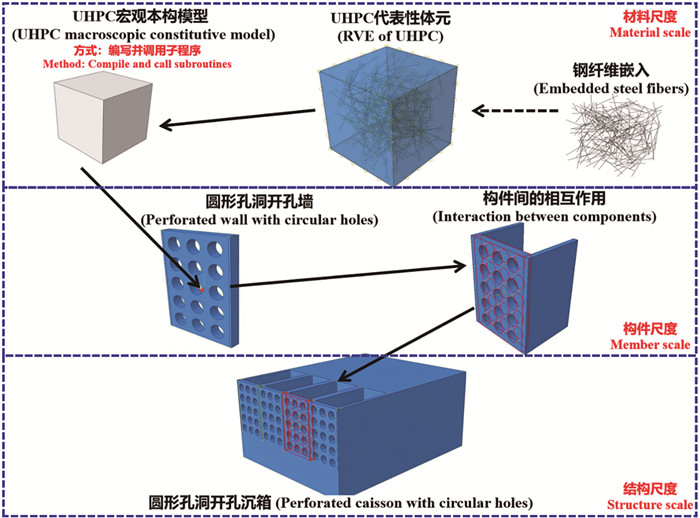
|
图 6 开孔沉箱承载性能的跨尺度优化分析[2] Fig. 6 Multiscale optimization analysis for the load-carrying performance of perforated caissons [2] |
海洋工程结构设计中,工程需求是从宏观结构层面上提出的,海洋环境作用下结构、构件、材料互相影响,失效源于材料微缺陷与所有尺度耦合的演化,即海洋环境流体-结构宏观响应-构件细观特性-材料微观特征的跨尺度耦合作用及演化,决定了结构承载、退化、破坏的综合性能。传统方法的特点是单一尺度独立分析、单向传递载荷信息,使得各尺度内在力学过程的相互作用弱化乃至消除,因此需要通过增大设计余量、降低性能指标以增加安全性,导致成本显著上升,但是结构损伤、破坏和倒塌等问题仍时有发生。在海洋结构物性能分析中,跨越了多个尺度阐明关键耦合机制并建立高效率同步计算模式,明确了海洋环境载荷下结构弹塑性从损伤至破坏的演化过程,形成了海洋结构物跨尺度耦合分析模拟方法,因此针对不同类型结构建立综合设计优化标准与规程,已成为工程发展中面临的关键科学问题与技术难题。
通过开展海洋结构物的跨尺度耦合分析。一方面提供海洋环境载荷下结构劣化分析的基本原理与方法,防止重大结构失效所引发的损伤和灾难,同时为结构运维的损伤监测与修复提供理论和技术支持。另一方面,可以为海洋工程结构设计基础理论和工程技术的发展提供新思路,即充分考虑流体、结构、构件和材料间跨越多个尺度相互影响和共同作用的关联特性,将海洋结构物性能分析由单一尺度计算、单向传递载荷提升至跨尺度耦合演化、双向传递载荷。
目前,材料层面多个尺度耦合研究已经发展到“材料基因组”工程,结构层面多个尺度耦合研究也取得了快速进展与广泛应用。海洋环境下结构-构件-材料的耦合分析跨越了多个尺度,因此不仅需要流体力学、结构力学、固体力学乃至材料学科的交叉融合,而且需要结合实际工程需求,推动跨尺度耦合分析方法的发展。针对流体与海洋结构物相互作用,水弹性研究已经具备了成熟的线性解析方法,然而实际中绝大多数的流固耦合作用为非线性问题,并包含流体、结构、构件、材料不同层次的关键要素,因此有必要发展非线性解析理论,同时提高数值方法效率。当前,极端海况下海洋结构物非线性大变形响应与材料弹塑性损伤相互作用的数值模拟技术是前沿性关键问题之一,今后的研究中若要进一步攻克该问题,必须全面阐明海洋环境载荷作用下微观材料、细观构件和宏观结构等物理性能的非线性演化特征与相互作用机制,创新力学模型与数值方法实现指向性定量分析,构建新型海洋结构物的跨尺度水弹塑性理论体系,为重大装备与工程研发奠定理论基础。
| [1] |
Fang H, Zhu H, Li A, et al. A multiscale material-structure-hydroelasticity coupled analytical model for floating sandwich structures with hierarchical cores[J]. Marine Structures, 2021, 79: 103055. DOI:10.1016/j.marstruc.2021.103055 (  0) 0) |
| [2] |
Jin Z, Fang H, Liu Y. A mesoscale material and macroscale structure joint design for perforated caissons made with ultrahigh-performance concrete[J]. Structures, 2022, 46: 765-792. DOI:10.1016/j.istruc.2022.10.099 (  0) 0) |
| [3] |
Li Z, Chen D, Feng X, et al. Hydroelastic analysis and structural design of a modular floating structure applying ultra-high performance fiber-reinforced concrete[J]. Ocean Engineering, 2023, 277: 114266. DOI:10.1016/j.oceaneng.2023.114266 (  0) 0) |
| [4] |
梅强中. 水波动力学[M]. 北京: 科学出版社, 1984. Mei Q Z. Water Wave Dynamics[M]. Beijing: Science Press, 1984. (  0) 0) |
| [5] |
吴一红, 谢省宗. 水工结构流固耦合动力特性分析[J]. 水利学报, 1995(1): 27-34. Wu Y H, Xie S Z. Dynamic characteristic analysis for fluid-structure interaction of hydraulic structures[J]. Journal of Hydraulic Engineering, 1995(1): 27-34. DOI:10.3321/j.issn:0559-9350.1995.01.004 (  0) 0) |
| [6] |
刘正兴. 计算固体力学[M]. 上海: 上海交通大学出版社, 2010. Liu Z X. Computational Solid Mechanics[M]. Shanghai: Shanghai Jiao Tong University Press, 2010. (  0) 0) |
| [7] |
Yu J, Zhang B, Chen W, et al. Experimental and multi-scale numerical investigation of ultra-high performance fiber reinforced concrete (UHPFRC) with different coarse aggregate content and fiber volume fraction[J]. Construction and Building Materials, 2020, 260: 120444. DOI:10.1016/j.conbuildmat.2020.120444 (  0) 0) |
| [8] |
Chen Q, Wang H, Jiang Z, et al. Reaction-degree-based multi-scale predictions for the effective properties of ultra-high-performance concrete[J]. Magazine of Concrete Research, 2021, 73(16): 853-864. DOI:10.1680/jmacr.19.00415 (  0) 0) |
| [9] |
Li Z X, Zhou T Q, Chan T H T, et al. Multi-scale numerical analysis on dynamic response and local damage in long-span bridges[J]. Engineering Structures, 2007, 29(7): 1507-1524. DOI:10.1016/j.engstruct.2006.08.004 (  0) 0) |
| [10] |
Li Y, Huang H, Zhang W, et al. Structural full-field responses reconstruction by the SVD and pseudo-inverse operator-estimated force with two-degree multi-scale models[J]. Engineering Structures, 2021, 249: 112986. DOI:10.1016/j.engstruct.2021.112986 (  0) 0) |
| [11] |
中国交通天津港湾工程研究院有限公司. JTS 151-2011水运工程混凝土结构设计规范[S]. 北京: 人民交通出版社, 2011. China Traffic Tianjin Dredging Harbour Construction Engineering Company Limited. JTS 151-2011 Code for Design of Concrete Structures in Water Transport Engineering[S]. Beijing: People's Communications Press, 2011. (  0) 0) |
| [12] |
徐策. 开孔沉箱结构的设计优化研究[D]. 大连: 大连理工大学, 2012. Xu C. Design Optimization Research on Perforated Caisson Structure[D]. Dalian: Dalian University of Technology, 2012. (  0) 0) |
| [13] |
American Society of Civil Engineers. Seismic Design of Piers and Wharves[M]. Reston, VA: American Society of Civil Engineers, 2014.
(  0) 0) |
| [14] |
李梦玥. 中美高桩码头抗震设计方法对比分析[D]. 大连: 大连理工大学, 2020. Li M Y. Comparative Analysis of Seismic Design Methods for High Pile Wharf in China and the United States[D]. Dalian: Dalian University of Technology, 2020. (  0) 0) |
| [15] |
Lehman D E, Brackmann E, Jellin A, et al. Seismic performance of pile-wharf connections[J]. TCLEE 2009: Lifeline Earthquake Engineering in a Multihazard Environment, 2009, 1-13. (  0) 0) |
| [16] |
Roeder C W, Graff R, Soderstrom J, et al. Seismic performance of pile-wharf connections[J]. Journal of Structural Engineering, 2005, 131(3): 428-437. DOI:10.1061/(ASCE)0733-9445(2005)131:3(428) (  0) 0) |
| [17] |
李玉成, 滕斌. 波浪对海上建筑物的作用[M]. 第3版. 北京: 海洋出版社, 2015. Li Y Y, Teng B. The Effect of Waves on Offshore Structures[M]. 3rd Edition. Beijing: Ocean Press, 2015. (  0) 0) |
| [18] |
倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1988. Ni Z H. Vibration Mechanics[M]. Xi'an: Xi'an Jiaotong University Press, 1988. (  0) 0) |
| [19] |
沈观林, 胡更开. 复合材料力学[M]. 北京: 清华大学出版社, 2006. Shen G L, Hu G K. Composite Material Mechanics[M]. Beijing: Tsinghua University Press, 2006. (  0) 0) |
| [20] |
徐伟, 李智, 张肖宁. 子模型法在大跨径斜拉桥桥面结构分析中的应用[J]. 土木工程学报, 2004, 137(16): 30-34. Xu W, Li Z, Zhang X N. The application of submodel method in the structural analysis of long-span cable stayed bridges[J]. Journal of Civil Engineering, 2004, 137(16): 30-34. DOI:10.15951/j.tmgcxb.2004.06.006 (  0) 0) |
| [21] |
Fang H, Wang T J, Chen X. Model updating of lattice structures: a substructure energy approach[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1469-1484. DOI:10.1016/j.ymssp.2011.01.002 (  0) 0) |
| [22] |
吴有生, 顾学康, 柳淑学, 等. 海洋超大型浮体重大科学问题的基础研究进展[J]. 中国基础科学, 2017, 4: 28-66. Wu Y S, Gu X K, Liu S X, et al. Basic research progress on major scientific issues of marine very large floating bodies[J]. China Basic Science, 2017, 4: 28-66. DOI:10.3969/j.issn.1009-2412.2017.04.008 (  0) 0) |
| [23] |
Suzuki H. Overview of Megafloat: Concept, design criteria, analysis, and design[J]. Marine Structures, 2005, 18(2): 111-132. DOI:10.1016/j.marstruc.2005.07.006 (  0) 0) |
| [24] |
Wei W, Fu S, Moan T, et al. A time-domain method for hydroelasticity of very large floating structures in inhomogeneous sea conditions[J]. Marine Structures, 2018, 57: 180-192. DOI:10.1016/j.marstruc.2017.10.008 (  0) 0) |
| [25] |
Strand I M, Faltinsen O M. Linear wave response of a 2D closed flexible fish cage[J]. Journal of Fluids and Structures, 2019, 87: 58-83. DOI:10.1016/j.jfluidstructs.2019.03.005 (  0) 0) |
| [26] |
Moan T, Eidem M E. Floating bridges and submerged tunnels in Norway—the history and future outlook[C]//WCFS2019 Proceedings of the World Conference on Floating Solutions. Berlin: Springer, 2019.
(  0) 0) |
| [27] |
Fu S, Li S, Cui W. Very Large Floating Structures (VLFS): Overview[M]//Cui W, Fu S, Hu Z. Encyclopedia of Ocean Engineering. Berlin: Springer, 2021.
(  0) 0) |
| [28] |
Ding J, Wu Y, Xie Z, et al. Overview: research on hydroelastic responses of VLFS in complex environments[J]. Marine Structures, 2021, 78: 102978. DOI:10.1016/j.marstruc.2021.102978 (  0) 0) |
| [29] |
Wang Y, Fu S, Moan T, et al. Hydroelasticity analysis of a vessel-shaped fish cage under incident, diffraction and radiation wave fields[J]. Journal of Ocean Engineering and Science, 2023, 16: 35. (  0) 0) |
| [30] |
Teng B, Gou Y, Cheng L, Liu S. Draft effect on wave action with a semi-infinite elastic plate[J]. Acta Oceanologica Sinica, 2006, 25(6): 116-27. (  0) 0) |
| [31] |
Fu S, Moan T, Chen X, et al. Hydroelastic analysis of flexible floating interconnected structures[J]. Ocean Engineering, 2007, 34(11-12): 1516-1531. DOI:10.1016/j.oceaneng.2007.01.003 (  0) 0) |
| [32] |
Zhao C, Hao X, Liang R, et al. Influence of hinged conditions on the hydroelastic response of compound floating structures[J]. Ocean Engineering, 2015, 101: 12-24. DOI:10.1016/j.oceaneng.2015.04.021 (  0) 0) |
| [33] |
Wu Y S, Ding J, Li Z W, et al. Hydroelastic responses of VLFS deployed near islands and reefs[C]//Ocean, Offshore and Arctic Engineering Division. Norway, Trondheim: ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, 2017.
(  0) 0) |
| [34] |
Mohapatra S C, Guedes Soares G. Interaction of ocean waves with floating and submerged horizontal flexible structures in three-dimensions[J]. Applied Ocean Research, 2019, 83: 136-154. DOI:10.1016/j.apor.2018.10.009 (  0) 0) |
| [35] |
Ding J, Xie Z Y, Wu Y S, et al. Numerical and experimental investigation on hydroelastic responses of an 8-module VLFS near a typical island[J]. Ocean Engineering, 2020, 214: 107841. DOI:10.1016/j.oceaneng.2020.107841 (  0) 0) |
| [36] |
Feng S, Zhang G, Wan D, et al. On the treatment of hydroelastic slamming by coupling boundary element method and modal superposition method[J]. Applied Ocean Research, 2021, 112: 102595. DOI:10.1016/j.apor.2021.102595 (  0) 0) |
| [37] |
Chen Y, Ma H, Li A, et al. Hydroelastic analysis of double-segment floating sandwich structures under wave action[J]. Ocean Engineering, 2022, 260: 111993. DOI:10.1016/j.oceaneng.2022.111993 (  0) 0) |
| [38] |
Huang S, Jiao J, Guedes Soares C. Uncertainty analyses on the CFD-FEA co-simulations of ship wave loads and whipping responses[J]. Marine Structures, 2022, 82: 103129. DOI:10.1016/j.marstruc.2021.103129 (  0) 0) |
| [39] |
Huang S, Hu Z, Chen C. Application of CFD-FEA coupling to predict hydroelastic responses of a single module VLFS in extreme wave conditions[J]. Ocean Engineering, 2023, 280: 114754. DOI:10.1016/j.oceaneng.2023.114754 (  0) 0) |
| [40] |
Li A J, Fang H, Liu Y. Hydroelastic analysis of interaction between water waves and a floating laminated disk[J]. Physics of Fluids, 2022a, 34: 047121. DOI:10.1063/5.0088675 (  0) 0) |
| [41] |
Li S, Fu S, Zhang S, et al. Second-order hydroelastic analysis of a flexible floating structure under spatially inhomogeneous waves[J]. Marine Structures, 2022b, 86: 103306. DOI:10.1016/j.marstruc.2022.103306 (  0) 0) |
| [42] |
Li A J, Ma H J, Fang H, et al. Fluid-structure-material coupling analysis for a floating laminated structure consisting of high-stiffness panels and a soft core[J]. Marine Structures, 2023a, 89: 103375. DOI:10.1016/j.marstruc.2023.103375 (  0) 0) |
| [43] |
Hamamoto T, Suzuki A, Tsujioka N, et al. 3D BEM-FEM hybrid hydroelastic analysis of module linked large floating structures subjected to regular waves[C]//International Society of Offshore and Polar Engineers. Montreal, Canada: Proceedings of the 8th International Offshore and Polar Engineering Conference, 1998.
(  0) 0) |
| [44] |
Wang C D, Meylan M H. A higher-order-coupled boundary element and finite element method for the wave forcing of a floating elastic plate[J]. Journal of Fluids and Structures, 2004, 19(4): 557-572. DOI:10.1016/j.jfluidstructs.2004.02.006 (  0) 0) |
| [45] |
Feng S, Zhang G, Wan D, et al. On the treatment of hydroelastic slamming by coupling boundary element method and modal superposition method[J]. Applied Ocean Research, 2021, 112: 102595. DOI:10.1016/j.apor.2021.102595 (  0) 0) |
| [46] |
Lu Y, Liu J, Teng B, et al. Modal investigation on a large-scale containership model for hydroelastic analysis[J]. Shock and Vibration, 2022(4): 2539870. (  0) 0) |
| [47] |
Wang H, Duan W, Chen J, et al. A numerical method to compute flexible vertical responses of containerships in regular waves[J]. Ocean Engineering, 2022, 266: 112828. DOI:10.1016/j.oceaneng.2022.112828 (  0) 0) |
| [48] |
Yoon J S, Lee P S. Hydro-elastoplastic analysis of floating plates in waves[C]//Ocean, Offshore and Arctic Engineering Division. Bodies, Bristol: ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, 2015.
(  0) 0) |
| [49] |
Iijima K, Fujikubo M. Hydro-elastoplastic behaviour of VLFS under extreme vertical bending moment by segmented beam approach[J]. Marine Structures, 2018, 57: 1-17. DOI:10.1016/j.marstruc.2017.09.008 (  0) 0) |
| [50] |
Morvarid M, Rezghi A, Riasi A, et al. 3D numerical simulation of laminar water hammer considering pipe wall viscoelasticity and the arbitrary Lagrangian-Eulerian method[J]. World Journal of Engineering, 2018, 15(2): 298-305. DOI:10.1108/WJE-08-2017-0236 (  0) 0) |
| [51] |
Gotod H, Khayyer A, Shimizu Y. Entirely Lagrangian meshfree computational methods for hydroelastic fluid-structure interactions in ocean engineering—reliability, adaptivity and generality[J]. Applied Ocean Research, 2021, 115: 102822. DOI:10.1016/j.apor.2021.102822 (  0) 0) |
| [52] |
Huang L, Li Y. Design of the submerged horizontal plate breakwater using a fully coupled hydroelastic approach[J]. Computer-Aided Civil and Infrastructure Engineering, 2022, 37(7): 915-932. DOI:10.1111/mice.12784 (  0) 0) |
| [53] |
Tran-Dus T, Meylan M H, Thamwattana N. Dynamical response of a floating plate to water waves using a smoothed particle hydrodynamics algorithm for nonlinear elasticity[J]. Physics of Fluids, 2022, 34: 053316. DOI:10.1063/5.0088536 (  0) 0) |
| [54] |
Brown S A, Xie N, Hann M R, et al. Investigation of wave-driven hydroelastic interactions using numerical and physical modelling approaches[J]. Applied Ocean Research, 2022, 129: 103363. DOI:10.1016/j.apor.2022.103363 (  0) 0) |
| [55] |
Hu Z, Huang L, Li Y. Fully-coupled hydroelastic modeling of a deformable wall in waves[J]. Coastal Engineering, 2023, 179: 104245. DOI:10.1016/j.coastaleng.2022.104245 (  0) 0) |
| [56] |
Andrianov A I, Hermans A J. Hydroelastic analysis of a floating plate of finite draft[J]. Applied Ocean Research, 2006, 28(5): 313-325. DOI:10.1016/j.apor.2006.12.002 (  0) 0) |
| [57] |
Gao R P, Tay Z Y, Wang C M, et al. Hydroelastic response of very large floating structure with a flexible line connection[J]. Ocean Engineering, 2011, 38(17-18): 1957-1966. DOI:10.1016/j.oceaneng.2011.09.021 (  0) 0) |
| [58] |
Hirdaris S E, Temarel P. Hydroelasticity of ships: Recent advances and future trends[J]. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2009, 223(3): 305-330. DOI:10.1243/14750902JEME160 (  0) 0) |
| [59] |
Iijima K, Sakai M, Fujikubo M, et al. Hydro-elastoplastic analysis for predicting collapse behavior of VLFS under large waves[C]//Ocean, Offshore and Arctic Engineering Division. Busan, South Korea: ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, 2016.
(  0) 0) |
| [60] |
Iijima K, Fujikubo M. Hydro-elastoplastic behaviour of VLFS under extreme vertical bending moment by segmented beam approach[J]. Marine Structures, 2018, 57: 1-17. DOI:10.1016/j.marstruc.2017.09.008 (  0) 0) |
| [61] |
Yu Z, Amdahl J, Greco M, et al. Hydro-plastic response of beams and stiffened panels subjected to extreme water slamming at small impact angles, PartⅠ: An analytical solution[J]. Marine Structures, 2019, 65: 53-74. DOI:10.1016/j.marstruc.2019.01.002 (  0) 0) |
| [62] |
Jin Z, Liu Y, Zhu M, et al. A novel analytical model coupling hydrodynamic-structural-material scales for very large floating photovoltaic support structures[J]. Ocean Engineering, 2023, 275: 114113. DOI:10.1016/j.oceaneng.2023.114113 (  0) 0) |
| [63] |
Hill R. Continuum micro-mechanics of elastoplastic polycrystals[J]. Journal of the Mechanics and Physics of Solids, 1965, 13(2): 89-101. DOI:10.1016/0022-5096(65)90023-2 (  0) 0) |
| [64] |
Mori T, Tanaka K. Average stress in matrix and average elastic energy of materials with misfitting inclusion[J]. Acta Metallurgica, 1973, 21(5): 571-574. DOI:10.1016/0001-6160(73)90064-3 (  0) 0) |
| [65] |
Bensoussan A, Lions J L, Papanicolaou G. Asymptotic Analysis for Periodic Structures[M]. Providence: American Mathematical Society, 1978.
(  0) 0) |
| [66] |
Fish J, Belsky V. Multigrid method for a periodic hetero-geneous medium, Part 2: Multiscale modeling and quality control in mutidimensional case[J]. Computer Methods in Applied Mechanics and Engineering, 1995, 126: 17-38. DOI:10.1016/0045-7825(95)00812-F (  0) 0) |
| [67] |
Cui J Z, Shin T M, Wang Y L. The two-scale analysis method for bodies with small periodic configurations[J]. Structural Engineering and Mechanics, 1999, 17: 601-614. (  0) 0) |
| [68] |
Qsymah A, Sharma R, Yang Z, et al. Micro X-ray computed tomography image-based two-scale homogenisation of ultra high performance fibre reinforced concrete[J]. Construction and Building Materials, 2017, 130: 230-240. DOI:10.1016/j.conbuildmat.2016.09.020 (  0) 0) |
| [69] |
Liu C, Wang F, Zhang M. Modelling of 3D microstructure and effective diffusivity of fly ash blended cement paste[J]. Cement and Concrete Composites, 2020, 110: 103586. DOI:10.1016/j.cemconcomp.2020.103586 (  0) 0) |
| [70] |
Wu Z, Zhang J, Yu H, et al. Three-dimensional mesoscopic investigation on the impact of specimen geometry and bearing strip size on the splitting-tensile properties of coral aggregate concrete[J]. Engineering, 2022, 17: 110-122. DOI:10.1016/j.eng.2021.02.024 (  0) 0) |
| [71] |
Zhang J, Liu X, Wu Z, et al. Fracture properties of steel fiber reinforced concrete: Size effect study via mesoscale modelling approach[J]. Engineering Fracture Mechanics, 2022, 260: 108193. DOI:10.1016/j.engfracmech.2021.108193 (  0) 0) |
| [72] |
章继峰, 王振清, 周健生, 等. 基于Python-Abaqus复合材料代表性体积元的数值模型[J]. 宇航材料工艺, 2009, 39(3): 25-29. Zhang J F, Wang Z Q, Zhou J S, et al. A numerical model based on representative volume elements of python-abaqus for composite materials[J]. Aerospace Materials Technology, 2009, 39(3): 25-29. DOI:10.3969/j.issn.1007-2330.2009.03.006 (  0) 0) |
| [73] |
Pan Y, Iorga L, Pelegri A A. Analysis of 3D random chopped fiber reinforced composites using FEM and random sequential adsorption[J]. Computational Materials Science, 2008, 43(3): 450-461. DOI:10.1016/j.commatsci.2007.12.016 (  0) 0) |
| [74] |
Ongaro F. Estimation of the effective properties of two-dimensional cellular materials: A review[J]. Theoretical and Applied Mechanics Letters, 2018, 8(4): 209-230. DOI:10.1016/j.taml.2018.04.010 (  0) 0) |
| [75] |
Ahmad S, Hakeem I, Azad A K. Effect of curing, fibre content and exposures on compressive strength and elasticity of UHPC[J]. Advances in Cement Research, 2015, 27(4): 233-239. DOI:10.1680/adcr.13.00090 (  0) 0) |
| [76] |
Ali S, Sama T, Behzad T. Effect of materials proportion on rheology and mechanical strength and microstructure of ultra-high performance concrete (UHPC)[J]. Construction and Building Materials, 2018, 187: 1103-1112. DOI:10.1016/j.conbuildmat.2018.08.070 (  0) 0) |
| [77] |
Park S H, Dong J K, Ryu G S, et al. Tensile behavior of ultra high performance hybrid fiber reinforced concrete[J]. Cement & Concrete Composites, 2012, 34(2): 172-184. (  0) 0) |
| [78] |
Bernard O, Ulm F J, Lemarchand E. A multiscale micromechanics-hydration model for the early-age elastic properties of cement-based materials[J]. Cement and Concrete Research, 2003, 33(9): 1293-1309. DOI:10.1016/S0008-8846(03)00039-5 (  0) 0) |
| [79] |
Sun C, Saffari P, Ranade R, et al. Finite element analysis of elastic property bounds of a composite with randomly distributed particles[J]. Composites Part A: Applied Science and Manufacturing, 2007, 38(1): 80-86. DOI:10.1016/j.compositesa.2006.01.010 (  0) 0) |
| [80] |
Su Y, Li J, Wu C, et al. Mesoscale study of steel fibre-reinforced ultra-high performance concrete under static and dynamic loads[J]. Materials & Design, 2017, 116: 340-351. (  0) 0) |
| [81] |
Borges D C, Pituba J J C. Analysis of quasi-brittle materials at mesoscopic level using homogenization model[J]. Advances in Concrete Construction, 2017, 5(3): 221-240. (  0) 0) |
| [82] |
Abbes F, Abbès B, Benkabou R, et al. A FEM multiscale homogenization procedure using nanoindentation for high performance concrete[J]. Journal of Applied and Computational Mechanics, 2020, 6(3): 493-504. (  0) 0) |
| [83] |
赵筠, 廉慧珍, 金建昌. 钢-混凝土复合的新模式—超高性能混凝土(UHPC/UHPFRC) 之三: 收缩与裂缝, 耐高温性能, 渗透性与耐久性, 设计指南[J]. 混凝土世界, 2013, 12: 60-71. Zhao Y, Lian H Z, Jin J C. A new mode of steel concrete composite—Ultra High Performance Concrete (UHPC/UHPFRC) part 3: Shrinkage and cracking, high temperature resistance, permeability and durability, design guidelines[J]. Concrete World, 2013, 12: 60-71. (  0) 0) |
| [84] |
Scheydt J, Muller H, Herold G. Long term behaviour of ultra-high performance concrete under the attack of chlorides and aggressive waters[J]. Procedia Technology, 2016, 22: 203-210. DOI:10.1016/j.protcy.2016.01.045 (  0) 0) |
| [85] |
Chuang T J, Lee S. Elastic flexure of bilayered beams subject to strain differentials[J]. Journal of Materials Research, 2000, 15(12): 2780-2788. DOI:10.1557/JMR.2000.0397 (  0) 0) |
| [86] |
Li Z X, Jiang F F, Tang Y Q. Multi-scale analyses on seismic damage and progressive failure of steel structures[J]. Finite Elements in Analysis and Design, 2012, 48(1): 1358-1369. DOI:10.1016/j.finel.2011.08.002 (  0) 0) |
 2023, Vol. 53
2023, Vol. 53