2. 海底科学与探测技术教育部重点实验室,山东 青岛 266100
反射地震勘探是油气勘探的主要方法之一,高信噪比和高分辨率的地震资料,是准确解释地层深部地质构造的必要条件之一。反褶积是提高地震资料分辨率最常用的方法,在高分辨率地震资料处理中起着至关重要的作用。
根据褶积模型,反射地震信号可以表示为地层反射系数和震源子波的褶积。由观测的反射地震信号推测地层反射系数,理想条件下,真实的地层反射系数可以得到恢复,然而实际勘探中,震源子波的带限的,这导致反褶积是一个不适定的反问题,直接求解难以得到稳定的反演结果。合适的正则化约束可以加强反问题求解的稳定性[1-2],基于地层的分层性质,只有较大的地层反射系数才影响反射地震信号,因此,反射系数在时间上是稀疏的,使用反射系数的稀疏性质作为正则化约束的反褶积方法即为稀疏反褶积[3-4]。基于反射系数的稀疏性质,Wang[5]建立了L1正则化反褶积模型,通过非单调梯度下降算法求解反射系数,然后采用递推方法求解地层的波阻抗剖面。Gholami和Sacchi[6]将反褶积问题转化为无约束优化问题,此优化问题采用Lp范数作为拟合项,L1范数作为正则化项,然后利用分裂Bregman法[7]求解,此方法在准确反演稀疏反射系数的同时,可以有效压制高斯和非高斯噪音。稀疏反褶积通常会导出一个Topelitz矩阵的线性系统[8],基于Topelitz矩阵的稀疏分解,Wang等[9]提出了一个多道稀疏脉冲反卷积方法,将震源子波和地层反射系数都作为反演对象,二者交替求解,从而达到同时反演震源子波和反射系数的目的,此方法缓解了传统方法中出现的空间不连续、信号受噪音影响、子波估计不准确等问题。反褶积问题的求解还需使用合适的最优化算法,如共轭梯度法[10],迭代阈值收缩法(ISTA)[11]等,最近,国内学者潘树林等[12]提出自适应步长的快速迭代阈值收缩法(FISTA)用于求解稀疏脉冲反褶积问题,FISTA算法[13]是在ISTA算法的基础上使用Nesterov[14-15]加速策略,使得算法具有超线性收敛速率。上述稀疏反褶积方法均属于正则化迭代方法,对反褶积问题施加稀疏正则化约束,降低反演结果的不稳定性,然后通过合适的优化算法迭代求解。求解过程通常需要反复迭代,每次迭代均需进行多次正演,因此,其计算代价较高。另外,正则化迭代方法还存在正则化参数选取困难的问题,正则化参数的作用是平衡拟合项和正则化项的权重,此参数的选取需进行多次试验,才能得到较合适的值。最后,正则化迭代方法的反演结果不精确,反演结果中较大的反射系数振幅有所损失,小的反射系数则难以得到恢复。
近几年,深度学习[16]方法因其强大的学习能力受到广泛关注,其中回归型深度神经网络在反问题的求解方面也取得了大量进展,如信号去噪[17],图像反卷积[18],图像重建[19]等。国内外学者已将深度学习推广到地球物理反演中。Kim和Nakata[20]以地震反射系数反演为例探讨了地球物理反演和机器学习之间的联系和区别。从数学的角度,二者的目标均为解决不适定的非线性反问题,且都需应用合适的优化算法。地球物理反演首先需要根据一定的物理规律建立反演模型,然后加入合理的先验假设降低反演问题的不适定性,最后利用优化算法求解。机器学习则属于数据驱动类方法,通过大量的数据训练,从数据中学习输入到输出的非线性关系,然后利用学习到的非线性关系对测试数据进行预测,从而达到求解反问题的目的。Yu等[21]利用DCNN对地震信号进行去噪,传统的信号去噪方法多是基于模型的,而DCNN则是数据驱动型方法,无需任何先验假设,经过训练的网络可以自适应的去除随机噪声、线性噪声、多次波等多种干扰噪音。然而上述工作使用的仍然是“黑盒式”的神经网络结构,网络的可解释性较差。近几年,对于反问题的求解,众多研究者开始关注深度学习网络与传统正则化迭代算法之间的关系,并由此构建高效的、可解释的深度神经网络。Gregor和LeCun[22]研究了ISTA算法和共享分层神经网络之间的相似性,并证明了多层神经网络可以作为一种快速的近似稀疏编码器。类似的,Jin等[23]提出一个深度卷积神经网络用于稀疏图像重建,并解释了此网络与传统迭代算法的关系。
受到上述研究工作的启发,针对传统正则化迭代算法存在的计算代价高,正则化参数难以选取,反演结果不精确等问题,本文构建一个深度卷积神经网络,用于地震反射信号的反褶积。首先使用训练数据集对此网络进行训练,使得其可以从数据中自动学得输入的地震反射信号与输出的地震反射系数之间的映射关系,然后利用训练好的网络对反射系数进行预测。所建网络融合了多尺度分解和残差学习[24]等技巧,提高了网络的表达能力。
1 方法原理 1.1 稀疏反褶积及ISTA算法由地震信号的褶积模型知,一道地震信号可表示为震源子波与反射系数的褶积,即
| $ d\left( t \right) = \omega \left( t \right) \times r\left( t \right) + n\left( t \right)。$ | (1) |
式中:d(t)为观测到的叠后地震信号;ω(t)为震源子波;n(t)表示噪声;×表示褶积运算。(1)式还可写成矩阵方程的形式,即
| $ d = \mathit{\boldsymbol{W}}r + n。$ | (2) |
式中:d∈RN;r∈RN和n∈RN分别表示d(t),r(t)和n(t)的离散采样;W∈RN×N为Toeplitz矩阵,且矩阵元素Wi, j=ωi-j+1;ωi-j+1是震源子波ω(t)的第i-j+1个采样点。反褶积即从观测到的反射地震信号d中推测反射系r。由于子波是带限的,由(2)式反演反射系数r是一个不适定的反问题,直接求解难以得到稳定的反演结果,因此引入合适的正则化约束是必要的。考虑到的反射系数的稀疏性质,引入L1正则化,可得反演反射系数的L1正则化模型如下
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{min}}{{\left\| r \right\|}_1},}\\ {s.t.Wr = d。{\rm{ }}} \end{array}} \right. $ | (3) |
其中
| $ \mathop {{\rm{min}}}\limits_r E\left( r \right) = \frac{1}{2}\left\| {Wr = d} \right\|_2^2 + \lambda {\left\| r \right\|_1}。$ | (4) |
上式中第一项通常称为拟合项,本文采用L2范数衡量拟合度,第二项为正则化项。(3)式或(4)式的求解可采用ISTA算法,ISTA为迭代优化算法,第k+1步的迭代格式为
| $ {r_{k + 1}} = {{\rm{T}}_{\lambda tk}}\left( {{r_k} - {t_k}{W^{\rm{T}}}\left( {W{r_k} - d} \right)} \right)。$ | (5) |
式中:
| $ {{\rm{T}}_\alpha }{\left( r \right)_i} = \left( {\left| {{r_i}} \right| - \alpha } \right) + {\rm{sgn}}\left( {{r_i}} \right)。$ |
sgn为符号函数。进一步的,(5)式可写为
| $ {r_{k + 1}} = {{\rm{T}}_\alpha }\left( {A{r_k} + Bd} \right)。$ | (6) |
式中:α=λtk;A=I-tkWΤW;B=tkWΤ。注意到,上式中正则化参数λ,步长tk均需人工选择,实际实验时,需反复尝试不同的数值;此外ISTA为迭代算法,需多次迭代才能最终得到最优解,计算代价较高。
1.2 深度卷积神经网络方法使用深度学习方法求解(4)式的基本思想是建立反射地震信号d和(4)式最优解r*之间的映射关系,其数学模型如下:
| $ {r^ * } = Net\left( {d, \theta } \right)。$ | (7) |
式中:r*=argminrE(r);Net表示神经网络的结构;θ为待学习的网络参数集合。网络通过极小化下式学习参数θ:
| $ \mathop {{\rm{min}}}\limits_\theta \frac{1}{{2N}}\sum\limits_{i = 1}^N {} \left\| {Net\left( {d, \theta } \right) - {r_i}^*} \right\|_2^2。$ | (8) |
其中
| $ Ne\:{t_{ir}}\left( {d;\theta } \right) = {\rm{ReLu}}\left( {\widetilde A \times d + \widetilde b} \right)。$ | (9) |
式中:
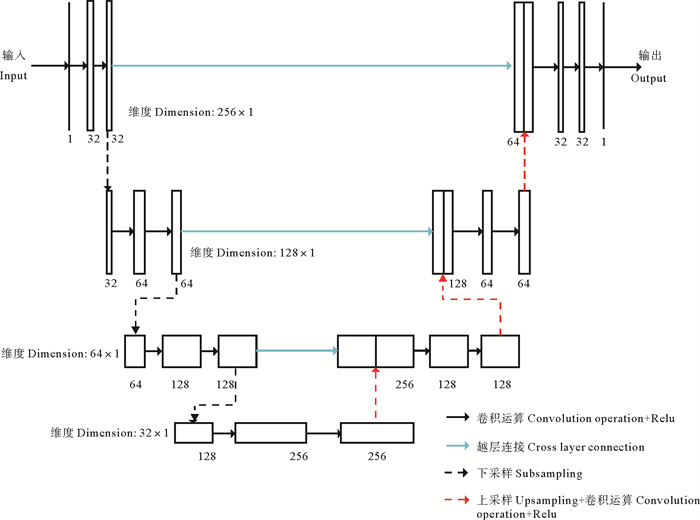
本文所建网络模型参考了U型网络[26]的结构(U型网络最初主要用于医学图像分割),网络结构呈对称形式,分为编码和解码两个部分。编码部分使用多个卷积核对输入地震信号提取不同的特征,并逐层增加卷积核的数量,这种多尺度分解方法是DCNN常用的方法。然后应用最大池化操作,降低输入数据的维度,提取主要特征,通过多次池化操作,原始数据将被映射到较低的维度,同时由于多个卷积核的作用,数据的主要特征即得到提取。解码部分与编码部分对称,使用上采样依次增加数据的维度,同时利用多个卷积核增加网络的表达能力。为避免网络训练时出现梯度弥散的问题,引入了残差学习,即将数据越层连接,网络实际学习的是输入与输出之差。所提网络模型的具体参数为:卷积核长度为5,步长为1,各层卷积核数量分别为32、64、128、256、128、64、32、1,最大池化长度为2,步长为1,网络结构的具体细节如图 1所示。
|
图 1 U型网络结构图 Fig. 1 U-net architecture |
数值实验包括两个方面,其分别使用模拟数据和实际数据,两部分实验均与ISTA方法对比。所有实验均在个人电脑上进行,电脑装配Intel i7-4790 CPU, 主频为3.60 GHz,内存为32 GB,GPU为NVIDIA GeForce GTX 1070。
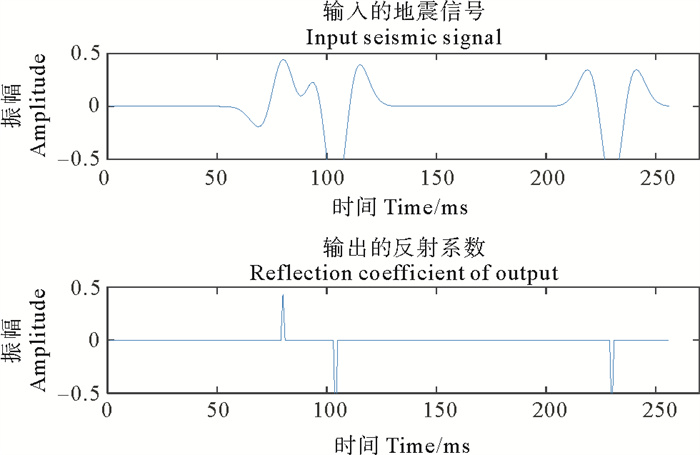
2.1 模拟实验模拟实验采用人工模拟的数据进行对比试验。使用DCNN方法进行反褶积之前,需要训练集对网络进行训练。训练数据由两部分组成,即地震信号和反射系数。离散反射系数长度为256,采样率为1 ms,于是可使用稀疏随机向量代替,向量中每个反射系数幅值范围为[-1, 1],位置是随机的。反射地震信号由反射系数和主频为35 Hz的Ricker子波褶积得到。为使网络得到充分训练,本文使用10 000组训练数据,1 000组测试数据用于测试DCNN方法的有效性,其中一组如图 2所示。网络结构已由上节给出,训练时,为防止网络出现过拟合现象,每层均舍弃20%的参数。为加快训练速度,每次输入64组数据,采用步长为1×e-4的Adam算法[27]进行训练,训练200次即终止。经训练后的网络即可用于地震信号的反褶积,反褶积结果的相对误差由下式给出
| $ Err = \frac{{\left\| {r - \bar r} \right\|}}{{\left\| {\bar r} \right\|}}。$ | (10) |
|
图 2 训练数据 Fig. 2 Training data |
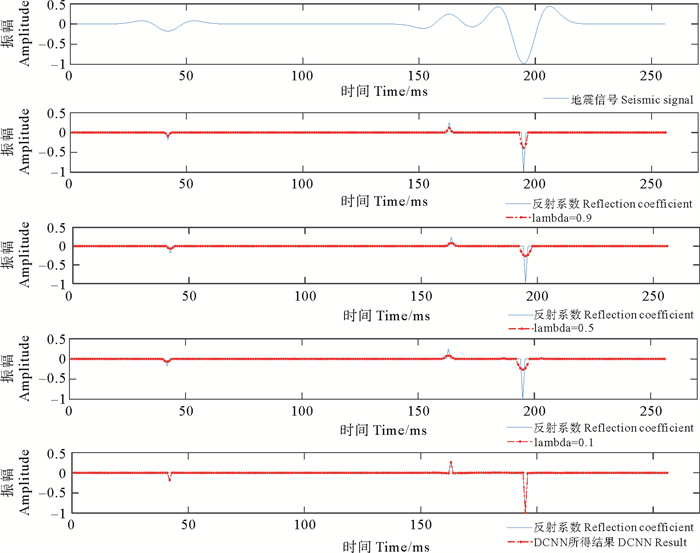
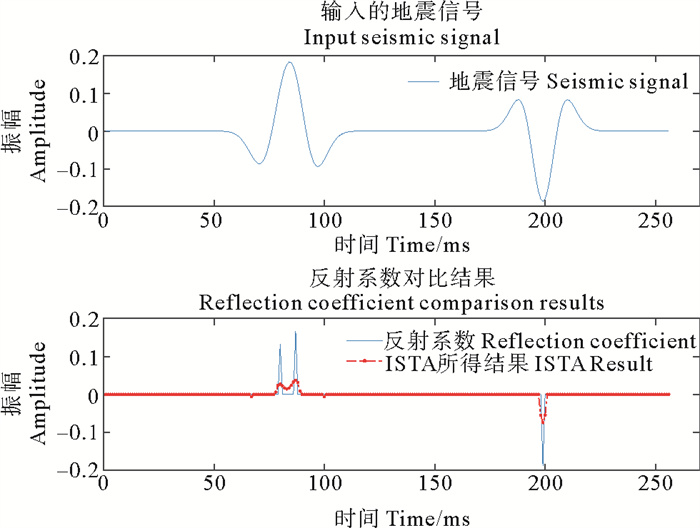
式中:r为算法求得的反褶积结果;r为真实反射系数。对于两种方法所得结果,相对误差越小,反演结果越好。对于测试数据,DCNN方法及与ISTA算法的反褶积结果如图 3所示,其中ISTA算法中的正则化参数分别取λ=0.9, 0.5, 0.1。计算可得三种情况下ISTA算法反演结果的相对误差分别为Err=0.718 2, 0.820 3, 0.821 4,而DCNN方法所得结果的相对误差则为Err=0.031 1。由图可知,ISTA和DCNN两种方法均可达到压缩子波的效果,然而ISTA方法的结果受到正则化参数λ的影响,实际使用时正则化参数的取值难以确定,此外,给定正则化参数后,ISTA所得结果的幅值损失较大,尤其对于振幅较大的情况。对于DCNN方法,此方法由数据驱动,无需建立数学模型,不受正则化参数的影响,且反演结果准确度更高。
|
图 3 ISTA及DCNN所得结果 Fig. 3 Results of ISTA and DCNN |
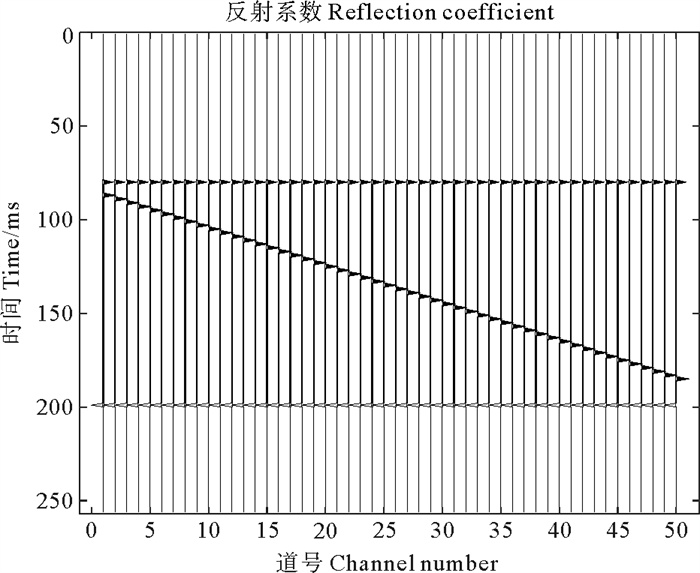
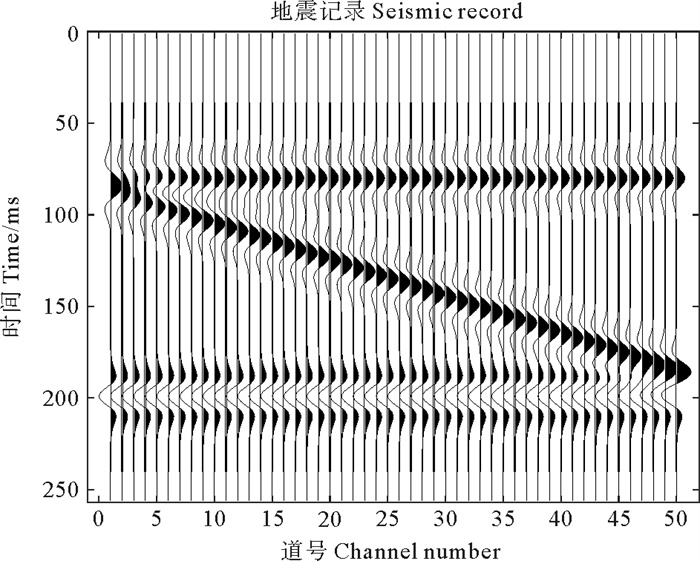
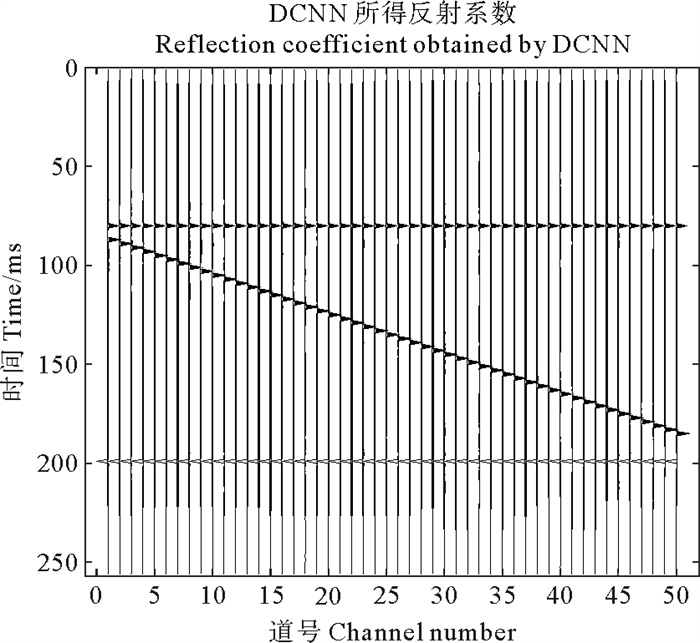
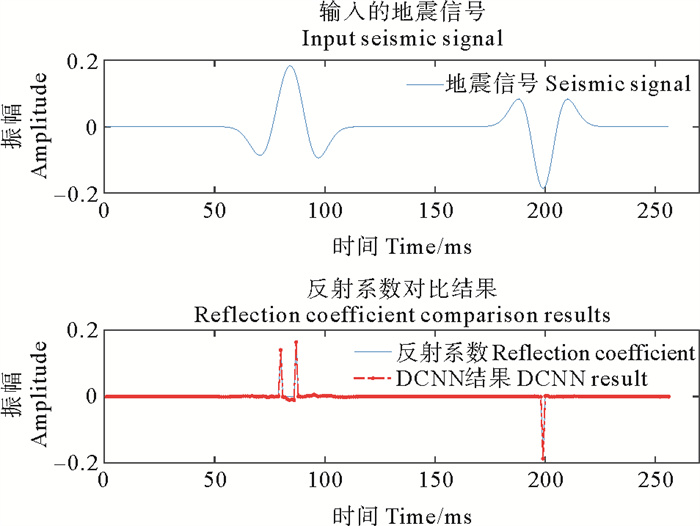
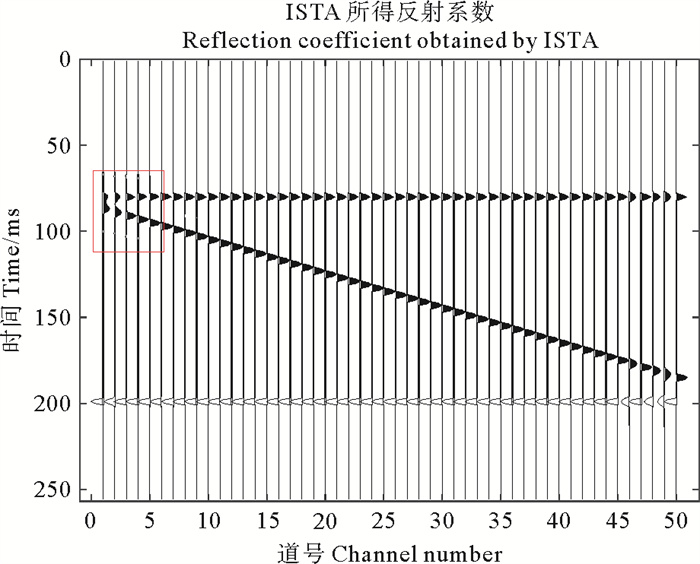
进一步的,为测试本文所提方法的有效性,设计一个四层的楔形模型,模型包含50道数据,采样率为1 ms,采样点数为256,如图 4所示。采用主频为35 Hz的Ricker子波与反射系数褶积得到地震记录,如图 5所示。反演时,使用训练好的深度卷积神经网络,将正演得到的地震记录作为输入,网络的输出即为反演得到的反射系数,如图 6所示,其相对误差Err=0.046 3。图 7对比了图 6中第一道反射系数与真实反射系数的差别,其相对误差Err=0.085 6。由图 6和图 7可知,DCNN方法反演得到的结果准确度较高,反射系数振幅真实反射系数振幅大小一致。作为对比,采用ISTA算法迭代求解(4)式,迭代格式由(5)式给出,取正则化参数λ=0.9。ISTA算法的反演结果分别由图 8、图 9给出,由图可知,ISTA算法可以压缩子波,反演反射系数的目的,然而由图 8可知ISTA算法对子波的压缩并不充分,图 8中楔形左上角处(即红色方框处)的反射系数未能得到正确的反演,其相对误差为Err=0.734 8,图 9亦显示了ISTA算法未能反演出相距较近的两个反射系数,且反射系数振幅损失较大,其相对误差为Err=0.798 0。综合对比图 4至图 9可知,ISTA方法反演的反射系数振幅损失较大,对于子波的压缩并不充分,并且不能有效分辨距离较近的两个反射系数,这使得楔形模型的左上角处出现了误差。而DCNN方法可以较准确的反演反射系数,即使相距较近的两个反射系数也能准确反演。
|
图 4 楔形模型 Fig. 4 Wedge model |
|
图 5 楔形模型的正演记录 Fig. 5 Forward modeling record of wedge model |
|
( 相对误差Err=0.046 3。Relative error Err=0.046 3. ) 图 6 DCNN所得反射系数 Fig. 6 Reflection coefficient obtained by DCNN |
|
( 相对误差Err=0.085 6。Relative error Err=0.085 6. ) 图 7 DCNN所得的单道反射系数 Fig. 7 Single channel reflection coefficient obtained by DCNN |
|
( 相对误差Err=0.734 8。Relative error Err=0.734 8. ) 图 8 ISTA所得反射系数 Fig. 8 Reflection coefficient obtained by ISTA |
|
图 9 ISTA所得的单道反射系数 Fig. 9 Single channel reflection coefficient obtained by ISTA |
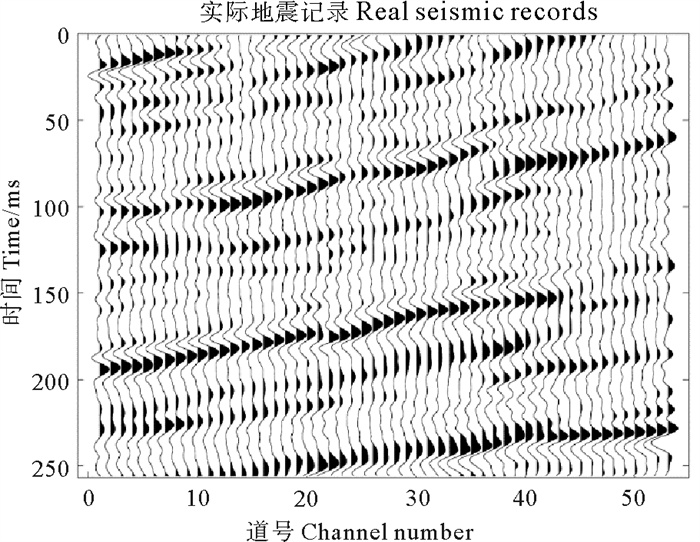
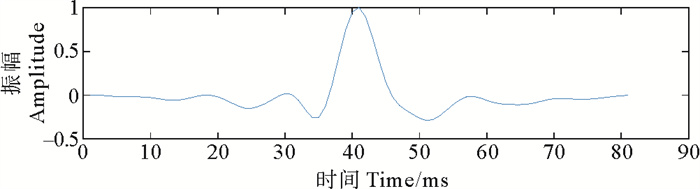
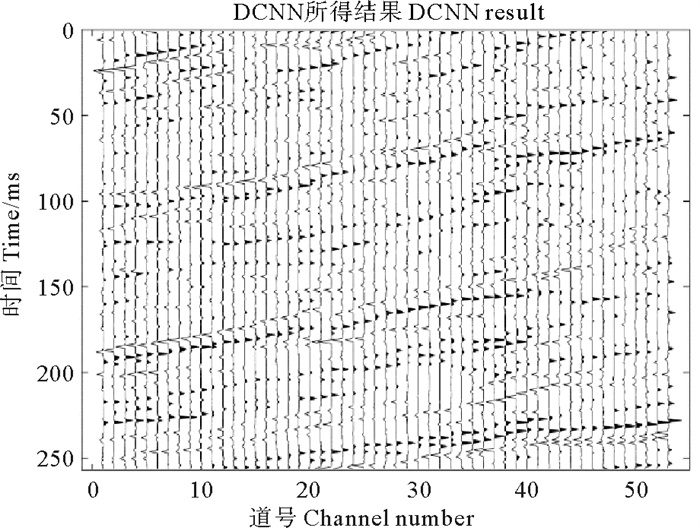
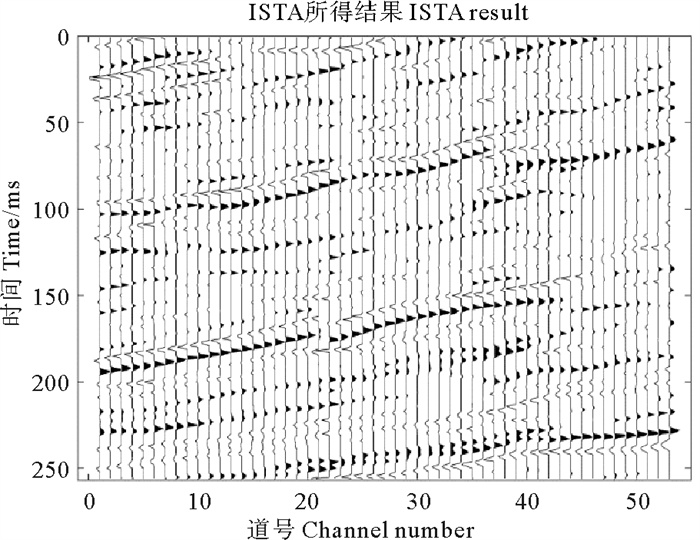
本部分实验采用实际数据检验所提方法的有效性。截取的某工区部分实际数据如图 10所示,此数据体包括53道地震反射信号,时间长度为256 ms,采样率为1 ms。利用统计方法估计的震源子波如图 11所示。得到震源子波后,使用随机产生反射系数序列与震源子波褶积得到模拟地震信号,由反射系数序列和模拟地震信号组成DCNN方法的训练数据集,训练输入为模拟地震信号,输出为反射系数序列。训练好的网络模型即可直接用于反褶积,结果如图 12所示,由图可知,相比地震数据剖面,反褶积得到的反射系数剖面中子波宽度得到压缩,分辨率较高,不仅大的反射系数得到恢复,较小的反射系数也被反演得到。作为对比,仍采用ISTA算法迭代求解(4)式,正则化参数λ=0.9时的计算结果如图 13所示,由图可知,相比地震数据剖面,反射系数剖面的分辨率有所提高,然而子波宽度未能得到充分压缩,且仅有较大的反射系数得到恢复,较小的反射系数并未出现。
|
图 10 实际地震数据 Fig. 10 Actual seismic data |
|
图 11 估计的子波 Fig. 11 Estimated wavelet |
|
图 12 DCNN方法的反褶积结果 Fig. 12 Deconvolution results of DCNN method |
|
图 13 ISTA算法的反褶积结果 Fig. 13 Deconvolution results of ISTA algorithm |
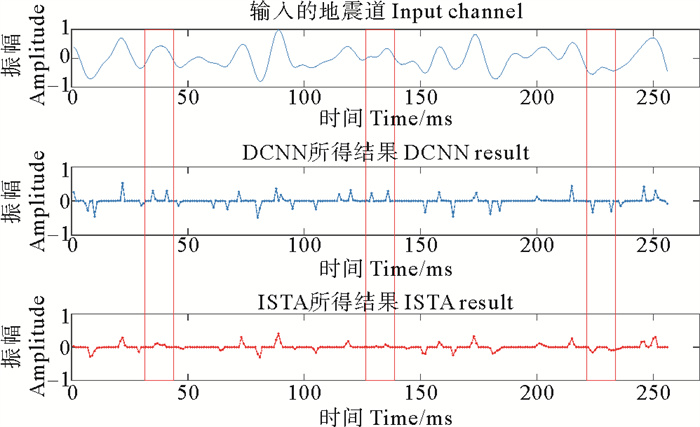
图 14给出了DCNN方法和ISTA方法反褶积结果的单道对比结果,两种方法均可以反演出较大振幅的反射系数,所得结果的主要差异由三个红色方框标记,三个红色方框中,DCNN方法可以较好的反演出距离较近的弱反射系数,而ISTA方法未能反演出反射系数。此外,相比DCNN方法所得结果,ISTA方法得到反射系数振幅损失较大。
|
图 14 DCNN和ISTA的反褶积结果对比 Fig. 14 Comparison of deconvolution results of DCNN and ISTA |
本文构建了一个DCNN模型,使用合适的训练集训练后,即可用于地震反射信号的反褶积。DCNN属于端到端的数据驱动方法,进行反演时,直接输入地震信号,输出即为反褶积结果。传统神经网络仅仅是建立了输入端到输出端的映射关系,网络结构的可解释性较差,本文阐述了所建的深度卷积神经网络模型与ISTA算法结构上的相似性,网络具有一定的可解释性。数值实验从模拟数据和实际数据两个方面验证了本文所提方法的有效性,与ISTA算法对比,DCNN方法所需时间少,反褶积结果更加准确,对于距离较近的弱振幅亦能较准确反演,反演得到的反射系数剖面分辨率更高。
| [1] |
王彦飞. 反演问题的计算方法及其应用[M]. 北京: 高等教育出版, 2007. Wang Y F. Inverse Problems in Geophysics and Solution Methods[M]. Beijing: Higher Education Press, 2007. (  0) 0) |
| [2] |
Tikhonov A N, Goncharsky A V, Stepanov V V, et al. Numerical Methods for the Solution of Ill-posed Problems[M]. USA: Springer Science & Business Media, 2013.
(  0) 0) |
| [3] |
朱振宇, 刘洪. 稀疏反褶积方法及其应用[J]. 中国石油大学学报(自然科学版), 2005, 29(6): 20-22. Zhu Z Y, Liu H. Sparse deconvolution method and its application[J]. Journal of the University of Petroleum, 2005, 29(6): 20-22. DOI:10.3321/j.issn:1000-5870.2005.06.005 (  0) 0) |
| [4] |
Latimer R B, Davidson R, Van Riel P. An interpreter's guide to understanding and working with seismic-derived acoustic impedance data[J]. The Leading Edge, 2000, 19(3): 242-256. DOI:10.1190/1.1438580
(  0) 0) |
| [5] |
Wang Y F. Seismic impedance inversion using l1-norm regularization and gradient descent methods[J]. Journal of Inverse and Ill-Posed Problems, 2010, 18(7): 823-838.
(  0) 0) |
| [6] |
Gholami A, Sacchi M D. A fast and automatic sparse deconvolution in the presence of outliers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 4105-4116. DOI:10.1109/TGRS.2012.2189777
(  0) 0) |
| [7] |
Goldstein T, Osher S. The split Bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343. DOI:10.1137/080725891
(  0) 0) |
| [8] |
刘喜武, 刘洪. 实现稀疏反褶积的预条件双共轭梯度法[J]. 物探化探计算技术, 2003, 25(3): 215-219. Liu X W, Liu H. The preconditional dual conjugate gradient algorithm for sparse deconvolution[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2003, 25(3): 215-219. DOI:10.3969/j.issn.1001-1749.2003.03.006 (  0) 0) |
| [9] |
Wang L, Zhao Q, Gao J, et al. Seismic sparse-spike deconvolution via Toeplitz-sparse matrix factorization[J]. Geophysics, 2016, 81(3): 169-182. DOI:10.1190/geo2015-0151.1
(  0) 0) |
| [10] |
崔岩, 王彦飞, 杨长春. 带先验知识的波阻抗反演正则化方法研究[J]. 地球物理学报, 2009, 52(8): 2135-2141. Cui Y, Wang Y F, Yang C C. Regularizing method with a prior knowledge for seismic impedance inversion[J]. Chinese Journal of Geophysics, 2009, 52(8): 2135-2141. DOI:10.3969/j.issn.0001-5733.2009.08.023 (  0) 0) |
| [11] |
Daubechies I, Defrise M, Mol C D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57: 1413-1457. DOI:10.1002/cpa.20042
(  0) 0) |
| [12] |
潘树林, 闫柯, 李凌云, 等. 自适应步长FISTA算法稀疏脉冲反褶积[J]. 石油地球物理勘探, 2019, 54(4): 737-743. Pan S. L, Yan K, Li L Y, et al. Sparse-spike deconvolution based on adaptive step FISTA algorithm[J]. Oil Geophysical Prospecting, 2019, 54(4): 737-743. (  0) 0) |
| [13] |
Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542
(  0) 0) |
| [14] |
Nesterov Y E. A method for solving the convex programming problem with convergence rate O (1/k.2)[J]. Soviet Mathematics Doklady, 1983, 27(2): 372-376.
(  0) 0) |
| [15] |
Nesterov Y. Gradient methods for minimizing composite functions[J]. Mathematical Programming, 2013, 140(1): 125-161. DOI:10.1007/s10107-012-0629-5
(  0) 0) |
| [16] |
LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521: 436-444. DOI:10.1038/nature14539
(  0) 0) |
| [17] |
Xie J, Xu L, Chen E. Image denoising and inpainting with deep neural networks[C]. Advances in Neural Information Processing Systems. [s. l. ]: Curran Associates Inc, 2012: 341-349.
(  0) 0) |
| [18] |
Xu L, Ren J S J, Liu C, et al. Deep convolutional neural network for image deconvolution[C]. Advances in Neural Information Processing Systems. [s. l. ]: Curran Associates Inc, 2014: 1790-1798.
(  0) 0) |
| [19] |
Kulkarni K, Lohit S, Turaga P, et al. ReconNet: Non-Iterative Reconstruction of Images from Compressively Sensed Measurements[C]. [s. l. ]: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016: 449-458.
(  0) 0) |
| [20] |
Kim Y, Nakata N. Geophysical inversion versus machine learning in inverse problems[J]. The Leading Edge, 2018, 37(12): 894-901. DOI:10.1190/tle37120894.1
(  0) 0) |
| [21] |
Yu S W, Ma J W, Wang W L. Deep learning for denoising[J]. Geophysics, 2019, 84(6): 333-350. DOI:10.1190/geo2018-0668.1
(  0) 0) |
| [22] |
Gregor K, Lecun Y. Learning Fast Approximations of Sparse Coding[C]. Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa: Omnipress, 2010: 399-406.
(  0) 0) |
| [23] |
Jin K H, McCann M T, Froustey E, et al. Deep convolutional neural network for inverse problems in imaging[J]. IEEE Transactions on Image Processing, 2017, 26(9): 4509-4522. DOI:10.1109/TIP.2017.2713099
(  0) 0) |
| [24] |
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]. [s. l. ]: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 770-778.
(  0) 0) |
| [25] |
LeCun Y A, Bottou L, Orr G B, et al. Efficient Backprop[M]. Berlin: Springer, 2012: 9-48.
(  0) 0) |
| [26] |
Ronneberger O, Fischer P, Brox T. U-net: Convolutional Networks for Biomedical Image Segmentation[C]. Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015. Berlin: Springer International Publishing, 2015: 234-241.
(  0) 0) |
| [27] |
Kingma DP,Ba J. Adam:A Method for Stochastic Optimization[C].Thaca:Cortribution to International Conference on LearningRepresentations,2015.
(  0) 0) |
2. The Key Laboratory of Submarine Geosciences and Prospecting, Ministry of Education, Qingdao 266100, China
 2021, Vol. 51
2021, Vol. 51


