钢悬链线立管(SCR)出现于1990年代中期, 由于成本相对较低以及对浮体升沉和漂移运动较好的顺应能力等特点而成为深水油气开发的首选立管形式[1]。随着油气资源勘测开发逐渐步入深海, 钢悬链线立管的设计、施工和安装方法已经成为油气勘探开发行业重要的技术问题。
钢悬链线立管(SCR)初始位形和初始内力分析是对其进行动力响应分析的基础, 当前国内外学者对SCR的静力位形的建模和求解等已进行了大量研究。Ghadimi[2]采用集中质量法建立立管模型, 对立管进行静态分析和动态分析, 并与实验结果对比分析, 表明该模型的合理性。O’Brien等[3]用类似悬链线索元确定了立管的平衡位形。Jain[4]用有限差分法对lazy-S型立管悬垂段部分进行了静力分析。Daniel等[5]基于悬链线位形附近小位移假设, 利用线性理论导出了平衡方程, 研究了在静力荷载作用下钢悬链线立管响应的分析方法。Chai等[6]考虑了悬链线立管的弯矩、扭矩、剪力, 提出了钢悬链线立管的三维集中质量公式。唐友刚等[7]采用集中质量法研究了深海平台系缆形状和张力分析方法, 指出需要考虑海底地形对系缆形状和张力的影响。Santillan等[8]基于几何-弯矩-曲率关系建立了立管平衡方程并采用有限差分法对陡峭型S立管和惰性S立管静力位形进行了数值模拟和实验对比。白兴兰等[9]基于大挠度柔性索理论, 采用具有弯曲刚度的细长梁模型模拟钢悬链线立管。李艳等[10]采用三维集中质量法, 建立了立管构型及张力的计算模型。
综上所述, 当前钢悬链线立管初始位形确定的方法主要有:根据悬链线方程建立钢悬链线立管模型, 忽略管道的弯曲刚度, 只考虑自重和浮力, 用有限元静力分析迭代求解获得立管的初始位形; 用集中质量法来模拟钢悬链线立管, 通过在节点之间增加伸长弹簧和旋转弹簧模拟立管的轴向及弯曲变形; 根据平衡原理对微元体列控制方程, 采用有限元法或有限差分法求解方程等。总之大都是通过各种结构动力学方法建立立管控制方程, 然后基于有限元方法或有限差分法等对控制方程进行数值求解, 控制方程和数值计算是彼此独立分离的概念。而对于复杂的立管几何构型来说控制方程的建立是一个及其复杂的过程, 而且一旦边界条件改变, 有可能需要重新建立计算模型。而基于向量式有限元(VFIFE)的分析方法是与上述方法截然不同的一种新型建模和数值计算方法。
由丁承先[11]教授提出的向量式有限元, 又称有限质点法, 以向量力学作为分析的理论基础, 并与数值计算结合, 是求解结构的大变形、大变位、弹塑性、碰撞、倒塌等非线性或不连续性力学行为的新方法[12]。向量式有限元基于结构的物理模式, 其计算步骤可概括为:将结构离散为满足牛顿第二定律的质点; 时间历程被分为一系列的途径单元; 在途经单元内, 采用虚拟的逆向运动, 通过单元的纯变形, 计算结构的内力; 采用中央差分的显示积分法求解运动公式。
本文基于向量式有限元提出了一种新的确定钢悬链线立管初始位形求解方案。基于该案方案将立管离散成一系列质点的集合, 质点间用只承受内力而无质量的弯曲杆件元连接, 采用牛顿第二定律来表达质点的运动行为, 并用中央差分的显式积分法求解质点各时刻的控制方程, 编制相应Matlab求解程序。分析了三种不同立管形式, 并与他人研究结果进行对比分析, 结果表明基于向量式有限元的位形求解方案是可行和正确的, 最后指出了向量式有限元法相较于传统有限元法存在的优势。
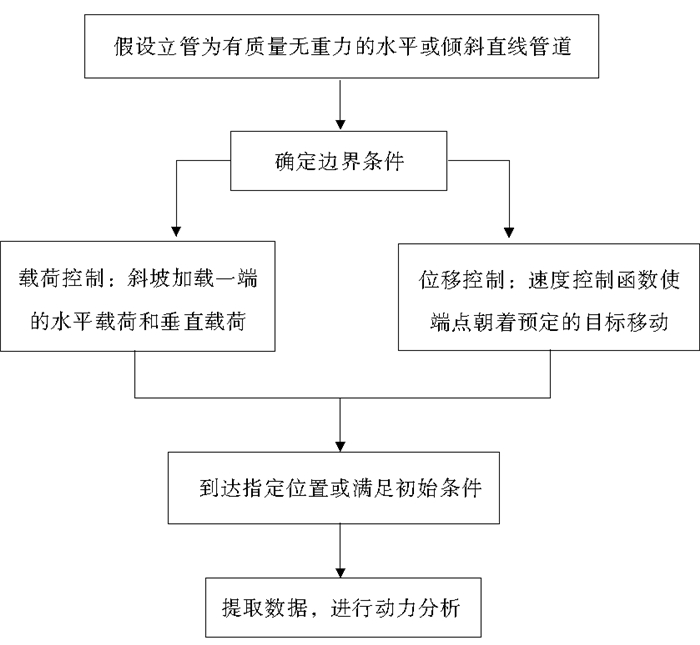
1 钢悬链线立管初始位形分析模型 1.1 初始位形建模方案要对立管展开静力和动力分析, 首先要确定立管的初始位形, 以初始形态作为计算位移、变形和应力等的基础架构。对于悬链线立管初始位形的确定可分为两类问题。一是初值问题:已知某一端的所有边界条件, 包括该端的位置坐标、张力的水平分量和竖直分量。二是边值问题:即两端的位置坐标均已知, 而其两端的张力分量均未知。本文采用如图 1所示方案解决立管的这两类问题。
|
图 1 向量式有限元法建模流程图 Fig. 1 Flow scheme for VFIFE |
基于上述方案, 假设立管在初始位置时是以一定角度倾斜的直管, 有质量且暂不考虑重力和浮力作用, 如图 1所示。确定立管整体坐标系, 坐标系定义如下:取立管底部为坐标原点, x轴与来流方向平行, y轴为水深方向, 向上为正, z轴垂直于x轴和y轴。
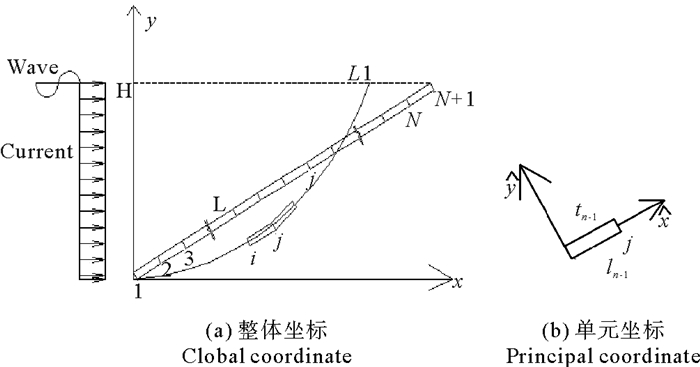
采用N+1(从底向上编号依次为1, 2, …, N, N+1)个等间距的质点模拟立管的直线状态, 质点之间利用平面弯曲杆单元相连接, 单元的质量平均分配到两端的质点上, 立管的初始张力通过单元的初始轴力来实现。立管底端铰接, 将N+1号质点在rtime时间内(假设位置到指定位置的模拟时间)水平运动到指定位置L1点, 同时在rtime时间内将重力和浮力以斜坡函数加载的方式作用在各质点上, 立管在重力、浮力与单元作用力下最终达到平衡状态, 即可得到如图 2(a)所示的钢悬链线立管的初始位形。
|
图 2 立管的变形及坐标示意图 Fig. 2 Diagram of the riser deformation and coordinate |
取一个标准途径单元tn-1≤t≤tn, 在时刻tn-1, 设立一组杆件元AB的主轴坐标(
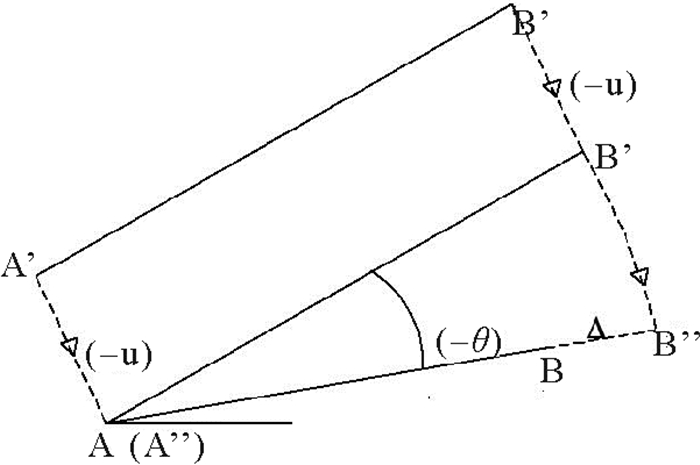
为获得单元节点的纯变形位移量, 可采用虚拟的逆向运动方法从单元节点全位移中得到刚体位移。刚体位移包括刚体平移和刚体转动, 本文只考虑平面内的情况。如图 3, 设定杆件在时刻的位置为, 称此形态为基础架构, 杆件两端点位置向量是(xAn-1, xBn-1),
| $ {单元长度} \;{l^{n - 1}} = \left| {x_B^{n - 1} - x_A^{n - 1}} \right| 。$ | (1) |
| $ {方向向量} \;\mathop {{e_x}}\limits^ \wedge = \left[{\begin{array}{*{20}{c}} {{l_1}}\\ {{m_1}} \end{array}} \right] = \mathop {e_x^{n - 1}}\limits^ \wedge = \frac{{\left( {x_B^{n - 1} - x_A^{n - 1}} \right)}}{{{l^{n - 1}}}} 。$ | (2) |
| $ \mathop {{e_y}}\limits^ \wedge = \mathop {e_y^{n- 1}}\limits^ \wedge = k \times \mathop {{e_x}}\limits^ \wedge = \left[{\begin{array}{*{20}{c}} {-{m_1}}\\ {{l_1}} \end{array}} \right] 。$ | (3) |
|
图 3 单元的逆向运动 Fig. 3 The retrogression of element |
在tn时刻运动到A′B′, 位置向量是(xAn, xBn), 单元长度ln=|xBn-xAn|, 方向向量
节点A的位移u1, 取杆件A′B′对参考元AB的转角Δθ为刚体转角
| $ {则:} \;\left\{ \begin{array}{l} {\Delta _e} = {l^n} - {l^{n - 1}}\\ {\theta _A} = {\theta _{A\prime }} + ( - \Delta \theta )\\ {\theta _B} = {\theta _{B\prime }} + ( - \Delta \theta ) \end{array} \right. 。$ | (4) |
以节点B为例, 先将节点B在tn-1时节点内力由域坐标分量转换成主轴分量, 取得
| $ \left[{\begin{array}{*{20}{c}} {\mathop {f_{Bx}^{n-1}}\limits^ \wedge }\\ {\mathop {f_{By}^{n-1}}\limits^ \wedge } \end{array}} \right] = \mathop Q\limits^ \wedge \left[{\begin{array}{*{20}{c}} {f_{Bx}^{n-1}}\\ {f_{By}^{n-1}} \end{array}} \right], \hat Q = \left[{\begin{array}{*{20}{c}} {\mathop {e_x^T}\limits^ \wedge }\\ {\mathop {e_y^T}\limits^ \wedge } \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{l_1}}&{{m_2}}\\ {-{m_1}}&{{l_1}} \end{array}} \right] 。$ | (5) |
单元B点的轴力:
将两个节点内力分量分别转换成域坐标分量,
| $ \begin{array}{l} {f_i}^n = \left[{\begin{array}{*{20}{c}} {{f_{ix}}^n}\\ {{f_{iy}}^n}\\ {{m_{iz}}^n} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{Q^{\rm{T}}}}&0\\ 0&1 \end{array}} \right]f = \\ \left[{\begin{array}{*{20}{c}} {{l_1}}&{-{m_1}}&0\\ {{m_1}}&{{l_1}}&0\\ 0&0&1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\mathop {{f_{ix}}^n}\limits^ \wedge }\\ {\mathop {{f_{iy}}^n}\limits^ \wedge }\\ {{m_{iz}}^n} \end{array}} \right]\;\;\;\;\;\;\;\;\left( {i = A, B} \right) \end{array} 。$ | (6) |
最后进行内力集成。
1.4 质点控制方程对于空间杆系结构, 质点有3个位移分量, 考虑阻尼的影响, 质点控制方程式为:
| $ \begin{array}{l} \left[{\begin{array}{*{20}{c}} {{m_i}}&0&0\\ 0&{{m_i}}&0\\ 0&0&{{I_i}} \end{array}} \right]\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{t^2}}}\left[{\begin{array}{*{20}{c}} {{x_i}}\\ {{y_i}}\\ {{\beta _i}} \end{array}} \right] = \\ \left[{\begin{array}{*{20}{c}} {{f_x}^{ext}}\\ {{f_y}^{ext}}\\ {{f_z}^{ext}} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {{f_x}^{{\rm{int}}}}\\ {{f_y}^{{\rm{int}}}}\\ {{f_z}^{{\rm{int}}}} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {{f_x}^{{dmp}}}\\ {{f_y}^{{dmp}}}\\ {{f_z}^{{dmp}}} \end{array}} \right] \end{array} 。$ | (7) |
其中:mi是质点i的质量, 包含质点i本身质量和相连单元的分配质量; Ii是其对z轴的质量惯性矩; βi是转角;
向量式有限元求解时采用中央差分的显示时间积分法, 这是为了避免隐式解法带来的复杂迭代和收敛问题。但为了计算的准确性, 必须控制时间步长h。
i质点的速度和加速度用i质点在n-1步, 第n步, 第n+1步的位移Χin-1、Χin、Χin+1以及h时间步长通过中央差分的显示时间积分法来表示, 并将其带入质点运动公式(8)中, 得到:
| $ \left\{ \begin{array}{l} {x_i}^{n + 1} = 2{C_1}{x_i}^n-{C_2}{x_i}^{n-1} + {C_1}{h^2}\left( {{f_{ix}}^{ext} + {f_{ix}}^{{\rm{int}}}} \right)/{m_i}\\ {y_i}^{n + 1} = 2{C_1}{y_i}^n-{C_2}{y_i}^{n - 1} + {C_1}{h^2}\left( {{f_{iy}}^{ext} + {f_{iy}}^{{\rm{int}}}} \right)/{m_i}\\ {\beta _i}^{n + 1} = 2{C_1}{\beta _i}^n - {C_2}{\beta _i}^{n - 1} + {C_1}{h^2}\left( {{m_{iz}}^{ext} + {m_{iz}}^{{\rm{int}}}} \right)/{I_i} \end{array} \right. 。$ | (8) |
其中C1=1/1+ζh/2;C2=C1(1-ζh/2)。
计算步骤可总结为:
首先, 由第n-1步和第n步的的位置向量xin-1、xin计算出第n+1步的位置向量xin+1;
然后, 根据xin+1计算该位置处各空间点上作用的内力;
之后, 用n步代替n-1步, 用n+1步代替n步, 更新位置向量, 重复上述步骤, 循环计算, 直到完成分析。
2 算例分析基于上述理论及计算方法, 本文编制相应的Matlab求解程序, 对钢悬链立管初始位形及内力进行分析, 为验证程序的可靠性, 本文选取三种立管进行计算。
选取的立管一为高秦岭[13]所采用的简单钢悬链线立管, 具体参数为:水深1 000 m, 长1 298 m, 外径0.274 m, 壁厚0.01 m, 海水密度为1 025 kg·m-3, 内部流体密度为1 000 kg·m-3, 立管管材密度7 850 kg·m-3, 弹性模量2.07 e11N·m-2; 本程序中rtime=450.0 s。
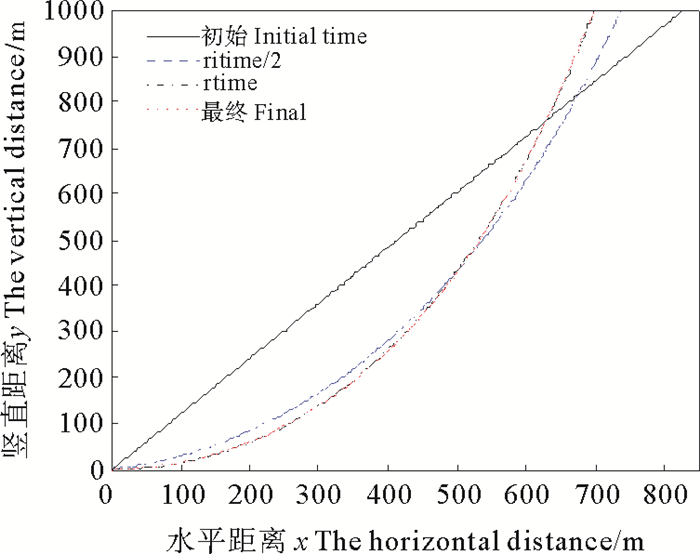
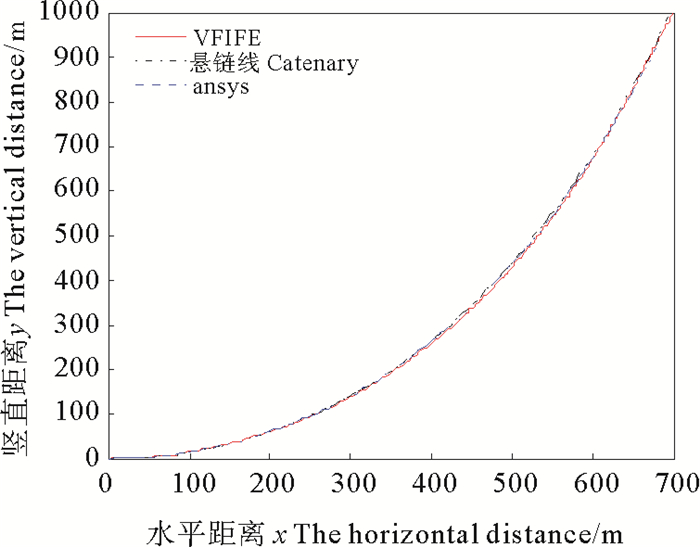
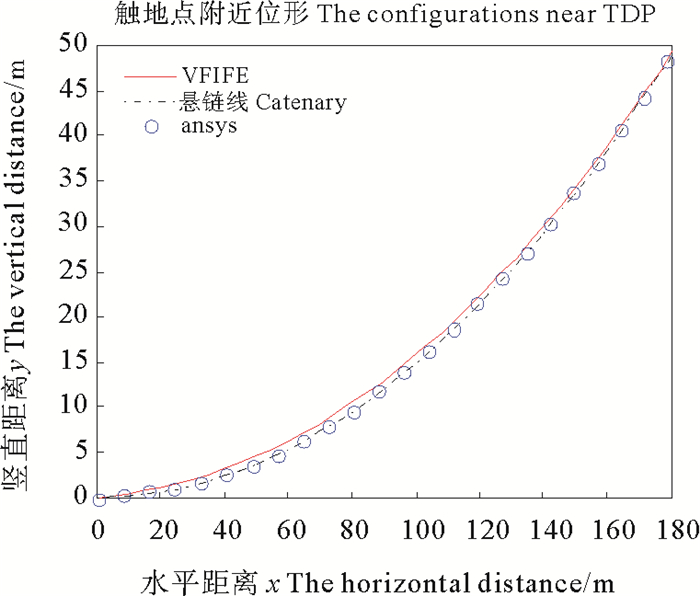
图 4绘制了立管一在初始时刻、rtime/2时刻、rtime时刻以及最终时刻的位形图, 显示了立管一从假设的虚拟斜直状态在重力和浮力等载荷作用下达到最终寻找的初始位形的形成过程。图 5是分别通过向量式有限元、经典悬链线方程以及Ansys软件分析计算出的立管一整体位形, 图 6是立管一在触地点附近的局部位形图。由图 5可看出向量式有限元法得出的整体位形与其他方法得出的结果相当吻合。从图 6可以看出三种方法得到的初始位形在触地点局部略有差异, 原因在于悬链线法忽略了弯曲刚度的影响, 文献[13]中通过设定位形判别条件, 一步步迭代, 使立管最终达到平衡状态即SCR立管的初始位形, 而采用向量式有限元计算时, 结构荷载可以在计算分析的初始步全部加在立管上, 立管在力的作用下形成初始位形, 向量式有限元是对立管的力学行为建立的模型, 位形的形成中不需要迭代求解, 所得结果相对精确。
|
图 4 不同时段立管一位形图 Fig. 4 The first riser's configuration at different times |
|
图 5 三种模型得到的立管一整体位形比较 Fig. 5 The configuration's comparison of three calculation models about the first riser |
|
图 6 三种模型在立管一触地点附近位形 Fig. 6 The configurations near TDP with three calculation models about the first riser |
本文立管二采用Chen[14]、Ghadimi[2]的长度为540 m的简单悬链线立管, 具体参数为:水平投影距离255 m, 竖直投影距离375 m, 外径0.276 6 m, 海水密度为1 025 kg·m-3, 立管干重102 kg·m-2, 轴向刚度3.27e8N, 抗弯刚度3.4e4N·m2; 本程序中rtime=550.0 s。
通过向量式有限元法、细长柔性杆模型[14]、理论计算和集中质量法[2]得到顶部张力分别为:163.535、166.6、165和167 kN, 误差不大于2.07%。得到的拖地段长度分别为:120、123.5、121.5和120 m, 误差不大于2.83%。
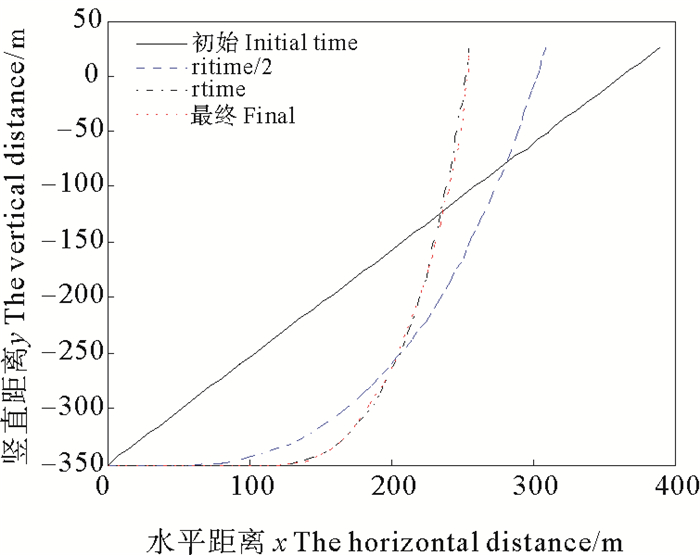
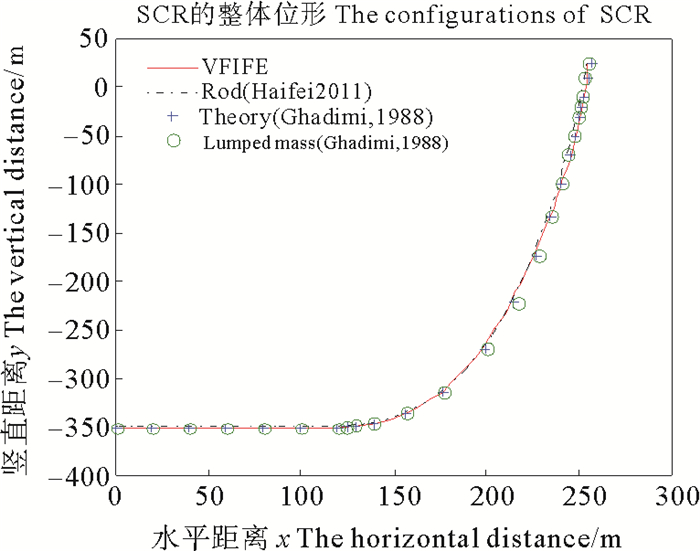
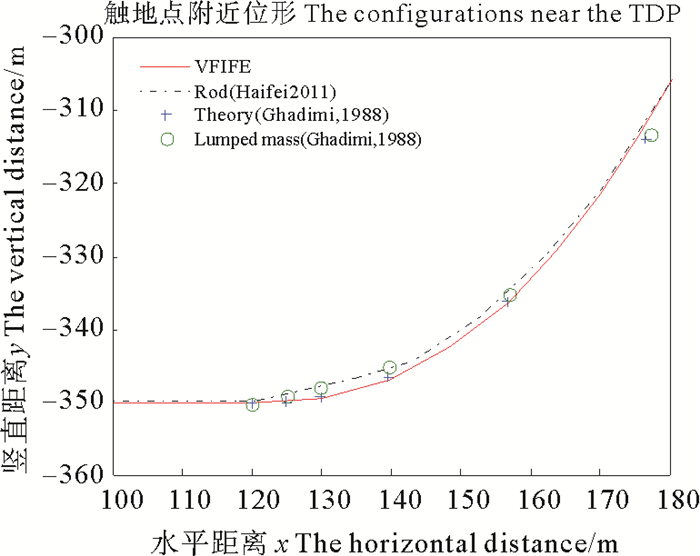
如图 7, 显示了立管二从假设的虚拟斜直立管在重力和浮力等载荷作用下达到初始位形的过程。图 8是分别通过向量式有限元法、细长柔性管模型[14]、理论计算和集中质量法[2]得到简单悬链线立管的整体位形, 由图可知四种方法得到的整体位形基本吻合。图 9是触地点附近局部位形, 从图中看出四种方法计算结果略有差异, 究其原因还是由于计算模型的差异所导致的, 集中质量法采用伸长弹簧和旋转弹簧分别模拟立管的轴向及弯曲变形, 而向量式有限元法采用质点及质点间的平面弯曲杆件模拟, 两者不同导致位形差异。
|
图 7 不同时段立管二位形 Fig. 7 The second riser′s configuration at different times |
|
图 8 四种模型得到的立管二整体位形比较 Fig. 8 The configuration's comparison of four calculation models about the second riser |
|
图 9 四种模型在立管二触地点附近位形 Fig. 9 The configurations near TDP with four calculation models about the second riser |
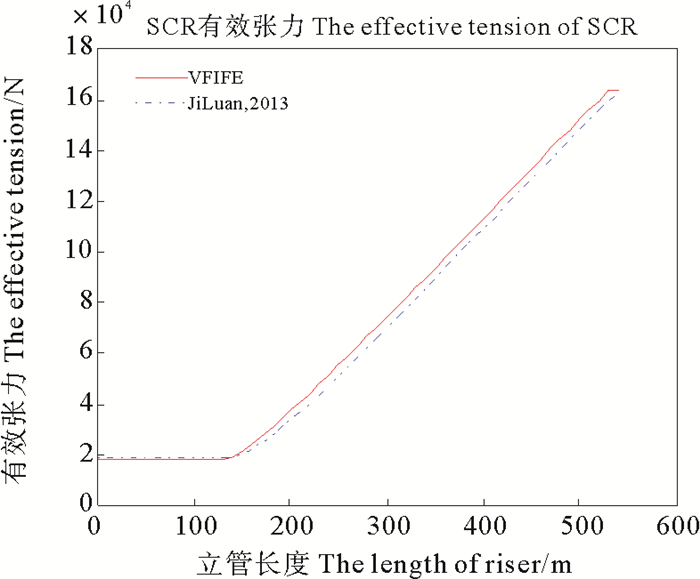
图 10绘制了540 m管道张力分布图, 与姬鸾[15]的结果比较可以看出两者差异很小。集中质量法是通过杆单元模拟单元节点, 用旋转弹簧-阻尼系统等效弯曲刚度, 并需要建立方程, 通过迭代求解; VFIFE使用的是梁单元, 用质点轨迹来模拟整体运动行为, 无需迭代求解。两者之间计算方式的不同造成计算结果有所差异。VFIFE是基于物理模型, 模拟立管的力学行为, 更符合实际受力情况。
|
图 10 两种计算模型得到的立管二张力比较 Fig. 10 The tension comparison of two calculation models about the second riser |
本文选取的立管三为Wang[16]所采用的缓波形钢悬链线立管, 具体参数为:水深1 850 m, 立管长度2 600 m, 悬垂段1 690 m, 浮子段520 m, 下降段390 m, 外径0.203 2 m, 壁厚0.019 1 m, 海水密度为1 024 kg·m-3, 内部流体密度为998 kg·m-3, 立管管材密度7 860 kg·m-3, 弹性模量2.06e11N·m-2; 本程序中rtime=2200.0 s。
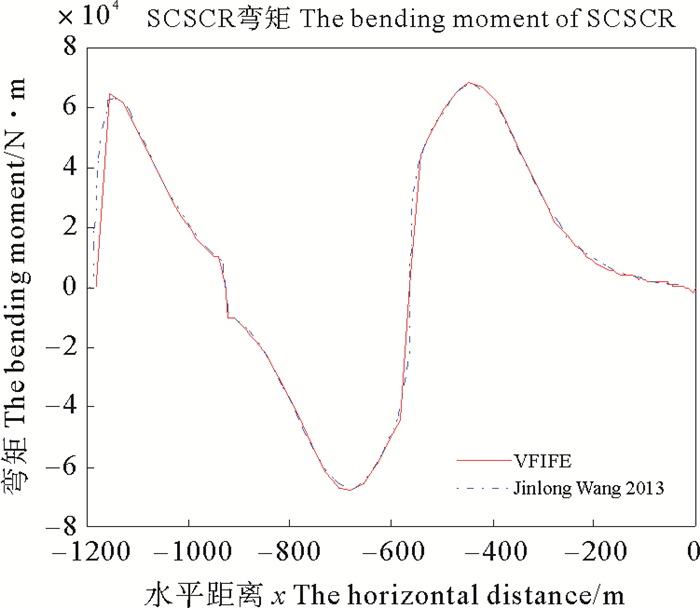
Wang[16]给出的数值计算和OrcaFlex计算得到的顶端张力分别是820.75、820.94 kN, 向量式有限元法得到的顶端张力为819.216 kN, 误差不大于0.21%。Wang[16]两种方法得到触地点处张力分别是75、75.056 kN, 向量式有限元法得到的结果是75.159 kN, 相比误差不大于0.212%。Wang[16]两种计算方法得到的最大弯矩分别是67.441、67.074 kN·m, 本文得到的最大弯矩为68.215 kN·m, 误差不大于1.70%。
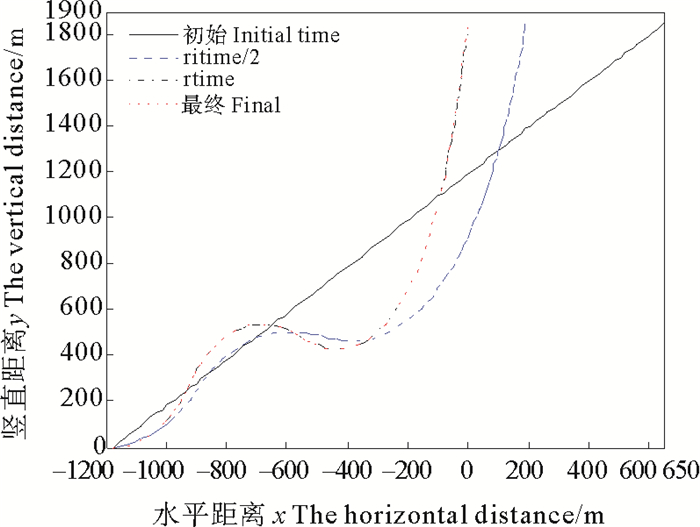
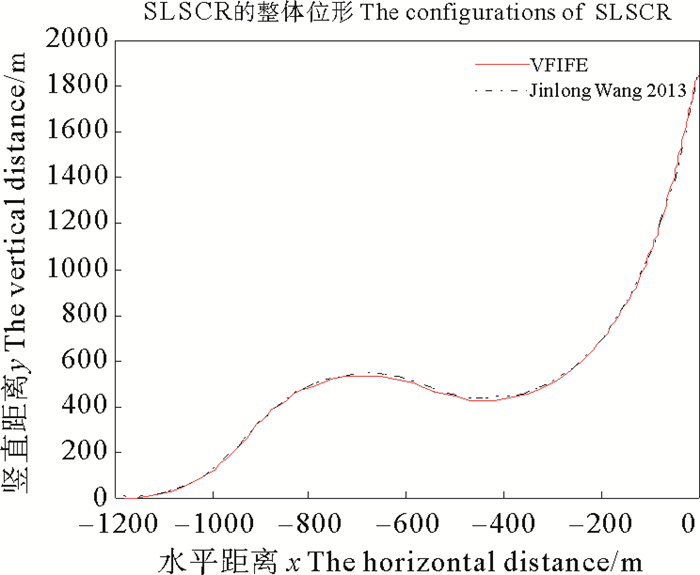
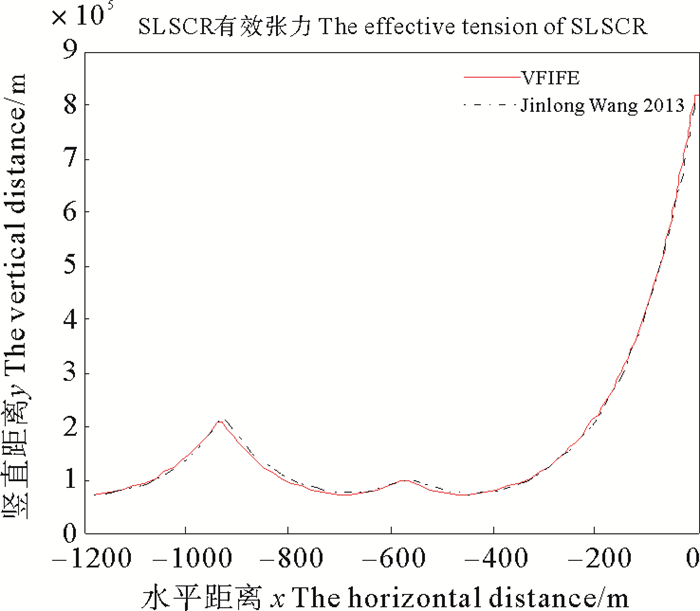
图 11显示的是立管三从假设的虚拟斜直立管在重力和浮力等载荷作用下达到初始位形的过程。图 12是通过向量式有限元法计算出的位形与Wang[16]给出的的位形比较图, 由图 12可看出向量式有限元法得出的位形图与其他方法得出的位形基本吻合。图 13和图 14分别是采用本文方法得到的缓波形立管的张力和弯矩, 与文献对比图。从图中可以看出结果相当吻合, 证明了向量式有限元法分析缓波形钢悬链线立管的可行性及正确性。
|
图 11 不同时段立管三位形 Fig. 11 The third riser′s configuration at different times |
|
图 12 四种模型得到的立管三整体位形比较 Fig. 12 The configuration′s comparison of four models about the third riser |
|
图 13 两种计算模型得到的立管三张力比较 Fig. 13 The tension comparison of two calculation models about the third riser |
|
图 14 两种计算模型得到的立管三弯矩比较 Fig. 14 The bending moment comparison of two calculation models about the third riser |
本文提出了一种确定钢悬链线立管初始位形新的求解方案, 基于向量式有限元对钢悬链线立管的整体位形和初始内力进行分析, 对比传统有限元分析过程和结果, 可以看出:
(1) 传统有限元方法基于变分原理, 需要由单元刚度矩阵集成为整体刚度矩阵, 计算过程中不容易增减单元和改变边界条件。向量式有限元采用的是物理模式, 对立管的力学行为建立计算理论, 计算中不需集成结构的刚度矩阵, 可方便更改单元和边界条件, 也不需迭代求解非线性方程组, 从而简化了立管分析的难度。
(2) 向量式有限元对立管的分析即使是初始静力位形分析都是动态的分析。不同于传统有限元方法的静态—动态分开分析, 向量式有限元分析初始时可以将荷载直接加载到立管上, 而且分析过程中可以任意改变荷载, 可以更好的模拟真实海洋环境下立管的运动, 使分析更加准确。
(3) 向量式有限元法计算程序更加简洁。向量式有限元法计算程序只存在质点位置计算和单元内力计算两个循环, 整体步骤呈系统化; 采用中央差分的显式时间积分求解, 避免了迭代和收敛问题, 从而使分析更加简洁。
结果表明, 基于向量式有限元法并采用本文提出的位形求解方案是完全可行的, 为悬链线立管初始位形和内力计算提供了一种条理清晰和高效的数学模型及可靠稳定的数值模拟方法。总之向量式有限元法在分析悬链线立管时具有很大的优势, 为进一步对各种形式的海洋立管复杂行为尤其是动力分析提供了一种新的可行的方法, 其结果亦可与其他求解方案对比分析以此保证立管服役期间的安全可靠运行。
| [1] |
黄维平, 李华军. 深水开发的新型立管系统—钢悬链线管(SCR)[J]. 中国海洋大学学报(自然科学版), 2006, 36(5): 775-780. Huang W P, LI H J. A new type of deepwater riser in offshore oil & gas production:the steel catenary riser(SCR)[J]. Periodical of Ocean University of China, 2006, 36(5): 775-780. (  0) 0) |
| [2] |
Rumbod G. A simple and efficient algorithm for the static and dynamic analysis of flexible marine Risers[J]. Computers and Structures, 1988, 29(4): 541-555. DOI:10.1016/0045-7949(88)90364-1
(  0) 0) |
| [3] |
O'Brien P J, McNamara J F. Significant characteristics of three-dimensional flexible riser analysis[J]. Engineering Structures, 1989, 11(4): 223-233. DOI:10.1016/0141-0296(89)90041-2
(  0) 0) |
| [4] |
Jain A K. Review of flexible risers and articulated storage systems[J]. Ocean Engineering, 1994, 21(8): 733-750. DOI:10.1016/0029-8018(94)90049-3
(  0) 0) |
| [5] |
Daniel A, Cedric L, David C.Analytical methods for predicting displacements and stresses in SCRs subjected to static loading[C].The Thirteenth International Offshore and Polar Engineering Conference(ISOPE2003): 2003, 70-75.
(  0) 0) |
| [6] |
Chai Y T, Varyani K S, Barltrop N D P. Three-dimensional lump-mass formulation of a catenary riser with bending, torsion and irregular seabed interaction effect[J]. Ocean Engineering, 2002, 29(12): 1503-1525. DOI:10.1016/S0029-8018(01)00087-7
(  0) 0) |
| [7] |
唐友刚, 易丛, 张素侠. 深海平台系缆形状和张力分析[J]. 海洋工程, 2007, 25(2): 9-14. Tang Y G, Yi C, Zhang S X. Analysis of cable shape and cable tension for platforms in deep sea[J]. The Ocean Engineering, 2007, 25(2): 9-14. (  0) 0) |
| [8] |
Santillan S T, Virgin L N. Numerical and experimental analysis of the static behavior of highly deformed risers[J]. Ocean Engineering, 2011, 38(13): 1397-1402. DOI:10.1016/j.oceaneng.2011.06.009
(  0) 0) |
| [9] |
白兴兰, 黄维平. 深水钢悬链线立管非线性有限元静力分析[J]. 工程力学, 2011, 28(4): 208-213. Bai X L, Huang W P. Static analysis of the deep steel catenary riser using nonlinear finite element method[J]. Engineering Mechanics, 2011, 28(4): 208-213. (  0) 0) |
| [10] |
李艳, 李欣. 深水钢悬链线立管非线性动力分析[J]. 船舶工程, 2013, 35(6): 106-111. LI Y, LI X. Nonlinear dynamic analysis of the steel catenary riser(SCR)[J]. Ship Engineering, 2013, 35(6): 106-111. (  0) 0) |
| [11] |
Edward C T, Chiang S, Yeon-Kang W.Fundamentals of a vector intrinsic finite element: Part1.Basic procedure and a plane frame element[J].Journal of Mechanics, 2004, 20(2): 113-122.
(  0) 0) |
| [12] |
丁承先, 段元锋, 吴东岳. 向量式结构力学[M]. 北京: 科学出版社, 2012. Ting E C, Duan Y F, Wu D Y. Vector Mechanics of Structures[M]. Beijing: Science Press, 2012. (  0) 0) |
| [13] |
高秦岭.钢悬链线立管的ANSYS非线性有限元分析[D].青岛: 中国海洋大学, 2011. GAO Q L.Nonlinear Finite Element Analysis by ANSYS for Steel Catenary Risers[D].Qingdao: Shandong: Ocean University of China, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1829759 (  0) 0) |
| [14] |
Chen H F, XU S P, GUO H Y. Nonlinear analysis of flexible and steel catenary risers with internal flow and seabed interaction effects[J]. Journal of Marine Science and Application, 2011, 10(2): 156-162. DOI:10.1007/s11804-011-1055-4
(  0) 0) |
| [15] |
姬鸾.柔性立管静态构型分析及防弯器设计[D].大连: 大连理工大学, 2013. JI L.Flexible Riser Static Configuration Analysisi and Bend Stiffener Design[D].Dalian: Dalian University of Technology, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2416776 (  0) 0) |
| [16] |
Wang J L, Duan M L, He T, et al. Numerical solutions for nonlinear large deformation behavior of deepwater steel lazy-wave riser[J]. Ships and Offshore Structures, 2014, 6(9): 655-668.
(  0) 0) |
 2018, Vol. 48
2018, Vol. 48

