2. 哈尔滨工程大学水下机器人技术重点实验室,黑龙江 哈尔滨 150001
随着海洋发展战略的实施及“一带一路”战略的推进,我国海洋科技取得了长足发展。为提高海洋资源勘查、油气矿产资源开发与利用等领域的水下作业水平,实现海洋资源开发装备的工程化和产业化,必须加强与之相关的高新技术,如水下作业装备的研究。其中,动密封件[1-2]作为水下作业装备的重要组成部分,旨在避免工作介质的泄漏以及外部海水的入侵。直线动密封作为一种水下作业装备的密封形式,其性能决定着系统的能耗特性、可靠性及寿命等。因此,有必要对其力学特性进行研究。
为了改善密封性能,国内外的学者对动密封性能展开了一系列的研究,如德国的Robert Bosch GmbH公司[3]利用有限元分析软件ABAQUS,建立了橡胶的超弹性和粘弹性材料模型,验证了O形圈密封面混合润滑理论的准确性;亚琛工业大学[4]运用自主研发的往复式液压杆件动密封特性试验台,对四种不同密封圈(斯特封、格莱圈、PU化合物密封圈、一种组合密封圈)在不同工况(不同压力(25~100 bar)、不同油温(30~70 ℃)、不同电机频率(2.8~12.5 Hz)、不同运动速度(0~10 m/s))下的直线动密封性能进行了试验研究,得出聚四氟乙烯和O型密封圈组成的组合密封和PU化合物密封件具有润滑性好、启动摩擦力小等优点,更适合动密封;阿拉巴马汉茨维尔大学[5]利用有限元分析软件ABAQUS,建立了O型密封圈的仿真模型,分析了O型密封圈在不同压缩率下密封圈载荷变化情况,得出O型密封圈的载荷速率随压缩率的增加而逐渐减小;清华大学[6-7]利用有限元分析软件ABAQUS,建立了丁腈橡胶O形圈的轴对称模型,对丁腈橡胶O形圈的静密封和微动密封性能进行了仿真与试验研究。研究结果表明:当O形圈用于静密封且压力≥6 MPa时,可以通过添加挡圈来避免剪切失效,以此提高其工作压力;用于微动密封时,O形圈所受的摩擦力随压缩率的增加而增大;武汉工程大学[8]利用有限元分析软件ANSYS,建立了格莱圈有限元分析模型,分析了不同工况下格莱圈密封面接触压力的分布情况,得出格莱圈密封面的最大接触压力随压缩率和气体压力的增加逐渐增大;浙江大学[9]利用有限元分析软件ANSYS,对航空液压作动器往复密封进行建模和仿真研究,从密封材料、密封机理、材料磨损失效和疲劳失效四个层面对其密封理论进行了阐述和分析,得出增大压缩率能有效提高密封性,但会带来动作迟缓、寿命降低等问题。此外,中北大学[10]、北京航空航天大学[11]、江苏大学[12]等高校也对密封圈的动密封性能进行了相关研究。
从上述研究可看出,第一,密封圈工作条件多为单侧受压,未考虑密封圈两侧受压情况,此与深海工况不符。因为水下作业装备工作时,密封圈为双侧受压;第二,密封介质多数是液压油,而以水为工作介质的研究少,且多数只进行了仿真研究,缺少试验论证。
在密封圈单侧受压的研究基础上,以格莱圈为研究对象,建立了直线动密封的二维轴对称模型,搭建了直线动密封特性试验平台,对格莱圈的直线动密封特性诸如预压缩率及工作压力对最大米塞斯应力的影响,工作压力及运动速度对摩擦力的影响等进行了仿真和试验研究。
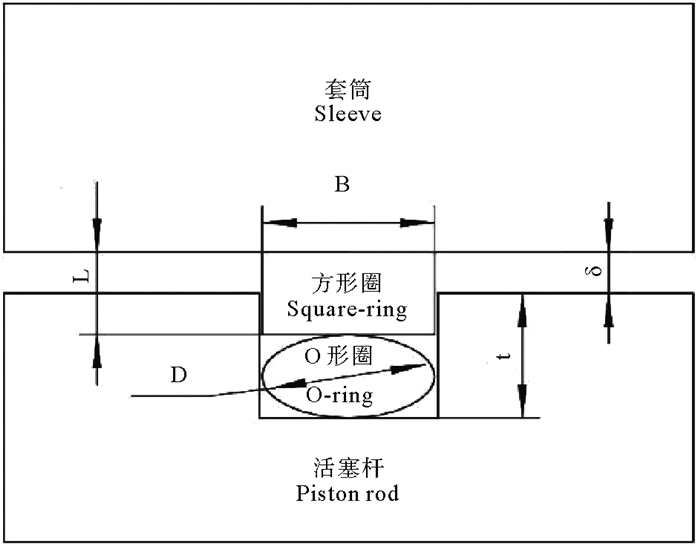
1 模型建立 1.1 物理模型直线动密封物理模型见图 1,选用格莱圈(即由一个填充PTFE方形密封圈和一个O形橡胶圈组合而成,适用于液压往复运动双向压力密封,其中O形圈提供径向施力,并对密封圈的磨损进行补偿。具有压力稳定性好、寿命高、低摩擦以及起动阻力小、运动平稳,动静摩擦力相等的特点,且可以用于水等低粘度介质的密封)为研究对象,其具体规格为RC11-Q-8 mm×12.9 mm×2.2 mm,尺寸参数如表 1所示。
|
图 1 直线动密封模型 Fig. 1 Model of linear motion seal |
|
|
表 1 格莱圈尺寸参数 Table 1 Glyd-ring size parameter |
格莱圈的O形圈为丁腈橡胶(NBR)材料,属于不可压缩的超弹性体[13],用应变能密度函数Mooney-Rivlin模型来描述,其应变能密度函数模型[14]为:
| $ W = \sum\limits_{i, j}^N {{C_{ij}}{{\left( {{I_1} - 3} \right)}^i}{{\left( {{I_2} - 3} \right)}^j}} + \sum\limits_{k = 1}^N {\frac{1}{{{d_k}}}} {\left( {J - 1} \right)^{2k}}。$ | (1) |
式中:W为应变能函数;Cij、dk为常数,通过材料测定实验确定;对于不可压缩材料J=1。
简化其应变能函数,采用二参数Mooney-Rivlin模型描述,其函数为:
| $ W = {C_{10}}\left( {{I_1} - 3} \right) + {C_{01}}\left( {{I_2} - 3} \right)。$ | (2) |
式中:W为应变能密度,J/m3;C10、C01为材料的Mooney-Rivlin系数;I1、I2为第一、第二张量不变量,J/m3。
综上分析,穆尼常数取C10=1.87,C01=0.47。方形圈的材料为聚四氟乙烯PTFE,套筒的材料为铝青铜QAL9-4,活塞杆的材料为不锈钢316L,O形圈的摩擦系数为0.3,方形圈的摩擦系数为0.05,各个材料属性参数如表 2所示。
|
|
表 2 材料属性参数 Table 2 Material property parameters |
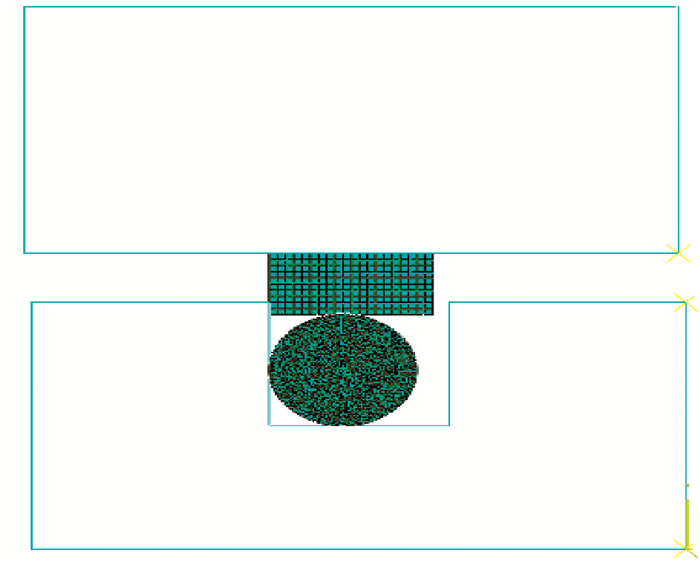
鉴于格莱圈的轴对称结构,将其简化为二维轴对称模型,在分析格莱圈的接触问题时,采用罚单元进行描述,方向为各向同性。为提高计算精度,细化了O形圈和方形圈的网格,网格模型如图 2所示。
|
图 2 直线动密封网格模型 Fig. 2 Grid model of linear motion seal |
考虑到实际情况及仿真的可行性,在误差允许范围内,作如下假设[15]:
(1) 聚四氟乙烯和NBR密封圈各向同性、均匀连续且完全弹性。
(2) 在仿真过程中忽略因摩擦造成的温度变化和磨损情况。
(3) 活塞杆和套筒材料的刚度是格莱圈刚度的数万倍,故可以忽略它们的形变,即在仿真分析时将其定义为解析刚体,不作任何处理。
(4) 格莱圈的预压缩率视为由活塞杆约束边界的位移引起的。
在上述基础上,设置三个分析步:第一步对格莱圈施加一定的预压缩率,即设定活塞杆Y轴方向的位移;第二步对格莱圈两侧分别施加一定的工作压力;第三步对活塞杆施加一定的往复运动速度。
仿真过程中,设定预压缩率为13%、15%、17%和19%,分析预压缩率对最大米塞斯应力分布的影响;设定预压缩率为17%,活塞杆运动速度为0.2 m/s,工作压力从0开始,以2 MPa为步差递增至10 MPa,分析工作压力对格莱圈单/双侧最大米塞斯应力分布的影响。
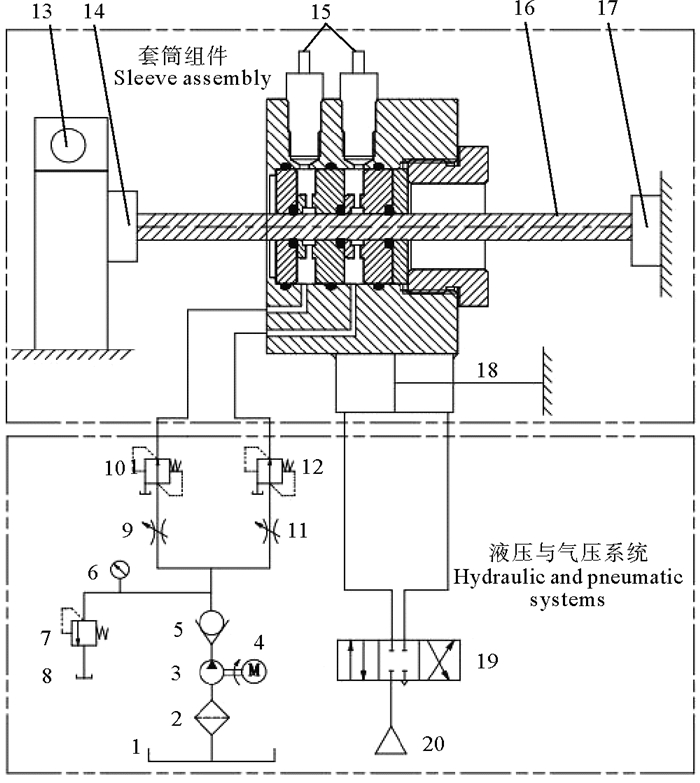
1.3 试验平台直线动密封摩擦特性试验原理图,如图 4所示,试验台实物如图 3所示。该试验台主要由活塞杆、套筒组件、密封圈、传感器(位移传感器、拉压力传感器、压力传感器)、气缸及壳体等组成。并将试验部分分为两个腔体,实现了密封圈在不同工况下摩擦特性的测定。
|
(1, 8.水箱(Water tank);2.过滤器(Filter);3.水液压泵(Water hydraulic pump);4.电机(Motor);5.单向阀(Check valve);6.压力表(Pressure gauge);7.溢流阀(Regulating valve);9, 11.节流阀(Choke valve);10, 12.定值减压阀(Fixed pressure reducing valve);13.位移传感器(Fixed pressure reducing valve);14, 17.拉压力传感器(Pull pressure sensor) 15.压力传感器(Pressure Sensor);16.活塞杆(Piston rod);18.气缸(Cylinder);19.三位四通换向阀(Three-position four-way reversing valve);20.气泵(Air pump).) 图 4 直线动密封摩擦特性试验原理图 Fig. 4 The working principle of linear motion seal friction characteristic test |

|
图 3 试验台实物图 Fig. 3 The photo of test bench |
试验时,(1)由水液压泵3泵出水,经单向阀5分别流向两个容腔;(2)定值减压阀10、12控制两个容腔的压力,节流阀9、11控制回路中的流量;(3)气泵20为气缸18提供气压源,使套筒组件实现往复直线运动;(4)两个容腔内水压力大小由压力传感器15测得,活塞杆16的速度由位移传感器13测得,密封圈所受摩擦力大小由拉压力传感器14、17测得;(5)最后通过试验台数据采集系统得到运动速度,并将速度、压力和摩擦力信号进行存储和处理。
1.4 试验研究向已排出空气的两个容腔注满水;启动气泵,待气泵压力稳定在0.3 MPa后,气缸开始动作,各个传感器正常工作,动密封特性试验台数据采集系统中示数显示正常,试运行几个周期。
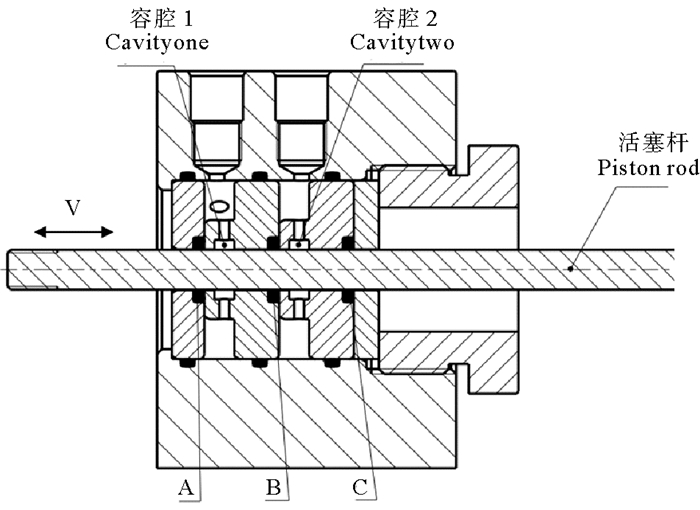
套筒组件格莱圈安装位置为A、B、C,如图 5所示,格莱圈受压情况结果分析如下:
|
图 5 格莱圈安装图 Fig. 5 Installation diagram of Glyd-ring |
(1) 格莱圈单侧受压力情况
在A、C处安装格莱圈,B处不安装格莱圈,容腔1、2相通。设定往复速度为一定值,记录两个容腔内水压力Pa为0~10 MPa时,拉压力传感器示数F1,此时获得的数据F1为两个格莱圈所受摩擦力,因此格莱圈在单侧受压力时摩擦力Fa1=F1/2。
调节容腔内水压力为定值,通过气泵压力控制往复速度大小,分别记录速度V为0~0.5 m/s时,拉压力传感器示数F2。同理,格莱圈单侧受压力的摩擦力Fa2=F2/2。
(2) 格莱圈两侧受相同压力情况
在A、B、C三处安装格莱圈,容腔1、2不相通。设定往复速度为一定值,调节容腔1、2的压力Pb(0~10 MPa)相同,记录拉压力传感器示数F3,对比情况a,得到格莱圈所受摩擦力Fb=F3-F1。
(3) 格莱圈两侧受不同压力情况
在A、B、C三处安装格莱圈,容腔1、2不相通。设定往复速度为一定值,调节容腔1中水的压力为一定值,当容腔2的压力Pc从0开始,以2 MPa为步差递增至10 MPa时,记录拉压力传感器示数F4。调节容腔1的压力与情况a中两个容腔的压力相同时,记录拉压力传感器示数F5。对比情况a,得到格莱圈所受摩擦力Fc=F4-F1-F5/2。
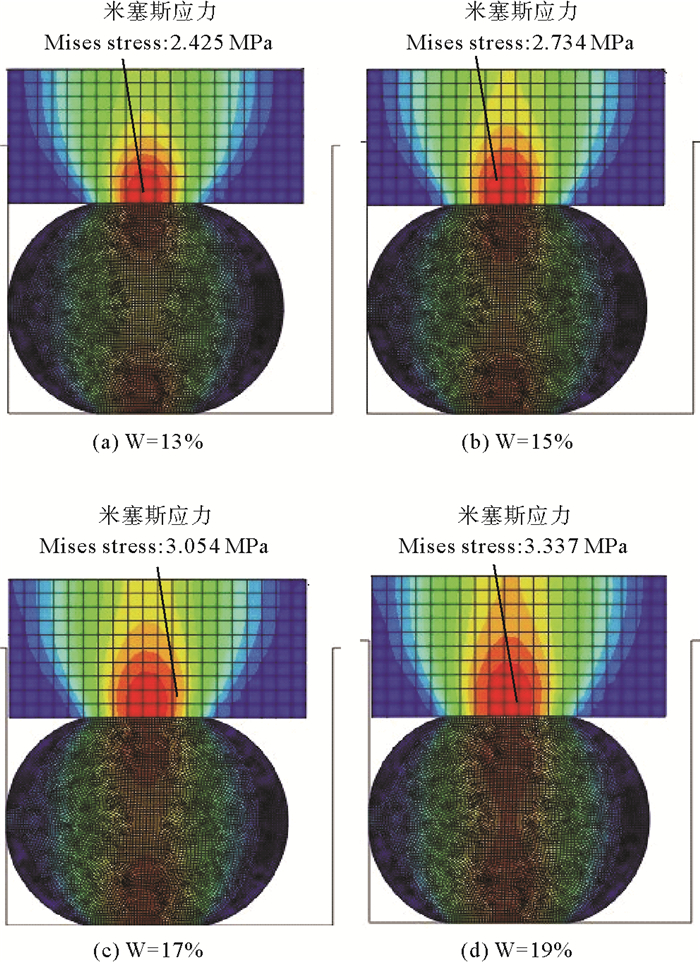
2 结果分析 2.1 预压缩率对最大米塞斯应力的影响图 6是格莱圈在不同预压缩率的条件下,最大米塞斯应力的分布情况,从图 6中可以看出:
|
图 6 不同预压缩率时格莱圈的最大米塞斯应力分布 Fig. 6 Maximum Von Mises stress distribution of the Glyd-ring with different pre-compression ratio |
(1) 在压力和速度载荷为零的工况下,当预压缩率W=13%时,格莱圈的最大米塞斯应力为2.425 MPa;当预压缩率递增至W=19%时,格莱圈的最大米塞斯应力增加至3.377 MPa。
(2) 格莱圈最大米塞斯应力位于方形圈与O形圈接触面,并随着预压缩率的增加而增大。而米塞斯应力越大,会加速密封材料的松弛,易出现裂纹,最终导致密封失效。故保证形成良好密封的前提下,适当减小预压缩率可以提高格莱圈的密封性能。
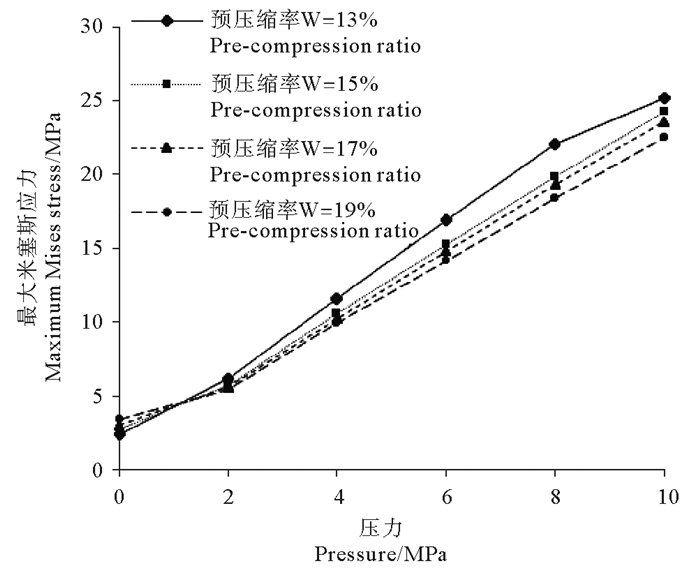
在上述基础上,设置活塞杆运动速度为0.2 m/s,并分别施加0 ~10 MPa的工作压力,得到不同预压缩率时,格莱圈的最大米塞斯应力与工作压力的关系曲线,如图 7所示。从图 7中可以看出,在工作压力和速度载荷不为零的工况下,格莱圈的最大米塞斯应力随着预压缩率的增加而减小,对比图 6可以看出压力对于格莱圈的米塞斯应力影响较大;在预压缩率一定的条件下,其最大米塞斯应力随着压力的增加而增大;其预压缩率W=17%的最大米塞斯应力随压力的增加变化趋势相对平稳,说明此预压缩率时,密封效果较好,将其确定为最优预压缩率。
|
图 7 格莱圈所受最大米塞斯应力与压力的关系 Fig. 7 Relationship between the maximum Von Mises stress and pressure in the Glyd-ring |
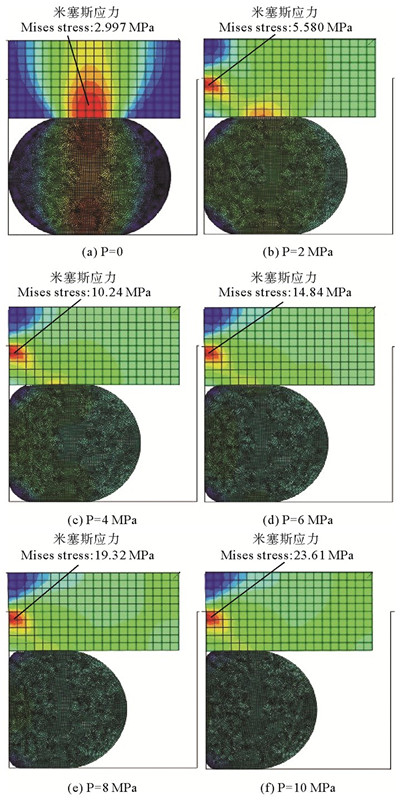
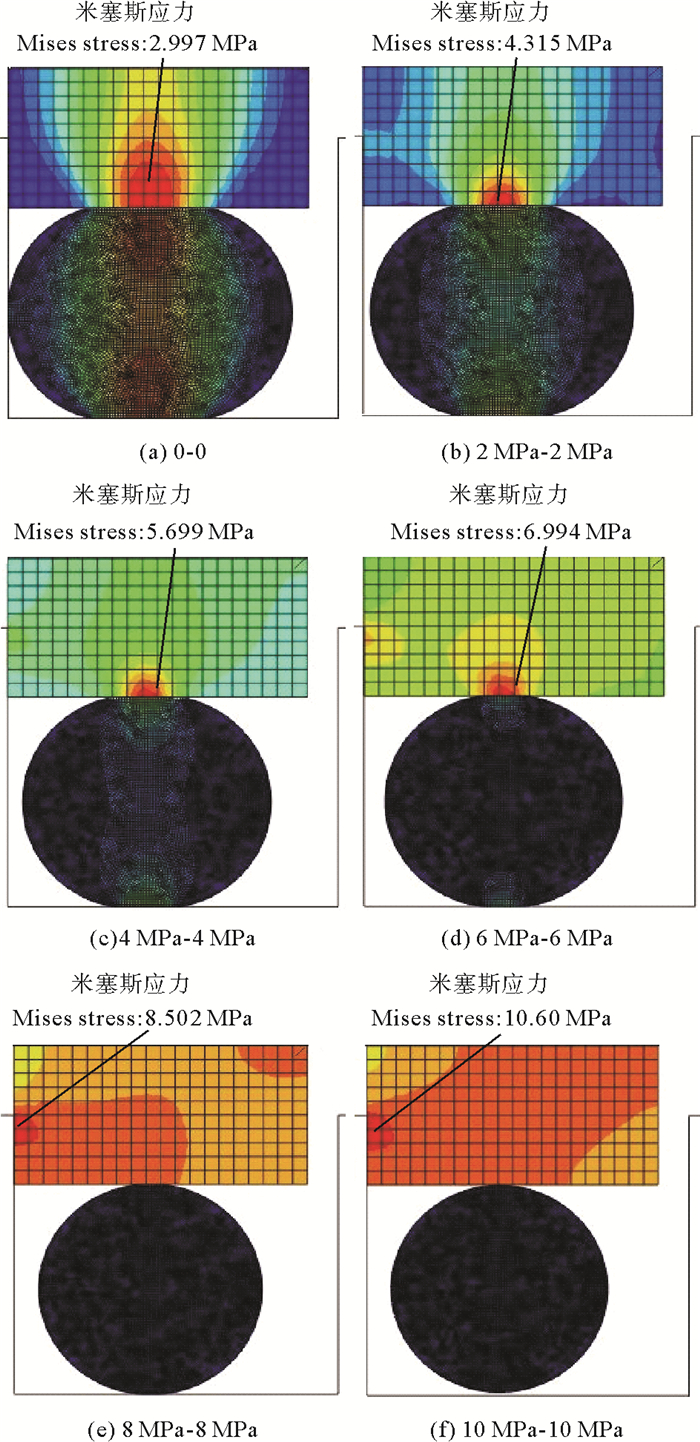
图 8~10分别是格莱圈在单侧受压、两侧受同压、两侧受不同压的条件下,最大米塞斯应力的分布情况。
|
图 8 单侧受压时格莱圈的最大米塞斯应力分布 Fig. 8 Maximum Mises stress distribution of the Glyd-ring under one side with pressures |
|
图 9 两侧受相同压力时格莱圈的最大米塞斯应力分布 Fig. 9 Maximum Von Mises stress distribution of the Glyd-ring under the same pressure on both sides |
|
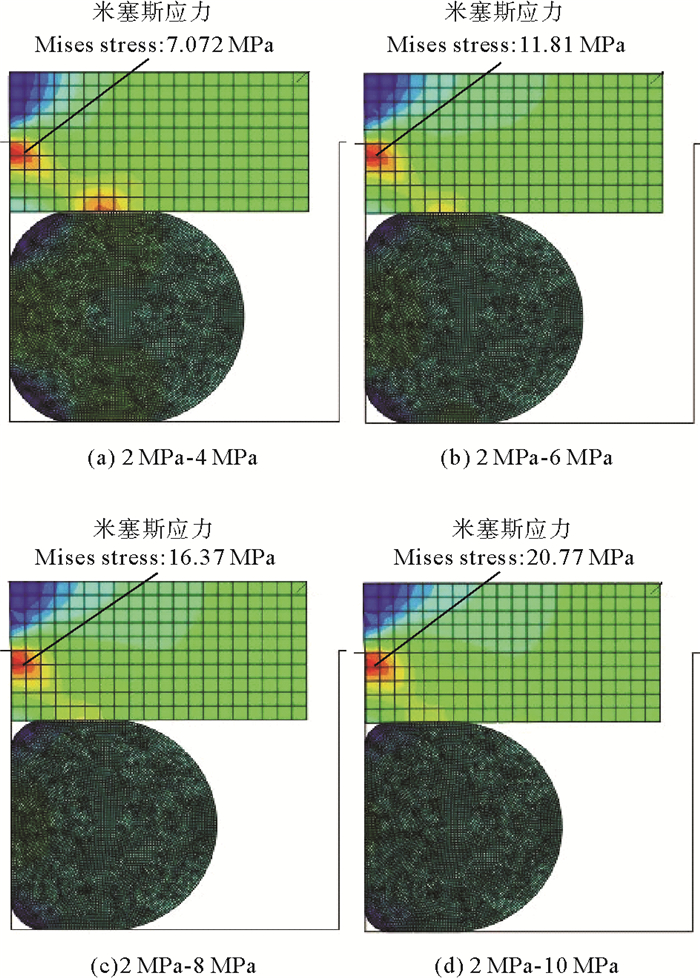
图 10 两侧受不同压力时格莱圈的最大米塞斯应力分布 Fig. 10 Maximum Von Mises stress distribution of the Glyd-ring under different pressures on both sides |
(1) 当格莱圈单侧受压和两侧受不同压时,方形圈和沟槽接触面米塞斯应力分布较集中,为格莱圈最易失效位置。这是因为沟槽拐角处不连续,易造成较大的局部应力集中,因此,可以对沟槽进行适当的倒角处理来减小局部应力集中,提高格莱圈的密封效果。
(2) 当格莱圈两侧受相同压力时,压力低于6 MPa时,方形圈与O形圈的接触面米塞斯应力分布较集中,为其最易失效位置;压力高于6 MPa时,方形圈和沟槽接触面米塞斯应力分布较集中,为格莱圈最易失效位置。
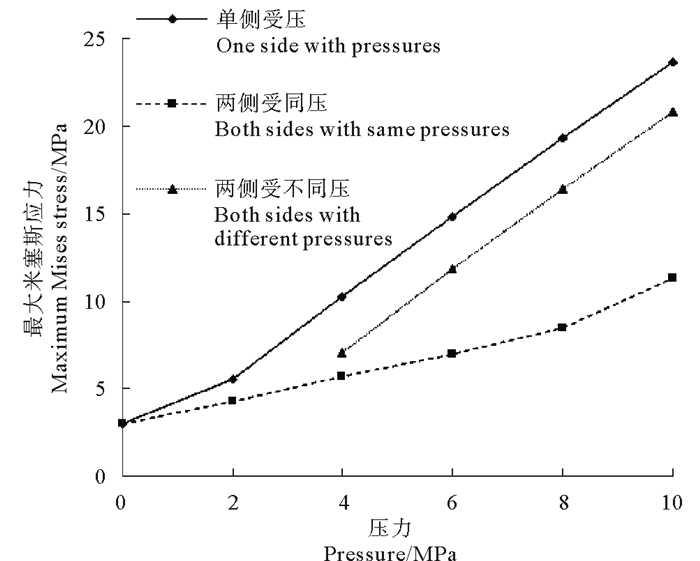
图 11给出了三种受压条件下,格莱圈最大米塞斯应力与工作压力的关系曲线,从图 11可以看出,格莱圈最大米塞斯应力随工作压力的增加逐渐增大,且近似成线性关系;两侧受压时格莱圈的最大米塞斯应力均小于单侧受压时的工况。
|
图 11 格莱圈最大米塞斯应力与压力的关系 Fig. 11 Relationship between maximum Von Mises stress and pressure in the Glyd-ring |
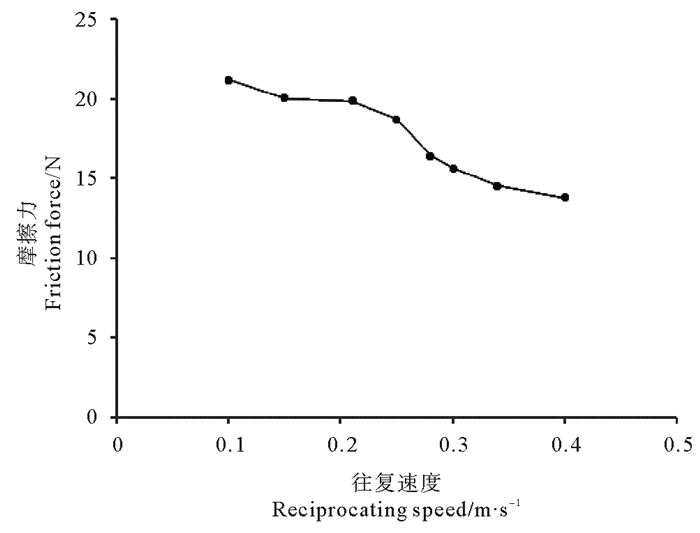
图 12是在格莱圈两侧施加不同压力(一侧受压为1 MPa,另一侧受压为2 MPa)的条件下,格莱圈所受摩擦力与往复速度的关系曲线,从图 12中可以看出:
|
图 12 格莱圈所受摩擦力与往复速度的关系 Fig. 12 Relationship between the friction force and the reciprocating speed of the Glyd-ring |
(1) 当速度为0.1 m/s时,格莱圈所受摩擦力为21.2 N;当速度逐渐递增至0.4 m/s时,摩擦力减小为13.81 N。
(2) 当压力一定时,格莱圈所受摩擦力随往复速度的增加逐渐减小,且变化趋势逐渐缩小。摩擦力越小,则密封圈与活塞杆之间的水膜厚度将会增加,从而使润滑效果更好。
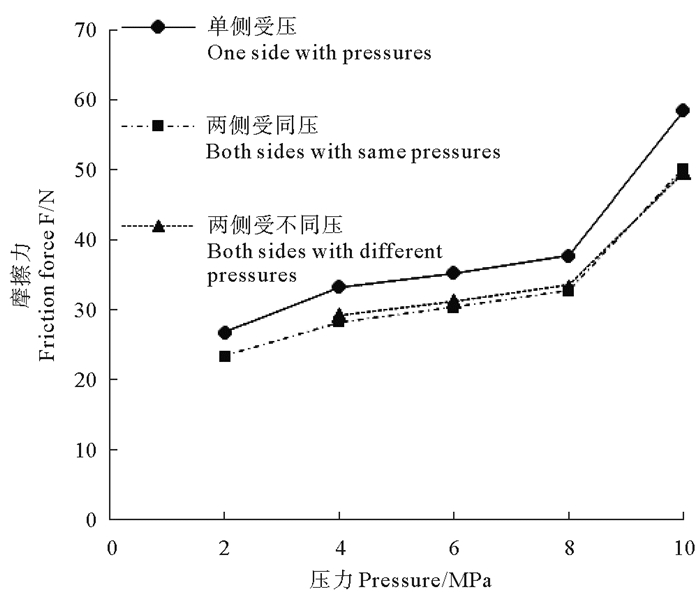
2.4 定速变压对摩擦力的影响图 13是格莱圈在两侧施加不同压力(一侧为2 MPa,另一侧为2~10 MPa)且密封效果良好的条件下,格莱圈摩擦力与工作压力的关系曲线。
|
图 13 格莱圈所受摩擦力与压力的关系 Fig. 13 Relationship between the friction force and the pressure of the Glyd-ring |
从图 13中可以看出,当往复速度一定时,格莱圈所受的摩擦力随工作压力的增加逐渐增大;当压力高于8 MPa时,变化趋势更加明显。此外,格莱圈两侧受压时的摩擦力均小于单侧受压时工况。这是因为格莱圈所受摩擦力与接触面积,压缩力及摩擦系数有关。当摩擦系数不变时,两侧受压时接触面积减小,摩擦力也变小;而单侧受压时,所受压缩力较双侧受压时压缩力会增大,根据摩擦力等于摩擦系数乘以压缩力可知,压缩力增大,摩擦力也会变大。所以,其两侧受压时的摩擦力均小于单侧受压时工况。
试验结果中格莱圈所受摩擦力与仿真结果中所受最大米塞斯应力相对应,即仿真中得到的最大米塞斯应力在试验中表现为摩擦力的变化。对比试验和仿真结果可以得出,试验中格莱圈所受摩擦力变化与仿真得到两侧受压时最大米塞斯应力小于单侧受压时工况相符。
3 结论以格莱圈为研究对象,搭建了直线动密封特性试验平台。通过仿真和试验对其在水润滑条件下的动密封力学特性进行了研究,得到以下结论:
(1) 工作压力及预压缩率对格莱圈最大米塞斯应力有较大影响,最大米塞斯应力随预压缩率及工作压力的增加而增大,确定了最优压缩率W=17%。
(2) 当格莱圈单侧受压力及两侧受不同压力时,最易失效位置为方形圈与沟槽倒角;两侧受相同压力时,方形圈与O形圈的接触面为最易失效位置。
(3) 格莱圈两侧受压时的最大米塞斯应力、摩擦力均小于单侧受压时的工况。
(4) 在工作压力一定时,格莱圈所受摩擦力随往复运动速度的增大而减小;在运动速度一定时,摩擦力随工作压力的增加而增大。本文的研究成果将对水下作业装备动密封的设计提供一定的依据和参考价值。
| [1] |
彭旭东, 王玉明, 黄兴, 等. 密封技术的现状与发展趋势[J]. 液压气动与密封, 2009(4): 4-11. PENG Xudong, WANG Yuming, HUANG Xing, et al. Present situation and development trend of sealing technology[J]. Hydraulic Pneumatic and Sealed, 2009(4): 4-11. DOI:10.3969/j.issn.1008-0813.2009.04.002 (  0) 0) |
| [2] |
蔡仁良, 等. 流体密封技术[M]. 北京: 化学工业出版社, 2013: 5. CAI Renliang, et al. Fluid Seal Technology[M]. BeiJing: Chemical Industry Press, 2013: 5. (  0) 0) |
| [3] |
Schmidt T, Andre M, Poll G. A transient 2D-finite-element approach for the simulation of mixed lubrication effects of reciprocating hydraulic rod seals[J]. Tribology International, 2010, 43(10): 1775-1785. DOI:10.1016/j.triboint.2009.11.012
(  0) 0) |
| [4] |
Heipl O, Murrenhoff H. Friction of hydraulic rod seals at high velocities[J]. Tribology International, 2015(85): 66-73.
(  0) 0) |
| [5] |
Bower M V. Design and analysis of seals for extended service life[N], NASA/ASEE Summer Faculty Fellowship Program N94-24408, 1994.
(  0) 0) |
| [6] |
吴琼, 索双富, 刘向峰, 等. 丁腈橡胶O形圈的静密封及微动密封特性[J]. 润滑与密封, 2012(11): 5-21. WU Qiong, SUO Shuangfu, LIU Xiangfeng, et al. The static seal and the micro-dynamic sealing characteristics of the rubber O-ring[J]. Lubrication and Sealing, 2012(11): 5-21. DOI:10.3969/j.issn.0254-0150.2012.11.002 (  0) 0) |
| [7] |
吴琼, 索双富, 廖传军, 等. 丁腈橡胶O形圈往复密封性能实验研究[J]. 润滑与密封, 2012(2): 28-33. WU Qiong, SUO Shuangfu, LIAO Chuanjun, et al. Experimental Study on Reciprocating Sealing Performance of Rubber O-ring[J]. Lubrication and Sealing, 2012(2): 28-33. (  0) 0) |
| [8] |
王成刚, 肖健, 刘慧, 等. 格莱圈密封性能非线性有限元分析[J]. 武汉工程大学学报, 2014(2): 42-47. WANG Chenggang, XIAO Jian, LIU Hui, et al. Nonlinear finite element analysis of grace circle sealing performance[J]. Journal of Wuhan Engineering University, 2014(2): 42-47. DOI:10.3969/j.issn.1674-2869.2014.02.009 (  0) 0) |
| [9] |
薛志全.航空液压作动器往复密封机理分析[D].杭州: 浙江大学, 2016. XUE Zhiquan. Analysis on Reciprocating Sealing Mechanism of Aviation Hydraulic Actuator[D]. Hangzhou: Zhejiang University, 2016. (  0) 0) |
| [10] |
赵河明, 韩宁. 动态压力下旋转动密封结构的有限元分析[J]. 现代制造工程, 2014(10): 81-85. ZHAO Heming, HAN Ning. Finite element analysis of rotating dynamic seal under dynamic pressure[J]. Modern Manufacturing Engineering, 2014(10): 81-85. DOI:10.3969/j.issn.1671-3133.2014.10.017 (  0) 0) |
| [11] |
胡殿印, 王荣桥. 橡胶O形圈密封结构的有限元分析[J]. 北京航空航天大学学报, 2005, 31(2): 255-260. HU Dianyin, WANG Rongqiao. Finite element analysis of rubber O-ring sealing structure[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(2): 255-260. DOI:10.3969/j.issn.1001-5965.2005.02.031 (  0) 0) |
| [12] |
韩彬, 鲁金忠, 李传君, 等. O形橡胶密封圈的热应力耦合分析[J]. 润滑与密封, 2015(1): 58-62. HAN Bin, LU Jinzhong, LI Chuanjun, et al. O-shaped rubber seal ring thermal stress coupling analysis[J]. Lubrication and Sealing, 2015(1): 58-62. DOI:10.3969/j.issn.0254-0150.2015.01.013 (  0) 0) |
| [13] |
魏泳涛, 于建华. 橡胶有限元分析之研究[J]. 四川联合大学学报(工程科学版), 1997(5): 78-84. WEI Yongtao, YU Jianhua. Study on finite element analysis of rubber[J]. Journal of Sichuan Union University (Engineering Science Edition), 1997(5): 78-84. (  0) 0) |
| [14] |
喻九阳, 高九阳, 王成刚, 等. 机械振打器活塞杆处O形圈不同密封结构下的性能分析[J]. 润滑与密封, 2010, 35(3): 65-68. YU Jiuyang, GAO Jiuyang, WANG Chenggang, et al. Performance analysis of O-rings with different sealing structures at piston rods of mechanical rammers[J]. Lubrication and Sealing, 2010, 35(3): 65-68. (  0) 0) |
| [15] |
谭晶, 杨卫民, 丁玉梅, 等. O形橡胶密封圈密封性能的有限元分析[J]. 润滑与密封, 2006(9): 65-69. TAN Jing, YANG Weimin, DING Yumei, et al. O-shaped rubber seal sealing performance of the finite element analysis[J]. Lubrication and Sealing, 2006(9): 65-69. DOI:10.3969/j.issn.0254-0150.2006.09.020 (  0) 0) |
2. Science and Technology on Underwater Vehicle Technology of Harbin Engineering University, Harbin 150001, China
 2018, Vol. 48
2018, Vol. 48

